The document discusses a levelwise pagerank computation method for processing graphs, enabling distributed analysis without per-iteration communication. It compares the performance of levelwise pagerank against traditional monolithic pagerank on both CPU and GPU, revealing that although levelwise is efficient on CPU, it faces slowdowns on GPU due to workload distribution issues. The experiments demonstrate varying performance impacts for edge insertions and deletions, highlighting the strengths and limitations of the levelwise approach.

1. 1
Levelwise PageRank with Loop-Based
Dead End Handling Strategy
Subhajit Sahu1
, Kishore Kothapalli1
, Dip Sankar Banerjee2
1
International Institute of Information Technology, Hyderabad
2
Indian Institute of Technology, Jodhpur
Abstract — Levelwise PageRank is an alternative method of PageRank computation
which decomposes the input graph into a directed acyclic block-graph of strongly
connected components, and processes them in topological order, one level at a time.
This enables calculation for ranks in a distributed fashion without per-iteration
communication, unlike the standard method where all vertices are processed in each
iteration. It however comes with a precondition of the absence of dead ends in the
input graph. Here, the native non-distributed performance of Levelwise PageRank
was compared against Monolithic PageRank on a CPU as well as a GPU. To ensure a
fair comparison, Monolithic PageRank was also performed on a graph where vertices
were split by components. Results indicate that Levelwise PageRank is about as fast
as Monolithic PageRank on the CPU, but quite a bit slower on the GPU. Slowdown
on the GPU is likely caused by a large submission of small workloads, and expected
to be non-issue when the computation is performed on massive graphs.
Index terms — PageRank algorithm, Levelwise PageRank, STIC-D based algorithmic
optimizations, Split components, Topological sort, Per-iteration communication free.
1. Introduction
We seem to live in a data rich world. As the volume of our datasets grows,
but not single-thread performance, it becomes essential for us to invest in
techniques that have the potential to enable distributed analyses on them.
Levelwise PageRank is one such technique for the PageRank algorithm. It
decomposes the input graph into a directed acyclic block-graph of strongly
connected components (SCCs), and processes them in topological order, one
level at a time [2]. Each SCC in a level can be processed, until convergence,
independently of the others in the same level. This enables one to perform
PageRank computation in a distributed fashion without per-iteration

2. 2
communication. In contrast, the standard method of PageRank computation
requires all vertices in the graph to be processed in each iteration, and
performing it in a distributed manner would require communicating ranks of
vertices between processors in every iteration.
It should however be noted that Levelwise PageRank only works on graphs
without dead ends (vertices with no outgoing edges, also commonly called
dangling nodes). This is discussed in detail later. However, this is usually a
non-issue as they can be dealt with by adding self-loops to such vertices.
Other possible alternatives include adding self-loops to all the vertices, or
even removing all dead ends recursively (as removing existing dead ends can
introduce new dead ends). It is also important to note that ranks obtained
with the use of each such dead-end handling strategies can be significantly
different, because of the semantic difference between each strategy.
2. Preliminaries
PageRank is an iterative link-analysis graph algorithm, which helped bring
order and ease of access on the web. It is equivalent to the iterative
determination of the stationary rank distribution of a Markov chain, whose
probability transition matrix is defined using the graph structure. It is also
equivalent to the random-surfer model where a surfer initially visits a
random web page, and then randomly follows one of the links in each page
[1]. But, since the PageRank algorithm usually operates on Web graphs, it
suffers from two problems namely: spider traps, and dead ends [2].
Spider traps are groups of vertices (or even just a single vertex) which only
out-link each other. This causes the random-surfer to get stuck in the trap.
Eventually, spider traps absorb all the importance, and this is not what we
want. A solution to this issue is to allow the surfer (with some probability) to
teleport to a random page at any time, thus preventing the surfer from being
stuck in a spider trap. This is done with the damping factor α (also called
taxation), which controls the probability with which the surfer follows one of
the links on a given page [2]. It is usually set to 0.85, which means there is a
15% chance of the surfer teleporting to a random page at any time.
On the other hand, dead ends (or dangling nodes) are vertices which have
no out-links. This means the random-surfer has nowhere to go. In the

3. 3
presence of such web pages (vertices), the probability transition matrix is not
column stochastic, which is a requirement for Markov chains [1]. This can
cause importance to leak out of the graph. The most commonly used solution
to this is to allow the surfer to always teleport to a random page upon
reaching a dead end [1] [2]. This however, is not an ideal strategy for
handling dead ends with dynamic PageRank since any affected dead end
(including dead ends in the previous snapshot) can affect the ranks of all
vertices in the graph. Note that, affected vertices are those which are either
changed vertices, or are reachable from changed vertices. Changed vertices
are those which have an edge added or removed between it and another
(changed) vertex.
Other possible strategies include adding self loops to dead ends, adding self
loops to all vertices, or removing all dead ends recursively. None of these
require a common teleport contribution calculation per iteration, or enable a
single affected vertex to affect ranks of all vertices (unlike teleport strategy).
This, including the difference in the probability transition matrix, affects the
iterations required for convergence. Additionally, these strategies allow for
distributed PageRank computation without per-iteration communication [3],
although that is not exploited here.
3. Method
Monolithic PageRank is the standard approach of PageRank computation,
where all vertices in the graphs are processed in every iteration. As the
graphs used are dead end free (self-loops are added to dead ends before
PageRank computation), common teleport contribution c0 does not need to
be computed every iteration, and is simply (1-α)/N. In addition, vertices are
split by components (optimization), as this enables better cache utilization
[split]. On CPUs, this means vertices are arranged in the requisite data
structures such that vertices within each component are adjacent to each
other (the order in which the components themselves are arranged does not
matter). On GPUs, in addition to this, components smaller than a minimum
compute size (min-compute) of 107
are combined, and vertices in each such
large component are partitioned by in-degree to help improve work
balancing between threads though a switch thread/block-per-vertex CUDA
kernel. In all cases, the Compressed Sparse Row (CSR) representation of the
graph is used for PageRank computation (due to its cache friendliness).

4. 4
The Levelwise PageRank algorithm, as described in the original paper [2],
works as follows. Strongly connected components (SCCs) of the given
graph are obtained in the preprocessing stage. A block-graph is then
obtained, where each vertex in the block-graph denotes an SCC in the
original graph, and the edges represent cross-edges between SCCs. The
block-graph is always a directed acyclic graph (DAG), and it denotes a
dependency relation of ranks between SCCs. PageRank computation on each
SCC is then performed in topological order of each SCC in the block-graph.
Multiple iterations of rank computation are performed on each SCC until it
converges. An SCC can only be processed after all the SCCs it is dependent
upon, as indicated by incoming edges in the block-graph, have converged.
This dependency relation between SCCs is what allows for the ranks of
independent SCCs to be computed separately, in a distributed manner.
Levelwise PageRank is the new approach of PageRank computation, where
vertices are processed in topological order. On GPUs, in addition to this,
vertices in each such level are partitioned by in-degree to help improve work
balancing between threads though a switch thread/block-per-vertex CUDA
kernel. For the Levelwise approach, each component was represented as a
vertex in a block-graph, and each cross-edge between the components was
represented as an edge. Multiple cross-edges between two components
were combined into a single edge on the block-graph. Vertices in the
block-graph were arranged into levels using algorithm X, such that ranks of
vertices in a level were dependent only upon vertices in previous levels.
Components in each level were combined, and processed together. On
GPUs, vertices in each combined level were partitioned by in–degree similar
to Monolithic PageRank. A simple example of this process is shown in figure
2.1. In all cases, the Compressed Sparse Row (CSR) representation of the
graph is used for PageRank computation (due to its cache friendliness).
4. Experimental setup
Two experiments were conducted, comparing the difference in performance
between dynamic Monolithic PageRank, with static and dynamic Levelwise
PageRank on temporal graphs. This was done for insertions and deletions
of edges with batch sizes of 500, 1000, and 10000. Insertions and deletions
were performed separately, with the deletions being modeled as a reversal

5. 5
of the insertions. A single-threaded CPU-based implementation was used
with the first experiment for comparing the approaches, and a switched
thread/block-per-vertex CUDA-based (GPU) implementation was used with
the second one.
Strongly connected components (SCCs) of the graph were obtained using
Kosaraju’s algorithm. As mentioned before, the vertex order obtained after
this process was used to arrange vertices in the CSR representation of the
graph, which was then used for PageRank computation. Unlike Levelwise
PageRank, all vertices (components) were processed in each iteration.
The PageRank algorithm used was the pull-based standard power-iteration
approach [4]. Let N be the total number of vertices in the graph. The rank of
a vertex in an iteration was calculated as (1-α)/N + αΣre/de, where (1-α)/N is
the contribution due to a teleport from any vertex in the graph due to the
damping factor, αΣre/de is contribution due to edges/links, α is the damping
factor (0.85), re is the previous rank of vertex with an incoming edge, and de
is the out-degree of the incoming-edge vertex. A damping factor of 0.85, and
a tolerance of 10-6
was used. Before PageRank computation, self-loops were
added to all dead ends.
For both Monolithic and Levelwise PageRank, convergence was reached
when the L∞-norm between the ranks of all vertices in the current and
previous iterations falls below the tolerance value. The maximum number of
iterations allowed was 500. It is however noted that nvGraph PageRank uses
L2-norm for convergence check [4], which has been observed to converge
slower than L∞-norm [5]. nvGraph PageRank also seems to use a per
iteration L2-norm rank scaling (such that sum of square of ranks equals 1)
followed by an L1-norm rank scaling (such that sum of absolute of ranks
equals 1) after the final iteration.
The PageRank computation was performed on a Compressed Sparse Row
(CSR) representation of the graph (its cache friendly). The execution time
measured for each test case only includes the time required for PageRank
computation, including error calculation. However, the time required to
generate the equivalent graph (if needed), find strongly connected
components (SCCs) in topological order (for Levelwise PageRank), generate
CSR, copy back results from CSR, or allocate memory is not included.

6. 6
The first experiment uses a single-threaded CPU-based implementation to
compare the difference in performance of dynamic Monolithic PageRank,
with static and dynamic Levelwise PageRank on temporal graphs. Edges
were inserted to the graph in batch sizes of 500, 1000, and 10000. For each
batch size, 10 different samples are taken at different points in time, and
their arithmetic mean (AM) is obtained. All thirteen temporal graphs used in
this experiment were stored in a plain text file in “u, v, t” plaintext format,
where u is the source vertex, v is the destination vertex, and t is the UNIX
epoch time in seconds. These include: CollegeMsg, email-Eu-core-temporal,
sx-mathoverflow, sx-askubuntu, sx-askubuntu-a2q, sx-askubuntu-c2a,
sx-askubuntu-c2q, sx-superuser, sx-superuser-a2q, sx-superuser-c2a,
sx-superuser-c2q, wiki-talk-temporal, and sx-stackoverflow. All of them
were obtained from the Stanford Large Network Dataset Collection [6].
The experiment was implemented in C++, and compiled using GCC 9 with
optimization level 3 (-O3). The system used was a Dell PowerEdge R740
Rack server with two Intel Xeon Silver 4116 CPUs @ 2.10GHz, 128GB
DIMM DDR4 Synchronous Registered (Buffered) 2666 MHz (8x16GB)
DRAM, 16GB Tesla V100 PCIe GPU (GV100GL), and running CentOS Linux
release 7.9.2009 (Core). Execution time was measured using
std::chrono::high_performance_timer, 5 times for each test case, and
averaged. Statistics of each test case was printed to standard output
(stdout), and redirected to a log file, which was then processed with a script
to generate a CSV file, with each row representing the details of a single test
case. This CSV file was imported into Google Sheets, and necessary tables
were set up with the help of the FILTER function to create the charts.
The second experiment is similar to the first experiment, except that it uses
a switched thread/block-per-vertex CUDA-based (GPU) implementation
[11]. Additionally, nvGraph’s static PageRank approach was also included for
reference. With (dynamic) Monolithic PageRank, small components were
combined together, and their vertices partitioned by in-degree, until they
satisfied a minimum compute size (min-compute) of 107
. Rest of the process
was similar to that of the first experiment.
5. Results

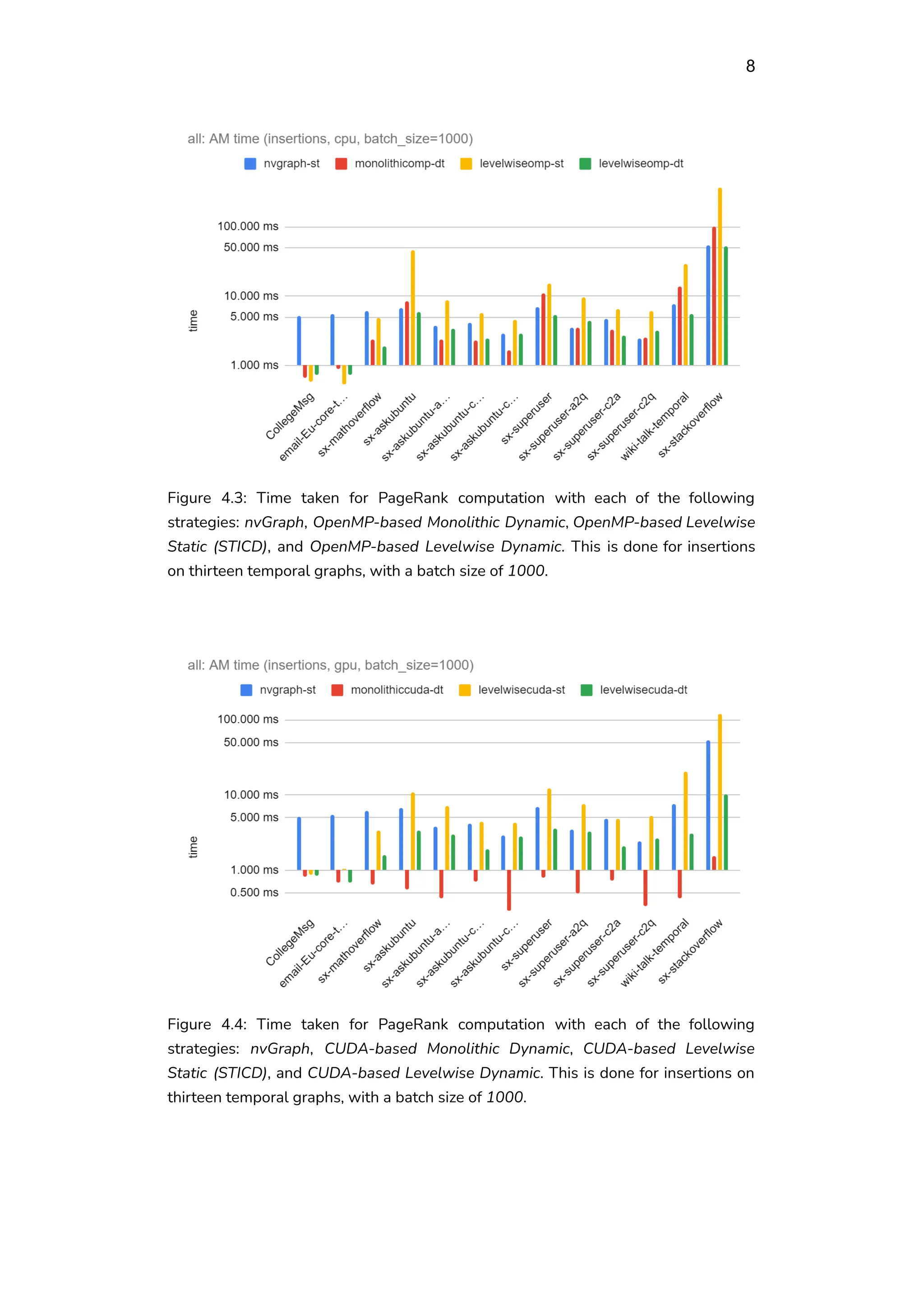
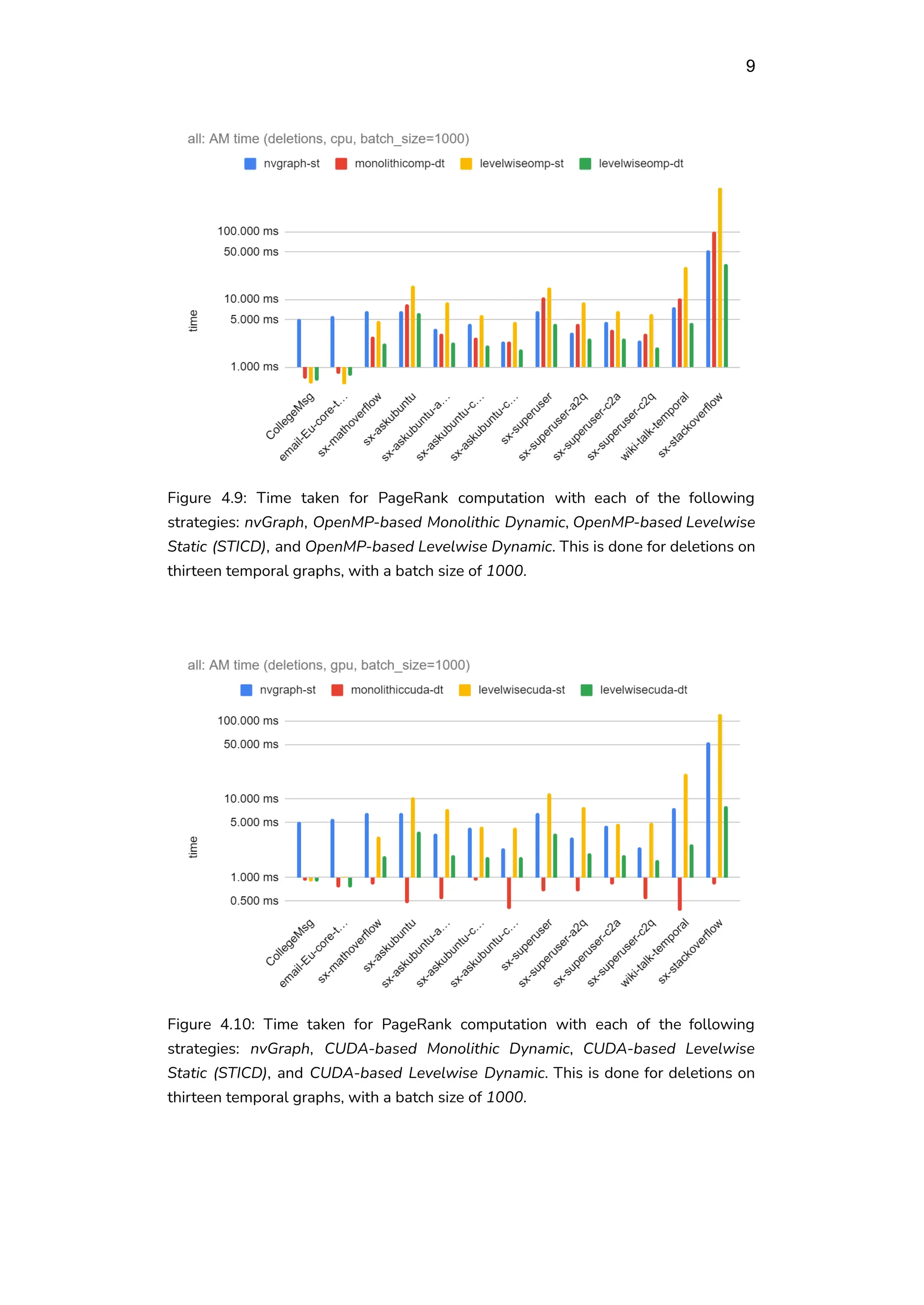
7. 7
From the results of the first experiment with a single-threaded CPU-based
implementation, it was observed that the PageRank computation time for
dynamic Levelwise PageRank increases by -5 to 2% for insertions, and by -7
to 36% for deletions, with respect to Monolithic approach (with vertices split
by components). For edge insertions, the AM-RATIOs between dynamic
Monolithic and Levelwise PageRank are 1.00:1.00, 1.00:1.00, and 1.00:1.01
for batch sizes of 500, 1000, and 10000 respectively. Thus, the Levelwise
approach completed in 0/0/1% more time than the Monolithic approach. For
edge deletions, the AM-RATIOs are 1.00:1.10, 1.00:1.10, and 1.00:1.06.
Thus, the Levelwise approach completed in 10/10/6% more time than the
Monolithic approach. Here, AM-RATIO was obtained by taking the arithmetic
mean (AM) of time taken for PageRank computation for insertions/deletions
of a particular batch size on all graphs, and then obtaining a ratio relative to
the Monolithic approach.
From the results of the second experiment with a switched
thread/block-per-vertex CUDA-based (GPU) implementation [11], it was
observed that the PageRank computation time for dynamic Levelwise
PageRank increases by -5 to 674% for insertions, and by -7 to 795% for
deletions, with respect to Monolithic approach (with vertices split by
components). For edge insertions, the AM-RATIOs between dynamic
Monolithic and Levelwise PageRank are 1.00:3.50, 1.00:3.46, and 1.00:3.78
for batch sizes of 500, 1000, and 10000 respectively. Thus, the Levelwise
approach completed in 250/246/278% more time than the Monolithic
approach. For edge deletions, the AM-RATIOs are 1.00:3.49, 1.00:3.50, and
1.00:3.63. Thus, the Levelwise approach completed in 249/250/263% more
time than the Monolithic approach.

8. 8
Figure 4.3: Time taken for PageRank computation with each of the following
strategies: nvGraph, OpenMP-based Monolithic Dynamic, OpenMP-based Levelwise
Static (STICD), and OpenMP-based Levelwise Dynamic. This is done for insertions
on thirteen temporal graphs, with a batch size of 1000.
Figure 4.4: Time taken for PageRank computation with each of the following
strategies: nvGraph, CUDA-based Monolithic Dynamic, CUDA-based Levelwise
Static (STICD), and CUDA-based Levelwise Dynamic. This is done for insertions on
thirteen temporal graphs, with a batch size of 1000.

9. 9
Figure 4.9: Time taken for PageRank computation with each of the following
strategies: nvGraph, OpenMP-based Monolithic Dynamic, OpenMP-based Levelwise
Static (STICD), and OpenMP-based Levelwise Dynamic. This is done for deletions on
thirteen temporal graphs, with a batch size of 1000.
Figure 4.10: Time taken for PageRank computation with each of the following
strategies: nvGraph, CUDA-based Monolithic Dynamic, CUDA-based Levelwise
Static (STICD), and CUDA-based Levelwise Dynamic. This is done for deletions on
thirteen temporal graphs, with a batch size of 1000.

10. 10
6. Conclusion
From the results of the first experiment using a single-threaded CPU-based
implementation, it can be inferred that the Levelwise approach to PageRank
computation, on a CPU, is slightly slower than the Monolithic approach. This
seems counter-intuitive as Levelwise PageRank processes components in
topological order, and convergence of components on higher levels of the
block-graph should ideally help accelerate the convergence of the lower
levels. However, it appears that this is not the case. Analysis of convergence
rate of components might help in understanding the issue, which may be
explored in future work. However, given the fact that Levelwise PageRank is
a suitable technique for distributed PageRank computation for dead ends
free graphs, it is a small price to pay.
The second experiment, which uses a switched thread/block-per-vertex
CUDA-based (GPU) implementation, suggests that Levelwise PageRank is
significantly slower than Monolithic PageRank. This overwhelming increase
in PageRank computation time is most likely due to the existence of a large
number of small sized levels, consisting of small components. This would
cause a large number of CUDA kernel calls to be made for each level, which
can in act as a major bottleneck on the system. Thus, the vanilla Levelwise
approach would be unsuitable for use with GPU unless measures are taken
to combine smaller levels/components in order to ensure sufficient workload
on the GPU per kernel call.
In conclusion, Levelwise PageRank would be a suitable approach for
PageRank computation on a distributed network of CPUs, as long as
strongly connected components of the input graph can be maintained on the
system. However, if one desires to use it for a distributed GPU network,
smaller levels/components should be combined and processed at a time in
order to help improve GPU usage efficiency. On a single machine however,
Monolithic PageRank (with vertices grouped by components) continues to
be the best approach to PageRank computation. The links to source code,
along with data sheets and charts, for both the experiments [2] is included in
references.

11. 11
References
[1] A. Langville and C. Meyer, “Deeper Inside PageRank,” Internet Math.,
vol. 1, no. 3, pp. 335–380, Jan. 2004, doi:
10.1080/15427951.2004.10129091.
[2] S. Sahu, “puzzlef/pagerank-adjust-damping-factor-stepwise.js:
Experimenting PageRank improvement by adjusting damping factor (α)
between iterations.”
https://github.com/puzzlef/pagerank-adjust-damping-factor-stepwise.js
(accessed Aug. 06, 2021).