The document discusses various sorting algorithms, including Bubble Sort, Merge Sort, and Quick Sort, explaining their implementations in C programming. It covers time complexity for each sort, with Bubble Sort having a complexity of O(n^2) in worst and best cases, while Merge and Quick Sort have complexities of O(n log n). Additionally, there are programming exercises related to geometric progressions, Floyd's triangle, and strong numbers.

1. PDS (Week-6)
Sorting and Example Programs
Jayanta Mukhopadhyay
jay@cse.iitkgp.ernet.in

2. Bubble Sort
In every iteration heaviest element
drops at the bottom.
The bottom moves upward.

3. Example
3 12 -5 6 72 21 -7 45
x:
Pass -1
3 12 -5 6 72 21 -7 45
x:
3 -5 12 6 72 21 -7 45
x:
3 -5 6 12 72 21 -7 45
x:
3 -5 6 12 72 21 -7 45
x:
3 -5 6 12 21 72 -7 45
x:
3 -5 6 12 21 -7 72 45
x:
3 -5 6 12 21 -7 45 72
x:

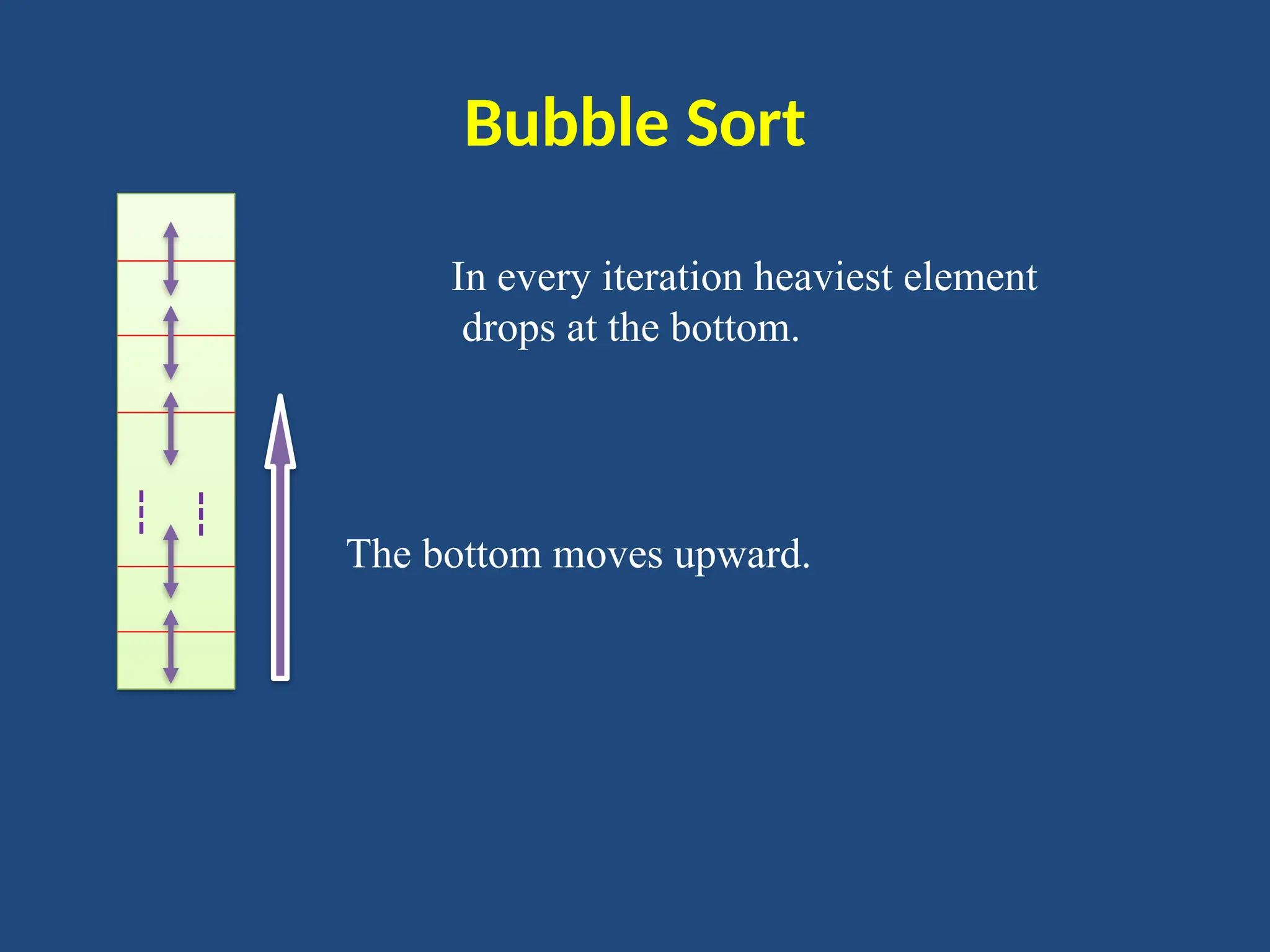
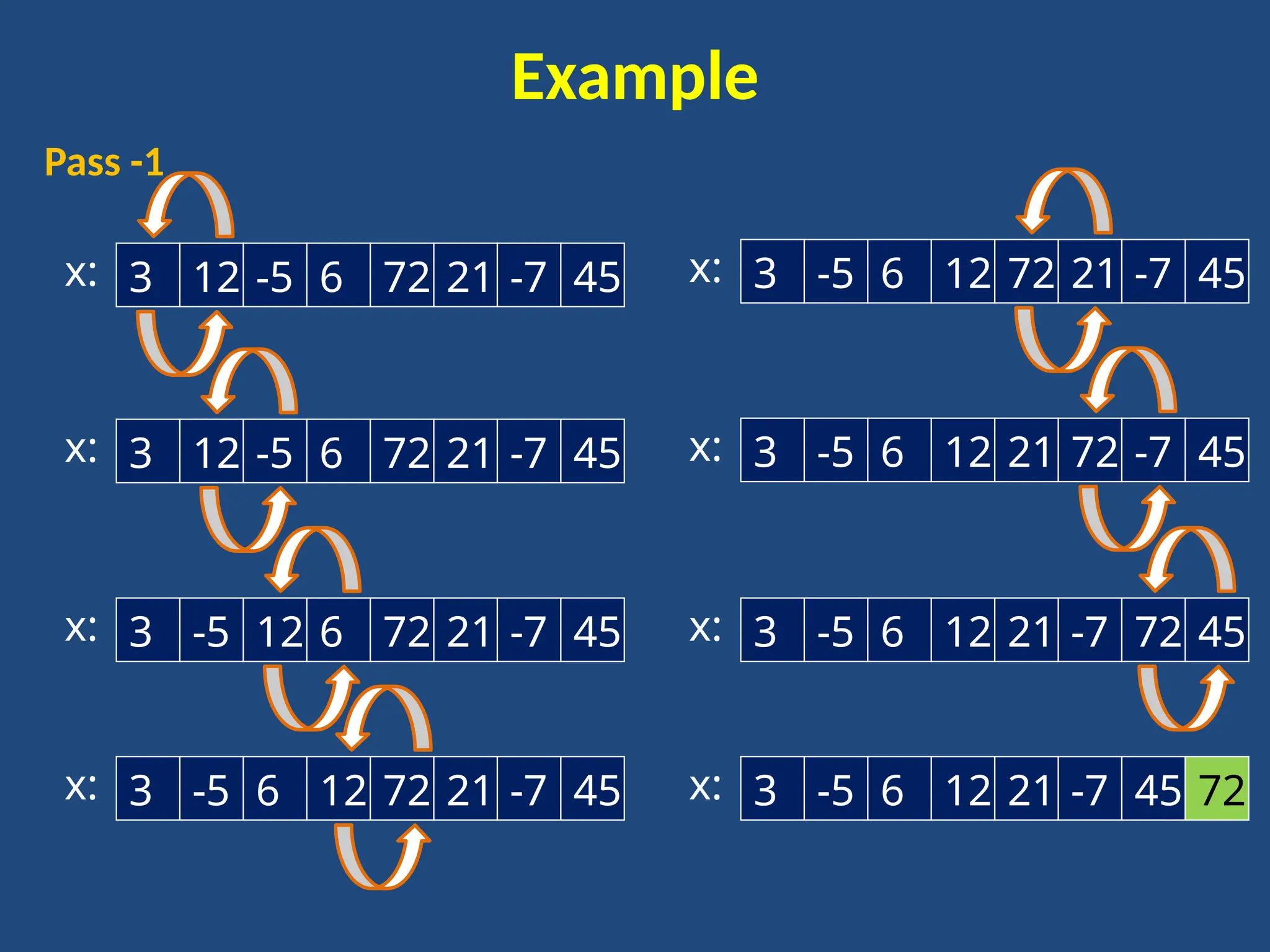
4. Bubble Sort
int pass,j,a[100],temp;
/* read number of elements as n and elements as a[] */
for(pass=0; pass<n; pass++) {
for(j=0; j<n-1; j++) {
if(a[j]>a[j+1]) {
temp = a[j+1];
a[j+1] = a[j];
a[j] = temp;
}
}
}
/* print sorted list of elements */

5. Example
3 12 -5 6 72 21 -7 45
x:
Pass: 1
3 12 -5 6 72 21 -7 45
x:
3 -5 12 6 72 21 -7 45
x:
3 -5 6 12 72 21 -7 45
x:
3 -5 6 12 72 21 -7 45
x:
3 -5 6 12 21 72 -7 45
x:
3 -5 6 12 21 -7 72 45
x:
3 -5 6 12 21 -7 45 72
x:

6. Example
3 -5 6 12 21 -7 45 72
x:
Pass: 2
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 21 -7 45 72
x:
-5 3 6 12 -7 21 45 72
x:
-5 3 6 12 -7 21 45 72
x:

7. Time Complexity
• Number of comparisons :
o Worst Case?
1+2+3+ …… +(n-1) = n(n-1)/2
o Best Case?
Same How do you make best case with
(n-1) comparisons only?

8. Bubble Sort
int pass,j,a[100],temp,swapflag;
/* read number of elements as n and elements as a[] */
for(pass=0; pass<n; pass++) {
swapflag=0;
for(j=0; j<n-1; j++) {
if(a[j]>a[j+1]) {
temp = a[j+1];
a[j+1] = a[j];
a[j] = temp;
swapflag=1;
}
}
if(swapflag==0)
break;
}
/* print sorted list of elements */

9. Can we improve the sorting time?

10. Basis of efficient sorting algorithms
• Two of the most popular sorting algorithms are
based on divide-and-conquer approach.
– Quick sort
– Merge sort
• Basic concept:
sort (list)
{
if the list has length greater than 1
{
Partition the list into lowlist and highlist;
sort (lowlist);
sort (highlist);
combine (lowlist, highlist);
}
}

11. Merge Sort

12. Merging two
sorted arrays
Splitting arrays
Example
3 12 -5 6 72 21 -7 45
x:
3 12 -5 6 72 21 -7 45
3 12 -5 6 72 21 -7 45
3 12 -5 6 72 21 -7 45
3 12 -5 6 21 72 -7 45
-5 3 6 12 -7 21 45 72
-7 -5 3
-7 -5 3 6 12 21 45 72

13. Merge Sort C program
lude<stdio.h>
mergesort(int a[],int i,int j);
merge(int a[],int i1,int j1,int i2,int j2);
main()
t a[30],n,i;
intf("Enter no of elements:");
anf("%d",&n);
intf("Enter array elements:");
r(i=0;i<n;i++)
scanf("%d",&a[i]);
ergesort(a,0,n-1);
intf("nSorted array is :");
r(i=0;i<n;i++)
printf("%d ",a[i]);
turn 0;
void mergesort(int a[],int i,int j)
{
int mid;
if(i<j) {
mid=(i+j)/2;
/* left recursion */
mergesort(a,i,mid);
/* right recursion */
mergesort(a,mid+1,j);
/* merging of two sorted sub-arrays */
merge(a,i,mid,mid+1,j);
}
}

14. Merge Sort C program
void merge(int a[],int i1,int j1,int i2,int j2)
{
int temp[50]; //array used for merging
int i=i1,j=i2,k=0;
while(i<=j1 && j<=j2) //while elements in both lists
{
if(a[i]<a[j])
temp[k++]=a[i++];
else
temp[k++]=a[j++];
}
while(i<=j1) //copy remaining elements of the first list
temp[k++]=a[i++];
while(j<=j2) //copy remaining elements of the second list
temp[k++]=a[j++];
for(i=i1,j=0;i<=j2;i++,j++)
a[i]=temp[j]; //Transfer elements from temp[] back to a[]
}

15. Splitting Trace
-56 23 43 -5 -3 0 123 -35 87 56 75 80
-56 -35 -5 -3 0 23 43 56 75 80 87 123
-56 23 43
23 43
-56 23 43 -5 -3 0 123 -35 87 56 75 80
-56 23 43 -5 -3 0
-3 0
-3 0
123 -35 87
-35 87
123 -35 87 56 75 80
56
75 80
75 80
Worst Case: O(n.log(n))
Space Complexity??

16. Quicksort
• At every step, we select a pivot element in the list
(usually the first element).
– We put the pivot element in the final position of the
sorted list.
– All the elements less than or equal to the pivot element
are to the left.
– All the elements greater than the pivot element are to the
right.

17. Partitioning
0 size-1
x:
pivot
Values smaller Values greater
Perform
partitioning
Perform
partitioning

18. Quick Sort program
#include <stdio.h>
void quickSort( int[], int, int);
int partition( int[], int, int);
void main()
{
int i,a[] = { 7, 12, 1, -2, 0, 15, 4, 11, 9};
printf("nnUnsorted array is: ");
for(i = 0; i < 9; ++i)
printf(" %d ", a[i]);
quickSort( a, 0, 8);
printf("nnSorted array is: ");
for(i = 0; i < 9; ++i)
printf(" %d ", a[i]);
}
void quickSort( int a[], int l, int r)
{
int j;
if( l < r ) { // divide and conquer
j = partition( a, l, r);
quickSort( a, l, j-1);
quickSort( a, j+1, r);
}
}
int partition( int a[], int l, int r)
{
int pivot, i, j, t;
pivot = a[l];
i = l;
j = r+1;
while( 1) {
do {
++i;
} while(a[i]<=pivot && i<=r);
do {
--j;
} while( a[j] > pivot );
if( i >= j ) break;
t = a[i];
a[i] = a[j];
a[j] = t;
}
t = a[l];
a[l] = a[j];
a[j] = t;
return j;
}

19. Trace of Partitioning
Input: 45 -56 78 90 -3 -6 123 0 -3 45 69 68
Output: -56 -6 -3 -3 0 45 45 68 69 78 90 123
45 -56 78 90 -3 -6 123 0 -3 45 69 68
-6 -56 -3 0 -3 45 123 90 78 45 69 68
-3 0 -3
-6
-56
0 -3
-3
-3 0
68 90 78 45 69 123
78 90 69
68
45
78
69 90

20. 2k
=n
Time Complexity
• Partitioning with n elements.
- No. of comparisons:
n-1
• Worst Case Performance:
(n-1)+(n-2)+(n-3)+………. +1= n(n-1)/2
• Best Case performance:
(n-1)+2((n-1)/2-1)+4(((n-1)/2-1)-1)/2-1) .. k steps
= O(n. log(n))
Choice of pivot element affects
the time complexity.

21. Exercise
• Implement non-recursive version of quick sort and
merge sort.

22. Multi-file programs

23. Example 1
• Determine the value of x which causes the
function
y = x cos(x)
to be maximized within a specified interval.

24. /* find the maximum of a function within a specified interval */
#include <stdio.h>
double a,b,xl,yl,xr,yr,cnst=0.0001; /* external variable declaration */
extern void reduce(void); /* external function prototype */
extern double curve(double xl); /* external function prototype */
int main()
{
double xmax, ymax;
printf("na= ");
scanf("%lf",&a);
printf("nb= ");
scanf("%lf",&b);
do
reduce();
while((yl!=yr) && ((b-a)>3*cnst));
xmax=0.5*(xl+xr);
ymax=curve(xmax);
printf("nxmax= %8.6lf ymax= %8.6lfn",xmax,ymax);
}
mainFile.c

25. extern double a,b,xl,yl,xr,yr,cnst;
extern double curve(double xl);
extern void reduce(void)
{
xl=a+0.5*(b-a-cnst);
xr=xl+cnst;
yl=curve(xl);
yr=curve(xr);
if(yl>yr) {
b=xr;
return;
}
if(yl<yr)
a=xl;
return;
}
intReduce.c
#include <math.h>
extern double curve(double x)
{
return (x*cos(x));
}
evalFunc.c

26. Example 1 – Compile and Execute
$ cc -c -Wall mainFile.c intReduce.c evalFunc.c
$ cc mainFile.o intReduce.o evalFunc.o -lm
$ ./a.out
a= 0
b= 3.141593
xmax= 0.860394 ymax= 0.561096

27. Example
Write a complete C program that will read N (to be read
from the user) number of integers and sort them. User
will input his/her choice of sorting technique from a pool
of Selection/Insertion/Bubble sort. Each sorting
technique will be implemented as separate function.
User choice will pick right sorting function using switch-
case statement.

28. Example
#include <stdio.h>
#define SIZE 100
void selSort(int a[],int n);
void insSort(int a[],int n);
void bubbleSort(int a[],int n);
int main()
{
char choice;
int k,x[SIZE],size;
do {
printf("Enter the number of elements: ");
scanf("%d",&size);
printf("Enter the elements: ");
for(k=0;k<size;k++)
scanf("%d",&x[k]);
printf("Sorting method [I/S/B]: ");
getchar();
choice=getchar();
switch(choice) {
case 'I':
case 'i': insSort(x,size);
break;
case 'S':
case 's': selSort(x,size);
break;
case 'B':
case 'b': bubbleSort(x,size);
break;
default: printf(“No Sorting");
}
for(k=0;k<size;k++)
printf("%d ",x[k]);
printf("Continue [Y/N]: ");
getchar();
choice=getchar();
} while(choice=='Y' || choice=='y');
return 0;
}

29. void bubbleSort(int a[],int n)
{
int pass,j,temp,swapflag;
for(pass=0; pass<n; pass++) {
swapflag=0;
for(j=0; j<n-1; j++) {
if(a[j]>a[j+1]) {
temp = a[j+1];
a[j+1] = a[j];
a[j] = temp;
swapflag=1;
}
}
if(swapflag==0)
break;
}
}
void insSort(int x[],int size)
{
int i,j,temp;
for (i=1; i<size; i++) {
temp = x[i] ;
for (j=i-1; (j>=0)&& (x[j] > temp); j--)
x[j+1] = x[j];
x[j+1] = temp ;
}
}
void selSort(int x[],int size)
{
int k,j,pos,temp;
for (k=0; k<size-1; k++) {
pos = k;
for (j=k+1; j<size; j++) {
if (x[j] < x[pos]) {
pos = j;
}
}
temp = x[k];
x[k] = x[pos];
x[pos] = temp;
}
}

30. EXAMPLE
PROBLEMS

31. Problem 1
Write a C program to print a Geometric
Progression (GP) series and its sum till N terms.
Expression for a GP Series:
where, a is the first term
r is the common ratio
n is the number of terms

32. Problem 1 (Gp-sum)
#include <stdio.h>
#include <math.h>
int main()
{
float a, r, sum, term;
int n, i;
printf("Give the first term, common ratio, and number of terms: n");
scanf("%f%f%d",&a,&r,&n);
sum=0;
term=a;
for (i=0; i<n; i++)
{ sum=sum+term;
term=term*r;
}
printf("Sum=%f n",sum);
return 0;
}

33. Problem 2
Write a C program to generate a FLOYD's triangle.
1
2 3
4 5 6
7 8 9 10
11 13 14 15
16 17 18 19 20 21

34. C Program Code (Floyd Triangle)
#include <stdio.h>
int main()
{
int rows, a, b, number = 1;
printf("Number of rows of Floyd's triangle to print:");
scanf("%d",&rows);
for ( a = 1 ; a <= rows ; a++ ) {
for ( b = 1 ; b <= a ; b++ ) {
printf("%d ", number);
number++;
}
printf("n");
}
return 0;
}

35. Problem 3
Write a C program to check whether a number is a
strong number or not.
What is a strong number ?
A number whose sum of the factorial of its digit is
equal to the number itself.
Example: 145 = 1! +4! +5! = 1 + 24 + 120 = 145 is a
strong number.

36. Problem 3 (Strong Number)
#include <stdio.h>
int factorial(int k);
int main()
{
int number, tmpnum, i, sum, digit;
printf("Input the number: n");
scanf("%d",&number);
sum=0;
tmpnum=number;
/* Get digits one by one and add their
factorials cumulatively */
while(tmpnum>0)
{
digit=tmpnum%10;
tmpnum=tmpnum/10;
sum=sum+factorial(digit);
}
int factorial(int k)
{
int prod=1, i;
for(i=1; i<=k;i++)
prod=prod*i;
return(prod);
}
if (sum==number)
printf("The number %d is a
strong number n",number);
else
printf("The number is NOT
a strong number n");
return 0;
} /* End of main() */

37. Problem 4
Write a C program to arrange elements in an array
in ascending order.

38. Problem 5
Write a C program to reverse a string (array of
characters) without using any extra array.

39. Problem 5 (String reversal w/o extra array)
/* String reversal without using extra array */
#include <stdio.h>
#include <string.h>
int main()
{
char S[100],tmpChar;
int i,j;
printf("Read the string n");
scanf("%s",S);
printf("The input string %s n", S);
i=0;
j=strlen(S)-1;
while(i<j)
{
tmpChar=S[i];
S[i]=S[j];
S[j]=tmpChar;
i++;
j--;
}
printf("The output string %s n", S);
return(0);
}

40. Problem 6
Write a C program to concatenate two strings
without using library function.

41. Problem 6 (String concatenation)
#include <stdio.h>
int main()
{
char S1[100], S2[100], S3[200];
int i,j;
printf("Read two strings n");
scanf("%s%s",S1,S2);
i=0;
j=0;
while(S1[i]!='0')
{
S3[j]=S1[i];
i++;
j++;
}
i=0;
while(S2[i]!='0')
{
S3[j]=S2[i];
i++;
j++;
}
S3[j]='0'; /* Denote end of string */
printf("Concatenated string %s n",S3);
return(0);
}

42. Problem 7
Given 2 positive numbers n and r, n>=r , write a C
function to compute the number of combinations(n
Cr)
and the number of permutations(n
Pr).
Permutations formula is P(n,r)=n!/(n-r)!
Combinations formula is C(n,r)=n!/(r!(n-r)!)

43. Problem 7- Program for testing permutaion
and combination
#include <stdio.h>
int permute(int n, int m);
int choose(int n,int r);
int main()
{
int n,m,r;
int permVal,combVal;
printf("Give n and m for n permute m n");
scanf("%d%d",&n,&m);
permVal=permute(n,m);
printf("Number of permutations=%d
n",permVal);
printf("Give n and r for n choose r n");
scanf("%d%d",&n,&r);
combVal=choose(n,r);
printf("Number of combinations=%d
n",combVal);
return(0);
}

44. permute() and choose() functions
int permute(int n,int m)
{
int i, val;
val=n;
for(i=n-1;i>=n-m+1;i--)
val=val*i;
return(val);
}
int choose(int n,int r)
{
int i;
float val;
val=n;
for(i=1;i<r;i++)
val=val* (float) (n-i)/ (float) (i+1);
return((int) val);
}

45. Problem 8
Scope of variable:
What is the output of the following code snippet?
#include <stdio.h>
int main(){
int i = 10;
for(int i = 5; i < 15; i++)
printf(“i is %dn”, i);
printf(“i=%d n”,i);
return 0;
}

46. Scope of variable: What is the output of the following code snippet?
#include <stdio.h>
int a = 20;
int sum(int a, int b) {
printf ("value of a in sum() = %dn", a);
printf ("value of b in sum() = %dn", b);
return a + b;
}
int main ()
{
int a = 10; int b = 20; int c = 0;
printf ("value of a in main() = %dn", a);
c = sum( a, b);
printf ("value of c in main() = %dn", c);
return 0;
}
Problem 9

47. Problem 10
Write a C program which display the entered
number in words.
Example:
Input:
Enter a number: 7
Output:
Seven

48. Problem 11
Write a C program to delete duplicate elements in
an array without using another auxiliary array.
Example:
Input:
5 8 5 5 6 9 8 2 1 1 3 3
Output:
5 8 6 9 2 1 3

49. Problem 12
Write a C program to print PASCAL’s triangle.

50. Problem 13
Given 2 numbers a and b, write a C program to
compute the Greatest Common Divisor(GCD) of the 2
numbers.
The GCD of 2 numbers is the largest positive integer
that divides the numbers without a remainder.
Example: GCD(2,8)=2; GCD(3,7)=1

51. Problem 14
Given 2 arrays of integers A and B of size n each, write a
C program to calculate the dot product of the 2 arrays.
If A=[a0, a1, a2,….,an-1] and
B= [b0, b1, b2,….,bn-1],
the dot product of A and B is given by
A.B=[a0*b0 + a1*b1 + a2*b2 + ……. + an-1*bn-1]

52. Problem 15
Given a non negative integer n, write a C function to
output the decimal integer(base 10) in its binary
representation (base 2).
Example: Binary representation of
3 is 11
8 is 1000
15 is 1111

53. Problem 16
Given two array of sorted numbers A and B, both are of
arbitrary sizes, write a C function named merge_arrays
that merges both the arrays in sorted order and returns
the sorted array C.