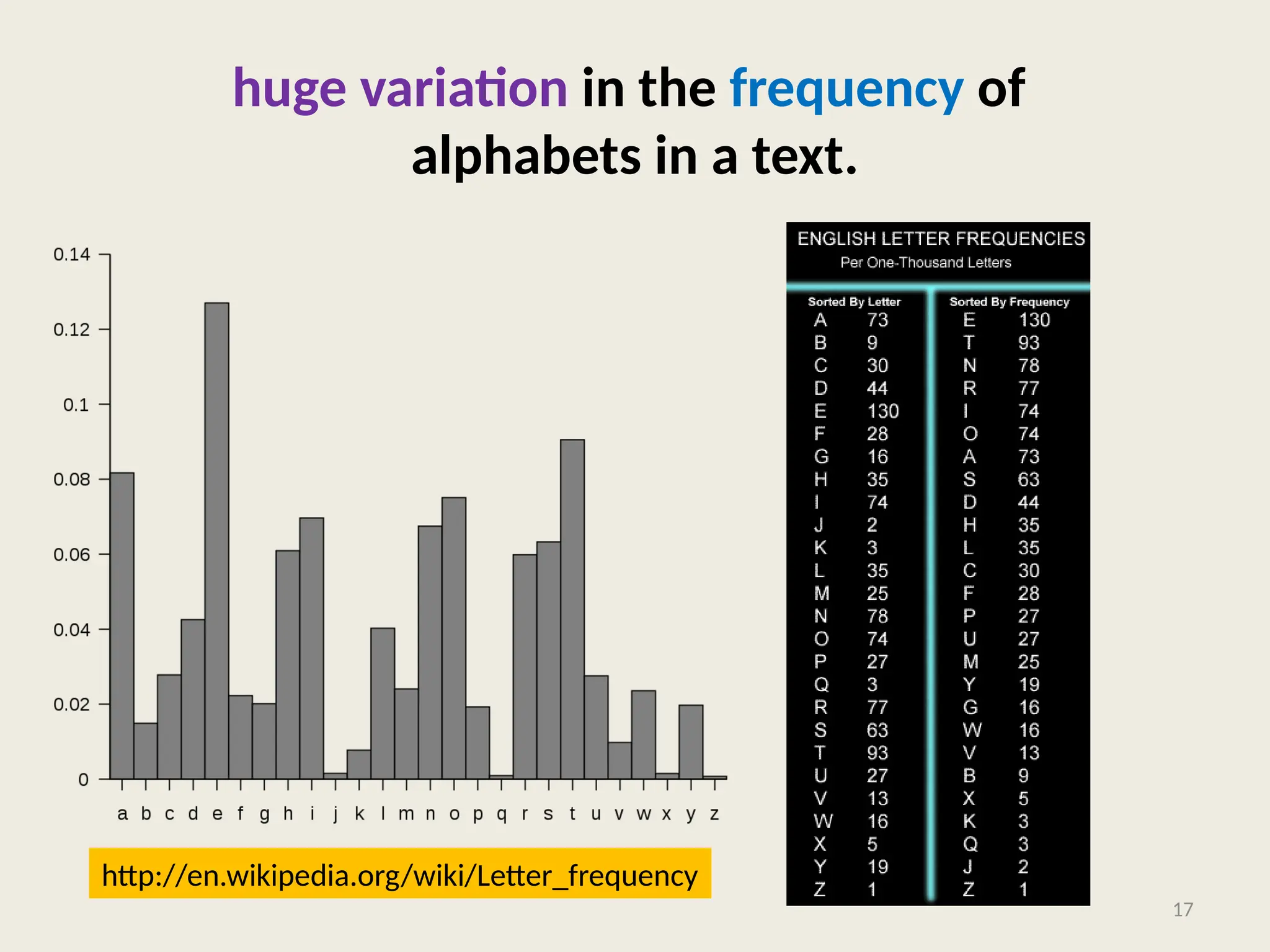
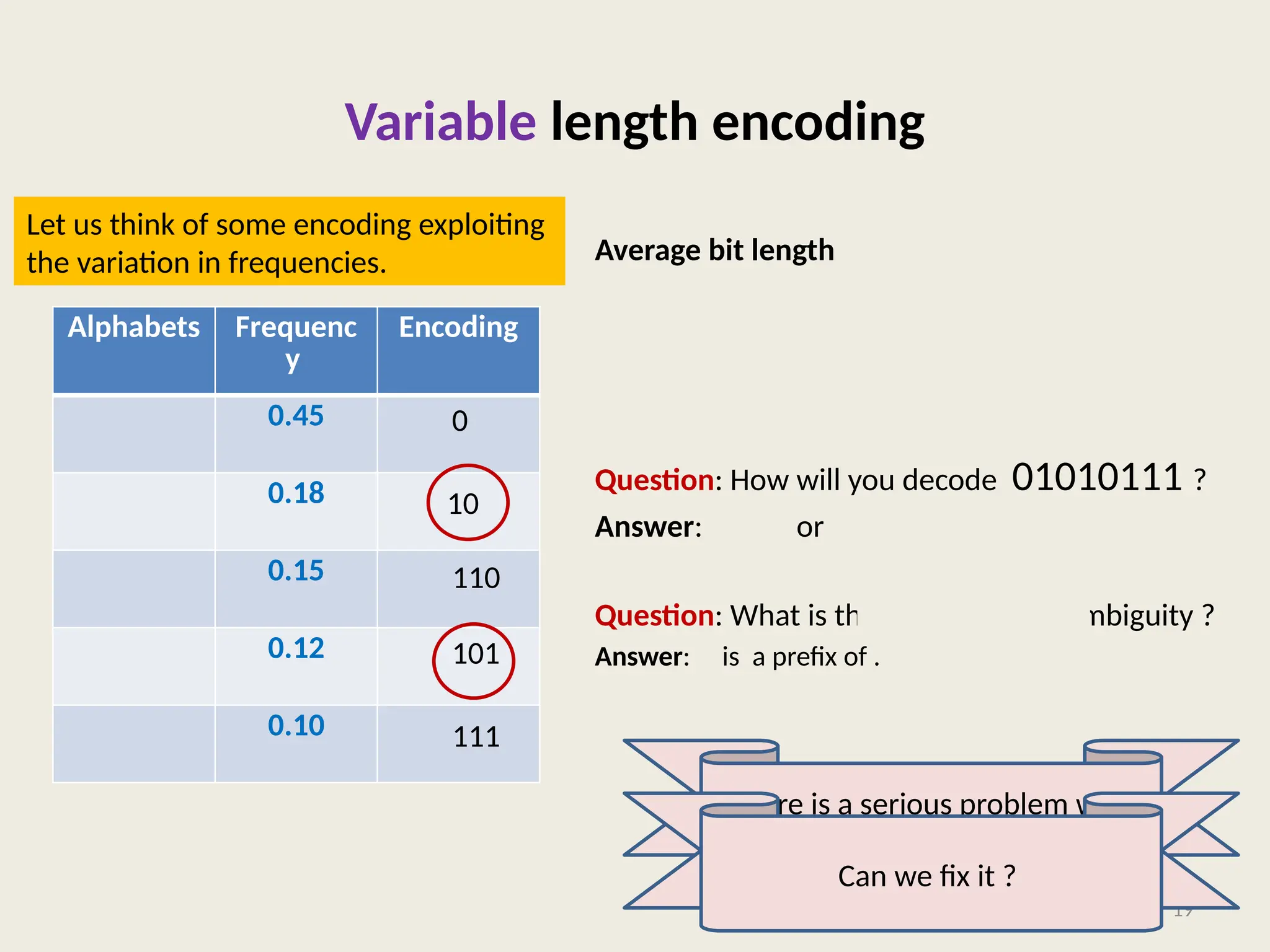
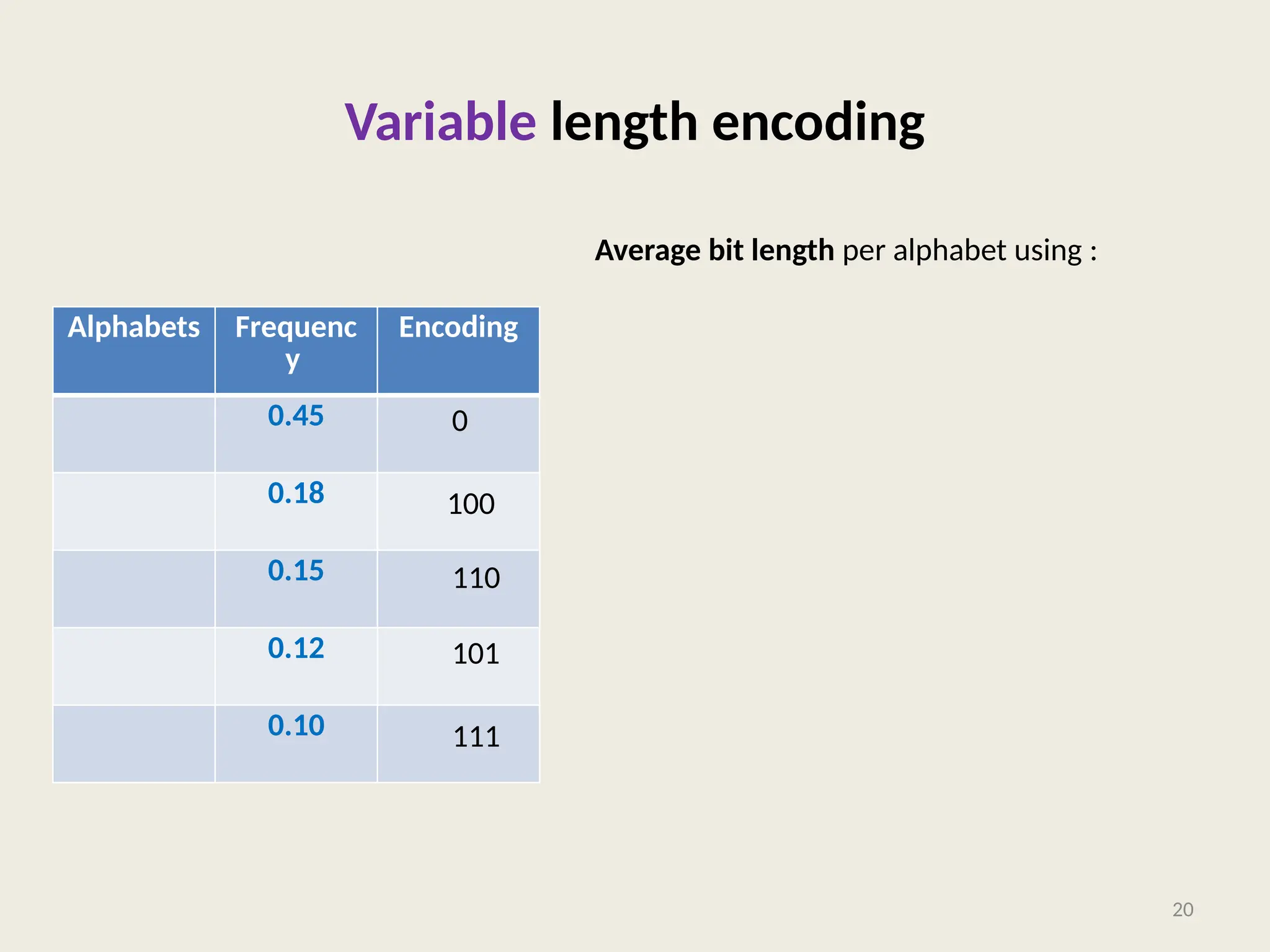
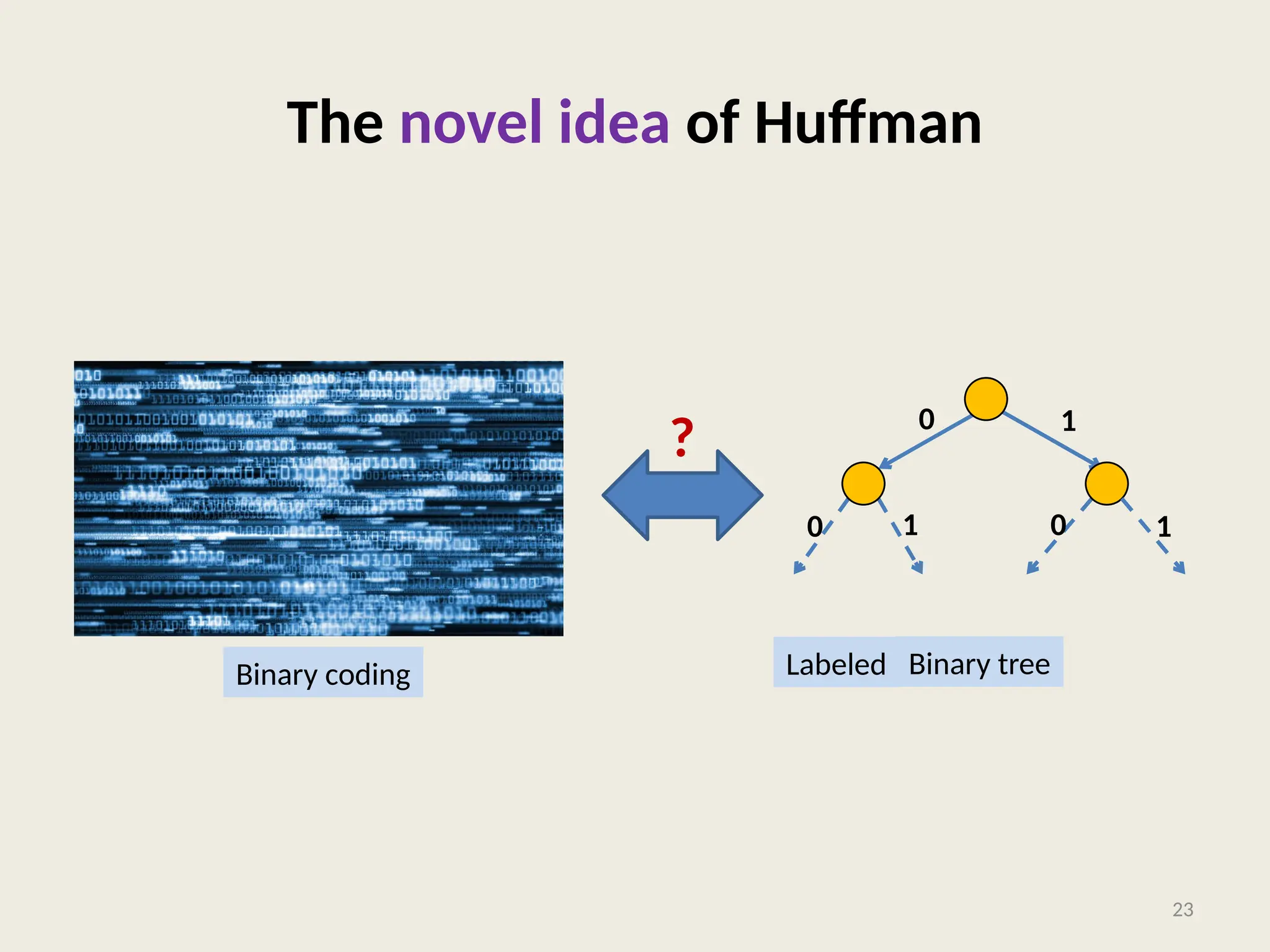
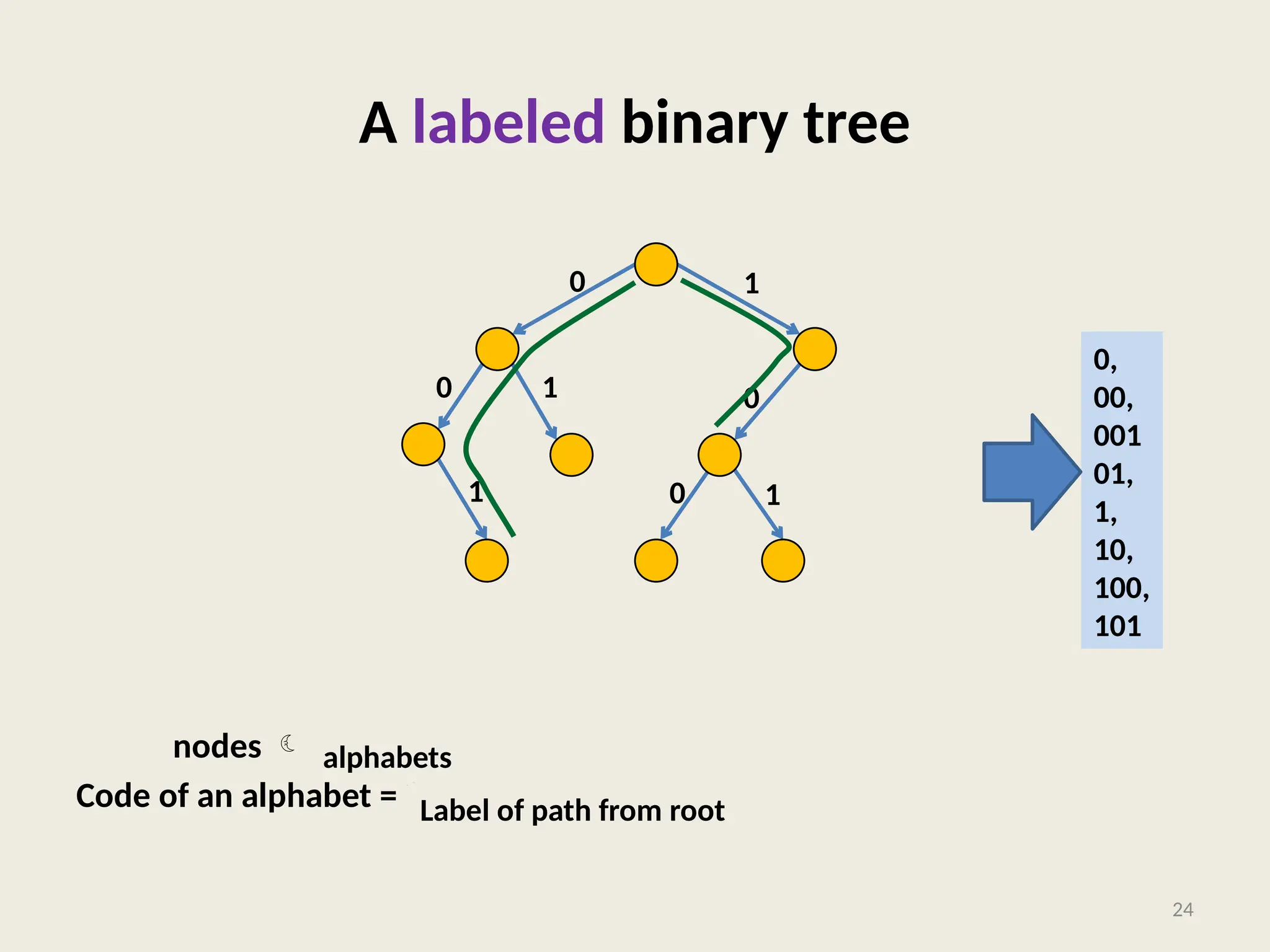
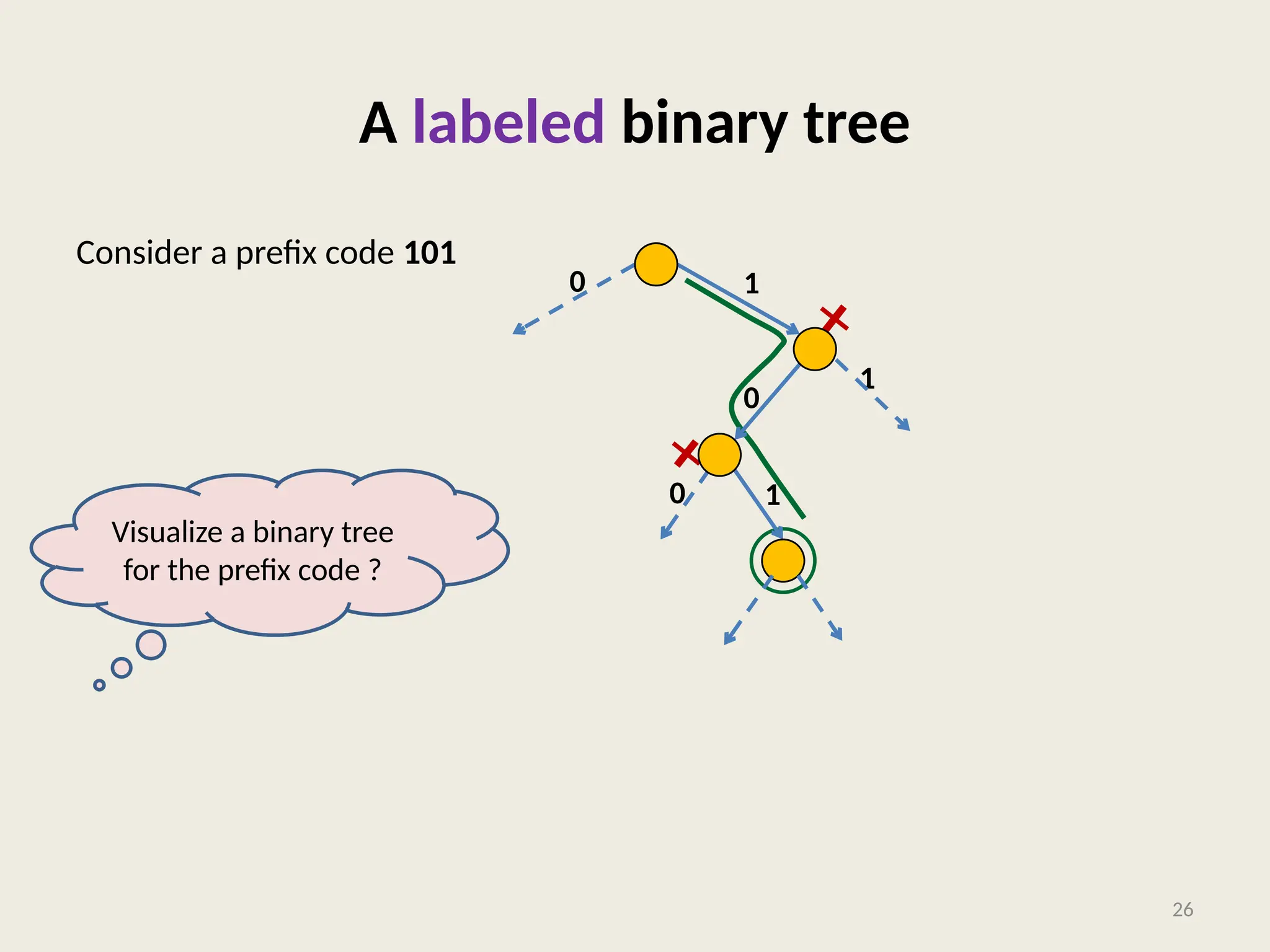
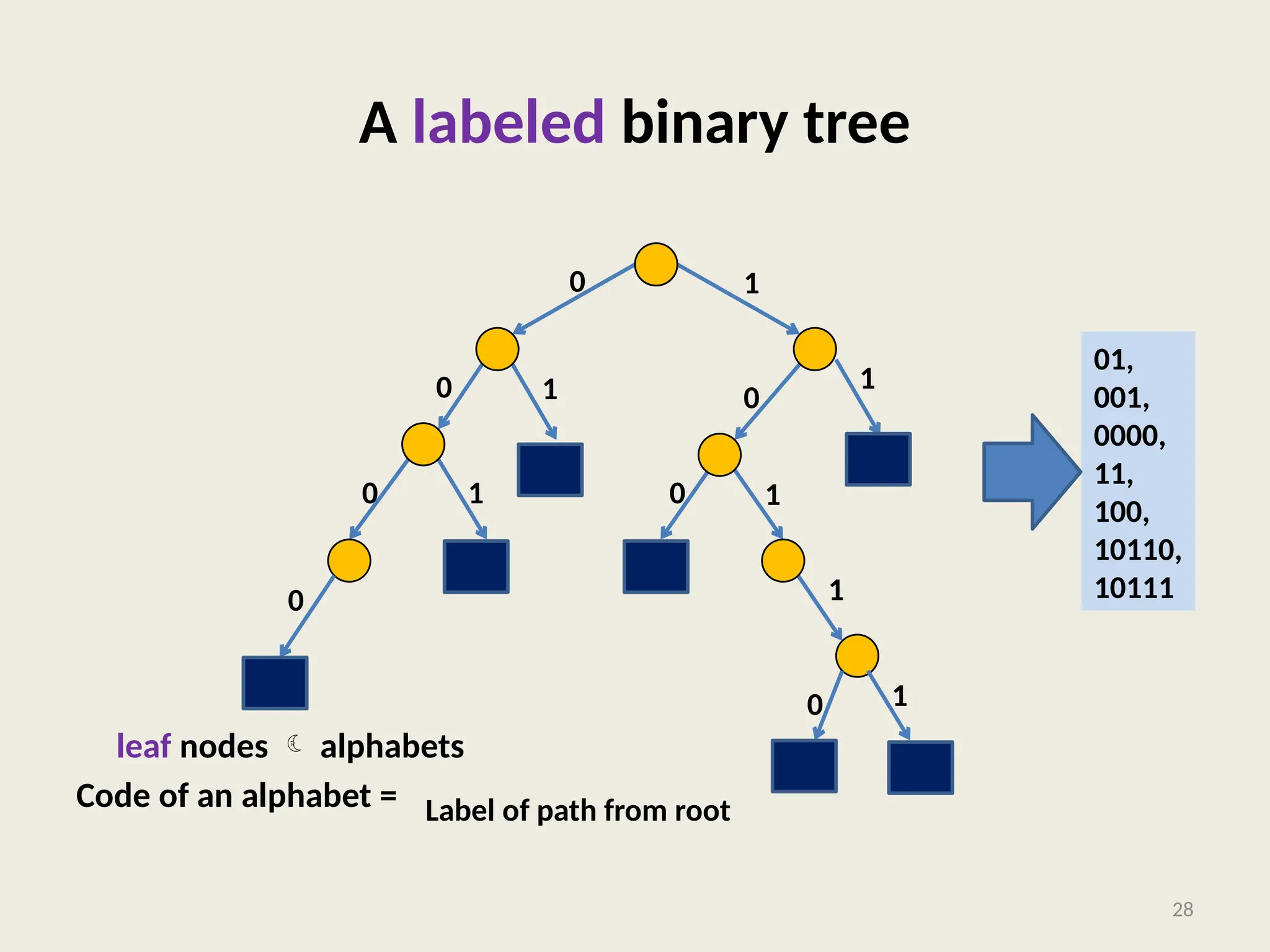
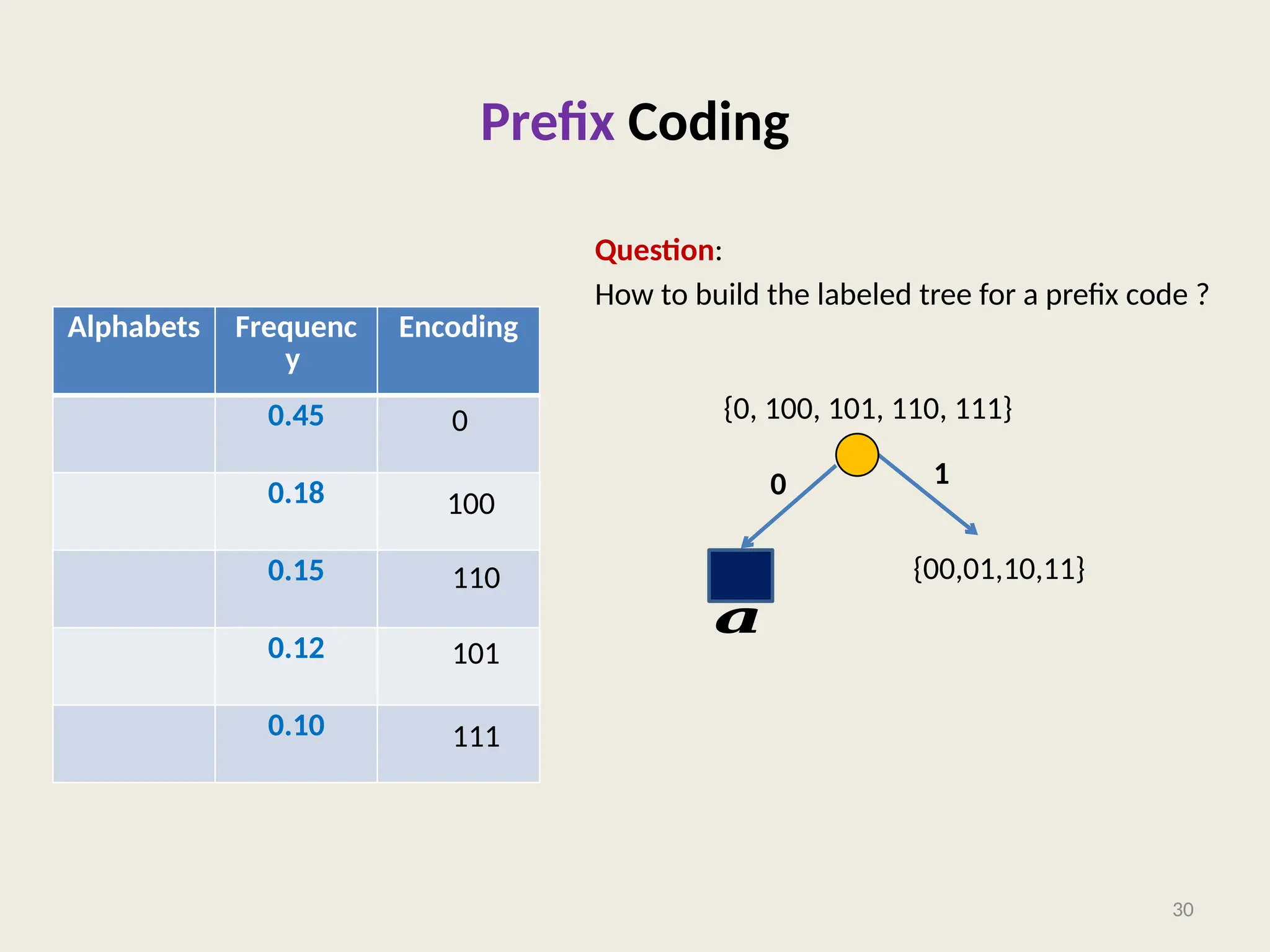
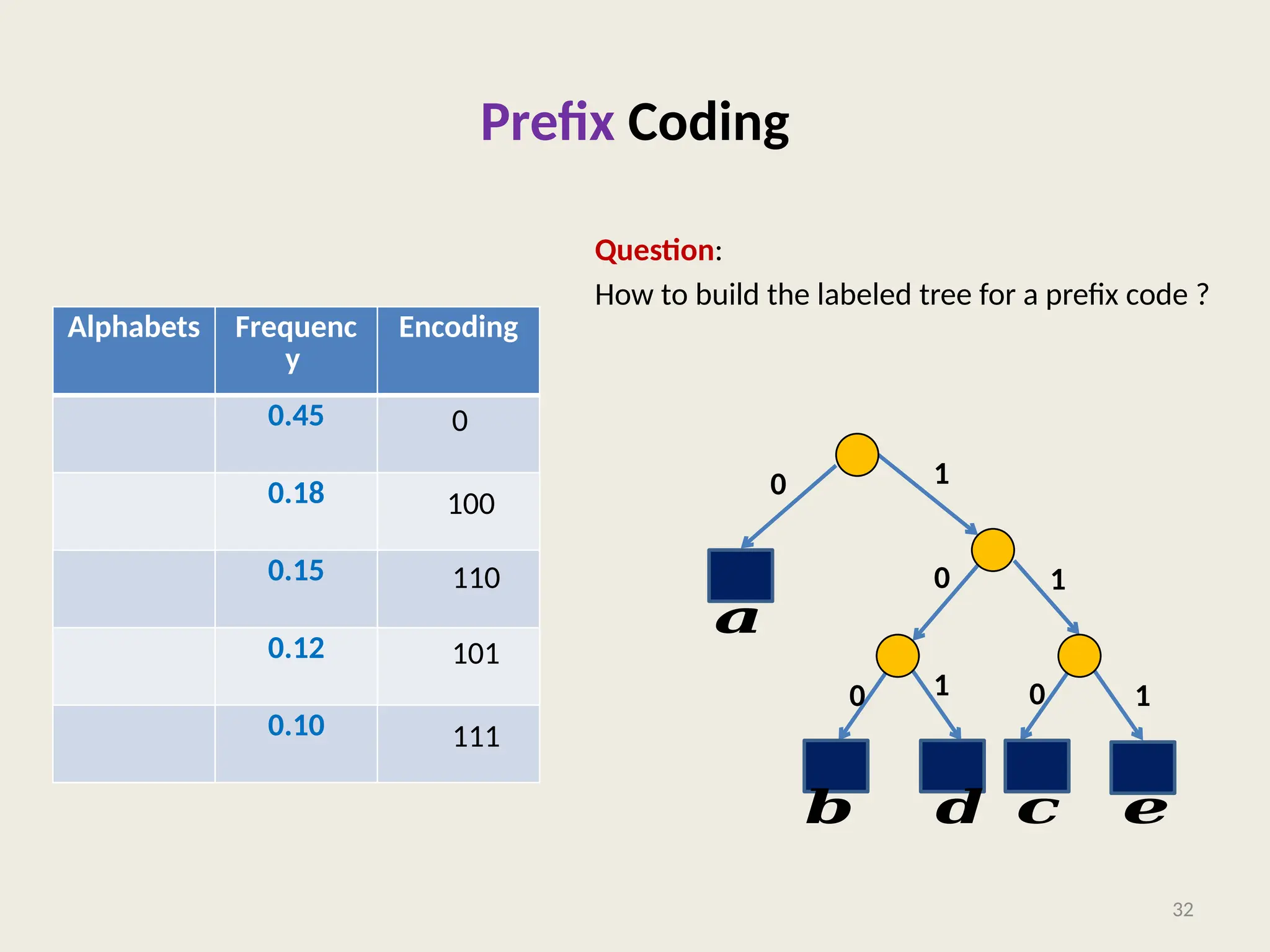
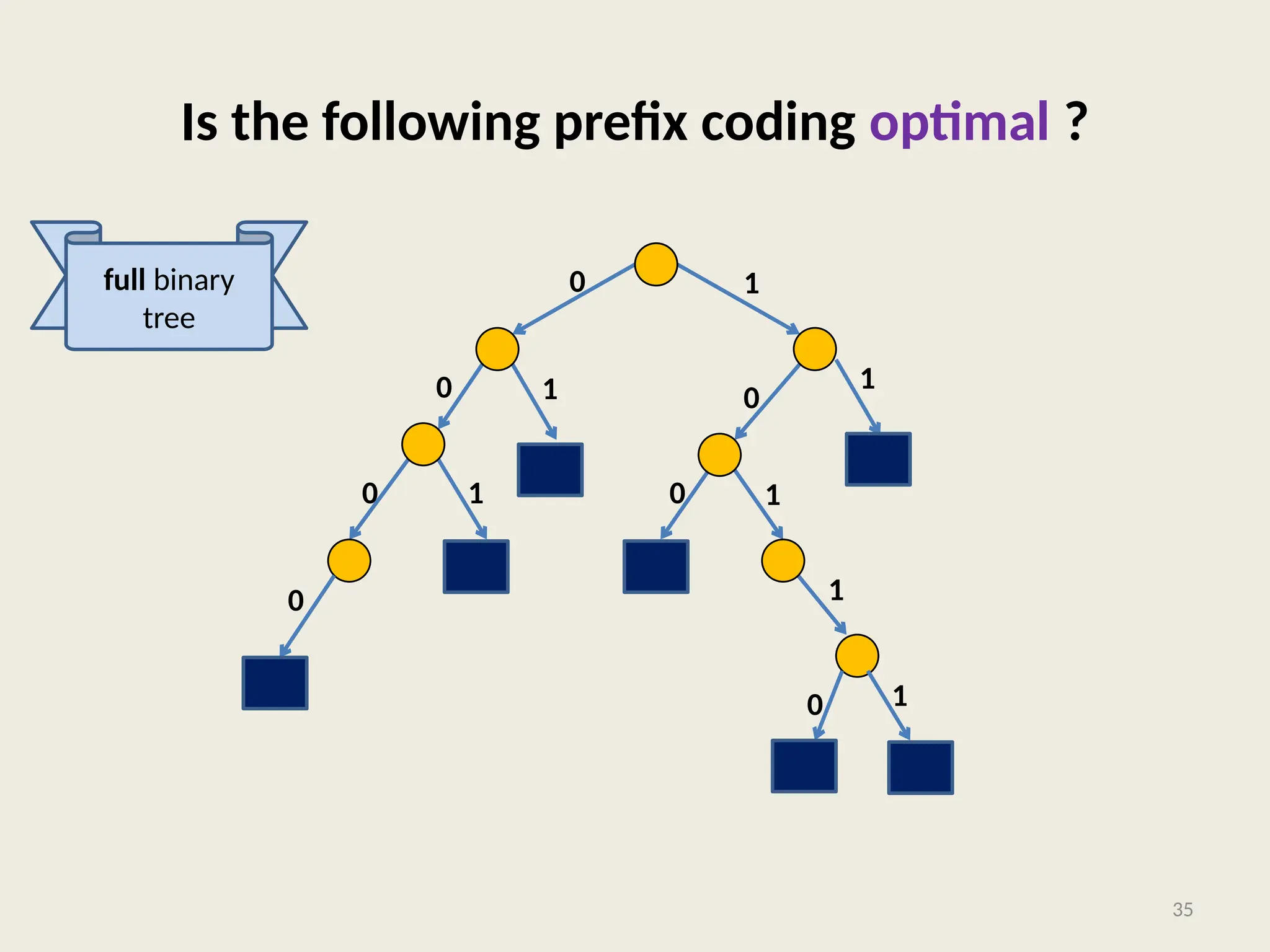
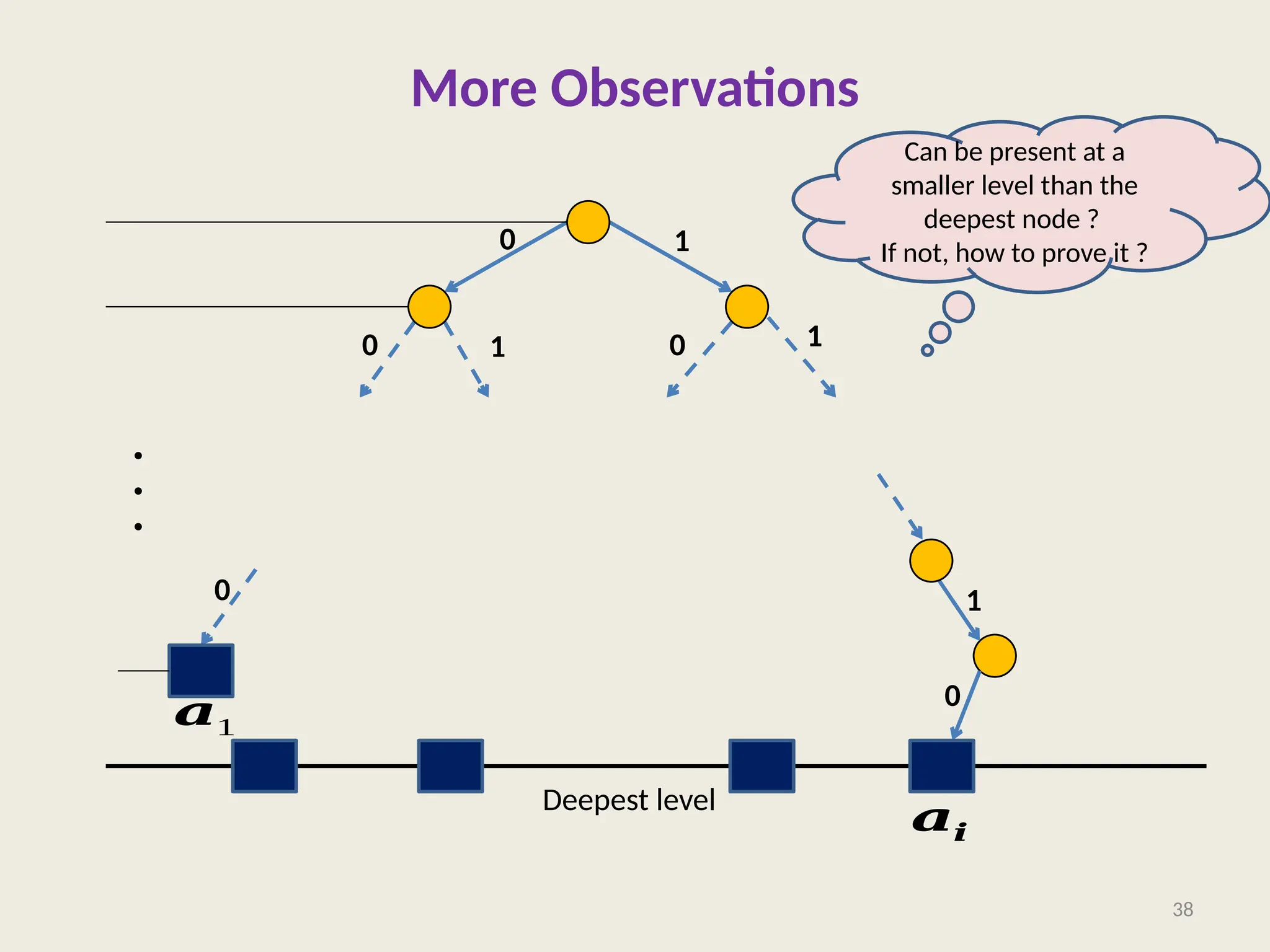
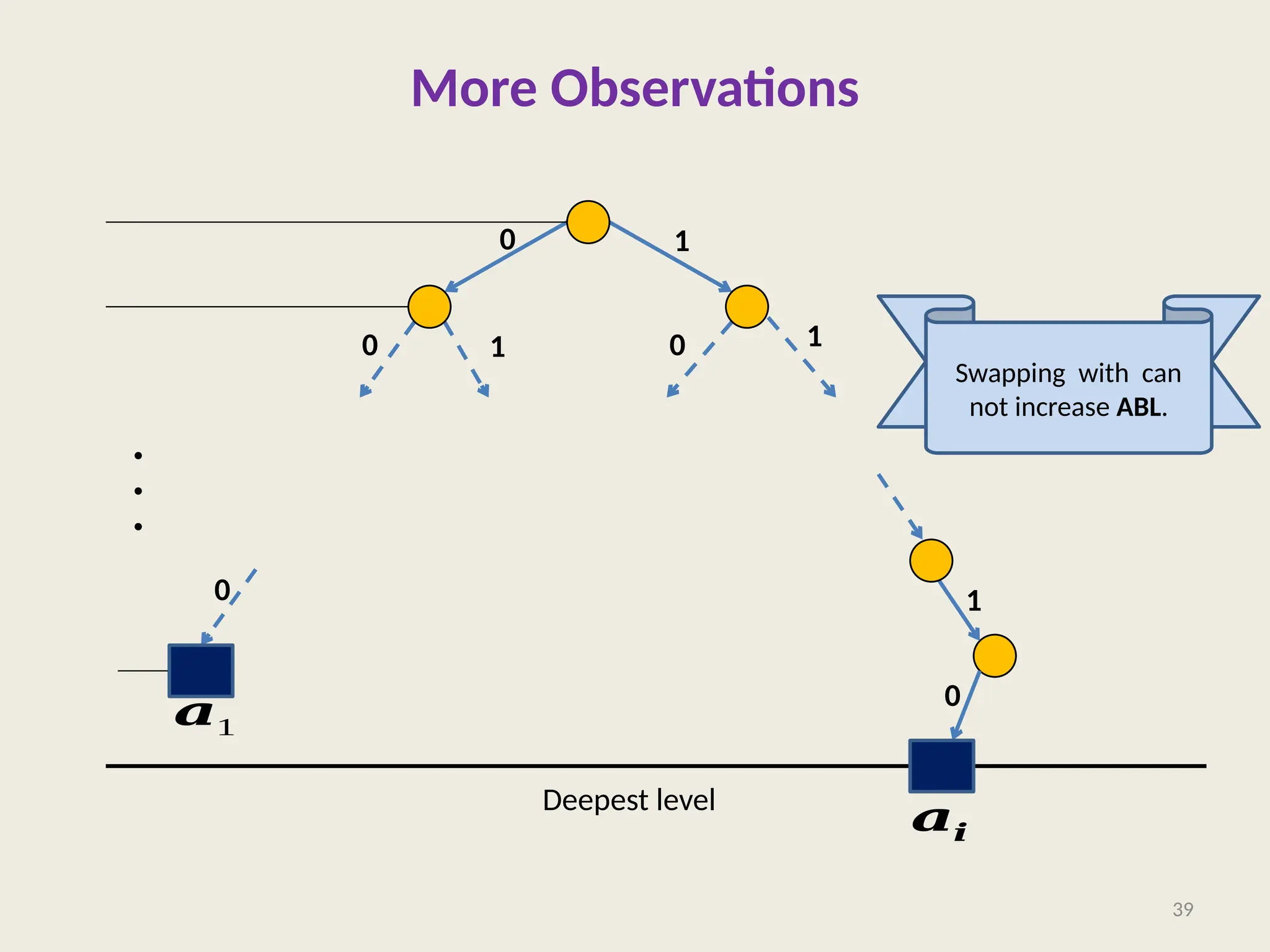
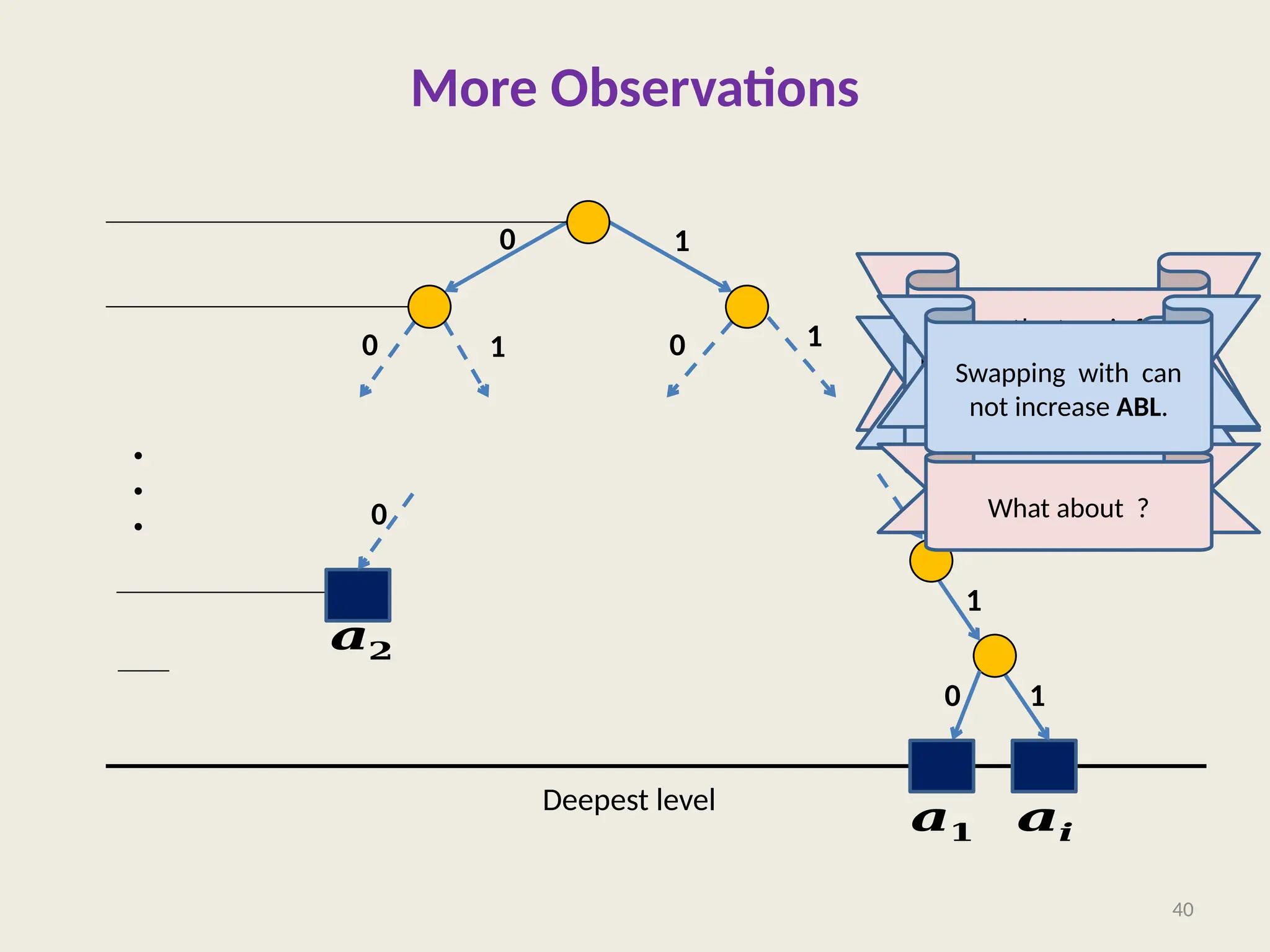
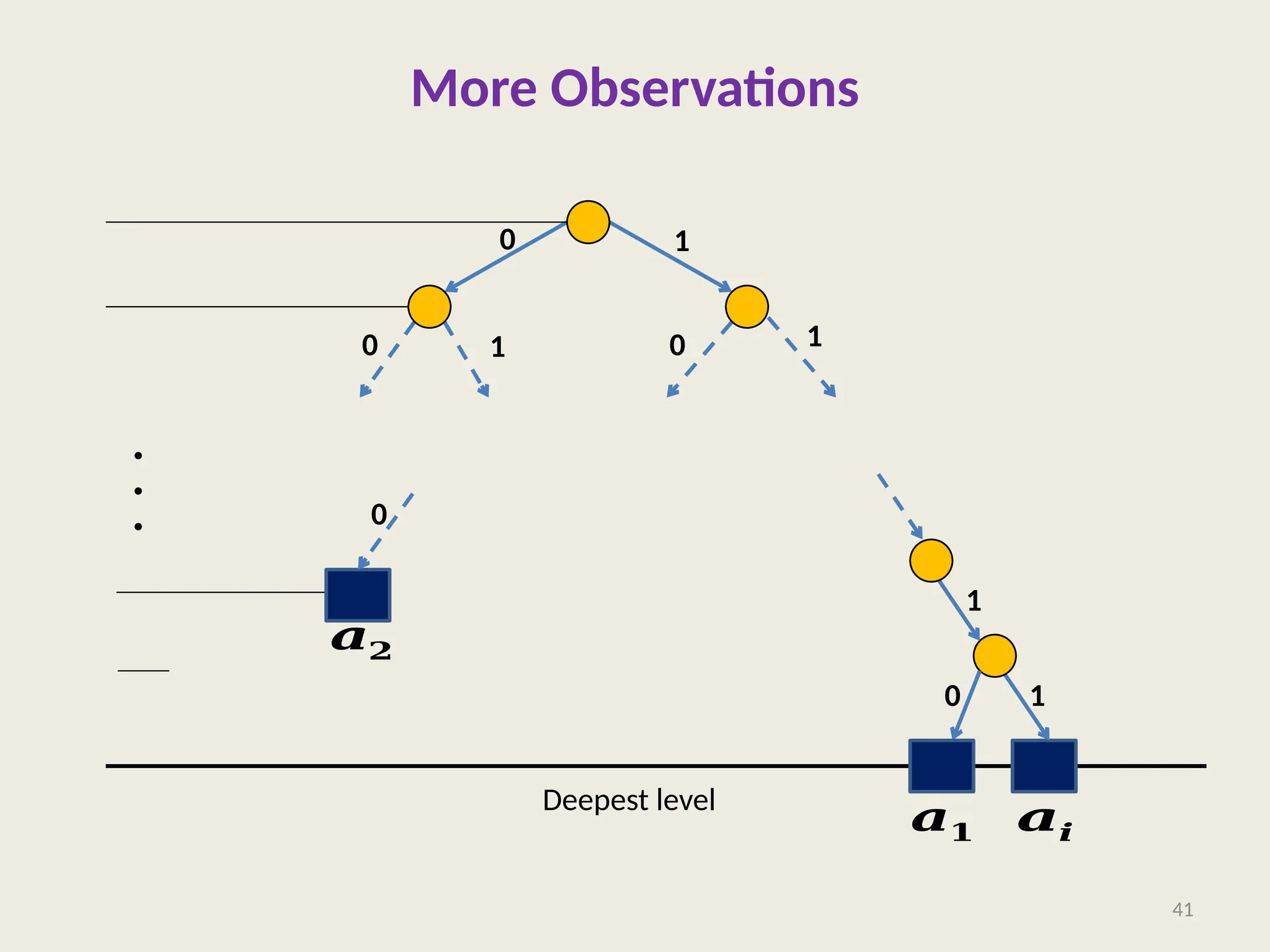
The document covers the proof of correctness for synchronizing circuits and the implementation of Huffman coding, emphasizing optimal solutions for delay enhancement and prefix coding. It discusses the principles of greedy algorithms, particularly how they can optimize binary coding according to character frequency. The text concludes by stressing the necessity of utilizing binary trees for creating optimal prefix codes, highlighting the importance of structuring algorithmic efficiency based on frequency analysis.

1. Design and Analysis of Algorithms
Lecture 9
• Proof of Correctness: Synchronzing the circuit problem
• Huffman Codes
1
Algorithms-II : CS345A

2. Recap of the last lecture
2

3. SYNCHRONIZING A CIRCUIT
with minimum delay enhancement
3

4. Claim :
There is an optimal solution where,
the delay enhancement by = ||
4

5. Observation 2
Question: In optimal sol., what is the max. delay along any path from to a leaf node ?
Guess: It remain unchanged.
In other words, it will still be max().
5
5
6
2
2
3 2
6
2 1 2 1
4
2 3
Delay 11 10 14 10 10 11 10 9
Electric signal
𝒖
+1
+1
+4
+1
+3
+3
+1
New Delay 14 14 14 14 14 14 14 14
The maximum delay from the root to
any leaf node remains unchanged in the
optimal solution. What can we say about
the maximum delay from any other
node to any leaf node in its subtree?

6. Proving the guess
Guess : In the optimal solution, the delay along any path from to any leaf
node is max().
Question: How to prove it ?
Answer: By contradiction.
6

7. What if the assertion fails at many nodes ?
8
𝒖

8. Proof:
must be synchronized in the optimal solution  ?
After alteration of delay enhancement, entire circuit is again synchronized.
The reduction in the delay-enhancement =
 solution is not optimal. Contradiction!! 9
𝒖
𝜷
𝜶
𝜸
Suppose
𝑫𝑹(𝒖)
𝑫𝑳(𝒖)
+𝜹𝟑
𝒖
𝜷
𝜶
𝜸
𝑫𝑹(𝒖)
𝑫𝑳(𝒖)
+𝜹𝟑
+𝜹𝟏
+𝑫𝑳(𝒖) − 𝑫𝑹 (𝒖
+𝜹𝟐− 𝜹𝟏
+𝜹𝟏 +𝜹𝟐
𝑫𝑳(𝒖)+𝜹𝟏=𝑫𝑹(𝒖)+𝜹𝟐
Since there was no red node here, so no extra delay
on this segment of the path corresponding to .
Since there was no red node here, so no extra delay
on this segment of the path corresponding to .
What does it
imply ?
What does it
imply ?
the maximum delay on any path from to any of its leaf node
is strictly greater than in an optimal solution .
Can you do some
manipulation to reduce
the total delay
enhancement ?

9. Homework
• Design an efficient implementation of the algorithm.
10

10. The last 2 problems we discussed
Synchronizing the delays in a circuit
Scheduling jobs to minimize maximum
lateness
11
5
6
2
2
3 2
6
2 1 2 1
4
2 3
Electric signal
𝟎 time
A local approach Optimizing a global function

11. Greedy Algorithms
• Unlike algorithms based on divide and conquer, the two greedy algorithms
we discussed were quite adhoc (problem specific) and so was their
analysis (proof of correctness)
• This leads to the following question :
• Does there exist any generic strategy to design and analyse Greedy
algorithms ?
• We shall now discuss a strategy of designing greedy algorithms that is
quite generic.
• To demonstrate this strategy, we address a very very nontrivial problem.
12

12. Huffman Codes
A novel and quite inspiring
application of greedy algorithms
13

13. Binary coding
alphabet set : {, ,…, }
A text File: a sequence of alphabets
Question: How many bits needed to encode a text file of size alphabets ?
Answer: bits.
14
once upon a time …………..
…………………………….
……………………………..
…………………
A text file F
Binary coding of F

14. Fixed length coding
alphabet set : {, ,…, }
Question: What is a binary coding of ?
Answer: : binary strings
Question: What is a fixed length coding of ?
Answer: each alphabet  a unique binary string of length .
Question: How to decode a fixed length binary coding?
Answer: easy 
15

15. Fixed length coding
alphabet set : {, ,…, }
Question: Can we use fewer than bits for each alphabet of ?
Answer: No.
Question: Can we use fewer than bits to store a file of length ?
Answer: Yes most likely.
16

16. huge variation in the frequency of
alphabets in a text.
17
http://en.wikipedia.org/wiki/Letter_frequency

17. huge variation in the frequency of
alphabets in a text.
Question: How to exploit variation in the frequencies of alphabets ?
Answer:
More frequent alphabets  coding with shorter bit string
Less frequent alphabets  coding with longer bit string
18

18. Variable length encoding
Alphabets Frequenc
y
Encoding
0.45
0.18
0.15
0.12
0.10
Average bit length per symbol using :
Question: How will you decode 01010111 ?
Answer: or
Question: What is the source of this ambiguity ?
Answer: is a prefix of .
19
10
0
110
101
111
There is a serious problem with
the encoding. Can you see?
Can we fix it ?
? ?
Let us think of some encoding exploiting
the variation in frequencies.

19. Variable length encoding
Alphabets Frequenc
y
Encoding
0.45
0.18
0.15
0.12
0.10
Average bit length per alphabet using :
20
100
0
110
101
111

20. Prefix Coding
Definition:
A coding is called prefix coding if
there does not exist such that
is prefix of
Algorithmic Problem: Given a set of alphabets and their frequencies,
compute coding such that
• is prefix coding
• is minimum.
21

21. The challenge of the problem
22
Among all possible binary coding of , how to find the optimal prefix coding ?
It looks too complex  because …
it is too difficult to see any structure underlying the set of binary strings

22. The novel idea of Huffman
23
Binary coding Binary tree
? 0 1
1
0 0
1
Labeled

23. A labeled binary tree
nodes  ?
Code of an alphabet = ?
24
0 1
0 0
0 1
1
1
Label of path from root
0,
00,
001
01,
1,
10,
100,
101
alphabets

24. PREFIX CODES AND LABELED BINARY TREE
25

25. A labeled binary tree
Consider a prefix code 101
26
0 1
0
0
1
1
Visualize a binary tree
for the prefix code ?

26. A labeled binary tree
27
0 1
0
0
0
0
0
0
1
1
1
1
1
1

27. A labeled binary tree
leaf nodes  alphabets
Code of an alphabet =
28
0 1
0
0
0
0
0
0
1
1
1
1
1
1
Label of path from root
01,
001,
0000,
11,
100,
10110,
10111

28. Homework
• Design an algorithm that given a prefix coding for a set of
alphabets, builds the corresponding labeled binary tree.
• The algorithm is sketched on the following slide.
29

29. Prefix Coding
Alphabets Frequenc
y
Encoding
0.45
0.18
0.15
0.12
0.10
Question:
How to build the labeled tree for a prefix code ?
30
100
0
110
101
111
0 1
𝒂
{0, 100, 101, 110, 111}
{00,01,10,11}

30. Prefix Coding
Alphabets Frequenc
y
Encoding
0.45
0.18
0.15
0.12
0.10
Question:
How to build the labeled tree for a prefix code ?
31
100
0
110
101
111
0 1
𝒂
{0,1}
1
0
{0,1}

31. Prefix Coding
Alphabets Frequenc
y
Encoding
0.45
0.18
0.15
0.12
0.10
Question:
How to build the labeled tree for a prefix code ?
32
100
0
110
101
111
0 1
1
1
1
0
0 0
𝒂
𝒃 𝒅 𝒄 𝒆

32. Theorem 1:
For each prefix code of a set of alphabets,
there exists a binary tree on leaves s.t.
• There is a bijective mapping between the alphabets and the leaves.
• The label of a path from root to a leaf node corresponds to the prefix code of
the corresponding alphabet.
Question: Can you express Average bit length of in terms of its binary tree ?
33

33. FINDING THE LABELED BINARY TREE FOR
34
the optimal prefix codes

34. Is the following prefix coding optimal ?
35
0 1
0
0
0
0
1
1
1
0
0 1
1
1
full binary
tree

35. Observations on
the binary tree of the optimal prefix code
Lemma:
The binary tree corresponding to optimal prefix coding must be a full binary tree:
Every internal node has degree exactly 2.
Question: What next ?
We need to see the influence of frequencies on the optimal binary tree.
36
, , … ,
Non-decreasing order of frequency
𝒇(𝒂¿¿𝒊)≤𝒇(𝒂¿¿𝒊+𝟏)¿¿

36. Observations on
the binary tree of the optimal prefix code
Intuitively, more frequent alphabets should be closer to the root and
less frequent alphabets should be farther from the root.
But how to organize them to achieve optimal prefix code ?
• We shall now make some simple observations about the structure of the
binary tree corresponding to the optimal prefix codes.
• These observations will be about some local property in the tree.
• Nevertheless, these observations will play a crucial role in the design of a
binary tree with optimal prefix code for given .
Please pay full attention on the next few slides.
37

37. More Observations
38
0 1
0 1 1
0
𝒂1
0 1
0
.
.
.
Deepest level
𝒂𝒊
Can be present at a
smaller level than the
deepest node ?
If not, how to prove it ?

38. More Observations
39
0 1
0 1 1
0
1
0
0
.
.
.
𝒂𝒊
Deepest level
Swapping with can
not increase ABL.
𝒂1

39. More Observations
40
0 1
0 1 1
0
𝒂𝟏 𝒂𝒊
1
1
0
.
.
.
𝒂𝟐
0
Deepest level
Since the tree is full
binary, must have a
sibling. What can we
say about it ?
It must be a leaf node.
Otherwise is not at
the deepest level.
What about ?
Swapping with can
not increase ABL.

40. More Observations
41
0 1
0 1 1
0
𝒂𝟏 𝒂𝒊
1
1
0
.
.
.
𝒂𝟐
0
Deepest level

41. More Observations
Theorem 2: There exists an optimal prefix coding
in which and appear as siblings 42
0 1
0 1 1
0
𝒂𝟏 𝒂𝟐
1
1
0
.
.
.
Deepest level

42. The important observation
Theorem 2: There exists an optimal prefix coding in which and appear as siblings.
Important note: It is inaccurate to claim that “In every optimal prefix coding, and
appear as siblings in the labeled binary string.” For example, if there are
alphabets with same frequencies and is odd.
But algorithmic implication of Theorem 2 mentioned above is quite important:
 We just need to focus on those binary trees in which and appear as siblings.
But there can still be exponential number of such trees .
43

43. Homework
Theorem 2: There exists an optimal prefix coding in which and appear as siblings.
Design an algorithm for optimal prefix coding.
Hint:
You don’t require anything more than Theorem 2.
So don’t try to prove properties for , ,…
Just use your creative skills to exploit Theorem 2 
44