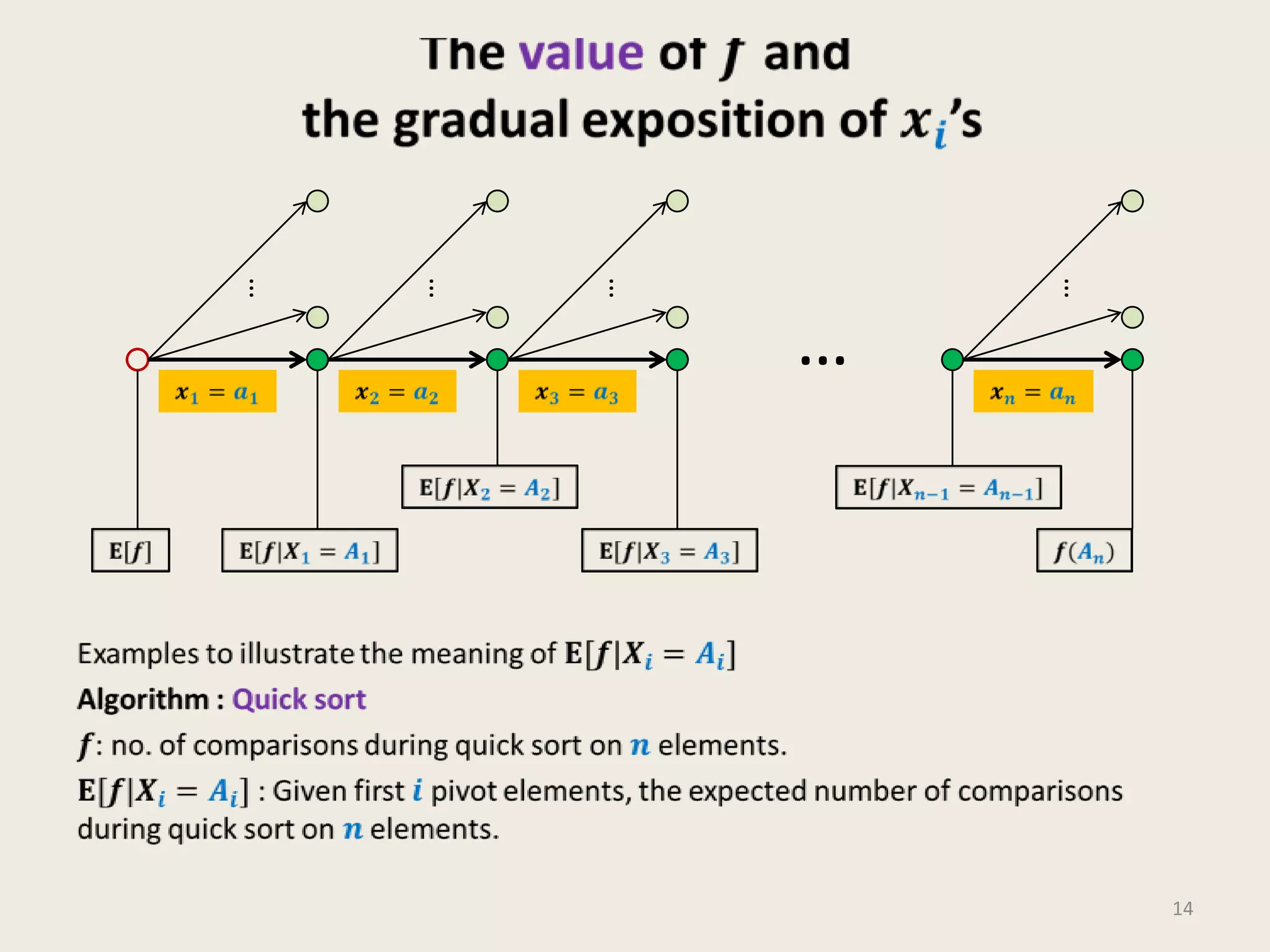
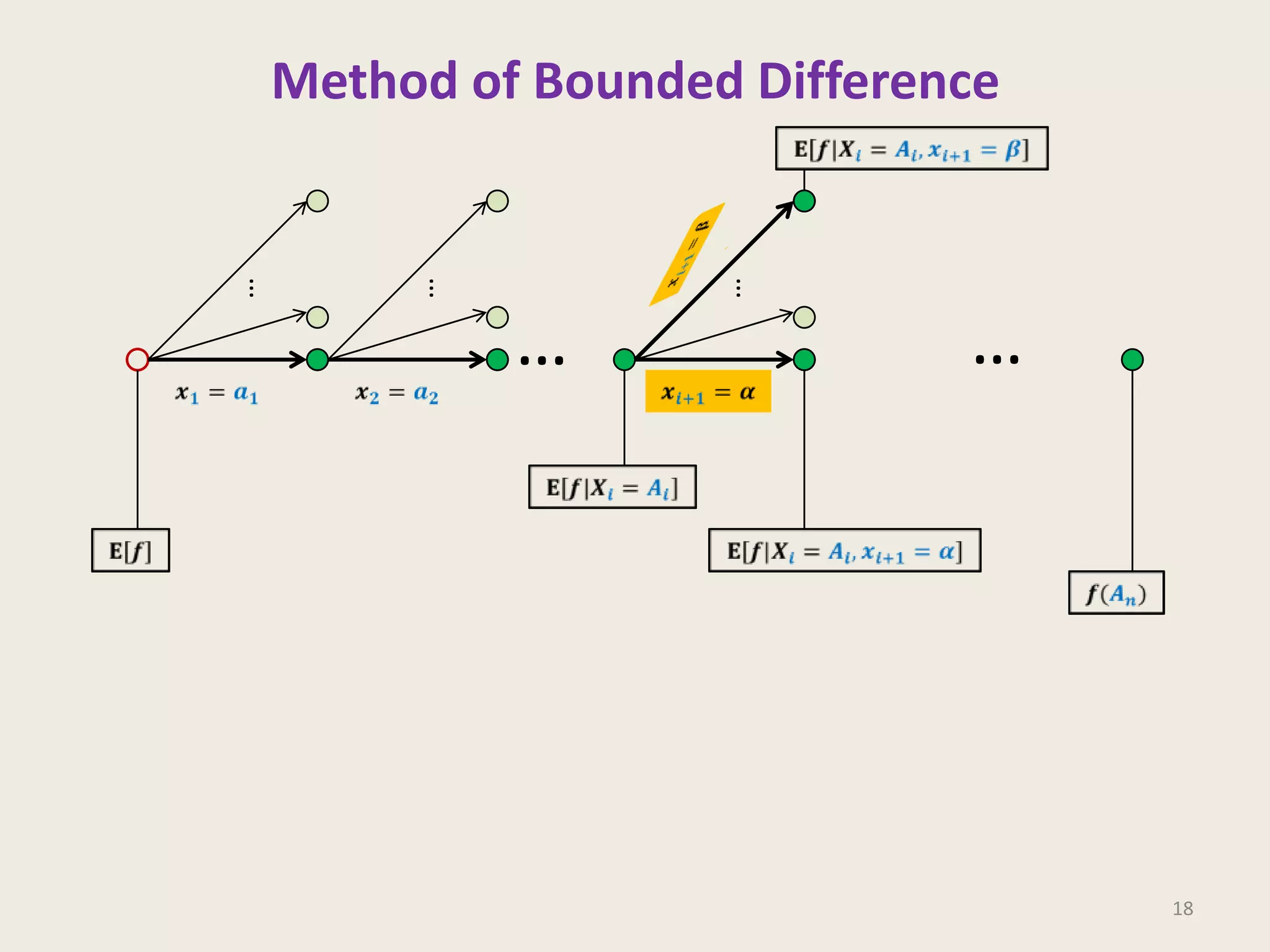
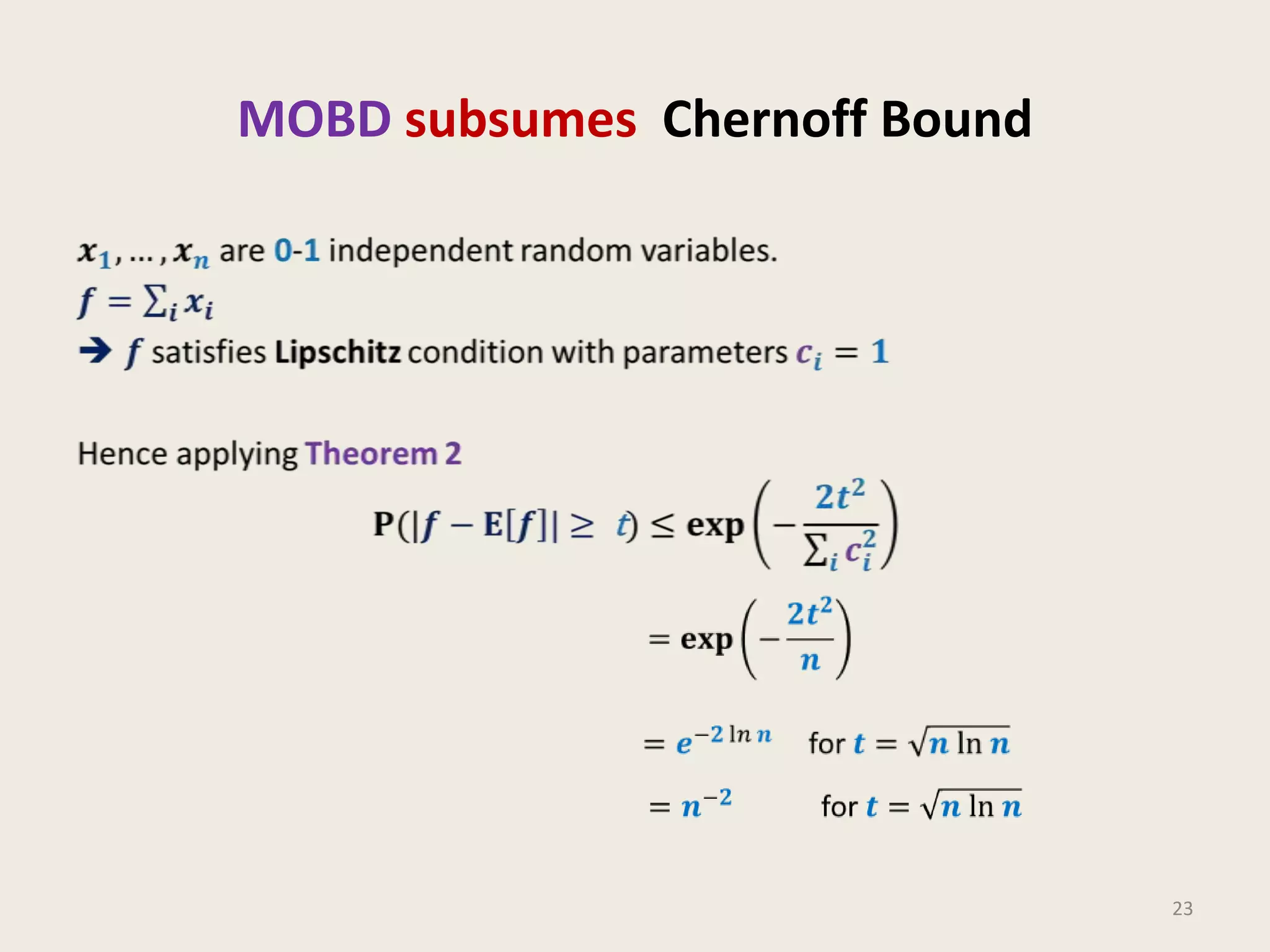
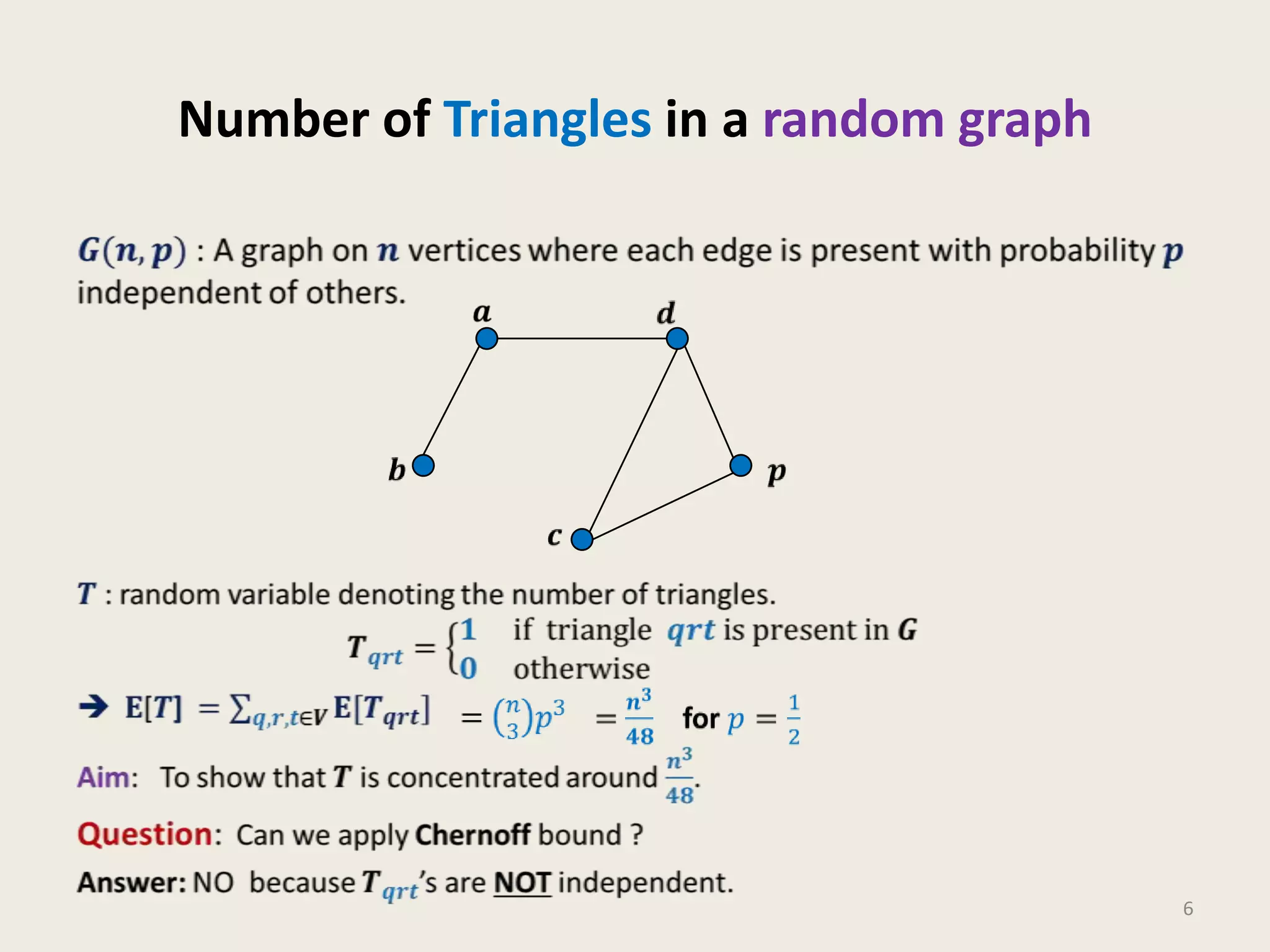
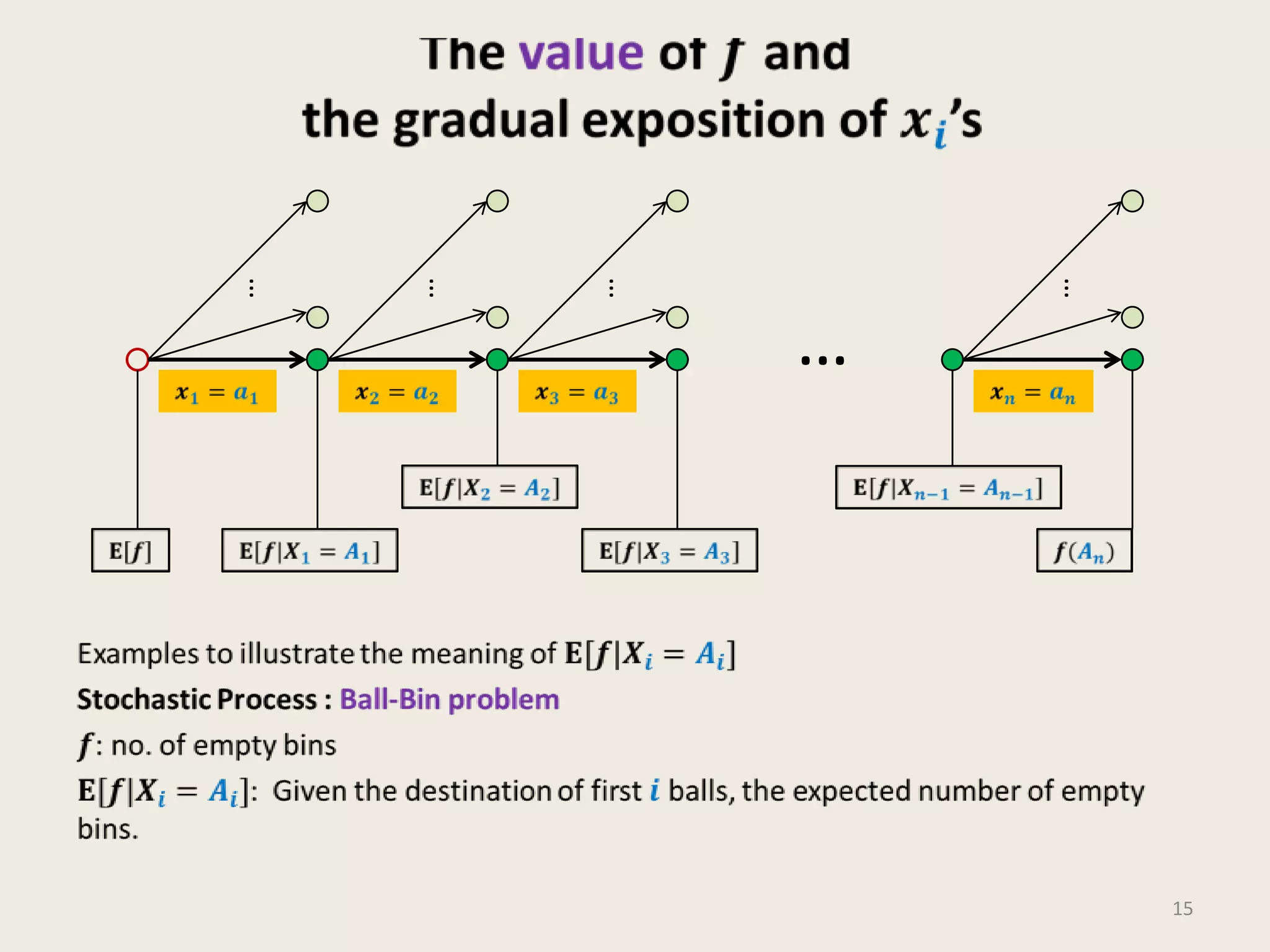
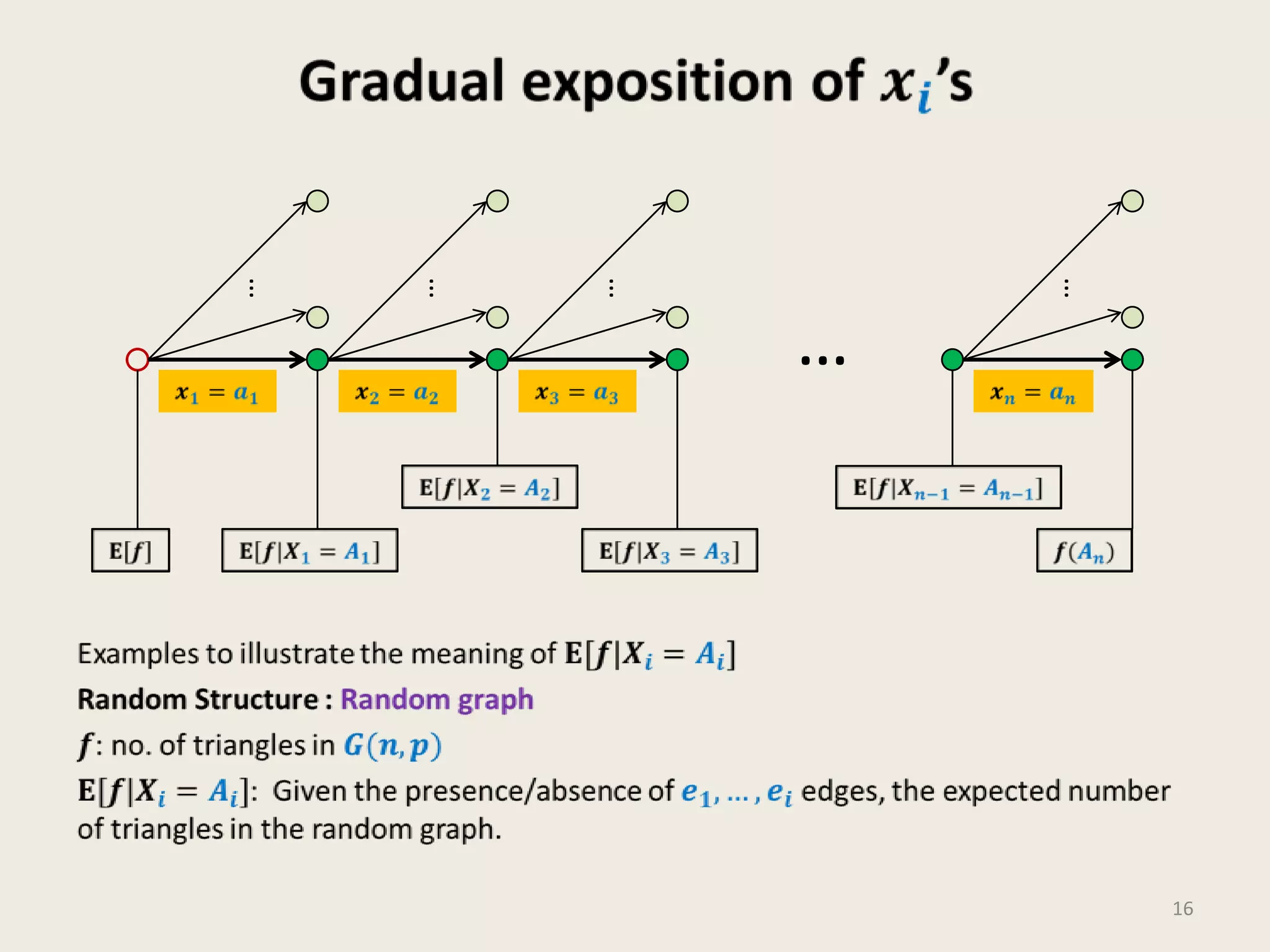
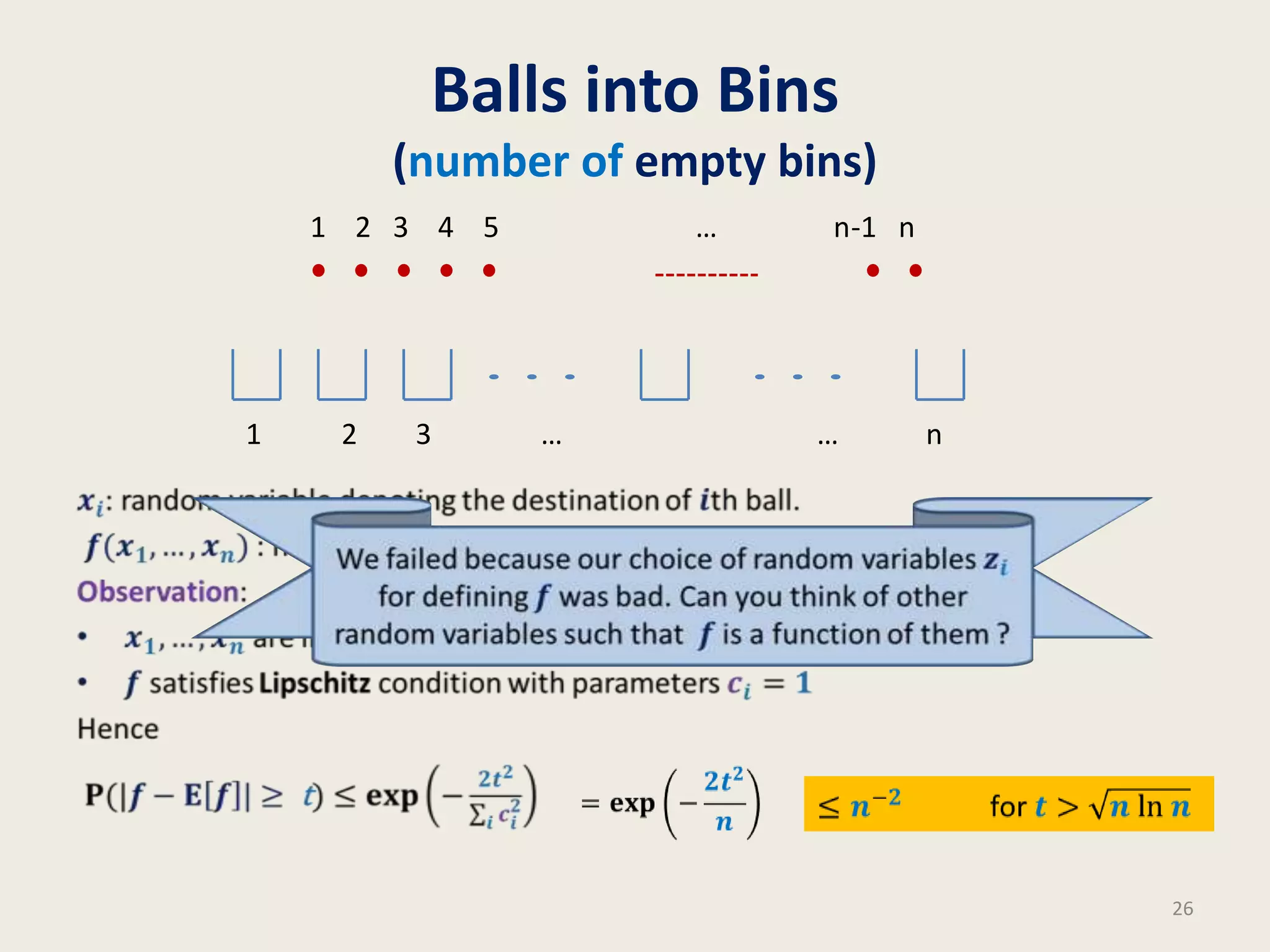
This document discusses randomized algorithms and covers several topics: - Chebyshev's Inequality and the Method of Bounded Difference (MOBD) for bounding the probability of deviation of a random variable from its expected value. - MOBD is described as the most powerful method for bounding this probability. - Three examples are presented to illustrate MOBD: balls into bins to calculate empty bins, red-blue balls drawn from a bin, and the number of triangles in a random graph.

1. Randomized Algorithms
CS648
Lecture 22
• Chebyshev Inequality
• Method of Bounded Difference
1

2. Chernoff Bound

3. THREE EXAMPLES TO ILLUSTRATE THE
INAPPLICABILITY OF CHERNOFF BOUND
3

4. Red-blue balls out of bin
4

5. Balls into Bins
(number of empty bins)
1 2 3 4 5
1
2
3
…
…
m-1 m
…
n
5

6. Number of Triangles in a random graph
6

7. CHEBYSHEV’S INEQUALITY
7

8. Chebyshev’s inequality
8

9. Chebyshev’s inequality
9

10. METHOD OF BOUNDED DIFFERENCE (MOBD)
The most powerful method for bounding
the probability of deviation of a random variable from expected value
10

11. The Power of MOBD
11

12. Notations
12

13. A new perspective
…
The next slide will give a visual description of the process
mentioned above.
But ponder over this slide before pressing the next button.
13

14. …
…
…
…
…
14

15. …
…
…
…
…
15

16. …
…
…
…
…
16

17. THE INTUITION
UNDERLYING MOBD
17

18. Method of Bounded Difference
…
…
…
…
…
18

19. Method of Bounded Difference
…
…
…
…
…
19

20. Method of Bounded Difference - I
…
…
…
…
…
20

21. Method of Bounded Difference - II
21

22. MOBD SUBSUMES CHERNOFF BOUND
22

23. MOBD subsumes Chernoff Bound
23

24. PROBLEM 1
NO. OF EMPTY BINS
24

25. Balls into Bins
(number of empty bins)
1 2 3 4 5
1
2
3
…
…
n-1 n
…
n
This will give very inferior bound
25

26. Balls into Bins
(number of empty bins)
1 2 3 4 5
1
2
3
…
…
n-1 n
…
n
26

27. Balls into Bins
(number of empty bins)
27

28. PROBLEM 2
RED-BLUE BALLS OUT OF BIN
28

29. Red-blue balls out of bin
29

30. Red-blue balls out of bin
…
…
…
30

31. Red-blue balls out of bin
31

32. PROBLEM 3
NO. OF TRIANGLES IN RANDOM GRAPH
Do it as exercise.
This problem will also be posted in practice sheet.
32