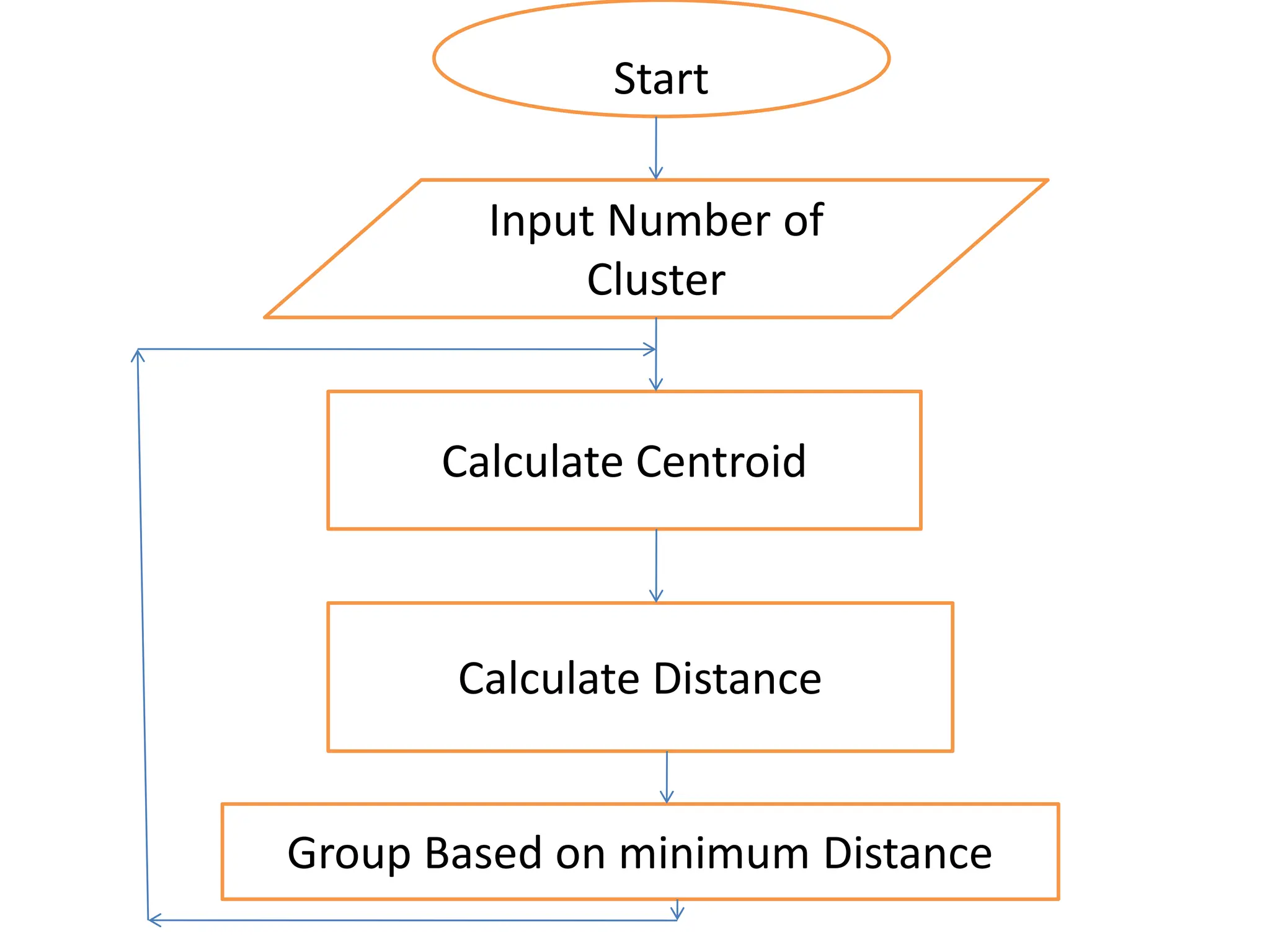
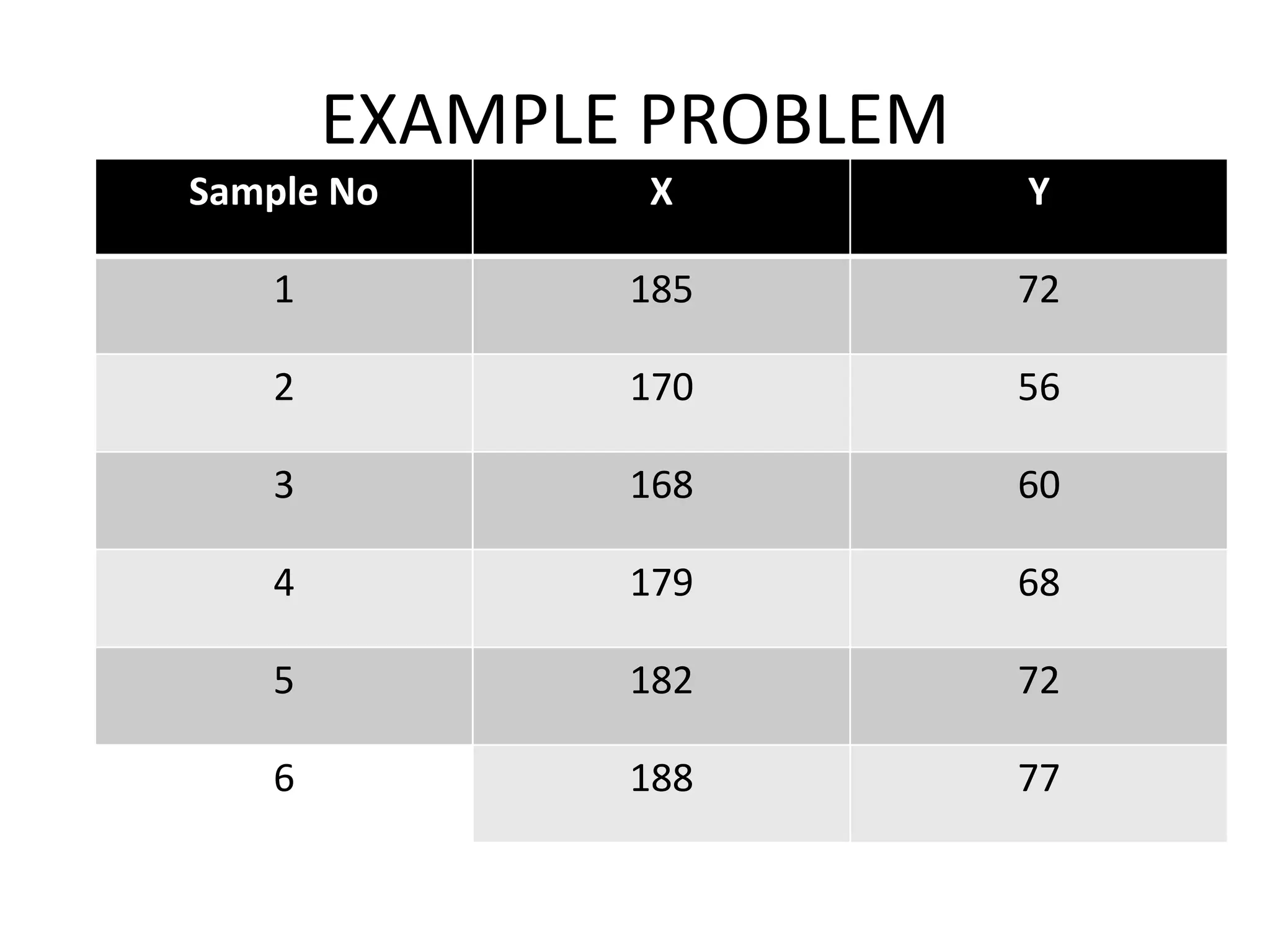
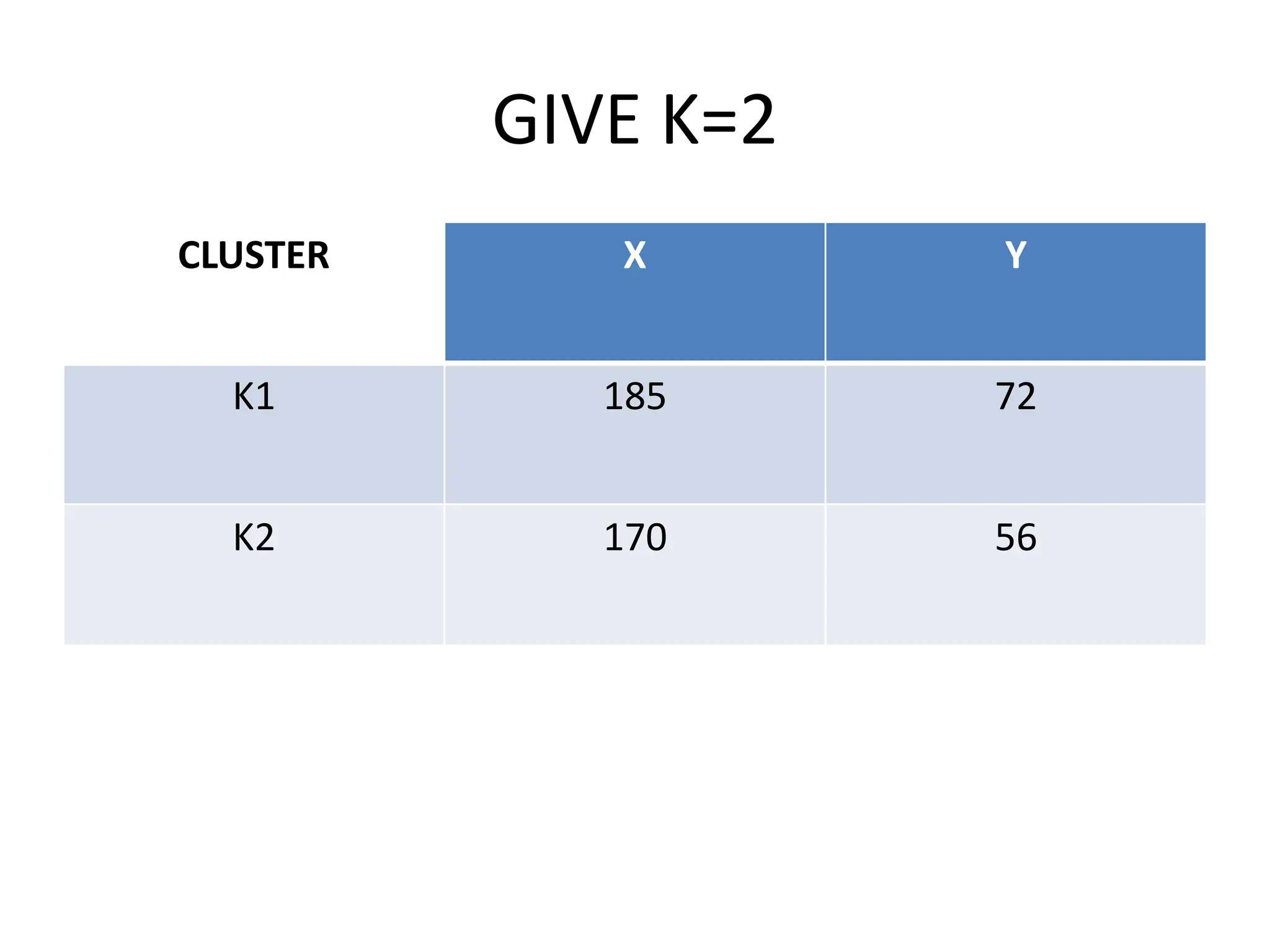
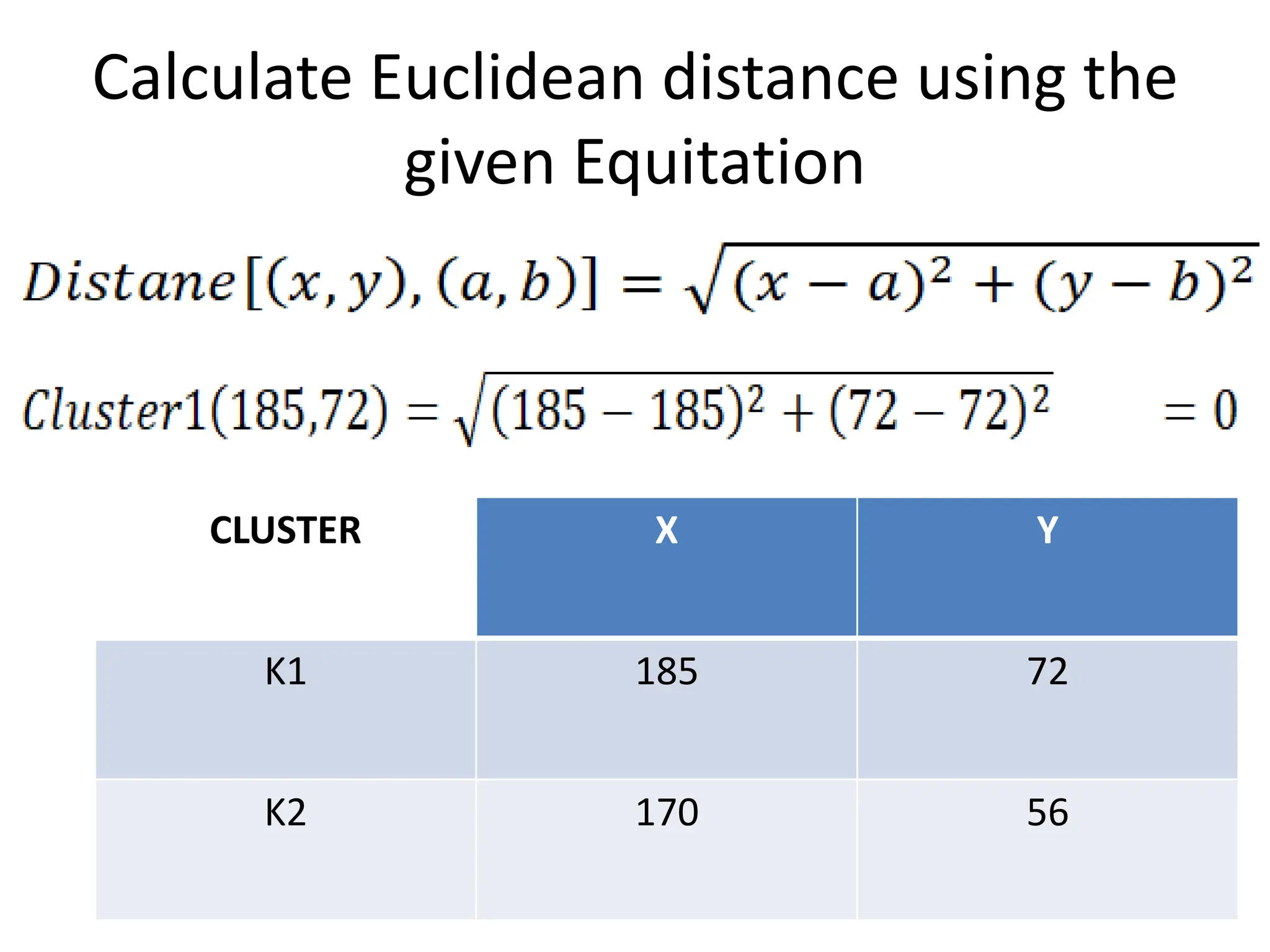
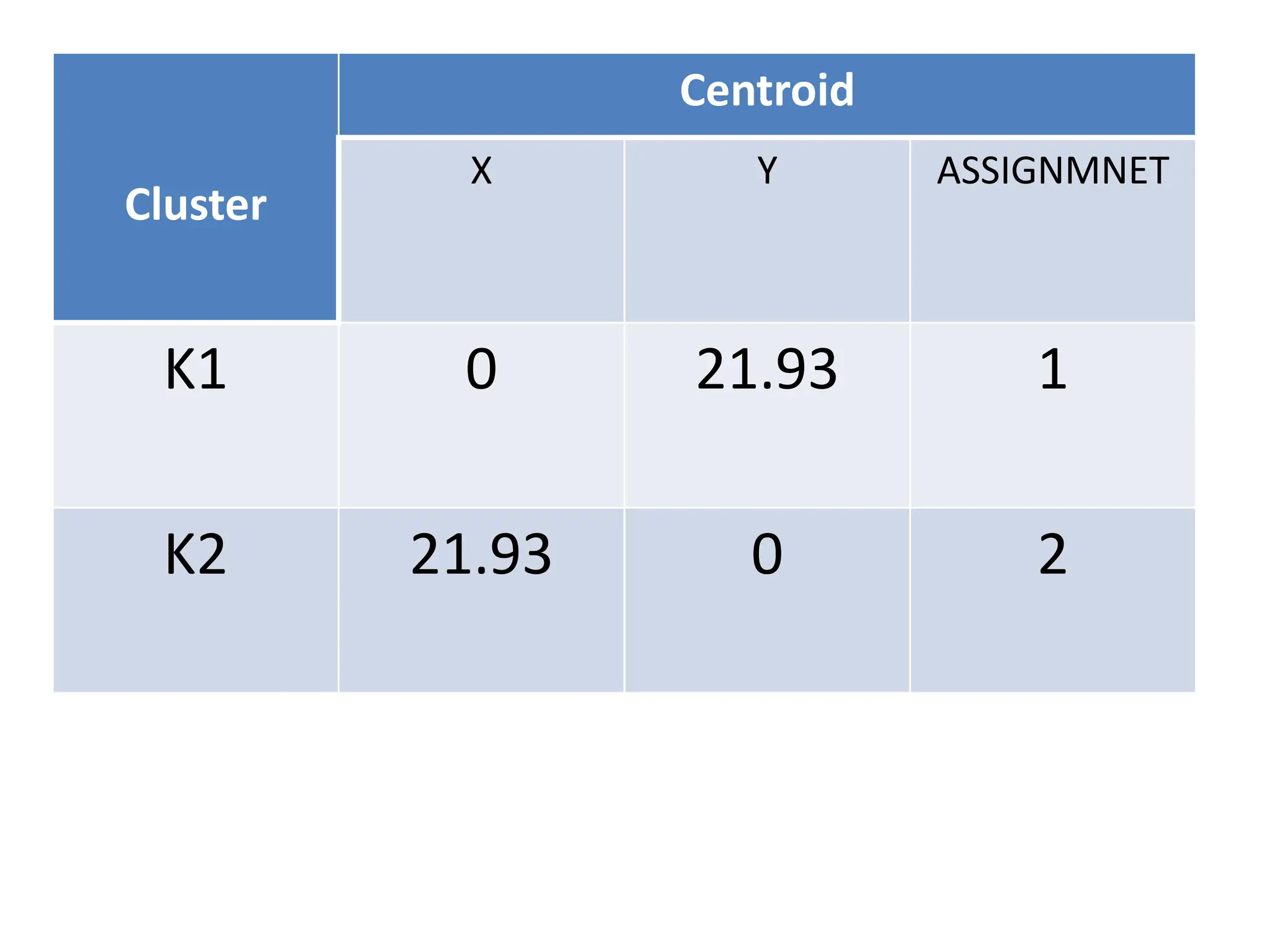
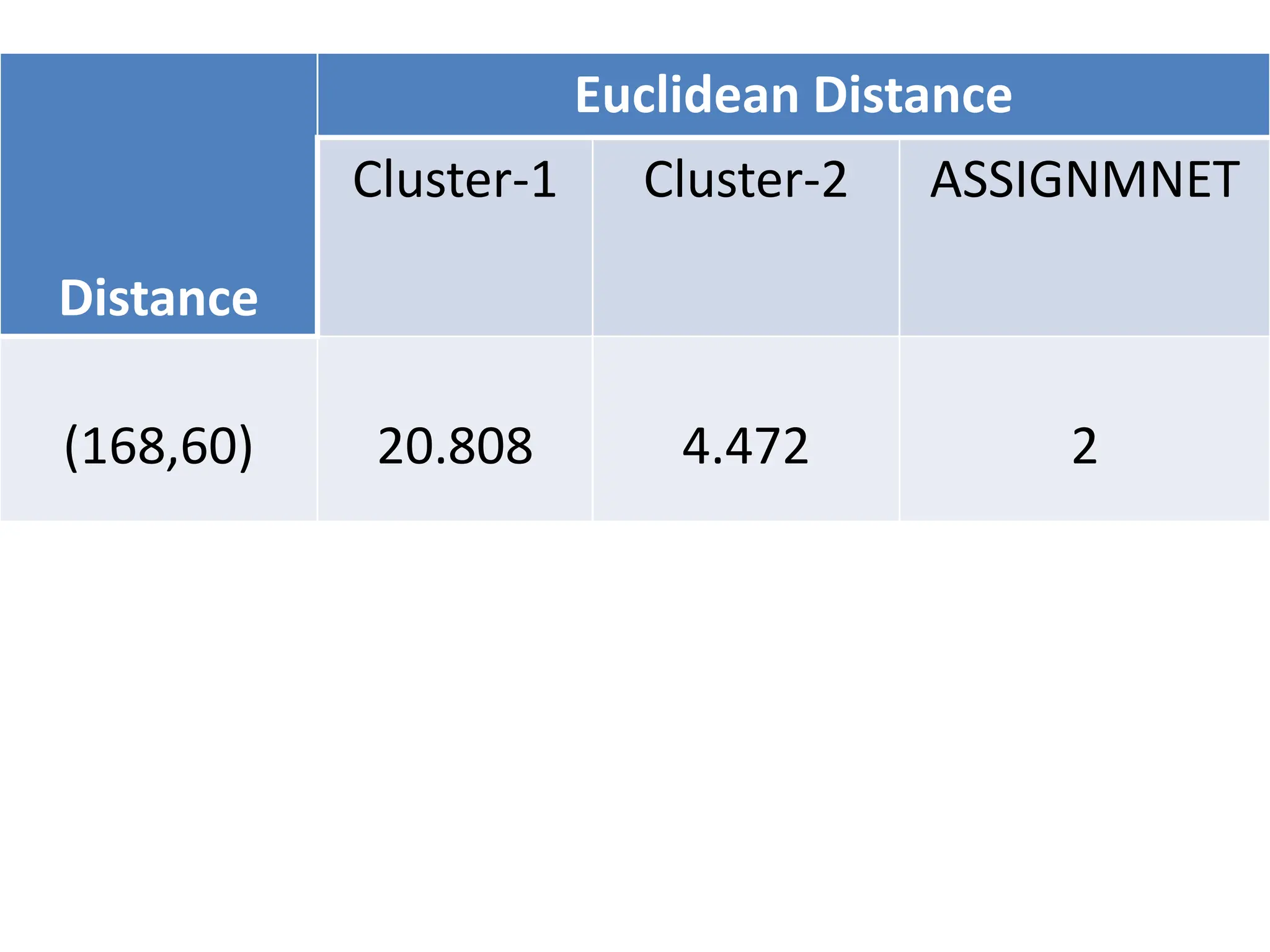
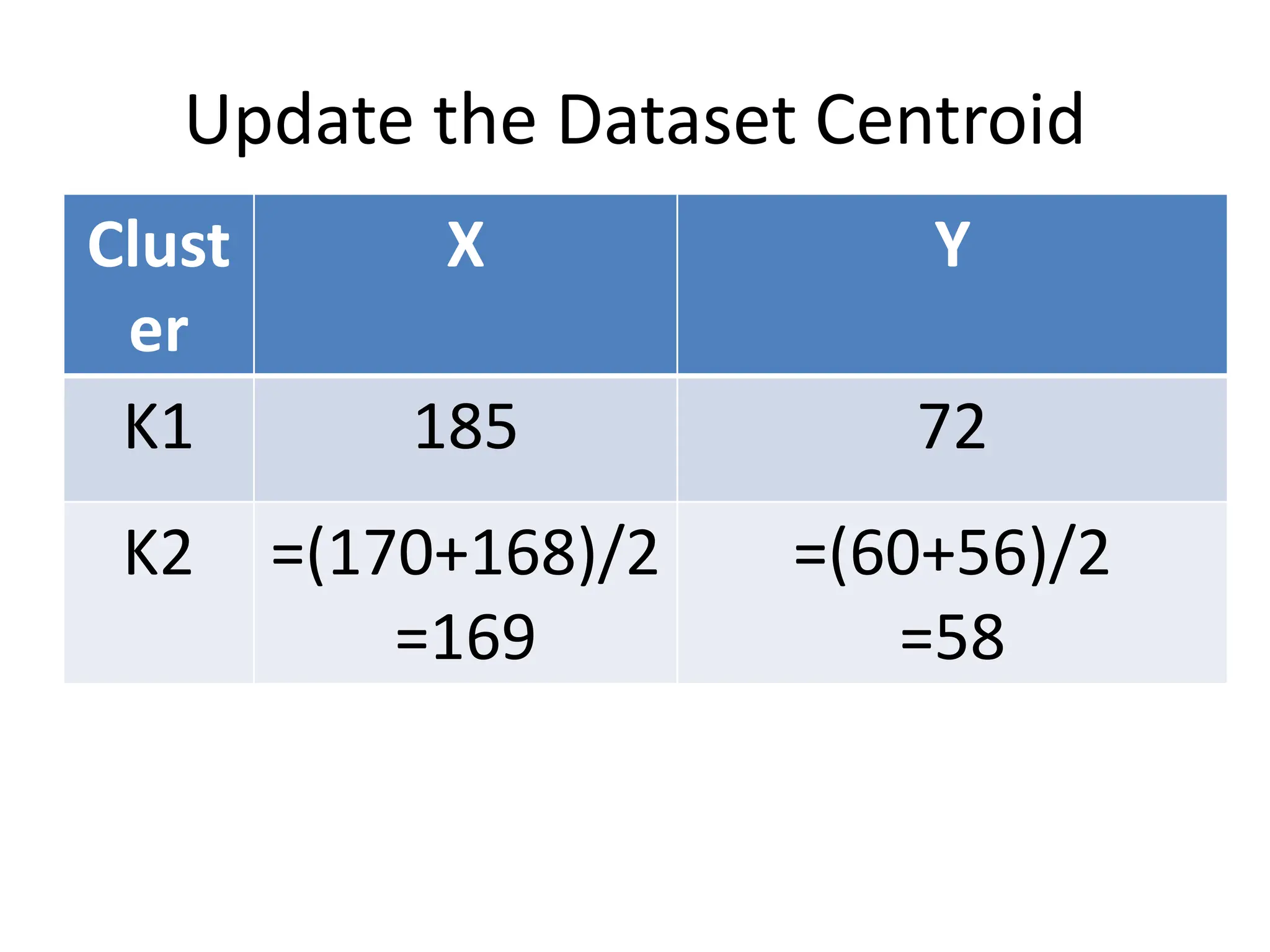
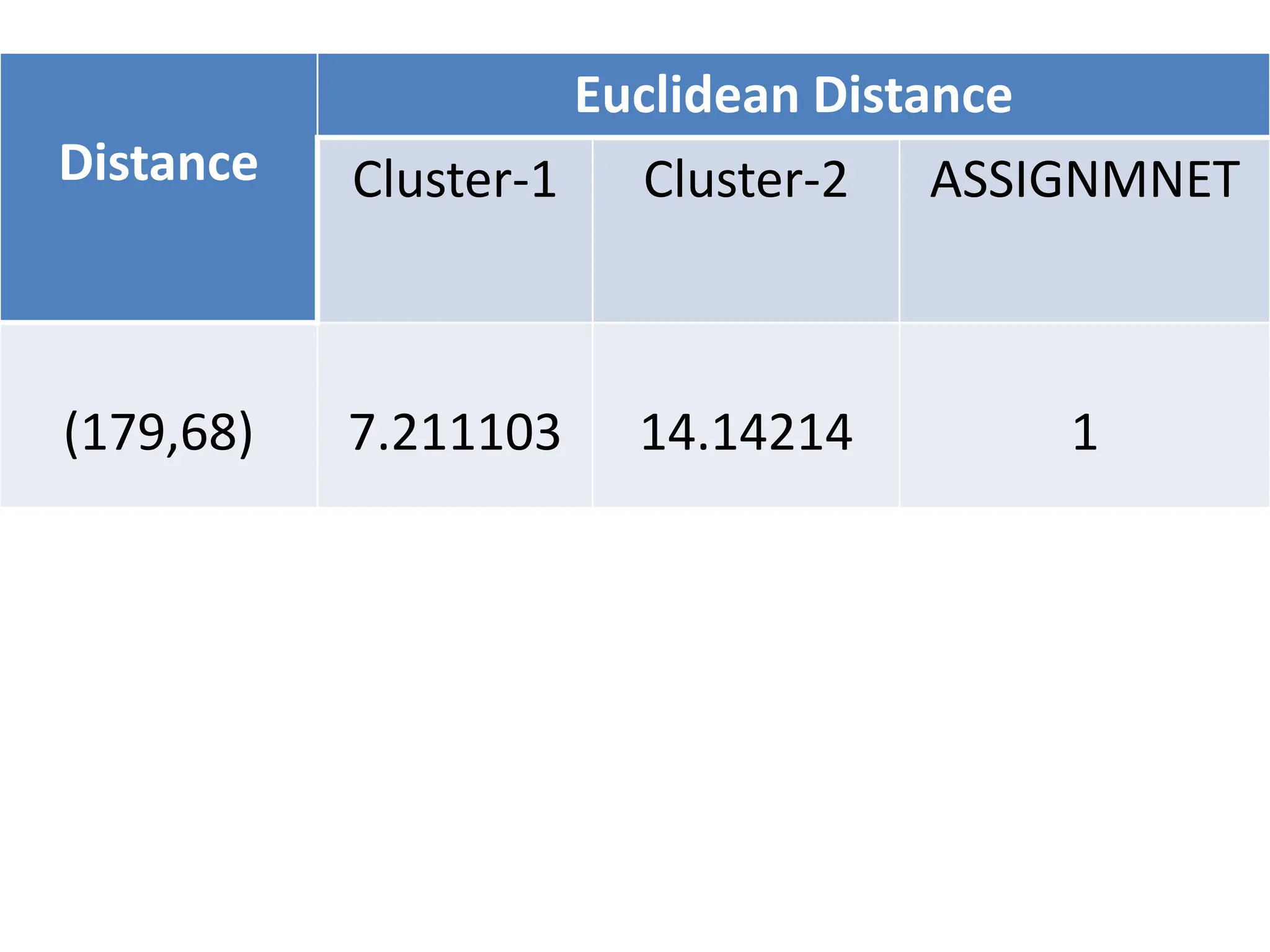
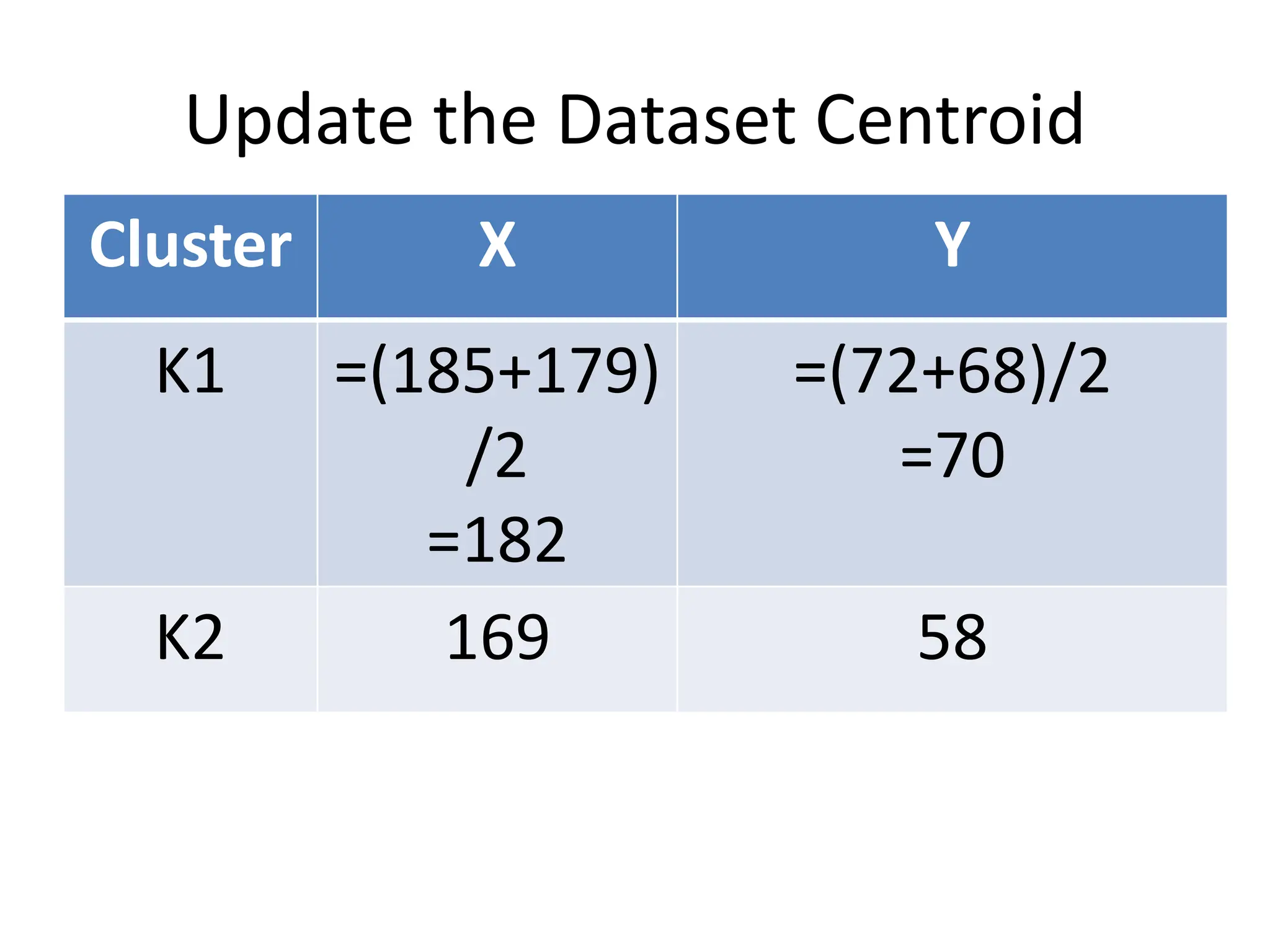
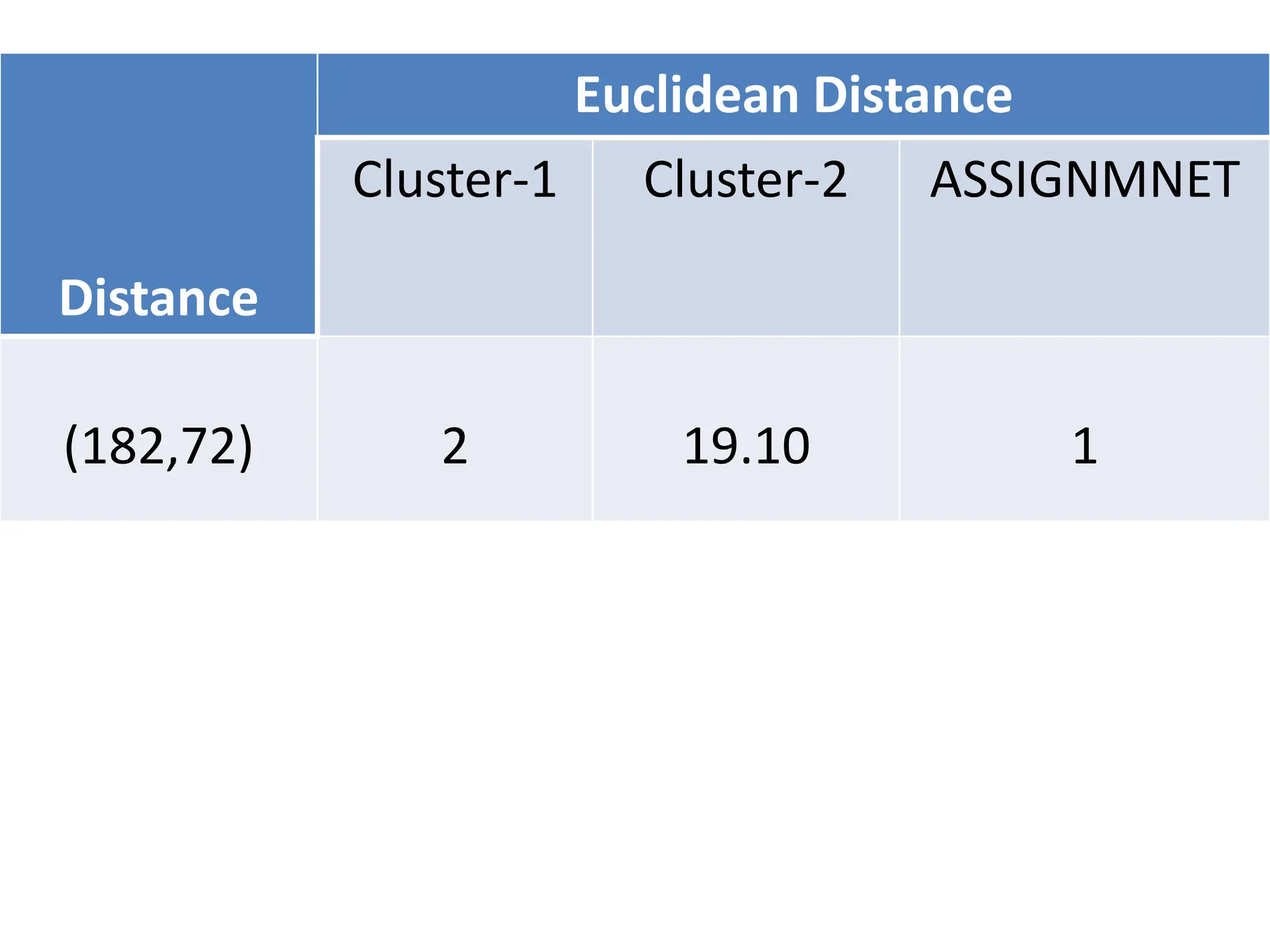
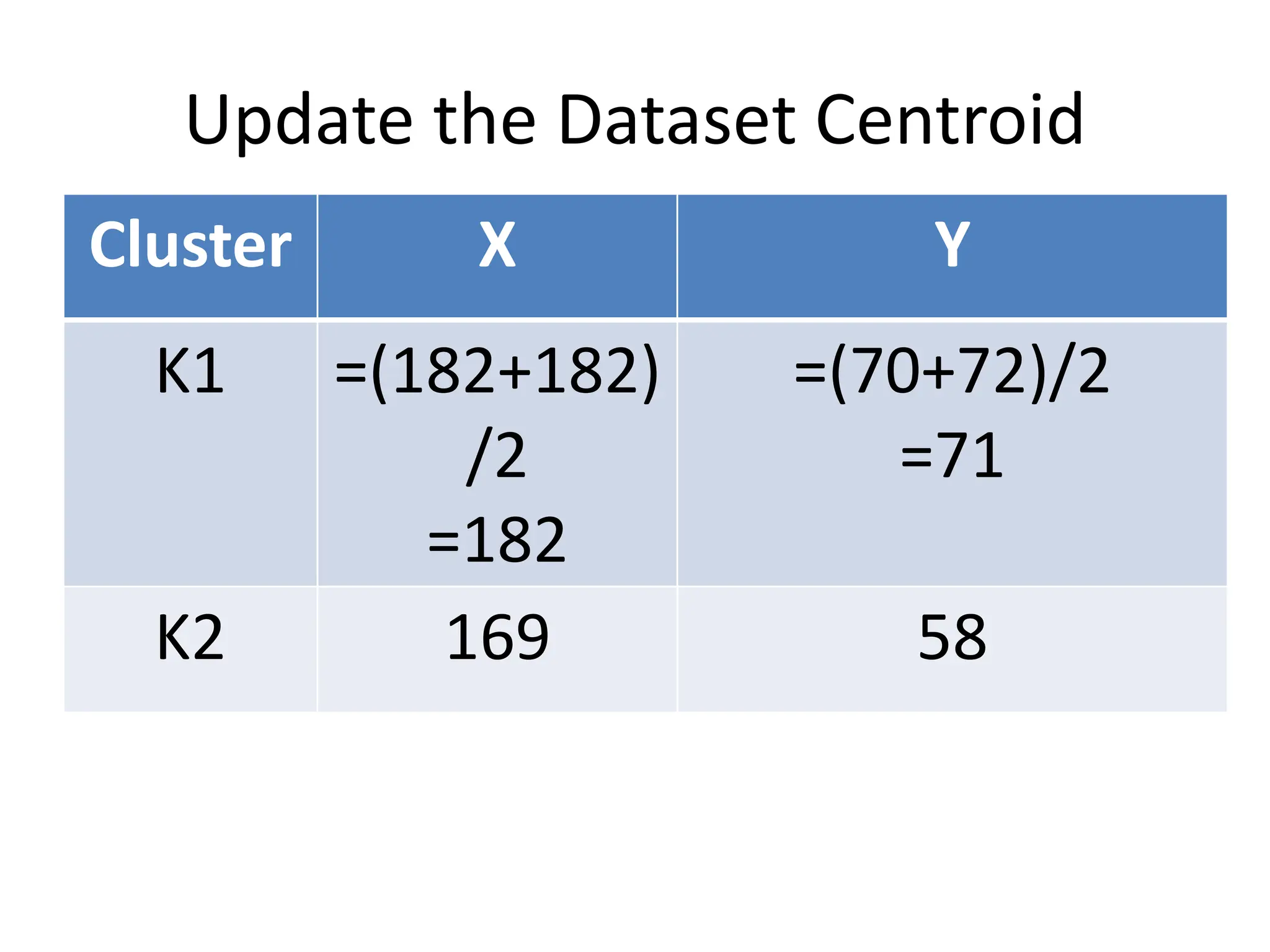
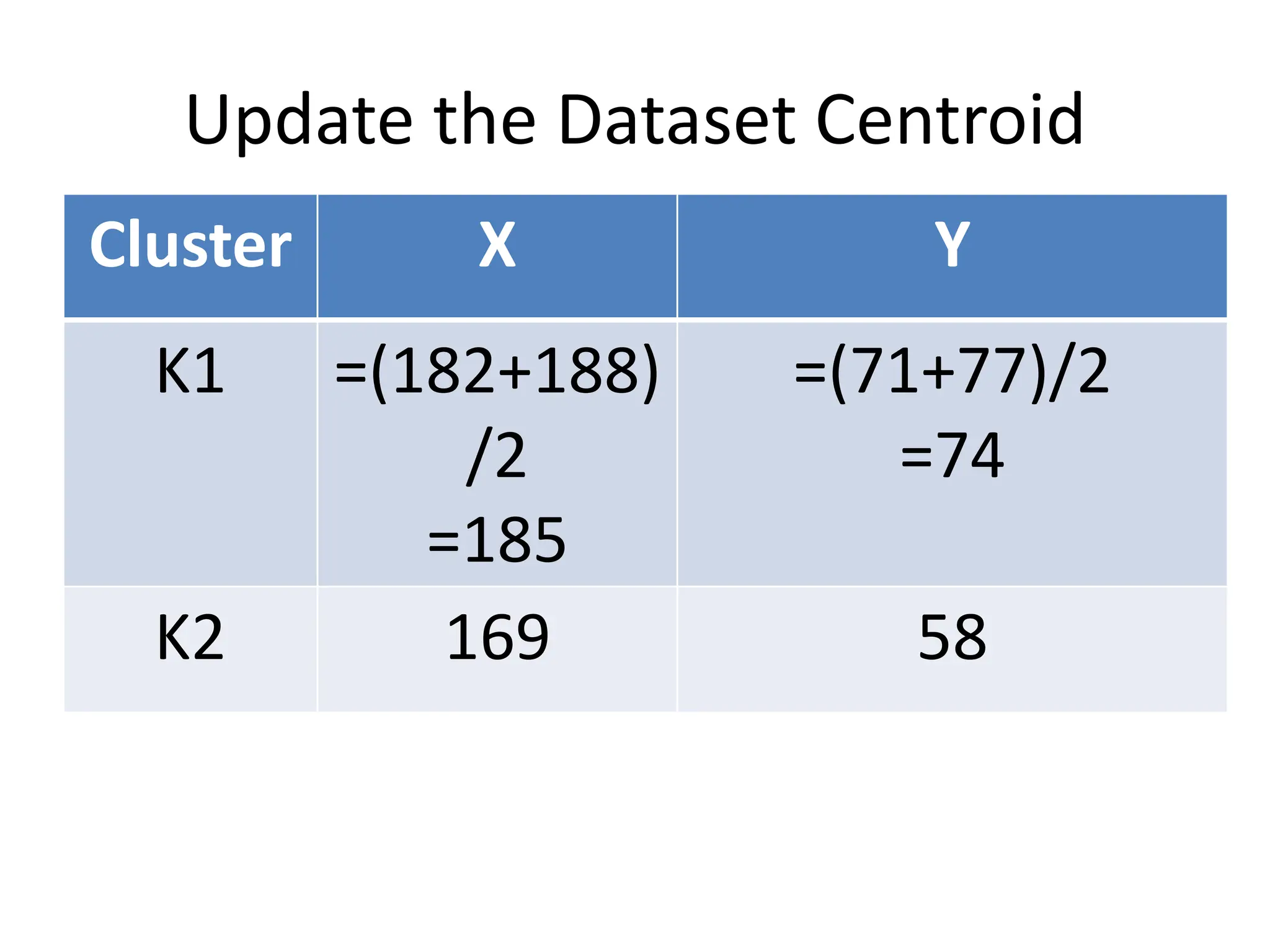
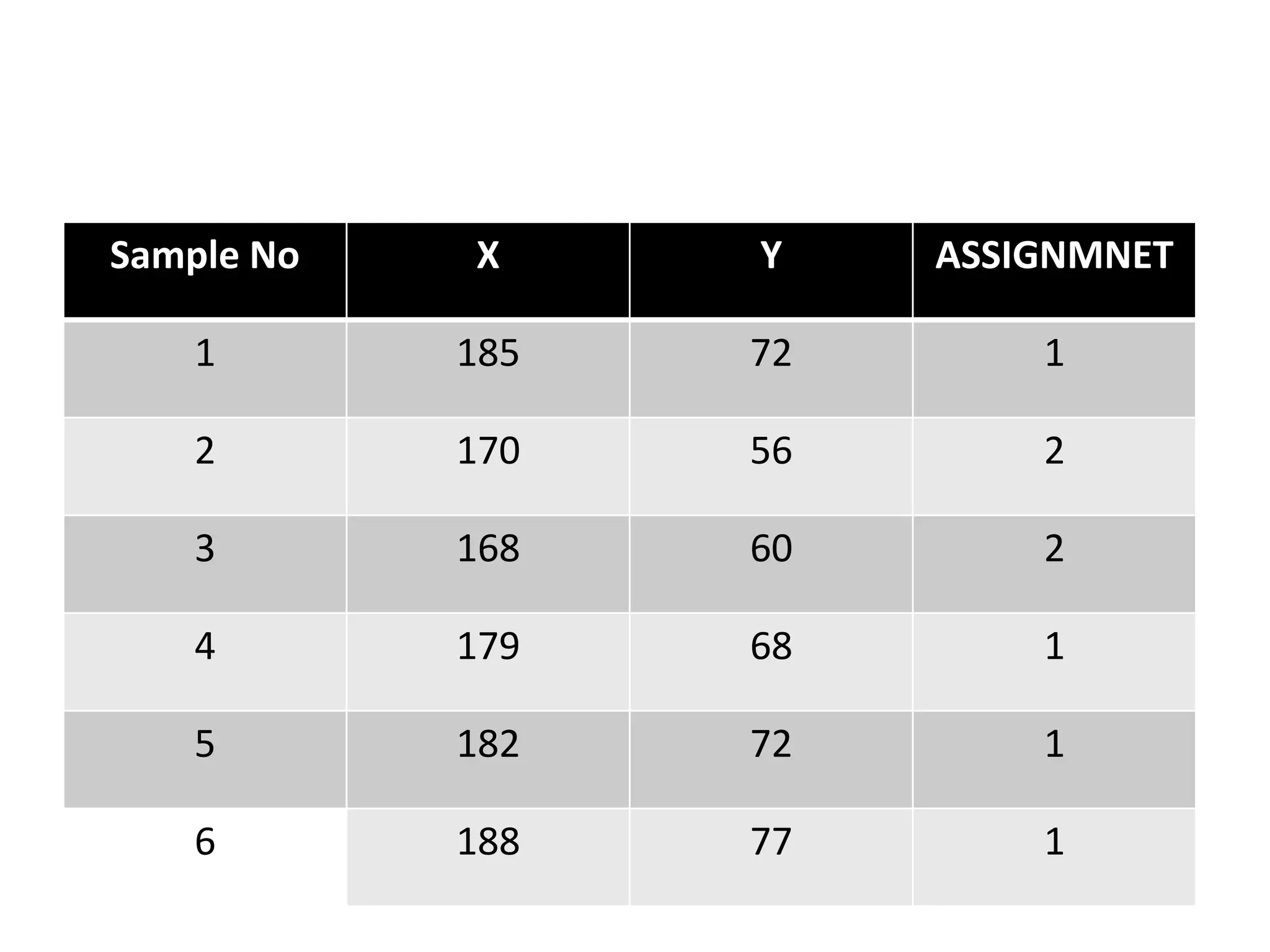
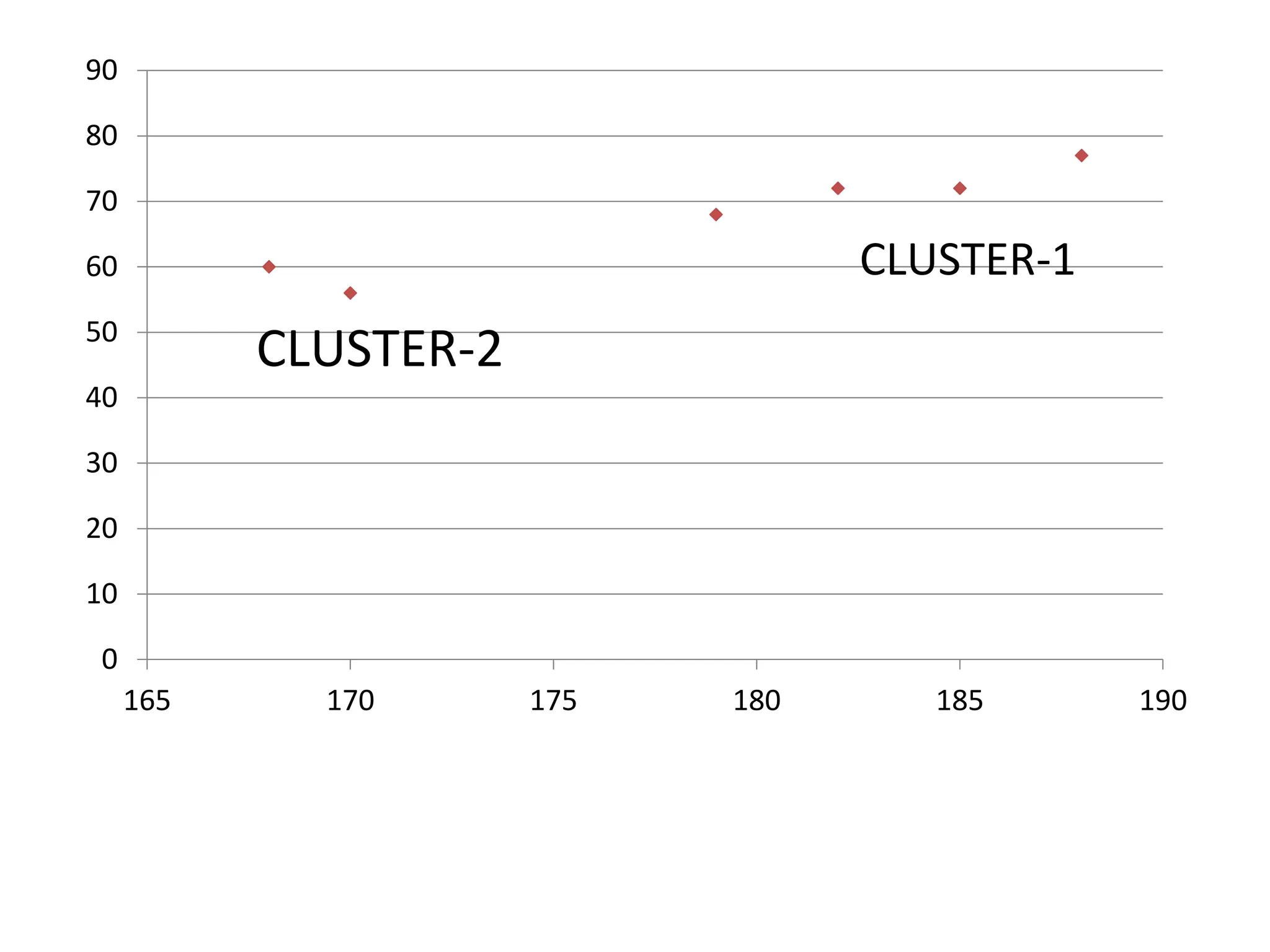
The document explains the k-mean clustering algorithm, a non-hierarchical method for grouping objects based on their minimum Euclidean distance to centroids. It details the process of calculating centroids, assigning data points to clusters, and updating cluster centroids as new distances are calculated. A sample problem is provided to illustrate the step-by-step clustering process with specific data points.

1. K-MEAN CLUSTERING
•Exploratory data analysis techniques
•Implements no hierarchical methods of grouping
object together
•Determines the centroid using the Euclidean
methods for distance calculation
•Groups the object based on minimum distance

2. Start
Input Number of
Cluster
Calculate Centroid
Calculate Distance
Group Based on minimum Distance

3. EXAMPLE PROBLEM
Sample No X Y
1 185 72
2 170 56
3 168 60
4 179 68
5 182 72
6 188 77

4. GIVE K=2
CLUSTER X Y
K1 185 72
K2 170 56

5. Calculate Euclidean distance using the
given Equitation
CLUSTER X Y
K1 185 72
K2 170 56

6. =21.93

7. Cluster
Centroid
X Y ASSIGNMNET
K1 0 21.93 1
K2 21.93 0 2

8. Calculate Euclidean distance for the
next distance(168,60)
=20.808

9. Calculate Euclidean distance for the
next distance(168,60)
=4.472

10. Distance
Euclidean Distance
Cluster-1 Cluster-2 ASSIGNMNET
(168,60) 20.808 4.472 2

11. Update the Dataset Centroid
Clust
er
X Y
K1 185 72
K2 =(170+168)/2
=169
=(60+56)/2
=58

12. Calculate Euclidean distance for the
next distance(179,68)
=7.211103

13. Calculate Euclidean distance for the
next distance(179,68)
=14.14214

14. Distance
Euclidean Distance
Cluster-1 Cluster-2 ASSIGNMNET
(179,68) 7.211103 14.14214 1

15. Update the Dataset Centroid
Cluster X Y
K1 =(185+179)
/2
=182
=(72+68)/2
=70
K2 169 58

16. Calculate Euclidean distance for the
next distance(182,68)
=2

17. Calculate Euclidean distance for the
next distance(182,68)
=19.10

18. Distance
Euclidean Distance
Cluster-1 Cluster-2 ASSIGNMNET
(182,72) 2 19.10 1

19. Update the Dataset Centroid
Cluster X Y
K1 =(182+182)
/2
=182
=(70+72)/2
=71
K2 169 58

20. Calculate Euclidean distance for the
next distance(188,77)
=8.4852

21. Calculate Euclidean distance for the
next distance(188,77)
=26.87

22. Update the Dataset Centroid
Cluster X Y
K1 =(182+188)
/2
=185
=(71+77)/2
=74
K2 169 58

23. Sample No X Y ASSIGNMNET
1 185 72 1
2 170 56 2
3 168 60 2
4 179 68 1
5 182 72 1
6 188 77 1

24. 0
10
20
30
40
50
60
70
80
90
165 170 175 180 185 190
CLUSTER-2
CLUSTER-1