Download as PDF, PPTX
![Hyperbolic geometry emerges from Newtonian model
and similarity × popularity optimization in growing network
S1
p(κ) ∝ κ−γ
r = 1
1+
[
d(θ,θ′)
µκκ′
]1/T
PRL 100, 078701](https://image.slidesharecdn.com/dpgmultiplex-160713210306/75/Hidden-geometric-correlations-in-real-multiplex-networks-9-2048.jpg)
![Hyperbolic geometry emerges from Newtonian model
and similarity × popularity optimization in growing network
S1 H2
p(κ) ∝ κ−γ ri = R − 2 ln κi
κmin
r = 1
1+
[
d(θ,θ′)
µκκ′
]1/T p(xij) = 1
1+e
xij−R
2T
PRL 100, 078701 PRE 82, 036106](https://image.slidesharecdn.com/dpgmultiplex-160713210306/75/Hidden-geometric-correlations-in-real-multiplex-networks-10-2048.jpg)
![Hyperbolic geometry emerges from Newtonian model
and similarity × popularity optimization in growing network
S1 H2 growing
1
2
3
p(κ) ∝ κ−γ ri = R − 2 ln κi
κmin t = 1, 2, 3 . . .
r = 1
1+
[
d(θ,θ′)
µκκ′
]1/T p(xij) = 1
1+e
xij−R
2T
mins [s × ∆θst]
PRL 100, 078701 PRE 82, 036106 Nature 489, 537–540](https://image.slidesharecdn.com/dpgmultiplex-160713210306/75/Hidden-geometric-correlations-in-real-multiplex-networks-11-2048.jpg)
![Geometric multiplex model allows to tune
correlations independently from layer topologies
Constituent layer
topologies by
hyperbolic model
Radial correlations
controlled by
ν ∈ [0, 1]](https://image.slidesharecdn.com/dpgmultiplex-160713210306/75/Hidden-geometric-correlations-in-real-multiplex-networks-40-2048.jpg)
![Geometric multiplex model allows to tune
correlations independently from layer topologies
Constituent layer
topologies by
hyperbolic model
Radial correlations
controlled by
ν ∈ [0, 1]
Angular corr.
controlled by
g ∈ [0, 1]](https://image.slidesharecdn.com/dpgmultiplex-160713210306/75/Hidden-geometric-correlations-in-real-multiplex-networks-41-2048.jpg)
Uploaded byKolja Kleineberg
Hidden geometric correlations in real multiplex networks
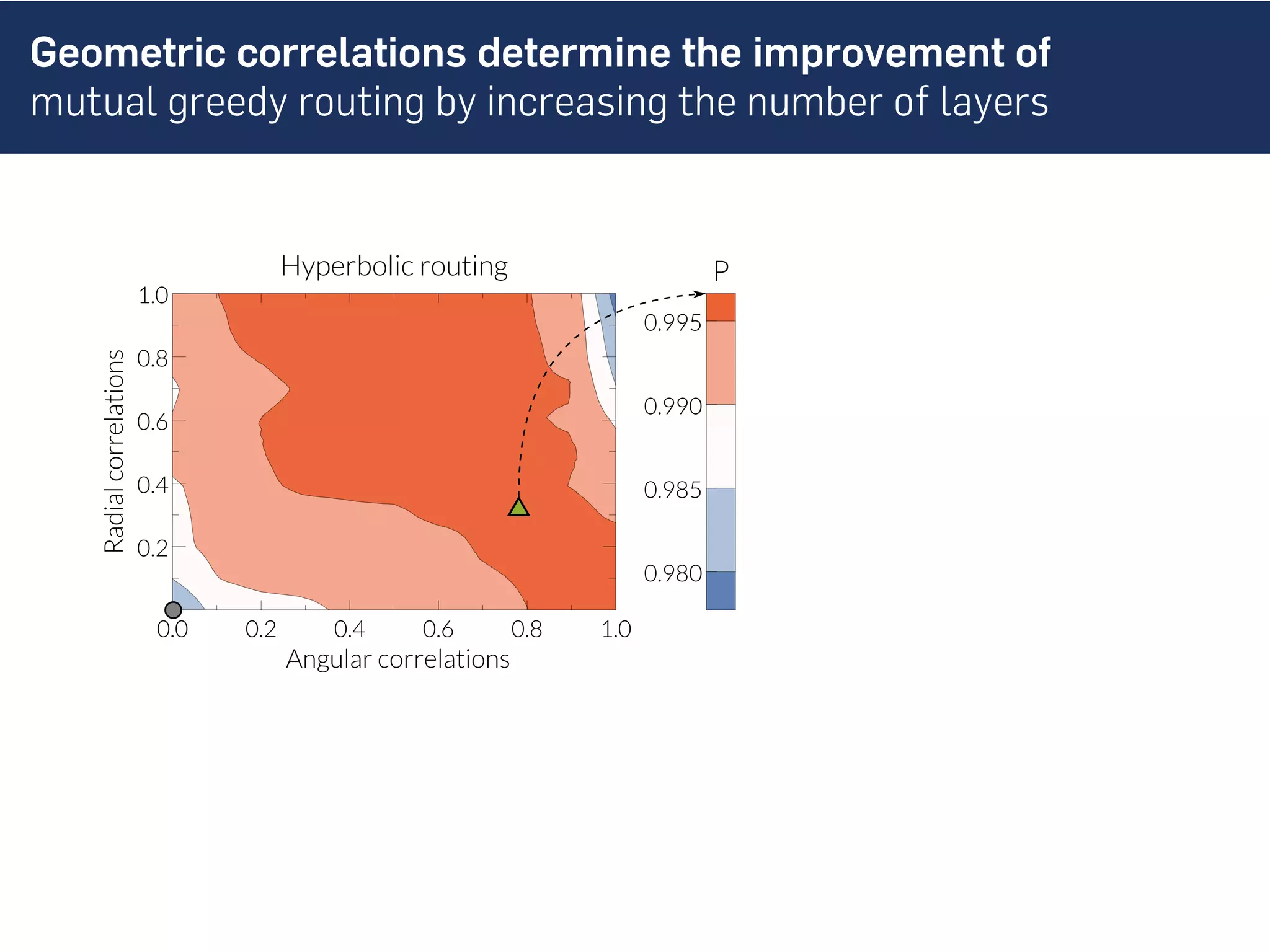
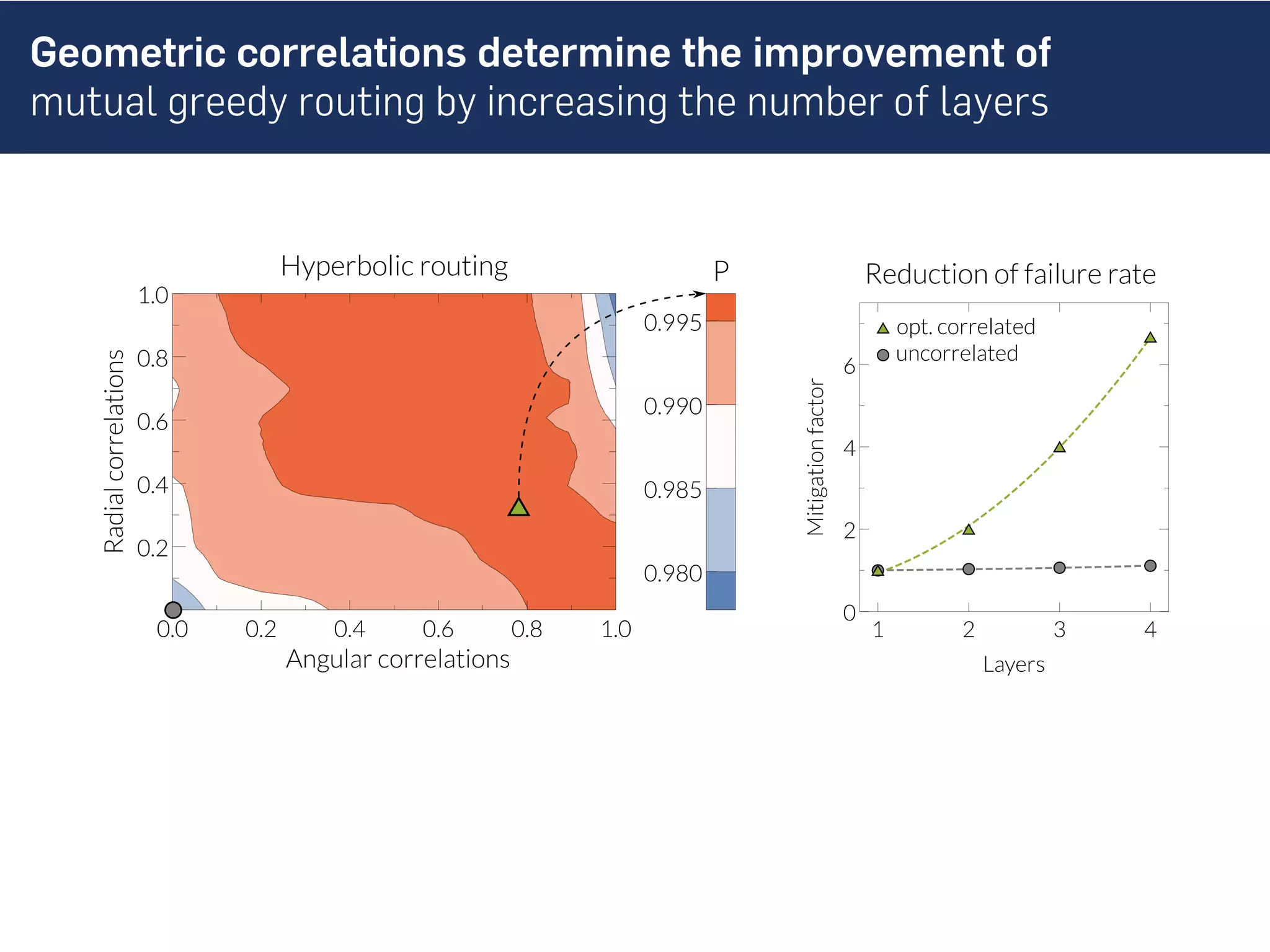
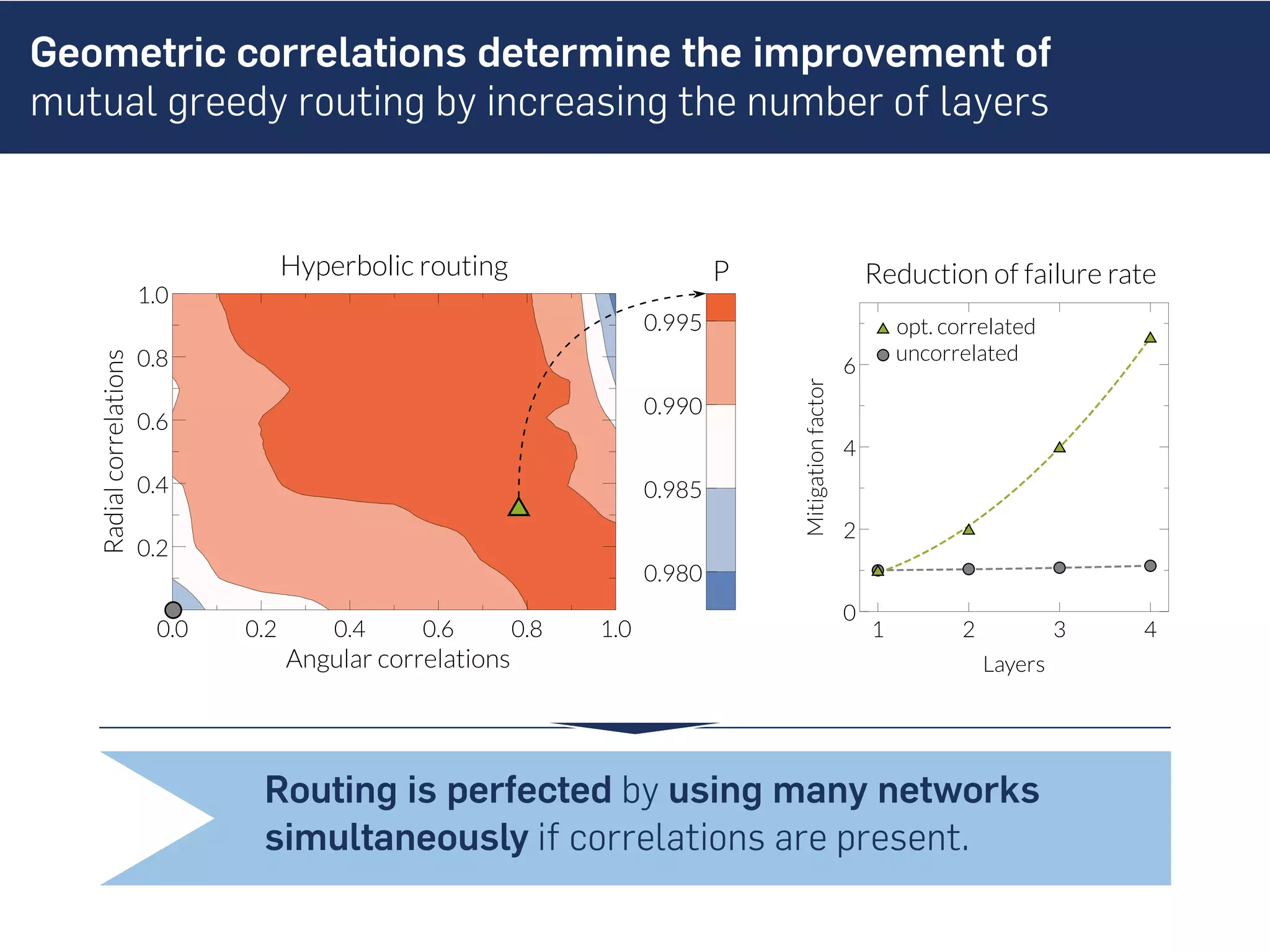
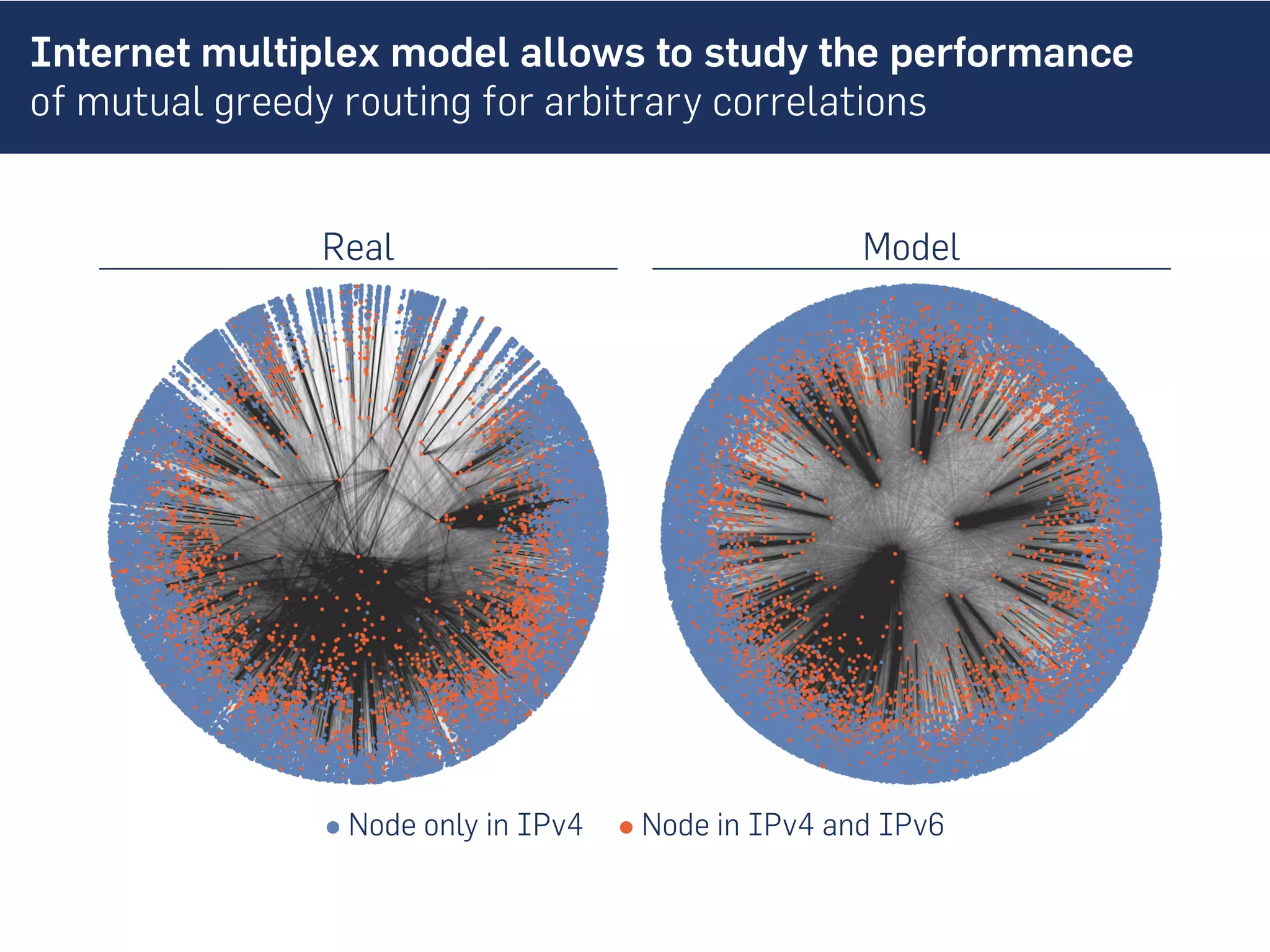
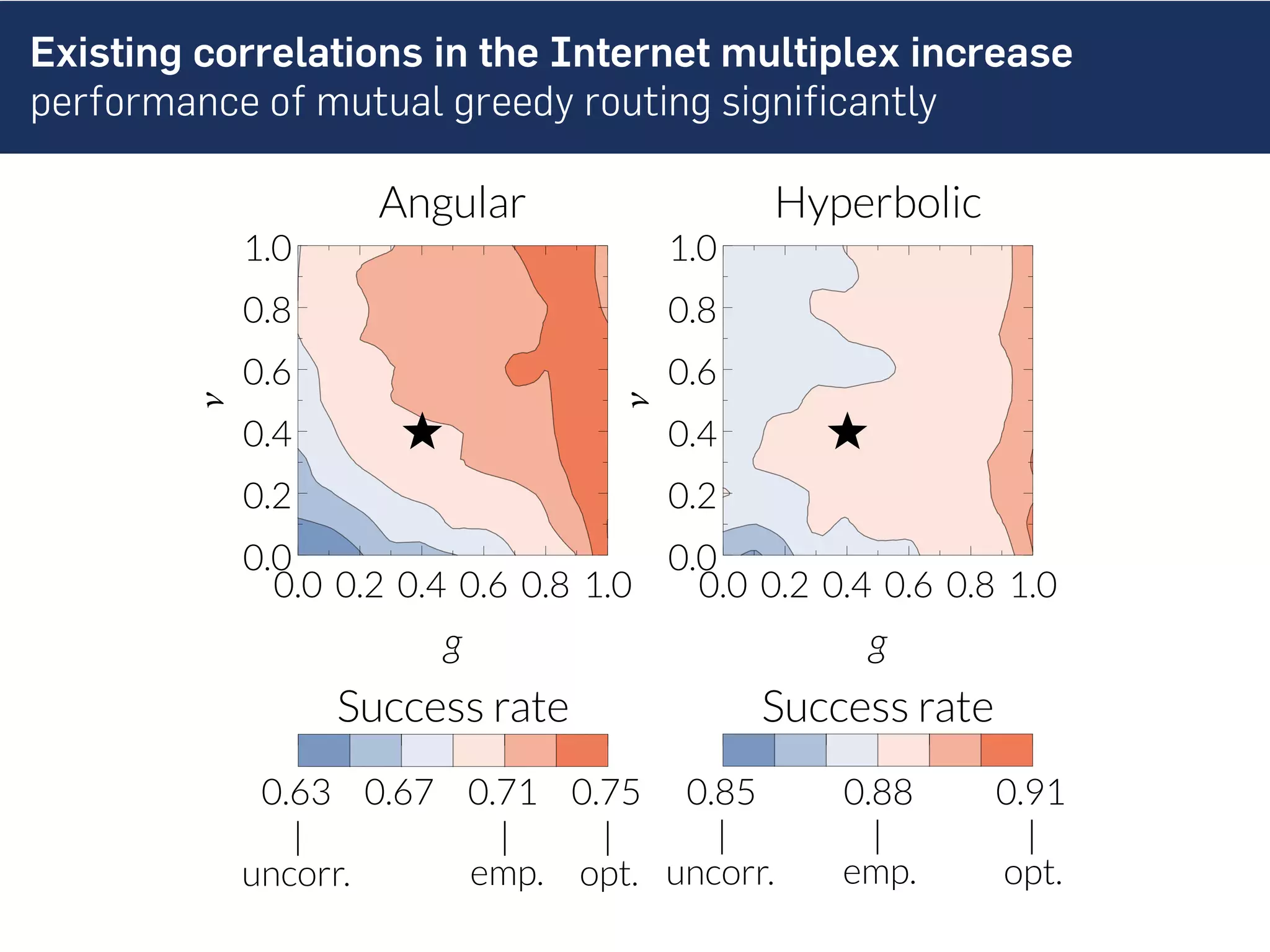
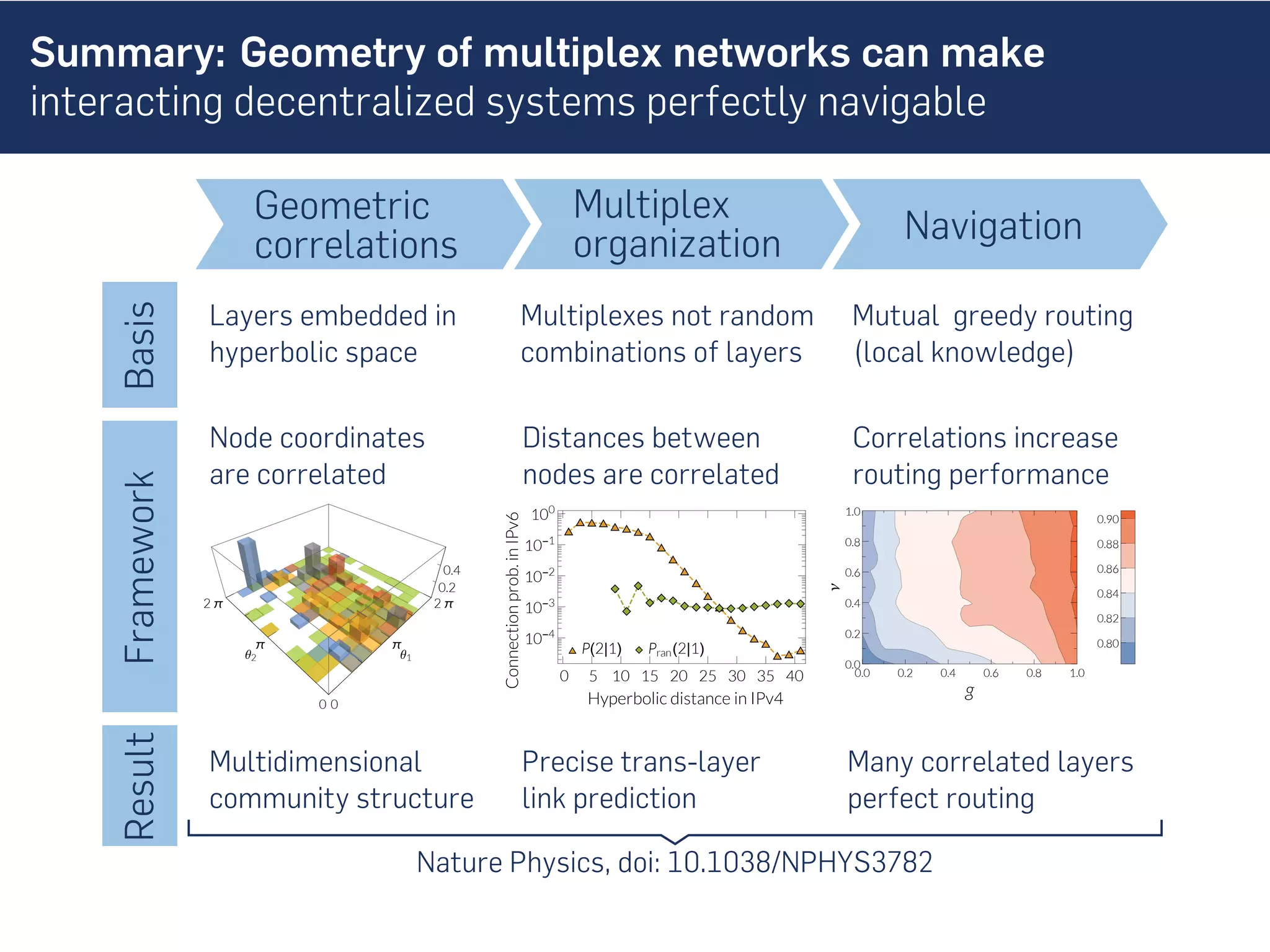
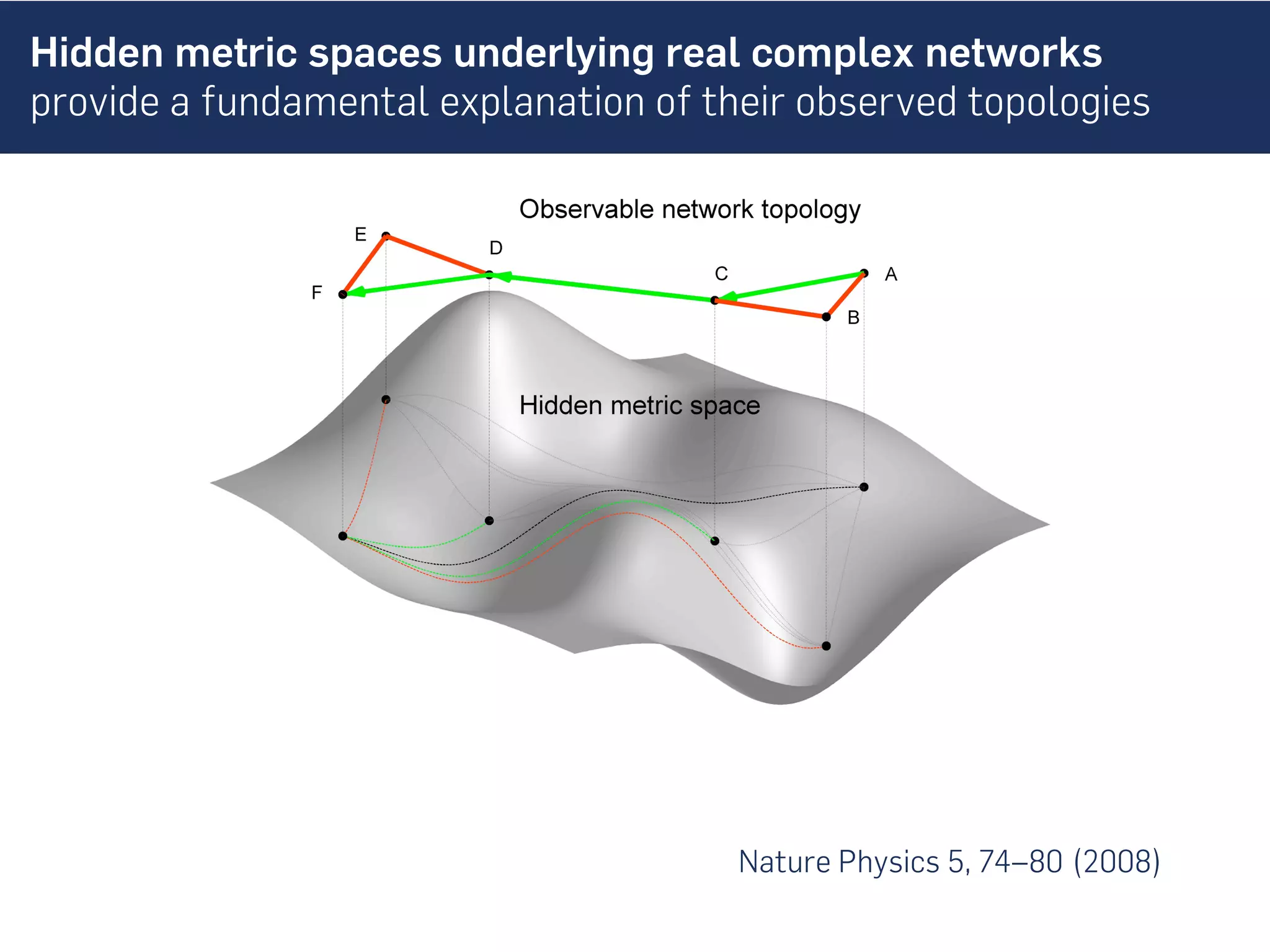
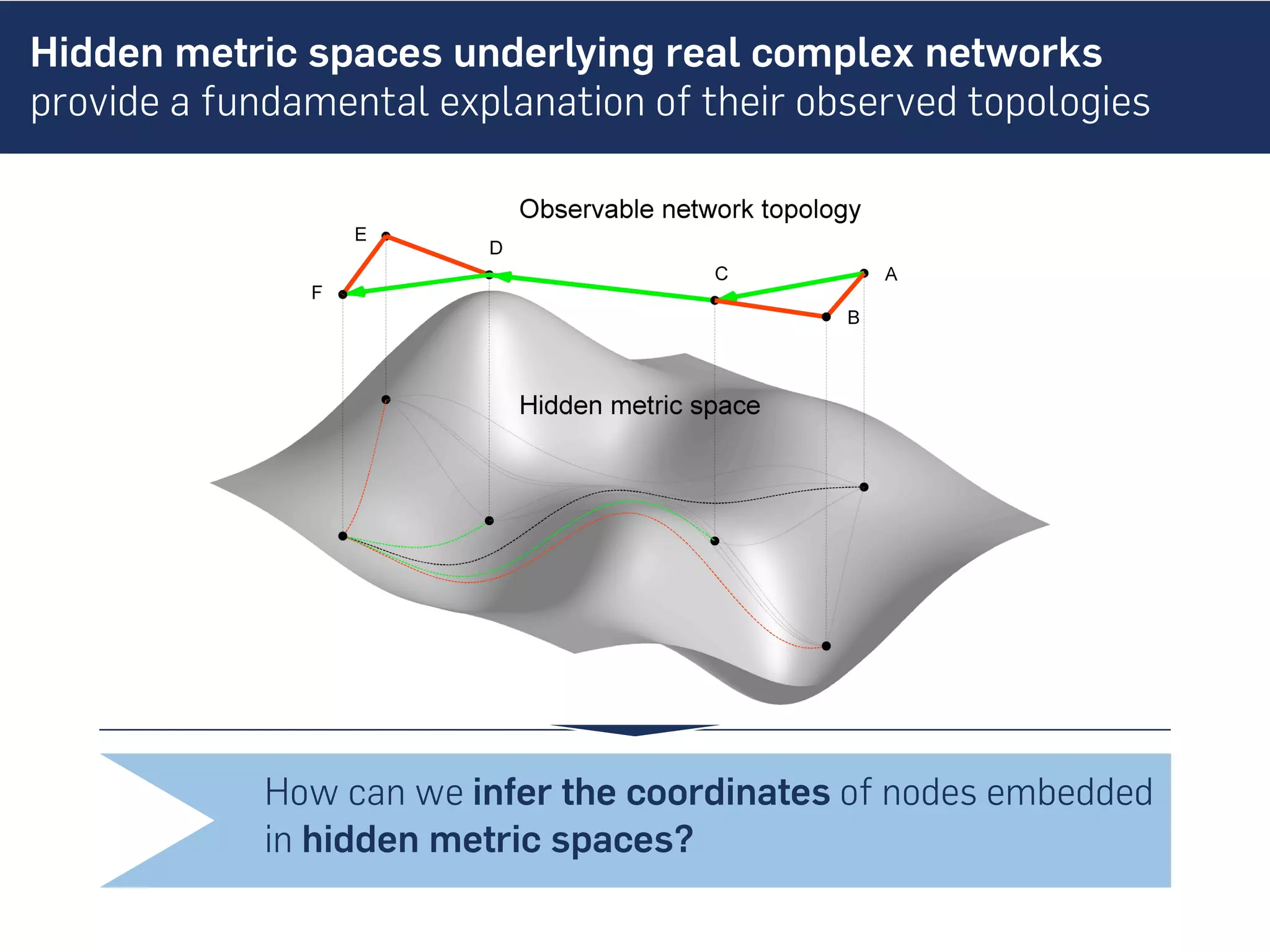
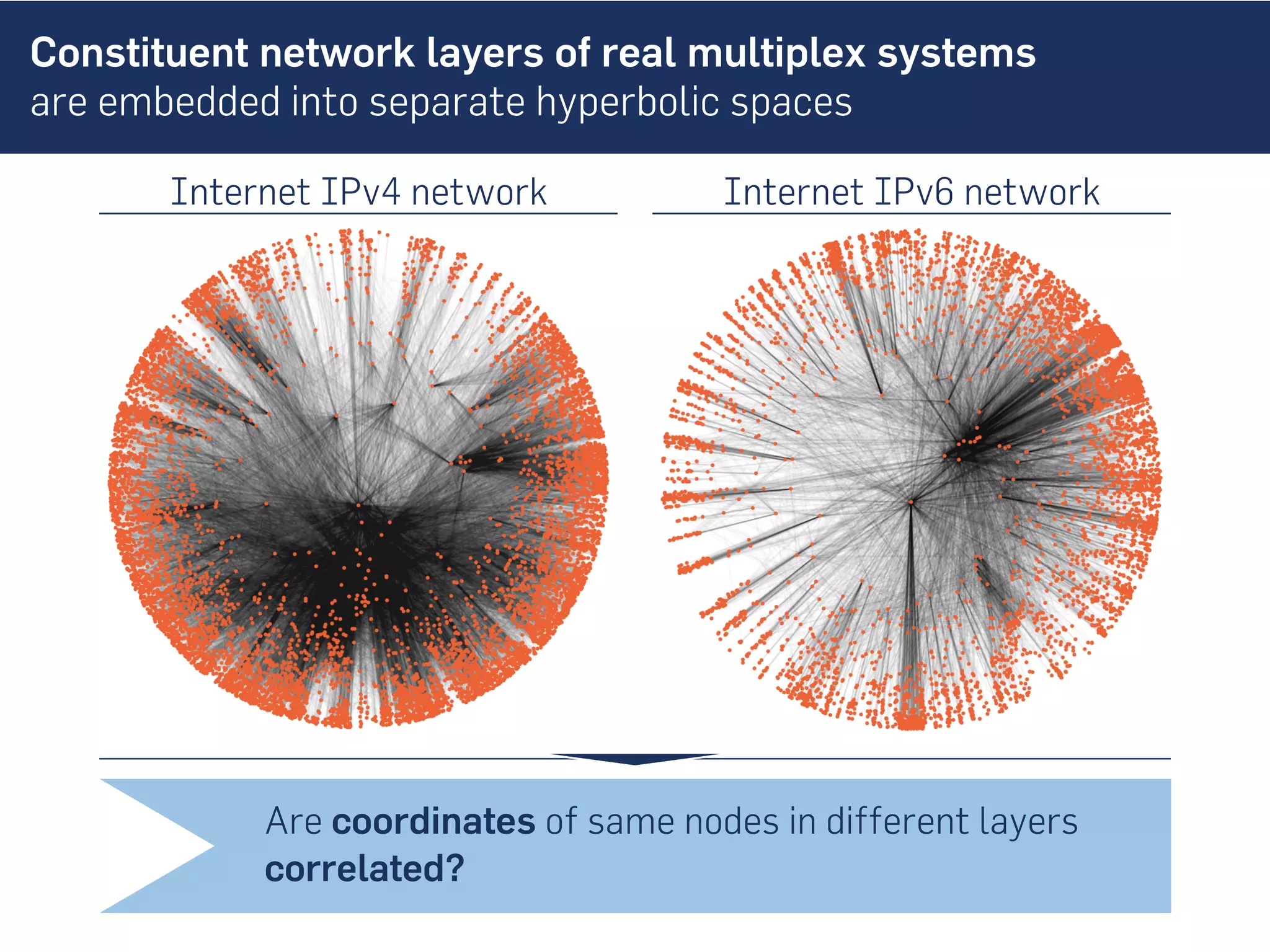
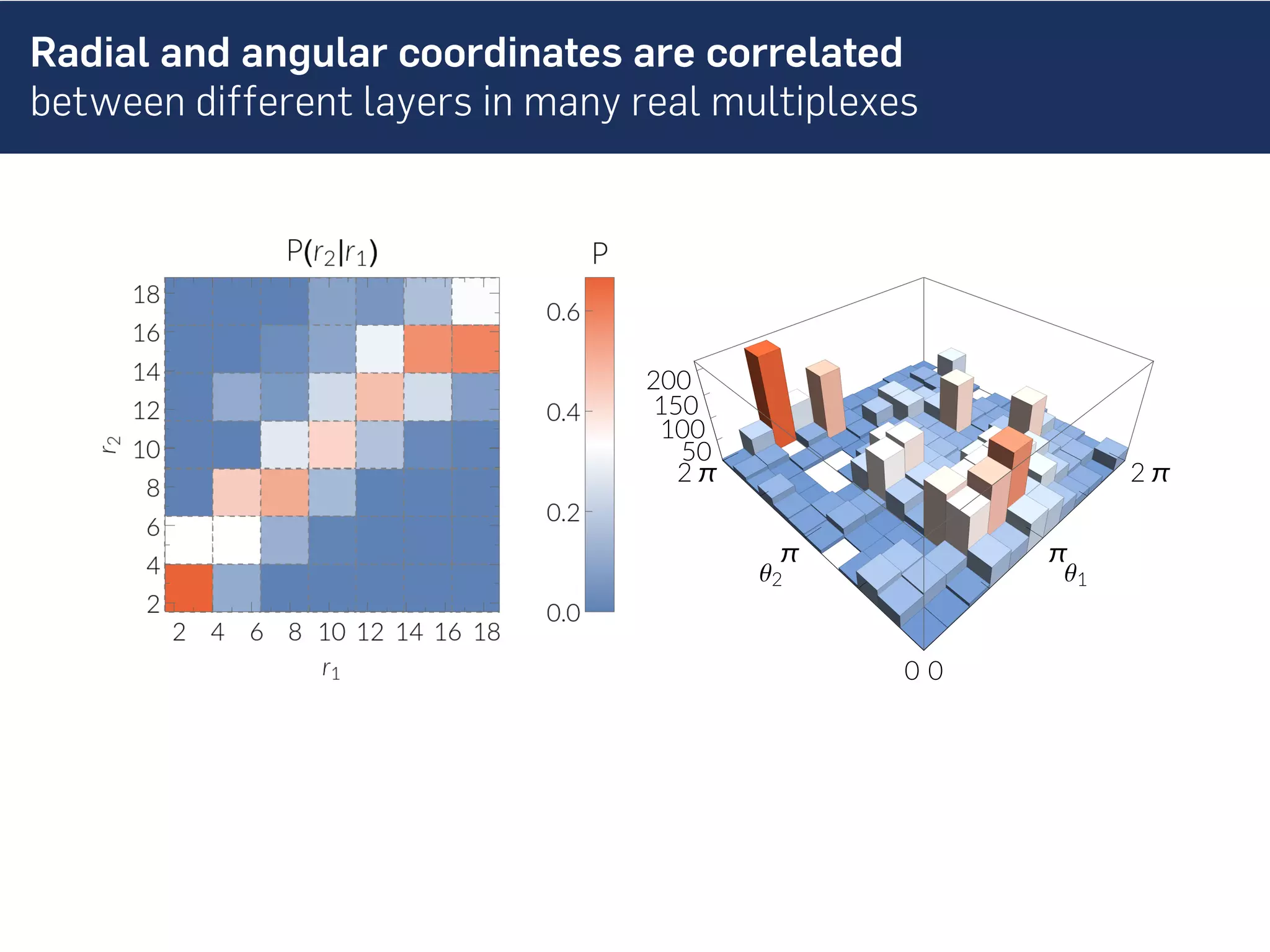
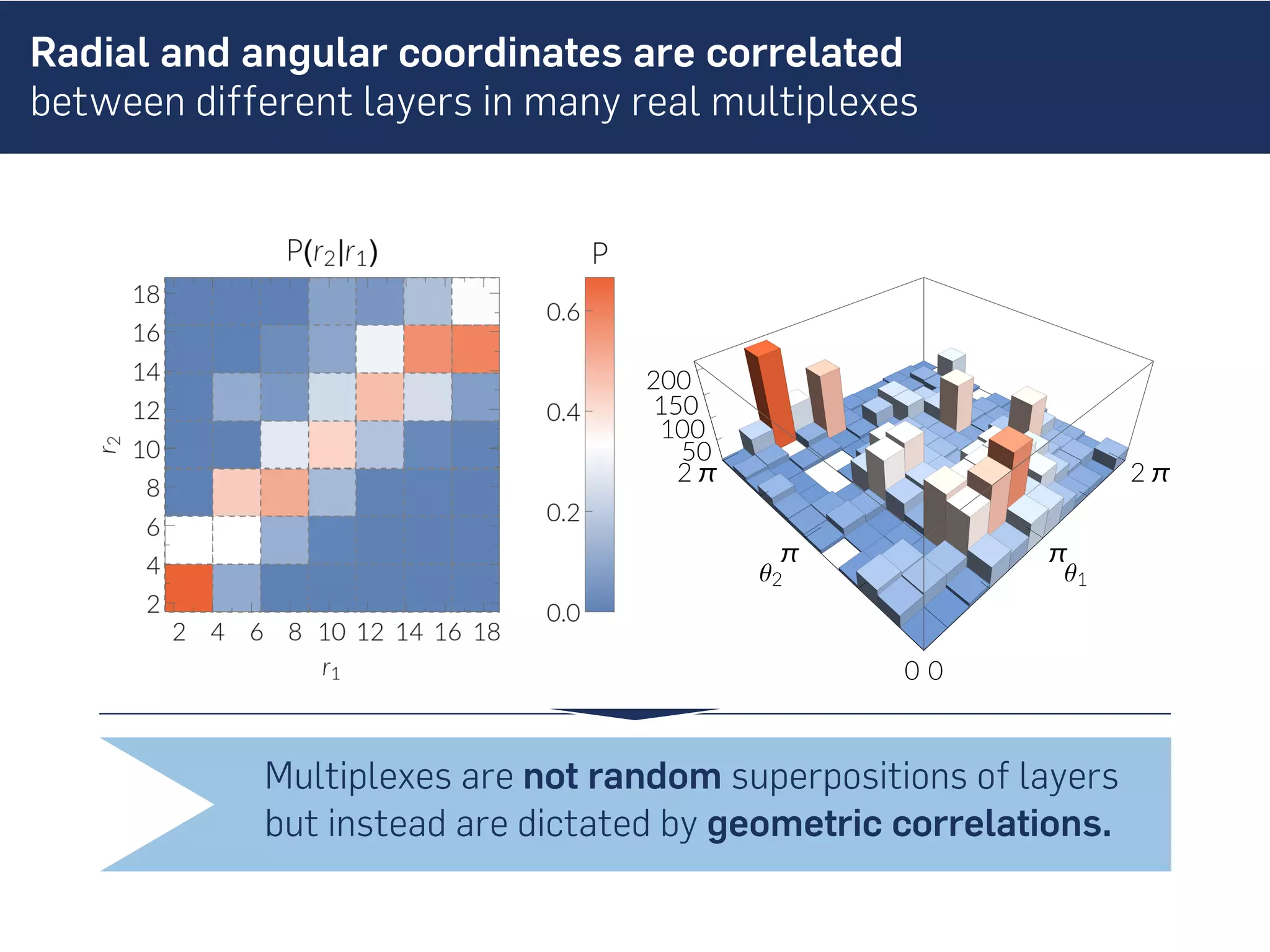
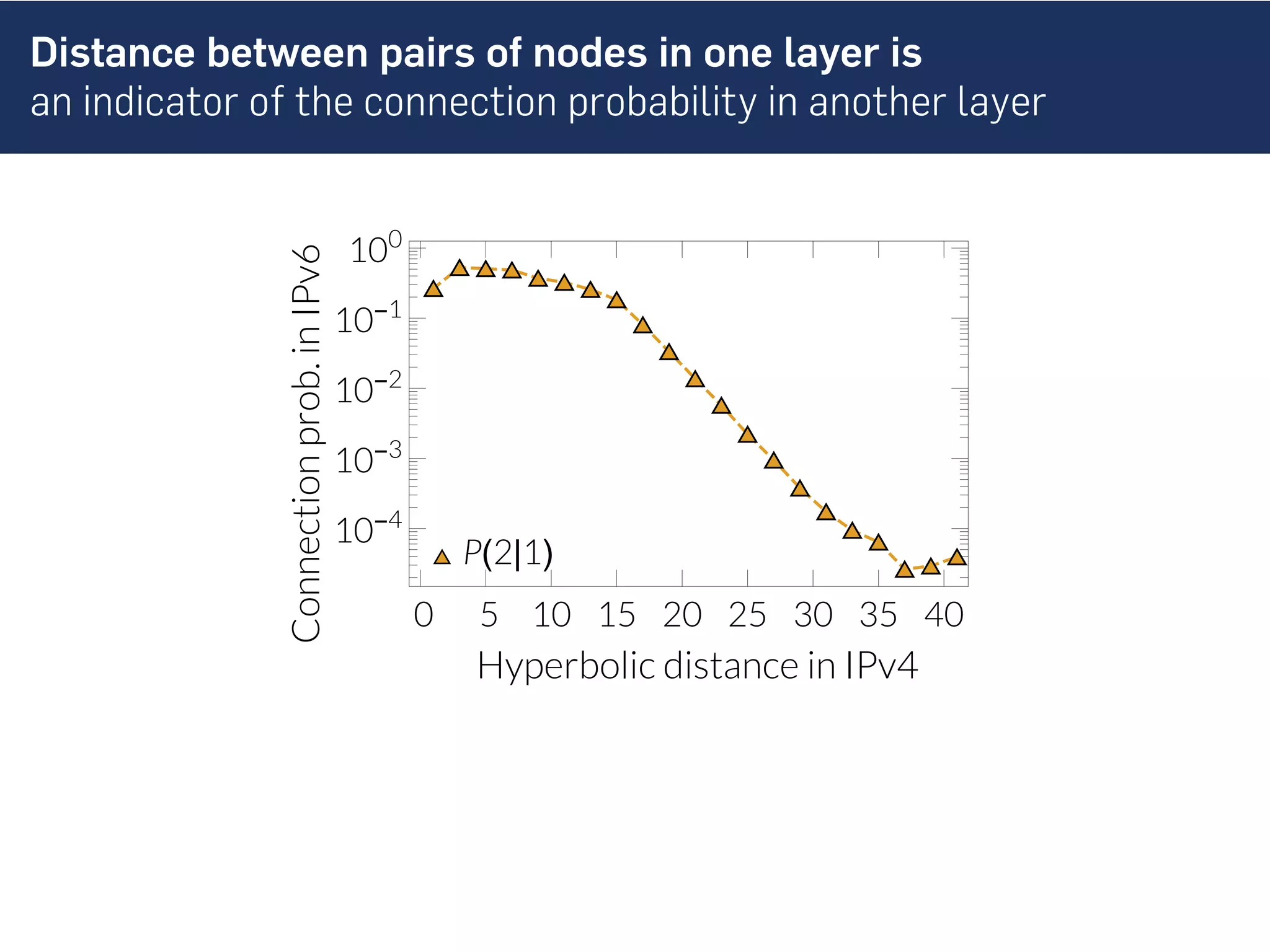
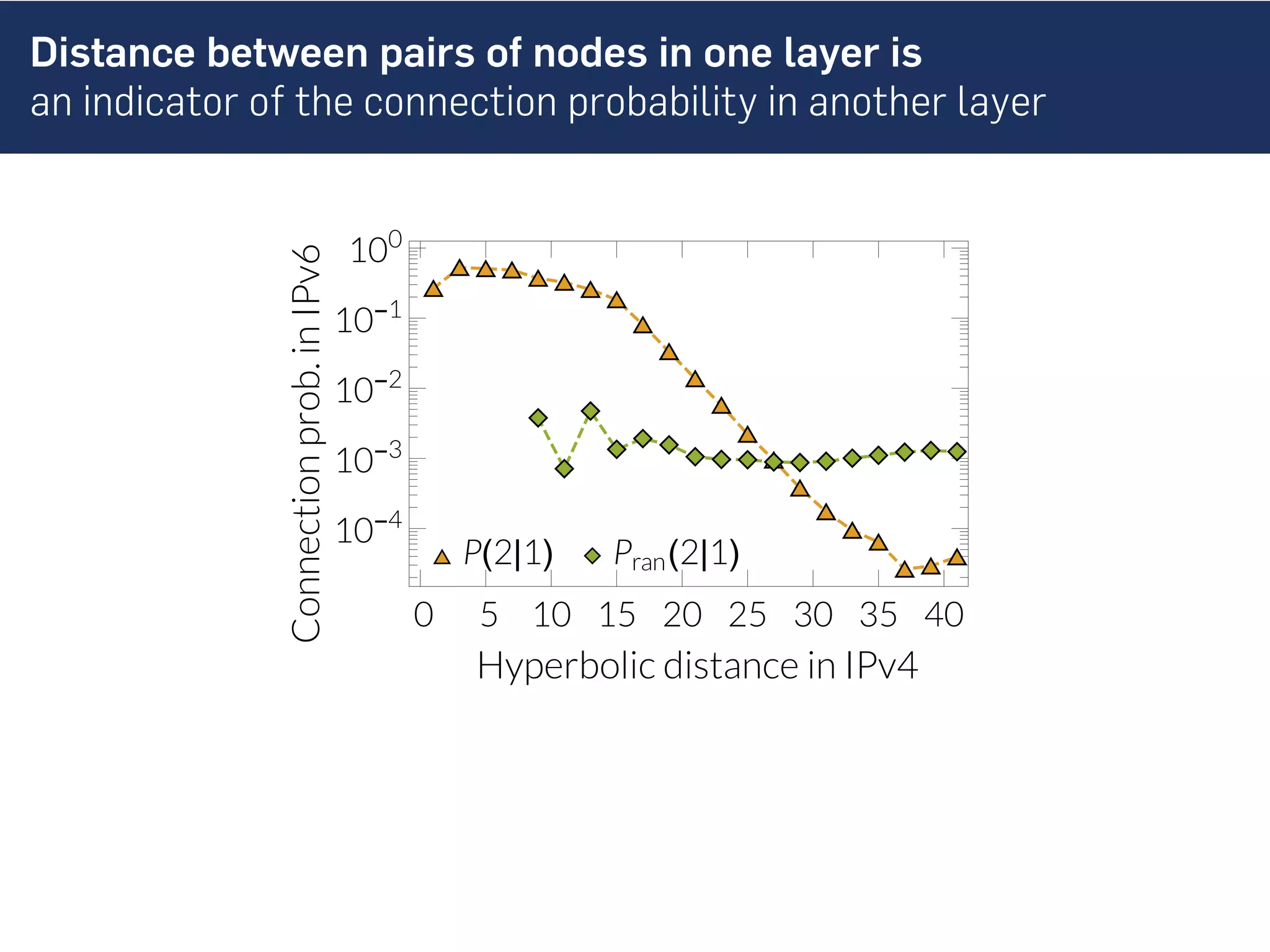
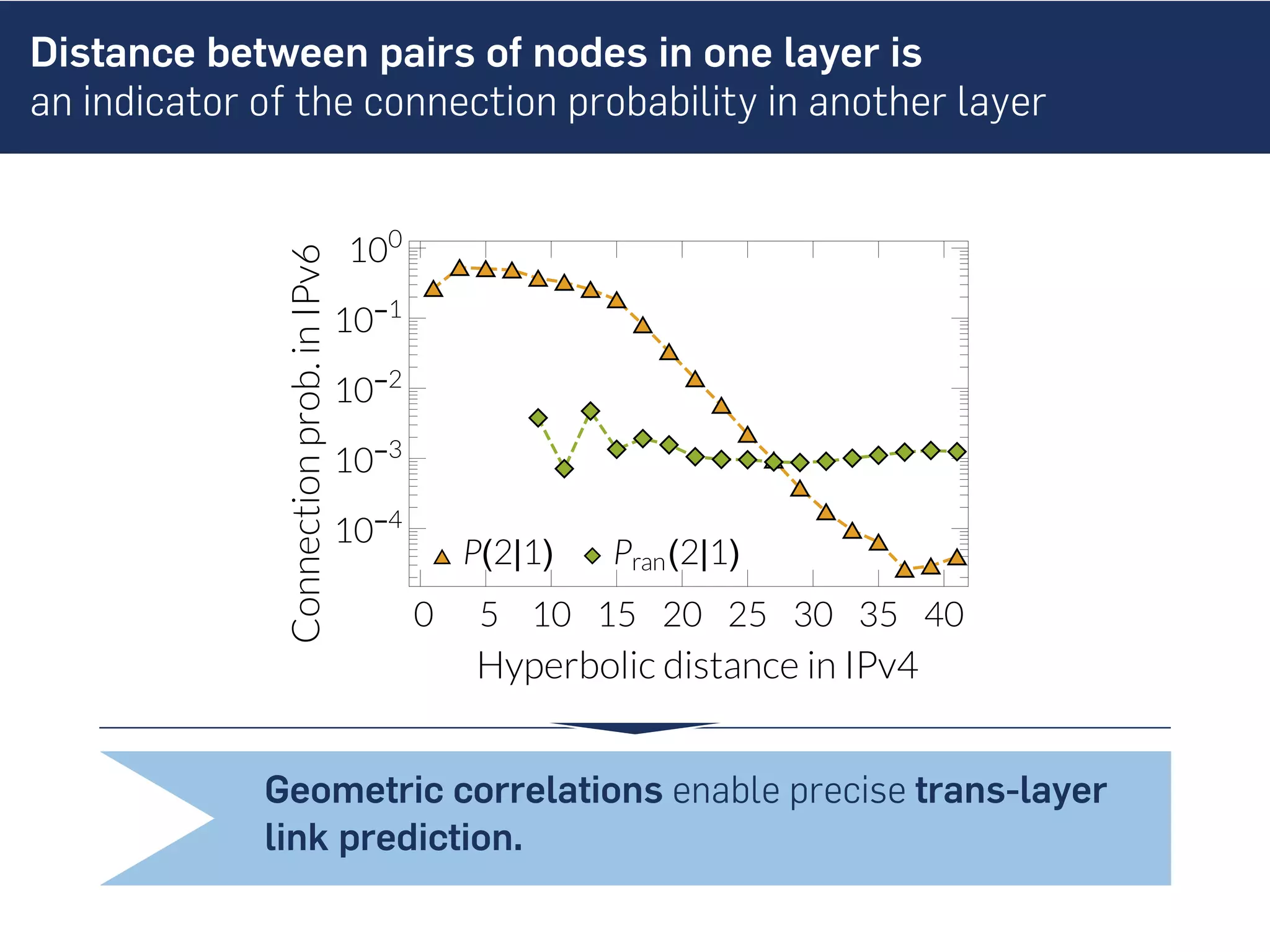
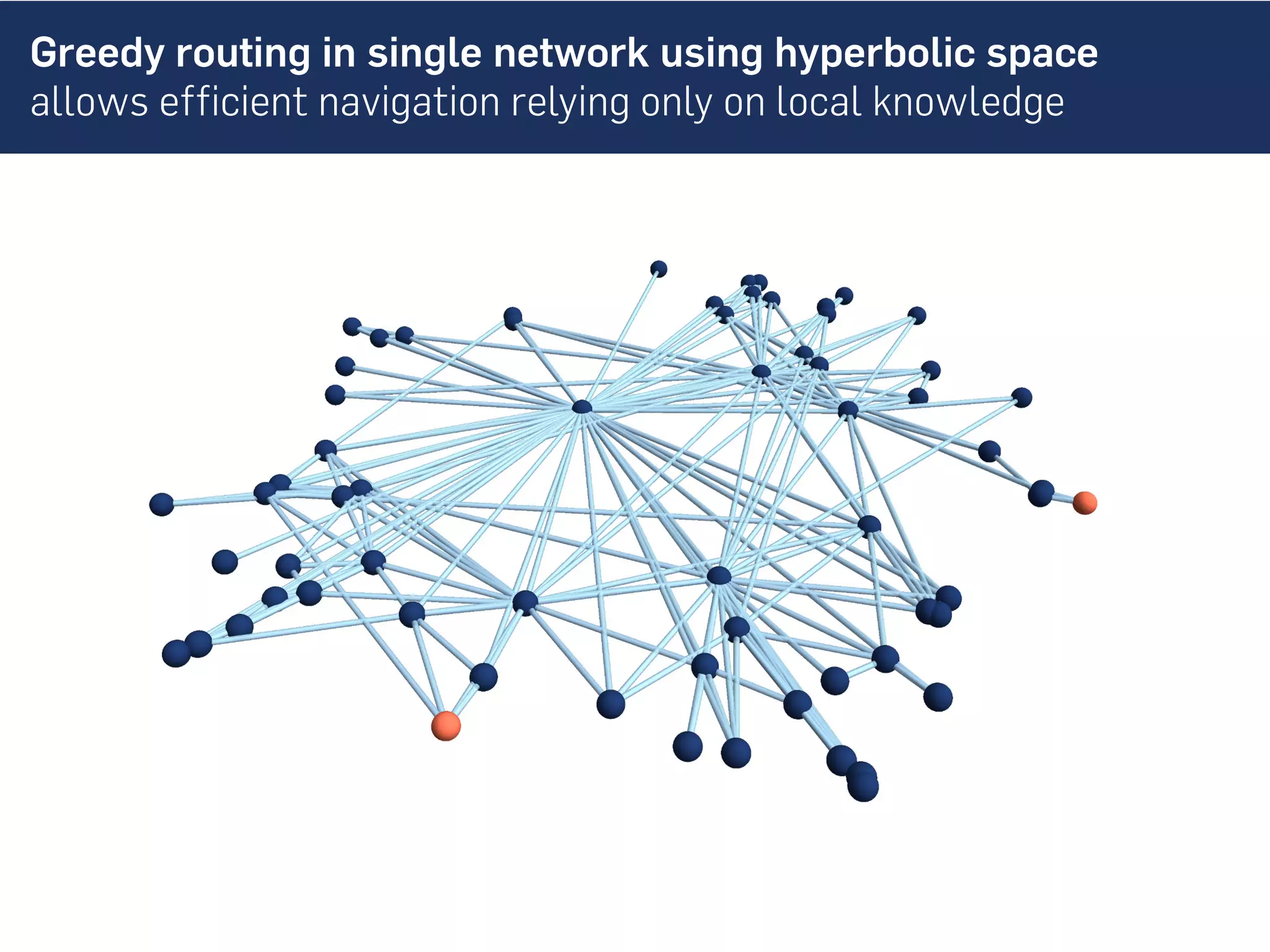
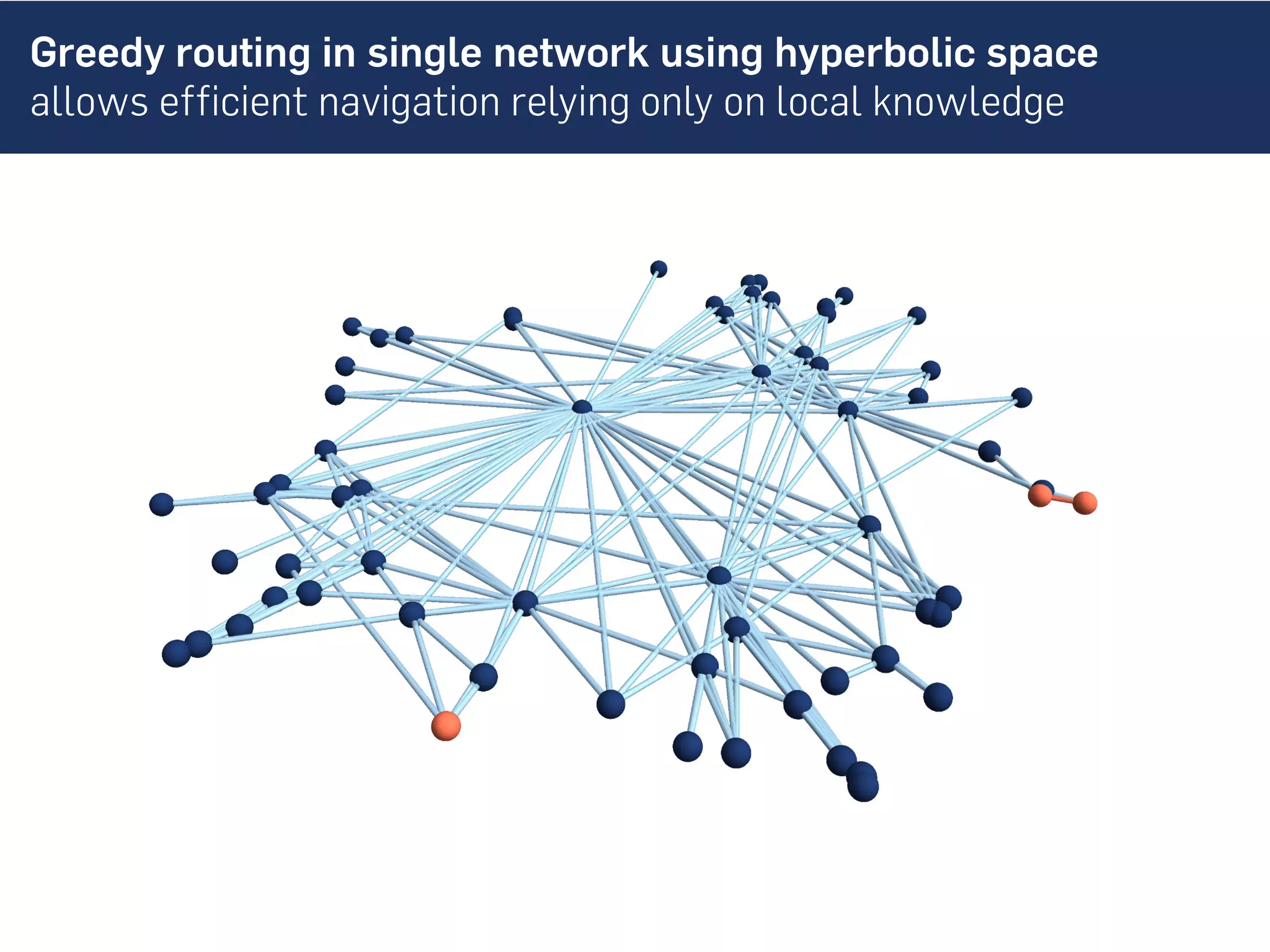
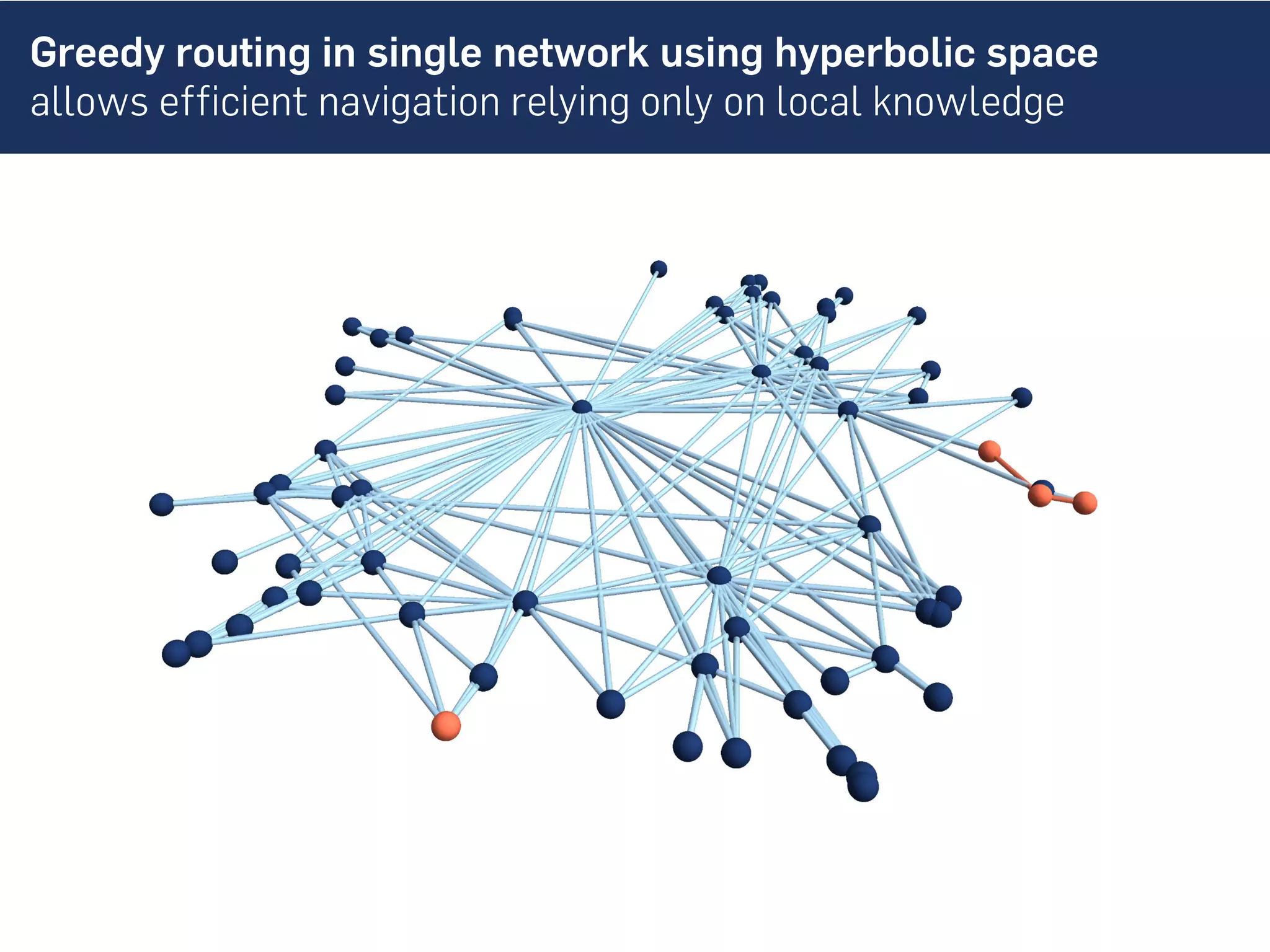
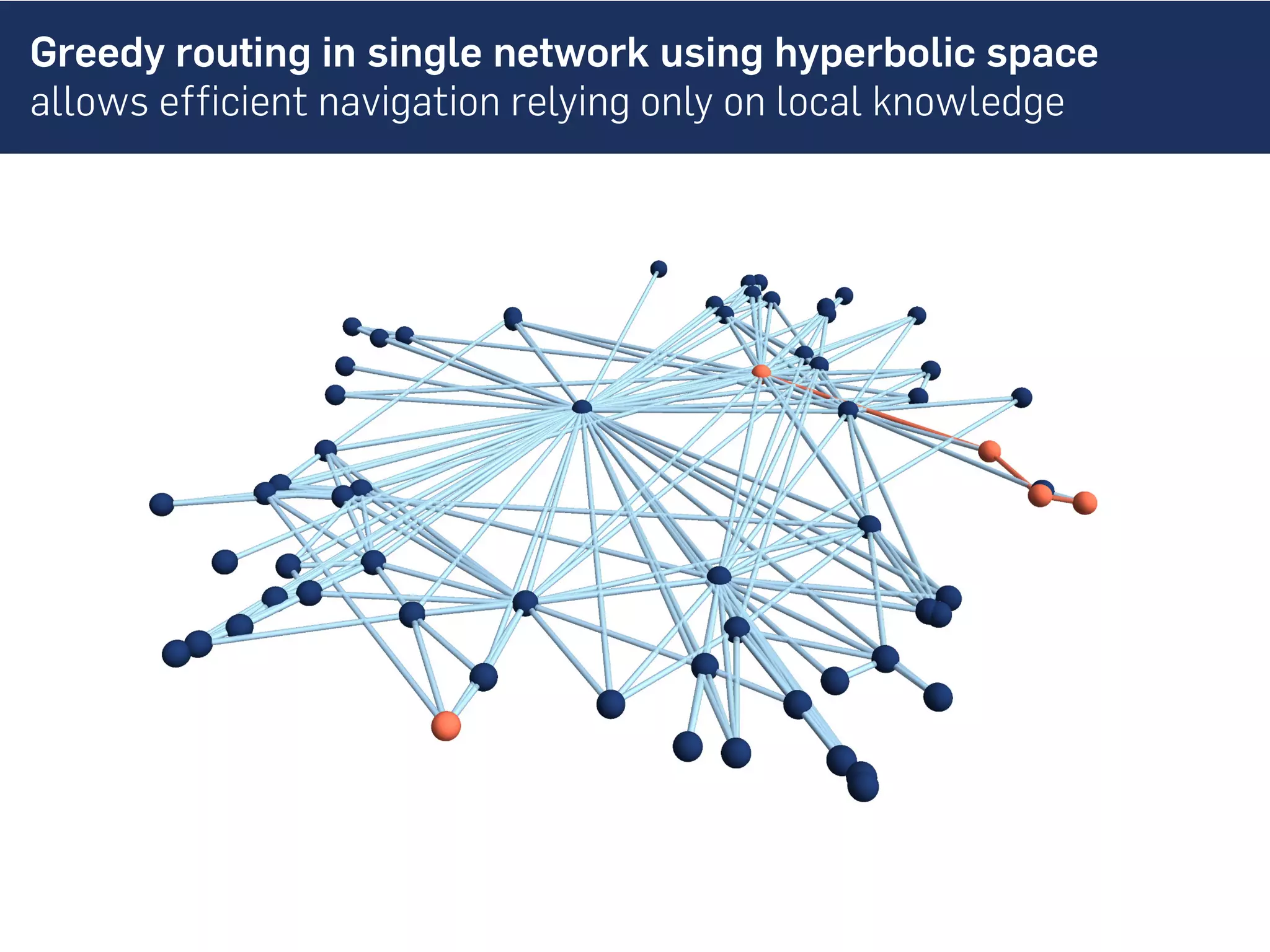
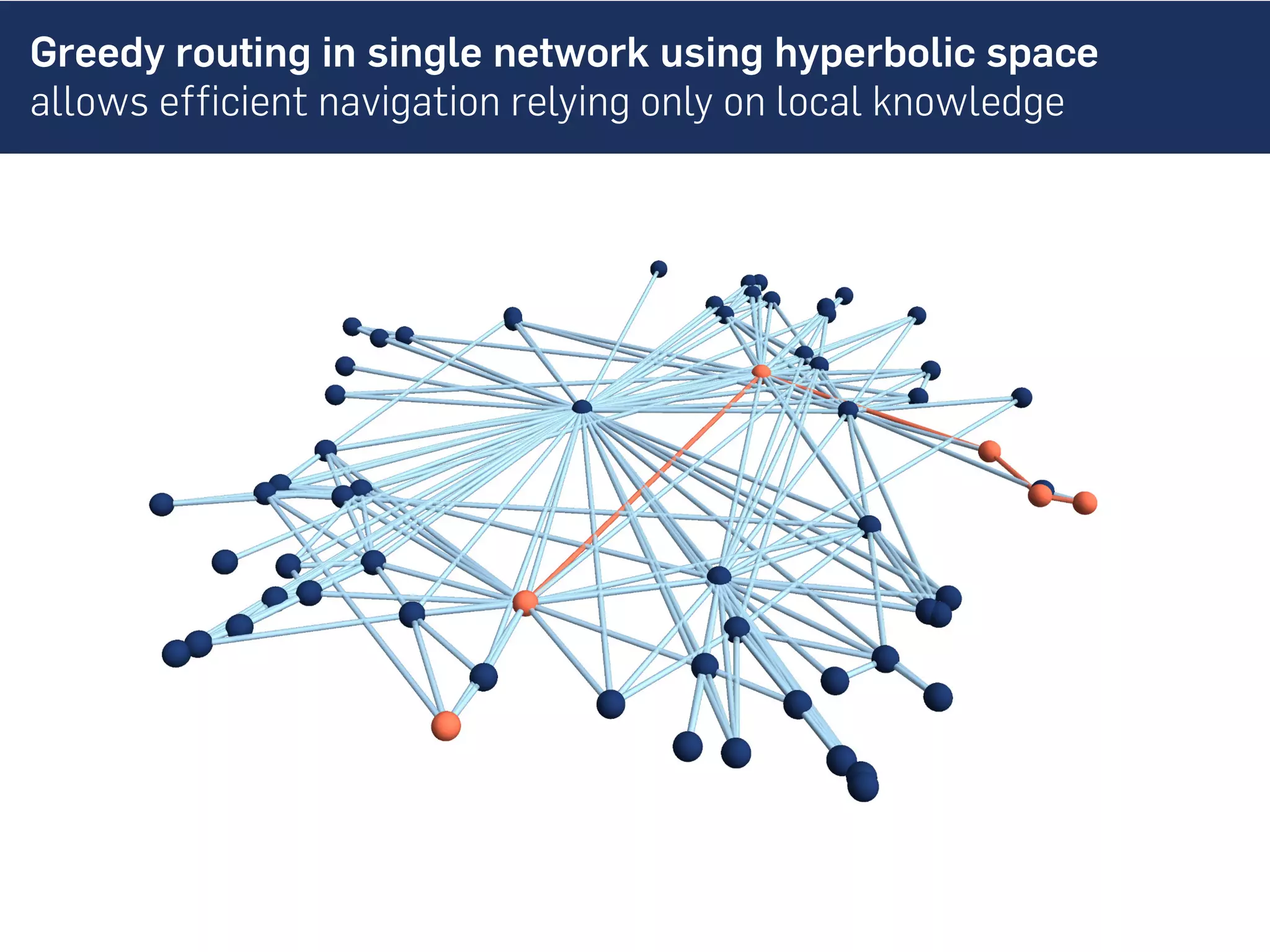
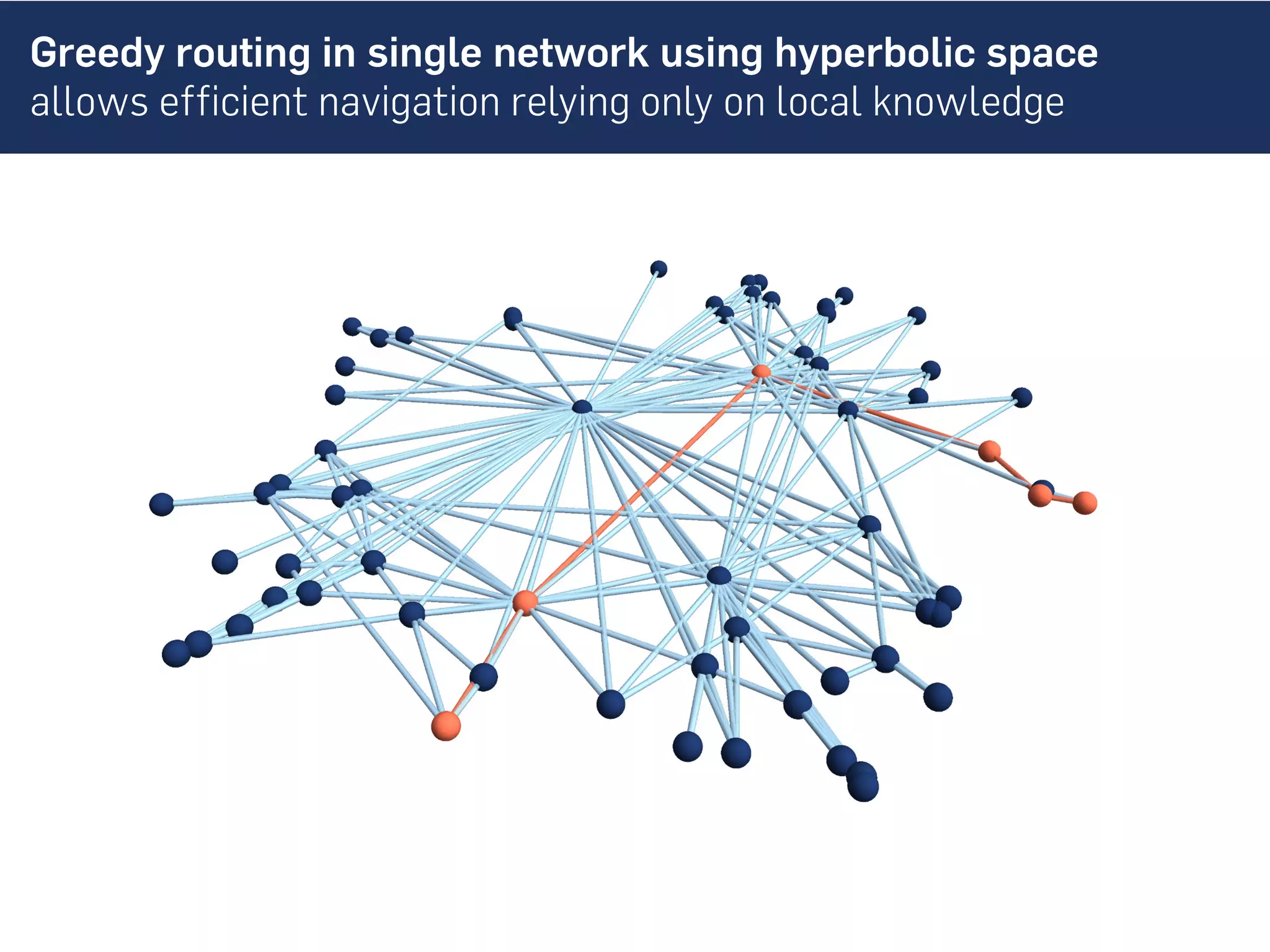
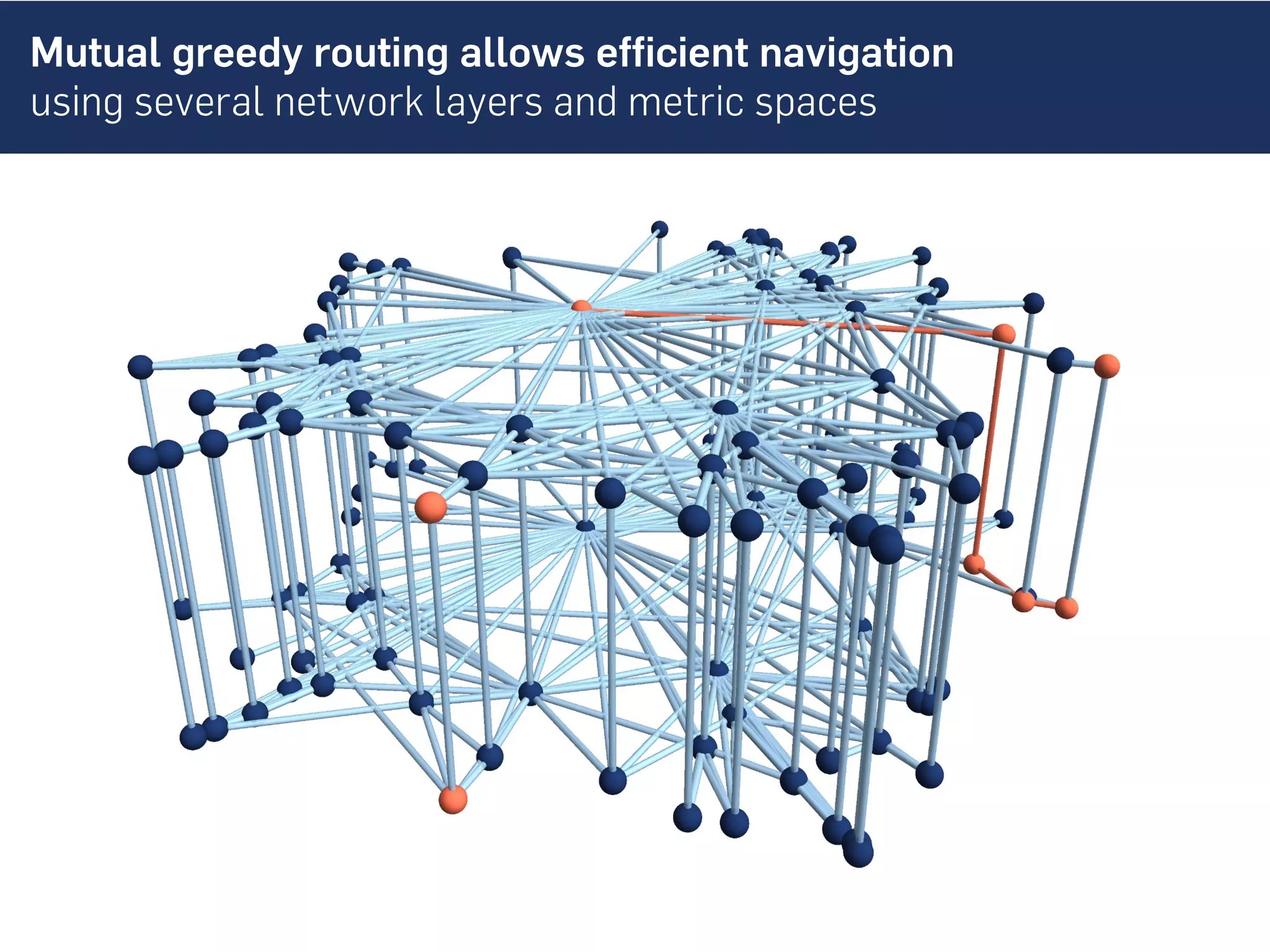
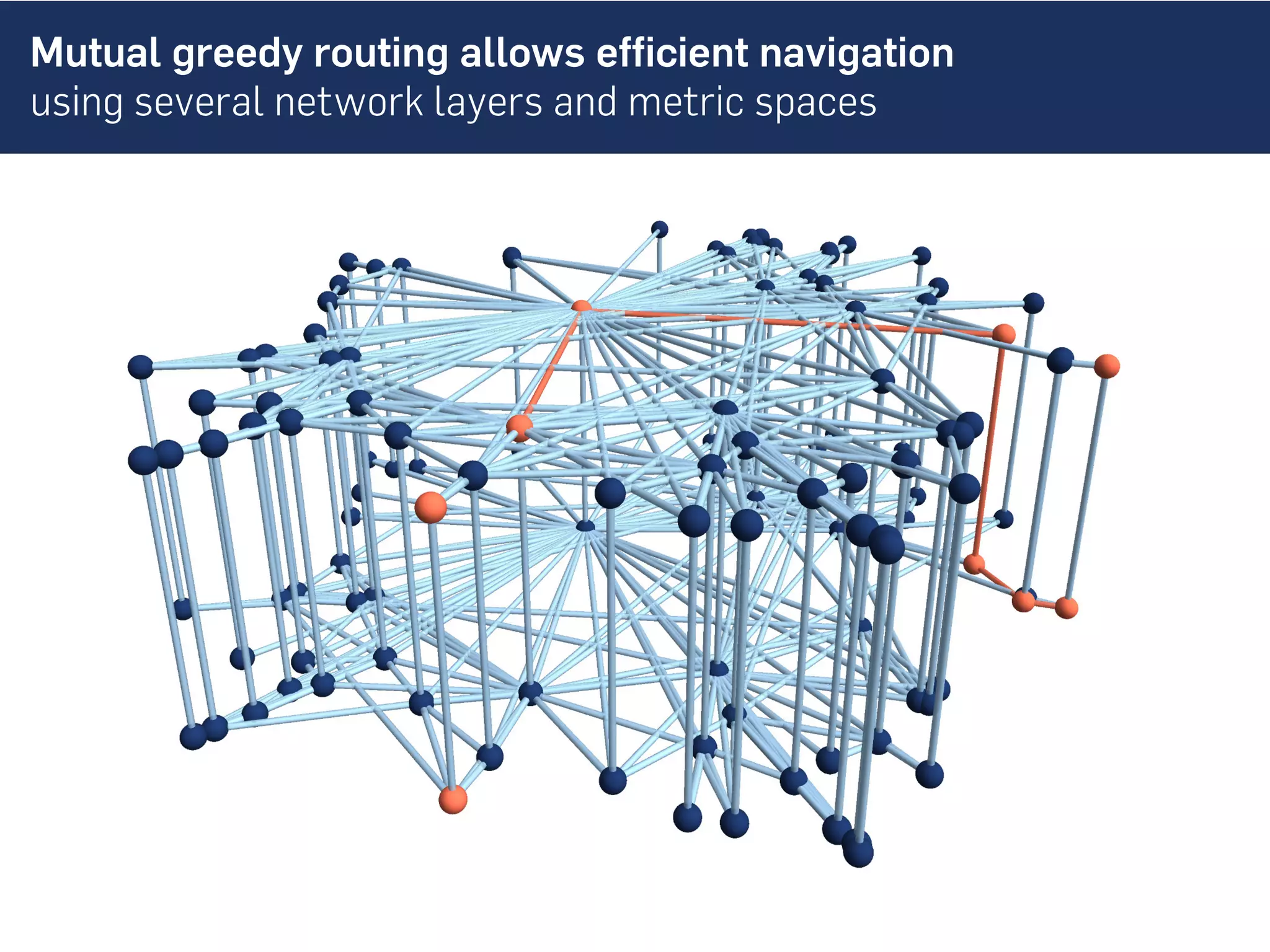
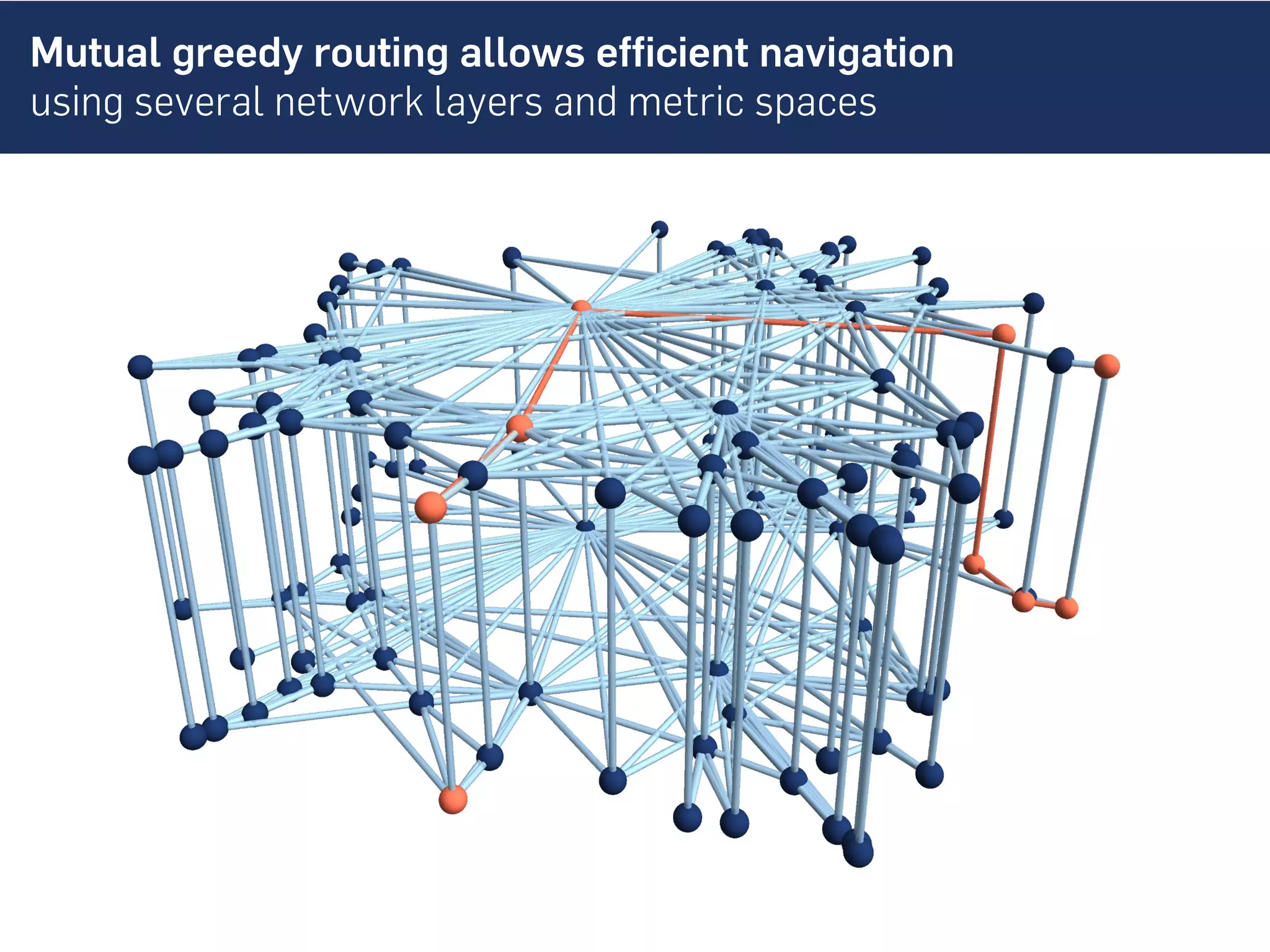
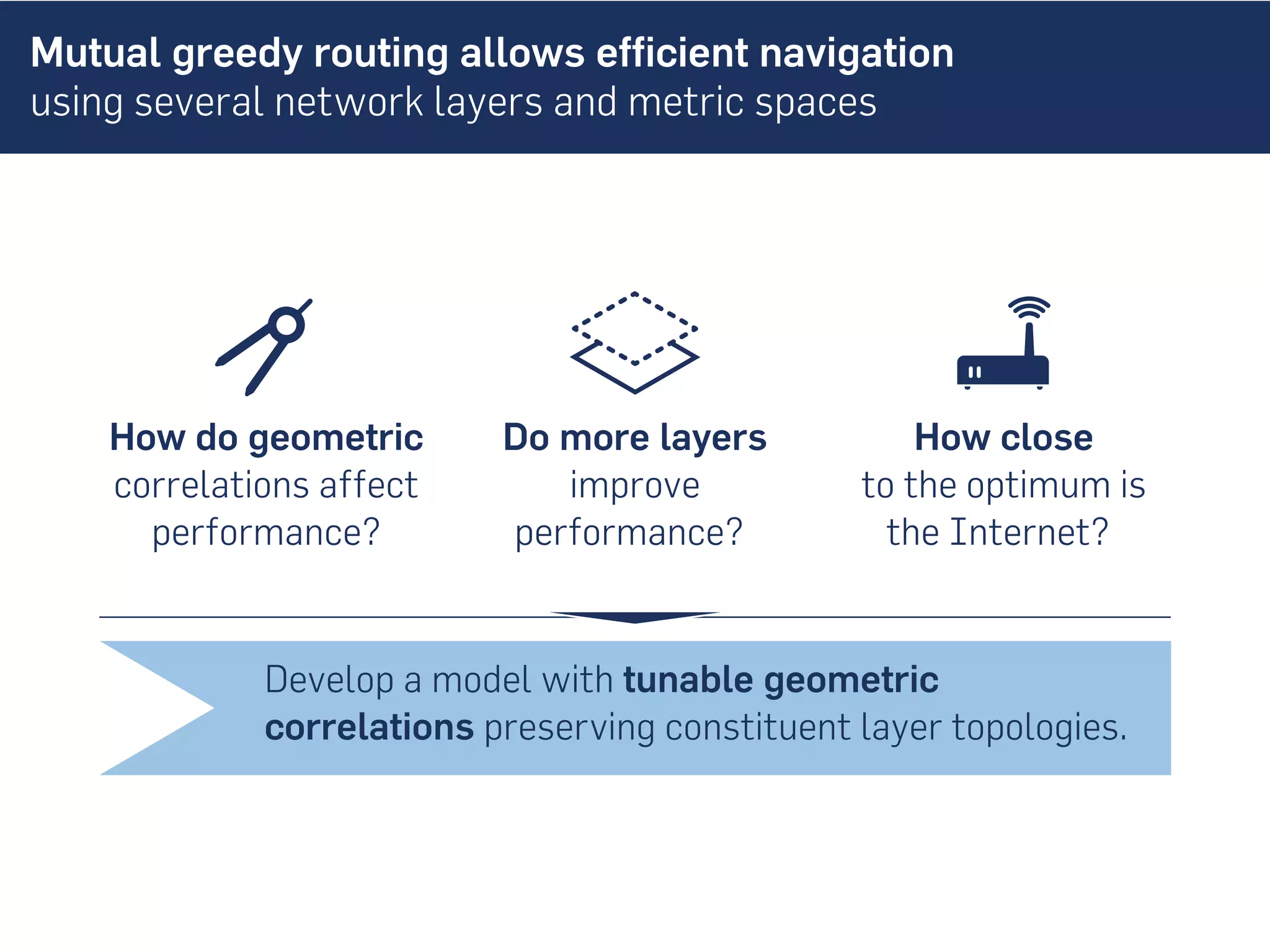
This document discusses the role of hidden geometric correlations in real multiplex networks, proposing that the structure and interaction of these networks can be understood through hyperbolic geometry. It highlights the relationship between node coordinates across layers, demonstrating that correlated distances influence connection probabilities and routing efficiency. The findings suggest that the geometry of multiplex networks can enhance navigation and performance in decentralized systems by improving routing methods such as mutual greedy routing.
More Related Content
Similar to Hidden geometric correlations in real multiplex networks
Hidden geometric correlations in real multiplex networks
- 1. Correlations in real MULTIPLEXES HIDDEN GEOMETRIC KajKolja KLEINEBERG Universitat de Barcelona @KoljaKleineberg kajkoljakleineberg@gmail.com
- 2. You have nomessage
- 3.
- 4.
- 5.
- 6. between maps oflayers?Relation
- 7. Hidden metric spacesunderlying real complex networks provide a fundamental explanation of their observed topologies Nature Physics 5, 74–80 (2008)
- 8. Hidden metric spacesunderlying real complex networks provide a fundamental explanation of their observed topologies How can we infer the coordinates of nodes embedded in hidden metric spaces?
- 9. Hyperbolic geometry emergesfrom Newtonian model and similarity × popularity optimization in growing network S1 p(κ) ∝ κ−γ r = 1 1+ [ d(θ,θ′) µκκ′ ]1/T PRL 100, 078701
- 10. Hyperbolic geometry emergesfrom Newtonian model and similarity × popularity optimization in growing network S1 H2 p(κ) ∝ κ−γ ri = R − 2 ln κi κmin r = 1 1+ [ d(θ,θ′) µκκ′ ]1/T p(xij) = 1 1+e xij−R 2T PRL 100, 078701 PRE 82, 036106
- 11. Hyperbolic geometry emergesfrom Newtonian model and similarity × popularity optimization in growing network S1 H2 growing 1 2 3 p(κ) ∝ κ−γ ri = R − 2 ln κi κmin t = 1, 2, 3 . . . r = 1 1+ [ d(θ,θ′) µκκ′ ]1/T p(xij) = 1 1+e xij−R 2T mins [s × ∆θst] PRL 100, 078701 PRE 82, 036106 Nature 489, 537–540
- 12. Constituent network layersof real multiplex systems are embedded into separate hyperbolic spaces Invert model → embed real networks: PRE 92, 022807 (2015) Internet Air and train Drosophila C. Elegans Human brain arXiv Rattus Physicians SacchPomb
- 13. Constituent network layersof real multiplex systems are embedded into separate hyperbolic spaces Invert model → embed real networks: PRE 92, 022807 (2015) Internet Air and train Drosophila C. Elegans Human brain arXiv Rattus Physicians SacchPomb
- 14. Constituent network layersof real multiplex systems are embedded into separate hyperbolic spaces Internet IPv4 network Internet IPv6 network
- 15. Constituent network layersof real multiplex systems are embedded into separate hyperbolic spaces Internet IPv4 network Internet IPv6 network Are coordinates of same nodes in different layers correlated?
- 16. Radial and angularcoordinates are correlated between different layers in many real multiplexes 0 π 2 π θ1 0 π 2 π θ2 50 100 150 200
- 17. Radial and angularcoordinates are correlated between different layers in many real multiplexes 0 π 2 π θ1 0 π 2 π θ2 50 100 150 200 Multiplexes are not random superpositions of layers but instead are dictated by geometric correlations.
- 18. Distance between pairsof nodes in one layer is an indicator of the connection probability in another layer Hyperbolic distance in IPv4 Connectionprob.inIPv6 P(2|1) 0 5 10 15 20 25 30 35 40 10-4 10-3 10-2 10-1 100
- 19. Distance between pairsof nodes in one layer is an indicator of the connection probability in another layer Hyperbolic distance in IPv4 Connectionprob.inIPv6 P(2|1) 0 5 10 15 20 25 30 35 40 10-4 10-3 10-2 10-1 100 Pran(2|1)
- 20. Distance between pairsof nodes in one layer is an indicator of the connection probability in another layer Hyperbolic distance in IPv4 Connectionprob.inIPv6 P(2|1) 0 5 10 15 20 25 30 35 40 10-4 10-3 10-2 10-1 100 Pran(2|1) Geometric correlations enable precise trans-layer link prediction.
- 21. navigation? How do geometriccorrelations affect
- 22. Greedy routing insingle network using hyperbolic space allows efficient navigation relying only on local knowledge
- 23. Greedy routing insingle network using hyperbolic space allows efficient navigation relying only on local knowledge
- 24. Greedy routing insingle network using hyperbolic space allows efficient navigation relying only on local knowledge
- 25. Greedy routing insingle network using hyperbolic space allows efficient navigation relying only on local knowledge
- 26. Greedy routing insingle network using hyperbolic space allows efficient navigation relying only on local knowledge
- 27. Greedy routing insingle network using hyperbolic space allows efficient navigation relying only on local knowledge
- 28. Mutual greedy routingallows efficient navigation using several network layers and metric spaces
- 29. Mutual greedy routingallows efficient navigation using several network layers and metric spaces
- 30. Mutual greedy routingallows efficient navigation using several network layers and metric spaces
- 31. Mutual greedy routingallows efficient navigation using several network layers and metric spaces
- 32. Mutual greedy routingallows efficient navigation using several network layers and metric spaces
- 33. Mutual greedy routingallows efficient navigation using several network layers and metric spaces
- 34. Mutual greedy routingallows efficient navigation using several network layers and metric spaces
- 35. Mutual greedy routingallows efficient navigation using several network layers and metric spaces How do geometric correlations affect performance?
- 36. Mutual greedy routingallows efficient navigation using several network layers and metric spaces How do geometric correlations affect performance? Do more layers improve performance?
- 37. Mutual greedy routingallows efficient navigation using several network layers and metric spaces How do geometric correlations affect performance? Do more layers improve performance? How close to the optimum is the Internet?
- 38. Mutual greedy routingallows efficient navigation using several network layers and metric spaces How do geometric correlations affect performance? Do more layers improve performance? How close to the optimum is the Internet? Develop a model with tunable geometric correlations preserving constituent layer topologies.
- 39. Geometric multiplex modelallows to tune correlations independently from layer topologies Constituent layer topologies by hyperbolic model
- 40. Geometric multiplex modelallows to tune correlations independently from layer topologies Constituent layer topologies by hyperbolic model Radial correlations controlled by ν ∈ [0, 1]
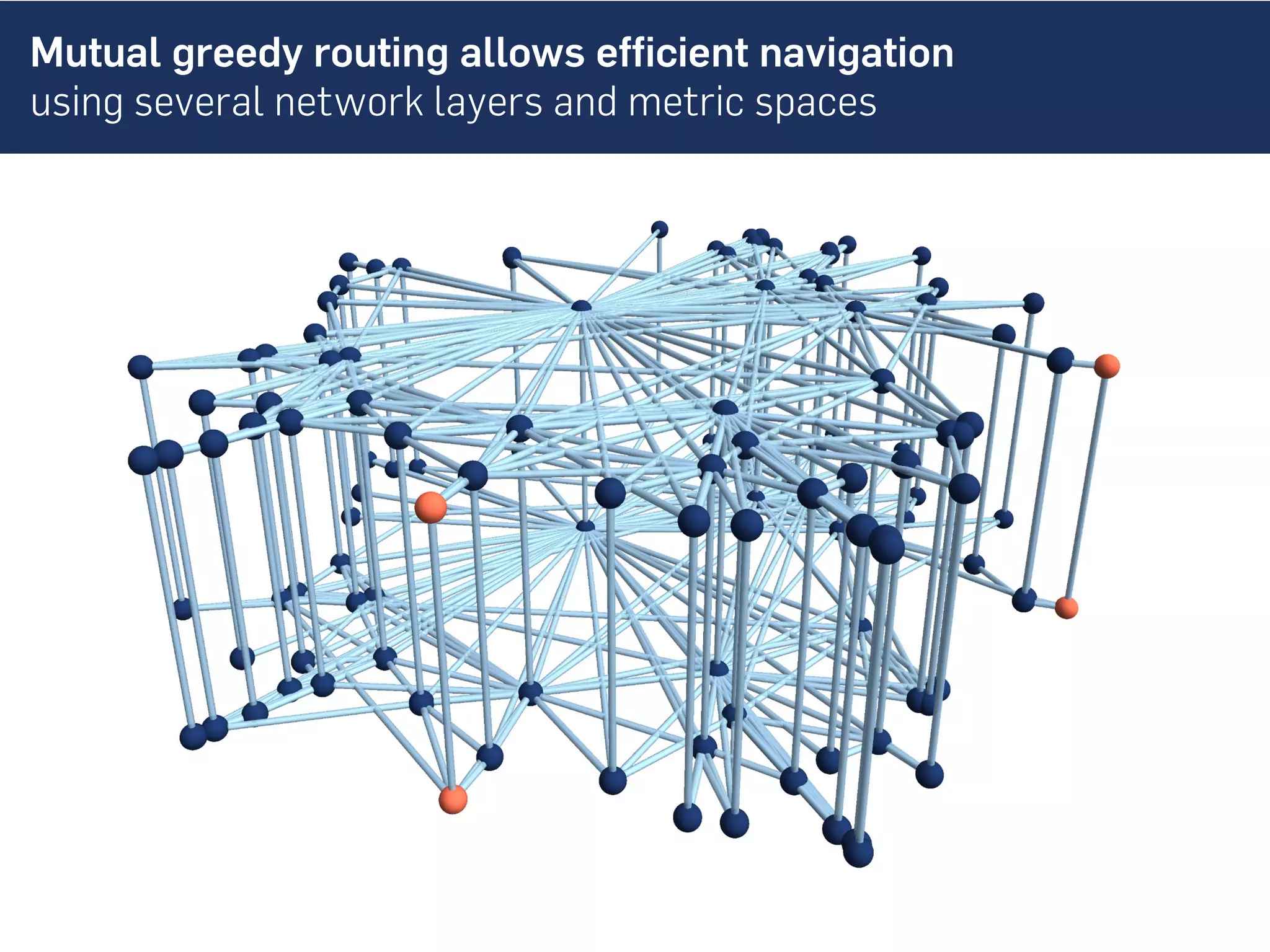
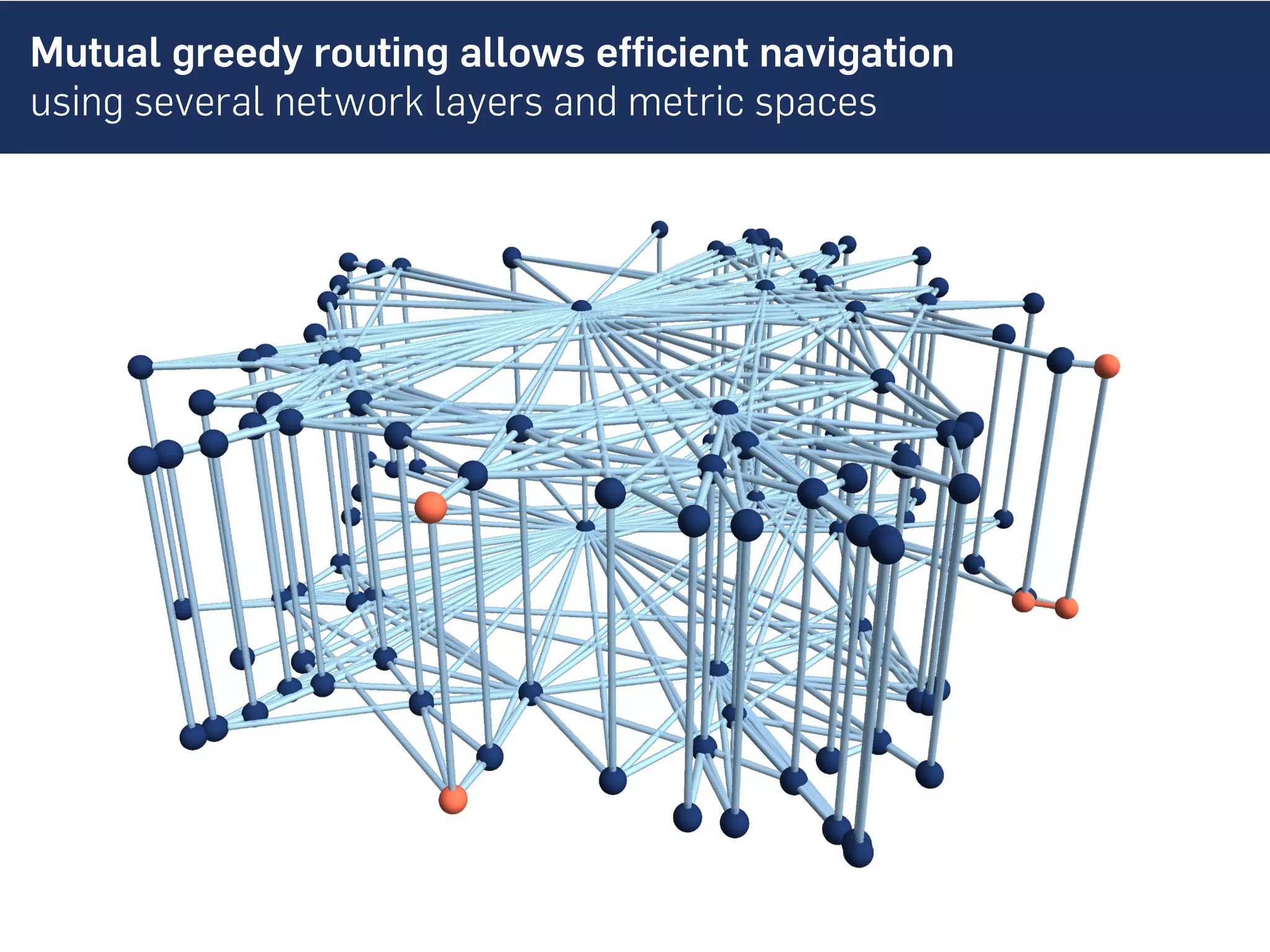
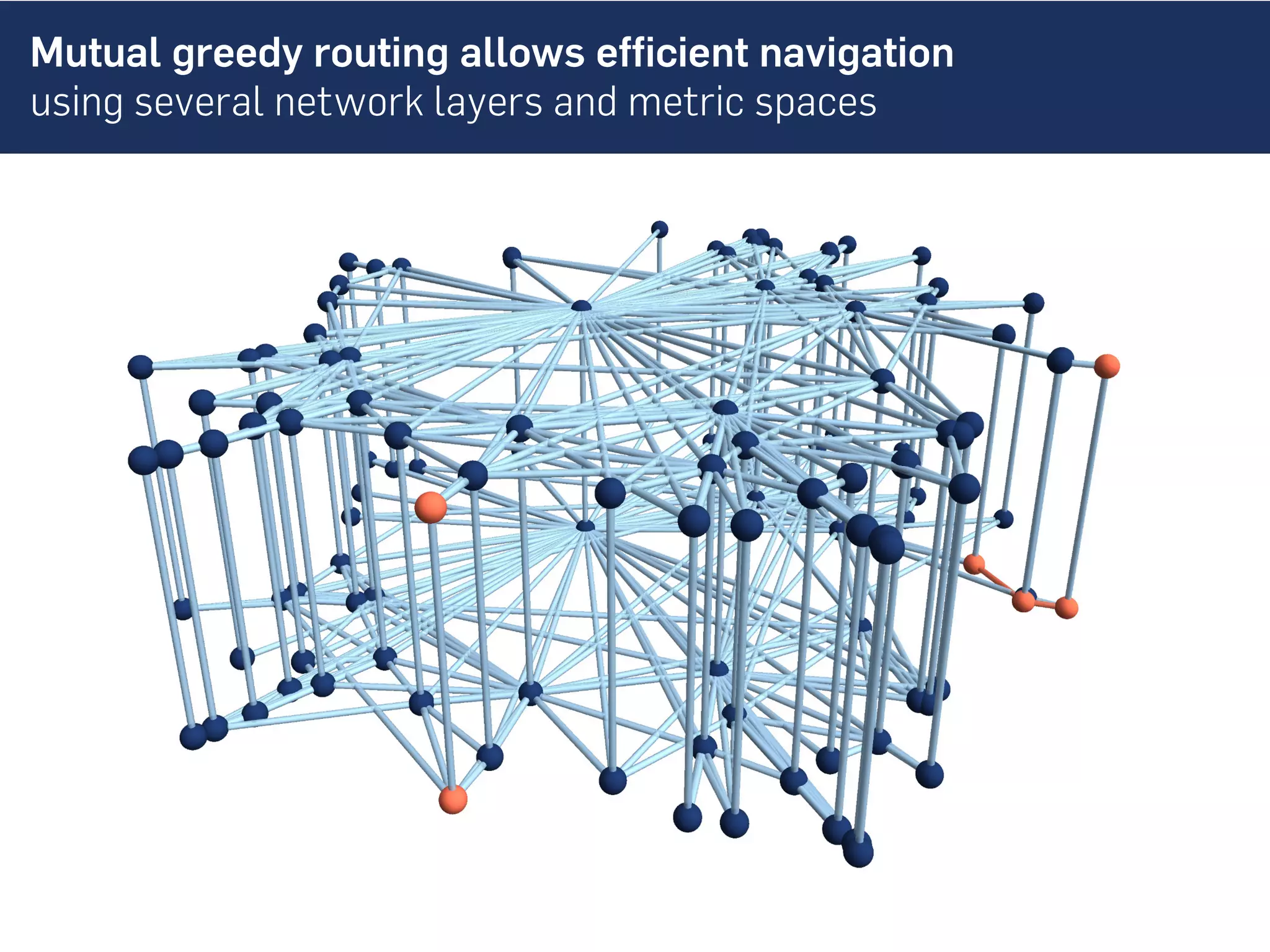
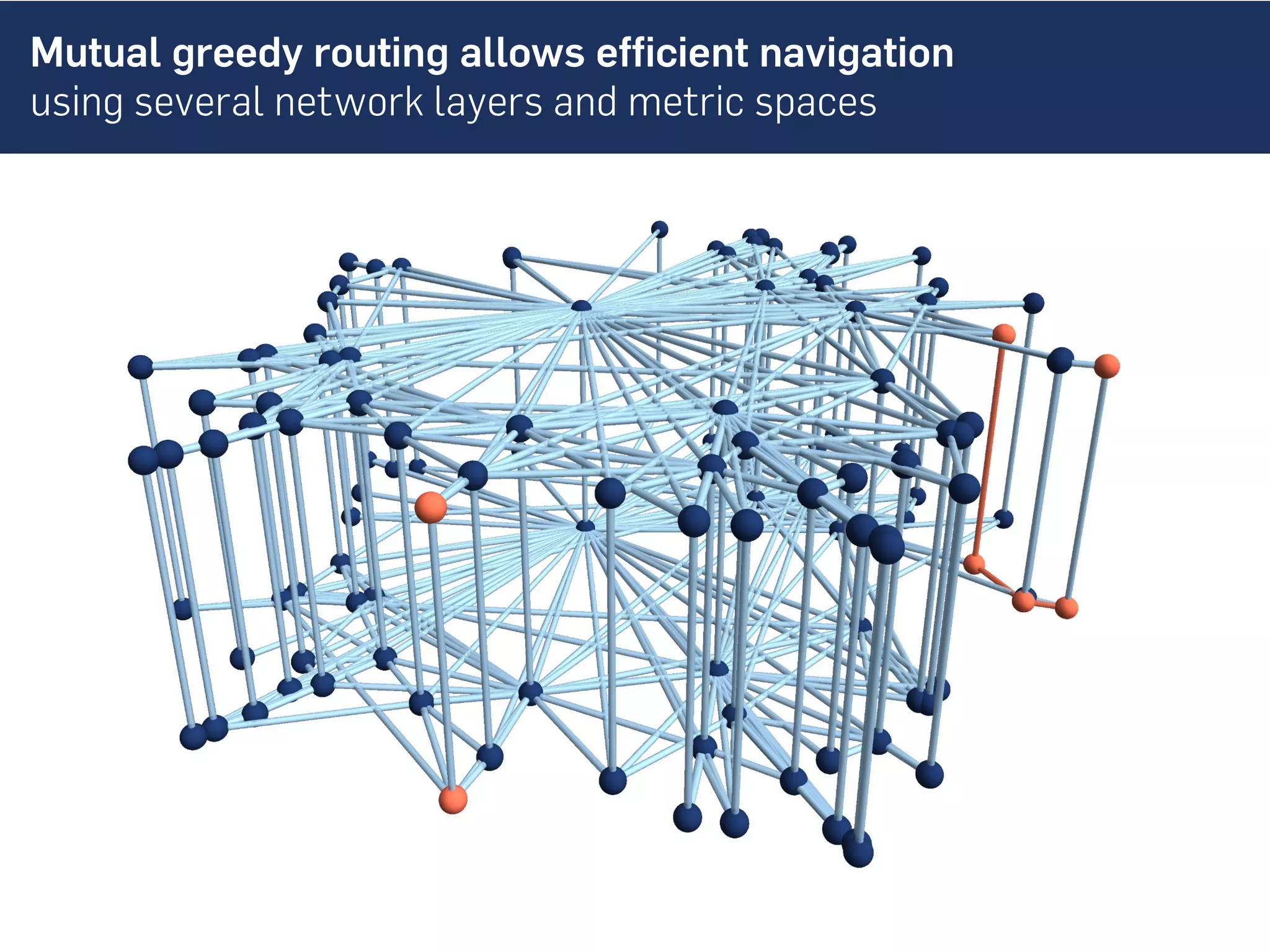
- 41. Geometric multiplex modelallows to tune correlations independently from layer topologies Constituent layer topologies by hyperbolic model Radial correlations controlled by ν ∈ [0, 1] Angular corr. controlled by g ∈ [0, 1]
- 42. Geometric correlations determinethe improvement of mutual greedy routing by increasing the number of layers 0.0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 Hyperbolic routing 0.980 0.985 0.990 0.995 P 1 2 3 4 0 2 4 6 Layers Mitigationfactor opt. correlated uncorrelated Angular correlations Radialcorrelations Reduction of failure rate
- 43. Geometric correlations determinethe improvement of mutual greedy routing by increasing the number of layers 0.0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 Hyperbolic routing 0.980 0.985 0.990 0.995 P 1 2 3 4 0 2 4 6 Layers Mitigationfactor opt. correlated uncorrelated Angular correlations Radialcorrelations Reduction of failure rate
- 44. Geometric correlations determinethe improvement of mutual greedy routing by increasing the number of layers 0.0 0.2 0.4 0.6 0.8 1.0 0.2 0.4 0.6 0.8 1.0 Hyperbolic routing 0.980 0.985 0.990 0.995 P 1 2 3 4 0 2 4 6 Layers Mitigationfactor opt. correlated uncorrelated Angular correlations Radialcorrelations Reduction of failure rate Routing is perfected by using many networks simultaneously if correlations are present.
- 45. Internet? Do correlations helpto navigate the real
- 46. Internet multiplex modelallows to study the performance of mutual greedy routing for arbitrary correlations Real Model • Node only in IPv4 • Node in IPv4 and IPv6
- 47. Existing correlations inthe Internet multiplex increase performance of mutual greedy routing significantly 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 g ν Angular 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 gν Hyperbolic 0.63 0.67 0.71 0.75 Success rate 0.85 0.91 Success rate uncorr. emp. opt. uncorr. emp. opt. 0.88
- 48. Summary: Geometry ofmultiplex networks can make interacting decentralized systems perfectly navigable 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 g ν 0.80 0.82 0.84 0.86 0.88 0.90 Framework 0 π 2 π θ1 0 π 2 π θ2 0.2 0.4 ResultBasis Navigation Mutual greedy routing (local knowledge) Geometric correlations Layers embedded in hyperbolic space Multidimensional community structure Precise trans-layer link prediction Correlations increase routing performance Many correlated layers perfect routing Distances between nodes are correlated Hyperbolic distance in IPv4 Connectionprob.inIPv6 P(2|1) 0 5 10 15 20 25 30 35 40 10-4 10-3 10-2 10-1 100 Pran(2|1) Nature Physics, doi: 10.1038/NPHYS3782 Node coordinates are correlated Multiplexes not random combinations of layers Multiplex organization
- 49. Summary: Geometry ofmultiplex networks can make interacting decentralized systems perfectly navigable 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 g ν 0.80 0.82 0.84 0.86 0.88 0.90 Framework 0 π 2 π θ1 0 π 2 π θ2 0.2 0.4 ResultBasis Navigation Mutual greedy routing (local knowledge) Geometric correlations Layers embedded in hyperbolic space Multidimensional community structure Precise trans-layer link prediction Correlations increase routing performance Many correlated layers perfect routing Distances between nodes are correlated Hyperbolic distance in IPv4 Connectionprob.inIPv6 P(2|1) 0 5 10 15 20 25 30 35 40 10-4 10-3 10-2 10-1 100 Pran(2|1) Nature Physics, doi: 10.1038/NPHYS3782 Node coordinates are correlated Multiplexes not random combinations of layers Multiplex organization
- 50. Summary: Geometry ofmultiplex networks can make interacting decentralized systems perfectly navigable 0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0 g ν 0.80 0.82 0.84 0.86 0.88 0.90 Framework 0 π 2 π θ1 0 π 2 π θ2 0.2 0.4 ResultBasis Navigation Mutual greedy routing (local knowledge) Geometric correlations Layers embedded in hyperbolic space Multidimensional community structure Precise trans-layer link prediction Correlations increase routing performance Many correlated layers perfect routing Distances between nodes are correlated Hyperbolic distance in IPv4 Connectionprob.inIPv6 P(2|1) 0 5 10 15 20 25 30 35 40 10-4 10-3 10-2 10-1 100 Pran(2|1) Nature Physics, doi: 10.1038/NPHYS3782 Node coordinates are correlated Multiplexes not random combinations of layers Multiplex organization
- 51. Geometric correlations inreal multiplexes: Reference and contact information Thanks to: M. Boguñá, M. A. Serrano, F. Papadopoulos Reference: »Hidden geometric correlations in real multiplex networks« Nature Physics, doi: 10.1038/NPHYS3782 K.-K. Kleineberg, M. Boguñá, M. A. Serrano, F. Papadopoulos Kaj Kolja Kleineberg: • kajkoljakleineberg@gmail.com • @KoljaKleineberg • koljakleineberg.wordpress.com
- 52. Geometric correlations inreal multiplexes: Reference and contact information Thanks to: M. Boguñá, M. A. Serrano, F. Papadopoulos Reference: »Hidden geometric correlations in real multiplex networks« Nature Physics, doi: 10.1038/NPHYS3782 K.-K. Kleineberg, M. Boguñá, M. A. Serrano, F. Papadopoulos Kaj Kolja Kleineberg: • kajkoljakleineberg@gmail.com • @KoljaKleineberg ← Slides • koljakleineberg.wordpress.com
- 53. IMAGE CREDITS Compass: MartinFisch Message in bottle: Susanne Nilsson Old globe: jayneandd Compass: Creative Stall Compass (navigate): Creative Stall Internet router: Thomas Uebe Train: Naomi Atkinson fly (drosophila): Daan Kauwenberg worm (celegans): anbileru adaleru bain network: parkjisun coauthor: Matt Wasser community: Edward Boatman Link: Rafaël Massé Icons: thenounproject Pictures: flickr