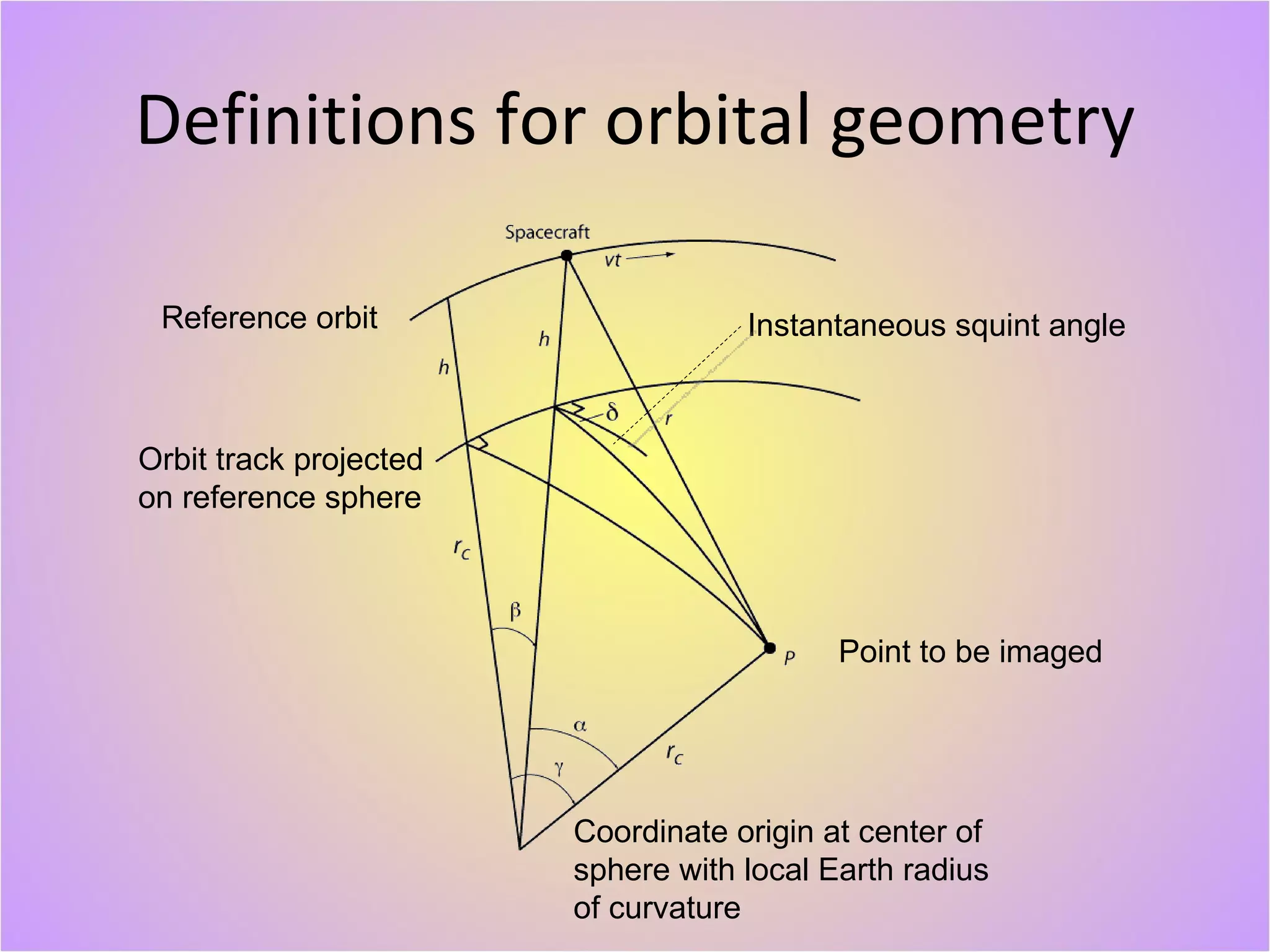
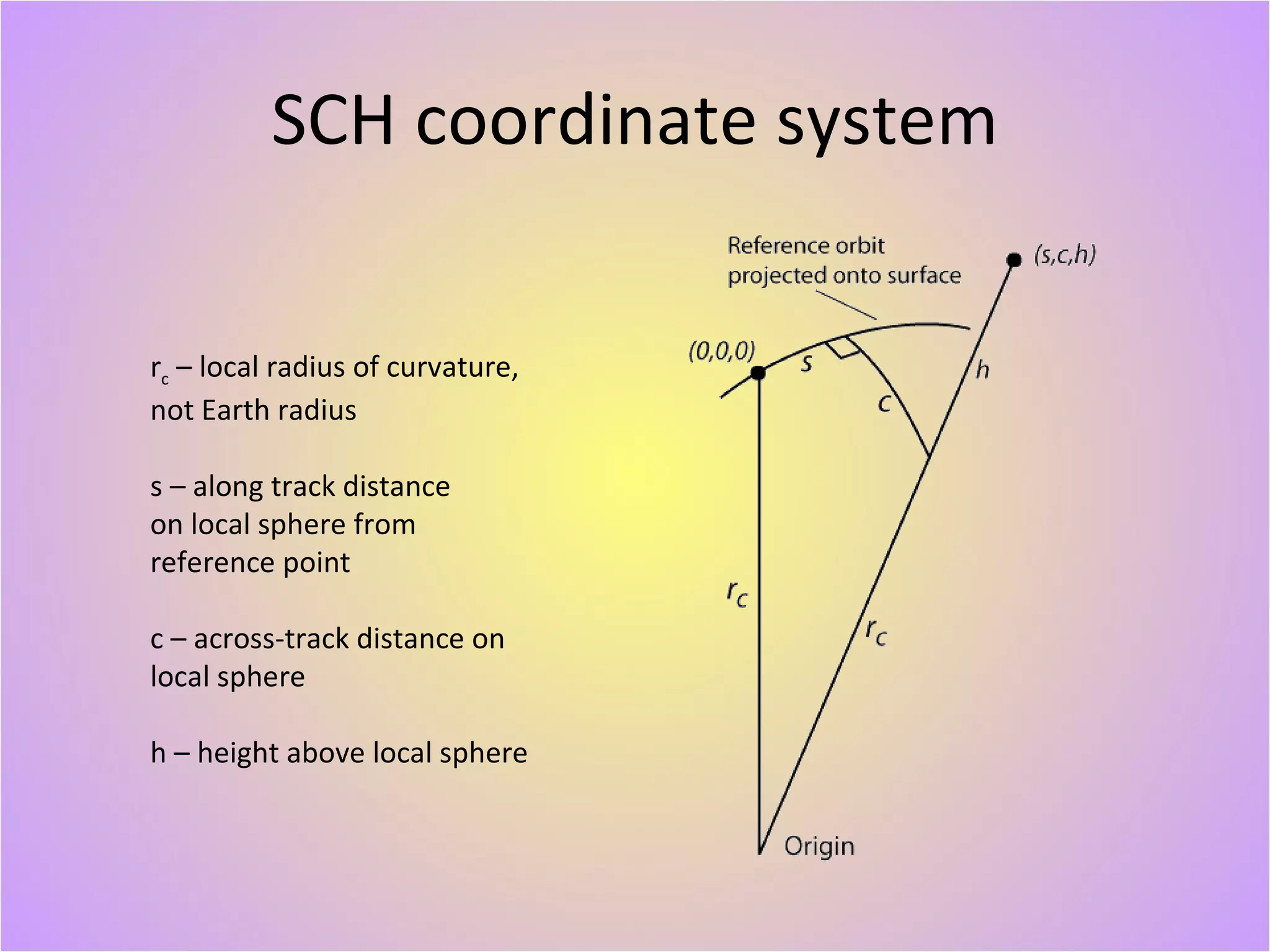
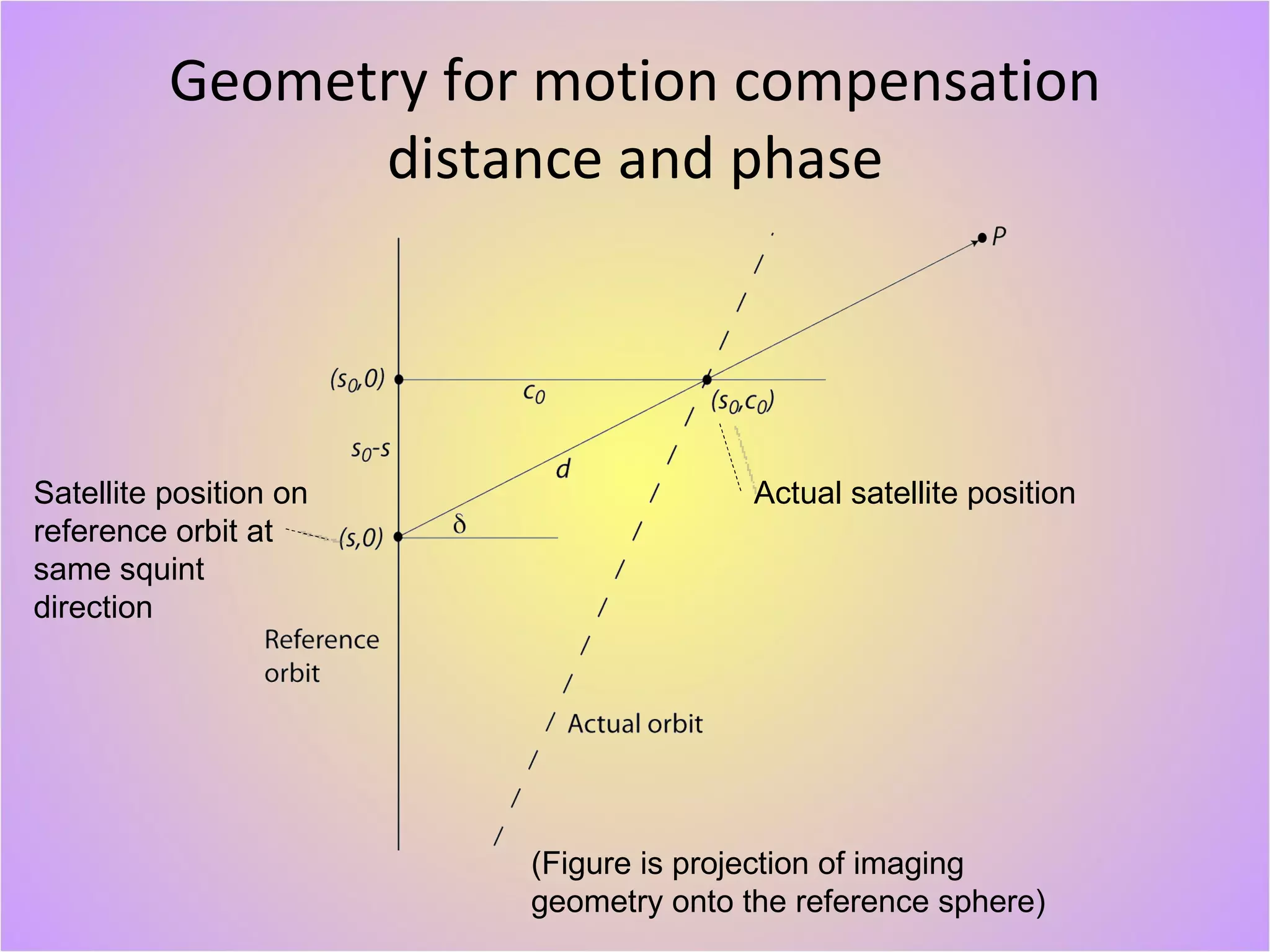
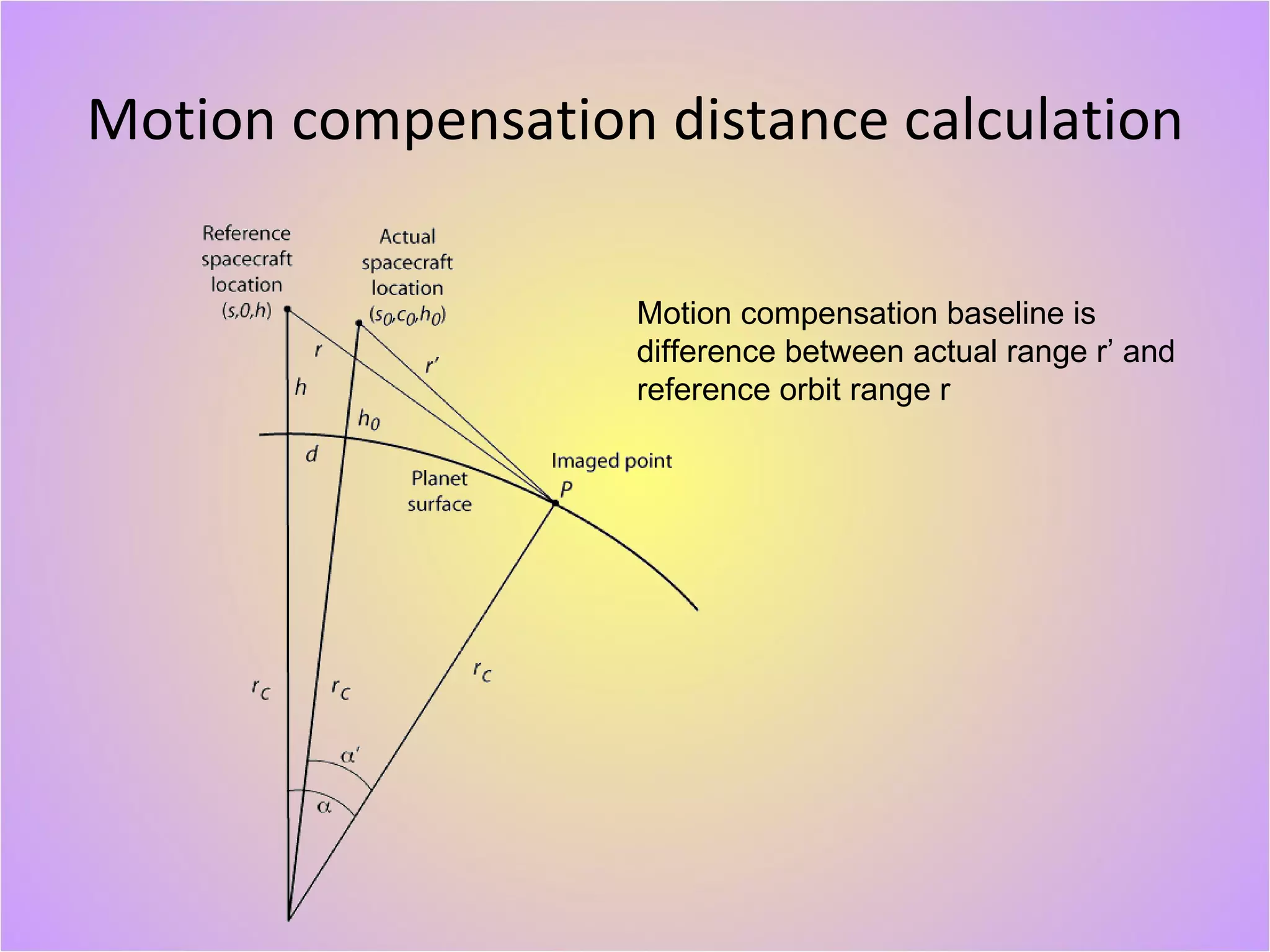
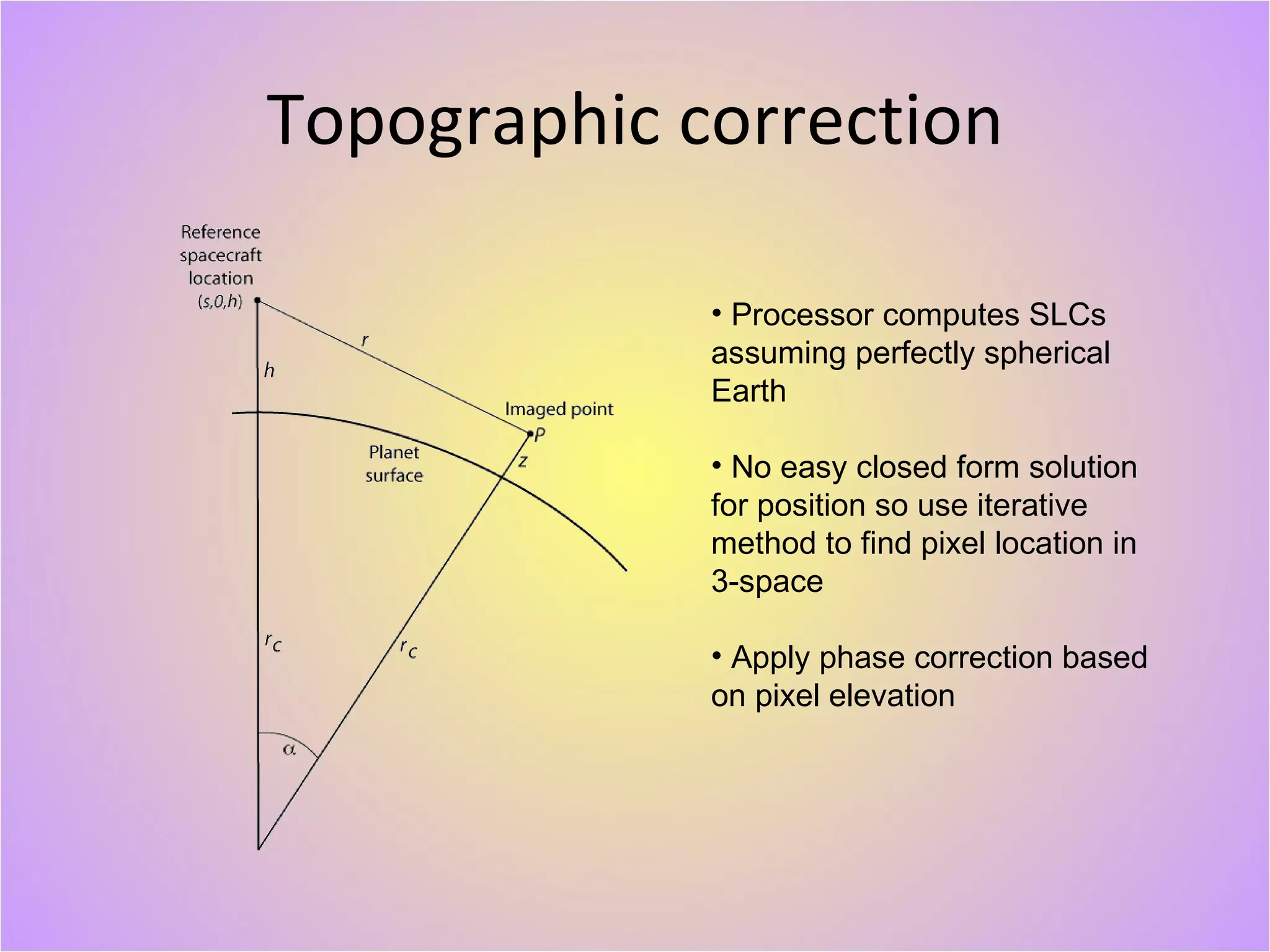
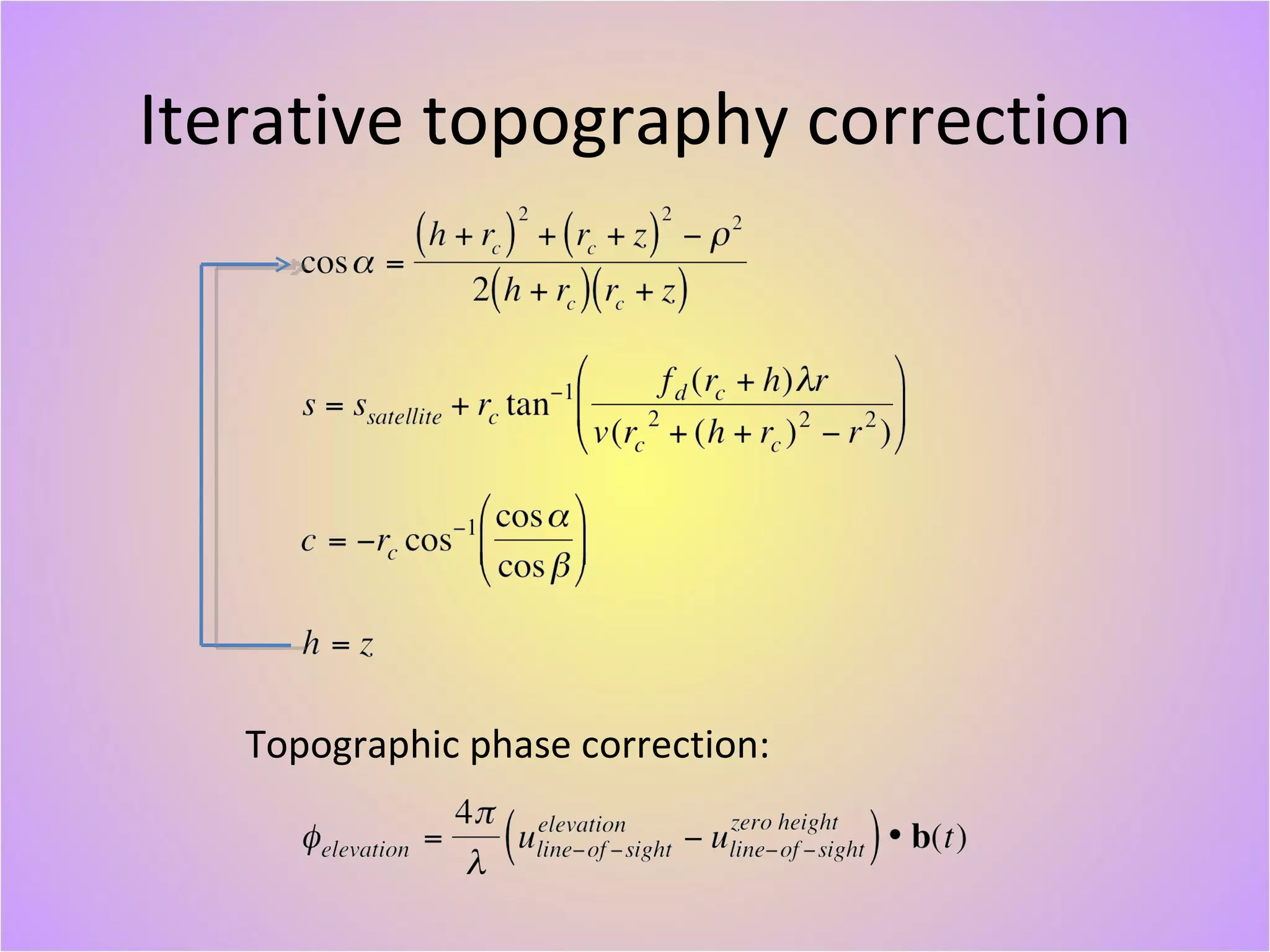
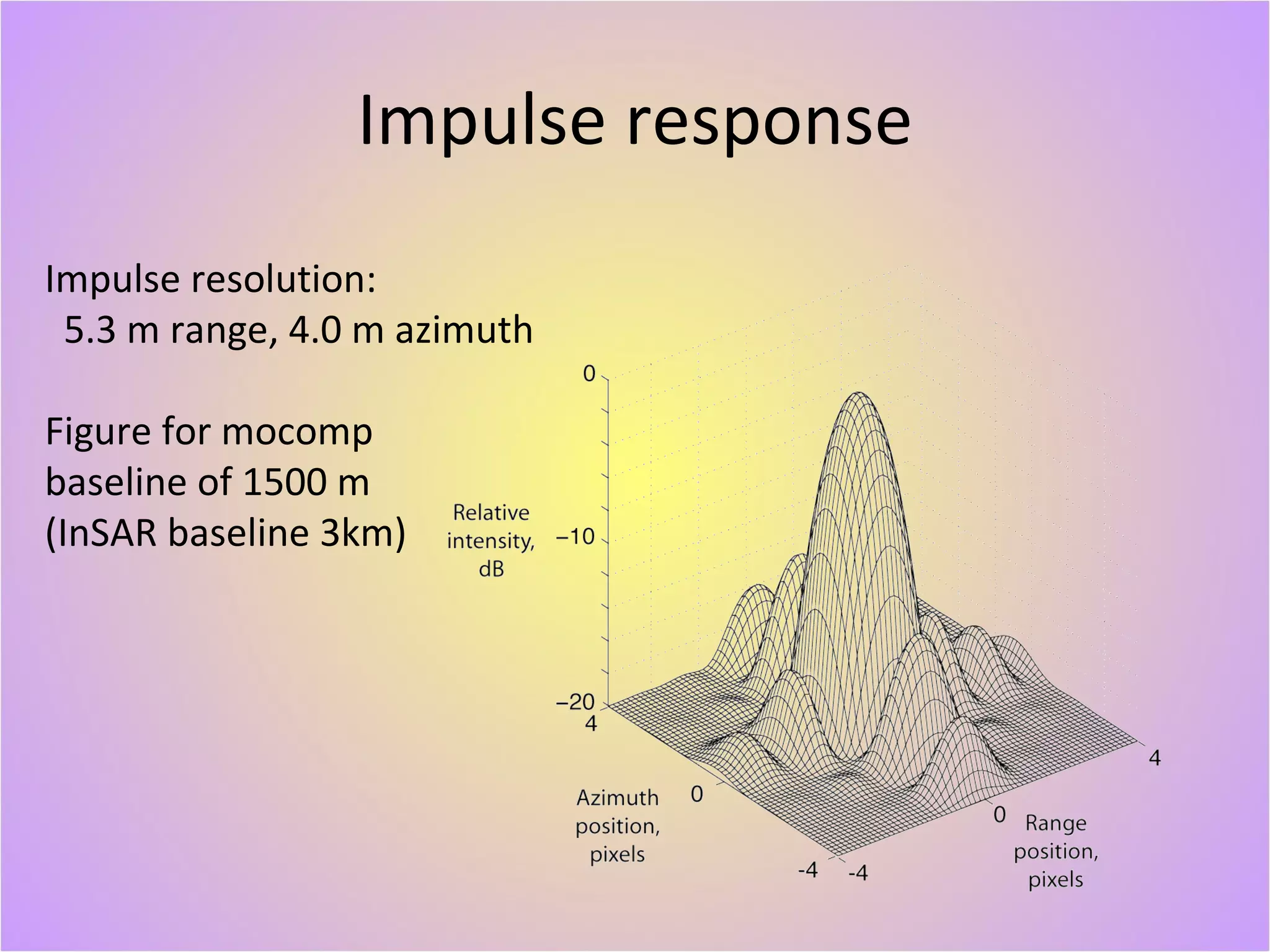
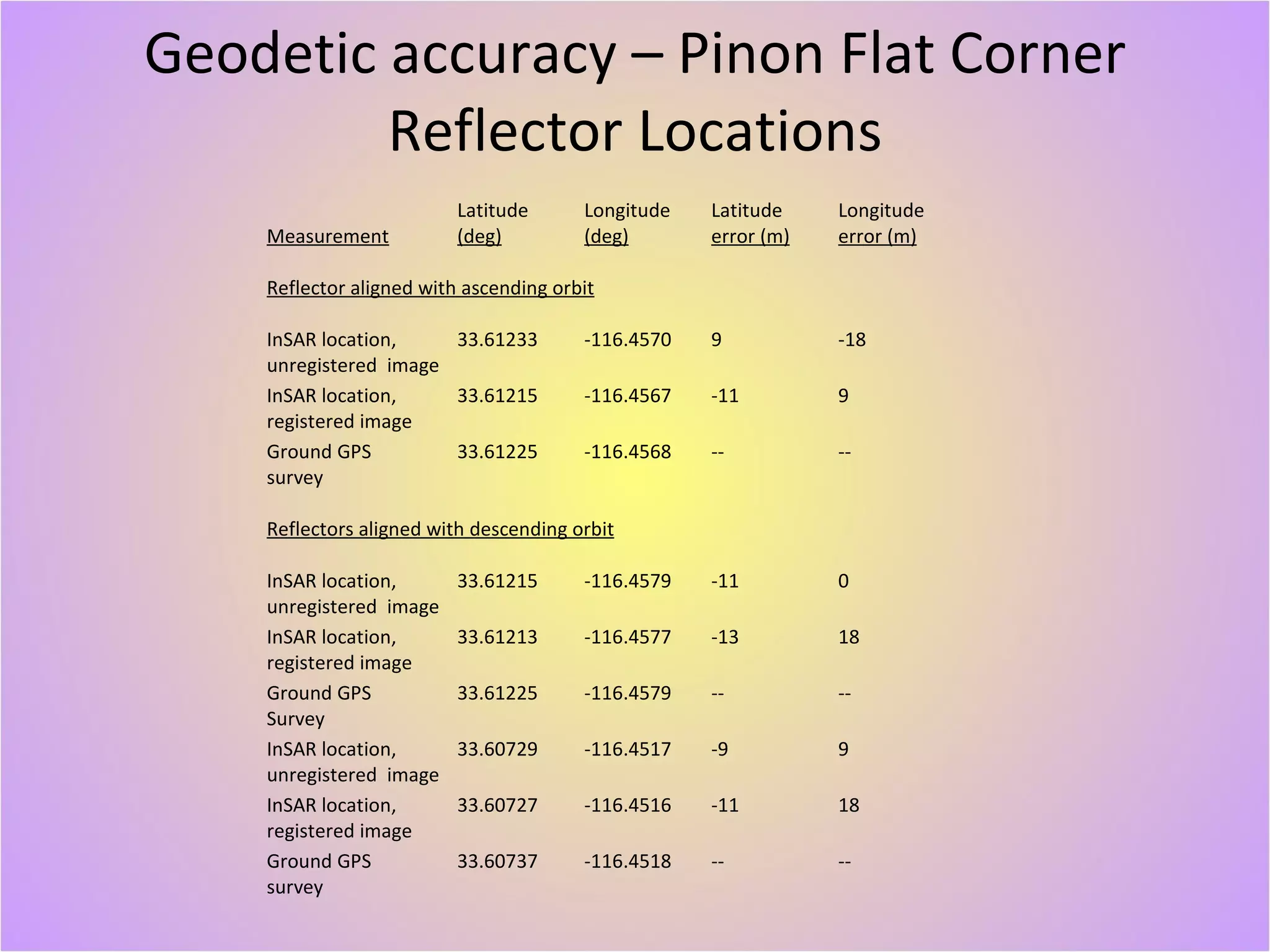
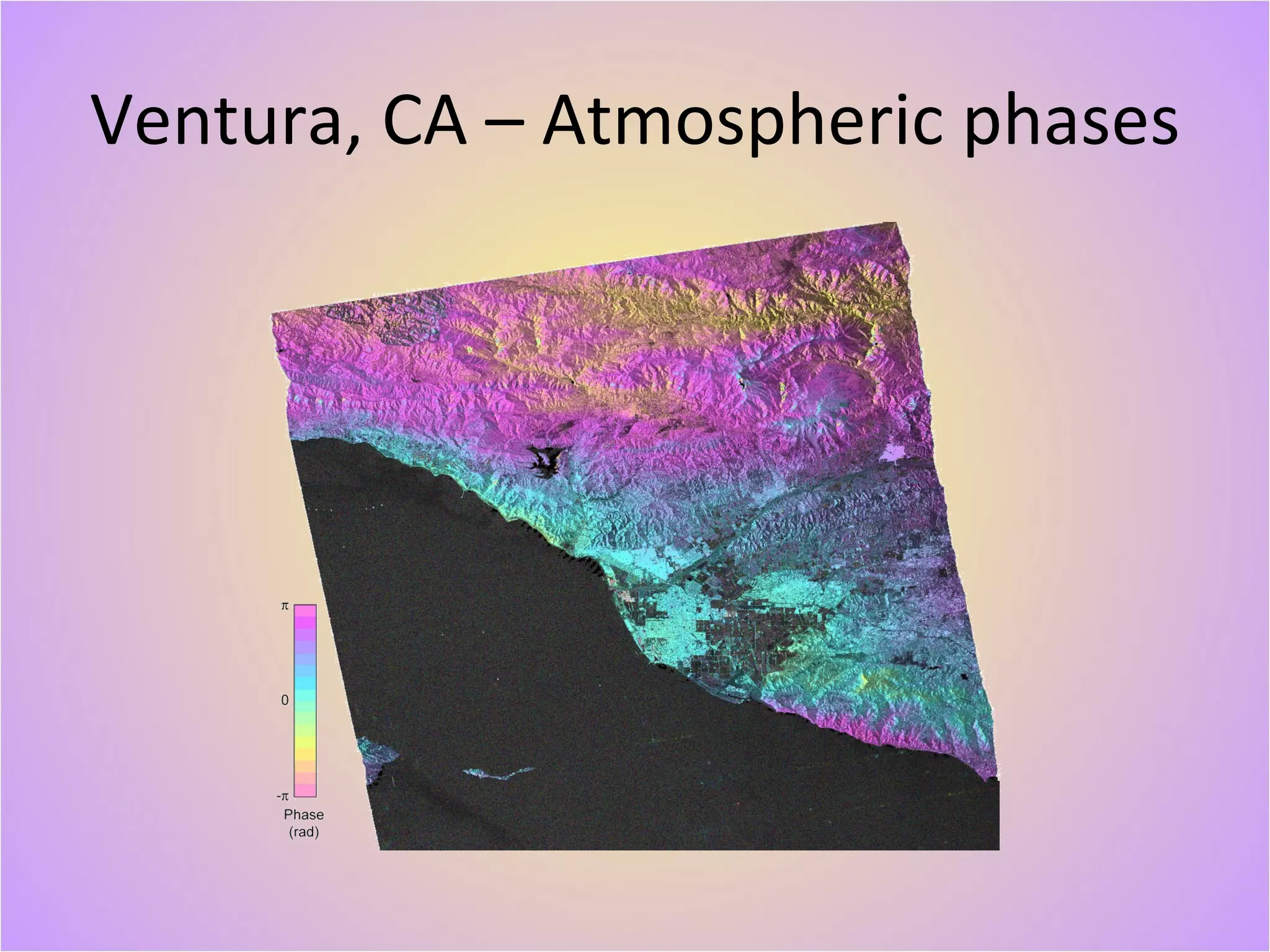
The document describes a new geodetically accurate InSAR data processor for time series analysis. The processor uses precise satellite orbits and a reference orbit to align Synthetic Aperture Radar (SAR) images with sub-meter accuracy. It employs a motion compensation algorithm to account for differences between the actual satellite position and reference orbit. The processor achieves accurate geolocation and is computationally efficient, processing interferograms for large areas in only a few minutes on a desktop computer. Validation tests using corner reflectors and SRTM elevation data demonstrate the processor's improved geodetic accuracy compared to existing tools.

1. Geodetically Accurate InSAR Data Processor for Time Series Analysis Howard Zebker, Piyush Shanker, Cody Wortham, Scott Hensley Stanford University and Jet Propulsion Laboratory

2. Modern applications need better geodetic accuracy InSAR and time series methods (PS, SBAS) require precise SLC alignment from a variety of orbits Merging SAR data with other types needs geolocated and orthorectified products Processing many scenes (typically dozens) of one area needs to be efficient and on the desktop

3. Need for new processor Existing processing packages largely geodetically inaccurate Pixels placed at wrong place Lots of resampling to find offsets, and this is where many processors fail Now have precise orbits Multicore processors have untapped cycles we can use to speed up processing time

4. Approach Use precise orbits to find exact (~10 cm error) satellite position Choose a reference orbit for multiple scenes so images are nearly aligned – small offsets Reference orbit not physically realizable without constant acceleration, so it’s “virtual” Use motion compensation method to make spacecraft “fly” on chosen trajectory Be careful to keep geometrical info throughout

5. Definitions for orbital geometry Reference orbit Orbit track projected on reference sphere Coordinate origin at center of sphere with local Earth radius of curvature Point to be imaged Instantaneous squint angle

6. Remember the basics Phase and range relations Doppler relations

7. Focus and position equations in our geometry

8. SCH coordinate system r c – local radius of curvature, not Earth radius s – along track distance on local sphere from reference point c – across-track distance on local sphere h – height above local sphere

9. Geometry for motion compensation distance and phase Actual satellite position Satellite position on reference orbit at same squint direction (Figure is projection of imaging geometry onto the reference sphere)

10. Finding the position on the reference orbit for an actual spacecraft location

11. Motion compensation distance calculation Motion compensation baseline is difference between actual range r’ and reference orbit range r

12. Motion compensation algorithm Derivation of reference distance r: Mocomp distance and phase corrections:

13. Phase history for mocomped scatterer Compare phase histories for r act (t) and r(t)

14. Focus corrections Quadratic phase correction from processing at wrong distance: Frequency domain phase term from range-varying motion compensation phase:

15. Topographic correction Processor computes SLCs assuming perfectly spherical Earth No easy closed form solution for position so use iterative method to find pixel location in 3-space Apply phase correction based on pixel elevation

16. Iterative topography correction Topographic phase correction:

17. Impulse response Impulse resolution: 5.3 m range, 4.0 m azimuth Figure for mocomp baseline of 1500 m (InSAR baseline 3km)

18. Single look complex image of SFO

19. Geodetic accuracy – Pinon Flat Corner Reflector Locations Latitude Longitude Latitude Longitude Measurement (deg) (deg) error (m) error (m) Reflector aligned with ascending orbit InSAR location, 33.61233 -116.4570 9 -18 unregistered image InSAR location, 33.61215 -116.4567 -11 9 registered image Ground GPS 33.61225 -116.4568 -- -- survey Reflectors aligned with descending orbit InSAR location, 33.61215 -116.4579 -11 0 unregistered image InSAR location, 33.61213 -116.4577 -13 18 registered image Ground GPS 33.61225 -116.4579 -- -- Survey InSAR location, 33.60729 -116.4517 -9 9 unregistered image InSAR location, 33.60727 -116.4516 -11 18 registered image Ground GPS 33.60737 -116.4518 -- -- survey

20. Geodetic accuracy – Image offsets from SRTM DEM Range offset Azimuth offset Additional stretch Scene at center (m) at center (m) Range (m) Azimuth (m) Ventura -15.8 18.2 9.4 15.2 Hawaii -21.5 24.0 14.1 25.4 Iceland 2.0 2.9 44.0 29.4

21. Ventura, CA – Atmospheric phases

22. Hawaii – deformation plus atmosphere

23. Iceland – significant ionospheric artifact

24. Correlation images Ventura Hawaii Iceland

25. Computational efficiency Implemented on multicore desktop using F90 and Python scripting Computational modules parallelized with OpenMP Typical ALOS interferogram ~2-4 minutes Working with JPL to produce a package to be distributed to community At present we use a standalone version compiled under *nix

26. Summary InSAR and time series analysis requires precise image pixel locations Imprecise locations make processing slow and unreliable With precise orbits, motion compensation, and particular geometry processor equations are fairly simple and efficient to compute Accuracies of 10 m easy to achieve, probably 1 m with further development