![Example application: sentiment analysis
• Use open-source pre-trained LLM to compute
sentiment score [-1, 1] on Fed Chair’s speech.
➢FinBERT. BERT is a pre-trained LLM by Google.
➢FinBERT is finetuned on financial data.
➢See our book on how to fine-tune a model using your own data.
➢Predict short term price moves in SPY during FOMC press
conferences using such sentiment scores every 30
second.](https://image.slidesharecdn.com/genaifortradingandassetmanagementwebinarv31-250411073104-298d833c/75/GenAI-for-Trading-and-Asset-Management-by-Ernest-Chan-18-2048.jpg)
Uploaded byQuantInsti
GenAI for Trading and Asset Management by Ernest Chan
Presentation from the power-packed webinar on AI-driven trading and automation, bringing together leading experts and a community of over 6000 traders, analysts, developers, and students. Participants got the chance to interact live with experts, ask questions, and gain practical, actionable skills in automated trading—making this webinar a useful resource for anyone serious about the future of trading technology. In Session 1, renowned quant expert Dr. Ernest Chan explores the evolving role of Generative AI in finance, diving into advanced trading strategies that go beyond traditional language models (LLMs). About the author: Dr. Ernest P. Chan is a recognized expert in applying statistical models and machine learning to finance. He is the Founder and Chief Scientist at PredictNow.ai, where he helps investors make informed decisions using advanced data-driven insights. Additionally, he is the Founder and Non-executive Chairman of QTS Capital Management, LLC, which focuses on systematic trading strategies. Dr. Chan has worked at notable organizations like IBM Research, Morgan Stanley, and Credit Suisse, gaining experience in pattern recognition, data mining, and quantitative trading. Dr. Chan obtained his PhD in Physics from Cornell University and his B.Sc. in Physics from the University of Toronto. He has also authored several influential books, including Quantitative Trading and Algorithmic Trading. He was an Adjunct Associate Professor of Finance at Nanyang Technological University in Singapore and an adjunct faculty at Northwestern University’s Masters in Data Science program. Dr. Chan combines extensive industry experience with deep technical knowledge, making him an excellent resource for understanding how to apply machine learning to trading effectively. This webinar was conducted on: Thursday, April 10, 2025
More Related Content
Similar to GenAI for Trading and Asset Management by Ernest Chan
GenAI for Trading and Asset Management by Ernest Chan
- 1. GenAI for Trading &Asset Management (GATAM) Hamlet Medina Ernie Chan Pre-order on Amazon.com!
- 2. Hamlet • Hamlet JesseMedina Ruiz holds the position of chief data scientist at Criteo. He specializes in time series forecasting, machine learning, deep learning, and Generative AI. He actively explores the potential of cutting-edge AI technologies, such as Generative AI across diverse applications. • He holds an electronic engineering degree from Universidad Rafael Belloso Chacin in Venezuela, as well as two master’s degrees with honors in mathematics and machine learning from the Institut Polytechnique de Paris and Université Paris-Saclay. Additionally, he earned a PhD in physics from Université Paris-Saclay. • Hamlet has consistently achieved first place and top ten rankings in global machine learning contests, earning the titles of Kaggle Expert and Numerai Expert for these challenges. Recently, he also earned a MicroMaster’s in finance from MIT’s Sloan School of Management.
- 3. Ernie • Ernie Chanis the founder and Chief Scientist of PredictNow.ai, machine learning SaaS for asset managers • He is the founder and non-executive chairman of QTS Capital Management, LLC., a commodity pool operator and trading advisor • Ernie is the author of“Quantitative Trading: How to Build Your Own Algorithmic Trading Business 2nd Ed”, “Algorithmic Trading: Winning Strategies and Their Rationale”,“Machine Trading”, and “Hands-On AI Trading” • Formerly ML researcher at language modeling group at IBM T.J. Watson Research Center. • Ph.D. Cornell U., B.Sc. University of Toronto
- 4. “Mirror, mirror, whois the best algorithmic trading author of them all?” • Perplexity:
- 5. GenAI vs. DiscriminativeAI • Discriminative AI / Supervised Learning: p(y|x)=? • Gen AI: p(x)=? p(x|y)=? p(x, y)=? • Bayes’ rule 𝑝 𝑥 𝑦 = 𝑝 𝑥 𝑝(𝑦|𝑥) 𝑝(𝑦)
- 6. Importance of p(x) •If feature x has a value never seen in train set (“outliers”), we want to know! • Can simulate (generate) new samples.
- 7. Importance of p(x|y) •Let x be images of dogs or cats. ➢p(x|y=”dog”) can generate images of dog conditioned on prompt y. • Let x be a returns series during bear markets. ➢p(x|y=“bear market” can generate returns distribution conditioned on prompt “bear market”.
- 8. Importance of p(x|y) •Let x be images of dogs or cats. ➢p(x|y=”dog”) can generate images of dog conditioned on prompt y. • Let x be a returns series during bear markets. ➢p(x|y=“bear market”) can generate returns distribution conditioned on prompt “bear market”.
- 9. Applications of p(x|y)or p(x, y) • Risk management e.g. VaR ➢Traditionally, simple parametric models such as t- distributions or even copulas are used. • Scenario testing: beyond backtesting ➢Would my trading strategy be more or less profitable during bull vs bear market? ➢Would entering into a position at a lower threshold be more profitable?
- 10. Applications of p(x|y)or p(x, y) • Downstream predictive (discriminative) or optimization (deep reinforcement learning) tasks ➢First pre-train with large amount of data e.g. all financial time series. ➢Then fine-tune with time series specific to asset of interest. ➢Mai D. 2024, “StockGPT: A GenAI Model for Stock Prediction and Trading”
- 11. Applications of p(x|y)or p(x, y) • Downstream predictive (discriminative) or optimization (deep reinforcement learning) tasks ➢First pre-train with large amount of data e.g. all financial time series. ➢Then fine-tune with time series specific to asset of interest. ➢Mai D. 2024, “StockGPT: A GenAI Model for Stock Prediction and Trading”
- 12. Applications of p(x|y)or p(x, y) • Outlier detection ➢If p(x) ~ 0, x is an outlier, therefore p(x, y) ~ 0: avoid making prediction p(y|x)! ➢Financial data often limited, especially if we train on only 1 asset: low confidence in p(y|x). ➢E.g. not enough bear market samples for p(x|”bear”). ➢Can, again, pre-train p(x) with large amount of general time series data and then fine-tune with specific time series data to improve estimation of p(y|x)=p(x, y)/p(x)
- 13. Types of GenerativeModels • Autoregressive Models 𝑝 𝑥1, … , 𝑥𝑇 = 𝑝(𝑥1)∙ 𝑝 𝑥2| 𝑥1 ∙ 𝑝 𝑥3| 𝑥1, 𝑥2 ∙ … ∙ 𝑝 𝑥𝑇| 𝑥1, 𝑥2, … , 𝑥𝑇−1 ➢Markov assumption/simplification: assume a finite lookback is enough. (W.L.O.G. lookback=1 with vector 𝑥) ➢Stationarity assumption/simplification: assume 𝑝 𝑥𝑡| 𝑥𝑡−1 is independent of time 𝑡 (a.k.a. weight sharing).
- 14. Autoregressive Models • Whenx is high dimensional (to accommodate long lookback), models can become complicated ➢Causal Masked Neural Network: masking future information as input ➢Recurrent Neural Network (RNN): incorporate all prior information as input (i.e. infinite lookback)
- 15.
- 16. Transformers • RNN hasexploding/vanishing gradient problem as time series gets lengthy/network gets deep. • LSTM/GRU alleviates this by adding gates: decide what information to discard at each time step. • Transformers: use attention to decide what input is relevant. ➢Attention apply weights to different inputs, with weights themselves trained on input-output series.
- 17. Transformers • Can regardattention as a sample-wise feature selection mechanism. • See our book for example on how to train attention weights on autoregressive time series predictions. • See also Cong et. al. (2021) “AlphaPortfolio: Direct construction through deep reinforcement learning and interpretable AI. “
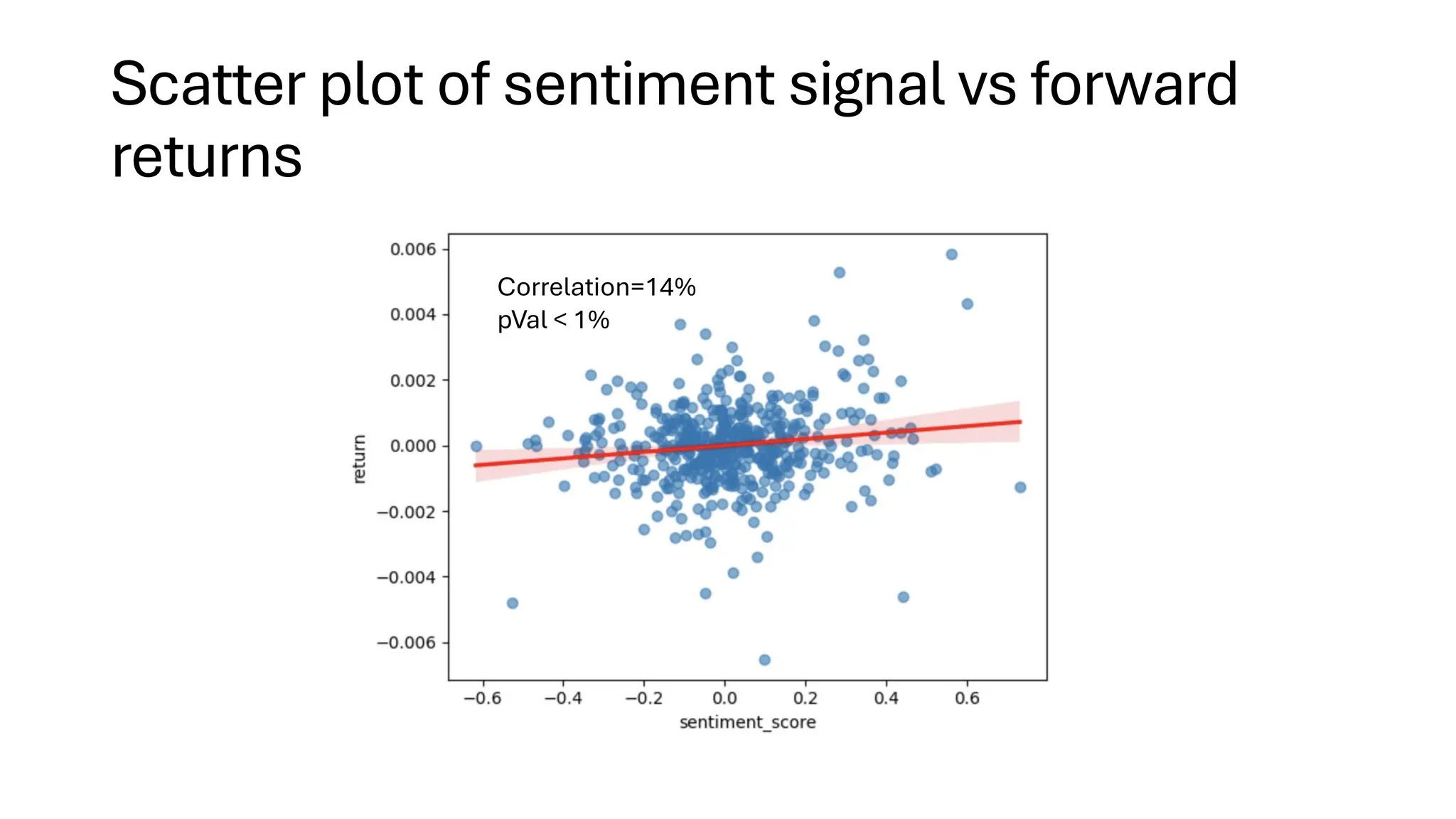
- 18. Example application: sentimentanalysis • Use open-source pre-trained LLM to compute sentiment score [-1, 1] on Fed Chair’s speech. ➢FinBERT. BERT is a pre-trained LLM by Google. ➢FinBERT is finetuned on financial data. ➢See our book on how to fine-tune a model using your own data. ➢Predict short term price moves in SPY during FOMC press conferences using such sentiment scores every 30 second.
- 19. Scatter plot ofsentiment signal vs forward returns Correlation=14% pVal < 1%
- 20. Backtest results Unnormalized Sharperatio Accuracy Pearson Correlation of Sentiment Signal vs SPY P-value 11,3844% 53,1532% 14,1458% 0,1999%
- 21. Conclusion • Generative AIis not just about LLMs. • You can use the technique to model distributions of anything: e.g. Returns. • Modeling feature x distribution let’s us simulate data and detect outliers. • Pre-training and fine-tuning models lets you overcome data scarcity. • Attention lets you apply sample-wise feature selection.
- 22.