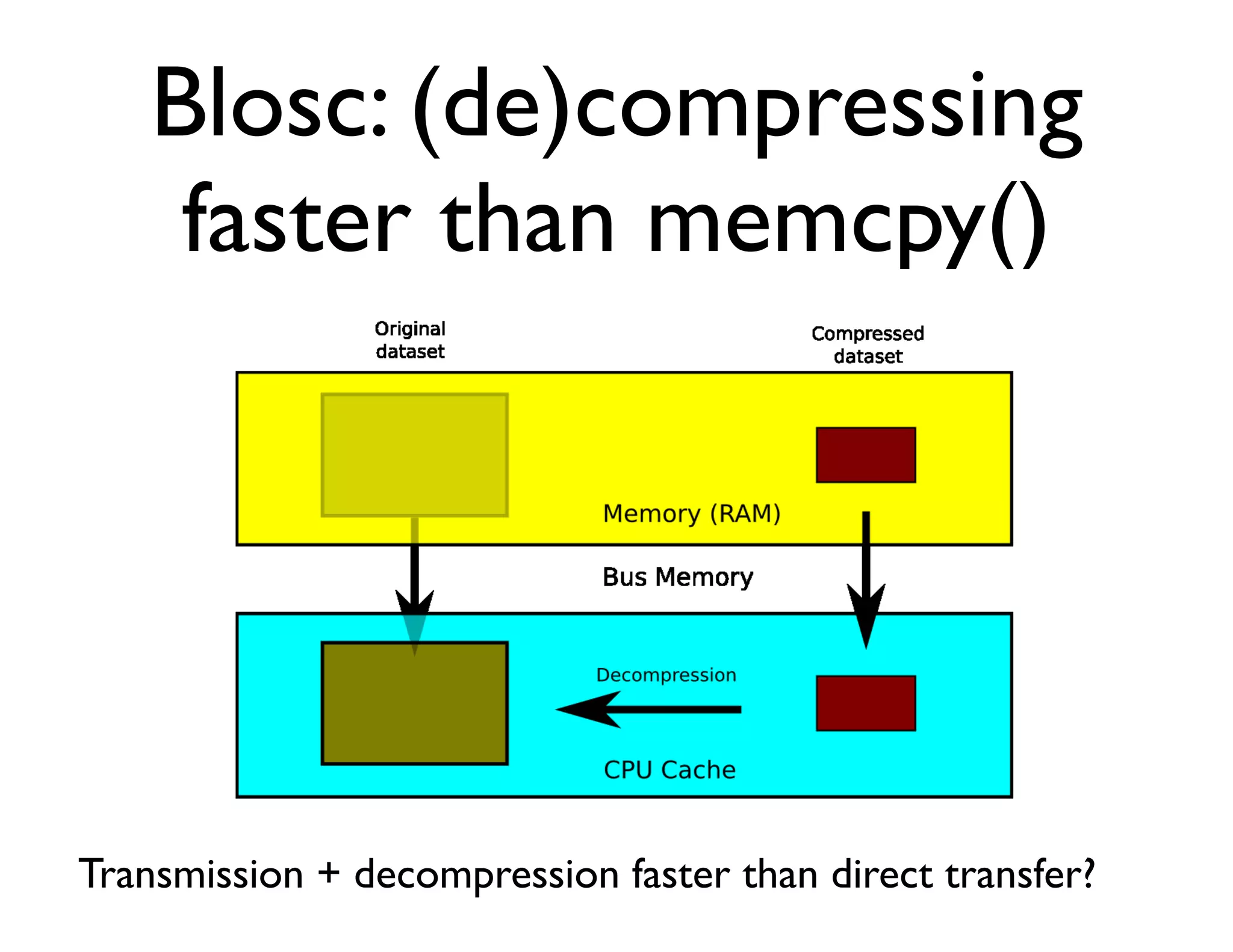
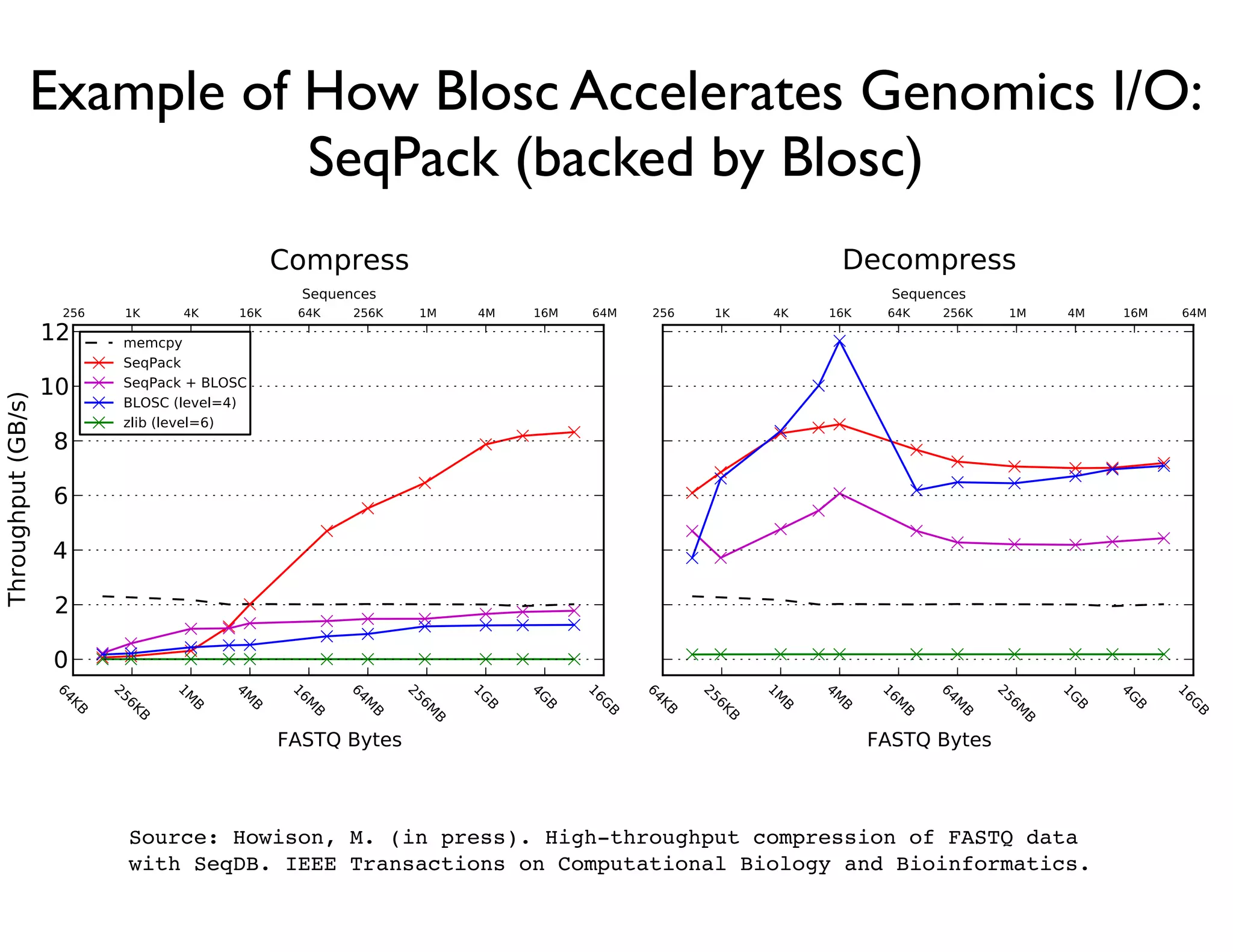
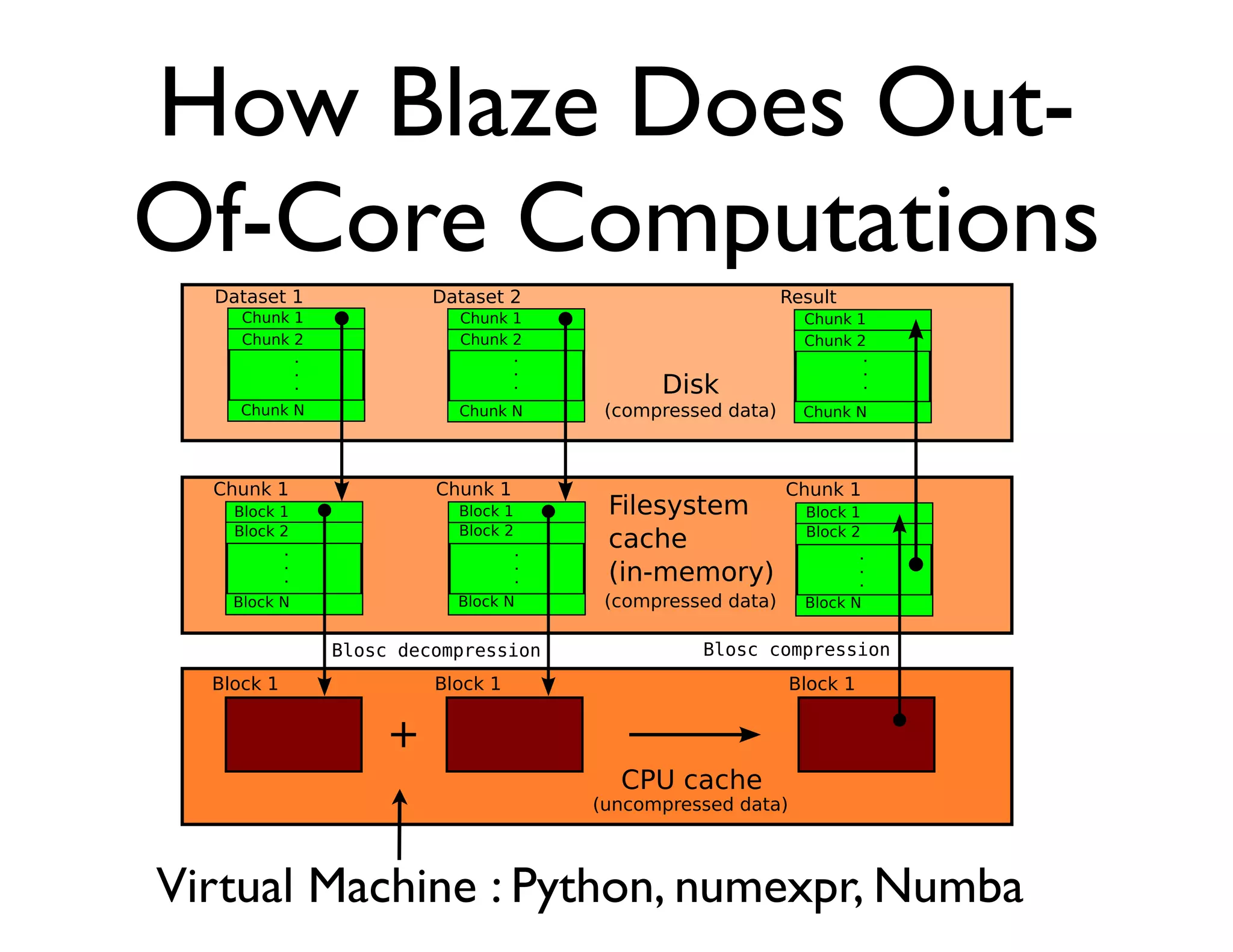
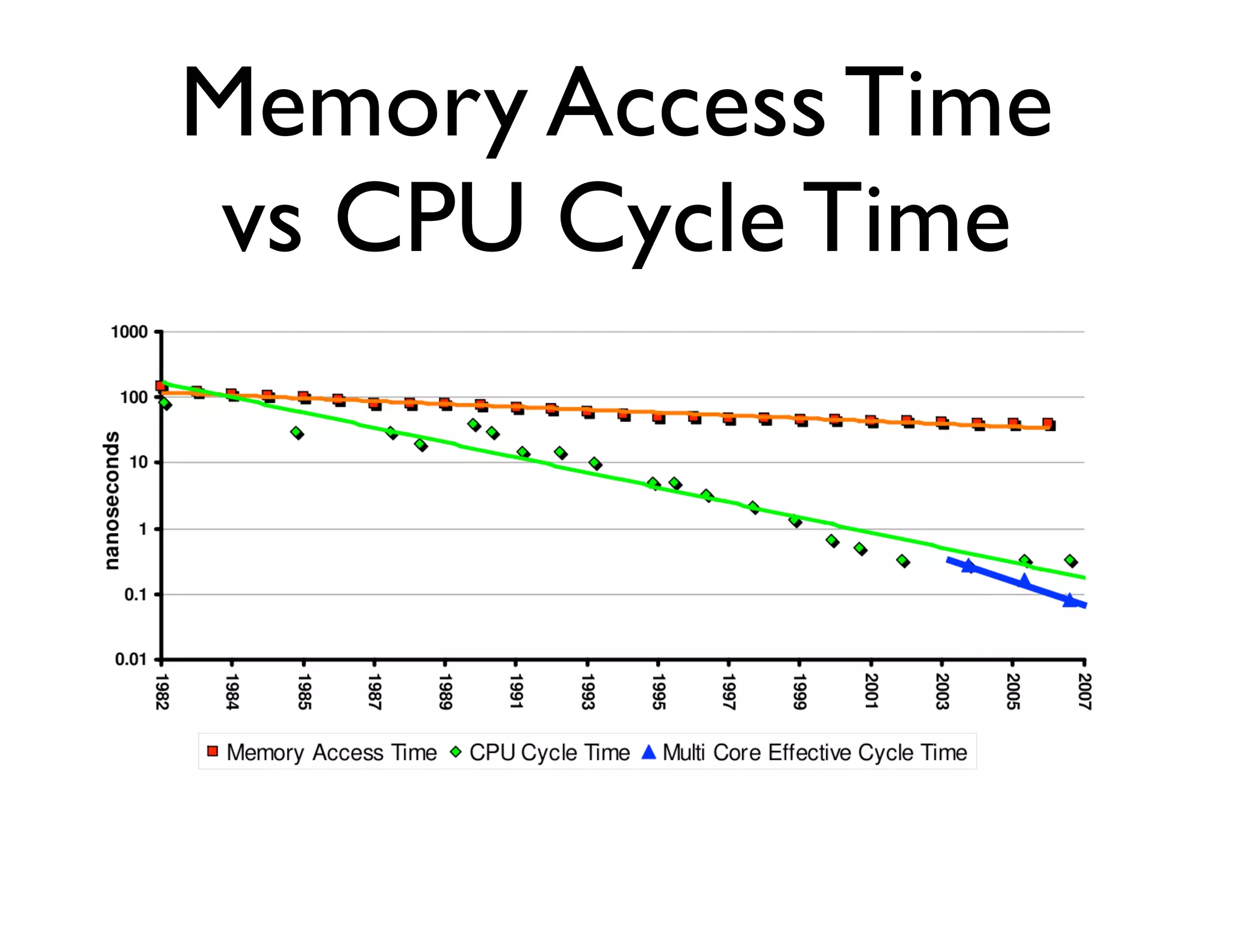
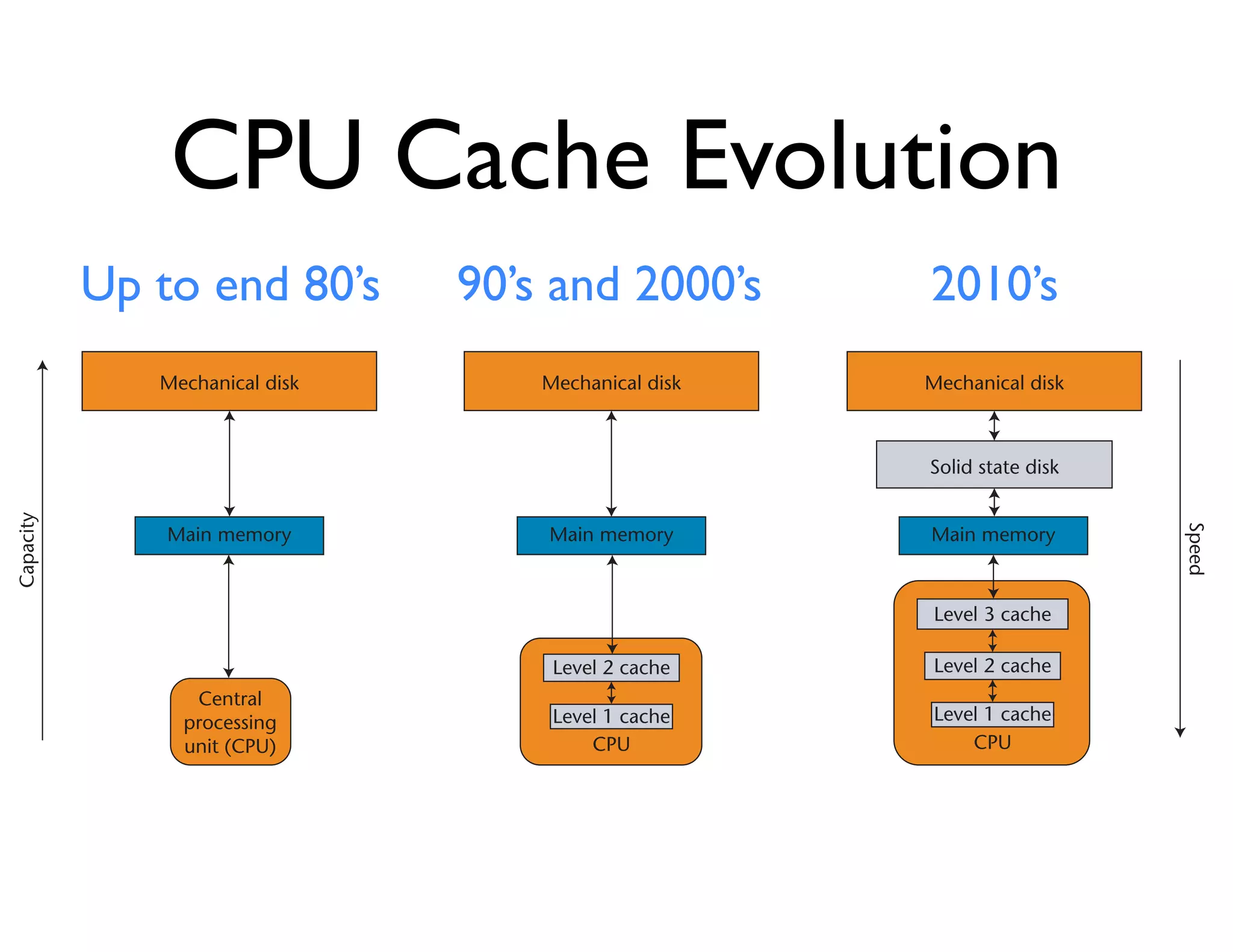
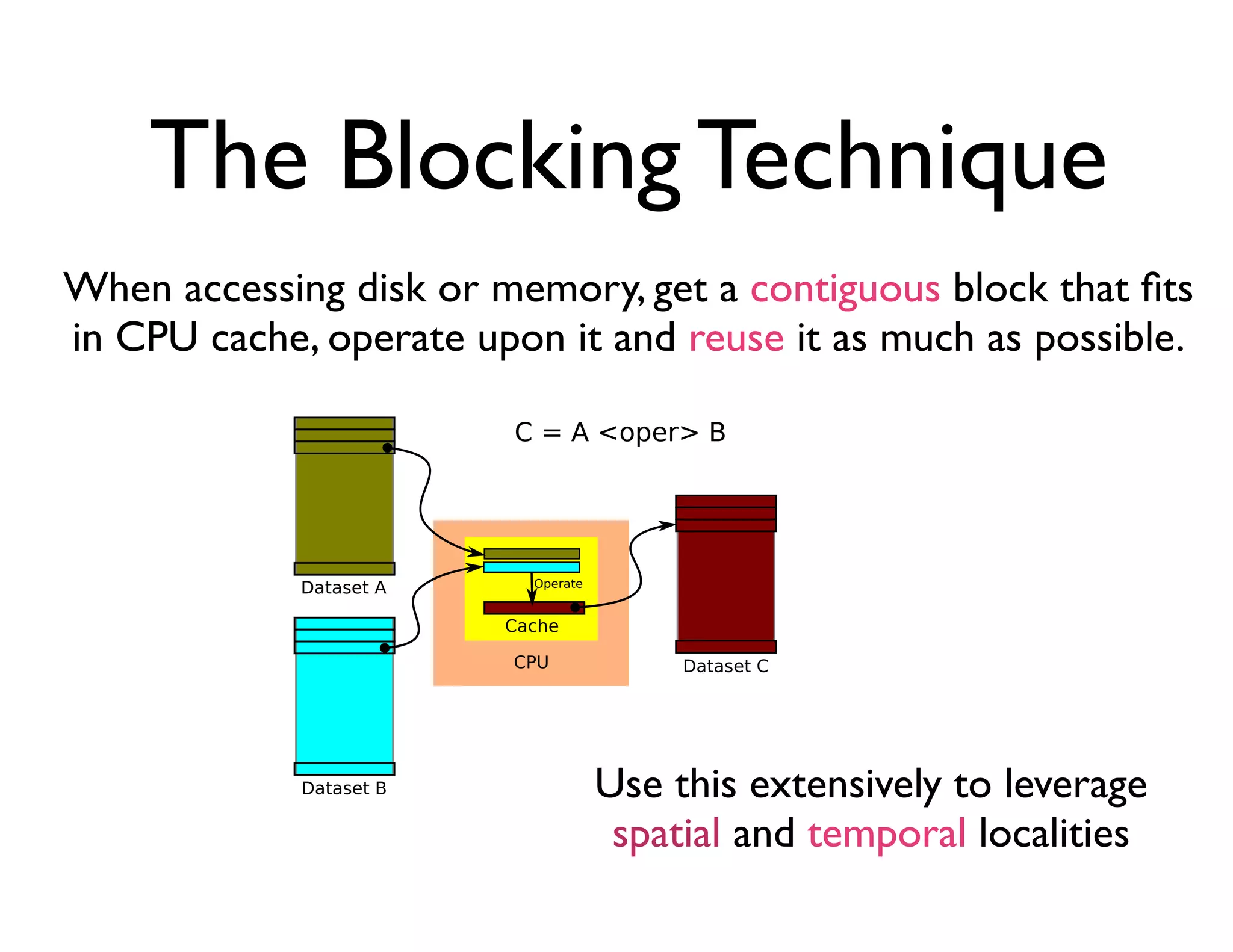
The document discusses the significance of memory access in handling big data, emphasizing that optimal data structures and containers are crucial for performance. It highlights the advantages of using Python and libraries like NumPy and Numba for data computation, illustrating the efficiency improvements through examples and comparisons. The presentation concludes by stressing the importance of selecting appropriate data containers for effective big data management.

1. It´s The Memory,
Stupid!
or:
How I Learned to Stop Worrying about CPU Speed
and Love Memory Access
Francesc Alted
Software Architect
Big Data Spain 2012, Madrid (Spain)
November 16, 2012

2. About Continuum
Analytics
• Develop new ways on how data is
stored, computed, and visualized.
• Provide open technologies for Data
Integration on a massive scale.
• Provide software tools, training, and
integration/consulting services to
corporate, government, and educational
clients worldwide.

3. Overview
• The Era of ‘Big Data’
• A few words about Python and NumPy
• The Starving CPU problem
• Choosing optimal containers for Big Data

4. “A wind of streaming data, social data
and unstructured data is knocking at
the door, and we're starting to let it in.
It's a scary place at the moment.”
-- Unidentified bank IT executive, as
quoted by “The American Banker”
The Dawn of ‘Big Data’

5. Challenges
• We have to deal with as much data as
possible by using limited resources
• So, we must use our computational
resources optimally to be able to get the
most out of Big Data

6. Interactivity and Big
Data
• Interactivity is crucial for handling data
• Interactivity and performance are crucial
for handling Big Data

7. Python and ‘Big Data’
• Python is an interpreted language and hence,
it offers interactivity
• Myth: “Python is slow, so why on the hell are
you going to use it for Big Data?”
• Answer: Python has access to an incredibly
powerful range of libraries that boost its
performance far beyond your expectations
• ...and during this talk I will prove it!

8. NumPy: A Standard ‘De
Facto’ Container

9. 


 

10. Operating
with NumPy
• array[2]; array[1,1:5, :]; array[[3,6,10]]
• (array1**3 / array2) - sin(array3)
• numpy.dot(array1, array2): access to
optimized BLAS (*GEMM) functions
• and much more...

11. Nothing Is Perfect
• NumPy is just great for many use cases
• However, it also has its own deficiencies:
• Follows the Python evaluation order in complex
expressions like : (a * b) + c
• Does not have support for multiprocessors
(except for BLAS computations)

12. Numexpr: Dealing with
Complex Expressions
• It comes with a specialized virtual machine
for evaluating expressions
• It accelerates computations mainly by
making a more efficient memory usage
• It supports extremely easy to use
multithreading (active by default)

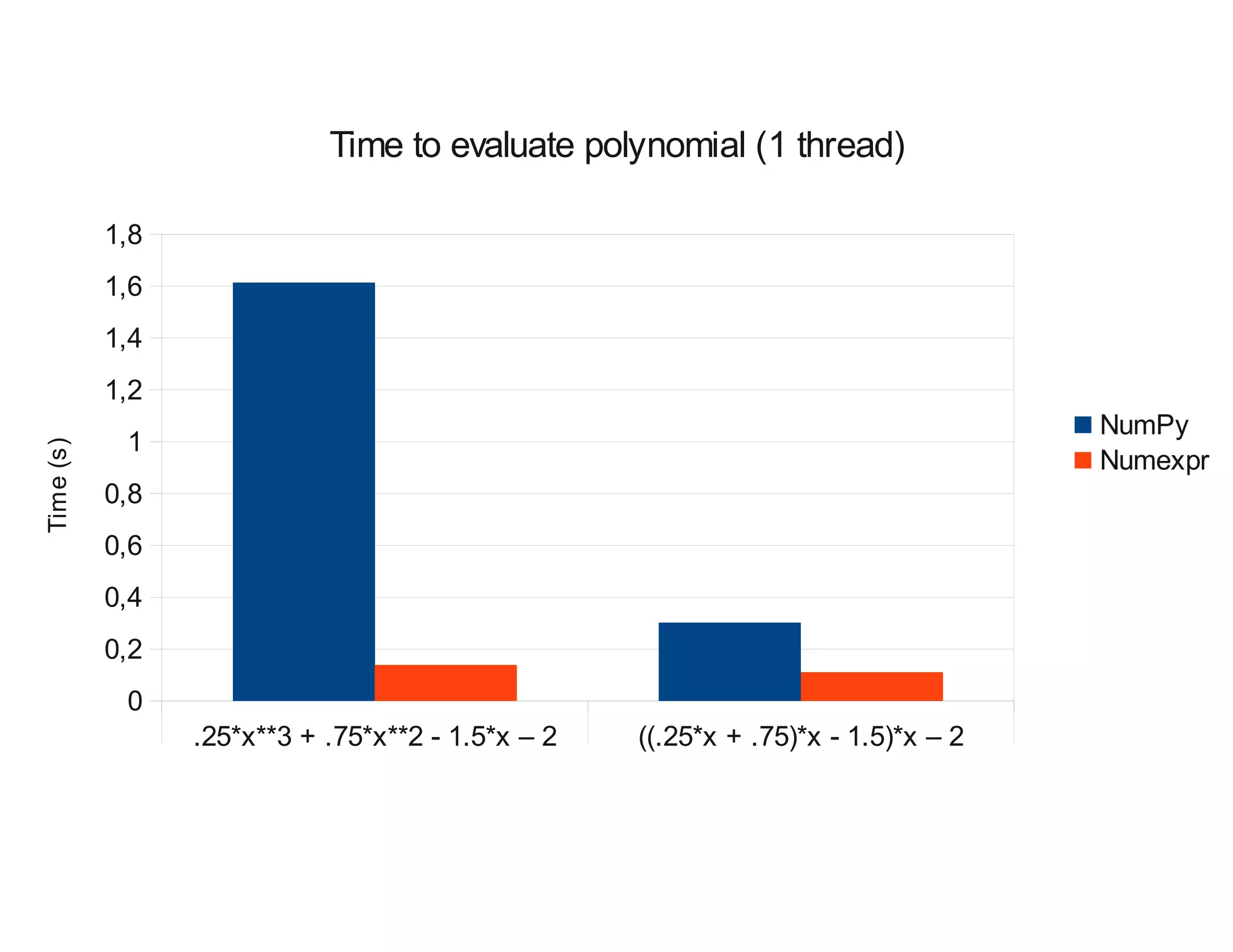
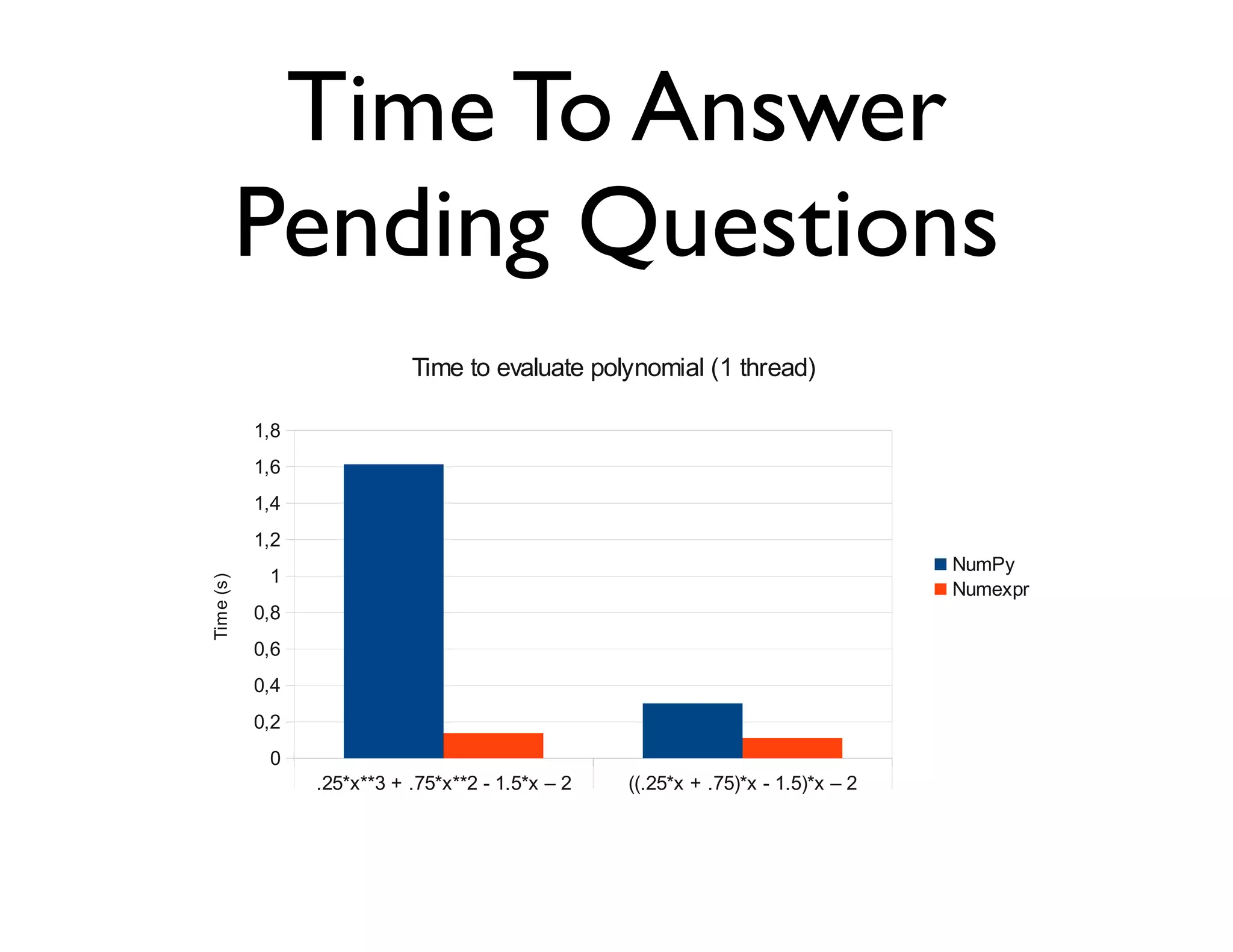
13. Exercise (I)
Evaluate the next polynomial:
0.25x3 + 0.75x2 + 1.5x - 2
in the range [-1, 1] with a step size of 2*10-7,
using both NumPy and numexpr.
Note: use a single processor for numexpr
numexpr.set_num_threads(1)

14. Exercise (II)
Rewrite the polynomial in this notation:
((0.25x + 0.75)x + 1.5)x - 2
and redo the computations.
What happens?

15. ((.25*x + .75)*x - 1.5)*x – 2 0,301 0,11
x 0,052 0,045
sin(x)**2+cos(x)**2 0,715 0,559
Time to evaluate polynomial (1 thread)
1,8
1,6
1,4
1,2
NumPy
1
Time (s)
Numexpr
0,8
0,6
0,4
0,2
0
.25*x**3 + .75*x**2 - 1.5*x – 2 ((.25*x + .75)*x - 1.5)*x – 2
NumPy vs Numexpr (1 thread)
1,8

16. Power Expansion
Numexpr expands expression:
0.25x3 + 0.75x2 + 1.5x - 2
to:
0.25x*x*x + 0.75x*x + 1.5x*x - 2
so, no need to use transcendental pow()

17. Pending question
• Why numexpr continues to be 3x faster
than NumPy, even when both are executing
exactly the *same* number of operations?

18. “Across the industry, today’s chips are largely
able to execute code faster than we can feed
them with instructions and data.”
– Richard Sites, after his article
“It’s The Memory, Stupid!”,
Microprocessor Report, 10(10),1996
The Starving CPU
Problem

19. Memory Access Time
vs CPU Cycle Time

20. Book in
2009

21. The Status of CPU
Starvation in 2012
• Memory latency is much slower (between
250x and 500x) than processors.
• Memory bandwidth is improving at a better
rate than memory latency, but it is also
slower than processors (between 30x and
100x).

22. CPU Caches to the
Rescue
• CPU cache latency and throughput
are much better than memory
• However: the faster they run the
smaller they must be

23. CPU Cache Evolution
Up to end 80’s 90’s and 2000’s 2010’s
Mechanical disk Mechanical disk Mechanical disk
Solid state disk
Capacity
Speed
Main memory Main memory Main memory
Level 3 cache
Level 2 cache Level 2 cache
Central
processing Level 1 cache Level 1 cache
unit (CPU) CPU CPU
(a) (b) (c)
Figure 1. Evolution of the hierarchical memory model. (a) The primordial (and simplest) model; (b) the most common current
implementation, which includes additional cache levels; and (c) a sensible guess at what’s coming over the next decade:
three levels of cache in the CPU and solid state disks lying between main memory and classical mechanical disks.

24. When CPU Caches Are
Effective?
Mainly in a couple of scenarios:
• Time locality: when the dataset is
reused
• Spatial locality: when the dataset is
accessed sequentially

25. The Blocking Technique
When accessing disk or memory, get a contiguous block that fits
in CPU cache, operate upon it and reuse it as much as possible.

 

 
 Use this extensively to leverage
spatial and temporal localities

26. Time To Answer NumPy
Pending Questions
.25*x**3 + .75*x**2 - 1.5*x – 2
((.25*x + .75)*x - 1.5)*x – 2
x
NumPy
1,613
0,301
0,052
Numexpr
0,138
0,11
0,045
sin(x)**2+cos(x)**2 0,715 0,559
Time to evaluate polynomial (1 thread)
1,8
1,6
1,4
1,2
NumPy
1
Time (s)
Numexpr
0,8
0,6
0,4
0,2
0
.25*x**3 + .75*x**2 - 1.5*x – 2 ((.25*x + .75)*x - 1.5)*x – 2
NumPy vs Numexpr (1 thread)
1,8

27. 


   



28. 


   



29. Beyond numexpr:
Numba

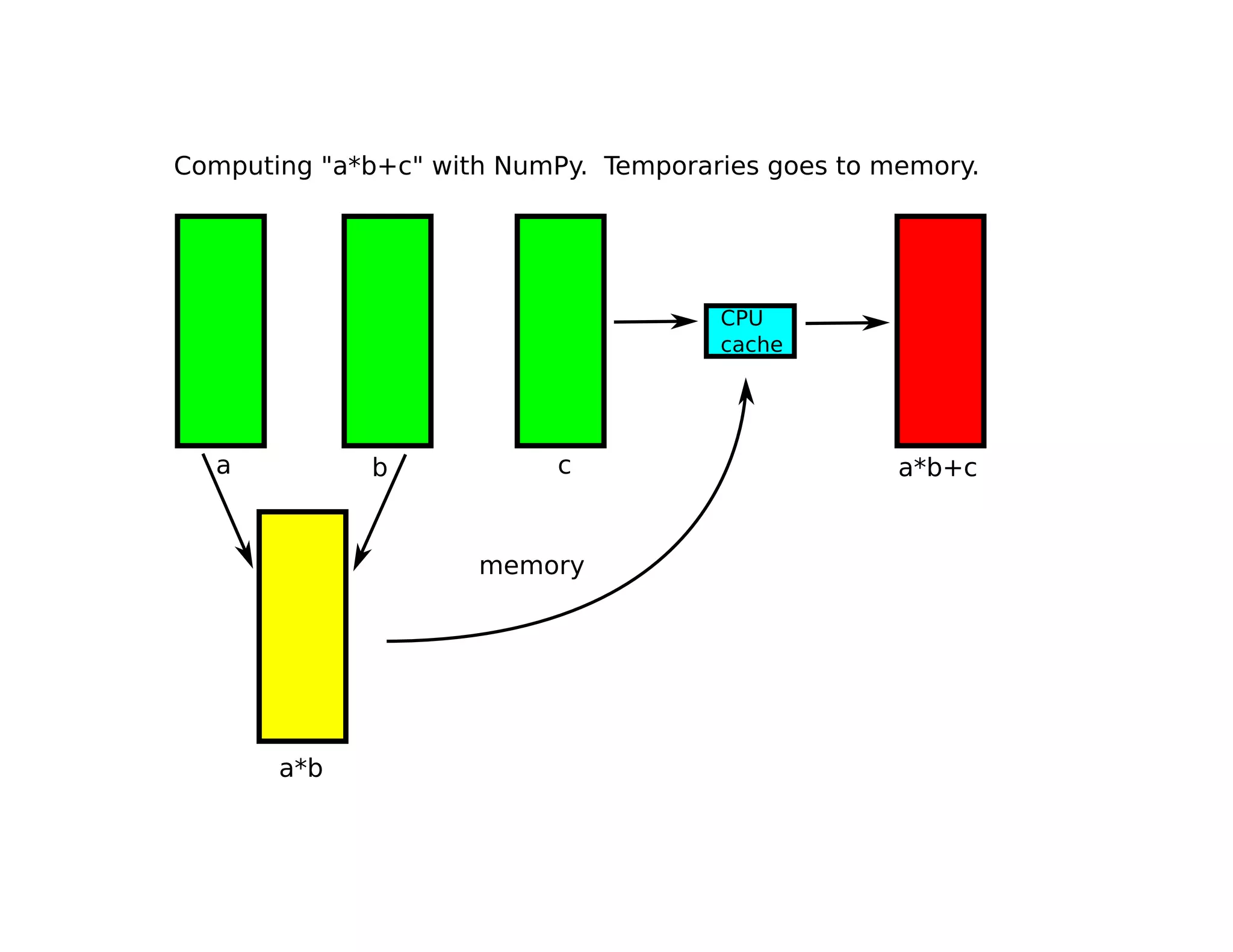
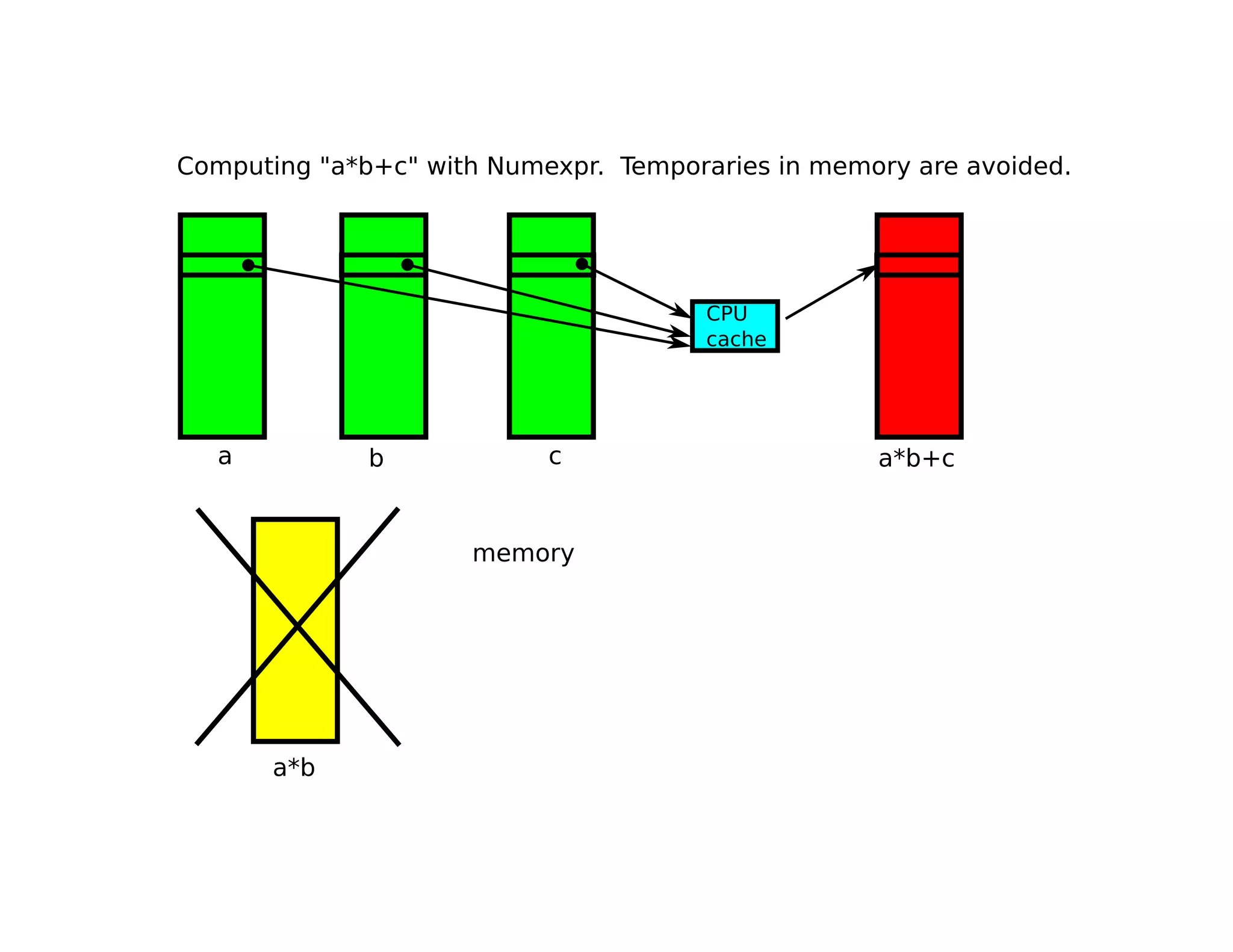
30. Numexpr Limitations
• Numexpr only implements element-wise
operations, i.e. ‘a*b’ is evaluated as:
for i in range(N):
c[i] = a[i] * b[i]
• In particular, it cannot deal with things like:
for i in range(N):
c[i] = a[i-1] + a[i] * b[i]

31. Numba: Overcoming
numexpr Limitations
• Numba is a JIT that can translate a subset
of the Python language into machine code
• It uses LLVM infrastructure behind the
scenes
• Can achieve similar or better performance
than numexpr, but with more flexibility

32. How Numba Works
Python Function Machine Code
LLVM-PY
LLVM 3.1
ISPC OpenCL OpenMP CUDA CLANG
Intel AMD Nvidia Apple

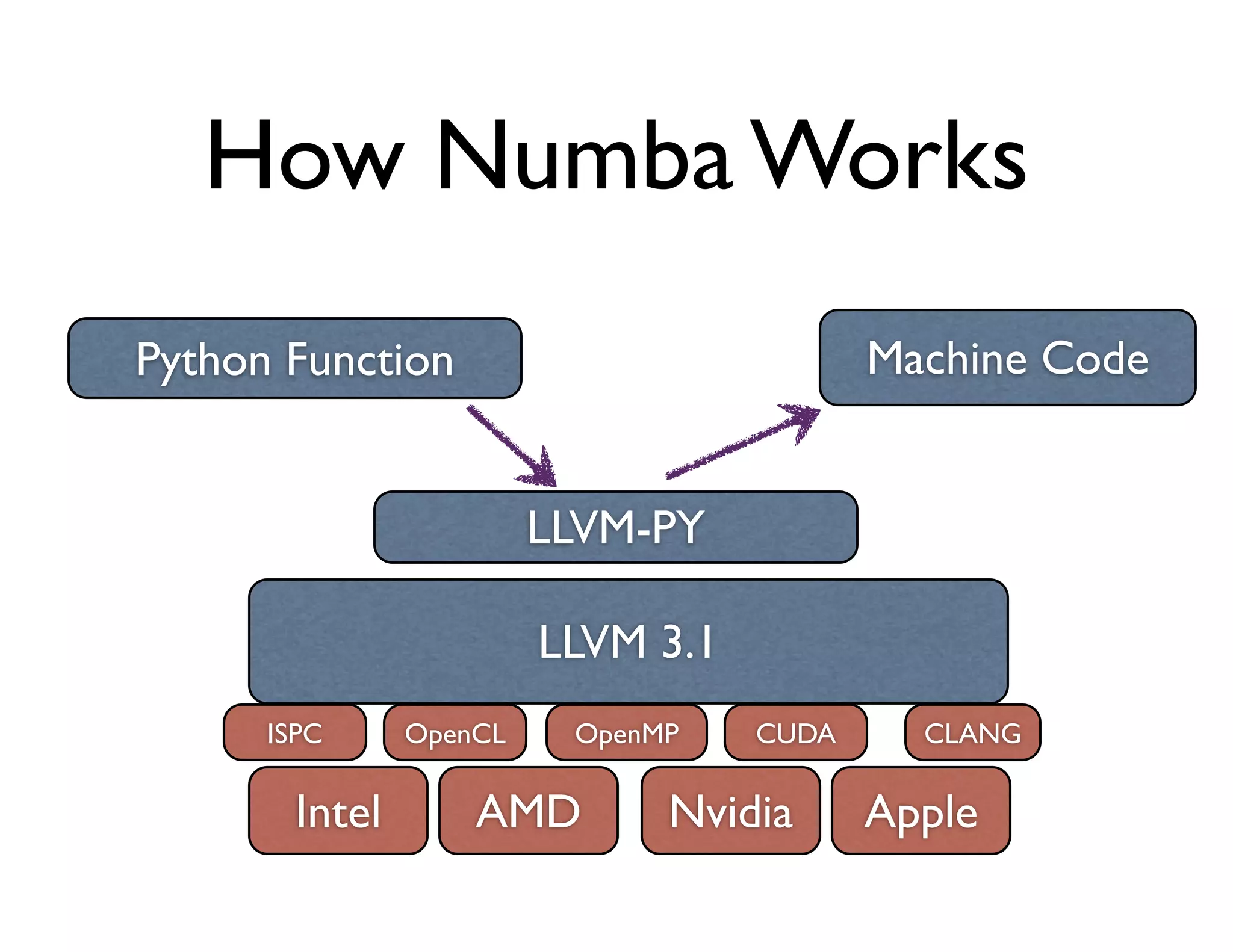
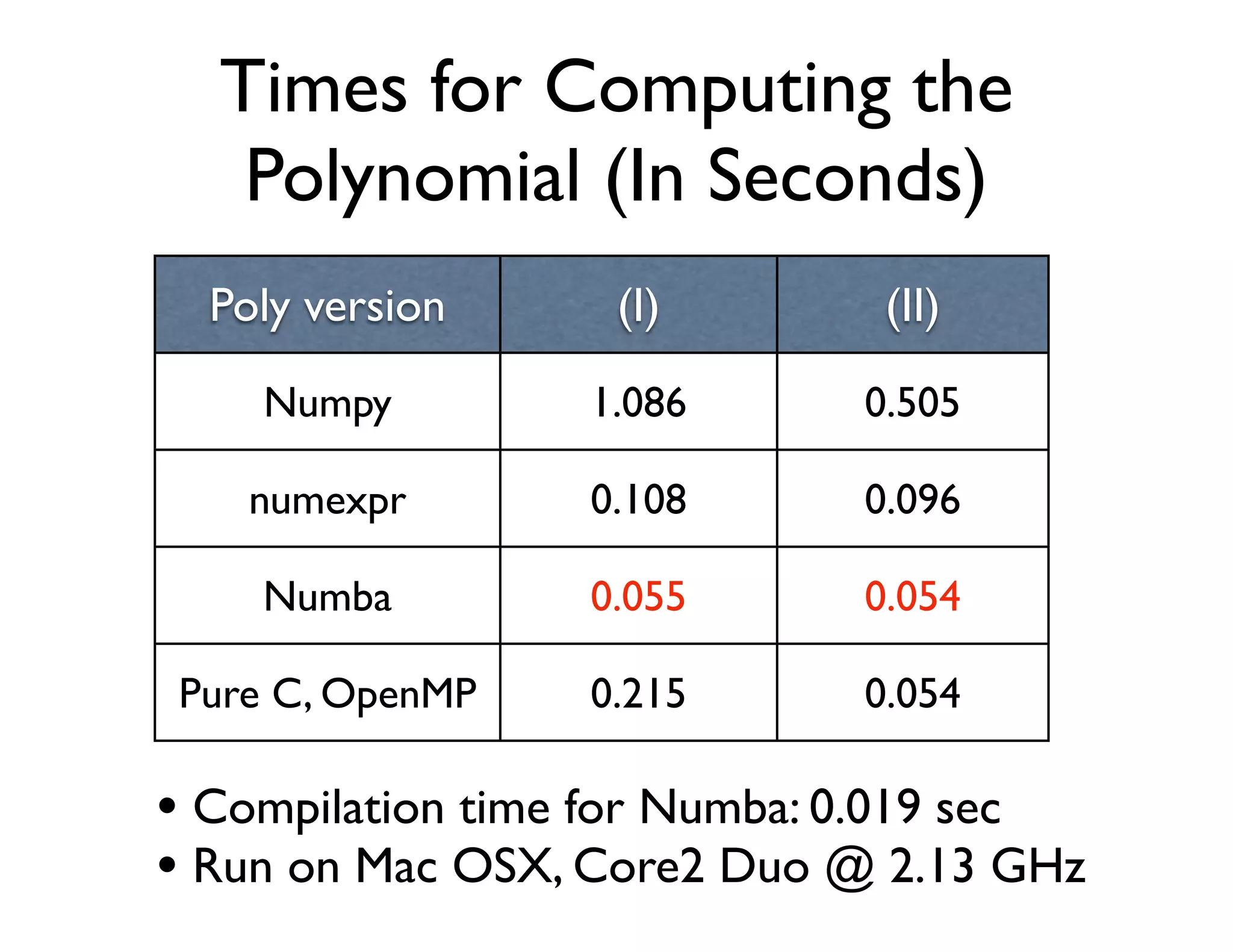
33. Numba Example:
Computing the Polynomial
import numpy as np
import numba as nb
N = 10*1000*1000
x = np.linspace(-1, 1, N)
y = np.empty(N, dtype=np.float64)
@nb.jit(arg_types=[nb.f8[:], nb.f8[:]])
def poly(x, y):
for i in range(N):
# y[i] = 0.25*x[i]**3 + 0.75*x[i]**2 + 1.5*x[i] - 2
y[i] = ((0.25*x[i] + 0.75)*x[i] + 1.5)*x[i] - 2
poly(x, y) # run through Numba!

34. Times for Computing the
Polynomial (In Seconds)
Poly version (I) (II)
Numpy 1.086 0.505
numexpr 0.108 0.096
Numba 0.055 0.054
Pure C, OpenMP 0.215 0.054
• Compilation time for Numba: 0.019 sec
• Run on Mac OSX, Core2 Duo @ 2.13 GHz

35. Numba: LLVM for
Python
Python code can reach C
speed without having to
program in C itself
(and without losing interactivity!)

36. Numba in SC 2012

37. Numba in SC2012
Awesome Python!

38. If a datastore requires all data to fit in
memory, it isn't big data
-- Alex Gaynor (in twitter)
Optimal Containers for
Big Data

39. The Need for a Good
Data Container
• Too many times we are too focused on
computing as fast as possible
• But we have seen how important data
access is
• Hence, having an optimal data structure is
critical for getting good performance when
processing very large datasets

40. Appending Data in
Large NumPy Objects
array to be enlarged final array object
Copy!
New memory
new data to append
allocation
• Normally a realloc() syscall will not succeed
• Both memory areas have to exist simultaneously

41. Contiguous vs Chunked
NumPy container Blaze container
chunk 1
chunk 2
.
.
.
chunk N
Contiguous memory Discontiguous memory

42. Appending data in Blaze
array to be enlarged final array object
X
chunk 1 chunk 1
chunk 2 chunk 2
compress
new data to append new chunk
Only a small amount of data has to be compressed

43. Blosc: (de)compressing
faster than memcpy()
Transmission + decompression faster than direct transfer?

44. TABLE 1
Test Data Sets
Example of How Blosc Accelerates Genomics I/O:
#
1
Source
1000 Genomes
Identifier
ERR000018
Sequencer
Illumina GA
Read Count
9,280,498
Read Length
36 bp
ID Lengths
40–50
FASTQ Size
1,105 MB
2
3 SeqPack (backed by Blosc)
1000 Genomes
1000 Genomes
SRR493233 1
SRR497004 1
Illumina HiSeq 2000
AB SOLiD 4
43,225,060
122,924,963
100 bp
51 bp
51–61
78–91
10,916 MB
22,990 MB
g. 1. In-memory throughputs for several compression schemes applied to increasing block sizes (where each
equence is 256 bytes Howison, M. (in press). High-throughput compression of FASTQ data
Source:
long).
with SeqDB. IEEE Transactions on Computational Biology and Bioinformatics.
to a memory buffer, timed the compression of block consistent throughput across both compression and

45. How Blaze Does Out-
Of-Core Computations
  
  
  
  
  
   
   
  
   
 
 
 




  

   
 
  



Virtual Machine : Python, numexpr, Numba

46. Last Message for Today
Big data is tricky to manage:
Look for the optimal containers for
your data
Spending some time choosing your
appropriate data container can be a big time
saver in the long run

47. Summary
• Python is a perfect language for Big Data
• Nowadays you should be aware of the
memory system for getting good
performance
• Choosing appropriate data containers is of
the utmost importance when dealing with
Big Data

48. “El éxito del Big Data lo conseguirán
aquellos desarrolladores que sean capaces
de mirar más allá del standard y sean
capaces de entender los recursos hardware
subyacentes y la variedad de algoritmos
disponibles.”
-- Oscar de Bustos, HPC Line of Business
Manager at BULL

49. ¡Gracias!