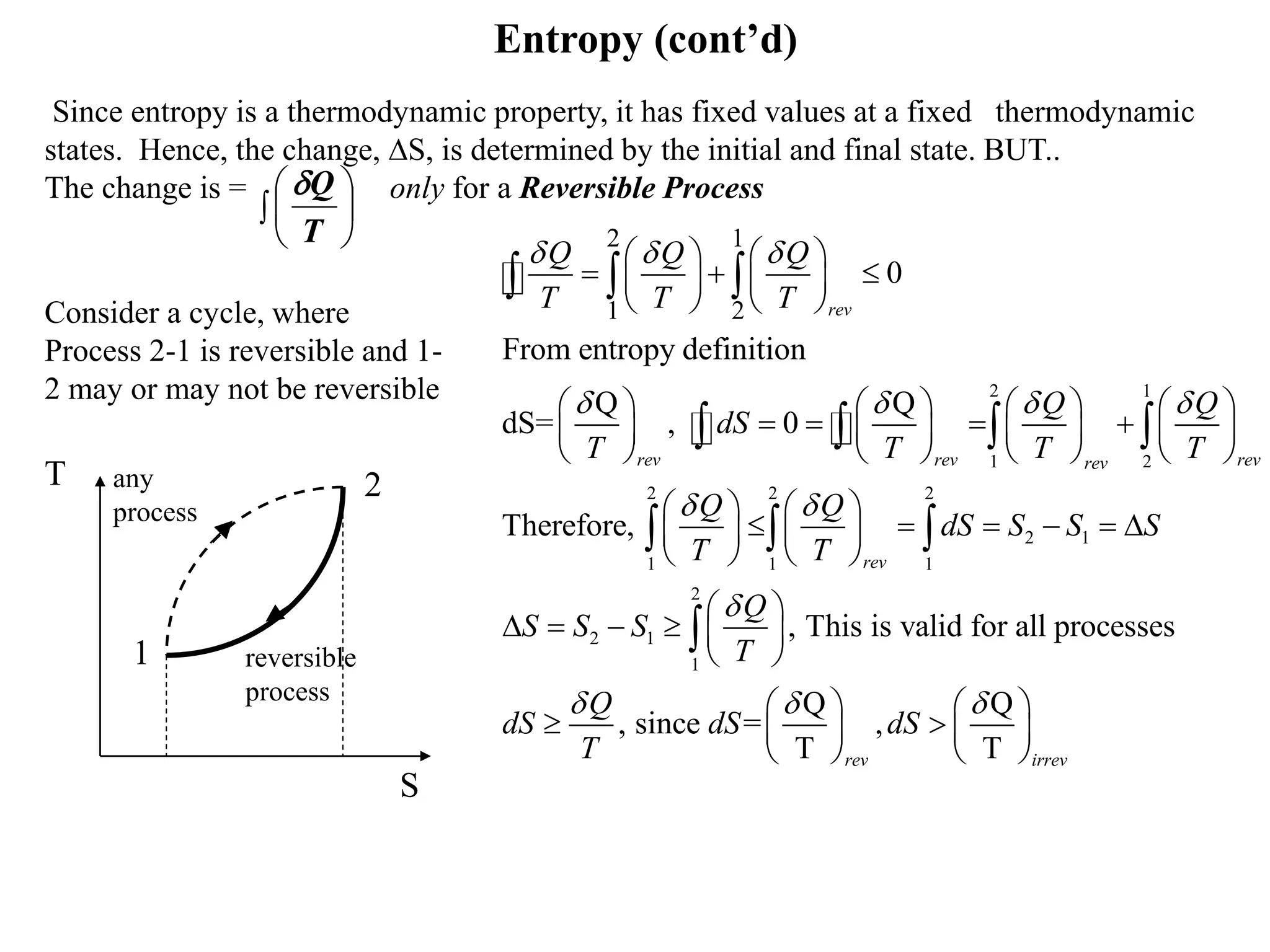
This document discusses entropy, a thermodynamic property that represents disorder in a system. It defines entropy using the Clausius inequality and introduces the increase of entropy principle, which states that entropy always increases or stays the same for isolated systems. The key points made are: - Entropy is defined using the Clausius inequality and can be viewed as a measure of disorder. - The increase of entropy principle is another formulation of the second law of thermodynamics and means entropy can increase but not decrease. - The entropy balance equation accounts for entropy changes, transfers, and generation in thermodynamic processes. Entropy generation must be greater than or equal to zero.

1. Entropy (YAC- Ch. 6)
• Introduce the thermodynamic property called Entropy (S)
• Entropy is defined using the Clausius inequality
• Introduce the Increase of Entropy Principle which states that
– the entropy for an isolated system (or a system plus its surroundings) is
always increases or, at best, remains the same.
– Second Law in terms of Entropy
• Learn to use the Entropy balance equation: entropy change = entropy
transfer + entropy change.
• Analyze entropy changes in thermodynamic process and learn how to
use thermodynamic tables
• Examine entropy relationships (Tds relations), entropy relations for
ideal gases.
• Property diagrams involving entropy (T-s and h-s diagrams)
In this Chapter, we will:
Entrpy.ppt, 10/18/01 pages

2. Entropy – A Property
• Entropy is a thermodynamic property; it can be viewed as a measure of disorder.
i.e. More disorganized a system the higher its entropy.
• Defined using Clausius inequality
where Q is the differential heat transfer & T is the absolute
temperature at the boundary where the heat transfer occurs
• Clausius inequality is valid for all cycles, reversible and irreversible.
• Consider a reversible Carnot cycle:
th, from Carnot efficiceny 1 1 ,
Q Q
Therefore, 0 for a reversible Carnot cycle 0
T T
H L L L L L
H L H H H H
rev
Q Q Q Q T Q T
T T T Q T Q T


 
      
 
  
 

 
• Since , i.e. it does not change if you return to the same state,
it must be a property, by defintion:
• Let’s define a thermodynamic property entropy (S), such that
2 2
2 1
1 1
, for any reversible process dS
The change of entropy can be defined based on a reversible process
rev rev
Q Q
dS S S
T T
 
    
0 





revT
Q
0 





revT
Q
True for a Reversible
Process only

3. Entropy (cont’d)
Since entropy is a thermodynamic property, it has fixed values at a fixed thermodynamic
states. Hence, the change, S, is determined by the initial and final state. BUT..
The change is = only for a Reversible Process
1
2
reversible
process
any
process
T
S
2 1
1 2
2 2 2
2 1
1 1 1
2 1
2 1
1 2
0
From entropy definition
Q Q
dS= , 0
Therefore,
rev
rev rev revrev
rev
Q Q Q
T T T
Q Q
dS
T T T T
Q Q
dS S S S
T T
Q
S S S
T
  
   
 

   
     
   
       
          
       
   
        
   
 
     
 
  
   
  
2
1
, This is valid for all processes
Q Q
, since = ,
T Trev irrev
Q
dS dS dS
T
     
    
   

 





T
Q
Consider a cycle, where
Process 2-1 is reversible and 1-
2 may or may not be reversible

4. Increase of Entropy Principle (YAC- Ch. 6-3)
2
2 1 gen
1
2 2
2 1
1 1
, define entropy generation S
where 0. If the system is isolated and "no" heat transfer
The entropy will still increase or stay
system gen
gen
Q
S S S
T
Q Q
S S S S
T T
S

 
 
     
 
   
        
   


 
the same but never decrease
0, entropy increase principlesystem genS S  
Implications:
•Entropy, unlike energy, is non-conservative since it is always increasing.
•The entropy of the universe is continuously increasing, in other words, it is becoming
disorganized and is approaching chaotic.
• The entropy generation is due to the presence of irreversibilities. Therefore, the higher the
entropy generation the higher the irreversibilities and, accordingly, the lower the efficiency
of a device since a reversible system is the most efficient system.
• The above is another statement of the second law
Entropy change
Entropy Transfer
(due to heat transfer)
Entropy Generation
The principle states that for an isolated Or a closed adiabatic Or System + Surroundings
A process can only take place such that Sgen 0 where Sge = 0 for a reversible process only
And Sge can never be les than zero.
Increase of Entropy Principle

5. Second Law & Entropy Balance (YAC- Ch. 6-4)
• Increase of Entropy Principle is another way of stating the Second Law of Thermodynamics:
Second Law : Entropy can be created but NOT destroyed
(In contrast, the first law states: Energy is always conserved)
•Note that this does not mean that the entropy of a system cannot be reduced, it can.
• However, total entropy of a system + surroundings cannot be reduced
• Entropy Balance is used to determine the Change in entropy of a system as follows:
Entropy change = Entropy Transfer + Entropy Generation where,
Entropy change = S = S2 - S1
Entropy Transfer = Transfer due to Heat (Q/T) + Entropy flow due to mass flow (misi – mese)
Entropy Generation = Sgen 0
For a Closed System: S2 - S1 = Qk /Tk + Sgen
In Rate Form: dS/dt = Qk /Tk + Sgen
For an Open System (Control Volume):
Similar to energy and mass conservation, the entropy balance equations can be simplified
Under appropriate conditions, e.g. steady state, adiabatic….
CVgeneeii
k
kcv
Ssmsm
T
Q
dt
dS
,




6. Entropy Generation Example
Show that heat can not be transferred from the low-temperature sink to the high-
temperature source based on the increase of entropy principle.
Source
800 K
Sink
500 K
Q=2000 kJ
S(source) = 2000/800 = 2.5 (kJ/K)
S(sink) = -2000/500 = -4 (kJ/K)
Sgen= S(source)+ S(sink) = -1.5(kJ/K) < 0
It is impossible based on the entropy increase principle
Sgen0, therefore, the heat can not transfer from low-temp. to
high-temp. without external work input
• If the process is reversed, 2000 kJ of heat is transferred from
the source to the sink, Sgen=1.5 (kJ/K) > 0, and the process can
occur according to the second law
• If the sink temperature is increased to 700 K, how about the entropy generation?
S(source) = -2000/800 = -2.5(kJ/K)
S(sink) = 2000/700 = 2.86 (kJ/K)
Sgen= S(source)+ S(sink) = 0.36 (kJ/K) < 1.5 (kJ/K)
Entropy generation is less than when the sink temperature is 500 K, less irreversibility.
Heat transfer between objects having large temperature difference generates higher degree
of irreversibilities