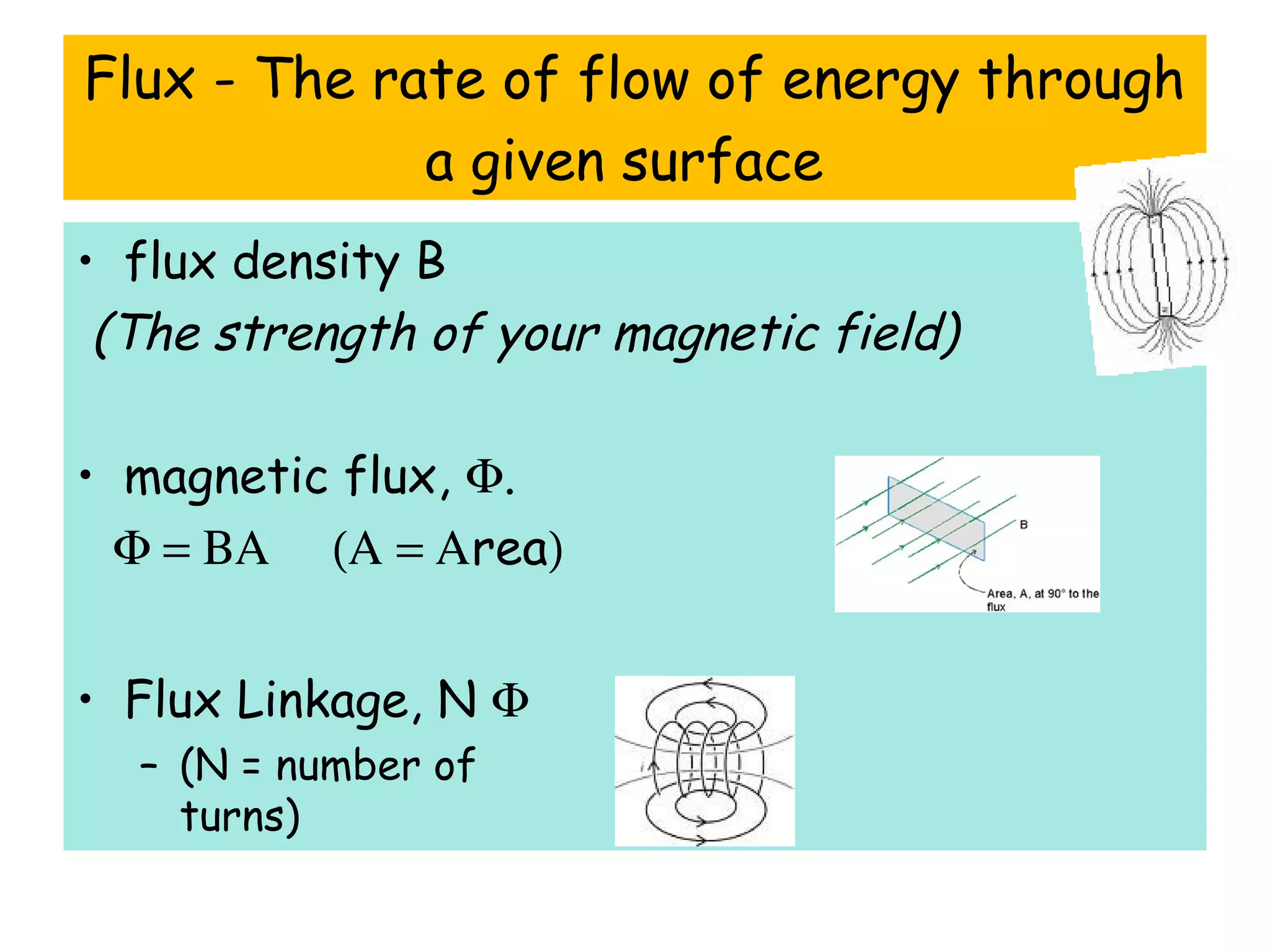
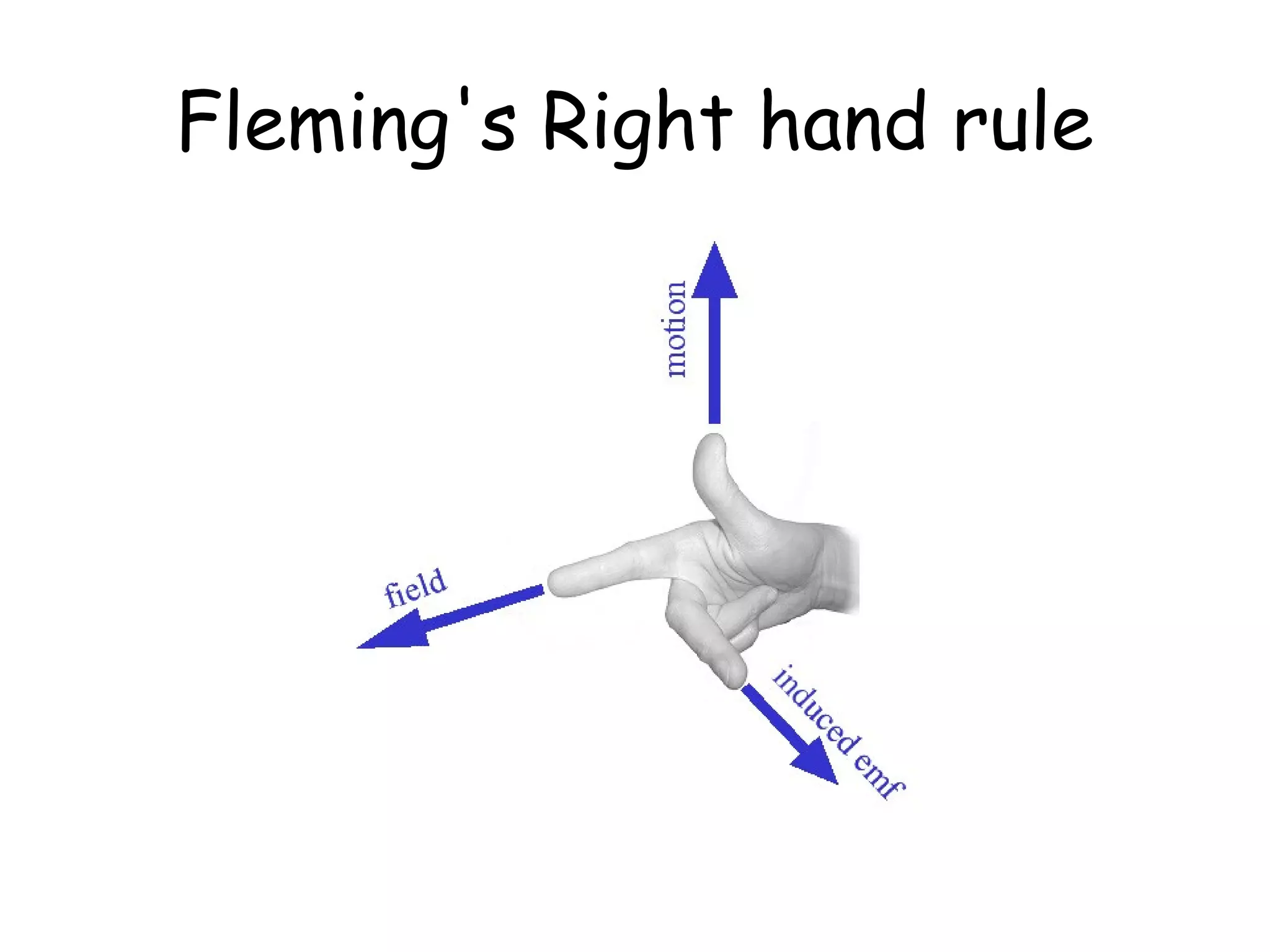
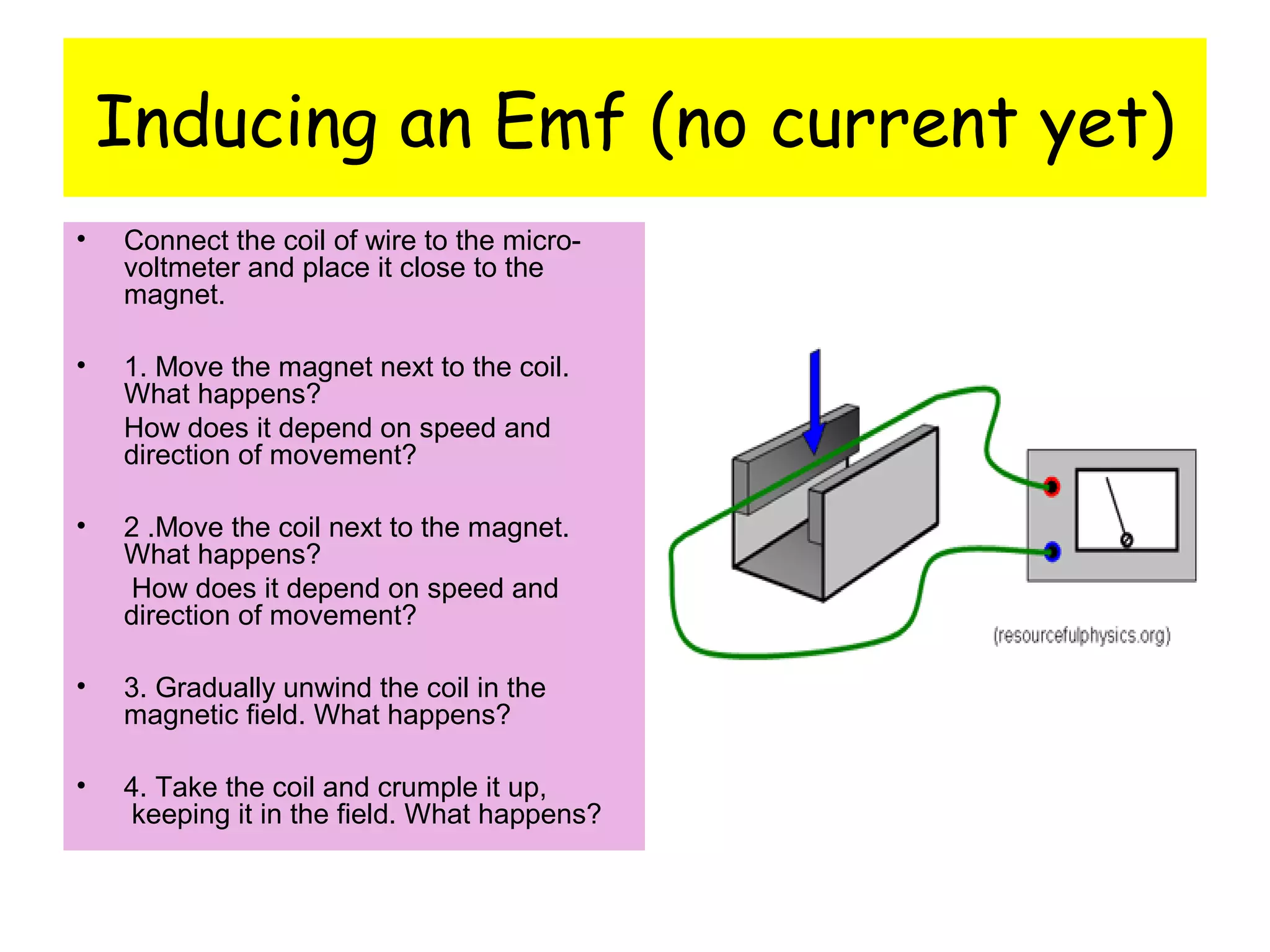
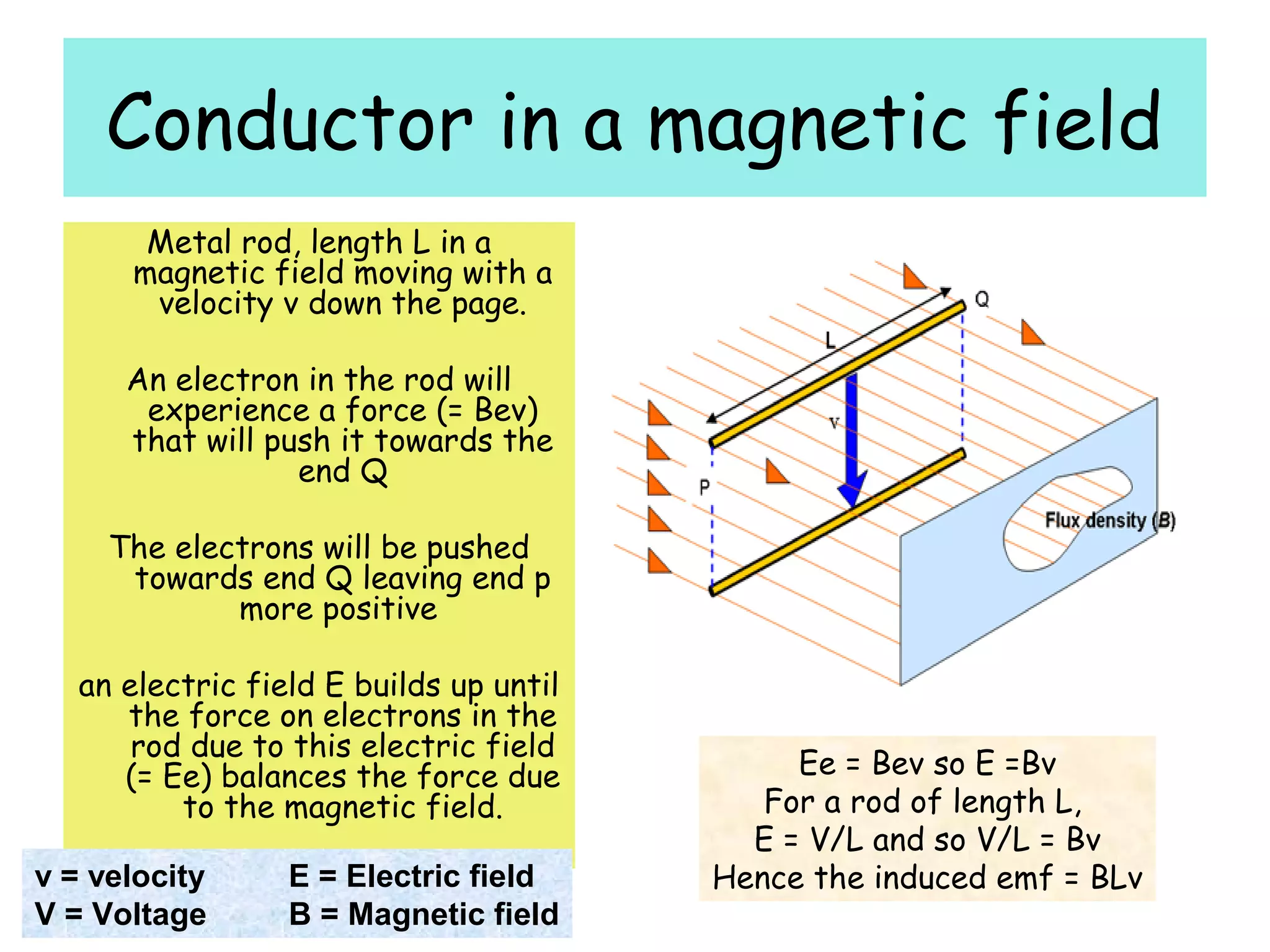
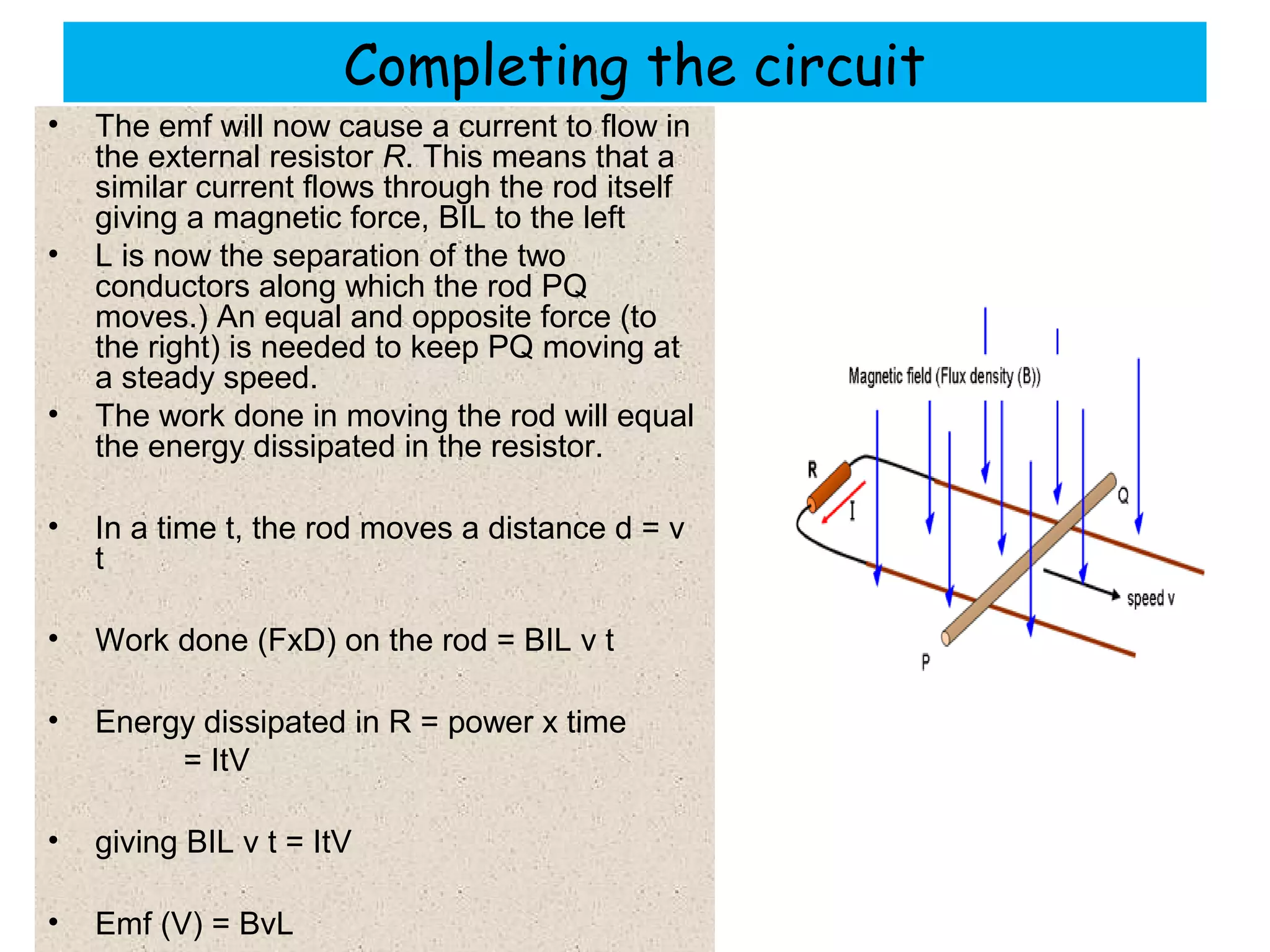
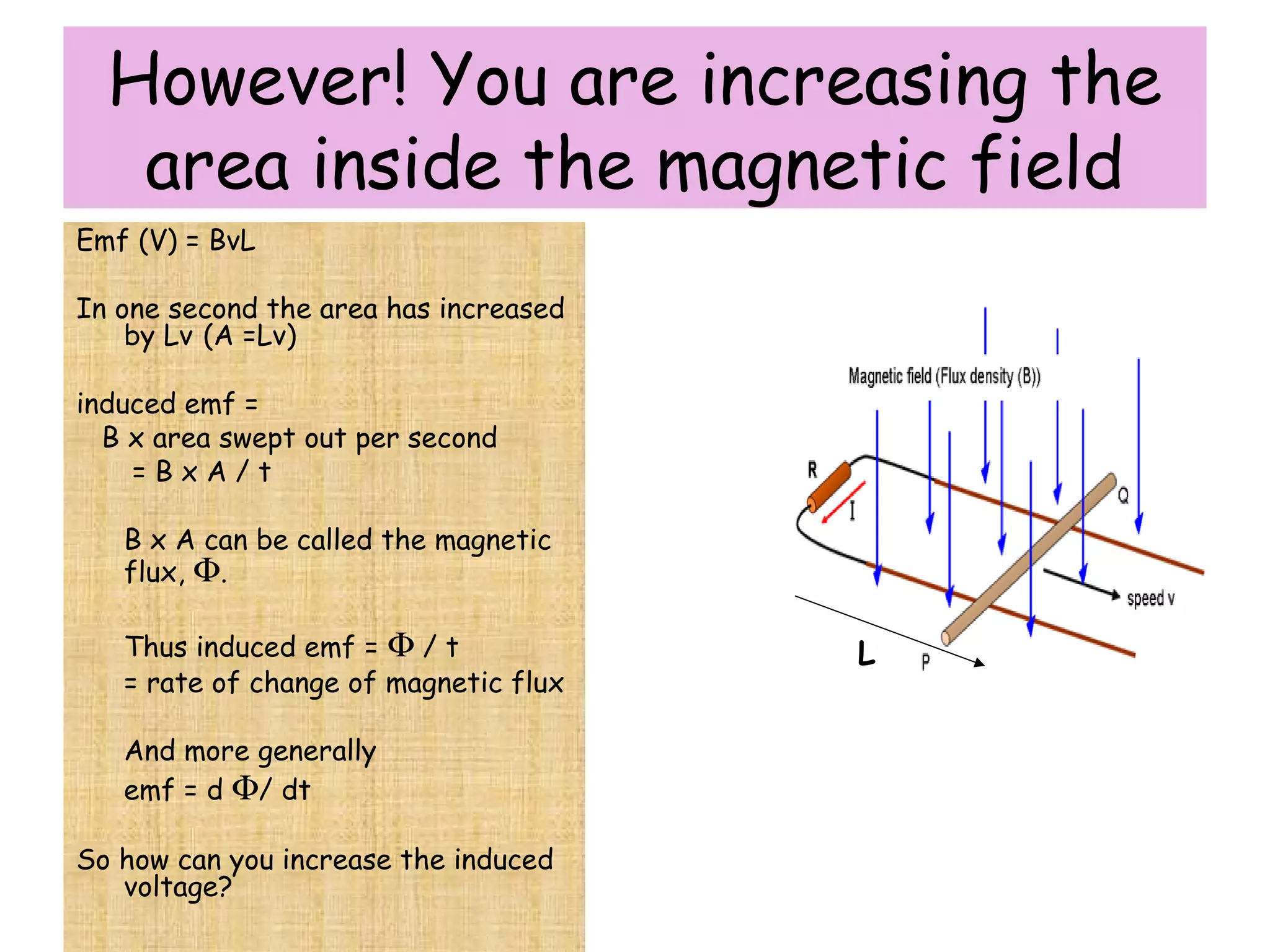
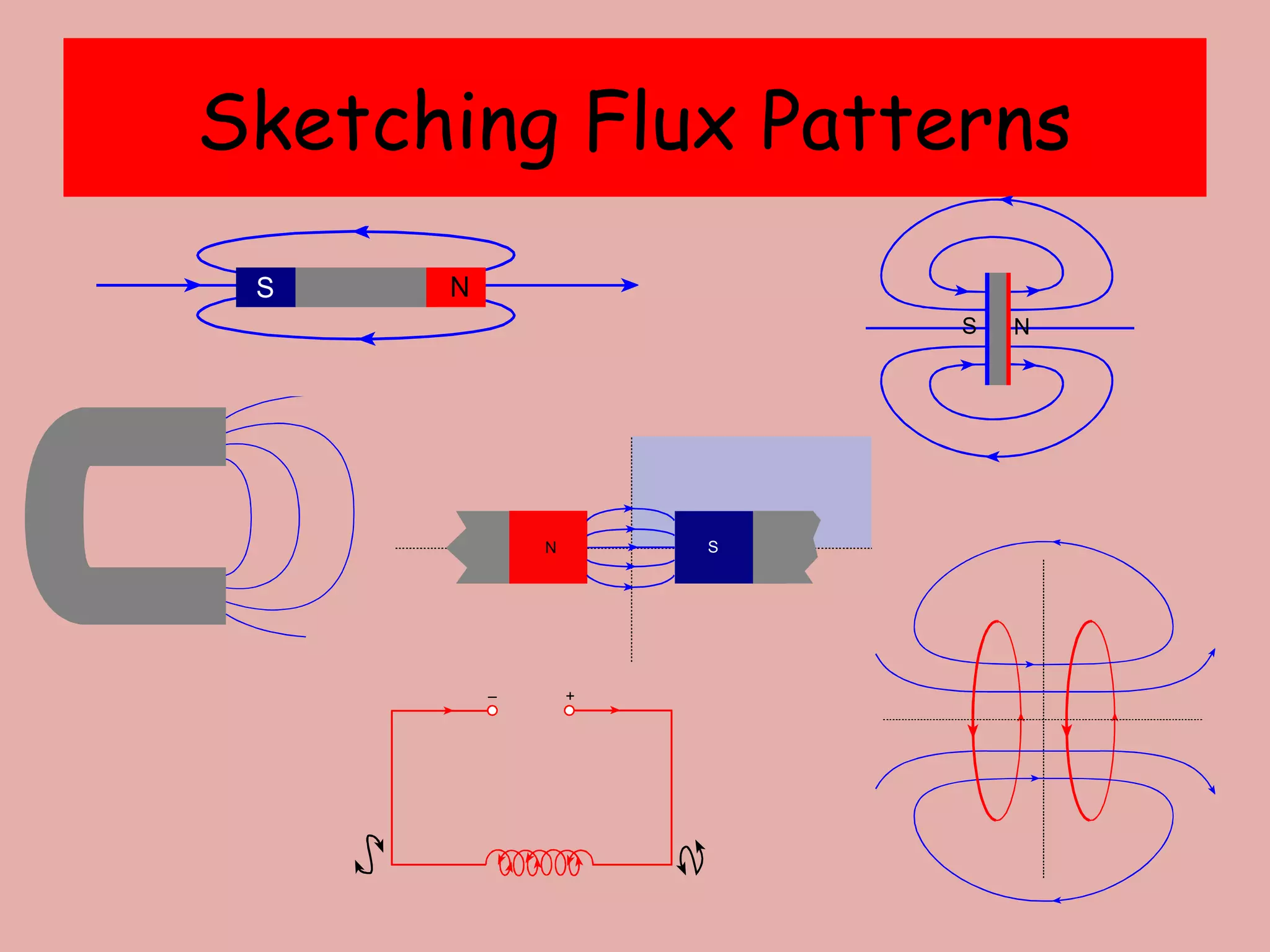
1) Electromagnetic induction occurs when there is a change in magnetic flux through a conductor. This can be caused by moving a magnet or coil, changing the area inside the magnetic field, or altering the number of turns in the coil. 2) The size of the induced emf depends on the speed of movement and strength of the magnetic field. A greater number of coil turns or larger area swept out also increases the induced emf. 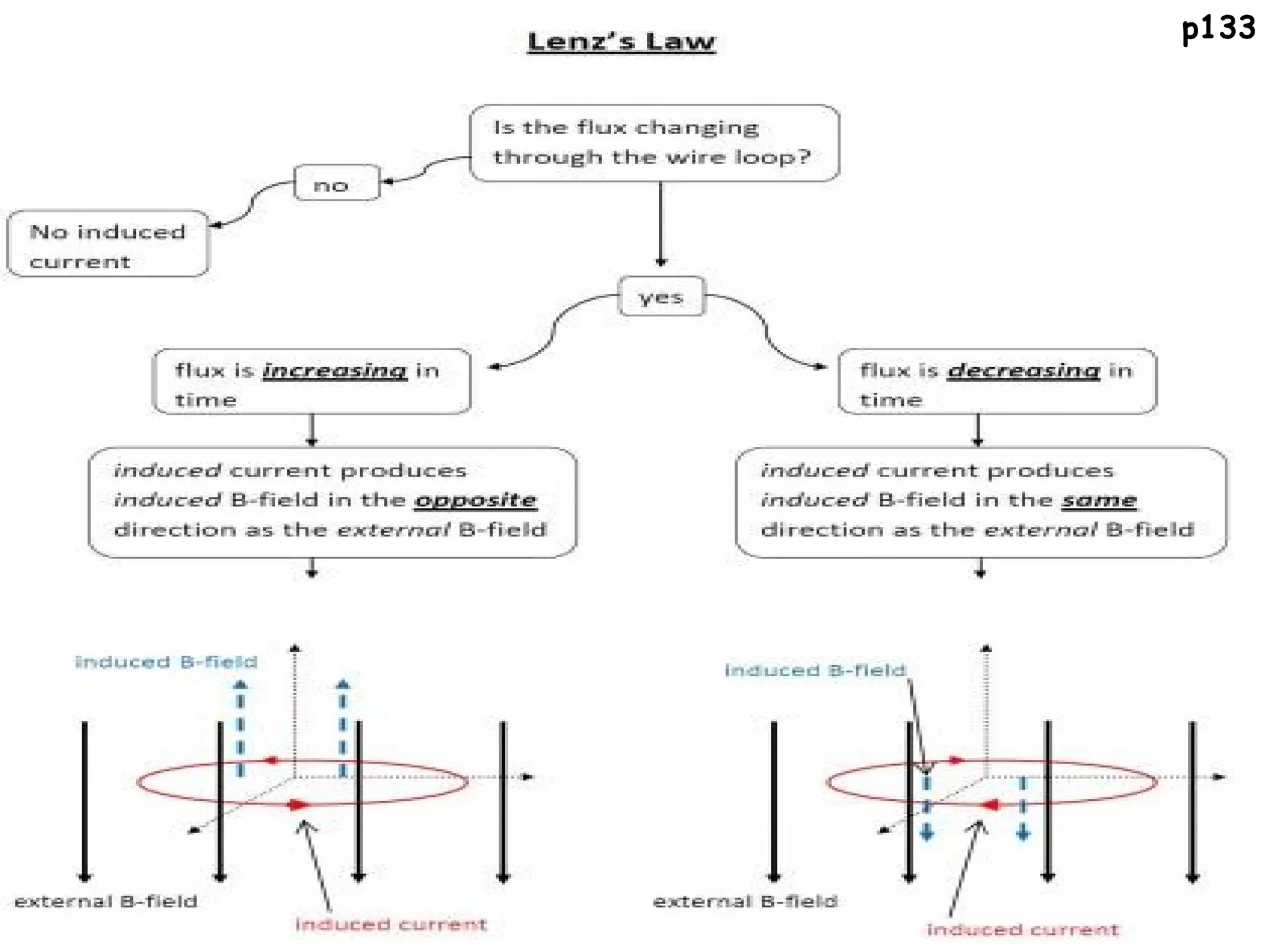3) Lenz's law states that the direction of the induced current will oppose the change causing it, as represented by a negative sign in the equation relating emf to the rate of change of magnetic flux linkage.

1. Electromagnetic induction

2. Important factors in inducing
currents
• 1. An emf is induced if the coil or the magnet
(or both) move (change in flux).
• 2. The size of the induced emf depends on
the speed of movement.
• 3. The induced emf depends on the strength
of the B field.
• 4. Changing the area inside the magnetic
field
• 5. Increasing the number of turns also
changes the flux linkage, and so induces a
greater emf.

3. What you are going to learn today
• What is magnetic flux, and magnetic flux linkage?
• What must happen to a conductor (or to the magnetic
field in which it’s placed) for electricity to be
generated?
• What factors would cause the induced emf to be
greater?
• What is Lenz’s law and what are the applications of
this law?

4. Flux - The rate of flow of energy through
a given surface
• flux density B
(The strength of your magnetic field)
• magnetic flux, Φ.
Φ = ΒΑ (Α = Αrea)
• Flux Linkage, N Φ
– (N = number of
turns)

5. Lenz’s Law
• Lenz’s Law states that the direction of
the induced current is always such as to
oppose the change that causes the
current.
• To include this idea in our formula, a
minus sign has to be introduced, giving;
• Emf = – N x dΦ/dt

6. Fleming's Right hand rule

7. p133

8. Kinetic energy recovery
systems
Toyota
• http://www.youtube.com/watch?v=evZ-
C8fVrP4
F1
• http://www.youtube.com/watch?
v=09knBT2gqqU

9. Inducing an Emf (no current yet)
• Connect the coil of wire to the micro-
voltmeter and place it close to the
magnet.
• 1. Move the magnet next to the coil.
What happens?
How does it depend on speed and
direction of movement?
• 2 .Move the coil next to the magnet.
What happens?
How does it depend on speed and
direction of movement?
• 3. Gradually unwind the coil in the
magnetic field. What happens?
• 4. Take the coil and crumple it up,
keeping it in the field. What happens?

10. Conductor in a magnetic field
Metal rod, length L in a
magnetic field moving with a
velocity v down the page.
An electron in the rod will
experience a force (= Bev)
that will push it towards the
end Q
The electrons will be pushed
towards end Q leaving end p
more positive
an electric field E builds up until
the force on electrons in the
rod due to this electric field
(= Ee) balances the force due
to the magnetic field.
Ee = Bev so E =Bv
For a rod of length L,
E = V/L and so V/L = Bv
Hence the induced emf = BLvv = velocity E = Electric field
V = Voltage B = Magnetic field

11. Completing the circuit
• The emf will now cause a current to flow in
the external resistor R. This means that a
similar current flows through the rod itself
giving a magnetic force, BIL to the left
• L is now the separation of the two
conductors along which the rod PQ
moves.) An equal and opposite force (to
the right) is needed to keep PQ moving at
a steady speed.
• The work done in moving the rod will equal
the energy dissipated in the resistor.
• In a time t, the rod moves a distance d = v
t
• Work done (FxD) on the rod = BIL v t
• Energy dissipated in R = power x time
= ItV
• giving BIL v t = ItV
• Emf (V) = BvL

12. However! You are increasing the
area inside the magnetic field
Emf (V) = BvL
In one second the area has increased
by Lv (A =Lv)
induced emf =
B x area swept out per second
= B x A / t
B x A can be called the magnetic
flux, Φ.
Thus induced emf = Φ / t
= rate of change of magnetic flux
And more generally
emf = d Φ/ dt
So how can you increase the induced
voltage?
L

13. Flux Linkage (N Φ)
• Increasing the number of turns of wire N in our circuit
increases the emf produced
• induced emf = rate of change of flux linkage
• emf = N x d Φ /dt

14. Sketching Flux Patterns
NS
NS
SN
– +