This master's thesis investigates efficiency optimization techniques for real-time GPU raytracing used in modeling car-to-car communication systems. Specifically, it aims to improve the simulation of the propagation channel through ray reordering and caching. The research analyzes existing caching schemes exploiting frame coherence, GPU data structures, and ray reordering techniques. It proposes algorithms for ray sorting on the CPU and caching tracing data. The thesis then implements and evaluates the proposed methods, analyzing system performance for static and dynamic scenes. Testing shows ray reordering significantly increases efficiency, though caching provides varying benefits depending on the scheme used.


















![1. Introduction
Software efficiency often refers to algorithmic efficiency which is one of the central topics
in computer science. According to Oxford Dictionary of Computing, algorithm efficiency
is “a measure of the average execution time necessary for an algorithm to complete work
on a set of data. Algorithm efficiency is characterized by its order.” [22]. On the other
hand, according to Robert Sedgewick [49], program optimization is a process of modifying
a software system to make some aspect of it work more efficiently or use fewer resources.
The latter implies that there is a software system that behaviour needs to be optimizied.
However, many experts in computer science (e.g Donald Knuth [25]) believe that the crit-
ical code sections have to be throughly verified and found before the optimization takes
place. In our case, efficiency optimization means that it is rather adding a new functional-
ity helping to increase performance then optimization of the existing code. With the term
optimization closely connected terms caching and performance analysis.
1.1. Thesis Statement
The aim of the project is modification of existing software system developed for modeling
of Car-to-Car Communication to increase its efficiency (decrease average time taken for
data processing). The system uses realtime GPU raytracing for simulation of wireless com-
munication between cars. A hypothesis of the research is that the tracing process could be
speeded up by taking into account an innerframe and outerframe coherence i.e. caching of
resulting data for future requests. It is also supposed that the efficiency optimization could
be achieved by altering tracing parameters, for example, by changing an order of rays shot
on a scene. Both hypothesis are tested using performance analysis (benchmarking).
1.2. Motivation
In the Motivation section, it is given a description of a general direction in which the cur-
rent work is carried out. In the first subsection it is briefly described Car-to-Car system,
its general purpose. In the second subsection, it is given some general information about
virtual testing of such systems. The last subsection considers an impact of realtime gpu
raytracing on the virtual drive system and on other urgent scientific areas.
1.2.1. Car-to-Car Communication System
Car-to-Car Communication system is a wireless network “between vehicles and their en-
vironment in order to make the vehicles of different manufactures interoperable and also
enable them to communicate with road-side units.[8]”. According to the Car2Car Com-
munication Consortium, the system shall provide the following top level features:
3](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-19-2048.jpg)
![1. Introduction
• automatic fast data transmission between vehicles and between vehicles and road
side units
• transmission of traffic information, hazard warnings and entertainment data
• support of ad hoc Car 2 Car Communications without need of a pre-installed net-
work infrastructure
• the Car 2 Car system is based on short range Wireless LAN technology
The Car 2 Car Communication System has the following goals:
• enable the cooperation between vehicles
• increase driver awareness
• extend driver’s horizon
• enable entirely new safety functions
• reduce accidents and their severity
• include active traffic management applications
• help to improve traffic flow
Thus, the main scenarios for which the system is designed include safety, traffic efficiency,
infotainment and some others.
1.2.2. VANET Simulation
In general, Car-2-Car communication systems represent a type of Vehicular ad-hoc Net-
works (VANET). Specifics of using a wireless connection in such networks requires an
active development of new network protocols suitable for the task. However, high costs of
full-scale real tests make them disadvantageous. An important part in simulation of such
systems is realistic motion model [12]. Another important issue in VANET simulation is
realistic modelling of propagation channel [26]. For the later problem there are two possi-
ble solutions: statistical and deterministic channel models. The deterministic method uses
a ray-tracing to model wave propagation [10]. The deterministic approach provides a real-
istic simulation taking into account geometrical and radio properties of the environment.
1.2.3. Simulation of Propagation Channel
In modelling of the propagation channel using the ray tracing, there are different ap-
proaches. Some authors, for example, create a radio map using a pre-calculation [15].
Others use a mixed (statistical and deterministic) approach for the channel simulation [6].
All authors, however, agree on that statistical models are unable to provide a necessary
precision in the network simulation. On the other hand, the ray tracing which provides
the seek accuracy suffers from low performance. Thus, the problem of increasing efficiency
of the realtime ray tracing becomes an important step towards building accurate VANET
simulators. The problem is also important in other areas of computer science, for example,
in computer graphics [16].
4](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-20-2048.jpg)
![1.3. Thesis Goals
1.3. Thesis Goals
The main goal of the thesis is to increase the efficiency of realtime GPU raytracing in a sys-
tem used for VANET simulation. The main functionality of the system has been developed
by the start of this work. So design goals can be formulated as follows:
1. Increase the system efficiency using the ray sorting
Design of sorting methods (algorithms)
Implementation of sorting methods (CPU)
Testing of the system performance with the ray reordering
2. Increase the system efficiency using caching
Design of caching method
Implementation of caching (GPU)
Testing of the system performance using caching
1.3.1. Ray Reordering
GPU performs calculations separating the streams on groups which are called ”warps“.
The main problem with warp is ”divergence” [4]. Such problem occurs, for example, in
code containing branches when some streams inside a ”warp“ take one branch of the ex-
ecution flow, other suspend on the evaluation point. When the first finish their execu-
tion, others take another branch, so the first group of threads now suspend till the second
group finish their execution. Presorting of rays helps to fully utilize the hardware such
that threads in one warp take the same execution paths.
1.3.2. Ray Cache
On the other hand, caching helps to reduce intensity of computational load. Cache stores
calculations which have been already computed in the system for future requests. The
main problem here is development of the caching schema and also implementation of the
caching on the GPU. The other important thing is testing and evaluation of testing results.
Tests development should be performed using automation tools as much as possible.
1.4. Contributions
The main contibution of this work is development of caching method for a system simulat-
ing VANET with low and medium intraframe coherence. This means that the geometrical
configuration of rays completely changes from frame to frame preserving a certain degree
of correlation. Other techniques use high ray coherence between frames, it means that par-
tially beam configuration stays stable between frames, this allows to reuse tracing results
between frames. In this case, radiation sources change their positions with relatively high
speed between frames.
5](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-21-2048.jpg)
![1. Introduction
The main problem solved in the implementation part is selection of efficient data struc-
ture allowing to build cache on the GPU side. Next, during testing of the data structure
for dynamic scenes, there have been an error that could be contributed to OptiX bugs.
The error has been solved by design of synchronization schema for writing/reading data
to/from buffer. The error in more detail will be described in the Testing chapter.
1.5. Software System Overview
In this section, it is given a brief system overview. Roughly the system contains the fol-
lowing modules:
Wavetracer This module is responsible for the ray tracing using OptiX engine: reading
of configuration file, creation of context, initialization of parameters, tracing programs,
launching of the tracing, processing of the output data, writing of the processed data to
the output file. This is the main module which will be amended.
Sceneviewer This module diplays results of the ray tracing both statically and dynami-
cally using OpenSceneGraph [41].
Osgloader Extracts information out of loaded 3D models.
Optix wrapper The module is a wrapper of OptiX api. C++ API of OptiX does not meet
needs of the application, for example, iterating the scene graph.
edgedetector Detection of diffraction edges.
adtf coupling The software component is responsible for encapsulation of modules into
ADTF [1]. These plugins are osgplugin, testdriverplugin, vtdplugin and wavetracer plu-
gin. All the plugins should inherit basic interfaces of the ADTF.
6](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-22-2048.jpg)


![2. Literature review
The study was conducted in the following directions: ray caching techniques & frame
coherence, GPU data structures and ray reordering. Also it has been written a review
on GPU programming model and memory types. Ray caching and frame coherence is
presented in one subsection while GPU data structures and ray reodering in separate.
2.1. Ray caching and frame coherence
Realtime ray tracing requires high computational power. One of the methods which
could be used to reduce computational expences is caching. Results of the tracing proce-
dure could be stored in a ray cache which will reduce a response time for future requests.
The main question is how to build an adequate and efficient caching strategy. Several au-
thors were selected which used caching techniques in their work (Chan [7], Debattista [9],
Popov [42], Ruff [46], Tole [50], Scherzer [48]).
The goals of the study:
1. find ”postulates“ for ray caching (how ray caching could be performed in general)
2. the seek strategy shall exploit ray coherence in rapidly changing environments
3. the seek strategy shall be implementationally gpu-compatible
The following literature review attempts to find such a strategy.
In a research by Chan et al. [7] the ray coherence is exploited to accelerate a sound
rendering process in an interactive environment. The article postulates the following prin-
ciples for the ray caching.
1. Rays with the same geometric properties (starting point, directions) as contained in
cache do not have to be traced again.
2. To maintain the intersection history objects are subdivided into discrete patches.
3. The cache represents a graph with object patches as nodes and rays as edges.
Once a ray hits a patch in the cache, the whole intersection history for the given patch
be taken which replaces costly intersection tests. Since this article is important for the
research, it is necessary to highlight some implementation details here.
Patch subdivision An object is subdivided into small patches so that two rays hitting the
same patch are considered have the same intersection points. Angular ray directions are
quantized
9](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-25-2048.jpg)
![2. Literature review
Coherence Intra-frame coherence occurs when several rays share the same path inside
one frame. Inter-frame coherence occurs when several rays share parts of paths contained
in the cache
Ray cache The cache consists of a tree and a graph attached to tree. Every node of the
tree is identified by a complex index (object, patch, patch, ..., division)
Purging The cache is purged according to Least Recently Used strategy using timestamp
Source movement When a ray source changes its position all cache entries connected
with it are removed from the cache.
Chan got significant performance improvements using the ray cache. The method was
beneficial in multi-user interactive environments with high ray coherence. Hovewer, the
method has several disadvantages. Firstly, the method is implemented on cpu using so-
phisticated data structures which will be hardly efficient on gpu. Secondly, the method
is limited to step - by - step movements with high correlations between frames. Thirdly,
the cache is purged when a source changes its position, it means that in succeeding frames
the cache cannot be reused. Nevertheless, the article states fundamental ideas for the ray
cache implementation.
Debattista et al. [9] used several techniques based on irradiance caching [54] in render-
ing dynamic scenes with global illumination [52]. The main contribution of the article is
detection of invalid ray paths after geometric transformations. Authors considered five
cases for invalidation of their instant cache.
Case 1 Occlusion of a light path by moving object (occlusion of a secondary light source)
Case 2 Deocclusion of a light path by moving object (deocclusion of a secondary light source)
Case 3 Occlusion of a visibility ray by moving object
Case 4 Deocclusion of a visibility ray by moving object
Case 5 Cache sample lies on a dynamic object
Figure 2.1 gives a summary of all cases. Overall, Debattista used caching for calculation of
a radiance integral where the cache stores illumination instead of visibility. Secondly, the
method is limited to static scene with moving objects. However, some of the ideas for ray
purging (ray invalidation) could be used in this work as well.
Popov et al. [42] in their work exploited an idea of lightcuts [53]. Authors introduced a
fundamental point-to-point visibility caching algorithm with could be incorporated in any
ray tracer. Also they developed an adaptive quantization scheme which helps to control
trade-off between performance and quality. The algorithm was implemented on gpu using
hash table which is of a particular interest for the research.
10](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-26-2048.jpg)
![2.1. Ray caching and frame coherence
Figure 2.1.: The five cases that invalidate the instant cache [9]
One of the main entities in Popov’s work is a binary visibility function. It is defined as
V (X, Y ) =
®
1 if X and Y are mutually visible
0 otherwise
(2.1)
The visibility function is approximated using quantization of path domain and mapping
K( ¯pe, ¯pl) → N which relates a pair of surface points to a unique cluster. The quantized
visibility function is defined as
¯V ( ¯pe, ¯pl) ≈ V C
(K( ¯pe, ¯pl)) (2.2)
The quantization error is controlled using equation
|A( ¯pe)||A(¯pl)| =
(CE)2
P( ¯pe)P(¯pl)Np
(2.3)
The figure 2.2 summarizes the concept.
To define K(.), the scene surface is divided into a set of virtual multi-resolution, overlap-
ping and differently oriented voxel grids. For vertex X with N(X) a quantized direction
is defined as
ωq
=
ñ
N(X) + 1
2
CN
ô
, dz =
2ωq
CN
− 1 (2.4)
K(.) returns a tuple of 14 integers: 3 for the orientation of X, 3 for the coordinates contain-
ing X, and 1 for the grid resolution R( ¯pe); integers for Y are chosen analogously.
11](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-27-2048.jpg)
![2. Literature review
Figure 2.2.: Similar paths are grouped together and share the same visibilty query [42]
The concept is illustrated by the figure 2.3.
Figure 2.3.: Visibility domain quantization [42]
Results of the visibility queries are stored in a hash table. To define a particular bin,
researchers calulate a 32 bit key k(j) from j = K(.) and use modulo division k(j) mod CT
where CT is the hash table size. They also employ a direct-mapped cache which does not
resolve collisions simply overwriting the data. One important implemenation detail is that
the algorithm uses a counter which controls how many threads in the warp need to trace
rays. If the counter is less then some predefined threshold, the local state of each thread is
saved in a small pre-warp queue and and the rays are not trace immediately. Whenever
the number of threads in the queue exceeds 32, the tracing is performed. This helps to
utilize a gpu performance and load it uniformely.
For the method assessment Popov uses three metrics: Quality metric, Performance met-
ric and Cache performance metric. As a quality writers employ a predictive QMOS pro-
posed by Mantiuk et. all [30]. As a performance estimation it is taken a shadow ray re-
duction and the total frame rendering time. The cache performance was measured using
ratio
(1 − HitRatio) = MissRatio = 1/(RayDirection + 1) (2.5)
Results show significant shadow ray reduction, up to 50×, preserving image quality with
QMOS above 77%. The total rendering speedup varies from 2.5× to 6.7× for different
scenes.
12](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-28-2048.jpg)
![2.1. Ray caching and frame coherence
All in all, the article is very valuable. Firstly, it gives a theoretical background for the
visibility caching. Secondly, the approach described could be used in rapidly changing
environments as in car driving since the quantization allows to exploit the inter-frame co-
herence when trace paths change entirely from frame to frame. Thirdly, the algorithm is
efficiently implemented on gpu using hash table and direct mapping which makes caching
very fast. On the other hand, quantization introduces too much parameters (14) which
makes hash table indexing a bit complicated using digest, prepending and modulo op-
erations. The higher performance makes memory utilization higher. On the hand, fast
changing scenes impose much stress on gpu buffers which could potentially cause mem-
ory destruction.
Ruff et al. [46] investigate the question of using caching textures for real time tracing
in OptiX. For each reflective object of the scene, researchers generate a set of 6 caching
textures. Before tracing a ray leaving the object the algorithm queries color information for
that ray in the caching textures. If the information is available it is taken from the cache,
otherwise the tracing procedure takes place. Authors introduce geometrical scheme how
reflection rays are saved in the textures. Results shows that the method produces pictures
that are visually equivalent to the reference images. A speed up achieved comparing to
conventional ray tracing varies from 2% to 168% depending on the number of additional
reflective objects.
Developers themself mention in their article that their method is tailored to static scenes
with convex objets and auto-reflection features. However, the idea of using the cubic box
as caching structure could be beneficial in this work as well.
Tole et al. [50] examine in their paper how to build a system for interactive computa-
tion of global illumination[52] in dynamic scenes. The system stores illumination samples
generated by pixel based rendering algorithms and then applies interpolation between
samples using graphics hardware. The shading cache represents a hierarchical patch tree
with every patch containing the last computed shading values for its vertices. The patch
could be used in three ways, either its value is used for interpolation or the patch could
be refined further or its value is updated. If the cache grows above the threshold, patches
which are not longer seen on the scene removed together with their children using ”not
recently used” strategy. When an object on the scene or light moves the patch values are
recalculated using ”age priority“. Comparison with other cache rendering systems, shows
that the system suits best for applications like interactive lighting design and modeling.
Altogether, the system likewise Debattista [9] uses illumination cache, spatial coherence is
exploited using interpolation, while temporal coherence maintained by reusage of patches
from previous frames. All this makes the approach practically useless in this study.
Work by Scherzer [48] is notes for the course with the same name: ”Exploiting Tempo-
ral Coherence in Real-Time Rendering”. He determines temporal (frame) coherence (TC)
as “the existence of a correlation in time of the output of a given algorithm”. He further
states that the coherence could be used to accelerate a given algorithm making it incre-
mental in time and for quality improvement by taking into account results obtained in the
13](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-29-2048.jpg)
![2. Literature review
previous frames. Next, Scherzer describes the Reverse Reprojection Cache which reuses
shading results from previously rendered frames. The basic idea of the method is to allow
renderer to use a shading information which is available for a given point in the previous
frame buffer. In order to do this Scherzer introduces a reverse reprojection operator. For
refreshing the cache, the screen is divided into n parts which are updated in a round-robin
fashion. The method shows good acceleration results for a few pixel shaders. It is used for
stereoscopic rendering, simulation of motion blur and depth of field effects, view frustum
culling techniques and others. Again, this method is basically designed to being used as
shading/illumination cache, it could be used for exploiting the temporal coherence in ob-
ject space in culling techniques but this does not help much in our task. The formulation
of the temporal coherence could be used to calculate how good frames correlate with each
other.
Upon the whole, the objectives are achieved. It has been selected the main strategy for
caching proposed by Chan et al. [7]. Based on work by Popov [42] the strategy could be
extended using the quantization (Chan also uses it intoducing divisions). Also the system
could be efficiently implemented on gpu using hash table and bin indexing. Some of the
policies for ray purging could be used from work by [9].
2.2. GPU data structures
In this subsection, it is given an overview for gpu data structures using book ”GPU Gems
2“ [31] and articles by Lefohn [28], Foley [13] and Prabhakar [34].
The main goal of the review to find an efficient parallel gpu data structure for the ray
cache implementation.
Lefohn, in chapter 33 of ”GPU Gems 2”[31] explains how fundamental data structures
are implemented using GPU programming model. According to Lefohn, GPU has the
following data structures: multidimensional arrays, static and dynamic sparse structures.
Multidimensional arrays 2-D textures with nearest-neighbour filtering are the substrate
on which most of the GPGPU structures are built. All multidimensional array use
address translation to convert N-D array address to 2-D texture. GPU implementa-
tion of the address translation suffers from limitations on floating-point addressing.
1-D array 1D arrays are implemented by mapping the data to 2D texture. Currently,
a maximum width for a 1D texture is 227 = 134, 217, 728 [37]. Each time an
element in a 1D array accessed by a GPU program, the address is translated
into a 2D texture indeces.
2-D array 2D arrays are represented as 2D textures. Their maximum size is limited
by the GPU driver.
14](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-30-2048.jpg)
![2.2. GPU data structures
Figure 2.4.: Representation of 1D arrays on GPU
3-D array 3D arrays can be implemented in three ways: as 3D textures, as several
levels of 2D textures or directly mapped to single 2D textures. Every implemen-
tation has its pluses and minuses. For example, the simplest 3D implementation
does not have an address translation and for this structure could be used native
GPU trilinear filtering to create high-quality data renderings. As a disadvan-
tage, this structure requires many passes to write to the whole array.
structures There are two possible solutions: a stream of structures and a structure of
streams. The stream of structures is a problematic solution because every member
of structure has a different stream index and they cannot be easily updated. Con-
trariwise, in the structure of streams, a separate flow is created for every structure
member.
sparse data structures Implementation of sparse data structures as lists, trees or sparse
matrices is problematic on the GPU. Firstly, because this involves writing to a com-
puted memory address (scattering). Secondly, traversing of such data structures in-
volves an inhomogenous number of pointer dereferencing operations to access data
which has difficulties based on processing properties of SIMD architecture. Elements
which are processed by single SIMD should contain exactly the same instructions.
static sparse structures The static sparse structures are not changed during the
GPU computation. All of these structures contain one or more levels of indirec-
tion.
There are two methods for solving the problem of irregular access in these pat-
terns: the first one is to divide the whole frame into blocks where all blocks
have the same random access model and can be handled together. The second
method is to have a stream to process one member from its scheduled list per
render passage.
dynamic sparse structures Dynamic sparse data structures is a very active research
area. One of two noticable works are Purcell et al. 2003 [44] and Lefohn at al
[17], [27].
15](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-31-2048.jpg)
![2. Literature review
Figure 2.5.: Purcell et al. 2002 [45]. Sparse Ray-Tracing Data Structure
A photon map [44] is a cache which stores intersection points and incoming di-
rections for light packets called photons.There are two techniques which allow
to build the photon map on the GPU. The first one computes addresses and data
for writing then it performs a scattering by performing parallel sorting opera-
tions on the buffers. The second method uses vertex processor.
Lefohn [27] created efficient dynamic data structure on GPU for implicit sur-
face deformation. He solves scattering problem by sending small messages to
the CPU when the GPU needs to be updated. The structure uses the blocking
strategy.
Weber et al. [55] presented efficient implementation for sparse matices on
GPU in solving of sparse linear systems in dynamic applications.
performance considerations In case of dependent memory reads there is a possibility
to create a memory-incoherent memory accesses. It could be prevented by creation
of coherent blocks of similar computations, small lookup tables and minimization of
dependency levels. Another important performance concerns include optimization
of computational frequency on the GPU, program specialization and a proper use of
pbuffers.
Foley and Sugerman [13] presents a GPU implementation for kd-tree traversal algorithm
suitable for raytracing but they build data structures on the CPU. This is of no interest for
the work.
Lefohn et al. [28] presented an abstract generic template library for complex random-
access data structures on the GPU. The structures, a stack, an octree, a quadtree are build
using standard library components. Firstly, ptx programs generated by nvcc compiler
should conform to restrictions imposed by OptiX API. This makes impossible usage of
16](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-32-2048.jpg)
![2.3. GPU programming model and memory types
some CUDA libraries. Secondly, we do not need so complicated data structures as octrees,
on the other hand functions for construction and utilization of data primitives as 1D, 2D,
3D arrays are built in OptiX API. All these make usage of the library unreasonable.
Lock-free data structures represent a certain interest in this work. Prabhakar and Chaud-
huri [34] evaluate their performance on the GPU. They consider lock-free linked list [18],
hash table, skip list [18] and priority queue [18]. The data structures are evaluated using a
mix of add, delete and search operations for different key ranges. For the lock-free linked
list, the GPU implementation has a moderate speedup up to 7.4 times for small to medium
key ranges comparing to the CPU implementation. The hash-table on the GPU outper-
forms the CPU implementation of the same structure in the all key ranges with the maxi-
mum speedup at 11.3. GPU realization of the lock-free skip-list is beneficial for small and
medium key ranges with the maximum speedup at 30.7. For the lock-free priority queue,
GPU benchmarks have the same pattern as for the skip-list with the maximum speedup
of 30.8. They close discussion by comparing performance of the GPU implementations of
hash-table and linked list. The hash-table is 36 to 538 times better then the linked-list. They
conclude that the GPU helps the hash-table to reveal its concurrent potential making it the
best data structure for arbitrary key ranges.
To sum up, in this subsection, it is considered problems of building data structures on
the GPU. It has been mentioned that the question of sparse data structures construction is
challenging task. However, many developers and researchers have already contributed to
this area. A lock - free data structures is of a particular interest since they offer efficient
GPU implementation. The hash table proved to be the best data structure of the afore-
mentioned due to its constant performance benefits and design well-suited for usage in
multithreaded GPU applications.
2.3. GPU programming model and memory types
In this section, it is given an overview of CUDA C programming model [37] and consid-
ered different types of GPU memory.
2.3.1. GPU programming model
Kernels
CUDA C allows a programmer to write C functions (kernels) which during invocation are
executed in parallel by N different CUDA threads. A kernel is defined using the global
identifier. The quantity of CUDA threads which are going to execute the kernel for the
given call is defined using a new syntax <<<...>>>. Each CUDA thread is given a unique
thread id which is accessible in the kernel body using the built-in threadIdx variable.
Thread hierarchy
For convenience, threadIdx is a three component vector so that every thread can have a 1-
dimensional, 2-dimensional or 3-dimensional index to form a 1-dimensional, 2-dimensional
17](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-33-2048.jpg)
![2. Literature review
or 3-dimensional block.
The thread id and it index inside the block is put in one-to-one correspondence using
the following equations:
for the 1D block: thread ID = x where (x) is the thread index
for the 2D block of size (Dx, Dy): thread ID = (x + yDx) where (x, y) is the thread index
for the 3D block of size (Dx, Dy, Dz): thread ID =(x + yDx + zDxDy)
There is a limit in the number of threads combined into one block since all the threads
should be processed by one processor core thus sharing the same memory. Presently, mod-
ern GPU allows to have blocks with a maximum of 1024 [37] threads per block.
Nonetheless, a kernel can be executed by a multiple blocks so the total number of
threads executing the kernal equals to the number of blocks multiplied by the number
of threads in the block. The blocks are organized in one-dimensional, two-dimensional,
three-dimensional grids as illustrated by figure 2.6.
Figure 2.6.: Grid of thread blocks [37]
18](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-34-2048.jpg)

![2. Literature review
Figure 2.7.: Memory hierarchy [37]
Serial code is executed on the host while parallel code is executed on the device.
Compute capability
Compute capability is defined by major and minor revision numbers. Devices that share
the same major revision number are of the same core architecture. The minor revisions
represent incremental improvement of the core architecture, possibly including new fea-
tures.
2.3.2. GPU memory types
In this subsection, it is given an overview of different GPU memory types.
20](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-36-2048.jpg)
![2.3. GPU programming model and memory types
Figure 2.8.: Heterogeneous programming [37]
Device memory accesses
An istruction which accesses a memory address could be performed multiple times de-
pending on the distribution of memory addresses across the threads within one warp.
How the distribution influences performance is peculiar to each memory type and de-
scribed in the following subsections. For instance, for the global memory, the rule of thumb
is that the more scattered addresses are the less performance is.
Global Memory
Global memory exists in device memory which is accessed using 32-, 64- and 128-byte [37]
memory transactions. These transactions should be naturally lined up: only 32-, 64- and
128-byte segments of device memory that are lined up to their size (i.e. the first address of
a segment is a multiple of its size) can be read or written by these transactions.
When a warp executes an istruction that accesses the global memory, it joins all memory
addresses for all threads within one warp into one or more memory transations depending
21](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-37-2048.jpg)
![2. Literature review
on the size of word accessed by each thread and distribution of the memory accesses across
the threads. The more transactions are necessary the more unused words are transferred
in addition to those words which are actually accessed by the threads reducing instruction
throughput.
How much transations are necessary and what the throughput of the device is fully
depends on the computing capability of the device. For devices of compute capability 1.0
and 1.1 [37] requirements to get any coalescense are very high. They are more relaxed for
devices with higher compute capability. For devices of compute capability 2.x and higher
[37] the memory transactions are cached so that data localization is used to reduce impact
on the throughput.
In order to maximize the throughput of the global memory it is necessary to maximize
the coalescing by:
• Following the most optimal patterns for devices with computing capabilities of 1.x,
2.x and 3.x [37]
• Utilizing data types which comply with requirements of data size and alignment
• Padding of data in some cases when, for example, accessing two-dimensional arrays
Size and Alignment Requirement
Instruction in global memory support writing and reading of words with size of 1,2,4,8 or
16 bytes [37]. Any access to data in the global memory compiled to a single istruction in
global memory if and only if the data size does not exceed these numbers and the data is
naturally aligned. If the requirements are violated then muliple instructions with different
access patterns are which hinder data coalescing.
The alignment is automatically done for built-in data types like char, short, int, long,
longlong, float, double like float2 or float4 [37].
For structures, the size and alignment requirements can be fullfilled using special speci-
ficators like align (8) or align (16).
Any variable which is located in the global memory is returned by a driver routine for
memory allocation or by runtime API aligned to at least with 256 bytes.
Reading of not naturally aligned 8-byte or 16-byte words [37] could lead to incorrect
results, a special attention should be paid to maintain alignment of a value or an array of
values of these types. This is a typical error which occurs when memory allocation for
multiple arrays using common calls to function cudaMalloc or cuMemAlloc are replaced by
allocation of a single large block in memory partitioned into multiple arrays. In this case
the starting addresses of the arrays are shifted with regard to the initial address of the
block.
22](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-38-2048.jpg)
![2.3. GPU programming model and memory types
Two-Dimensional Arrays
A common access pattern is when a thread with index tx, ty tries to access an element in
2D array of width width using the following mapping BaseAddress + width ∗ ty + tx. In
order these accesses are fully coalesced, the width of the thread block as well as the width
of the array should be be a multiple of the warp size.
Local Memory
Only automatic variables could be placed to the local memory. The automatic variables
are:
• Arrays for which cannot be detemined that they are indexed with constant values
• Large structures of arrays which otherwise consume too much register memory
• Any variable if kernel uses more registers then available
The local memory is located in device memory and as a consequence has a high latency
and a low bandwidth as the global memory and is a subject to the same requirements for
memory coupling. However the local memory is organized in that way that consecutive
32-bit words accesses are performed by threads with consecutive IDs. Therefore the ac-
cesses are coalesced as long as all threads in one warp access the same relative address.
For devices with compute capability 2.x and higher [37], all accesses to the local memory
are cached in the same way as accesses to the global memory.
Shared Memory
Shared memory has much lower latency and much higher instruction throughput then lo-
cal or global memory because it is placed directly on the chip. To achieve high bandwidth,
the shared memory is divided into equally-sized memory modules called banks which can
be accessed simultaniously. Thus processes of reading and writing to memory which refer
to locations seating in n memory banks can served simultaneously resulting in n times
overall bandwidth increase.
If two threads access addresses in the same bank then serialization is necessary. These
requests are divided into as many conflict-free queries as necessary. If thus n queries oc-
curs, the initial memory request is said to cause n-way bank conflicts. In order to maximize
performance it is necessary to minimize bank conflicts. This is specific to different device
types because of mechanisms of mapping memory addresses to memory banks.
Constant Memory
Constant memory lies in device memory and cached in constant cache for devices with
compute capabilities of 1.x and 2.x [37]. For devices with compute capability 1.x [37] a
request to constant memory for a warp is divided into two requests for an every half-
warp which then served independently. These requests are further divided to subrequests
depending on the number of memory addresses contained in the initial query. The overall
23](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-39-2048.jpg)
![2. Literature review
throughput is reduced by the number of subrequests. These subrequests are served at the
cache bandwidth in case of cache hit or at device bandwidth otherwise.
Texture and Surface Memory
Texture and surface memory reside in device memory and are cached in texture cache,
thus the cost of texture and surface memory access equals to cost of reading from the
device memory in case the data is not in cache, otherwise it costs reading from the texture
cache. The texture cache is optimized for 2D spatial localization, threads of the same warp
located in 2D space near each other achieve the best performance. Therefore the cache is
designed for streaming ingress with constant latency. Thus a number of cache hits reduces
the DDRAM bandwidth demand but not the fetch latency.
Reading of device memory using texture or surface memory has a number of benefits
which makes it advantageous alternative comparing to reading the device memory from
global or constant memory:
• If accesses to global or constant memory are carried out with violation of perfor-
mance rules, a higher bandwidth can be achieved providing that there is a localiza-
tion in texture fetches or surface reads.
• Operations of addresses calculation are performed outside of the kernel using special
units
• Packed data can be transferred to separate variables using single operation
• 8 or 16-bit integers can be cast to 32 floating-point values in the range of [0.0,1.0] or
[-1.0, 1.0] [37]
2.4. Ray Reordering
In this subsection, some ray reordering techniques are considered using articles by Garanzha
and Loop [14] and Moon et al. [35].
The goal here is to find suitable for the task ray reordering methods.
Garanzha and Loop [14] use ray sorting to boost efficiency of ray tracing by revealing
of coherence between rays and reducing a number of execution branches within SIMD
processor. For the ray sorting they propose a method based on compression of key-index
pair. Then the compressed data is sorted and decompressed.
The sequence of key-index pairs is generated by using a ray id as the index and a hash
value for the given ray as the key. Coordinates of ray sources are quantized using virtual
uniform 3D grid within the volume bounding the scene. Ray directions are also quan-
tized using virtual uniform grid. Using these grids, authors calculate ray ids which then
merged into a 32-bit hash value. Rays which have the same hash value are considered to
24](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-40-2048.jpg)
![2.4. Ray Reordering
be coherent in space. Then compressed data is sorted using radix sort. After the data is de-
compressed, packet ranges are extraced uing the same compression procedure. Once the
ranges are extracted, the next step is to create a frustum for each packet. The frustums are
traversed using the breadth-first algorithm. Next, the active frustums are decomposed into
chunks of 32 rays max analogously to CUDA warp. This eliminates execution branches
within a CUDA warp. Primary rays are indexed and sorted according to a screen-space
Z-curve. Binary BVH is build on CPU using binning algorithm. The algorithm is com-
pared with Depth-first algorithm for the ray tracing. They get significant performance
improvements for soft shadow rays at 1024 × 768 × 16 samples. Comparing to CPU, GPU
implementation is 4× faster. However, authors assume that memory consumption could
be sufficient. Also the bad case for the algorithm if one frustum captures all of the BVH
leaves which could cause very unbalanced workload.
Moon et al. [35] implemented the ray tracing with cache-oblivious ray reordering. For
the ray sorting, authors introduce a Hit Point Heuristic. A hit point is computed as the first
intersection point between the scene and a line starting from the ray origin pointing in the
ray direction. After this, points are reordered using a space-filling curve (Z-curve). Dur-
ing implementation stage, Hilbert curves were also considered but they gave only slight
performance benefits (e.g. 2%) while having much more complex implementation. The
ray tracer is implemented on the CPU. The method is tested for path tracing as well as
for photon mapping. For the path tracing, their method achieves a significant 16.83 times
performance improvement compared to without reodering. For the photon mapping, the
method in different configurations gives from 3.77 to 12.28 times performance improve-
ment. Rays reordering is also the cause of a higher cache utilization. Also ray reodering
based on Hit Point Heuristic shows better performance then ray reodering based on ori-
gin + direction reordering. However, authors mention that there is no guarantee that the
method will improve performance of the ray tracing because of the overhead.
Altogether, the goal is accomplished, it have been considered methods for ray reordering
using different techniques. Hash values for the rays could be generated using ray origin
and direction quantization as well as based on quantization of spatial information like hit
points coordinates. Rays according to their hash values could be sorted in different ways.
For example, using radix sort or space-filling curves. Also, in considered articles authors
report about significant performance improvements for tracing with ray sorting.
25](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-41-2048.jpg)

![3. Problem and Solution
3.1. An experiment with dimensionality of context launches
The first problem that is considered is the problem of how dimensionality of a computa-
tional problem affects efficiency of ray tracing.
3.1.1. Problem Description
The problem described in Redmine ticket #155 ”Experiment with dimensionality of context
launches“. The ticket has the following content:
”Chapter 9.Performance Guidelines” of OptiX Programming Guide [38] states that the
maximum coherence between threads of a tile is achieved by choosing an appropri-
ate dimensionality for the launch. For example, common problems with 2D images
has 2D complexity. Thus the problem is reduced to the determination of the launch
dimension and investigation of how this affects efficiency.
3.1.2. Theory
To describe the solution to the problem it is necessary to start from definitions for space-
filling and Hilbert curves.
Space-filling Curve
The space-filling curve is defined in the following way [3]:
Given a mapping f : I → Rn, then the corresponding curve f∗(I) is called a space-filling
curve, if the Jordan content of f∗(I) is larger then 0.
Hilbert Curve
The Hilbert curve is defined as [3]:
• each parameter t ∈ I = [0, 1] is contained in a sequence of intervals
I ⊃ [a1, b1] ⊃ ... ⊃ [an, bn] ⊃ ...
where each interval results from a division-by-four of the previous interval
• each such sequence of intervals can be uniquely mapped to a corresponding se-
quence of 2D intervals (subsquares)
• the 2D sequence of intervals converges to a unique point q in q ∈ Q = [0, 1] × [0, 1] -
q is defined as h(t)
f : I → Q defines a space-filling curve, the Hilbert curve.
27](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-43-2048.jpg)
![3. Problem and Solution
Grammar for 2D Hilbert Curve
Grammar for 2D Hilbert curve can be constructed in the following way [3]:
• No-terminal symbols: H, A, B, C, start symbol H
• terminal characters: ↑, ↓, ←, →
• productions:
H ← A ↑ H → H ↓ B
A ← H → H ↑ H ← B
B ← C ← H ↓ H → B
C ← B ↓ H ← H ↑ B
• replacement rule: in any word, all non-terminals have to be replaced at the same
time → L-System (Lindenmayer)
Arrows describe the iterations of the Hilbert curve in ”turtle graphics“[43]. Figure shows
a sample 2D Hilbert curve generated using the grammar.
Figure 3.1.: An example of 2D Hilbert curve
Grammar for 3D Hilbert Curve
L-Systems in three dimensions could be described using ”turtle graphics” [43]. The ba-
sic idea is to represent the turtle orientation in 3D space using a set of vectors [ ˆH, ˆL, ˆU]
representing the turtle’s heading, left direction and upward direction accordingly. Vectors
[ ˆH, ˆL, ˆU] form an orthonormal basis. Spatial rotations of the turtle can be described:
[ ˆH , ˆL , ˆU ] = [ ˆH, ˆL, ˆU]R (3.1)
where R is a 3 × 3 rotation matrix. Rotations by angle α around vectors ¯U,¯L and ¯H are
represented by the following matrices:
28](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-44-2048.jpg)
![3.1. An experiment with dimensionality of context launches
Figure 3.2.: Controlling turtle in 3D [43]
RU (α) =
cos(α) sin(α) 0
−sin(α) cos(α) 0
0 0 1
RL(α) =
cos(α) 0 −sin(α)
0 1 0
sin(α) 0 cos(α)
RH(α) =
0 0 1
0 cos(α) −sin(α)
0 sin(α) cos(α)
(3.2)
The following symbols determine turtle’s orientation in space:
+ Turn left by angle δ, using rotation matrix RU (δ)
- Turn left by angle δ, using rotation matrix RU (−δ)
& Pitch down by angle δ, using rotation matrix RL(δ)
∧ Pitch up by angle δ, using rotation matrix RL(−δ)
Roll left by angle δ, using rotation matrix RH(δ)
/ Roll right by angle δ, using rotation matrix RH(δ)
— Turn around, using rotation matrix RU (180◦)
An interested reader could find a grammar for 3D Hilbert curve in appendix A.3.
Z Curve
Z-curves are defined in terms of Morton codes [24]. In order to calculate Morton codes it is
necessary to consider a binary representation of point coordinates in 3D space, as shown
by figure 3.3. Firstly, for each coordinate, the binary code is expanded by insertion of two
additional ”gaps“ after each bit. Secondly, the binary codes of all coordinates are joined
(interleaved) to form one binary number. If thus resulting codes are sorted in ascending
order, this will determine the sequence of z-curve in 3D space (the left part of figure 3.3).
The sorting could be performed using radix sort.The expansion and interleaving of bits
could be done efficiently by utilizing the arcane bit-swizzling properties of integer multi-
plication. A curious reader will find a listing in appendix A.1.
29](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-45-2048.jpg)
![3. Problem and Solution
Figure 3.3.: Generation of Morton codes [24]
3.1.3. Problem Solution
The problem solution could be sketched in the following way:
1. Sort ray buffer according to spatial ray coordinates
2. Initialize the sorted buffer with the context depending on the dimensionality
For 1D, –
For 2D, map 1D indeces to 2D array structure using 2D Hilbert curve
For 3D, map 1D indeced to 3D array structure using 3D Hilbert curve
Next will be discussed in more details points of this sketch.
Sorting
Histogram and Hilbert Curve The first approach is to generate indices for every ray in
3D and sort them according to Hilbert curve.
Ray indices Rays generated for the wavetracer represent uniformely distributed
points on a unit sphere. Their coordinates could be quantized. The quanti-
zation is the same as the redistribution of rays on a three-dimensional spatial
data structure (a histogram) according to their directions. For each element in-
side the ray buffer could be generated indices depending on the number of bins
in the histogram. Using these indices the ray could be added to a bin of the
histogram. A pseudocode for the algorithm is shown by Algorithm 1. A geo-
metrical interpretation of the algorithm is shown by figure 3.4.
Hilbert curve Once, the data structure is obtained, it could be sorted using a 3D
Hilbert curve or, which is the same, mapped from 3D to 1D data structure. The
sorted buffer could be used directly for the context initialization. The Hilbert
curve generated for 16 × 16 × 16 bins is shown by figure 3.5.
Morton codes and Radix Sort The second approach is a logical continuation of the pre-
vious. Morton codes sort rays according to their spatial neighborhood in z-order.
Using morton codes, rays could be sorted with radix sort.
30](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-46-2048.jpg)
![3.2. Application of frame coherence
Algorithm 1 Algorithm for histogram generation
for all element in Buffer do
x0 ⇐ (element.x + 1)/2)
y0 ⇐ (element.y + 1)/2)
z0 ⇐ (element.z + 1)/2)
x ⇐ floor(x0 ∗ bin num/2)
y ⇐ floor(y0 ∗ bin num/2)
z ⇐ floor(z0 ∗ bin num/2)
list ⇐ histogram[x][y][z]
v.x ⇐ x0
v.y ⇐ y0
v.z ⇐ z0
list.pushBack(v)
histogram[x][y][z] ⇐ list
end for
Morton codes Efficient implementation for generation Morton codes was shown
in the previous subsections. The figure 3.6 shows a pattern generated by the
algorithm when sorting rays.
Radix Sort CUDA already has an efficient implementation for this algorithm.
Transformation between Spacial Structures
To experiment with dimensionality, it is necessary to transform spatial structures from 1D
to 2D or 3D data structures. This also could be achieved using Hilbert curves.
Mapping from 1D to 2D The sorted buffer could be mapped from 1D to 2D using 2D
Hilbert curve.
Mapping from 1D to 3D The mapping between 1D and 3D could be achieved using 3D
Hilbert curve.
Implementation details will be discussed in the appropriate chapter.
3.2. Application of frame coherence
The second problem is an investigation of influence of frame coherence on the wavetracer
performance.
3.2.1. Problem Description
The task is formulated in Redmine ticket # 218 ”Exploit frame coherence”. The task has
the following objectives:
1. Find types of coherence which exist in the system
a) Measure coherence
31](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-47-2048.jpg)
![3. Problem and Solution
Figure 3.4.: Uniformely distributed rays & histogram bins
2. Find schemas(algorithms) which allow to exploit them
3. Propose efficient implementation for the algorithms
4. Implement the proposed solution
5. Measure performance
6. What are the costs for coherence utilization in the system?
In the following subsections, the first two points will be considered.
3.2.2. Coherence
According to ”A Dictionary of Statistics” [51], coherence is a “term used to describe the
resemblance between the fluctuations displayed by two time series; an analogue of corre-
lation”.
Innerframe Coherence
In the context of the given work, the innerframe coherence means that there is a correlation
between results of ray tracing inside one frame. Rays with high coherence could be com-
32](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-48-2048.jpg)
![3.2. Application of frame coherence
Figure 3.5.: Hilbert curve generated for 16 × 16 × 16 bins
bined into groups. Inside these groups it necessary to trace only one ray [42]. Questions
which could be posed here:
1. How to know what rays have to be coalesced into one group?
2. How results of the tracing are to be stored in the cache?
3. How to calculate the error which introduces this approach?
Intraframe Coherence
The intraframe coherence means that there is a correlation between results of ray tracing
procedure for different frames. A result of the tracing procedure for any ray could be
stored in cache and used in the next frames. Questions which could be posed here:
1. How to measure coherence between frames?
2. How to know what data could be reused in the next frames?
3. What caching strategy to choose to purge the cache?
Coherence Measurement
Both innerframe and intraframe coherence could be measured using Pearson product cor-
relation coefficient [32].
rxy =
N
i=1(xi − ¯x)(yi − ¯y)
»
n
i=1(xi − ¯x)2 n
i=1(yi − ¯y)2
(3.3)
Where x and y are two random variables with N observations.
For the innerframe coherence could be used autocorrelation function [32].
rk =
N−k
i=1 (xi − ¯x)(xi+k − ¯x)
n
i=1(xi − ¯x)2
(3.4)
33](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-49-2048.jpg)
![3. Problem and Solution
Figure 3.6.: Z-curve
The quantity rk is called the autocorrelation coefficient at lag k. Calculation of these values
will be covered in more detail in the chapter dedicated to testing.
3.2.3. Formulation of Caching Scheme
In the Literature Review it has been done already a survey of caching schemas. Using
ideas stated by Chan [7] it is possible to build a caching system for the given task.
Cache Tree
In Chan’s [7] work, each object consists of several surfaces, each surface is divided into
several levels of patches and every patch is further quantized depending on angular values
of incident rays.
Objects In this work, there is only one type of objects: a model instance. Models are
distinguished using their ids which are defined in the configuration file. An environment
is also loaded as a model instance which usually has -1 as id. So roots of cache trees could
be featured using these identificators.
Patches There is a natural division of such objects into patches which are called primitive
indices. These primitive indices introduce patches of native precision for the objects. So
results cached for the given object could be discriminated using these indices.
Divisions Patches or primitive indices are responsible for spatial accuracy. However,
rays have to be distinguished also by angular precision. Angular values of incident rays
represent spatial coordinates within a sphere of unit length. These coordinates are also
quantized using some big number introducing quantization precision. Quantized coordi-
nates introduce divisions which further dinstinguish incident rays.
34](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-50-2048.jpg)









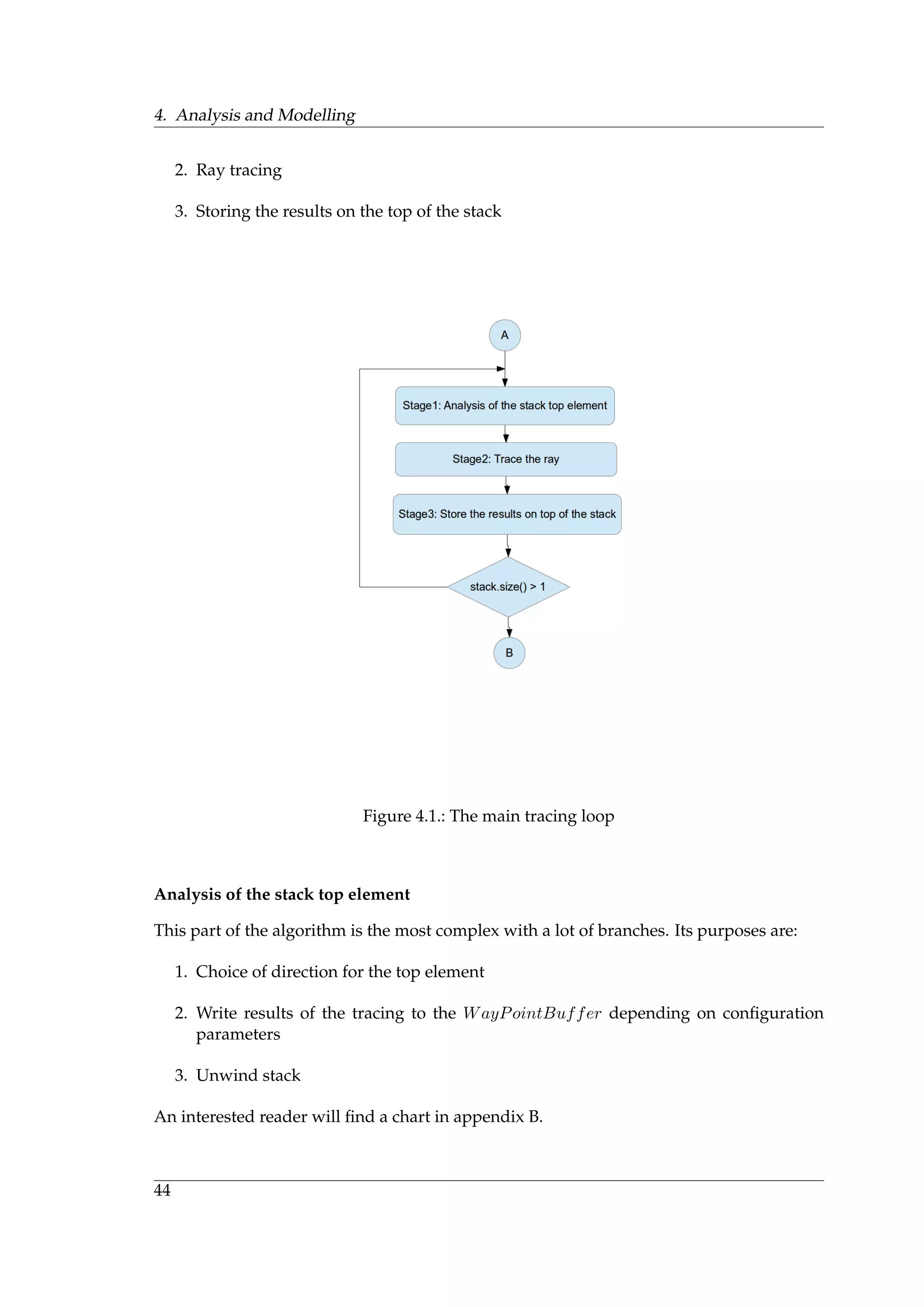
![4. Analysis and Modelling
Figure 4.3.: Saving data
2. If such trees can be efficiently constructed, how to maintain them?
3. How to implement a fast data search in such trees?
In our case, the cache trees cannot be implemented directly as they described by Chan [7],
firstly, because it requires a dynamic allocation of memory which is disabled in OptiX. Sec-
ondly, a search of elements in such data structures is challenging. In order to make it more
convenient, it is necessary to maintain additional data structures performing indexation.
Assuming all these, construction of such trees will be difficult.
Binary Tree
The first idea that comes is to use a binary tree. It has an easy construction and main-
tainance. Complexity of search in binary tree is O(log(n)). An object hierarchy could be
maintained using hashing of multicomponet indices. On the other hand, hash values could
be used to determine a total ordering of elements of the tree. Selection of an appropriate
hash function is a separate issue which will be regarded later. The problem with dynamic
allocation could be solved using a buffer with predefined elements. The tree is illustrated
using the figure 4.4.
However, the binary tree has one major defect: all elements of the tree have to be added
using the root element. The root element has to contain a counter which indicates the next
element in the buffer of predefined elements. In case of massively parallel computations,
GPU streams have to access the counter successively in order to provide data consistency.
This counter introduces the main bottleneck of the binary tree.
Chained Hash Table
A natural solution to the problem described in the previous paragraph is to constuct trees
in parallel. This resolves collisions of streams trying to access the counter and reduces the
waiting time in the queue. The streams are distributed by various root elements depending
on the hash value of added element. Such data structure is called a chained hash table [29].
It is more preferred then the binary tree, however, performance analysis of the chained
table shows that access to the root elements (buckets) and to chained elements of the table
46](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-62-2048.jpg)
![4.2. Frame Coherence
Figure 4.4.: Binary Tree
have different times. This difference overall reduces the table performance making it not
very profitable. Also since the element buffer has a fixed size, it is necessary to reserve a
certain number of elements for each bucket. This creates a fragmentation of the element
buffer. The data structure is illustrated by figure 4.5.
Implementation of the chained hash table is described in Implementation of Data Struc-
ture 5.2.2. Performance analysis is described in the Testing chapter 6.
Open-Addressed Hash Table
Further improvement of the data structure is permission of the direct access to elements of
the table. This solution has several benfits:
1. Further reduction of stream collisions
2. Absence of buffer fragmentation
3. A fast access to elements
Direct mapping allows to further reduce collisions of GPU streams. Absence of trees con-
struction solves the probem of buffer fragmentation. Direct access to buffer elements pro-
vides a possibility of fast read/write cache operations implementation. Nevertheless, there
exists an implementation pitfall connected with OptiX buffer which will be described in
the implementation subsection.
Implementation of the open-addressed hash table [29] is described in Implementation of
Data Structure subsection 5.2.2. Performance analysis is described in the Testing chapter
6.
47](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-63-2048.jpg)



![4.2. Frame Coherence
The first condition is necessary in order to distribute elements accross all buckets in uni-
form manner so that all the buckets contain approximately equal number of elements. The
second condition ensures that any element is identified in unique way.
However, based on the task solution approach, it is necessary to add another condition,
namely that keys with similar parameters should have close hash values. The question is
whether the conditions one and two are compatible. This should not be a problem because
rays are already uniformely distributed on a unit sphere.
Hash Function with Uniform Distribution
The key represents an array of integers. It is necessary to generate a hash value based on
the array. The code for such function could be taken, for example, from Morin [36]. Listing
4.2 shows the code.
Listing 4.2: Hash function for integer array
unsigned hashCode ( ) {
long p = (1L<<32)−5; / / prime : 2ˆ32 − 5
long z = 0x64b6055aL ; / / 32 b i t s from random . org
int z2 = 0x5067d19d ; / / random odd 32 b i t number
long s = 0;
long zi = 1;
for ( int i = 0; i < x . length ; i ++) {
/ / reduce to 31 b i t s
long long xi = ( ods : : hashCode ( x [ i ] ) * z2 ) >> 1;
s = ( s + zi * xi ) % p ;
zi = ( zi * z ) % p ;
}
s = ( s + zi * (p−1)) % p ;
return ( int ) s ;
}
In this listing, x is an array of integers. Integers are hashed using a multiplicative hash
function with d = 31 to reduce a hash code to 31 bits representation. This is done in order
additions and multiplications can be carried out using a 63-bit arithmetic. Probability for
two sequences to contain have the same hash code is defined as [36]
2
231
+
r
(232 − 5)
(4.1)
Hash Function Preseving Data Locality
Space filling curves again could be used to generate codes for multicomponent keys. The
key represents an integer array with 5 componets: instanceId, primitiveIndex, ,div x,
div y, div z. Listing 4.3 shows how the Morton Codes generator could be altered for 5D
[20].
51](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-67-2048.jpg)
![4. Analysis and Modelling
Listing 4.3: Morton Codes generator for 5D
unsigned int SeparateBy4 ( unsigned int x ) {
x &= 0 x0000007f ;
x = ( x ˆ ( x << 16)) & 0x0070000F ;
x = ( x ˆ ( x << 8 ) ) & 0x40300C03 ;
x = ( x ˆ ( x << 4 ) ) & 0x42108421 ;
return x ;
}
MortonCode MortonCode5 ( unsigned int x ,
unsigned int y ,
unsigned int z ,
unsigned int u ,
unsigned int v ) {
return SeparateBy4 ( x ) |
( SeparateBy4 ( y ) << 1) |
( SeparateBy4 ( z ) << 2) |
( SeparateBy4 (u) << 3) |
( SeparateBy4 ( v ) << 4 ) ;
}
SeparateBy4 inserts four blank bits between every two bits in the binary representation of
an integer. MortonCode5 interleaves binary representations using shift and or operations.
Double Hashing
In open-addressed hash tables, it is also used a mixed hash function [29]. The function for
double hashing is defined as:
h(k, i) = (h1(k) + i ∗ h2(k)) mod m (4.2)
where h1 and h2 are two auxilliary hash functions and i goes from 1 to m − 1 where m is
the number of positions in the table. In this work, however, it is used a simpler equation
where i and m are set to 1. Justification for this is that probing of hash table is not used,
i.e. insertion code does not look for unoccupied places in the table. Instead entire range of
hash function values is mapped directly to a discrete set of buffer indices. The mapping
function discribed in the next subsection.
4.2.5. Selection of Mapping Function
A mapping function associates a range of hash function values to the set of buffer indices.
The following formula performs the mapping:
f(h) = (1.0 + h/INT MAX) ∗ m/2; (4.3)
where h is a hash value, INT MAX is a constant denoting the maximum integer in a
system, m is the hash table size. The size of INT MAX is defined by ANSI standard. For
unix 32-bit systems it is 2,147,483,648 [56]. Thus for m = 500000 a range of hash values for
one bucket is approximately 8590.
52](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-68-2048.jpg)
![4.2. Frame Coherence
4.2.6. Selection of Synchronization Mechanism
Selection of synchronization mechanism depends on the data structure which is going to
be implemented. In case of chained hash tables, it is possible to use a lock-free synchro-
nization [34]. Synchronization of reading/writing access in open-addressed hash tables
could be implemented using atomic locks [47].
Lock-free Synchronization
In lock-free style of programming [40], at least one thread always do a progress. All threads
try to write their results to the concurrent data structure. On failure, a thread repeats the
operation. For synchronization, atomic operation are used usually. The following code
shows the atomicCAS operation how it is defined in CUDA [40].
Listing 4.4: atomicCAS [40]
int atomicCAS ( int *p , int cmp, int v){
exclusive single thread
{
int old = *p ;
i f (cmp == old ) *p = v ;
}
return old ;
}
The next listing shows insertion of element to a lock-free linked list.
Listing 4.5: Insertion to lock-free linked list [40]
void i n s e r t ( ListNode mine , ListNode prev )
{
ListNode old , link = prev−>next ;
do{
old = link ;
mine−>next = old ;
link = atomicCAS(&prev−>next , link , mine ) ;
}while ( link != old )
}
Idea behind the lock-free data updates is that on every new cycle it is generated a new
value based on current data. Then performed an atomicCAS operation trying to change
the current data to the new value. If the operation unsuccessful it is repeated again.
Atomic Lock Synchronization
In the locking style of programming [40], all threads are trying to get the lock. One thread
aquires the lock, does its work and release the lock and so on. The next listing shows a
mutex synchronization using atomic locking.
53](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-69-2048.jpg)
![4. Analysis and Modelling
Listing 4.6: Addition using atomic lock [40]
int locked = 0;
bool try lock ( )
{
int prev = atomicExch(&locked , 1 ) ;
i f ( prev == 0)
return true ;
return false ;
}
bool unlock ( )
{
int prev = atomicExch(&locked , 0 ) ;
i f ( prev == 1)
return true ;
return false ;
}
double atomicAdd ( double * data , double val )
{
while ( try lock ( ) == false ) ;
double old = * data ;
* data = old + val ;
unlock ( ) ;
return old ;
}
54](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-70-2048.jpg)
![5. Implementation
5.1. Implementation of Ray Reordering
During the research stage, it have been implemented 2D and 3D Hilbert curves, Z-curve
and the ray histogram. The implementation is performed on the CPU side, because the task
that is to explore how the ray sorting affects efficiency. On the basis of investigation results,
it is found that the most efficient solution is a combination of Z-curve and Radix sort. An
implementation of Z-curve has been described in the previous chapter and CUDA has
already an efficient implementation for Radix sort algorithm. Thus there exists a standard
GPU implementation. Results of the benchmarking are described in the next chapter.
Hilbert Curves
2D Hilbert Curve The curve is implemented using a turtle graphics with at most one
turn after a step [21]. An interested reader could find the implementation in appendix A.2
3D Hilbert Curve Implementation of the 3D Hilbert curve on the CPU is a straightfor-
ward. It follows the syntax given in appendix A.3. Showing the implementation would be
tedious for the reader.
Z Curve
Implementation for Z-curve strictly follows the algorithm given in appendix A.1.
Ray Histogram
Ray histograming is described by algorithm 1. The implementation exactly corresponds to
the algorithm.
Radix Sort
The algorithm for Radix sort has already an efficient implementation in CUDA, see, for
example [33].
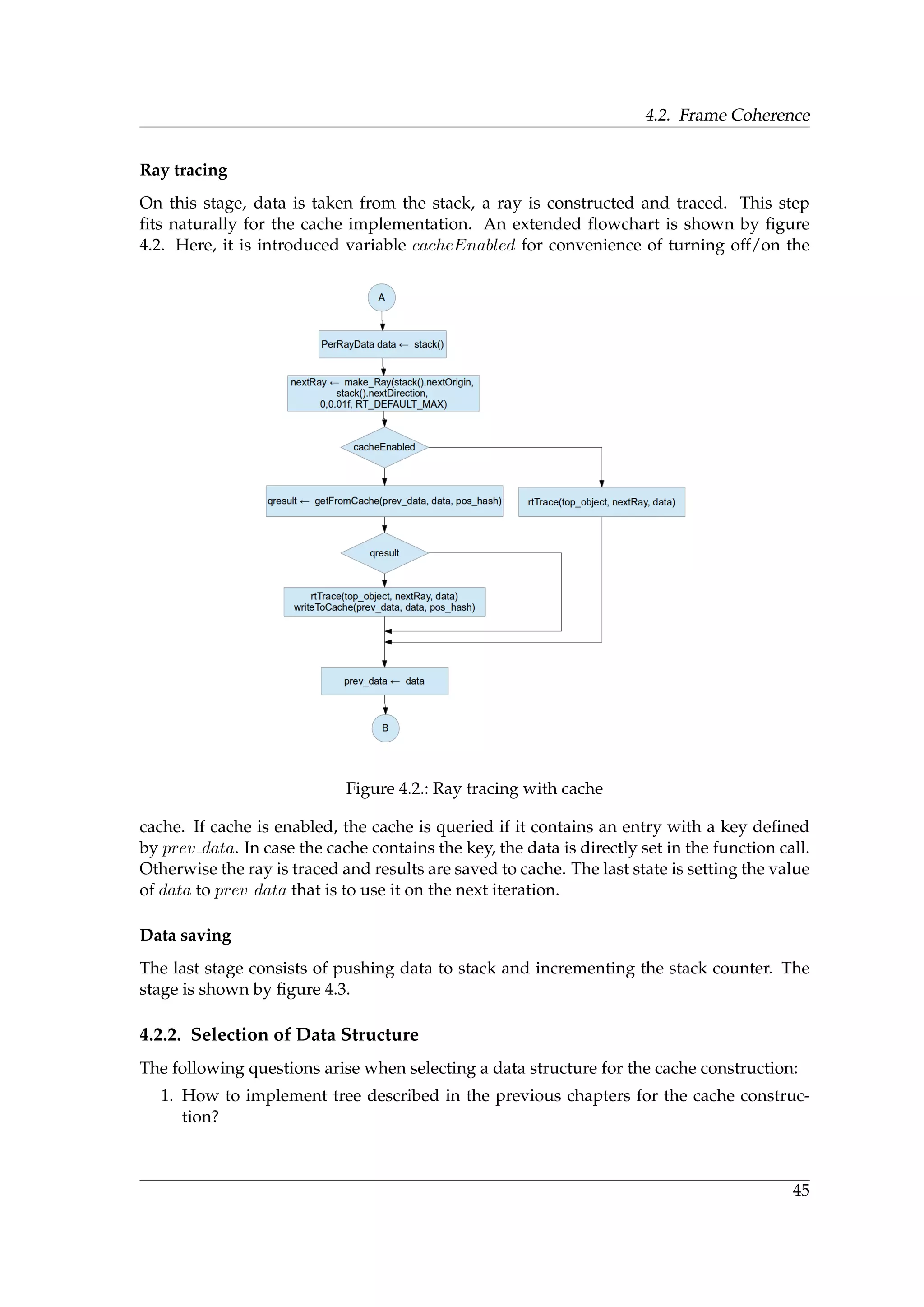
5.2. Implementation of Frame Coherence
In this section, it is described an implementation of frame coherence according to selected
data model 4.2.3 and data structure 4.2.2.
55](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-71-2048.jpg)
![5. Implementation
5.2.1. Implementation of Data Model
The implementation of data model includes implementation of CacheKey and CacheNode.
Cache Key
CacheKey is a data structure which contains parameters of a multicomponent key 3.2.3.
Interface
setIndices
device void setIndices(uint16 t instanceId, uint32 t primitiveIndex, float3 inc dir, int
hash method, int div)
Return value void
Parameters
instanceId : identificator of loaded model
primitiveIndex : identificator of mesh triangle
inc dir : a ray direction angle
hash method : id of hash function
div : quantization precision
Description Set the key members and calculate the hash value for the key data.
equals
device bool equals(Key other)
Return value boolean
Parameters
other : a key for comparison
Description Returns true if the key is equal to the key provided
calc hash1
device bool calc hash1()
Return value unsigned integer
Description Calculates a hash value from key members using uniform random distribu-
tion [36]
56](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-72-2048.jpg)
![5.2. Implementation of Frame Coherence
calc hash2
device bool calc hash2()
Return value unsigned integer
Description Calculates a hash value from key members using morton codes [20]
calc hash3
device bool calc hash2()
Return value unsigned integer
Description Calculates a hash value using a mix of two hashing functions [29]
separateBy4
device unsigned int separateBy4(unsigned int x)
Return value unsigned integer
Parameters
x : a number which binary representation to be shifted by 4
Description Separate bits by 4 bit places in binary representation of a number provided
in the method [20]
mortonCode5
device unsigned int mortonCode5(unsigned int x, unsigned int y, unsigned int z, unsigned
int u, unsigned int v)
Return value unsigned integer
Parameters
x : x coordinate
y : y coordinate
z : z coordinate
u : u coordinate
v : v coordinate
Description Constructs morton codes by interleaving x, y, z, u, v using oring and shifting
[20]
57](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-73-2048.jpg)
![5. Implementation
Interface Implementation A curious reader could find the interface implementation of
the cache key in appendix C.1
5.2.2. Implementation of Data Structure
The present subsection describes implementation of data strutures selected in the previous
subsections.
Chained Hash Table
Configuration Parameters Two parameters are added to a configuration file. These pa-
rameters are:
1. cache buffer size
2. cache load factor
cache buffer size is necessary to define a size of buffer which elements are used to build
the hash table on the device side. The buffer is created on the CPU side using OptiX
context. This buffer is filled with elements of CacheNode type. The initial state of these
elements is set and then the buffer passed to the device side. The primary cause why the
buffer is used for the hash table construction is impossibility for dynamic allocation of the
table elements on the device side using OptiX [38]. There are also some efficiency consid-
erations why using such buffer could be beneficial [34] for the hash table construction. The
following listing shows the buffer initalization on the CPU through the context.
Listing 5.1: Nodes buffer initialization
nodeBuffer = context−>createBuffer (RT BUFFER INPUT OUTPUT ) ;
nodeBuffer−>setElementSize ( sizeof ( CacheNode ) ) ;
context−>setBuffer ( BufferVariable : : CACHE NODE BUFFER) ( nodeBuffer ) ;
cache load factor defines a maximun number of elements which could be expected in
a bucket. The number of buckets for the hash table is determined using the following
formula:
number of bins =
cache buffer size
cache load factor
(5.1)
Key Parameters CacheKey has the same parameters as described in 4.2.3. Divisions are
calculated using the following code:
Listing 5.2: Divisions
div x = ( i n c d i r . x + 1)* div /2;
div y = ( i n c d i r . y + 1)* div /2;
div z = ( i n c d i r . z + 1)* div /2;
Here, inc dir is variable of type float3 containing direction cosines of a ray. Directions
are always aligned to positive floating numbers by adding one, after that the floats are
multiplied by large integer variable which is denoted by div. The variable is responsible
for the quantization precision, large values are responsible for greater accuracy.
58](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-74-2048.jpg)

![5. Implementation
hasKey
inline device bool hasKey(PerRayData data)
Return value Returns true if the requested element is in the cache, false otherwise
Parameters
data - data structure with results of the previous tracing (key)
Description Indicates an element’s existance in the cache by its key generated from data
get bucket index
inline device uint get bucket index(int hash)
Return value Returns true if the requested element is in the cache, false otherwise
Parameters
data - data structure with results of the previous tracing (key)
Description Indicates an element’s existance in the cache by its key generated from data
Interface Implementation
writeToCache constructs a binary tree in the bucket determined by the hash value of
node being inserted. Method writeToCache uses a lock-free synchronization paradigm
[19]. Before the loop which seeks a vacant place starts, the method gets pointers to the
root node of the tree and to the node in buffer which has to be inserted. Then the loop
starts, in both subtrees the method tries to atomicCAS indices pointing to the left and right
elements. If the operation successful, the loop terminated, otherwise to root is assigned a
new value, root− > left or root− > right and the operation repeats again.
getFromCache acesses elements of a tree located in a bucket obtained using the hash code
of the search element. If the element is found, returns it, otherwise returns NULL. No syn-
chronization is necessary. The only modification which is done is counter incrementation.
hasKey returns true if getFromCache returns value which is not NULL.
getBucketIndex maps hash values to the buffer indices. It first divides a hash value by
the maximum integer, adds one and multiplies the resulting number by a number of ele-
ments in the element buffer divided by 2.
A curious reader could find the implementation of the chained hash table in appendix
C.2
60](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-76-2048.jpg)



![5. Implementation
calculateResidual
inline device float calculateResidual(float3 origin, float3 otherOrigin)
Return value float
Parameters
origin : the first point
otherOrigin : the second point
Description Calculates L1 distance between two points provided in the function call.
checkIntersections
inline device bool checkIntersections(const CacheNode∗ node, float R)
Return value boolean
Parameters
node : node to be checked
R : radius of antenna
Description Returns true if coordinates of the node provided in the method call are within
a unit sphere of any of the receivers which present currently on the scene. This
method checks a validity of RECEIV ER HIT 3.2.3
Interface Implementation
writeToCache writes data to cache using prev data as a key. Synchronization of both
write and read accesses is performed using an atomic locking pardigm [47]. In the write
method, after the pointer to the bucket is obtained, a stream tries to lock the node on
writing using atomicCAS operation and writeLock. If the operation successful, then the
stream change the data inside the node and unlock the readLock. This operation unlocks
the object for reading. If the operation is not successful the stream simply leaves the section
without writing since, firstly, both results cannot be stored and, secondly, it could be faster
to trace ray then wait on the writeLock.
getFromCache reads from the cache data using data provided in the method call as key.
The method also uses the same synchronization [47] paradigm as writeToCache. A stream
gets a pointer to bucket and then tries to acquire the readLock. Every stream which ac-
quires the readLock check whether position stamp of the bucket is valid. If it is not, then
the method sets readN to 0, unlocks the bucket for writing setting writeLock to 0 and
64](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-80-2048.jpg)
![5.2. Implementation of Frame Coherence
returns false. This means that data of the given bucket will be automatically overwrit-
ten. If the stamp is valid, then, firstly, the stream increments the total number of reads for
the given bucket, this number is denoted by variable readN. If this number is less then
cache readers number defined in the configuration file, the stream after reading the data
releases the readLock. Otherwise, it sets the total number of reads readN to 0 and unlocks
the bucket for writing setting the writeLock to 0.
getFromCacheRes reads from cache data using data variable provided in the method call
as key. The method uses the same synchronization mechanism as in readFromCache.
The only difference is that the method uses a different approach for purging 3.2.3. In case
hashes of the requested element and that of the bucket are not equal, the method calculate a
residual value. If the residual value is less then a threshold denoted by cache residual value
provided in the configuration file then the stream reads data and returns true. Otherwise
it returns false which means that data in the bucket will be overwritten.
makeKey is an auxiliary method which serves for construction of key from prev data.
getBucketIndex returns an index in the node buffer for the hash provided in the method
call. The method implementation differs from the chained hash-table in that instead of
INT MAX it uses UINT MAX because hash values have now unsinged int type.
searchInMap is an auxiliary method helping to determine on offset for a particular model.
The buffer cache emitter map has an associated offset index which shall be multiplied by
the number of elements in the buffer divided by the number of models loaded.
calculateResidual is an auxiliary method helping to determine L1 [5] distance between
two points provided in the method call. The method is used in getFromCacheRes to
calculate the residual value.
checkIntersections checks coordinates of node provided in the method call against coor-
dinates of receivers are currently on the scene. If the node coordinates are within radius R
provided in the method call, the method returns true, otherwise returns false.
A curious reader could find the implementation in the appendix C.3
65](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-81-2048.jpg)





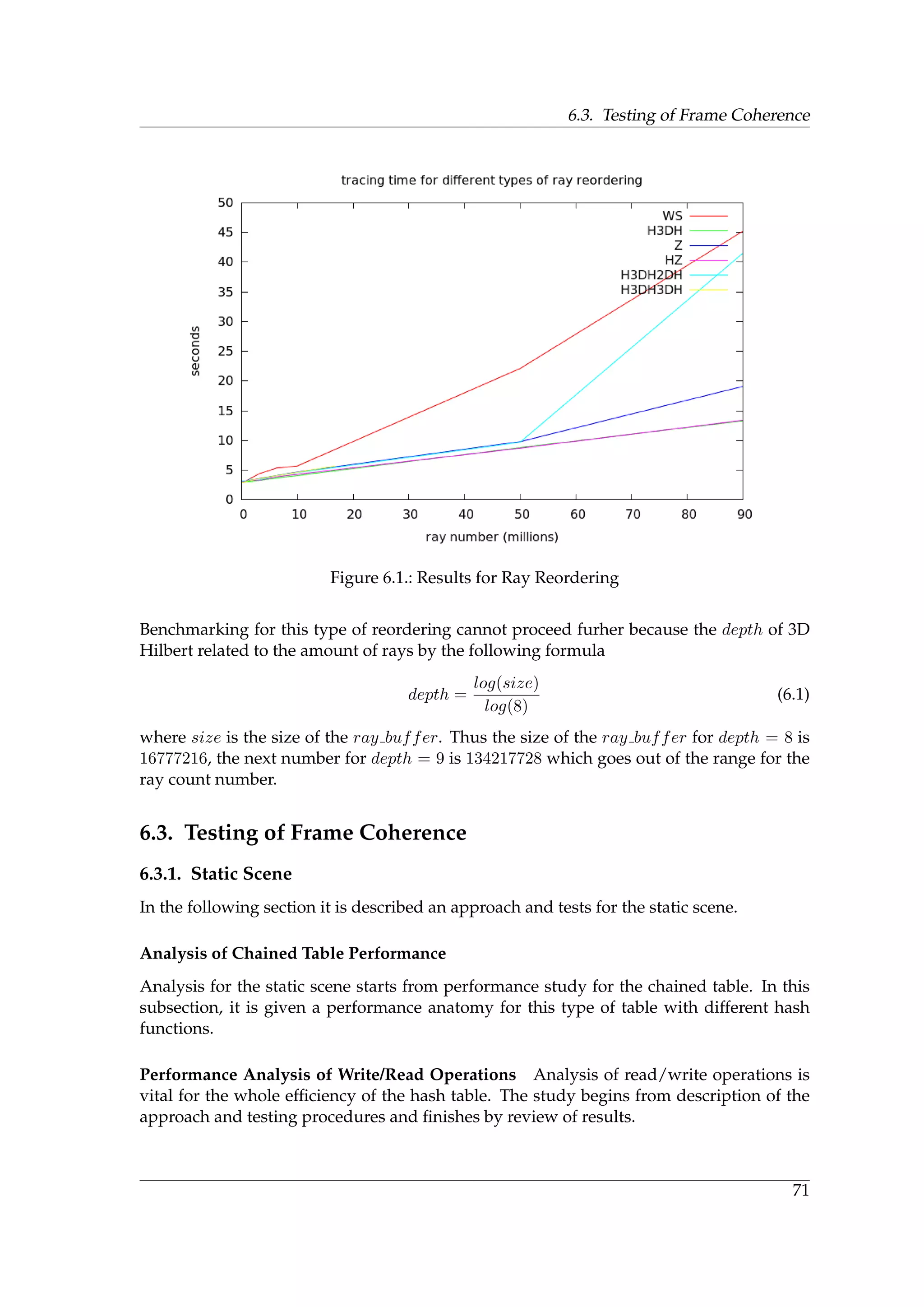

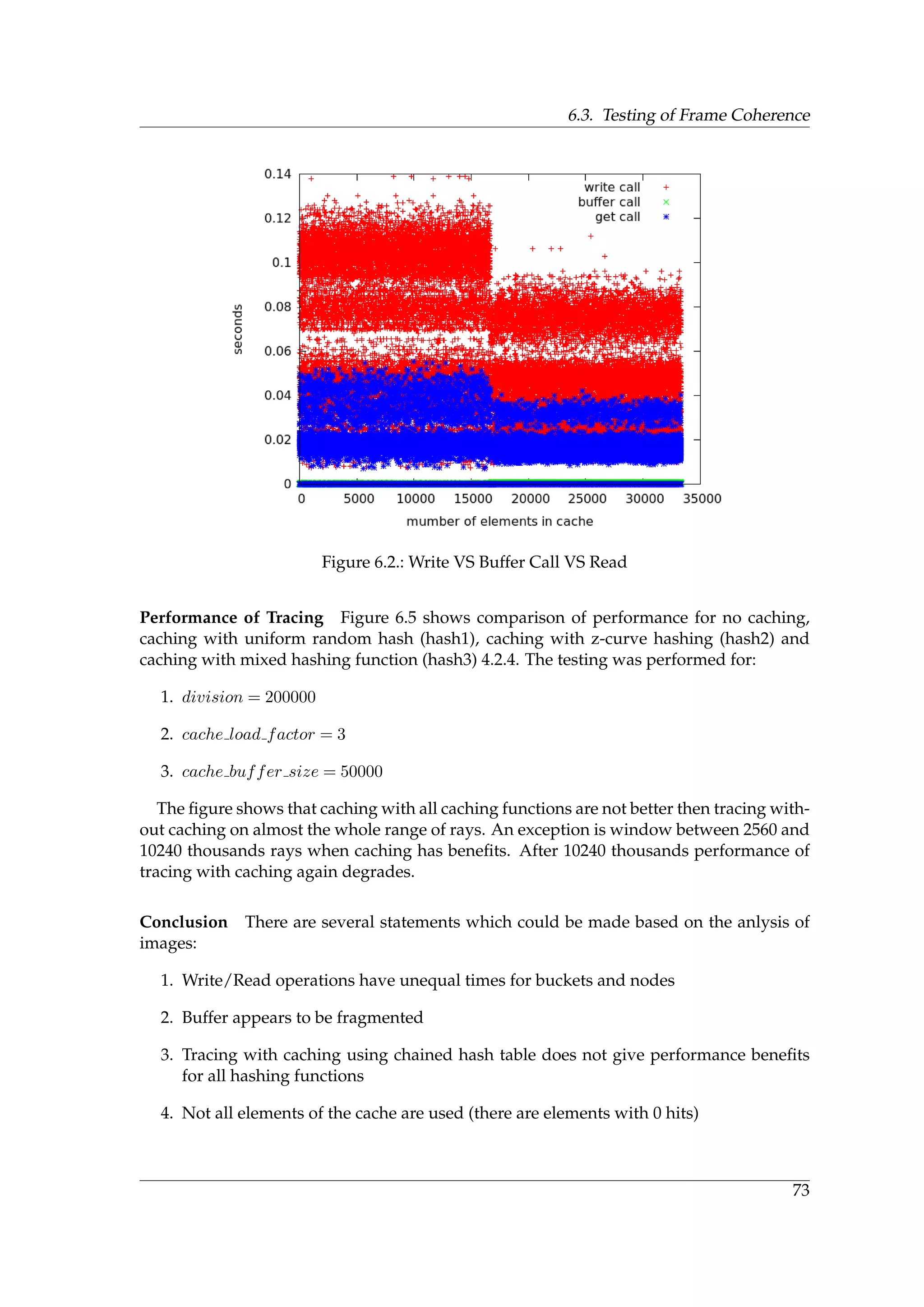
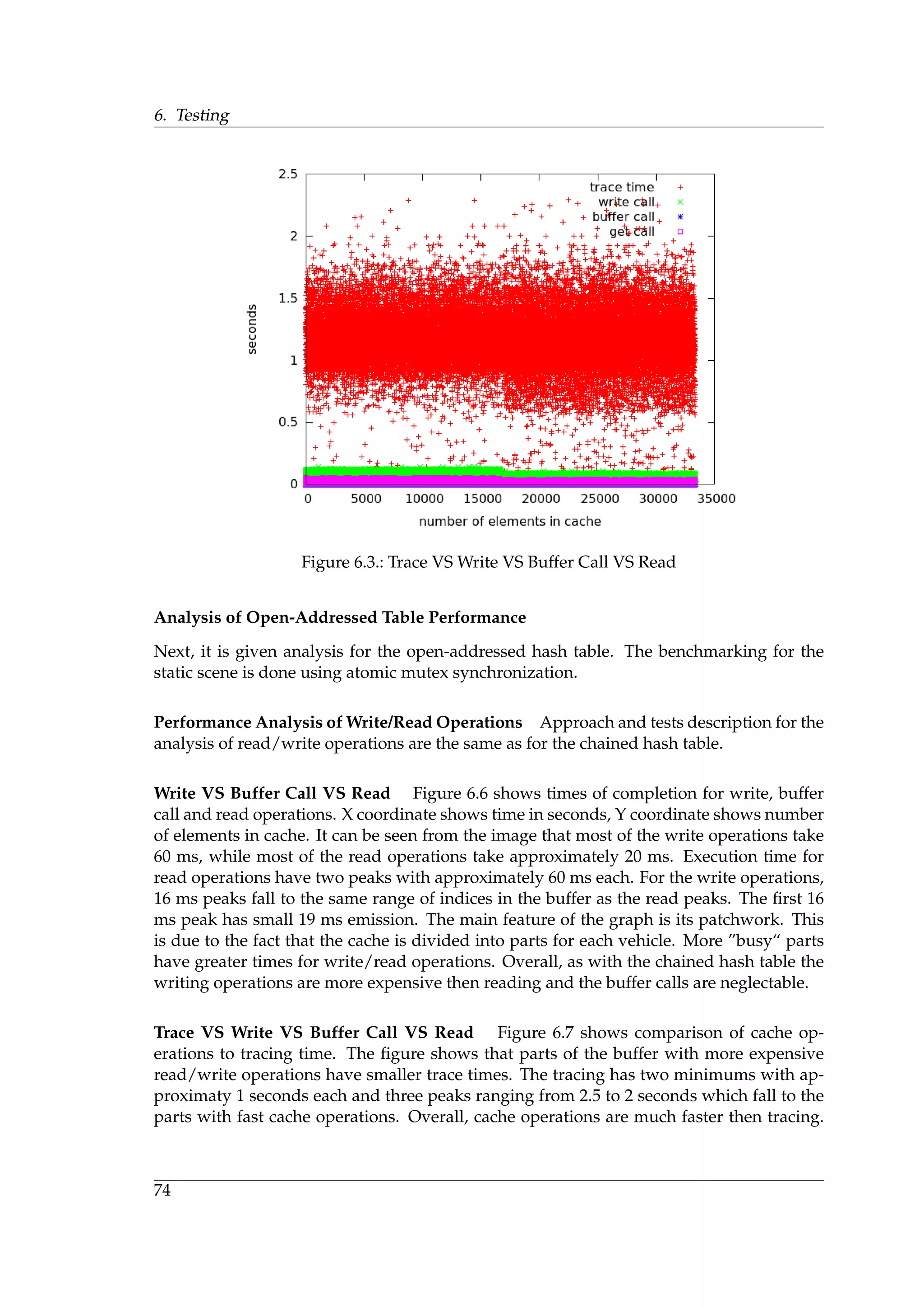
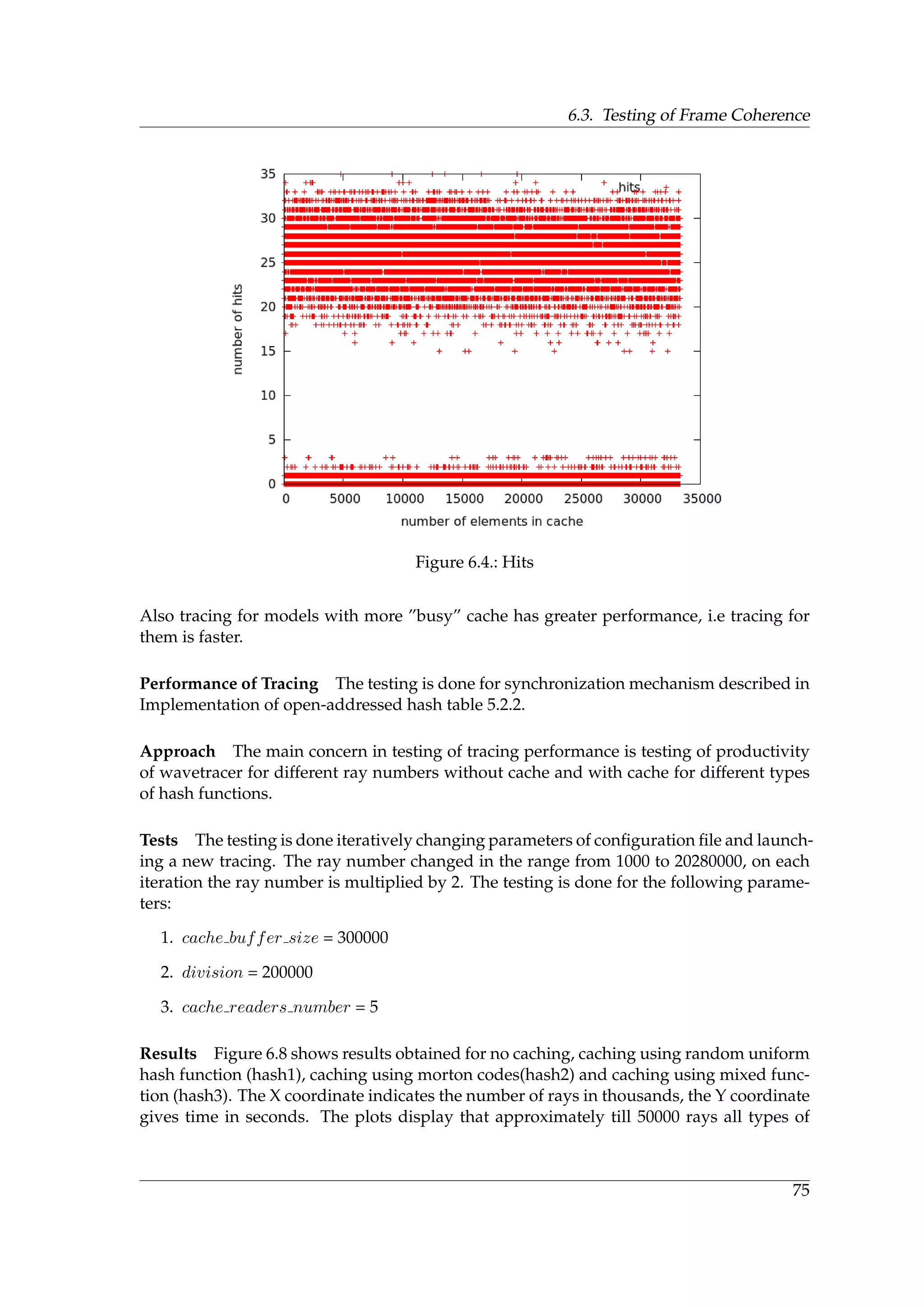
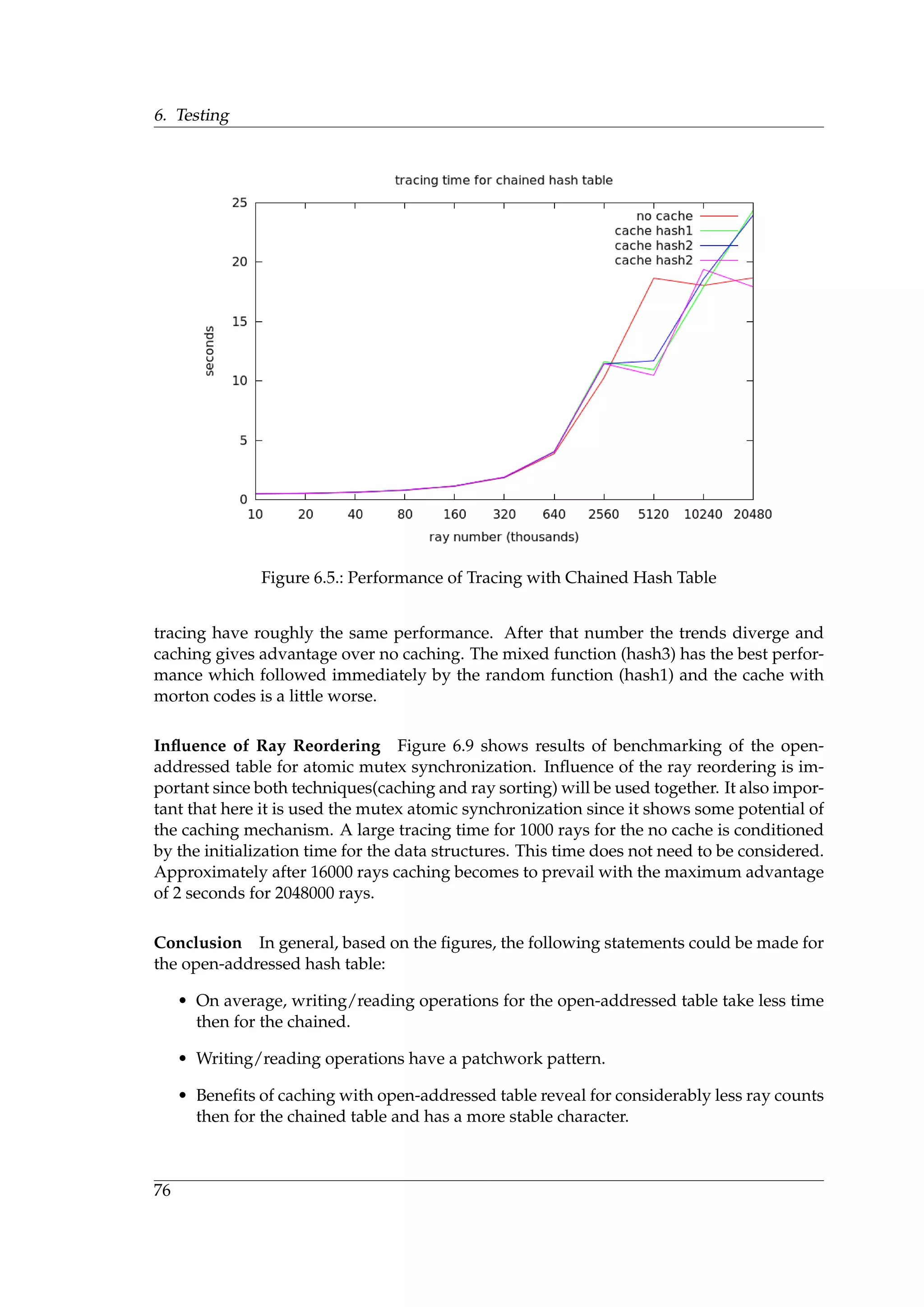
![6.3. Testing of Frame Coherence
Figure 6.6.: Write VS Buffer Call VS Read
6.3.2. Dynamic Scene
In this subsection, it is discussed a testing for dynamic scenes. The type of structure anal-
ysed is the open-addressed hash table which has better performance then the chained ta-
ble.
Approach
For dynamic testing, the following parameters are important:
• Temporal tracing metrics
• Accuracy of tracing with cache
• Calculation of correlation between frames
The first is obvious, the second item is necessary to estimate what error introduces caching
comparing to performance benefits. The last item is essential to assess the coherence be-
tween frames because high coherence correspond to high caching benefits.
Temporal Metrics As a temporal metric, it is chosen an average time of tracing for 500
working cycles of wavetracer. The average time could be calculated incrementally using
the following formula [11]:
An+1 = An +
vn+1 − An
n + 1
(6.2)
where An is the average number obtained on the previous cycle, vn+1 is tracing time for
n + 1th cycle and n + 1 is current number of cycles.
77](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-93-2048.jpg)
![6. Testing
Figure 6.7.: Trace VS Write VS Buffer Call VS Read
Accuracy of Tracing For correct error calculation, it is necessary to solve the following
issues:
• What output parameters of the ray tracing could be taken for error calculation?
• What is the ground truth in this assessment?
• How to calculate the error algorithmically?
As parameters for error calculation could be taken points on a trace path contained in the
waypoint buffer. The union Waypoint contains the following members:
• WP Reflection
• WP Diffraction
• WP Miss
• WP Hit
• WP Launch
As a tracing path could be taken positions of WP Reflection and WP Hit. As the ground
truth, it could be used a trace path obtained without caching. The error could be calculated
using the following approach. The trace paths represent point clouds, these clouds could
be compared with each other using many ways. One of the possible assessment is to
calculate length between point clouds centers, this length introduces a measure for two
clouds difference. The length could be calculated using the following formula [2]:
D1 = L1(cA, cB) and D2 = L2(cA, cB) (6.3)
78](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-94-2048.jpg)
![6.3. Testing of Frame Coherence
Figure 6.8.: Performance of Tracing with Open-Addressed Hash Table
where L1 and L2 are distances and cA and cB are centroids of point clouds.
Statistical Correlation between Frames Correlation between frames could be estimated
using the same data (point clouds). Every cycle of work of the wavetracer produces an
output written to the waypoint buffer. For example, correlation is calculated for two
sets of x coordinates in produced ouputs. Similar coefficients are calculated for y and z
coordinte. Normalized sum of these coefficients is considered as correlation coefficient
between frames. If this correlation coefficient is high then it means also that coherence
between frames is also high. Mathematically this could be expressed as following
rx1x2 =
N
i=1
(x1i− ¯x1)(x2i− ¯x2)
√ n
i=1
(x1i− ¯x1)2 n
i=1
(x2i− ¯x2)2
ry1y2 =
N
i=1
(y1i− ¯y1)(y2i− ¯y2)
√ n
i=1(y1i− ¯y1)2 n
i=1(y2i− ¯y2)2
rz1z2 =
N
i=1
(z1i− ¯z1)(z2i− ¯z2)
√ n
i=1
(z1i− ¯z1)2 n
i=1
(z2i− ¯z2)2
c12 =
r2
x1x2+r2
y1y2+r2
z1z2
1
(6.4)
where O1 = {x1, y1, z1} and O2 = {x2, y2, z2} are two ouputs of tracing pocedures and
xi, yi, zi are coordinate sets and rx1x2, ry1y2, rz1z2 are correlation coefficients between two
coordinate sets. c12 is normalized length of the correlation vector [rx1x2, ry1y2, rz1z2].
79](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-95-2048.jpg)
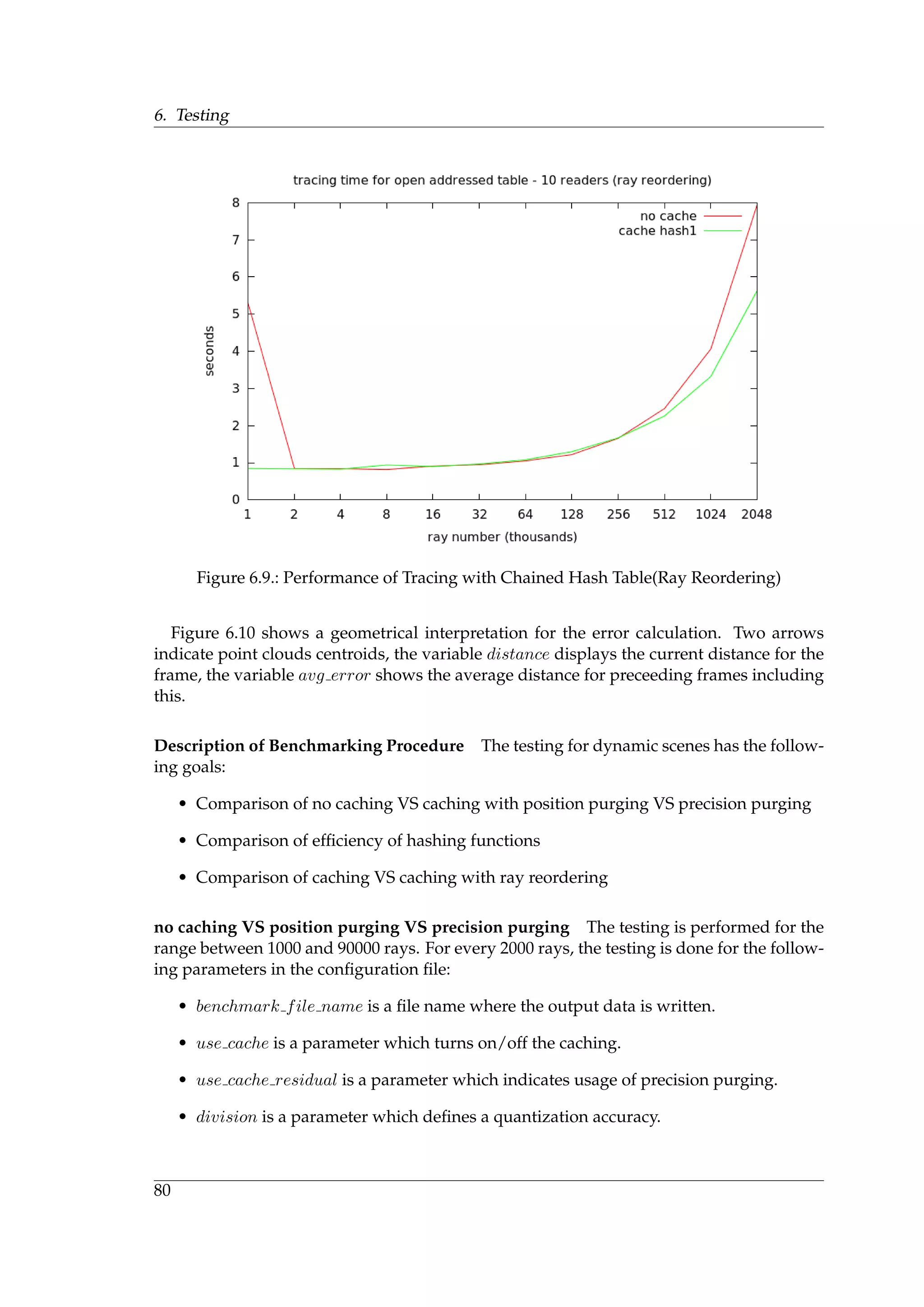

![6. Testing
Results In the following paragraph results of the testing procedures for dynamic scenes
are described.
OptiX error It is necessary to mention that while testing the system for dynamic scene,
there have been an exception with copying data from the host to device. An interested
reader will find the exception description in the following nvidia thread [39]. In order
to avoid the exception, there have been implemented a synchronization mechanism for
saving/reading data to/from buffer. The mechanism considerably reduces the caching
performance both for static and dynamic scenes but it cannot be not used since a pure mu-
tex synchronization does not ensure safe execution of the program. Moreover, developers
have not answered a question why such an error can occur. It is possible that such error
can occur when there is a big stress on the buffer. It is to be hoped that the error will be
resolved in the future version of the program.
no caching VS position purging VS precision purging Figure 6.11 shows results of the
benchmarking for no caching (green), caching with position stamp purging and division
200000(red) and caching with precision purging, residual value 0.0125 and division 10000
(blue). The X coordinate indicates a number of rays, while the Y coordinate shows average
Figure 6.11.: no caching VS position purging VS precision purging
tracing time in seconds. Caching with position stamp purging is constantly better then
tracing with no caching. The difference becomes bigger for higher ray numbers. Caching
with precision purging has better performance then both no caching and caching with po-
sition stamp purging. Simple caching gives approximately 10% performance improvement
for small and medium ray numbers with increase to 15 % for high ray count. Caching with
residual has around 30% improvement over no caching for small and medium ray num-
bers with decrease to aprroxiamtely 17% for higher ray counts.
82](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-98-2048.jpg)
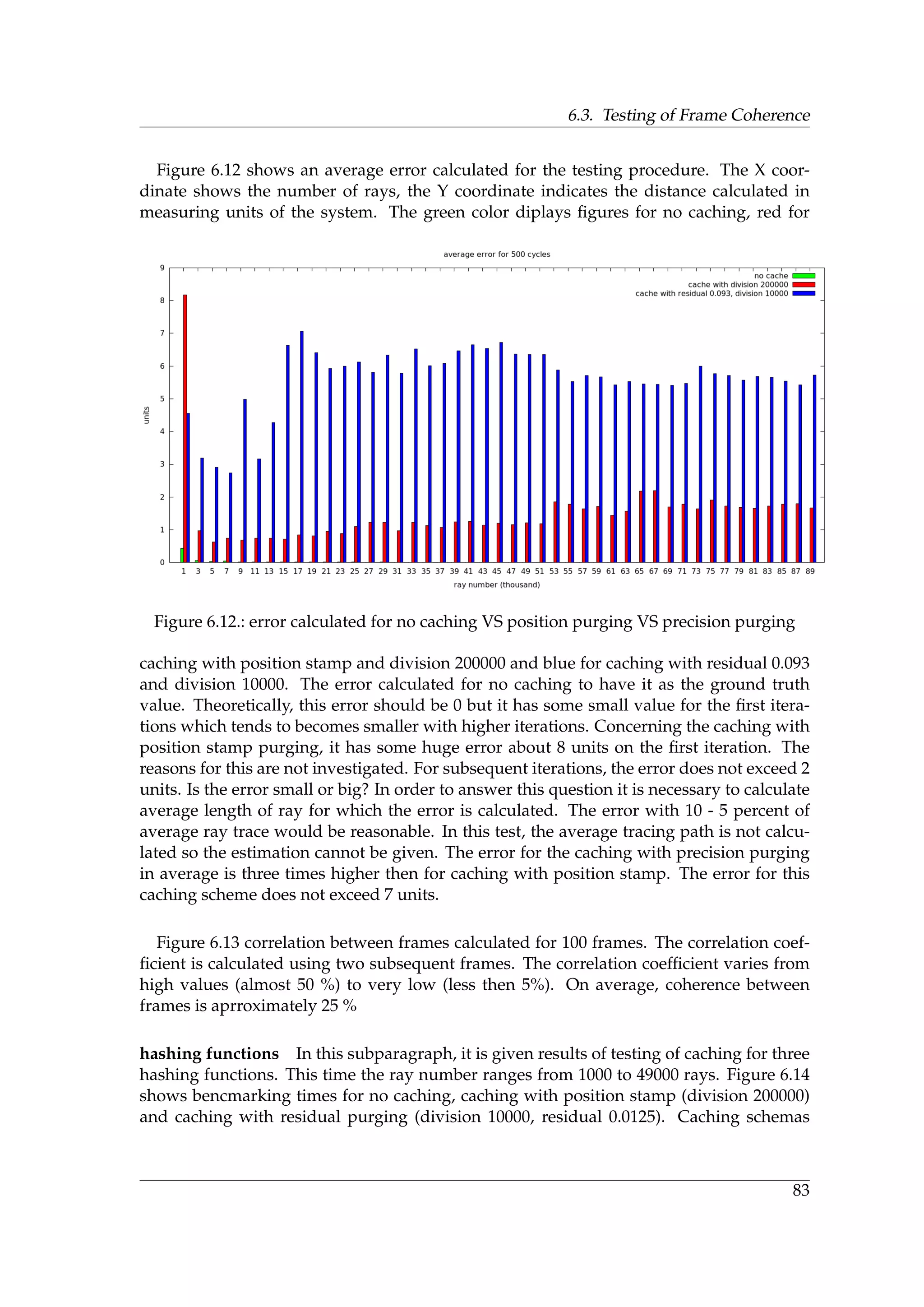
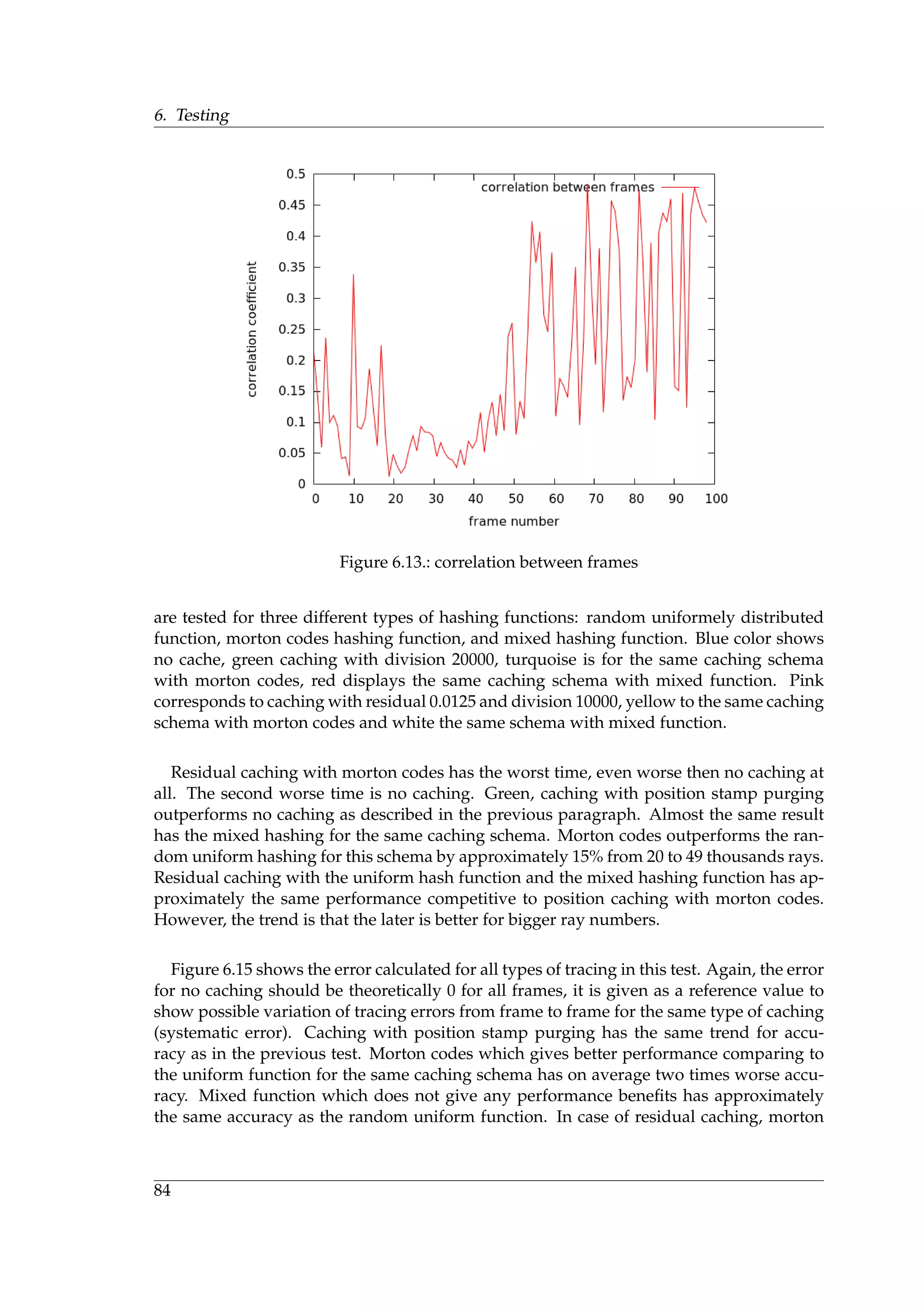
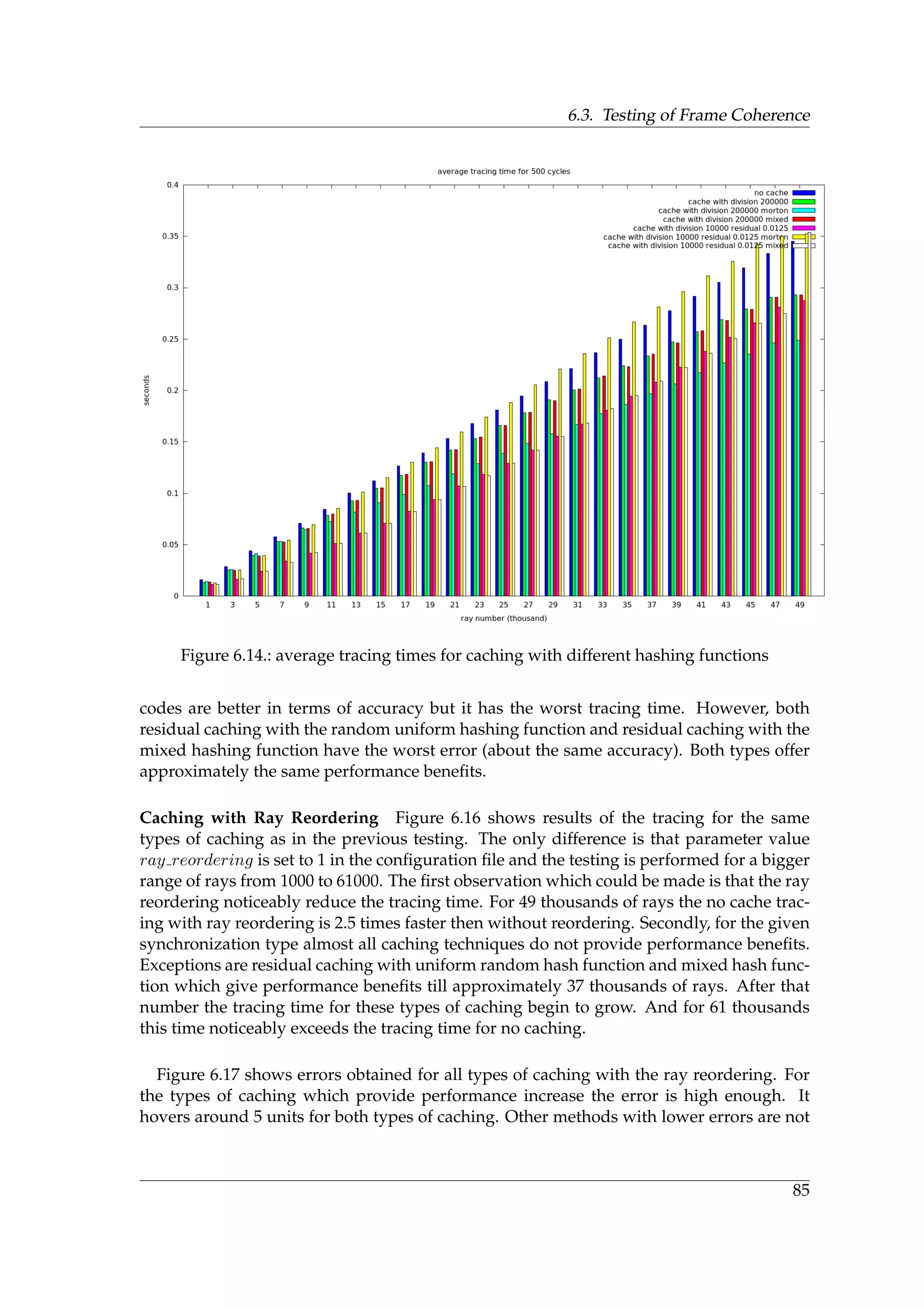

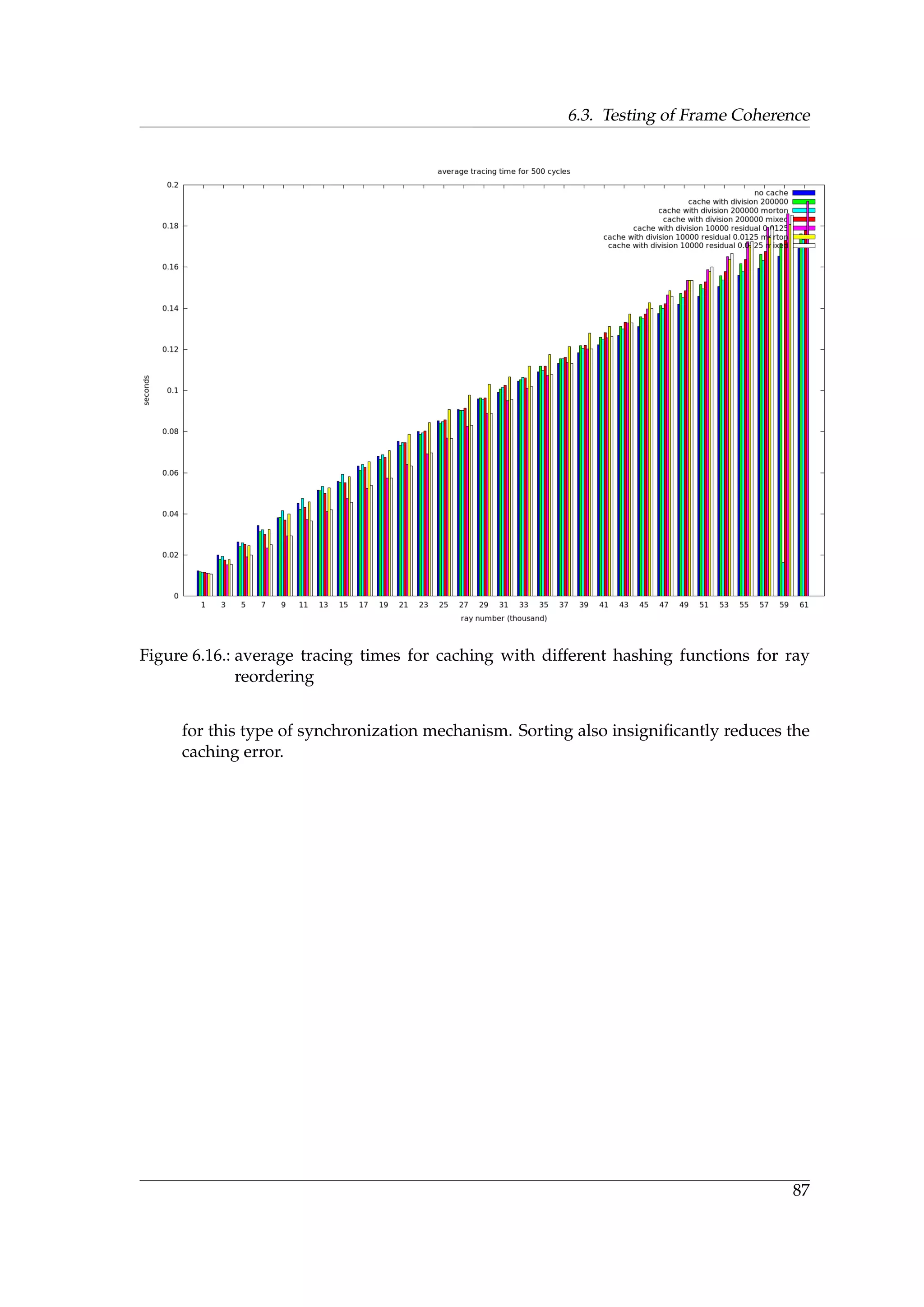
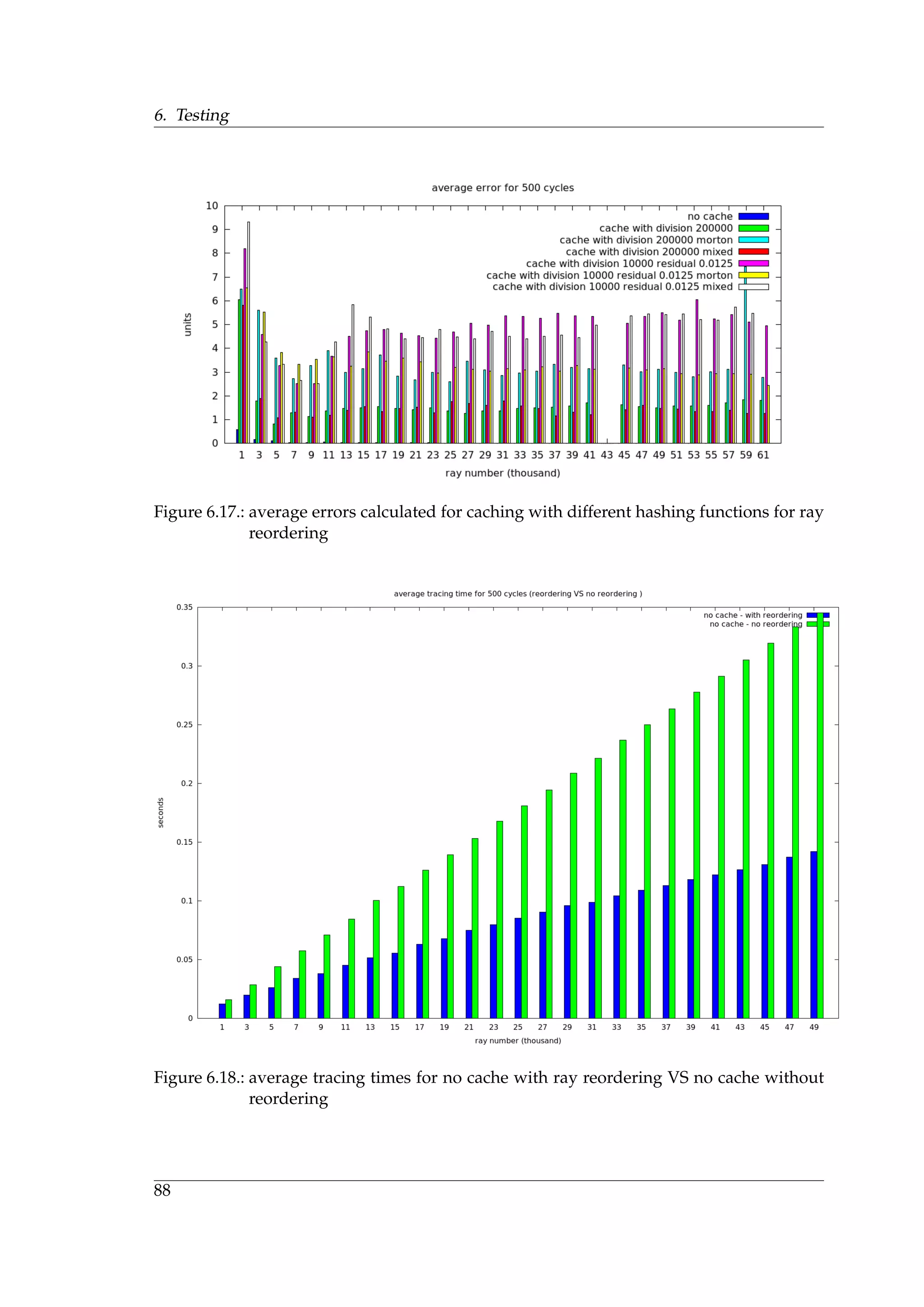


![7. Discussion
In the project, the following tasks have been performed and problems solved.
7.1. Ray Reordering
The task of ray reordering has been successfully solved using the space-filling curves. The
space-filling curves are also used for the BVH construction in the ray tracing. For example,
refer to [23]. It have been tried different versions for solution:
1. Construction of ray histogram and bypassing the histogram using the 3D Hilbert
curve.
2. Construction of ray histogram and bypassing the histogram using the Z-curve
3. Sorting initial ray coordinates using the Z-curve
4. Mapping of the obtained sorted ray list to 2D buffer using the 2D Hilbert curve
5. Mapping of the obtained sorted ray list to 3D buffer using the 3D Hilbert curve
Launching of the tracing procedure with 2D and 3D ray buffer gives no obvious results.
Overall, the most efficient implementation occurs to be the ray reordering using the Z-
curve. The curve could be easely implemented on the GPU side, the sorting could be
implemented using the radix sort. Results of the ray sorting will be discussed in the Con-
clusions chapter.
7.2. Frame Coherence
7.2.1. Caching Method
The main task that is solved here is construction of caching method for simulation of the
propagation channel in VANET simulation. The simulation is performed when practically
all the ray sources dynamically change their positions from frame to frame. Thus it is
solved a problem of cache construction, reusage of data from the previous launches and
cache purging.
7.2.2. Data Structure
In the implementation part, it is solved a problem of cache trees construction using ray
hashes. A research of hashing functions allows to detect their influence to the peformance.
It have been studied random uniform hasing function, hashing with Morton codes and
mixed hash function. They all differently influence the system perfomance, the results will
be discussed in the Conclusions chapter.
91](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-107-2048.jpg)





![A. Space-Filling Curves
A.1. Morton Codes Generator
Listing A.1: Morton codes generator
unsigned int expandBits ( unsigned int v ) {
v = ( v * 0x00010001u ) & 0xFF0000FFu ;
v = ( v * 0x00000101u ) & 0x0F00F00Fu ;
v = ( v * 0x00000011u ) & 0xC30C30C3u ;
v = ( v * 0x00000005u ) & 0x49249249u ;
return v ;
}
unsigned int morton3D ( float x , float y , float z ) {
x = min( std : : max( x * 1024.0 f , 0.0 f ) , 1023.0 f ) ;
y = min( std : : max( y * 1024.0 f , 0.0 f ) , 1023.0 f ) ;
x = min( std : : max( z * 1024.0 f , 0.0 f ) , 1023.0 f ) ;
unsigned int xx = expandBits ( ( unsigned int ) x ) ;
unsigned int yy = expandBits ( ( unsigned int ) y ) ;
unsigned int zz = expandBits ( ( unsigned int ) z ) ;
return xx * 4 + yy * 2 + zz ;
}
A.2. 2D Hilbert Curve Implementation
The 2D Hilbert curve is implemented using an algorithm when the turtle turns at most
only once after doing a step [21].
Listing A.2: 2D Hilbert Curve Implementation
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−−−−− hilbert2D . h −−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
# ifndef HILBERT2D H
#define HILBERT2D H
/ * *
* Maps 1D b u f f e r to 2D b u f f e r using H i l b e r t curve and t u r t l e g r a p h i c s .
* /
97](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-113-2048.jpg)


![A. Space-Filling Curves
return pow(2 , depth ) ;
}
} ;
#endif / * HILBERT2D H * /
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−− hilbert2D . cpp −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−− t u r t l e s t e p −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
void Hilbert2D : : step ( ) {
/ / here we increment b u f f e r index to get a new element from i n i t i a l
/ / b u f f e r
miles ++;
/ / depending on the t u r t l e o r i e n t a t i o n we increment / decrement x or y
/ / x and y in f a c t i n d i c e s o f the r e s u l t i n g b u f f e r
switch ( t u r t l e ) {
case 0:{
y++;
break ;
}
case 1:{
x++;
break ;
}
case 2:{
y−−;
break ;
}
case 3:{
x−−;
break ;
}
default :
break ;
}
/ / write ray d i r e c t i o n from i n i t i a l to r e s u l t i n b u f f e r
ray buffer2D [ x ] [ y ] . x = ray buffer [ miles ] . v . x ;
ray buffer2D [ x ] [ y ] . y = ray buffer [ miles ] . v . y ;
ray buffer2D [ x ] [ y ] . z = ray buffer [ miles ] . v . z ;
}
100](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-116-2048.jpg)




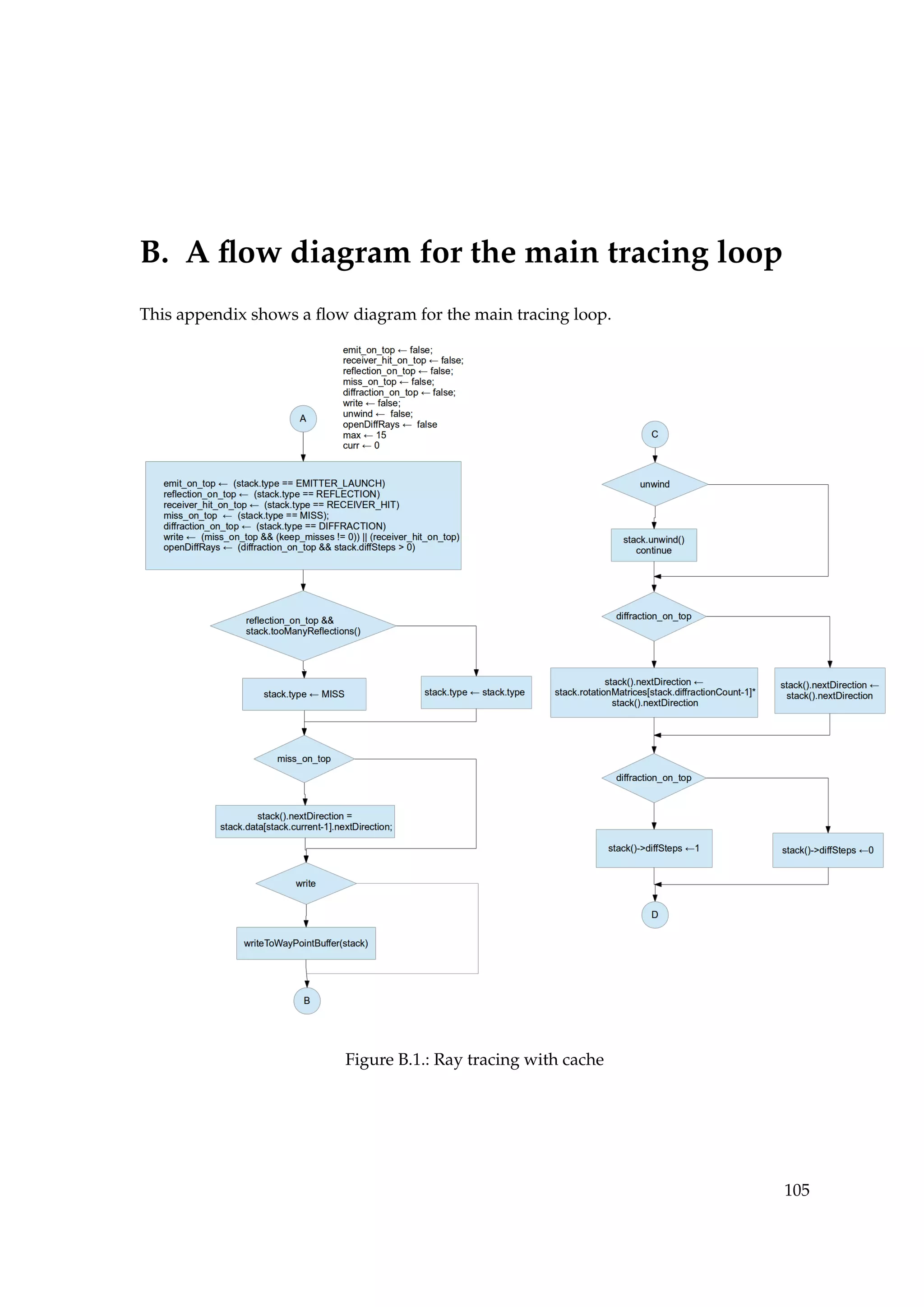


![C. Implementation Hash Tables
i f ( this−>instanceId != other . instanceId )
return false ;
i f ( this−>div x != other . div x )
return false ;
i f ( this−>div y != other . div y )
return false ;
i f ( this−>div z != other . div z )
return false ;
return true ;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−− c a l c h a s h 1 −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
d e v i c e unsigned int calc hash1 ( ) {
int x [ 5 ] = { primitiveIndex , instanceId , div x , div y , div z } ;
long p = (1L << 32) − 5;
long z = 0x64b6055aL ;
int z2 = 0x5067d19d ;
long s = 0;
long zi = 1;
for ( int i = 0; i < 5; ++ i ) {
long xi = ( x [ i ] * z2 ) >> 1;
s = ( s + zi * xi ) % p ;
zi = ( zi * z ) % p ;
}
s = ( s + zi * (p − 1 ) ) % p ;
end trace = clock ( ) ;
hash gen= ( float ) ( end trace−s t a r t t r a c e )/CLOCKS PER SEC ;
return ( unsigned int ) s ;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−− c a l c h a s h 2 −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
d e v i c e unsigned int calc hash2 ( )
{
return mortonCode5 ( div x , div y , div z , instanceId ,
primitiveIndex ) ;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−− separateBy4 −−−−−−−−−−−−−−−−−−−−−−− *
* *
108](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-124-2048.jpg)

![C. Implementation Hash Tables
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−− get bucket −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
int buf s = node buffer . size ( ) ;
Key key ;
key = makeKey( key , prev data , false ) ;
int bucket ind = get bucket index ( key . hash ) ;
CacheNode* root = &node buffer [ bucket ind ] ;
CacheNode* node = NULL;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−− i n s e r t data −−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
i f ( ! root−>used )
{
root−>hash = key . hash ;
root−>data = data ;
root−>used = true ;
node = root ;
atomicAdd(&( root−>counter ) , 1 ) ;
} else
{
int counter = atomicAdd(&( root−>counter ) , 1 ) ;
int node ind = bucket ind + counter * num of buckets ;
i f ( node ind >= buf s )
return ;
node = &node buffer [ node ind ] ;
node−>hash = key . hash ;
node−>data = copyData ( data , node−>data ) ;
node−>used = true ;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−− s e a r c h f o r vacant p o s i t i o n −−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
while ( true )
110](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-126-2048.jpg)
![C.2. Implementation of the Chained Hash Table
{
i f ( node−>hash <= root−>hash )
{
i f ( atomicCAS(&( root−>l e f t ) , −1, node ind ) == −1)
{
atomicCAS(&(node−>parent ) , −1, root−>index ) ;
return ;
} else
root = &node buffer [ root−>l e f t ] ;
} else
{
i f ( atomicCAS(&( root−>right ) , −1, node ind ) == −1)
{
atomicCAS(&(node−>parent ) , −1, root−>index ) ;
return ;
}
else
root = &node buffer [ root−>right ] ;
}
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−− l i n k elements o f one path −−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
i f ( cachedNodeWrite != NULL)
{
cachedNodeWrite−>queue = node−>index ;
}
cachedNodeWrite = node ;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−−− getFromCache −−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e CacheNode* getFromCache ( PerRayData data , bool benchmark )
{
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−− get bucket −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
int buf s = node buffer . size ( ) ;
111](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-127-2048.jpg)
![C. Implementation Hash Tables
Key key ;
key = makeKey( key , data , false ) ;
int bucket ind = get bucket index ( key . hash ) ;
CacheNode* root = &node buffer [ bucket ind ] ;
i f ( ! root−>used )
return NULL;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−− s e a r c h f o r element with equal key −−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
while ( true ){
i f ( root−>hash == key . hash )
{
root−>hi t ++;
return root ;
}
else i f ( key . hash <= root−>hash )
i f ( root−>l e f t == −1)
return NULL;
else
root = &node buffer [ root−>l e f t ] ;
else
i f ( root−>right == −1)
return NULL;
else
root = &node buffer [ root−>right ] ;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−−−−−− hasKey −−−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e bool hasKey ( PerRayData data )
{
CacheNode* node = getFromCache ( data , false ) ;
i f ( node == 0)
return false ;
return true ;
}
C.3. Implementation of the Open-Addressed Hash Table
Listing C.3: Implementation of open-addressed table interface
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
112](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-128-2048.jpg)
![C.3. Implementation of the Open-Addressed Hash Table
* *
* −−−−−−−−−−−−−−−−−−−− writeToCache −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e void writeToCache ( int base index ,
PerRayData prev data ,
PerRayData data ,
CacheNode* &cachedNodeWrite ,
unsigned int pos hash )
{
i f ( c a c h e i n i t )
{
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−get bucket from t a b l e −−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
CacheKey key ;
key = makeKey( key , prev data , false ,
cache division , hash method ) ;
int iind = getBucketIndex ( key . hash ) ;
int bucket ind = base index + iind ;
i f ( bucket ind < node buffer . size ( ) )
{
CacheNode *node = &node buffer [ bucket ind ] ;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−− a c q u i r e write l o c k and write data −−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
i f ( atomicCAS(&(node−>writeLock ) , 0 , 1) == 0)
{
node−>hash = key . hash ;
node−>nextOrigin = prev data . nextOrigin ;
node−>nextDirection = prev data . nextDirection ;
node−>data = data ;
node−>used = true ;
node−>traceTime = trace time ;
node−>hashGen = key . hash gen ;
node−>pos hash = pos hash ;
node−>timestamp = time ;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−− r e l e a s e r e a d l o c k l o c k −−−−−−−−−−−−−−−−−−− *
113](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-129-2048.jpg)
![C. Implementation Hash Tables
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
atomicExch (&(node−>readLock ) , 0 ) ;
}
}
}
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−− getFromCache −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e bool getFromCache ( int base index ,
PerRayData prev data ,
PerRayData &data ,
unsigned int pos hash )
{
i f ( c a c h e i n i t )
{
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−− get bucket by hash −−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
CacheKey key ;
key = makeKey( key , prev data , false ,
cache division , hash method ) ;
int iind = getBucketIndex ( key . hash ) ;
int bucket ind = base index + iind ;
i f ( bucket ind < node buffer . size ( ) )
{
CacheNode* node = &node buffer [ bucket ind ] ;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−− a c q u i r e the r e a d l o c k −−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
i f ( atomicCAS(&(node−>readLock ) , 0 , 1) == 0)
{
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−− purge i f node has d i f f e r e n p o s i t i o n stamp −−−−−−−− *
114](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-130-2048.jpg)

![C. Implementation Hash Tables
* −−−−−−−−−−−−−−−− get bucket by hash −−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
CacheKey key ;
key = makeKey( key , prev data , false ,
cache division , hash method ) ;
int iind = getBucketIndex ( key . hash ) ; ;
int bucket ind = base index + iind ;
CacheNode* node = &node buffer [ bucket ind ] ;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−− a c q u i r e the r e a d l o c k −−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
i f ( atomicCAS(&(node−>readLock ) , 0 , 1) == 0)
{
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−− i f hashes are not equal c a l c u l a t e r e s i d u a l −−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
i f ( node−>hash != key . hash )
{
float res1 =
calculateResidual ( node−>data . nextDirection ,
prev data . nextDirection ) ;
float res2 =
calculateResidual ( node−>data . nextOrigin ,
prev data . nextOrigin ) ;
float res = res1 + res2 ;
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−− i f r e s i d u a l e x c e e d s the t h r e s h o l d , purge −−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
i f ( res > cache residual value )
{
atomicExch (&(node−>readN ) , 0 ) ;
atomicExch (&(node−>writeLock ) , 0 ) ;
return false ;
}
}
116](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-132-2048.jpg)

![C. Implementation Hash Tables
r t P r i n t f ( ” div x %d n” , key . div x ) ;
r t P r i n t f ( ” div y %d n” , key . div y ) ;
r t P r i n t f ( ” div z %d n” , key . div z ) ;
}
return key ;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−− getBucketIndex −−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e uint getBucketIndex ( unsigned int hash )
{
return ( ( float ) hash/UINT MAX) * ( num of buckets − 1)/2;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−−−−− searchInMap −−−−−−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e int searchInMap ( int modelInstanceId )
{
int mapSize = cache emitter map . size ( ) ;
for ( int i = 0; i < mapSize ; ++ i )
{
EmitterMapEntry * entry = &cache emitter map [ i ] ;
i f ( entry−>modelInstanceId == modelInstanceId )
return entry−>base index ;
}
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
* *
* −−−−−−−−−−−−−−−−−− c a l c u l a t e R e s i d u a l −−−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e float calculateResidual ( f l o a t 3 origin ,
f l o a t 3 otherOrigin )
{
float res = abs ( origin . x − otherOrigin . x ) +
abs ( origin . y − otherOrigin . y ) +
abs ( origin . z − otherOrigin . z ) ;
return res ;
}
/ * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
118](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-134-2048.jpg)
![C.3. Implementation of the Open-Addressed Hash Table
* *
* −−−−−−−−−−−−−−−−−− c h e c k I n t e r s e c t i o n s −−−−−−−−−−−−−−−−−−− *
* *
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * /
inline d e v i c e
bool checkIntersections ( const CacheNode* node , float R)
{
const PerRayData * data = &(node−>data ) ;
for ( int i = 0; i < antenna buffer . size ( ) ; ++ i )
{
const AntennaBufferEntry * antenna = &antenna buffer [ i ] ;
i f ( data−>type == RECEIVER HIT)
{
f l o a t 3 recPos = antenna−>position ;
f l o a t 3 pos = data−>nextOrigin ;
float dx = abs ( recPos . x − pos . x ) ;
float dy = abs ( recPos . y − pos . y ) ;
float dz = abs ( recPos . z − pos . z ) ;
i f ( dx < R && dy < R && dz < R)
return true ;
}
}
return false ;
}
119](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-135-2048.jpg)

![Bibliography
[1] Users manual. eb assist adtf 2.9.0. Elektrobit Automotive GmbH.
[2] Luis A. Alexandre. Set distance functions for 3d object recognition. Progress in Pattern
Recognition, Image Analysis, Computer Vision, and Applications, pages 57–64, 2013.
[3] Michael Bader. Space-Filling Curves. Springer Berlin Heidelberg, 2013.
[4] James Balfour. Cuda threads and atomics, 25 April 2011. NVIDIA Research.
[5] Margherita Barile. Taxicab metric, mathworld–a wolfram web resource, 2014.
[6] Mate Boban, Jao Barros, and Ozan K. Tonguz. Geometry-based vehicle-to-vehicle
channel modeling for large-scale simulation. IEEE Transactions on Vehicular Technology.
[7] Ken Chan, Rynson W.H. Lau, and Jianmin Zhao. Dynamic sound rendering based on
ray-caching.
[8] CAR 2 CAR Communication Consortium. Car 2 car communication consortium man-
ifesto.
[9] Kurt Debattista, Piotr Dubla, Francesco Banterle, Luis Paulo Santos, and Alan
Chalmers. Instant caching for interactive global illumination.
[10] F. Escarieu, V. Degardin, and L. Aveneau. 3d modelling of the propagation in an
indoor environment : a theoretical and experimental approach. Proceedings of the Eu-
ropean Conference on Wireless Technologie, 2001.
[11] Tony Finch. Incremental calculation of weighted mean and variance, 2009. University
of Cambridge Computing Service.
[12] M. Fiore, J. Harri, F. Filali, and C. Bonnet. Vehicular mobility simulation for vanets.
Simulation Symposium, 2007. ANSS ’07. 40th Annual.
[13] Tim Foley and Jeremy Sugerman. Kd-tree acceleration structures for a gpu raytracer.
In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS conference on Graphics hard-
ware, 2005.
[14] Kirill Garanzha and Charles Loop. Fast ray sorting and breadth-first packet traversal
for gpu ray tracing. EUROGRAPHICS, 29, 2010.
[15] T. Gaugel, L. Reichardt, J. Mittag, T. Zwick, and H. Hartenstein. Accurate simulation
of wireless vehicular networks based on ray tracing and physical layer simulation.
Transactions of the High Performance Computing Center, Stuttgart (HLRS) 2011, pages
619–630.
121](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-137-2048.jpg)
![Bibliography
[16] J. Gunther, S. Popov, and P. Slusallek. Realtime ray tracing on gpu with bvh-based
packet traversal. Interactive Ray Tracing, 2007. RT ’07. IEEE Symposium on, pages 113 –
118, 2007.
[17] M. Harris, D. Luebke, I. Buck, N. Govindaraju, J. Kr ˜A¼ger, A. Lefohn, T. Purcell,
and J. Wooley. Gpgpu: General-purpose computation on graphics processing units.
SIGGRAPH 2004 Course Notes.
[18] M. Herlihy and N. Shavit. The Art of Multiprocessor Programming, 1st Edition. Morgan
Kaufmann, 2008.
[19] Maurice Herlihy. Wait-free synchronization. ACM Transactions on Programming Lan-
guages and Systems, Volume 13 Issue 1:124–149, 1991.
[20] Asger Hoedt. Morton codes, 2014.
[21] Denis Jarema. Grammars for space-filling curves. WWW. Solution for Worksheet 11.
Algorithms of Scientific Computing - Summer 2013. Technical University Munich.
[22] Edmund Wright John Daintith. A Dictionary of Computing (6 ed.). Oxford University
Press, 2008.
[23] Tero Karras. Maximizing parallelism in the construction of bvhs, octrees, and k-d
trees. High Performance Graphics, 2012.
[24] Tero Karras. Thinking parallel, part iii: Tree construction on the gpu, December 2012.
[25] Donald Knuth. The Art of Computer Programming. Addison-Wesley, 1995.
[26] Jonathan Ledy, Herve Boeglen, Anne-Marie Poussard, Benoit Hilt, and Rodolphe
Vauzelle. A semi-deterministic channel model for vanets simulations. International
Journal of Vehicular Technology, Volume 2012.
[27] A. E. Lefohn, J. M. Kniss, C. D. Hansen, and R. T. Whitaker. Interactive deformation
and visualization of level set surfaces using graphics hardware. IEEE Visualization,
page 75ˆa82, 2003.
[28] Aaron E. Lefohn, Shubhabrata Sengupta, Joe Kniss, Robert Strzodka, and John D.
Owens. Generic, efficient, random-access gpu data structures. ACM Transactions on
Graphics, 25 Issue 1:60–99, January 2006.
[29] Kyle Loudon. Mastering Algorithms with C. O’Reilly Media, 1999.
[30] R. Mantiuk, K. J. Kim, A. G. Rempel, and W. Heidrich. Hdr-vdp-2: a calibrated vi-
sual metric for visibility and quality predictions in all luminance conditions. ACM
Transactions on Graphics, 30, 4, 2011.
[31] Randima Fernando Matt Pharr, editor. GPU Gems 2: Programming Techniques For High-
Performance Graphics And General-Purpose Computation. Pearson Addison Wesley Prof,
2005.
122](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-138-2048.jpg)
![Bibliography
[32] David Meko. Applied time series analysis. Notes for lessons.
[33] Duane Merrill and Andrew Grimshaw. High performance and scalable radix sort-
ing: A case study of implementing dynamic parallelism for GPU computing. Parallel
Processing Letters, 21(02):245–272, 2011.
[34] Prabhakar Misra and Mainak Chaudhuri. Performance evaluation of concurrent lock-
free data structures on gpus. Parallel and Distributed Systems (ICPADS), pages 53 – 60,
2012.
[35] Bochang Moon, Byun Yongyoung, Kim Tae-Joon, Claudio Pio, Kim Hye-sun, Ban
Yun-ji, Nam Seung Woo, and Yoon Sung-eui. Cache-oblivious ray reordering. ACM
Transactions on Graphics, 29, 2010.
[36] Pat Morin. Open Data Structures (in C++).
[37] Nvidia. Cuda c programming guide, October 2012.
[38] Nvidia. Optix ray tracing engine. programming guide., November 2012.
[39] NVIDIA. Ray cache, 2014.
[40] Lars Nyland and Stephen Jones. Understanding and using atomic memory opera-
tions. In GPU Technology Conference. NVIDIA, 2013.
[41] OpenSceneGraph. The openscenegraph project website, 2014.
[42] Stefan Popov, Iliyan Georgiev, Philipp Slusallek, and Carsten Dachsbacher. Adaptive
quantization visibility caching. EUROGRAPHICS 2013, Volume 32, 2013.
[43] Przemyslaw Prusinkiewicz and Aristid Lindenmayer. The Alogirthmic Beauty of Plants.
Springer-Verlag, New York, 1996.
[44] C. Donner M. Cammarano H. W. Jensen Purcell, T. J. and P. Hanrahan. Photon map-
ping on programmable graphics hardware. Proceedings of the SIGGRAPH/Eurographics
Workshop on Graphics Hardware, page 41ˆa50., 2003.
[45] I. Buck W. R. Mark Purcell, T. J. and P. Hanrahan. Ray tracing on programmable
graphics hardware. ACM Transactions on Graphics(Proceedings of SIGGRAPH),
21(3):703ˆa712, 2002.
[46] Christian F. Ruff, Esteban W. G. Clua, and Leandro A. F. Fernandes. Dynamic per
object ray caching textures for real-time ray tracing. Graphics, Patterns and Images
(SIBGRAPI), 2013, pages 258 – 265, 2013.
[47] Jason Sanders and Edward Kandrot. CUDA by Example: An Introduction To General-
Purpose GPU Programming. Addison-Wesley, 2010.
[48] Daniel Scherzer, Lei Yang, and Oliver Mattausch. Exploiting temporal coherence in
real-time rendering. Proceedings of ACM SIGGRAPH, 2010.
[49] Robert Sedgewick. Algorithms (1st ed.). Addison-Wesley, 1983.
123](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-139-2048.jpg)
![Bibliography
[50] Parag Tole, Fabio Pellacini, Bruce Walter, and Donald P. Greenberg. Interactive global
illumination in dynamic scenes.
[51] Graham Upton and Ian Cook, editors. A Dictionary of Statistics. Oxford University
Press, 2008.
[52] I. Wald, C. Benthin, and P. Slusallek. Interactive global illumination in complex and
highly occluded environments. Proceedings of the 14th Eurographics Workshop on Ren-
dering, 2003.
[53] B. Walter, S. Fernandez, A. Arbree, K. Bala, M. Donikian, and Greenberg D. P.
Lightcuts: a scalable approach to illumination. ACM Transactions on Graphics, 24,
3:1098ˆa1107, 2005.
[54] G. J. Ward, F. M. Rubinstein, and Clearr. D. A ray tracing solution for diffuse inter-
reflection. SIGGRAPH, page 85ˆa92, 1988.
[55] Daniel Weber, Jan Bender, Markus Schnoes, Andre Stork, and Dieter Fellner. Efficient
gpu data structures and methods to solve sparse linear systems in dynamics applica-
tions. Computer Graphics Forum, 32, issue 1:16–26, February 2013.
[56] Wikipedia. Integer (computer science) — Wikipedia, the free encyclopedia, 2014.
124](https://image.slidesharecdn.com/main-190806080204/75/Efficiency-Optimization-of-Realtime-GPU-Raytracing-in-Modeling-of-Car2Car-Communication-140-2048.jpg)