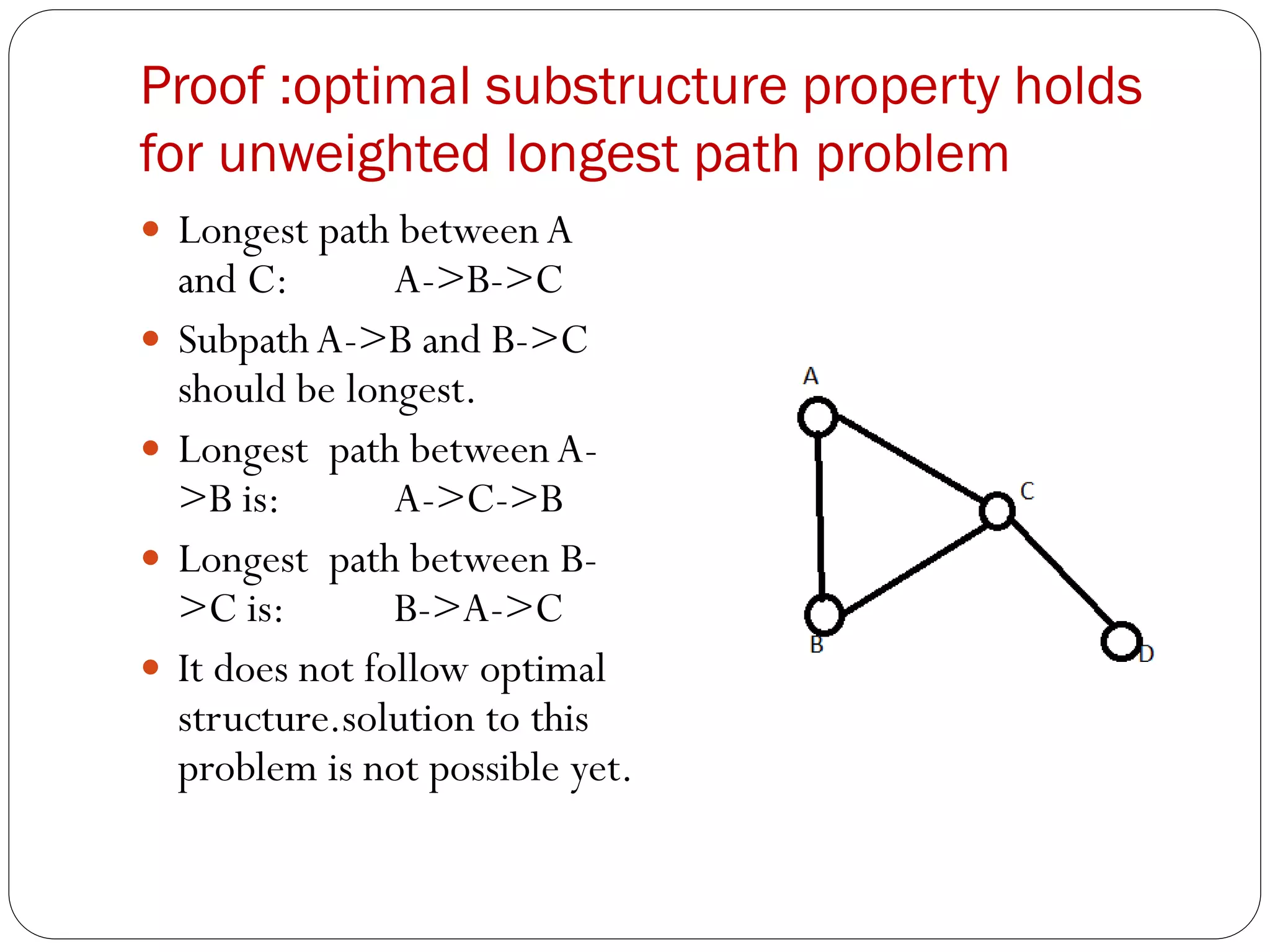
The document discusses dynamic programming techniques for finding the optimal number of scalar multiplications in matrix multiplication. It provides an example of calculating the optimal parenthesization of matrix multiplications using a 6x6 matrix. The complexity of the algorithm is O(n^3). Dynamic programming is more efficient than brute force or divide and conquer approaches for this problem. Optimal substructure and overlapping subproblems are elements that allow dynamic programming to be applied. Proofs are given that the unweighted shortest path problem has optimal substructure but the unweighted longest path problem may not.



![contd
According to algorithm to
find the optimal number of
scaler product if
i=j,m[i,i]<-0](https://image.slidesharecdn.com/dynamicprogrammng2-140422092145-phpapp02/75/Dynamic-programmng2-4-2048.jpg)
![contd
According to algorithm
m[i,j]=m[i,k]+m[k+1,j]
m[1,2]=m[1,1]+m[1,2]
=0+30*35*15=15750
m[2,3]=m[2,2]+m[2,3]
=0+35*15*5=2625
m[3,4]=m[3,3]+m[3,4]
=0+15*5*10=750
m[4,5]=m[4,4]+m[4,5]
=0+5*10*20=1000
m[5,6]=m[5,5]+m[5,6]
=0+10*20*25=5000](https://image.slidesharecdn.com/dynamicprogrammng2-140422092145-phpapp02/75/Dynamic-programmng2-6-2048.jpg)
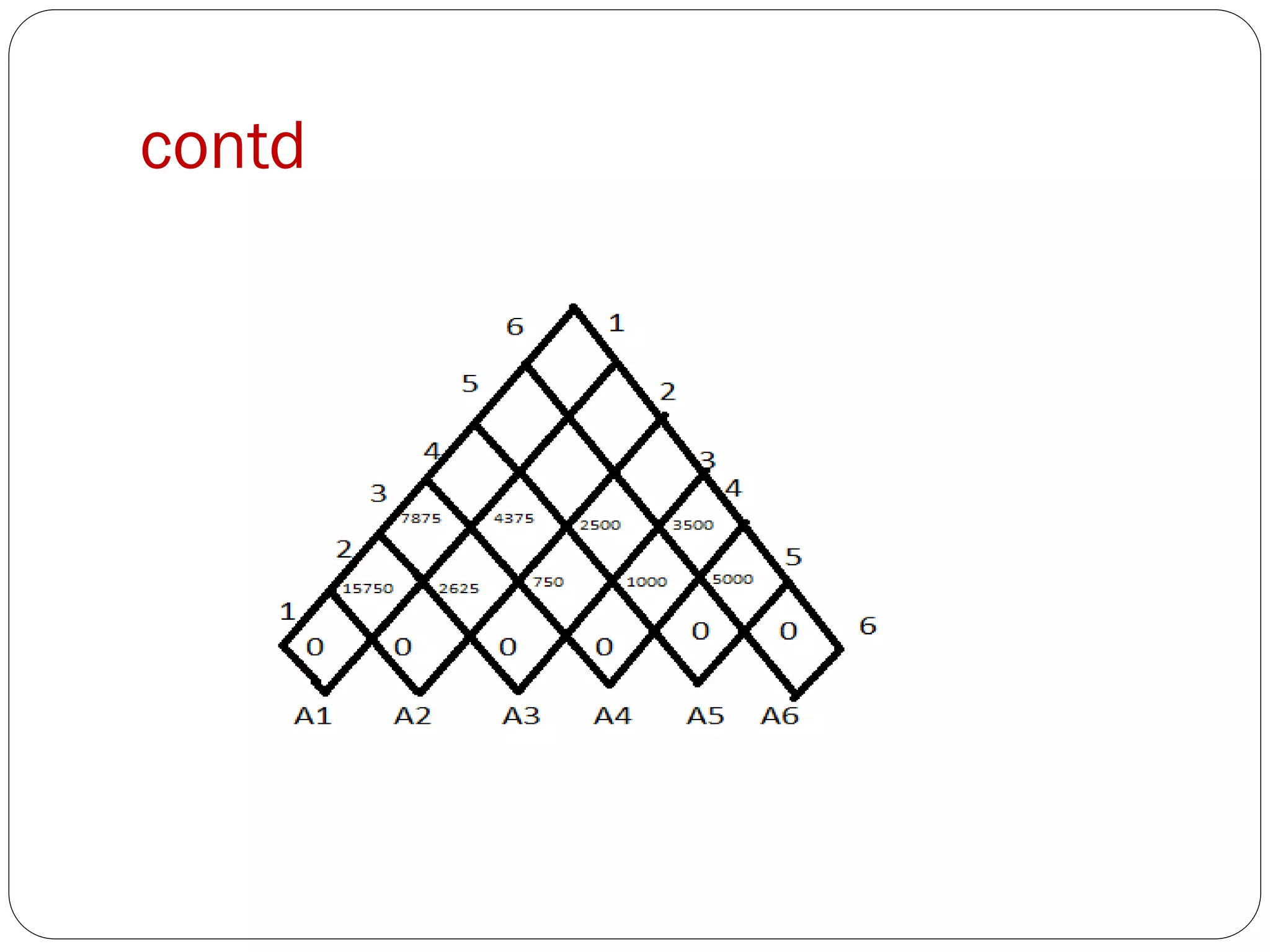
![contd
m[1,3]=min m[1,1]+m[2,3]+
P0.P1.P3=7875 =
m[1,2]+m[3,3]+P0.P2.P3=
18000
=7875
m[2,4]=min m[2,2]+m[3,4]+
P1.P2.P4=6000
m[2,3]+m[4,4]+
P1.P3.P4=4375
=4375
m[3,5]=min m[3,3]+m[4,5]+
P2.P3.P5=2500
m[3,4]+m[5,5]+
P2.P4.P5=3750
= 2500
m[4,6]= min m[4,4]+m[5,6]+
P3.P4.P6=6250
m[4,5]+m[6,6]+
P3.P5.P6=3500
= 3500](https://image.slidesharecdn.com/dynamicprogrammng2-140422092145-phpapp02/75/Dynamic-programmng2-7-2048.jpg)
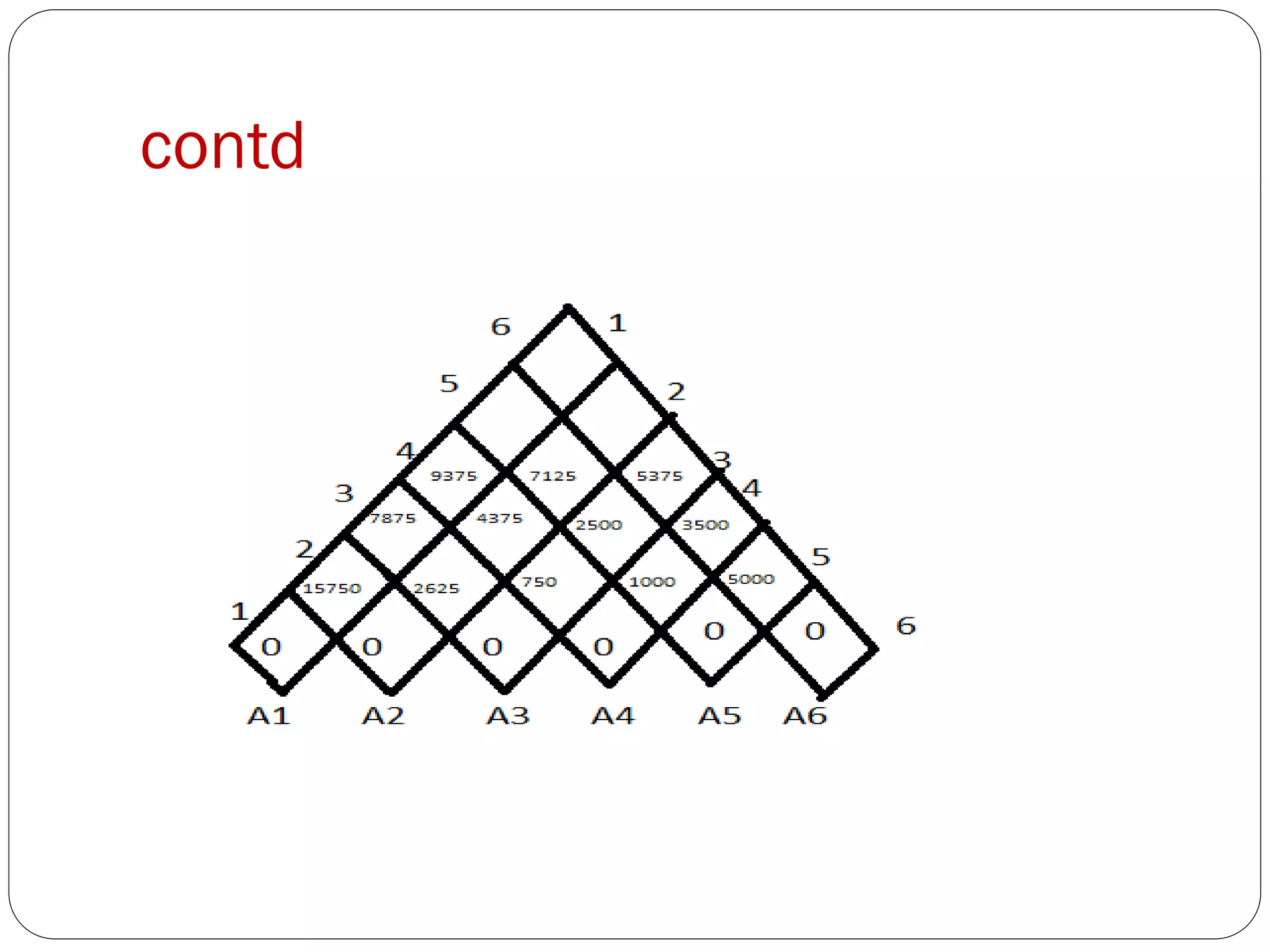
![contd
m[1,4]=min m[1,1]+m[2,4] +
P0.P1.P4 =14875
m[1,2]+m[3,4]+P0.
P2.P4=21000
m[1,3]+m[4,4]+P
0.P3.P4=9375=9
357
m[2,5]=min m[2,2]+m[3,5] +
P1.P2.P5 =13000
m[2,3]+m[4,5]+P1.
P3.P5=7125
m[2,4]+m[5,5]+P
1.P4.P5=9375
=11375
m[3,6]=min m[3,3]+m[4,6] +
P2.P3.P6 =5375
m[3,4]+m[5,6]+P2.
P4.P6=9500
m[3,5]+m[6,6]+P
2.P5.P6=10000
=5375](https://image.slidesharecdn.com/dynamicprogrammng2-140422092145-phpapp02/75/Dynamic-programmng2-9-2048.jpg)
![contd
m[1,5]=min m[1,1]+m[2,5]+
P0.P1.P5=28125
m[1,2]+m[3,5]+
P0.P2.P5=27250
m[1,3]+m[4,5]+
P0.P2.P5=11875
m[1,4]+m[5,5]+
P0.P4.P5=15375
= 11875
m[2,6]=min m[2,2]+m[3,6]+
P1P2.P6=18500
m[2,3]+m[4,6]+
P2.P3.P6=10500
m[2,4]+m[5,6]+
P2.P4.P6=18125
m[2,5]+m[6,6]+
P1P5.P6=24625
= 10500](https://image.slidesharecdn.com/dynamicprogrammng2-140422092145-phpapp02/75/Dynamic-programmng2-11-2048.jpg)
![contd
m[1,6]=min m[1,1]+m[2,6]+
P0.P1.P6=36750
m[1,2]+m[3,6]+
P0.P2.P6=37000
m[1,3]+m[4,6]+
P0.P3.P6=15125
m[1,4]+m[5,6]+
P0.P4.P6=21875
m[1,5]+m[6,6]+
P0.P5.P6=26875
= 15125](https://image.slidesharecdn.com/dynamicprogrammng2-140422092145-phpapp02/75/Dynamic-programmng2-12-2048.jpg)








![Proof :optimal substructure property holds
for unweighted shortest path problem
There are 2 vertices u and v.
P path is optimal if it contains
minimum number of vertices.2
subpaths
p1[u w] and p2[w->v] if the path
is optimal then the subpaths must
be optimal.
We will proof this by contradiction.
Let we have a path p1’between u and
w which is not optimal,by
combining 2 subpaths we get the
final path p’which take less number
of vertices than p.but p is
optimal.so byy contradiction we
have prooved that unweighted
shortest path problem follows
optimal substructure problem.](https://image.slidesharecdn.com/dynamicprogrammng2-140422092145-phpapp02/75/Dynamic-programmng2-21-2048.jpg)