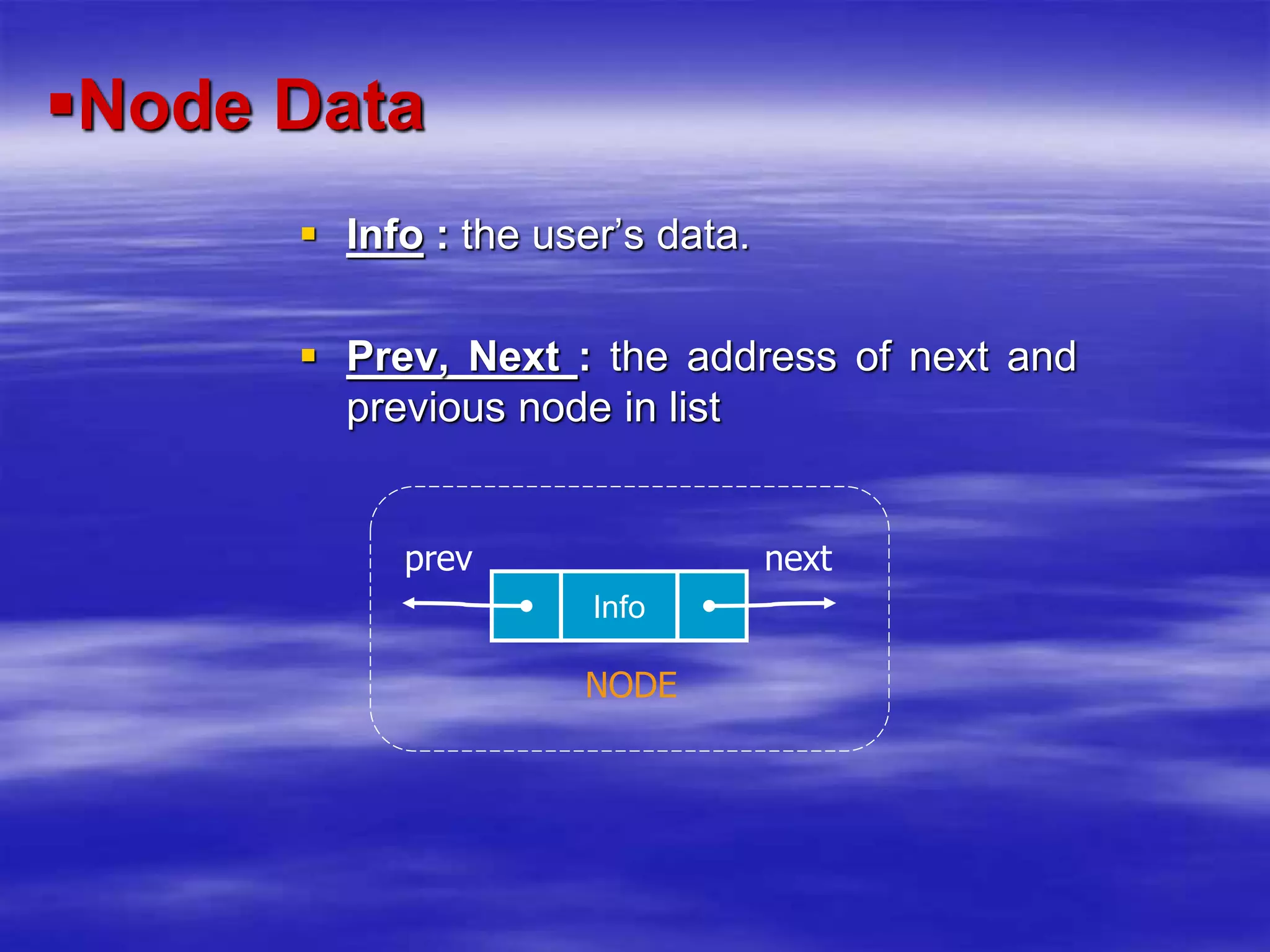
The document describes a doubly linked list data structure. Each node in a doubly linked list contains pointers to both the next and previous nodes, allowing traversal in either direction. Common operations on doubly linked lists include inserting and deleting nodes at the beginning, end, or anywhere in the list. Pseudocode algorithms are provided to demonstrate how to implement these operations by updating the pointer references between nodes.

1. Doubly-Linked List

2. Doubly Linked List
 In doubly linked list each node contains two points.
 which points has a reference to both the next point
and pervious point of node in list.
 A doubly linked list is a two-way list because one
can move in either from left to right or from right to
left

3. prev next
Info
NODE
Node Data
 Info : the user’s data.
 Prev, Next : the address of next and
previous node in list

4. Operations on a Doubly linked list
o Create list.
o Insert element at beginning in list.
o Insert element at end in list.
o Insert element at any place in list.
o Delete element from the beginning of list.
o Delete element from the end of list.
o Delete element from any place from list.

5. Create doubly linked list
NULL
7 X
X 9 X

6. Algorithm
Step 1: [initially list is empty]
First = NULL
last = NULL
Step 2: [allocate space to newly created node]
new1= create new node
Step 3: [assign value to information part of node]
info[new1]= Value
Step 4: [assign NULL to the address part for the next]
next[new1]= NULL
Step 5: [check for list is empty]
if first =NULL then
first = new1
last = new1
prev[new1]= NULL
else
next[last]= new1
prev[new1]=last
last=new1
end if
Step 6: exit

7. Insert an element at beginning
doubly linked list
We assume linked list
first last
7 9 X
X 2 X

8. Algorithm
Step 1: [allocate space to newly created node]
new1= create new node
Step 2: [check for free space]
if new1=NULL then
Write “Memory full”
Step 3: [check for list is empty]
if first=NULL then
Write “list is empty”
return
Step 4: [assign value to information part of node]
info[new1]= Value
Step 5: [store the node at first]
next[new1]= first
prev[new1]= NULL
prev[first]= new1
first=new1
Step 6: exit

9. Insert an element at last of
doubly linked list
We assume linked list
first last
X 2 7 9
X 4 X

10. Algorithm
Step 1: [check for list is empty]
if first=NULL then
Write “list is empty”
return
Step 2: [allocate space to newly created node]
new1= create new node
Step 3: [assign value to information part to node]
info[new1]= Value
Step 4: [store the node at last]
next[new1]= NULL
next[last]= new1
prev[new1]= last
last=new1
Step 5: exit

11. Insert an element at Any place
doubly linked list
first last
X 2 7 9
4 X
We assume linked list and
Insert after 7 valued node
6
tra
t1

12. Algorithm
Step 1: [check for list is empty]
if first=NULL then
Write “list is empty”
return
Step 2: [allocate space to newly created node]
new1= create new node
Step 3: [read values of information part of new node]
info[new1]=value
Step 4: [initialization]
tra=first
Step 5: [perform insertion operation]
repeat through step 7 while tra != NULL

13. Step 6: if info[tra] =no then
if tra=last then
next[tra]=new1
next[new1]=NULL
prev[new1]=tra
last=new1
else
t1=next[tra]
next[tra]=new1
next[new1]=t1
prev[t1]=new1
prev[new1]=tra
Step 7: [increment temp value]
tra=next[tra]
Step 8: exit

14. Delete an element at beginning
of doubly linked list
first last
X 2 7 9
4 X
We assume linked list
ffirst
X

15. Algorithm
Step 1: [check for list is empty]
if first=NULL then
Write “list is empty”
return
Step 2: [perform deletion opration]
if first=last then
first=NULL
last=NULL
free(first)
else
ffirst=next[first]
free(first)
first=ffirst
prev[first]=NULL
end if
Step 3: exit

16. Delete an element at last of
doubly linked list
first last
X 2 7 9
4 X
We assume linked list
t
X

17. Algorithm
Step 1: [check for list is empty]
if first=NULL then
Write “list is empty”
return
Step 2: [perform deletion opration]
if first=last then
first=NULL
last=NULL
free(first)
else
t=prev[last]
free(last)
last=t
next[last]=NULL
Step 3: exit

18. Delete an element at any place
doubly linked list
We assume linked list and
Delete 7 valued node
first last
X 2 7 9
4 X
tra
t1
pr1

19. Algorithm eny delete
Step 1: [check for list is empty]
if first=NULL then
Write “list is empty”
return
Step 2: [perform deletion opration]
if first=last then
first=NULL
last=NULL
free(first)
Step 3: [initialization]
tra=first
Step 4: [perform insertion operation]
repeat through step 7 while tra != NULL

20. Step 5: IF info[tra]=number then
if tra=first then
ffirst=next[first]
free(first)
first=ffirst
else if tra=first then
free(last)
last=pr1
next[last]=NULL
else
t1=next[tra]
next[pr1]=t1
prev[t1]=pr1
free(tra)
last=t1
Step 6: [Assign previous value of tra to prev]
pr1=tra
Step 7: [increment temp value]
tra=next[tra]
Step 8: exit