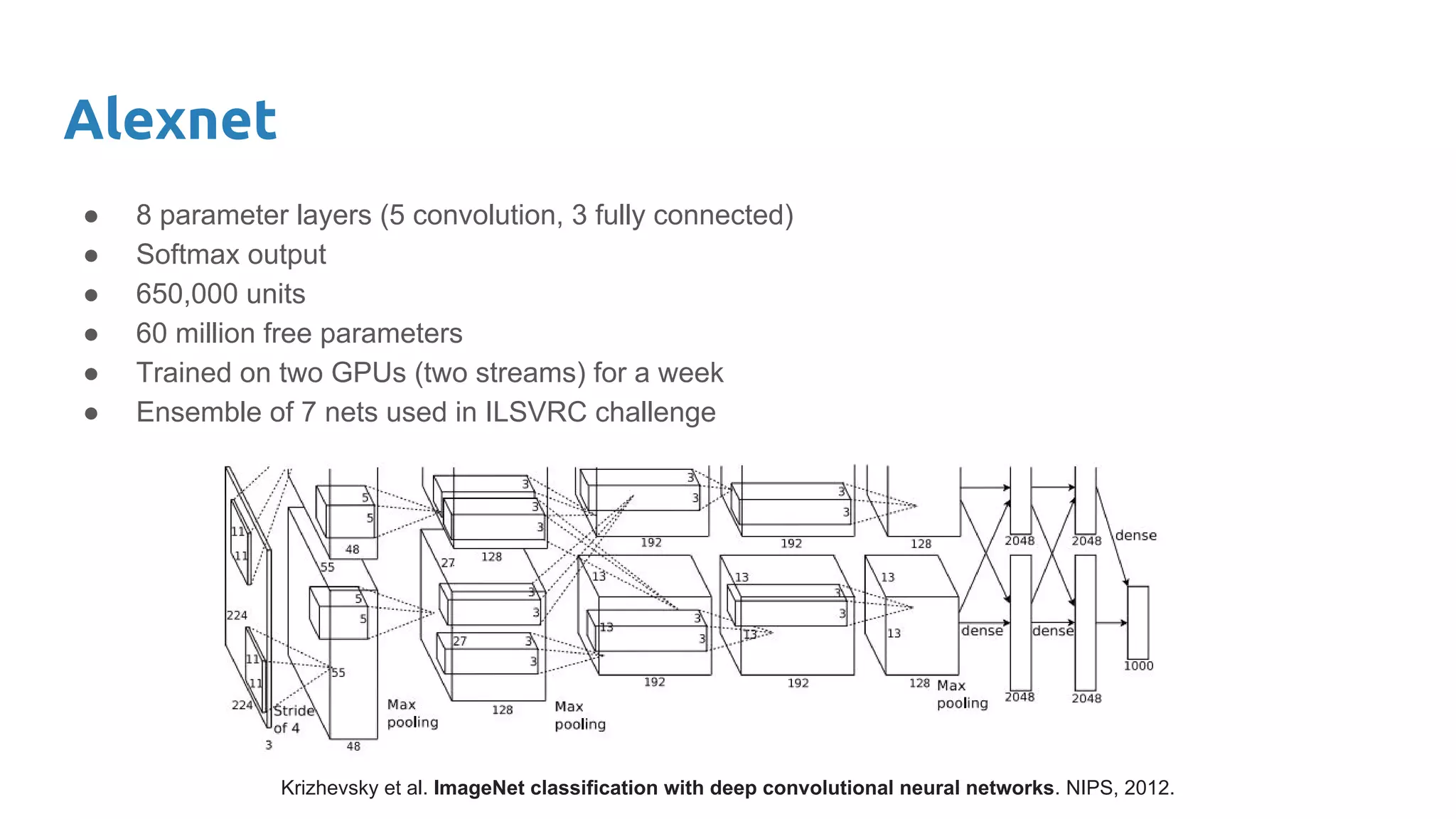
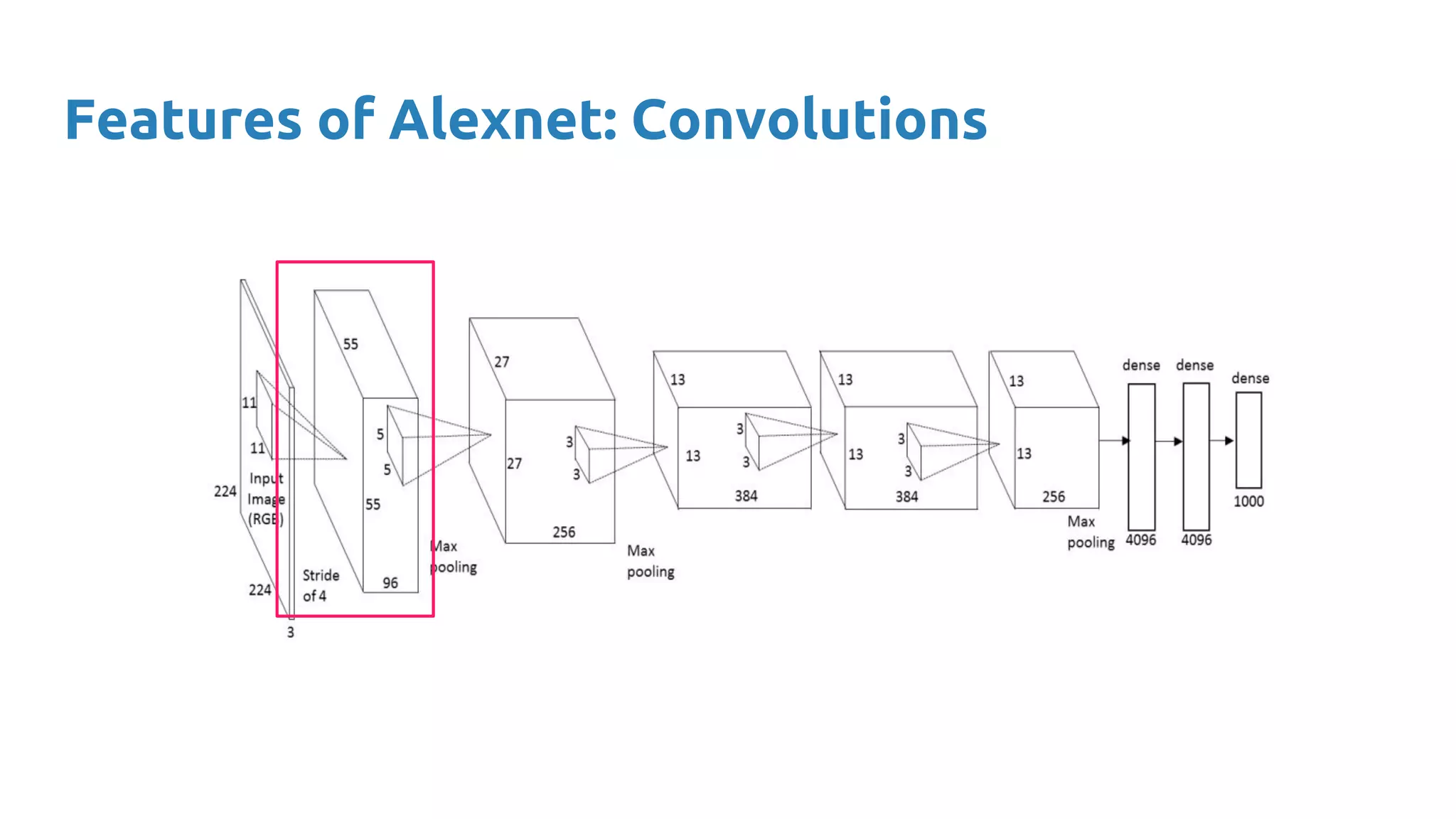
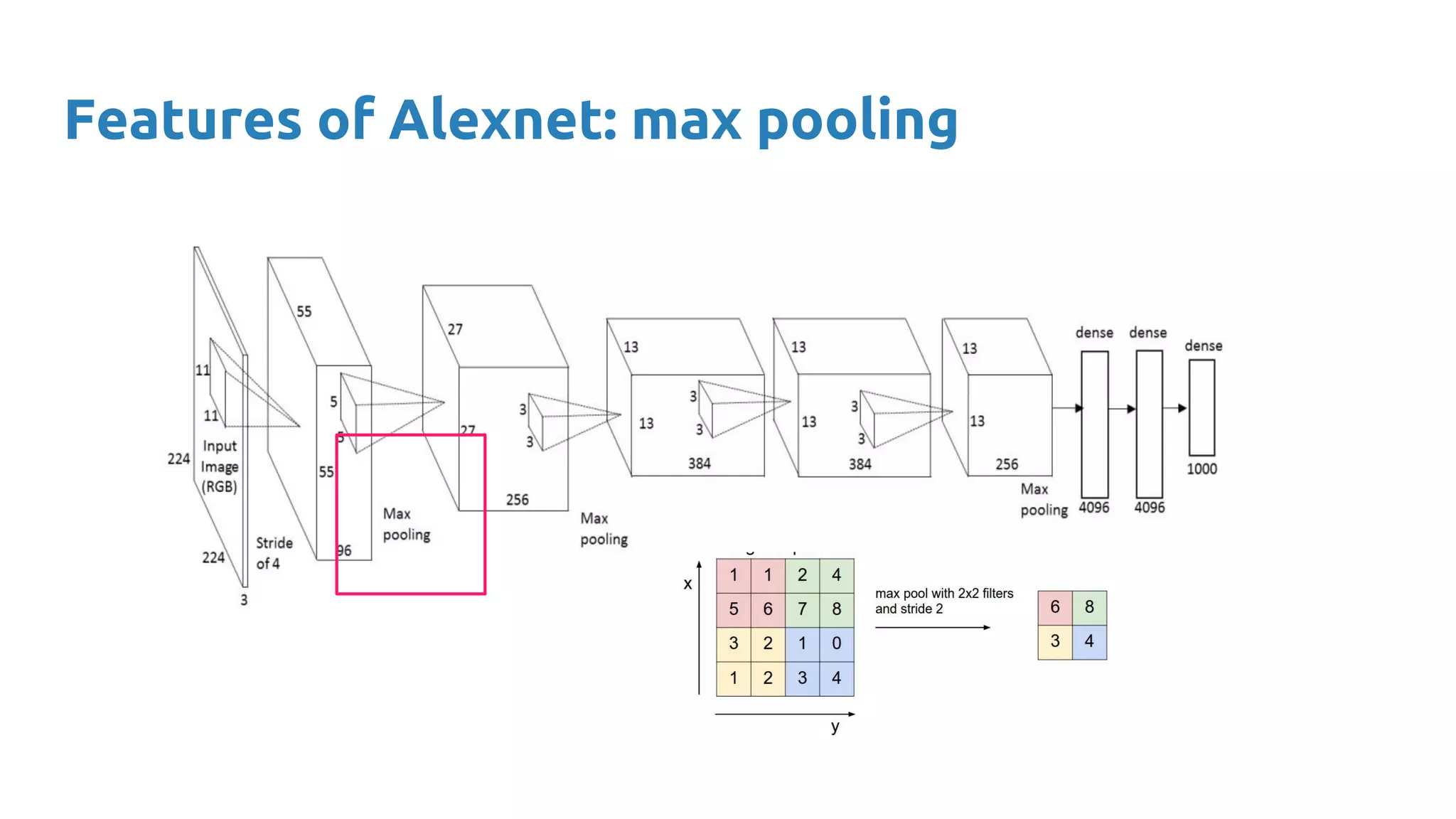
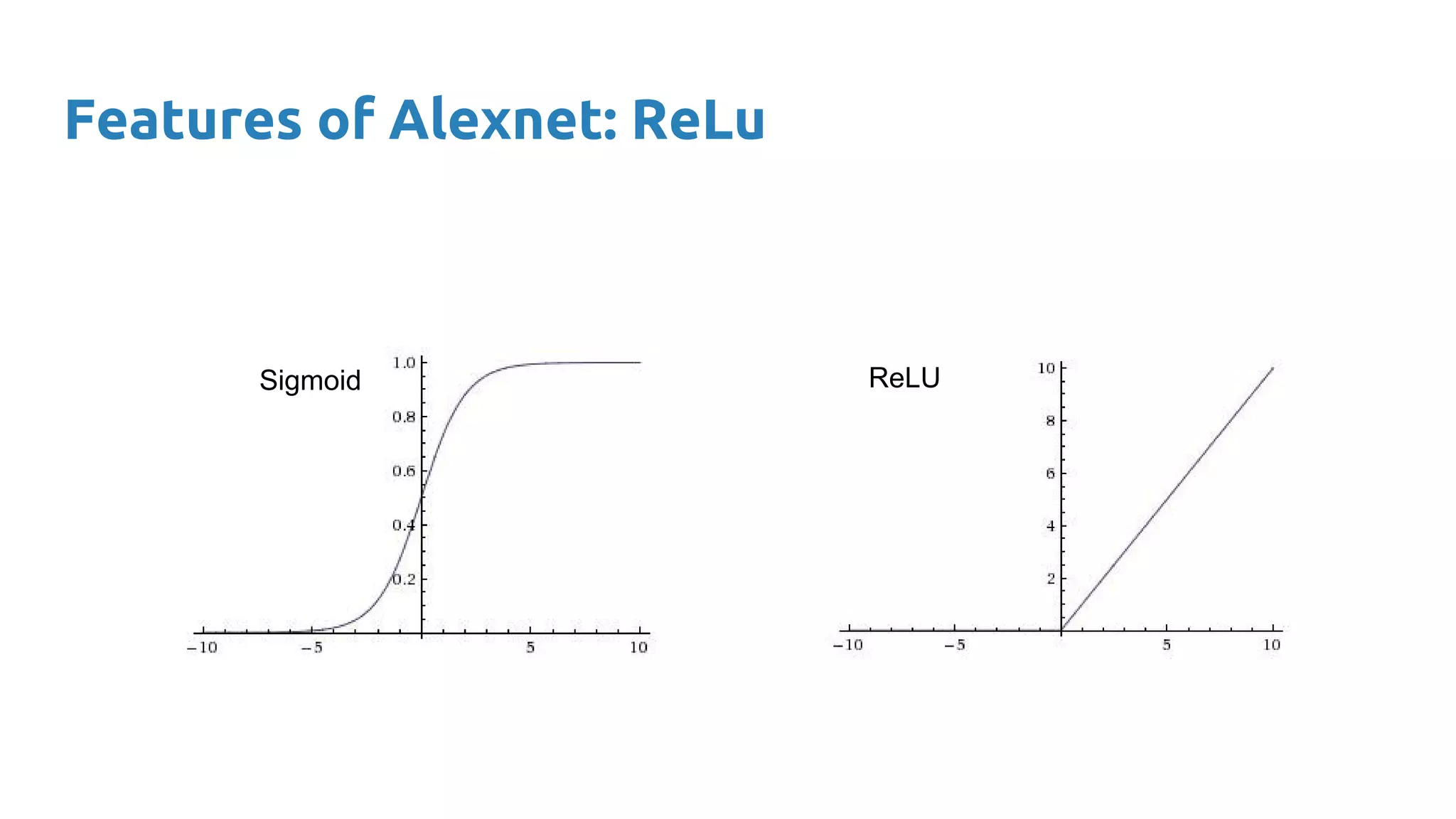
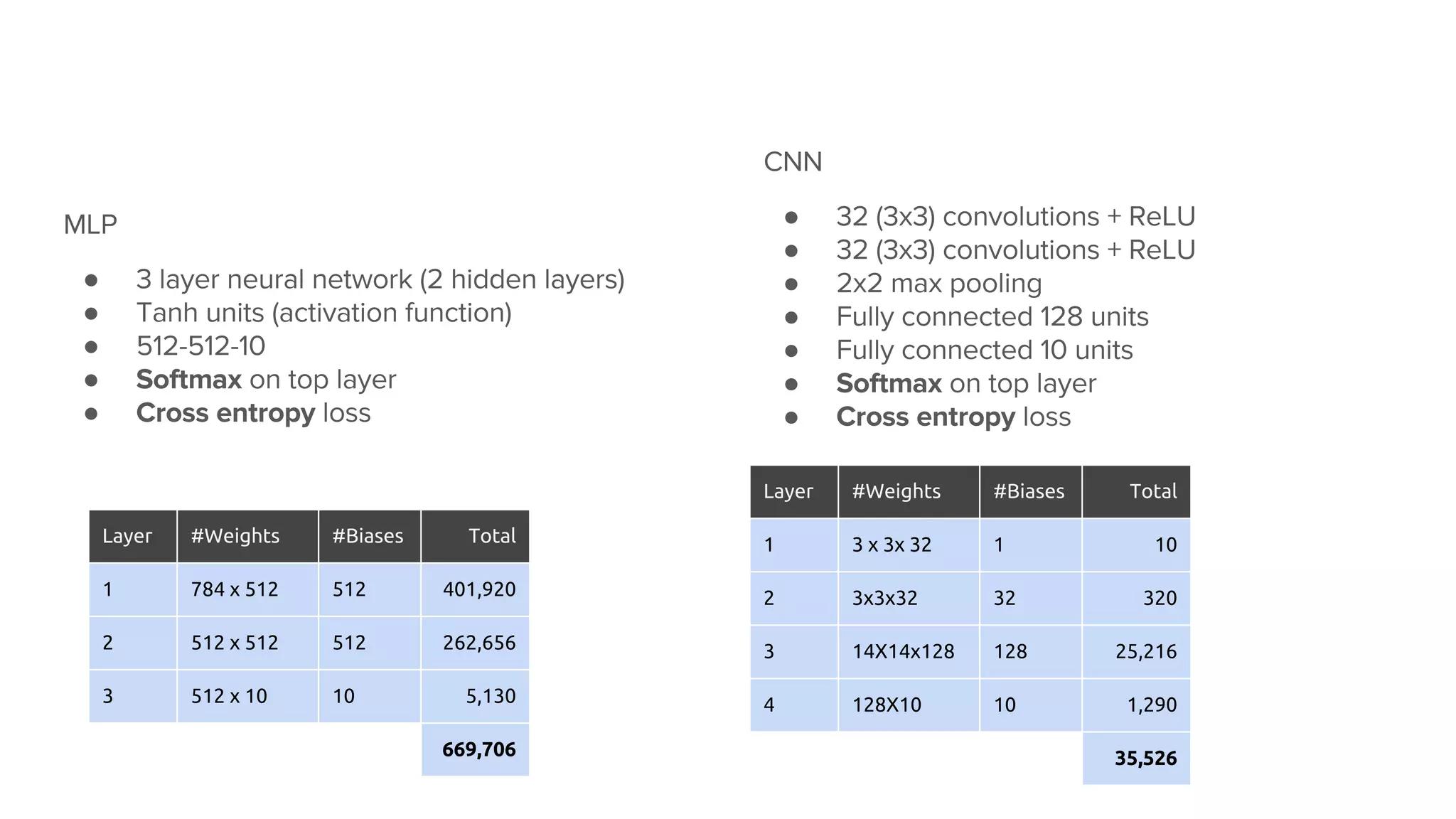
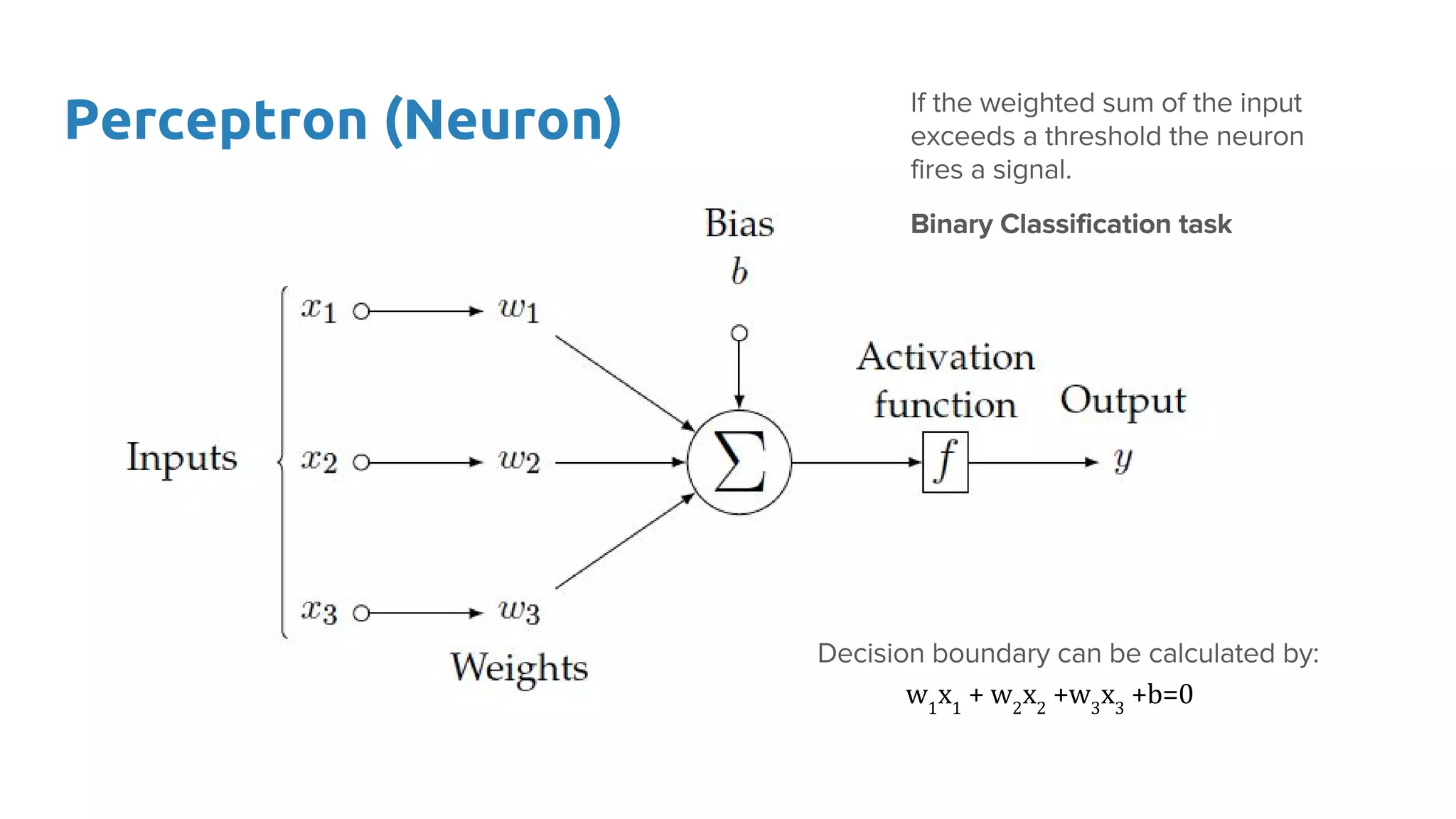
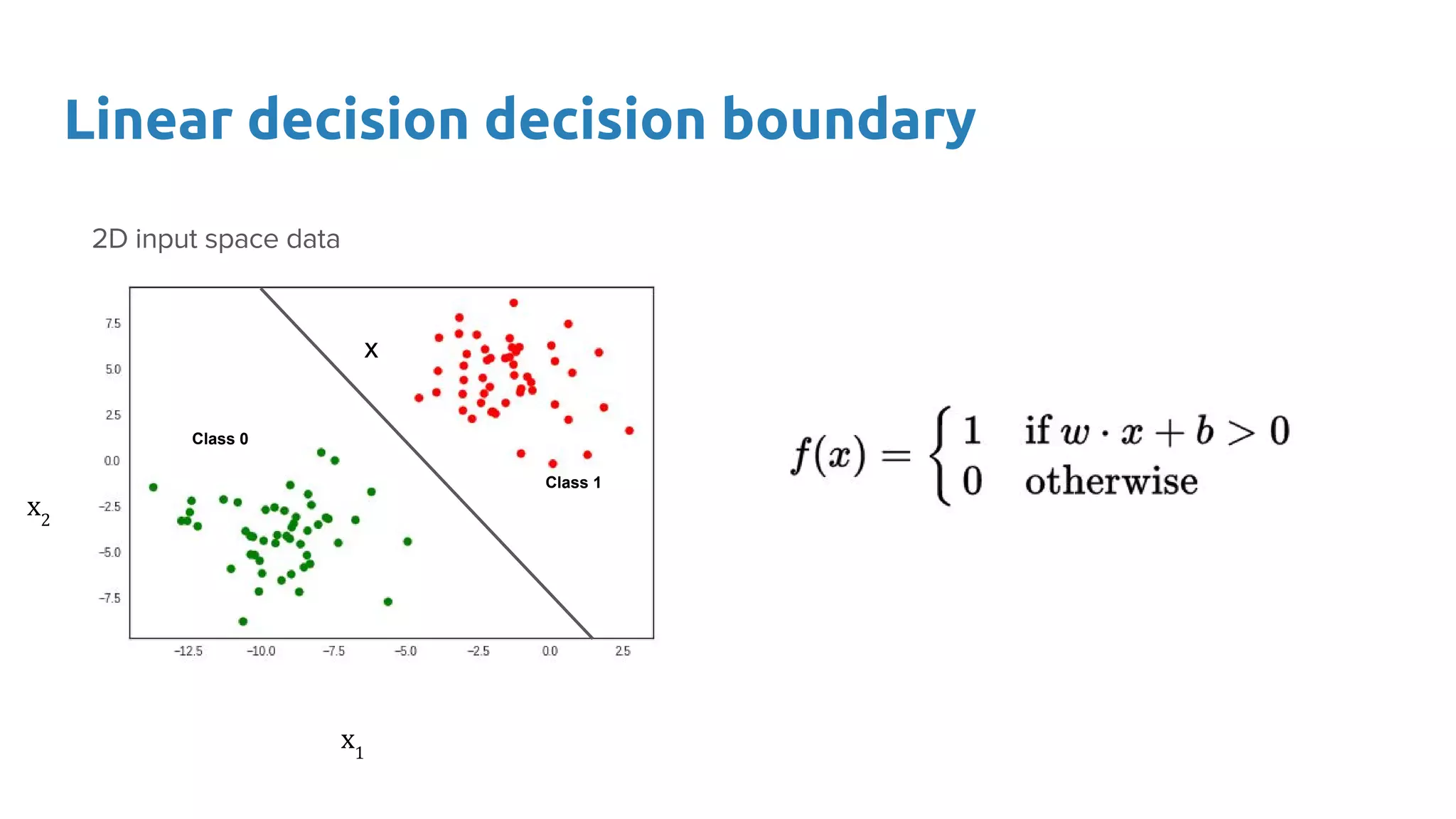
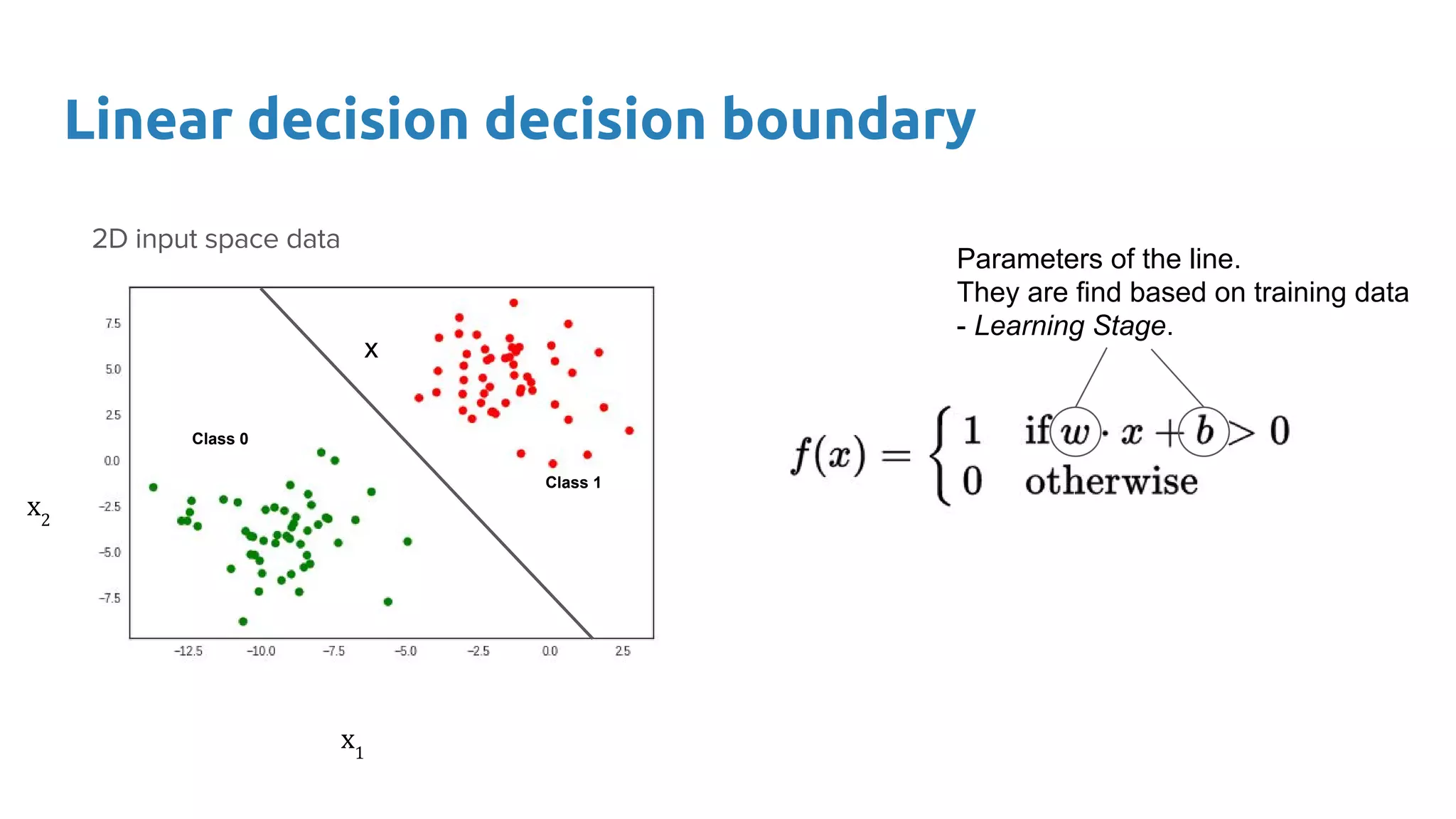
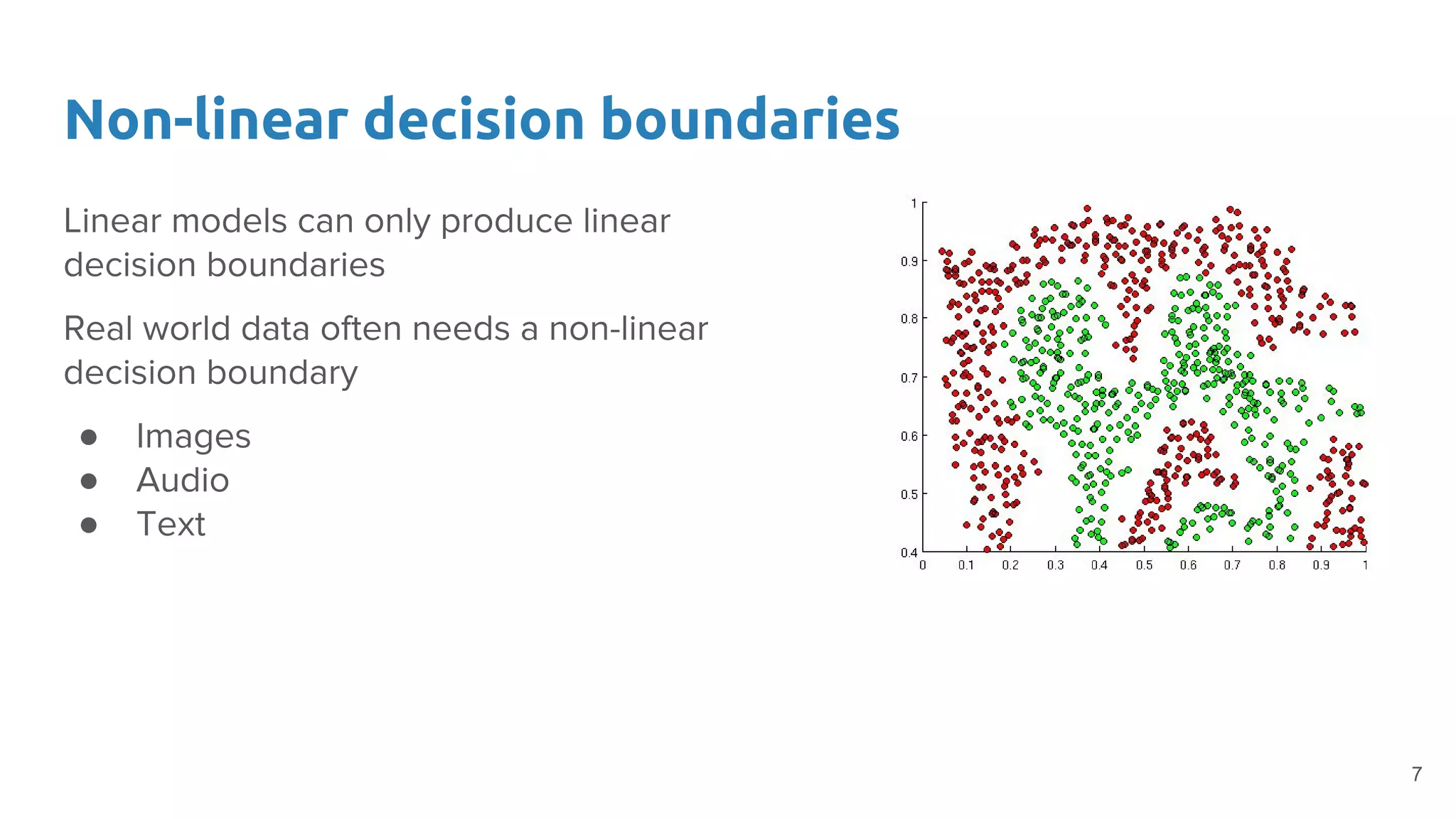
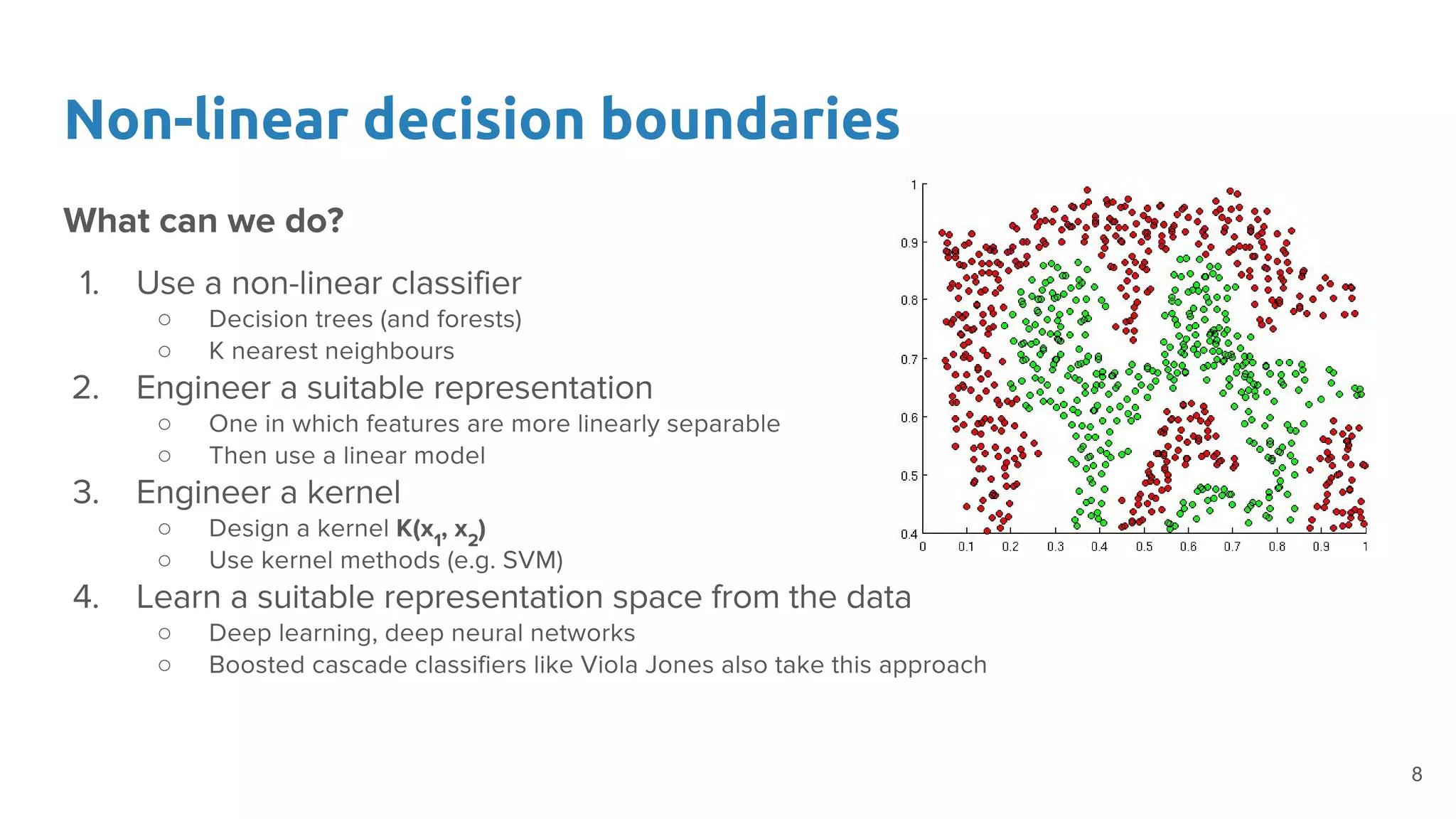
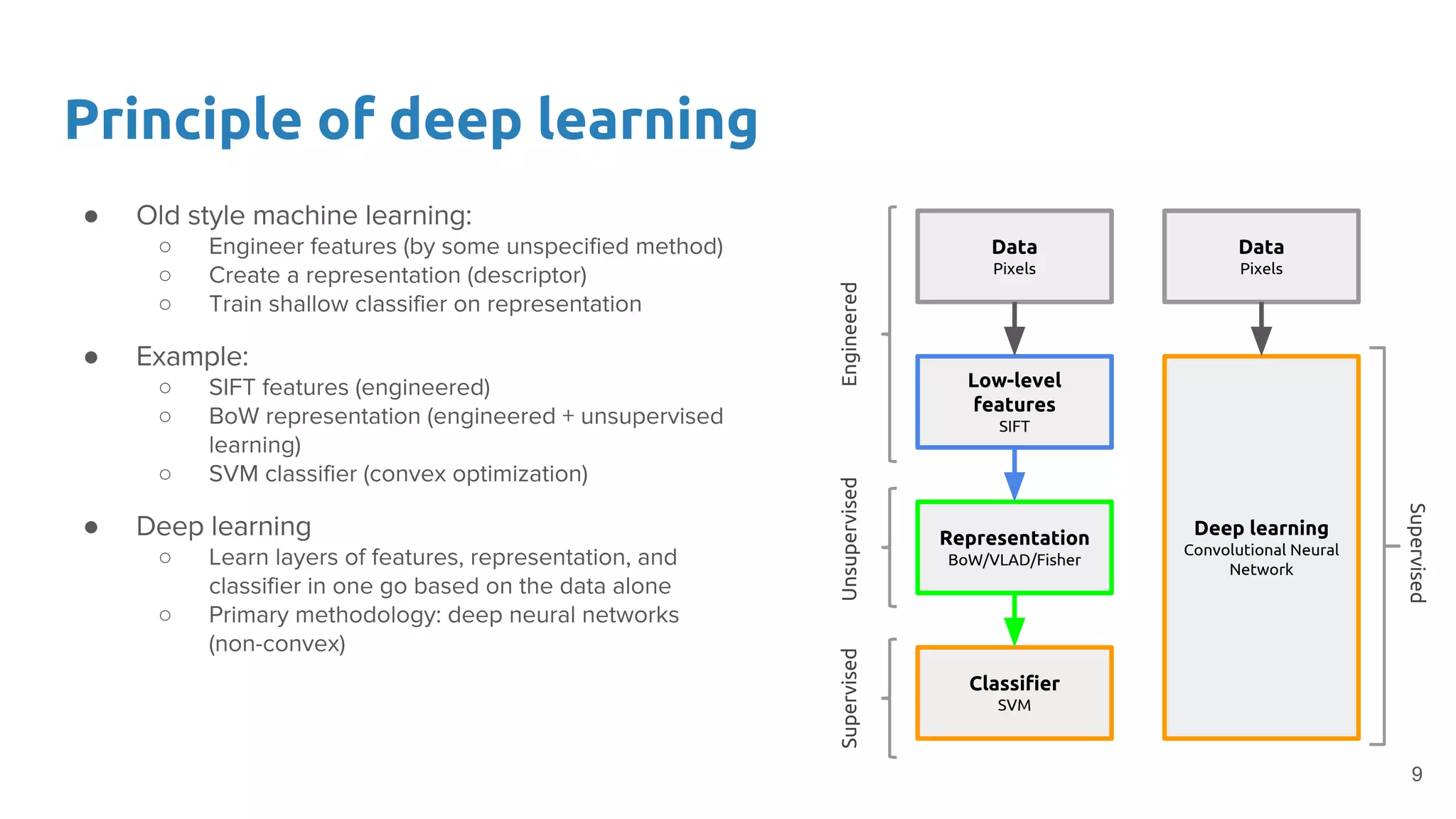
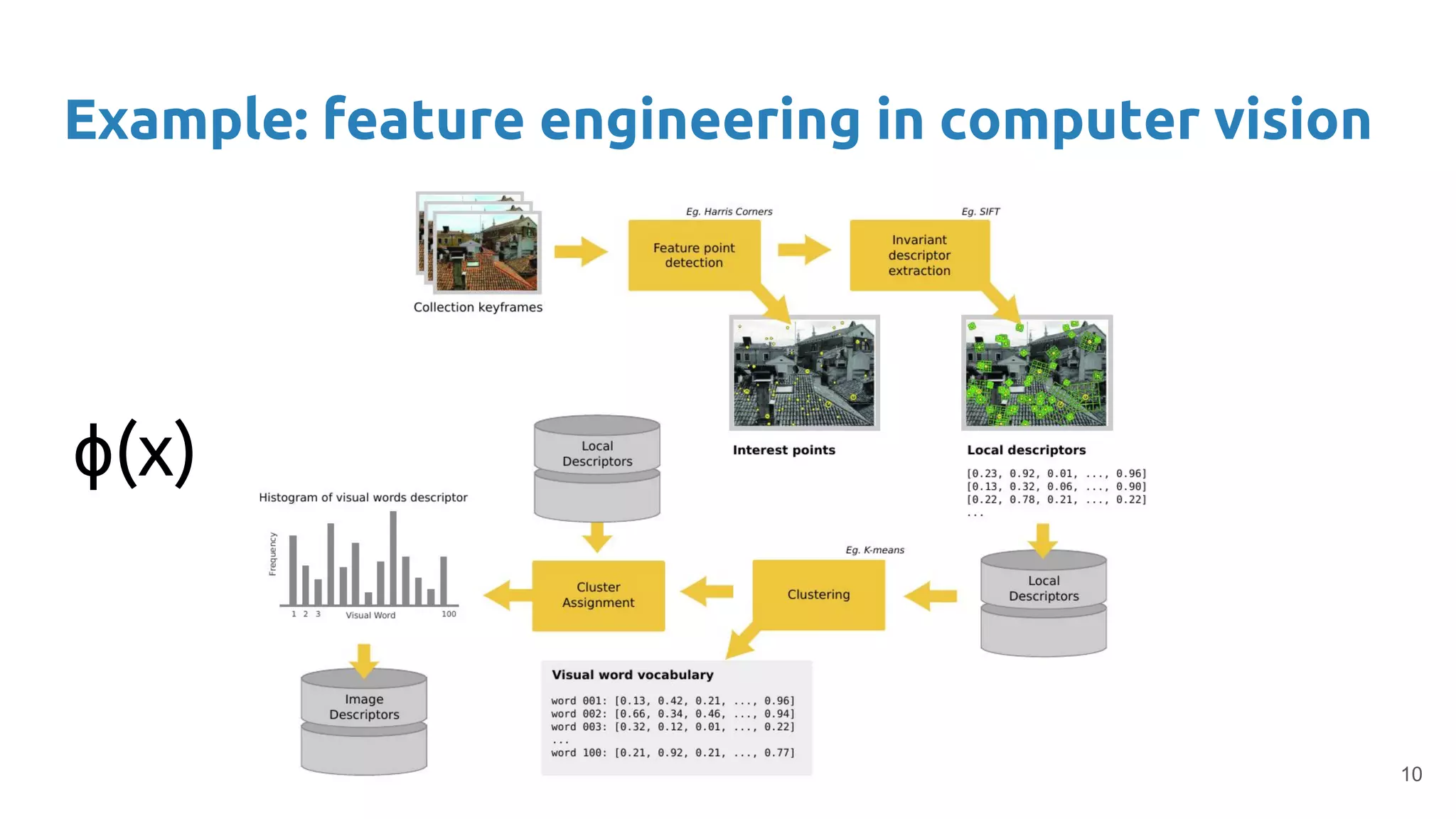
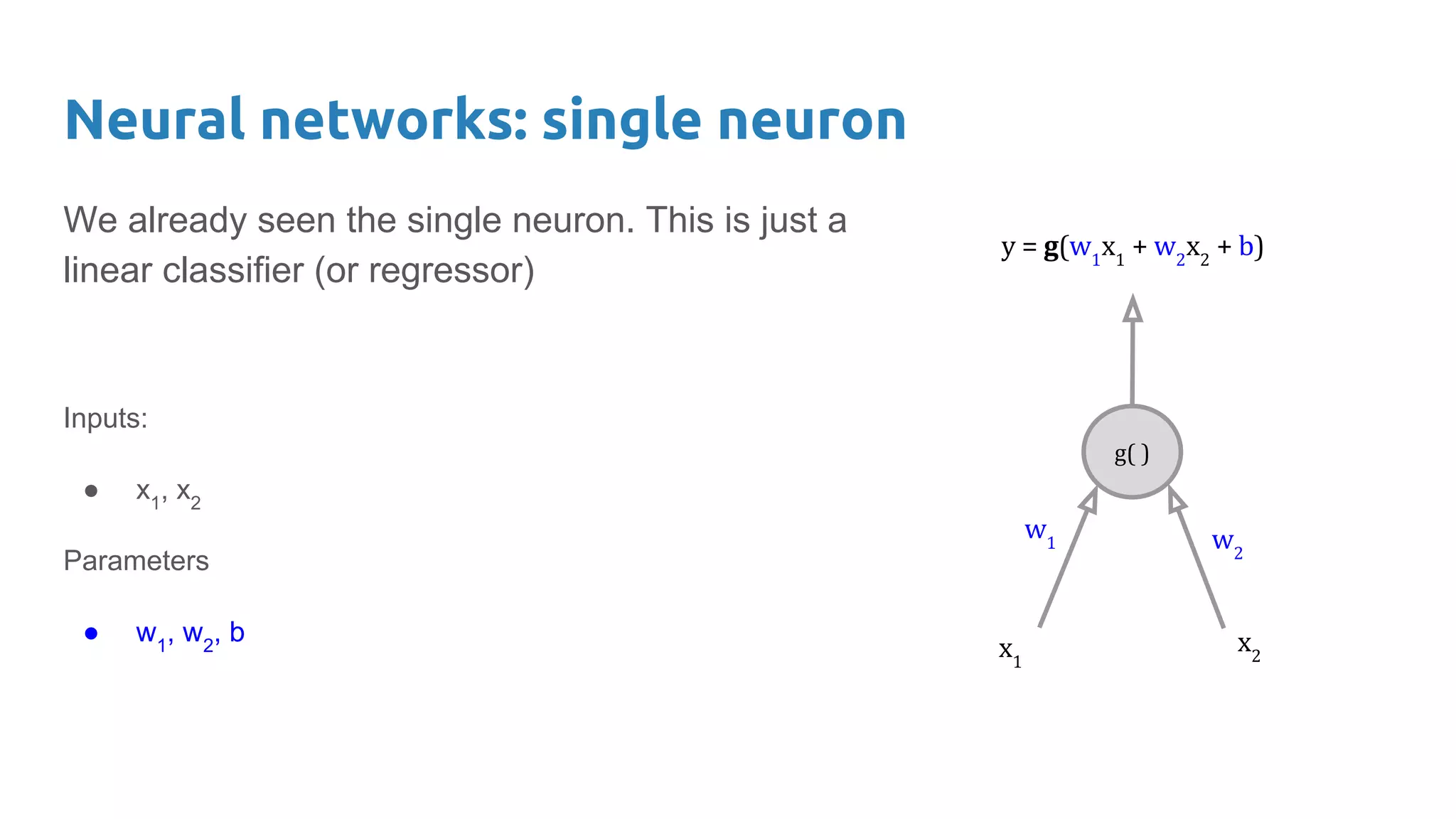
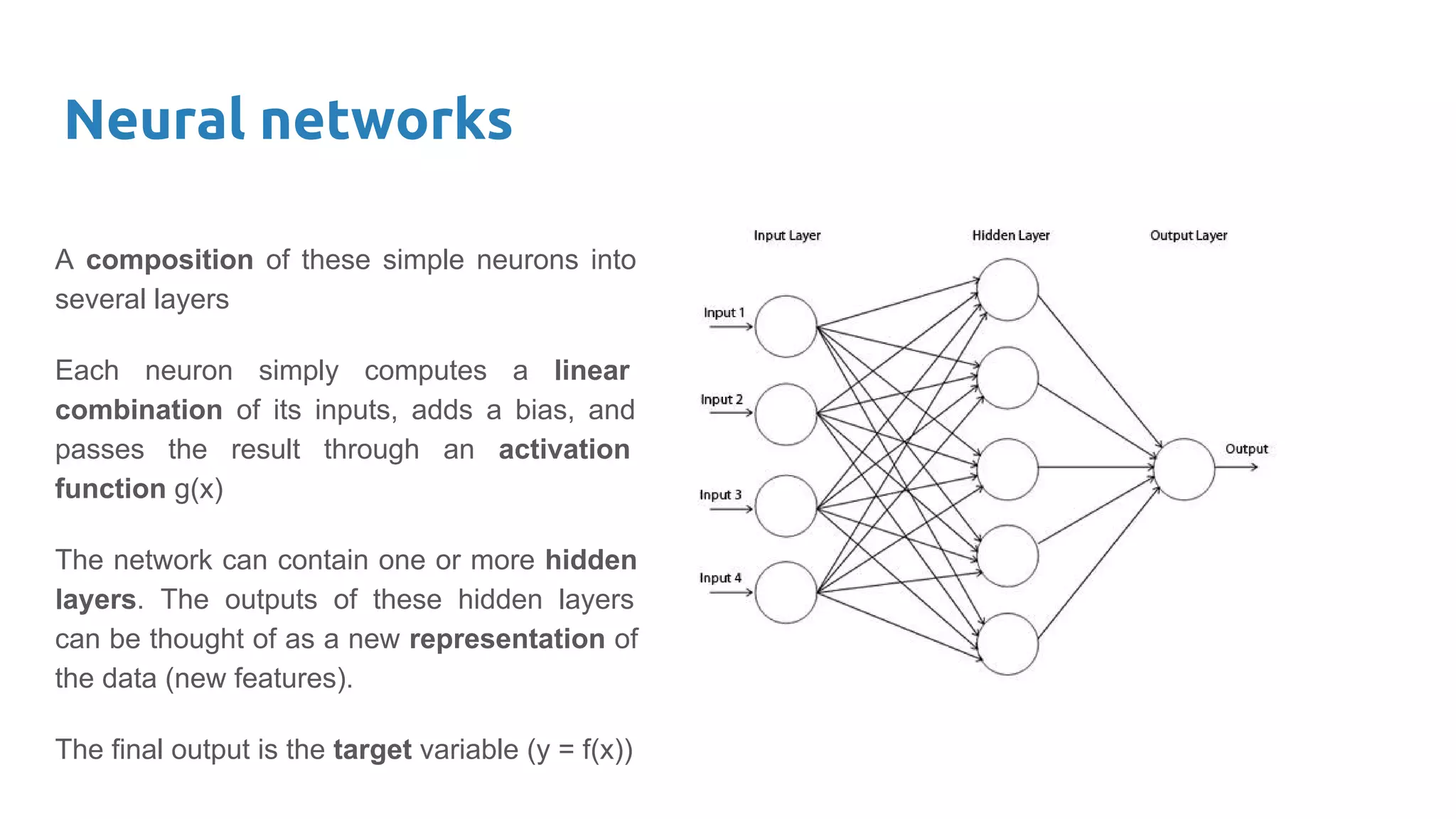
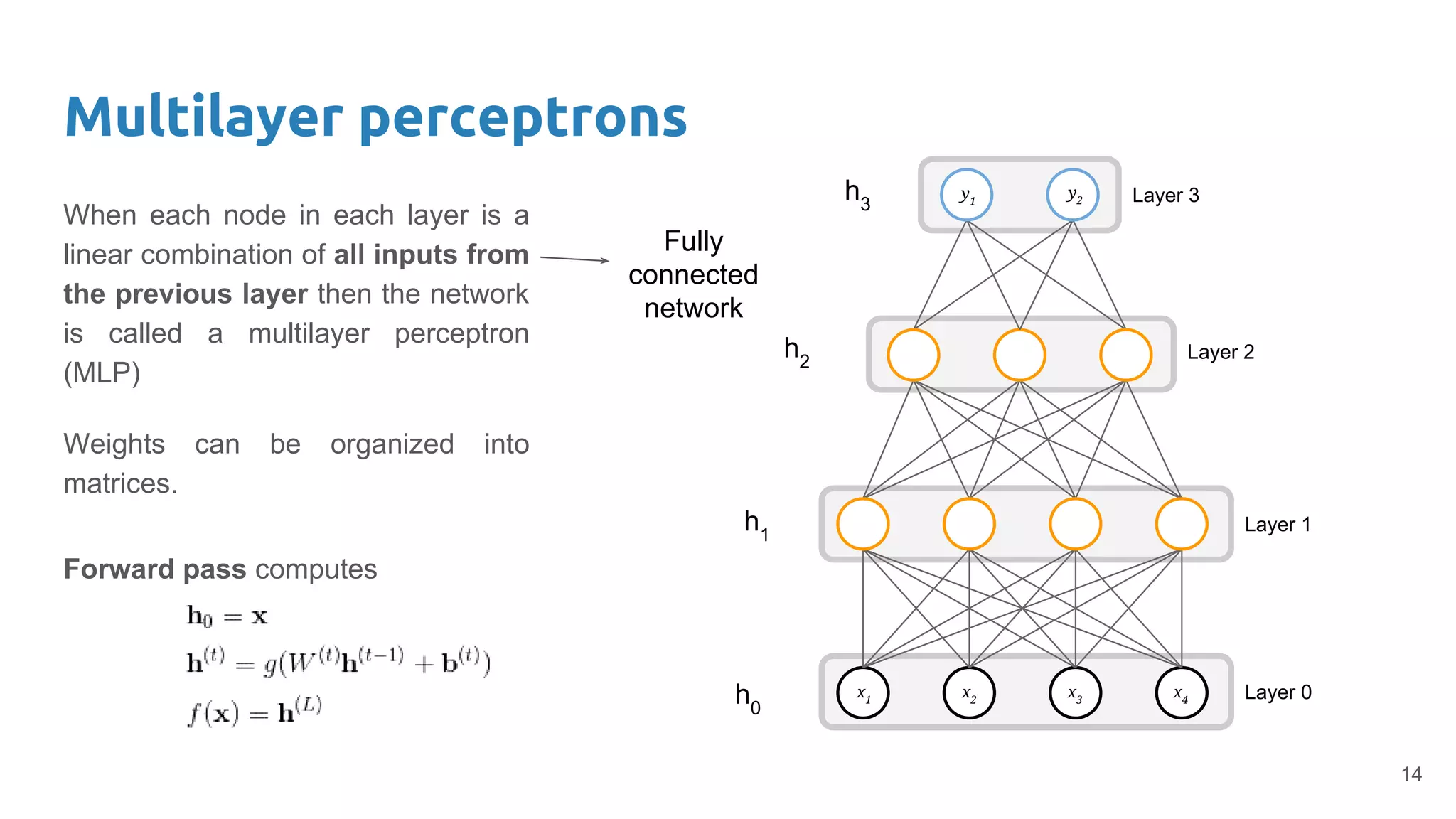
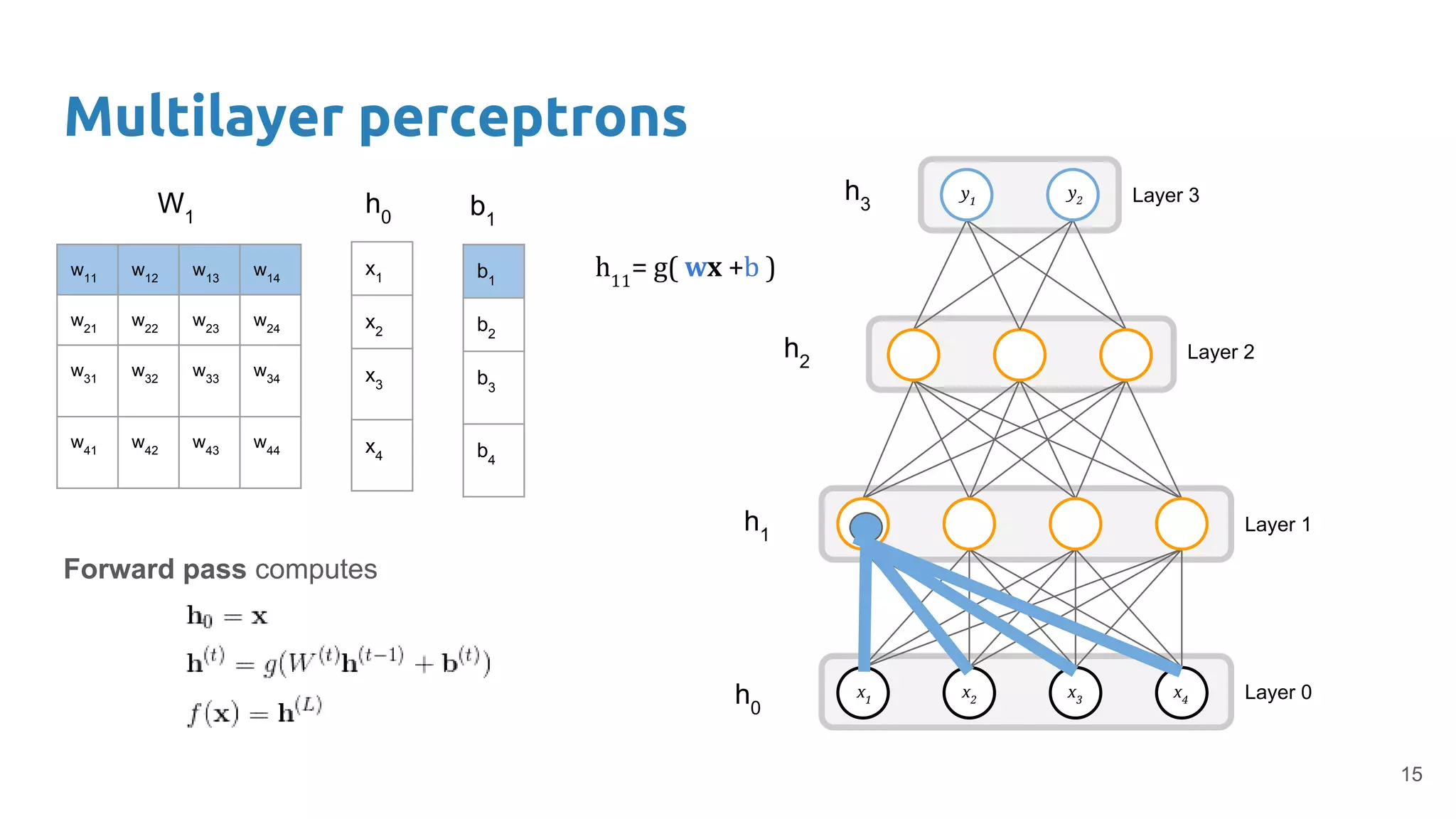
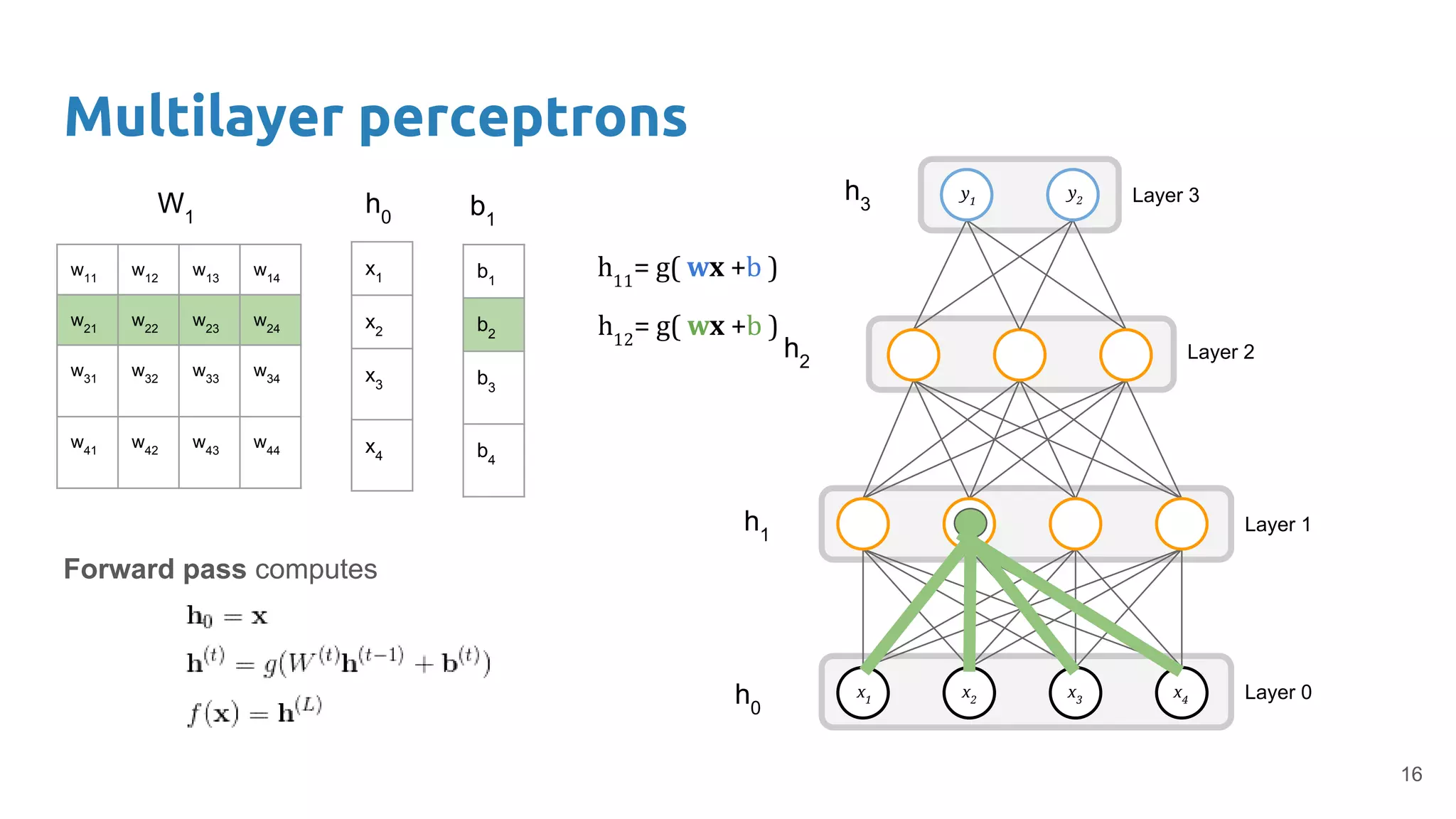
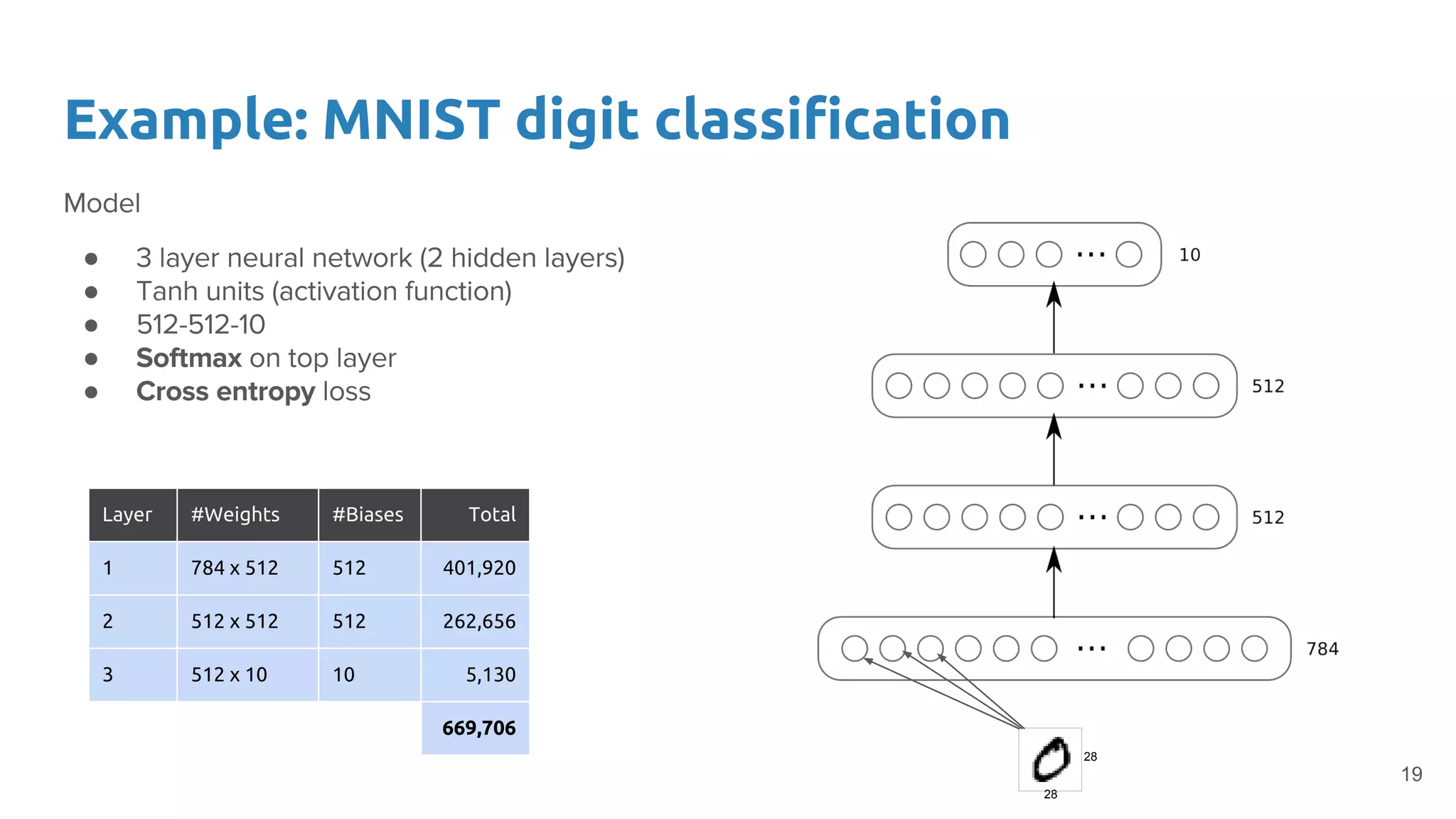
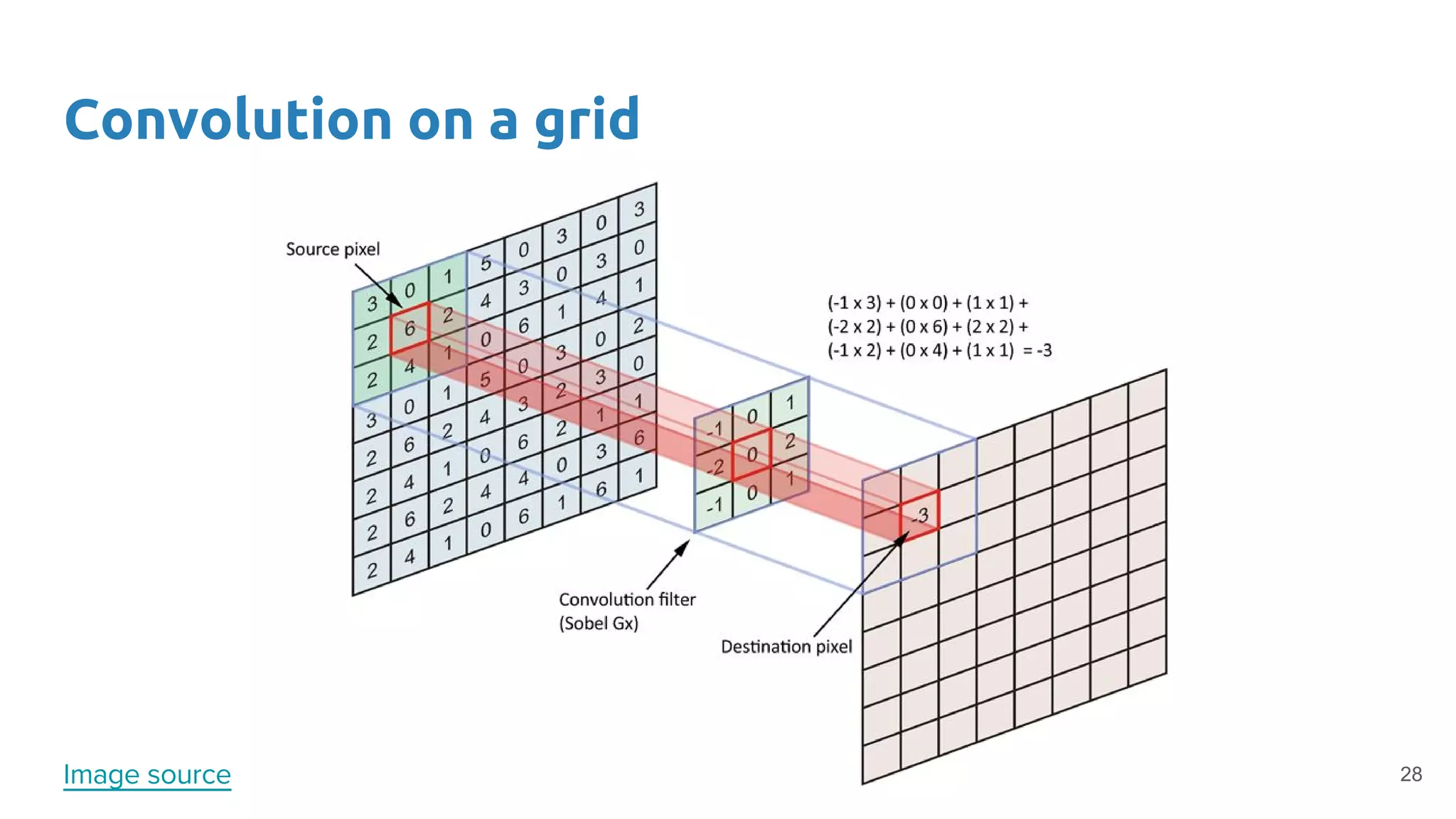
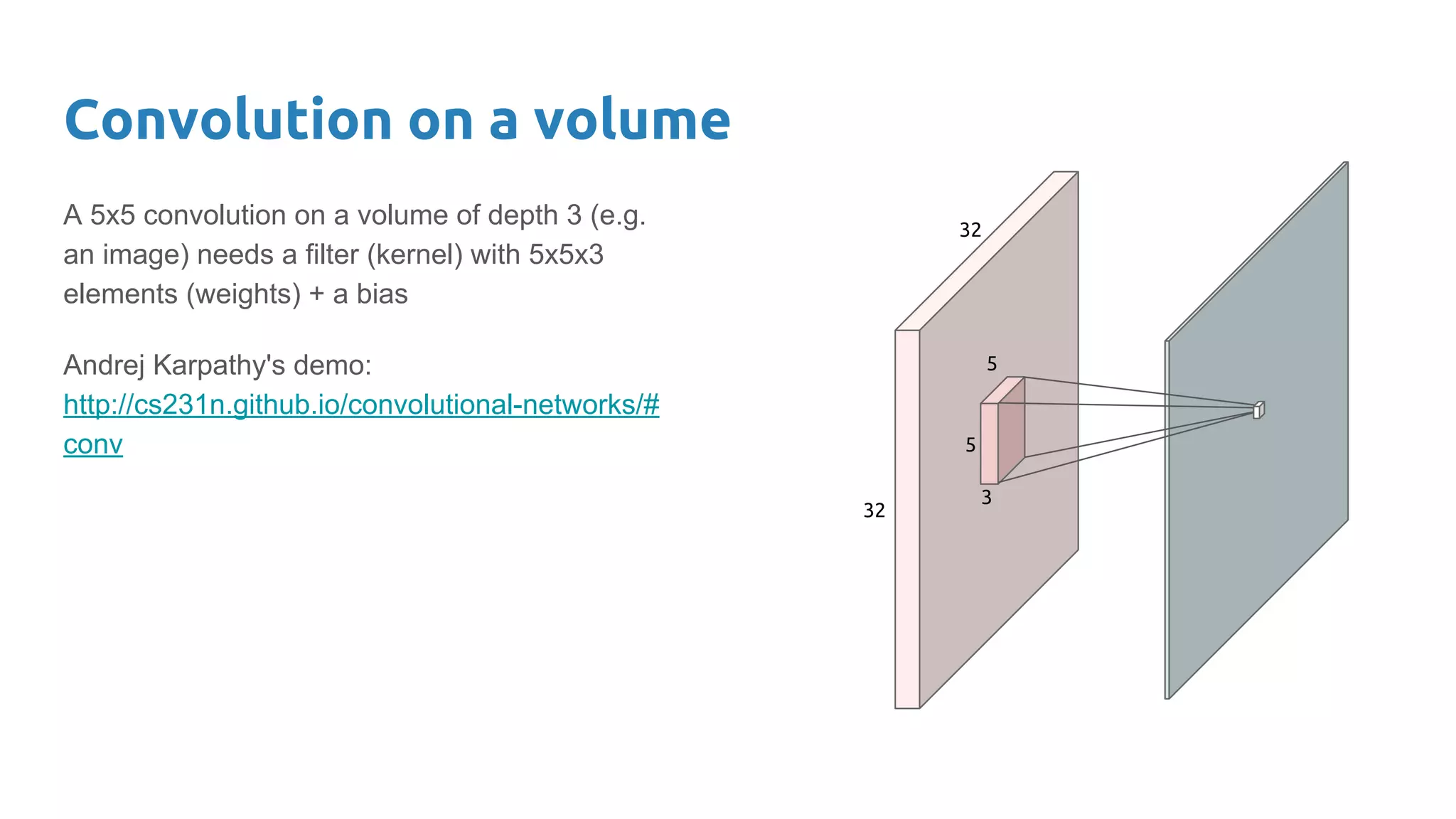
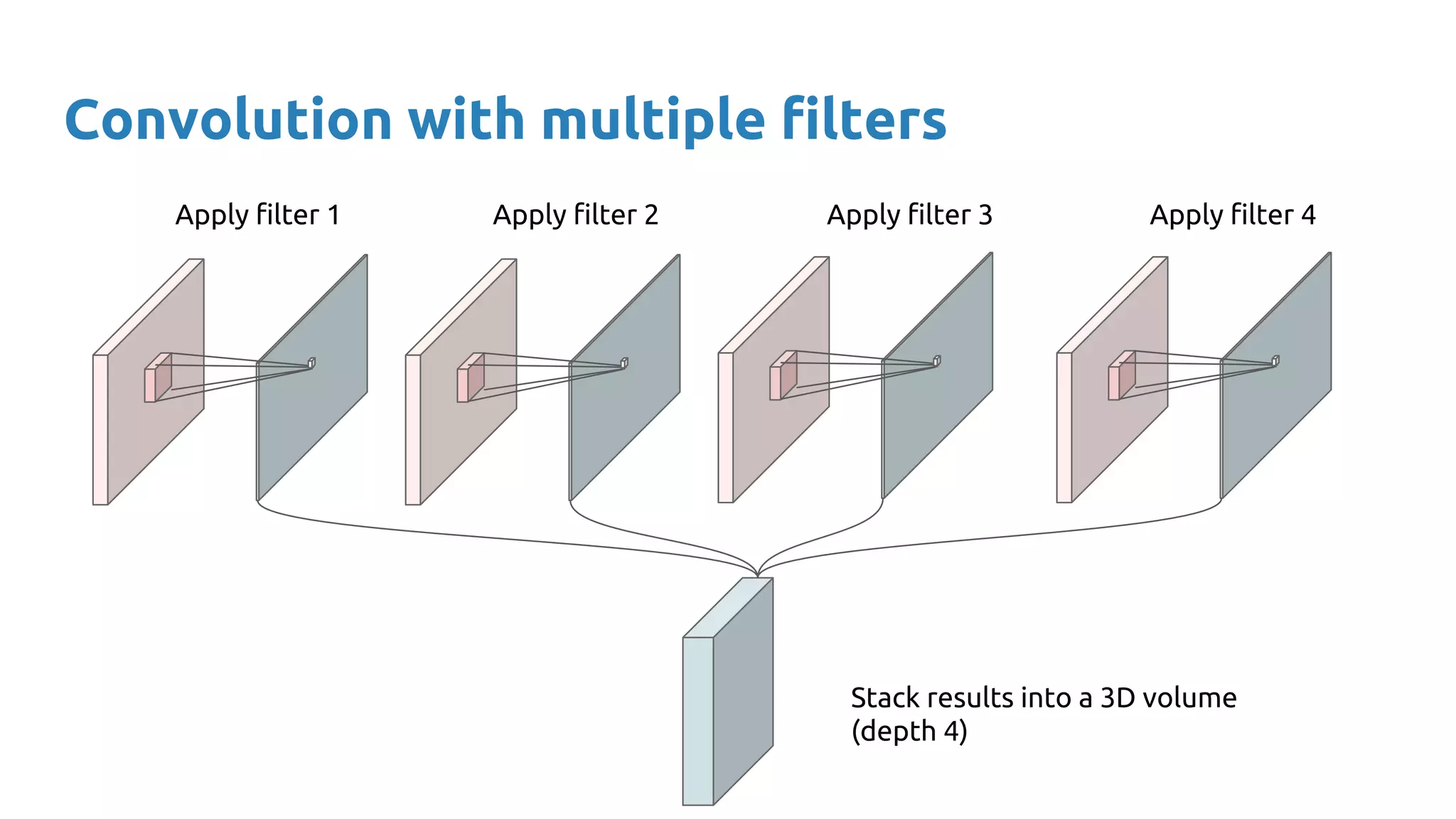
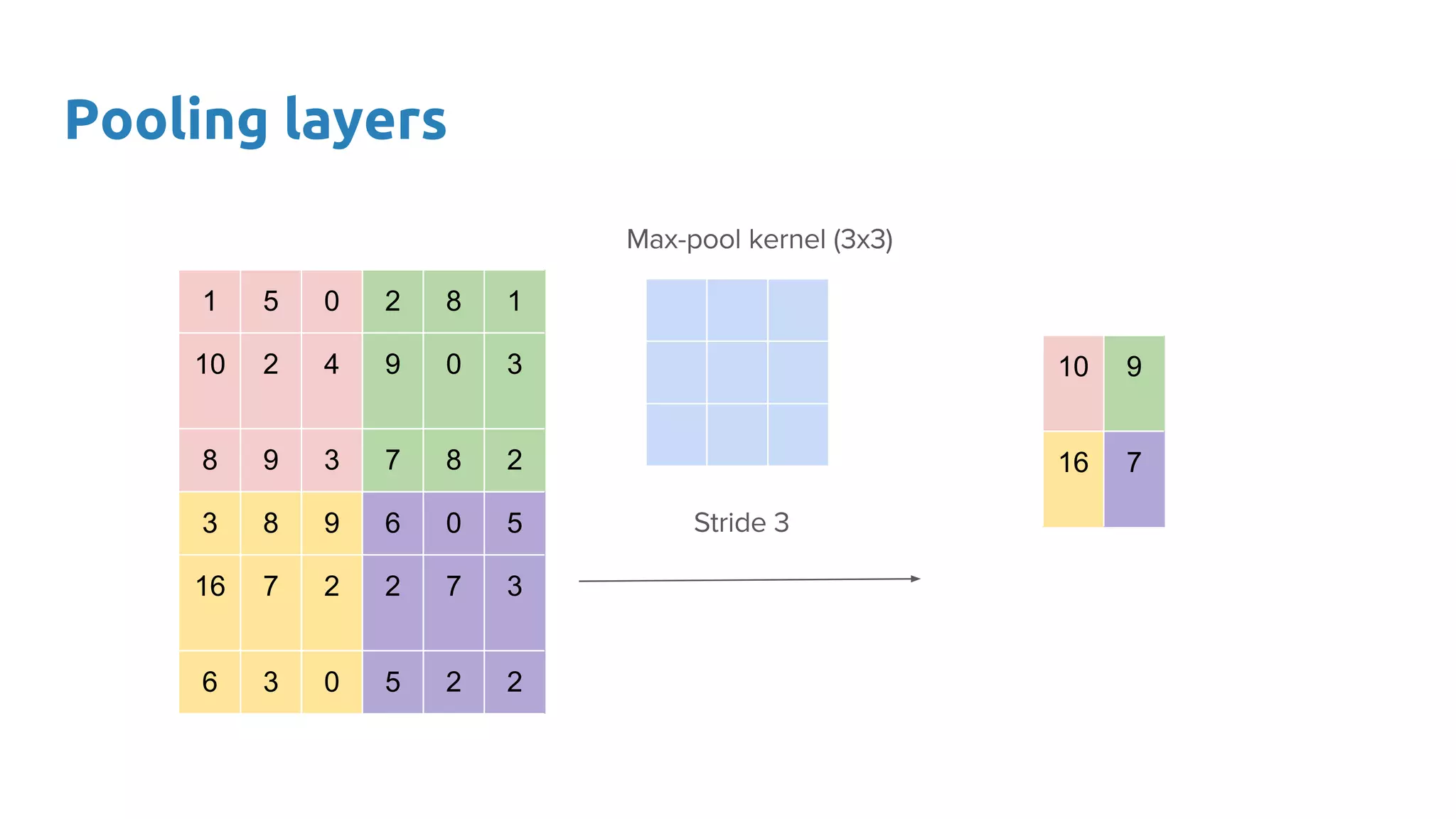
The document provides an overview of deep neural networks, including concepts like perceptrons, multilayer perceptrons, and convolutional neural networks (CNNs). It discusses the limitations of linear decision boundaries, the importance of activation functions, and the universal approximation theorem that supports the use of deep networks in complex function approximation. Additionally, it presents examples from the MNIST digit classification and highlights key features of CNNs such as filtering and pooling layers.

1. Eva Mohedano
eva.mohedano@insight-centre.org
PhD Student
Insight Centre for Data Analytics
Dublin City University
Deep Neural Networks

2. Overview
●
●
●
●

3. Perceptron (Neuron)

4. Linear decision decision boundary
Class 0
Class 1
x

5. Linear decision decision boundary
Class 0
Class 1
Parameters of the line.
They are find based on training data
- Learning Stage.
x

6. Limitations: XOR problem
Input 1 Input 2 Desired
Output
0 0 0
0 1 1
1 0 1
1 1 0
XOR logic table
1
0
0
1 Input 1
Input 2
?

7. Non-linear decision boundaries
●
●
●
7

8. Non-linear decision boundaries
○
○
○
○
○
○
○
○
8

9. Principle of deep learning
●
○
○
○
●
○
○
○
●
○
○
Data
Pixels
Deep learning
Convolutional Neural
Network
Data
Pixels
Low-level
features
SIFT
Representation
BoW/VLAD/Fisher
Classifier
SVM
EngineeredUnsupervisedSupervised
Supervised
9

10. Example: feature engineering in computer vision
10
ϕ(x)

11. Neural networks: single neuron
We already seen the single neuron. This is just a
linear classifier (or regressor)
Inputs:
● x1
, x2
Parameters
● w1
, w2
, b

12. Neural networks
A composition of these simple neurons into
several layers
Each neuron simply computes a linear
combination of its inputs, adds a bias, and
passes the result through an activation
function g(x)
The network can contain one or more hidden
layers. The outputs of these hidden layers
can be thought of as a new representation of
the data (new features).
The final output is the target variable (y = f(x))

13. Activation functions
●
●
●
●
●
●
Sigmoid
Tanh
ReLU
13
If we only use linear layers we are only able to
learn linear transformations of our input.

14. Multilayer perceptrons
14
x1
x2
x3
x4
y1
Layer 1
Layer 2
Layer 3
Layer 0
y2
When each node in each layer is a
linear combination of all inputs from
the previous layer then the network
is called a multilayer perceptron
(MLP)
Weights can be organized into
matrices.
Fully
connected
network
Forward pass computes
h0
h1
h2
h3

15. Multilayer perceptrons
15
Forward pass computes
w11
w12
w13
w14
w21
w22
w23
w24
w31
w32
w33
w34
w41
w42
w43
w44
W1
x1
x2
x3
x4
b1
b2
b3
b4
b1
h0
x1
x2
x3
x4
y1
Layer 1
Layer 2
Layer 3
Layer 0
y2
h0
h1
h2
h3

16. Multilayer perceptrons
16
Forward pass computes
w11
w12
w13
w14
w21
w22
w23
w24
w31
w32
w33
w34
w41
w42
w43
w44
W1
x1
x2
x3
x4
b1
b2
b3
b4
b1
h0
x1
x2
x3
x4
y1
Layer 1
Layer 2
Layer 3
Layer 0
y2
h0
h1
h2
h3

17. Universal approximation theorem
Universal approximation theorem states that “the standard multilayer feed-forward network with a single hidden layer,
which contains finite number of hidden neurons, is a universal approximator among continuous functions on compact
subsets of Rn
, under mild assumptions on the activation function.”
If a 2 layer NN is a universal approximator, then why do we need deep nets??
The universal approximation theorem:
● Says nothing about the how easy/difficult it is to fit such approximators
● Needs a “finite number of hidden neurons”: finite may be extremely large
In practice, deep nets can usually represent more complex functions with less total neurons (and
therefore, less parameters)

18. Example: MNIST digit classification
●
●
●
●
●
●
●
●
18

19. Example: MNIST digit classification
●
●
●
●
●
28
28
19
Layer #Weights #Biases Total
1 784 x 512 512 401,920
2 512 x 512 512 262,656
3 512 x 10 10 5,130
669,706

20. Example: MNIST digit classification
●
●
●
●
●
●
●
●
●
●
●
●
●
●
20

21. Permutation invariant MNIST
●
●
●
●
●
●
Permute
21

22. Convolutional neural networks (CNNs, convnets)
●
●
22

23. 1D convolution
23
0 1 5 0 2 8 1 0
-1 2 -1
Signal
Kernel/filter
dot product
-3
=
.

24. 1D convolution
24
0 1 5 0 2 8 1 0
-1 2 -1
Signal
Kernel/filter
-3 9
. .

25. 1D convolution
25
0 1 5 0 2 8 1 0
-1 2 -1
Signal
Kernel/filter
-3 9 -7
. . .

26. 1D convolution
26
0 1 5 0 2 8 1 0
-1 2 -1
Signal
Kernel/filter
-3 9 -7 -4 13 -6
. . . . . .

27. 1D convolution
27
0 1 5 0 2 8 1 0
-1 2 -1
Signal
Kernel/filter
-3 -7 13
. . . Hyperparameters

28. Convolution on a grid
28

29. Convolution on a volume
32
32
5
5
3
A 5x5 convolution on a volume of depth 3 (e.g.
an image) needs a filter (kernel) with 5x5x3
elements (weights) + a bias
Andrej Karpathy's demo:
http://cs231n.github.io/convolutional-networks/#
conv

30. Convolution with multiple filters
Stack results into a 3D volume
(depth 4)
Apply filter 1 Apply filter 2 Apply filter 3 Apply filter 4

31. Pooling layers
1 5 0 2 8 1
10 2 4 9 0 3
8 9 3 7 8 2
3 8 9 6 0 5
16 7 2 2 7 3
6 3 0 5 2 2
10 9
16 7

32. Convnets
●
●
LeNet-5 [LeCun et al. 1998] 32

33. Alexnet
● 8 parameter layers (5 convolution, 3 fully connected)
● Softmax output
● 650,000 units
● 60 million free parameters
● Trained on two GPUs (two streams) for a week
● Ensemble of 7 nets used in ILSVRC challenge
Krizhevsky et al. ImageNet classification with deep convolutional neural networks. NIPS, 2012.

34. Features of Alexnet: Convolutions

35. Features of Alexnet: max pooling

36. Features of Alexnet: ReLu
Sigmoid ReLU

37. Filters learnt by Alexnet
Visualization of the 96 11 x 11 filters learned by bottom layer
Krizhevsky et al. ImageNet classification with deep convolutional neural networks. NIPS, 2012.

38. Example: a convnet on MNIST
●
●
●
●
●
●
●
●
●
●
https://github.com/fchollet/keras/blob/master/examples/mnist_cnn.py 38

39. Advantages of convnets
●
○
○
●
○
●
○
●
○
●
○
●
39

40. Summary
●
●
●
●
●
40

41. Questions?
41

42. ●
●
●
●
●
Layer #Weights #Biases Total
1 784 x 512 512 401,920
2 512 x 512 512 262,656
3 512 x 10 10 5,130
669,706
●
●
●
●
●
●
●
Layer #Weights #Biases Total
1 3 x 3x 32 1 10
2 3x3x32 32 320
3 14X14x128 128 25,216
4 128X10 10 1,290
35,526