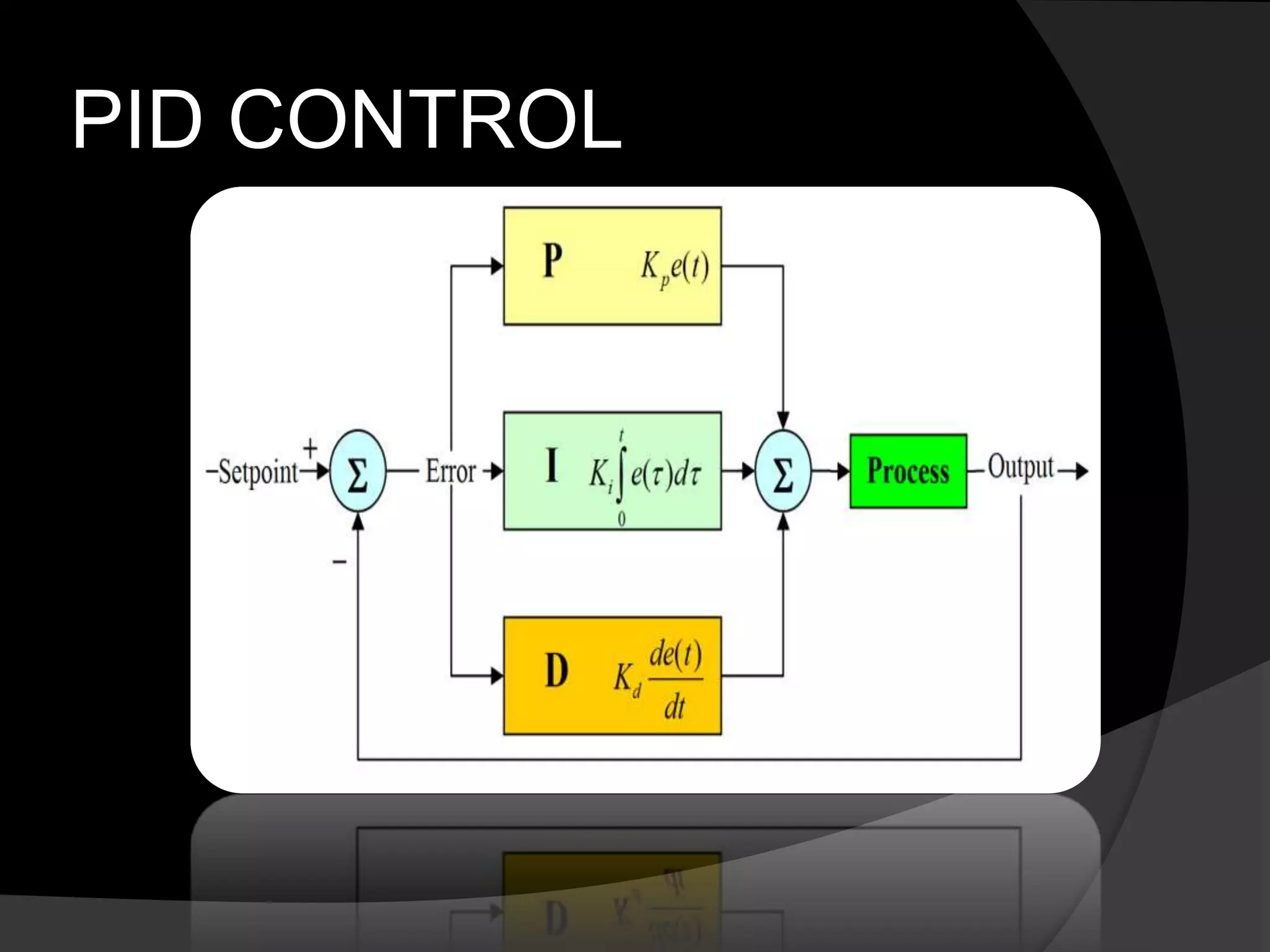
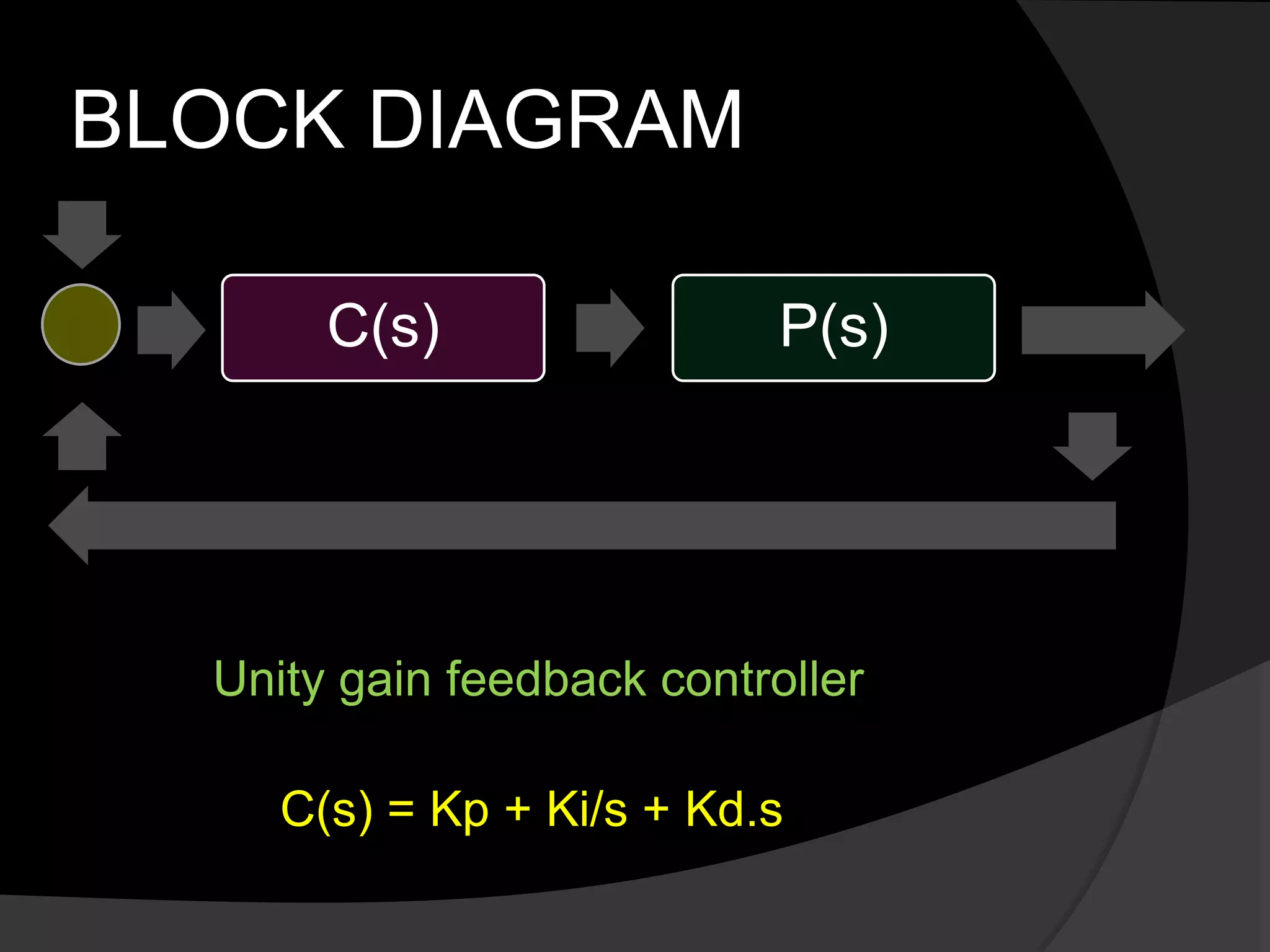
Cruise control systems use feedback control to maintain a constant vehicle speed set by the driver. A cruise control system measures the current vehicle speed, compares it to the desired speed, and automatically adjusts the throttle according to a control law to account for external disturbances. Modeling the vehicle as a first order mass-damper system and applying Newton's second law derives the system transfer function. A proportional controller meets some performance criteria, but a lag controller is also needed to reduce the steady-state error to within acceptable limits.

1. ADVANCING SMOOTHLY

2. CRUISE CONTROL

3. CRUISE CONTROL
 Cruise control (speed control, auto-cruise
or tempomat) is a system that automatically
controls the speed of a motor vehicle. The system
takes over the throttle of the car to maintain a
steady speed as set by the driver.

4. CRUISE CONTROL

5. SYSTEM MODELLING
 feedback control system
 purpose is to maintain a constant vehicle
speed despite external disturbances, such
as changes in wind or road grade.
 accomplished by
i. measuring the vehicle speed
ii. comparing it to the desired or reference speed
iii. automatically adjusting the throttle according
to a control law

6. PHYSICAL SETUP: FBD
bv u
 Mass m
 Control force u
 Resistive forces bv
 Vehicle velocity v
 u = force generated at the road/tire
interface
 we will assume that :
i. u can be controlled directly
ii. the dynamics of the
powertrain, tires, etc are 0
iii. bv, due to rolling resistance and wind
drag varies linearly with the vehicle
velocity, v, and act in the direction
opposite the vehicle's motion

7. FIRST ORDER EQUATION
We are considering a first order mass-damper
system.
Summing forces in the x-direction and applying
Newton's 2nd law, we arrive at the following
system equation:
m(dv/dt)+bv=u
Since v is the required output:
y = v

8. TRANSFER FUNCTION
Taking the Laplace transform and assuming
zero initial conditions, we find the transfer
function of the cruise control system to be:
P(s) = V(s)/U(s)
= 1/(ms+b)

9. PID CONTROL

10. PARAMETERS
 m vehicle mass 1000 kg
 b damping coefficient 50 N.s/m
 r reference speed 10 m/s
 Rise time < 5 s
 Overshoot < 10%
 Steady-state error < 2%

11. BLOCK DIAGRAM
C(s) P(s)
Unity gain feedback controller
C(s) = Kp + Ki/s + Kd.s

12. PROPORTIONAL
CONTROL
 The root-locus plot shows the locations of
all possible closed-loop poles when a single
gain is varied from zero to infinity.
 Only a proportional controller Kp will be
considered to solve this problem. The
closed-loop transfer function becomes:
Y(s)/R(s) = Kp/(ms + ( b + Kp ) )

13. PROPORTIONAL
CONTROL
 MATLAB command sgrid
 Used to display an acceptable region of the
root-locus plot
 Damping ratio (zeta) and the natural
frequency (Wn) need to be determined

14. PROPORTIONAL
CONTROL

15. PROPORTIONAL
CONTROL
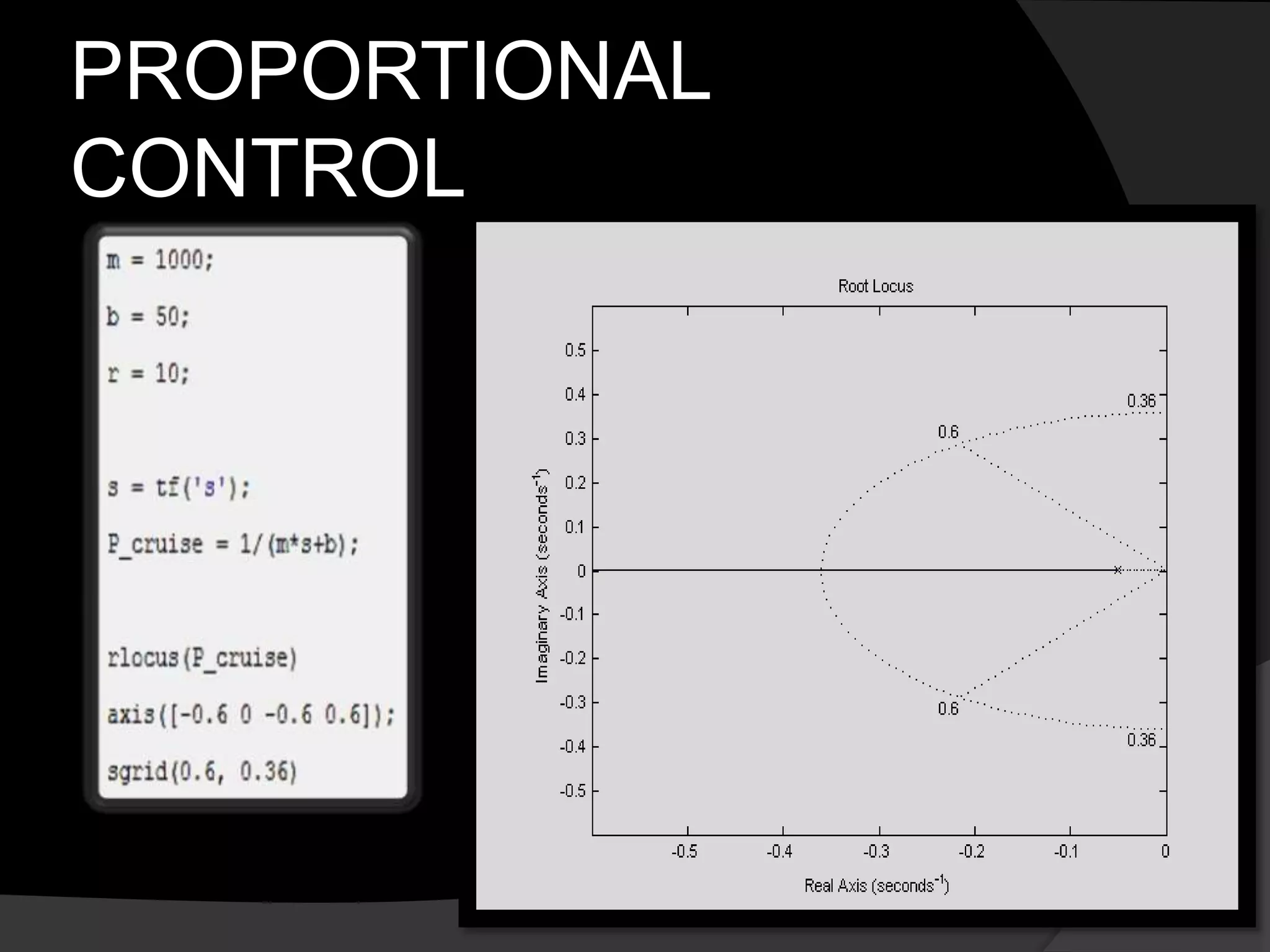
 We can then find a gain to place the closed-
loop poles in the desired region by
employing the rlocfind command
 specific loop gain
[Kp,poles]=rlocfind(P_cruise)
 In between the dotted lines (zeta > 0.6) and
outside the semi-ellipse (wn > 0.36)

16. LAG CONTROLLER
 With the gain Kp being the only functional
gain and Ki and Kd being zero, the rise time
and the overshoot criteria have been met
 A steady-state error of more than 10%
remains
 To reduce the steady-state error, a lag
controller is added to the system

17. LAG CONTROLLER
 To reduce the steady-state error, a lag
controller will be added to the system.
 A pole and a zero, not too distant spacing-
wise are introduced i.e:

18. LAG CONTROLLER
 With the gain Kp being the only functional
gain and Ki and Kd being zero, the rise time
and the overshoot criteria have been met
 A steady-state error of more than 10%
remains
 To reduce the steady-state error, a lag
controller is added to the system
 the steady-state error will be reduced by a
factor of zo/po

19. LAG CONTROLLER
 With the gain Kp excluded for the moment, the
transfer function of PID becomes:
 Adding Kp to the equation, the transfer function of
PID becomes:

20. LEAD CONTROLLER
 The lead controller is basically added to
improve the transient response of the
system i.e. Ts and Tp mainly
 Not used here as it is not needed and the
desired parameters are already being
achieved