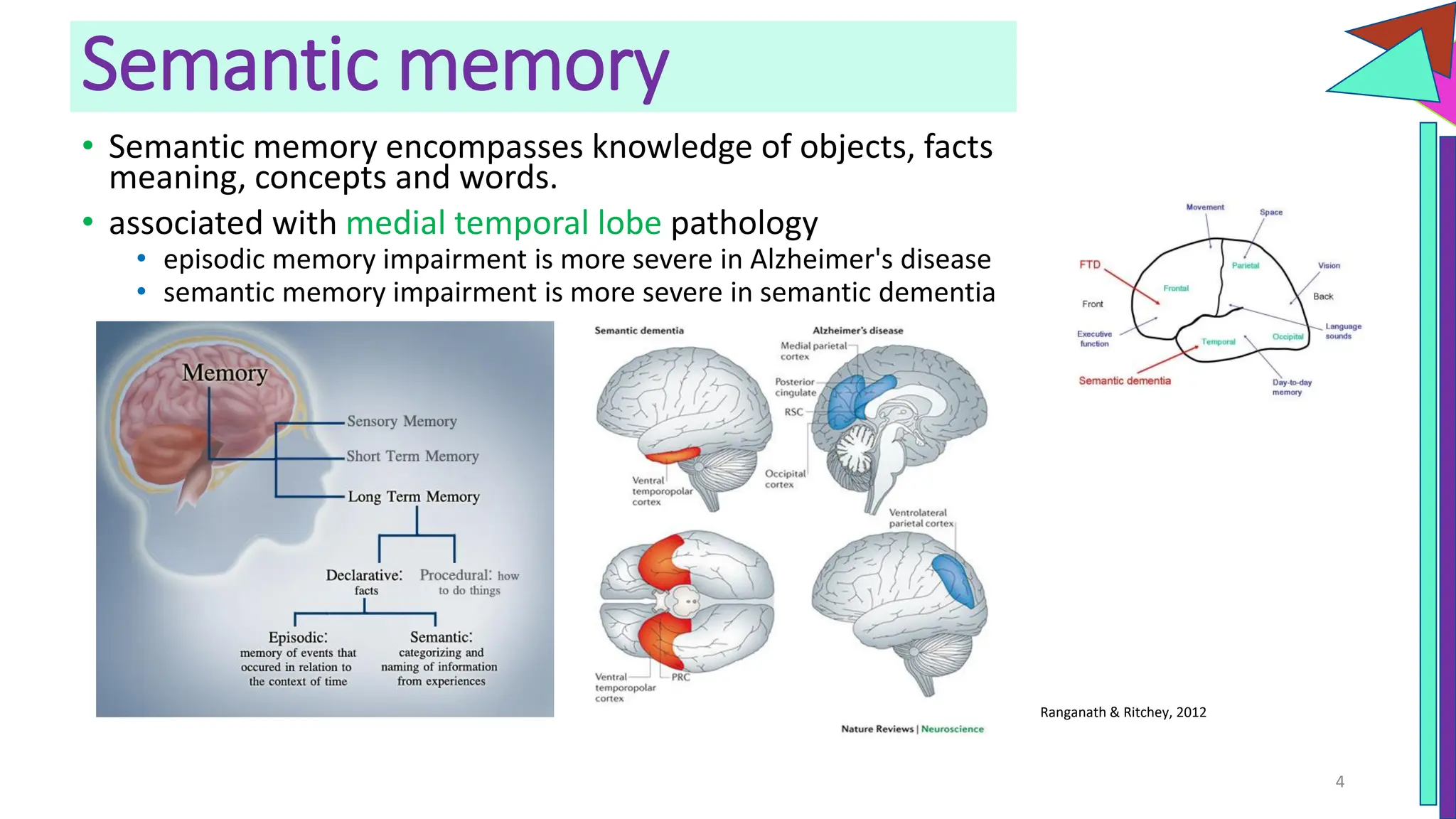
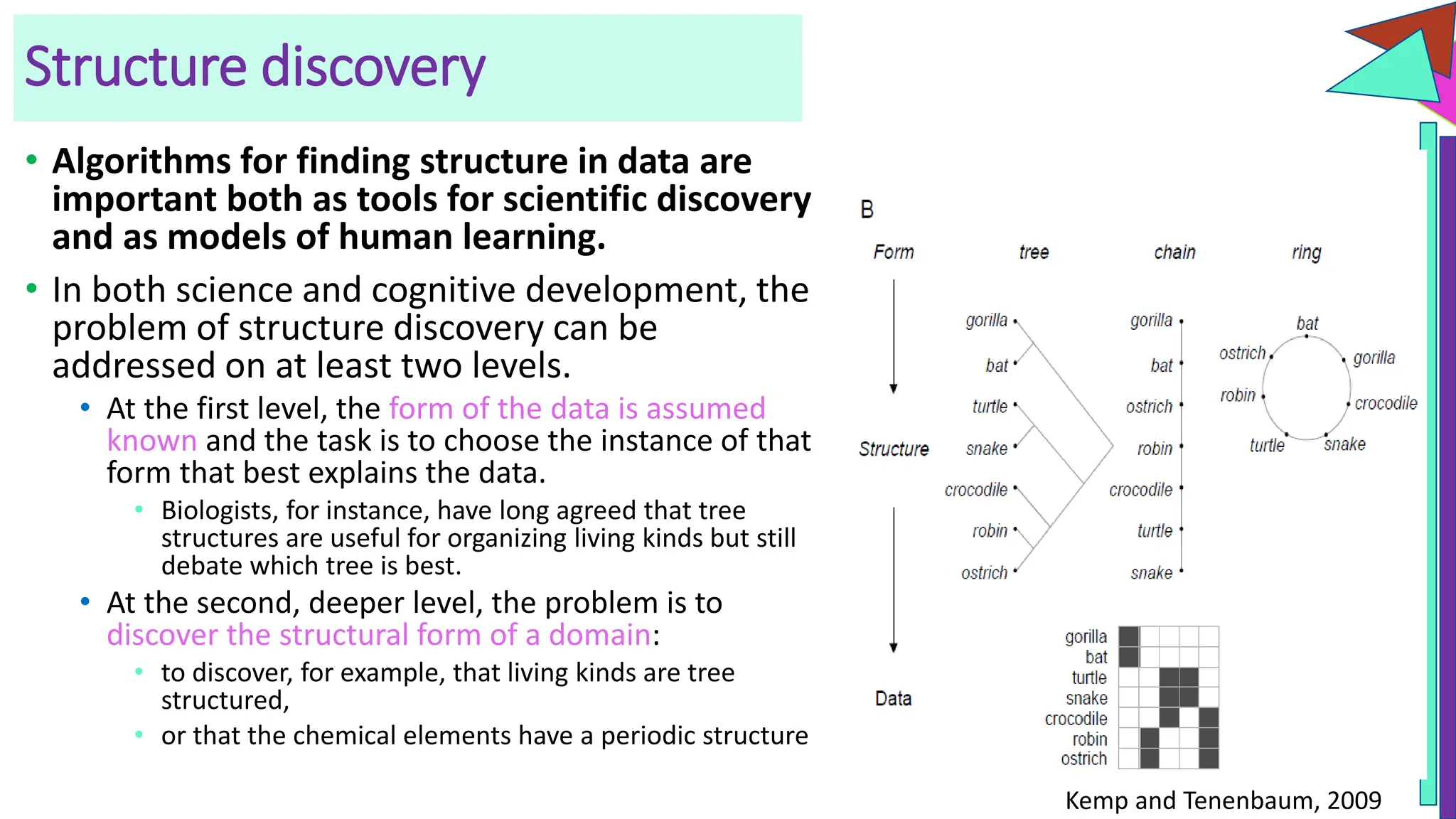
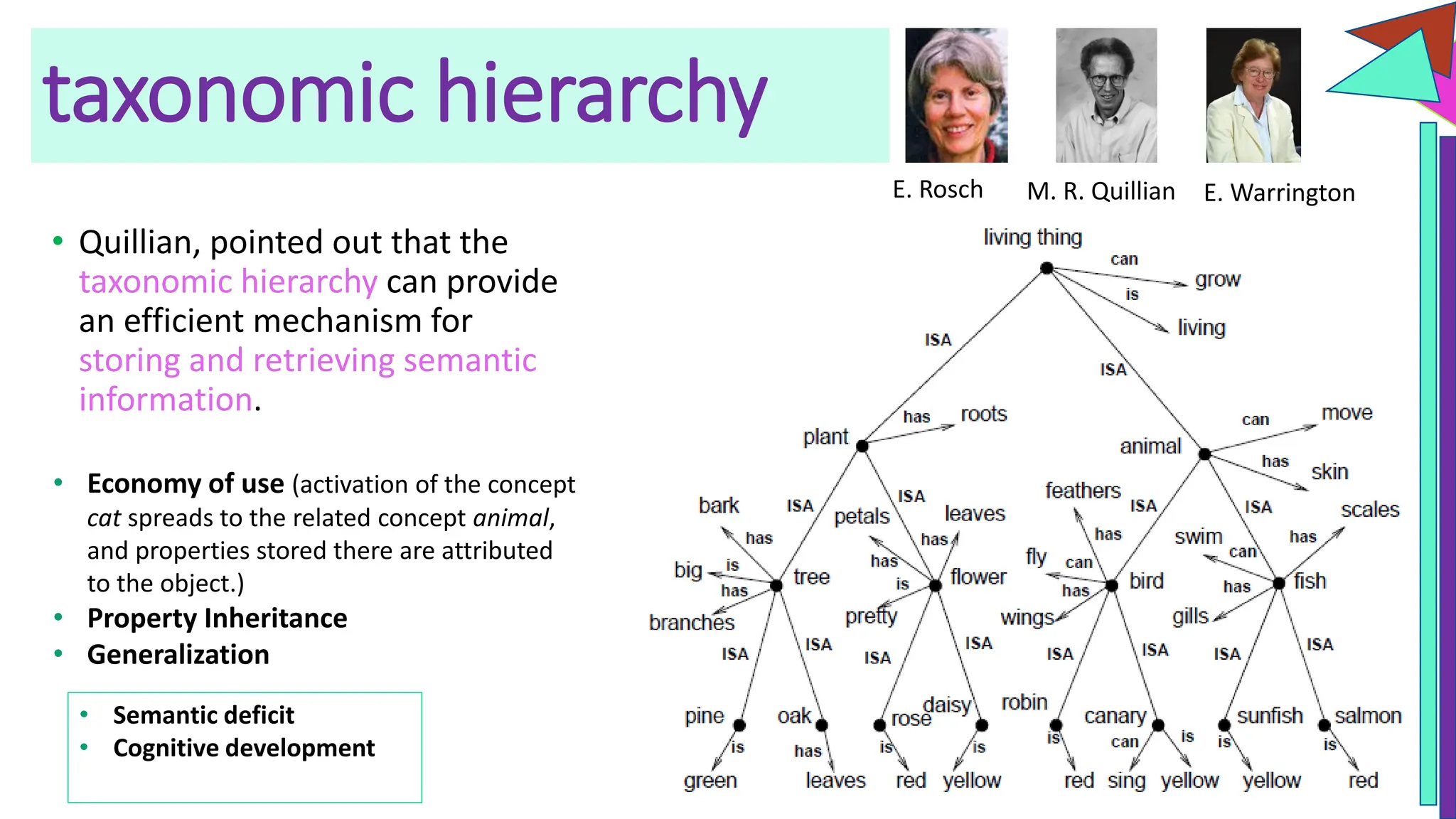
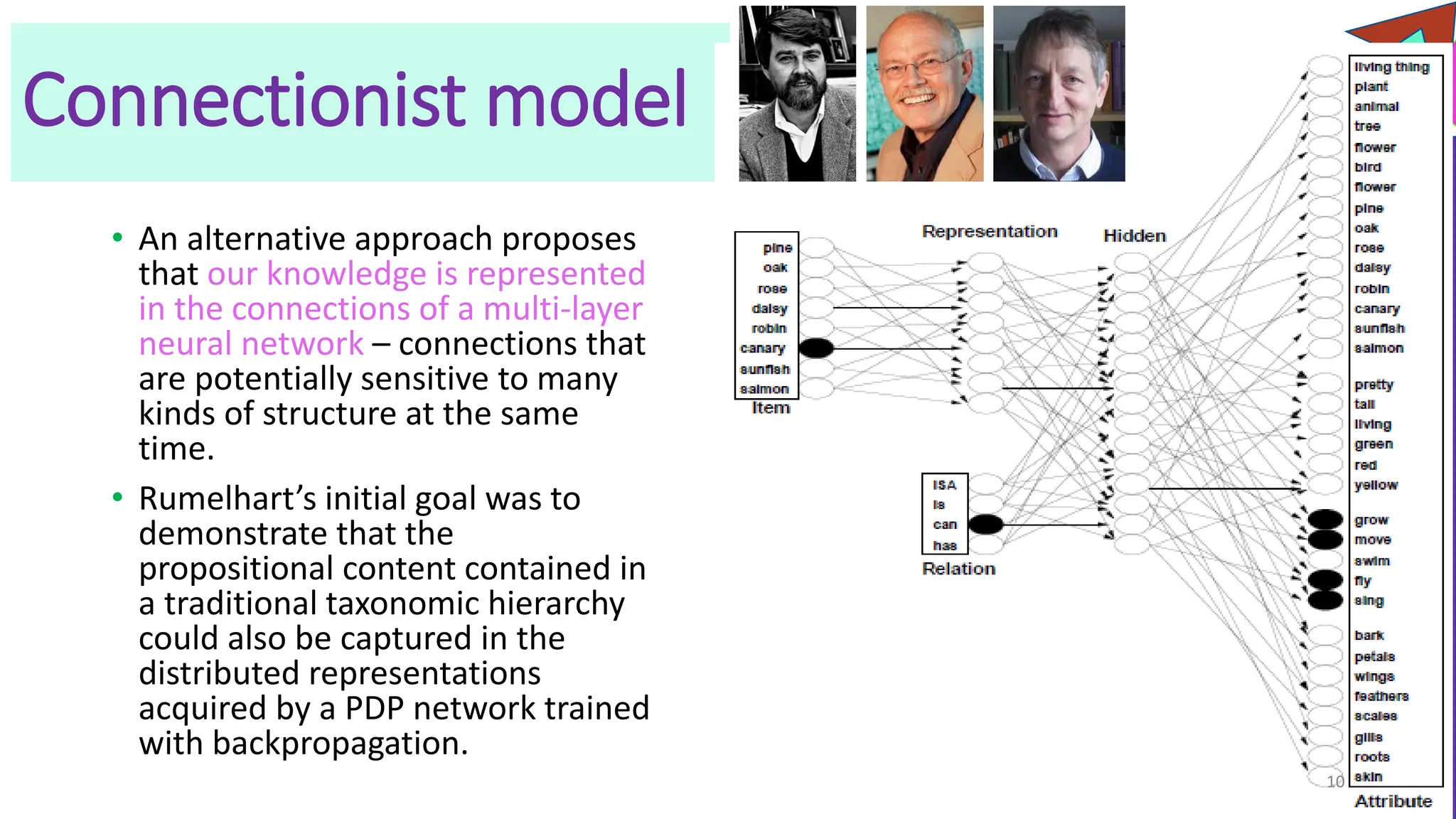
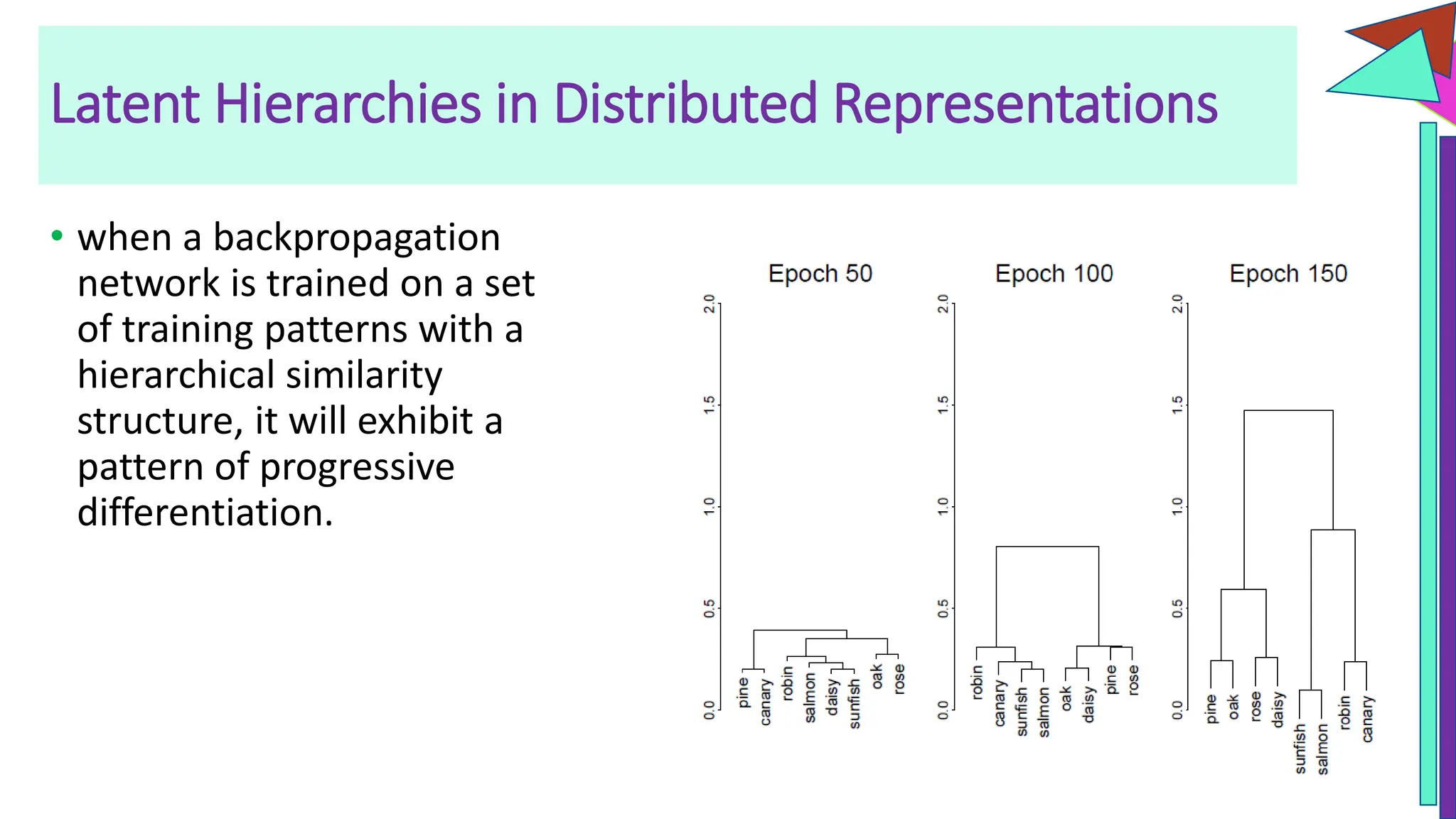
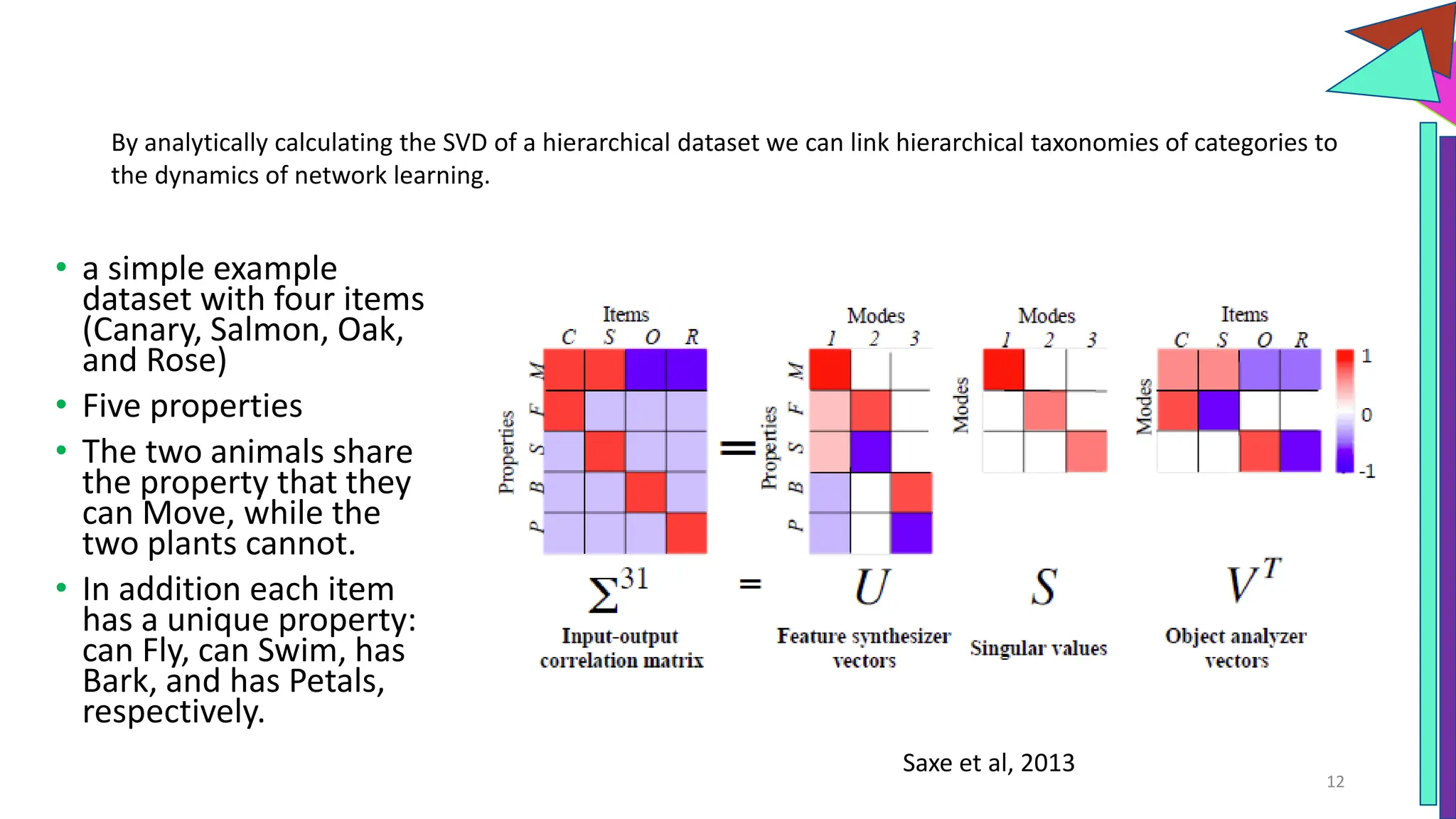
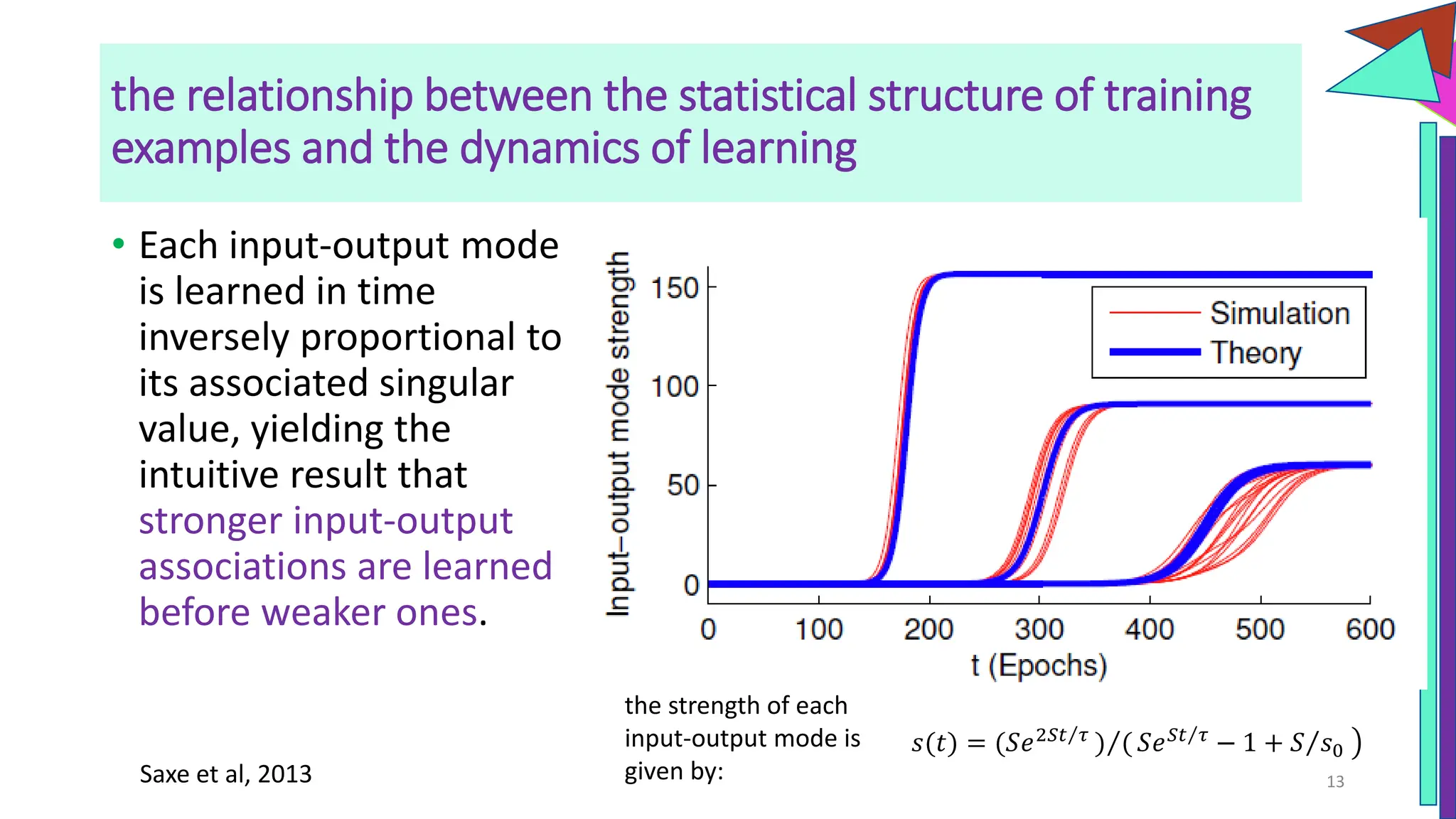
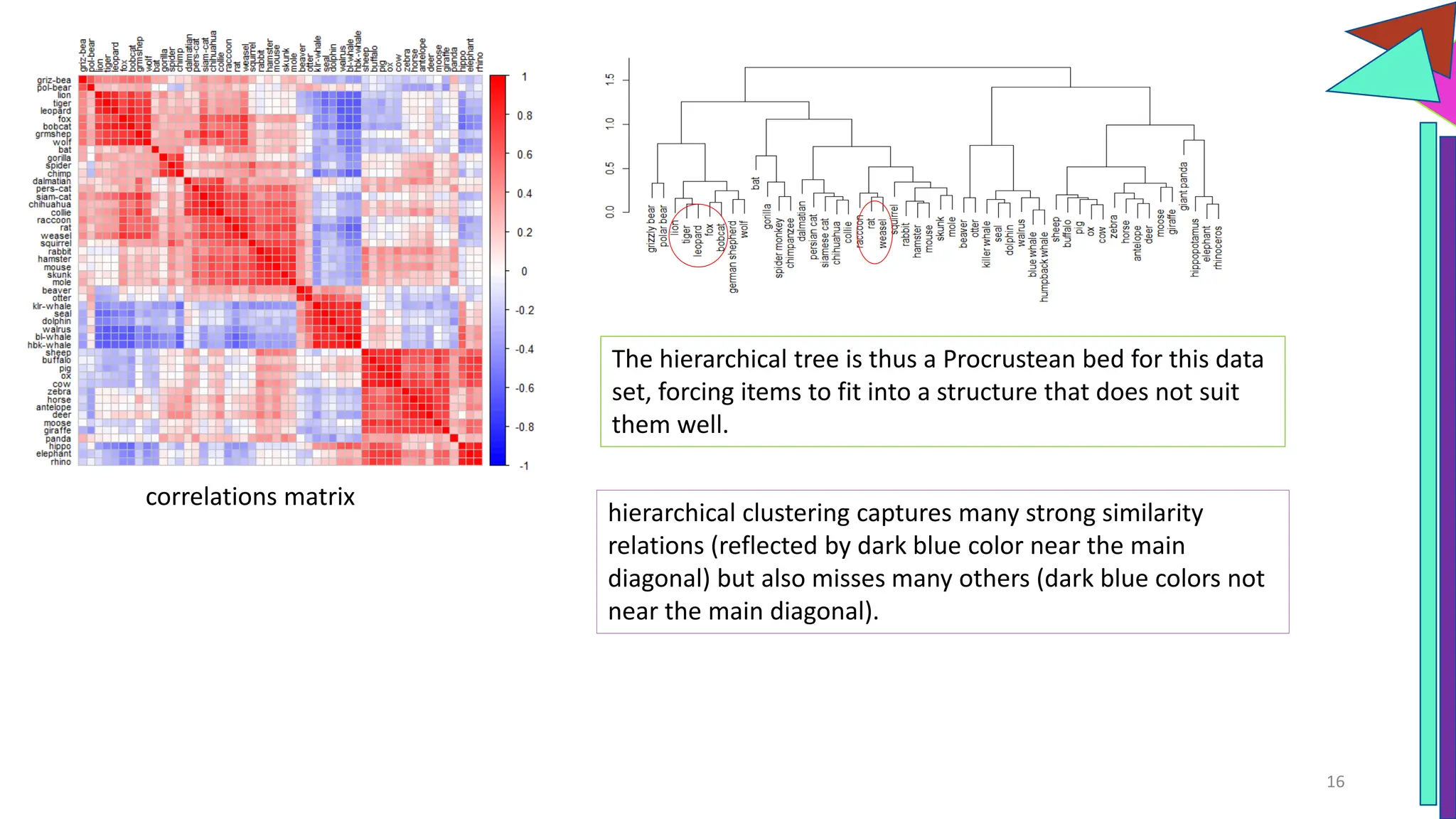
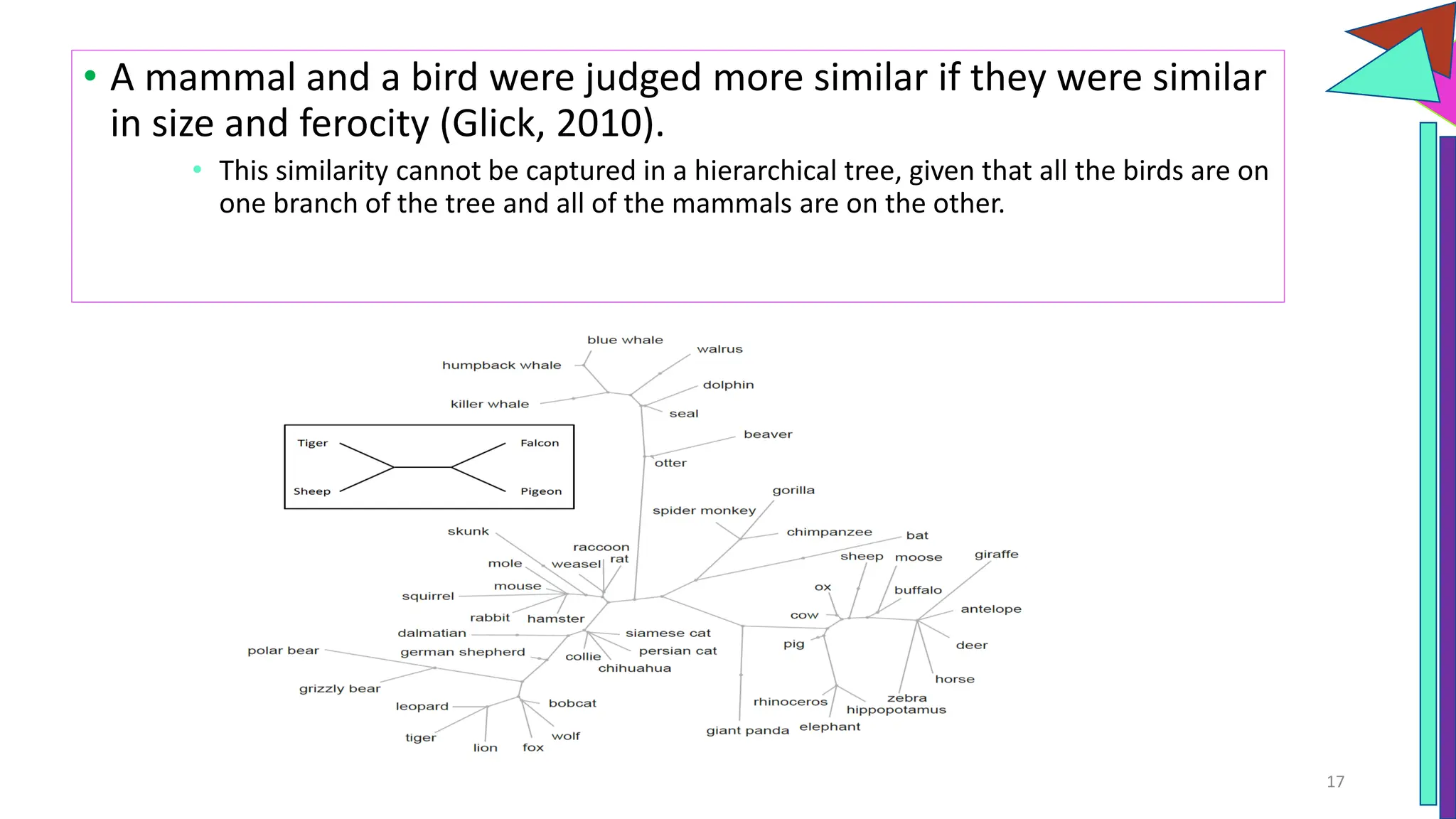
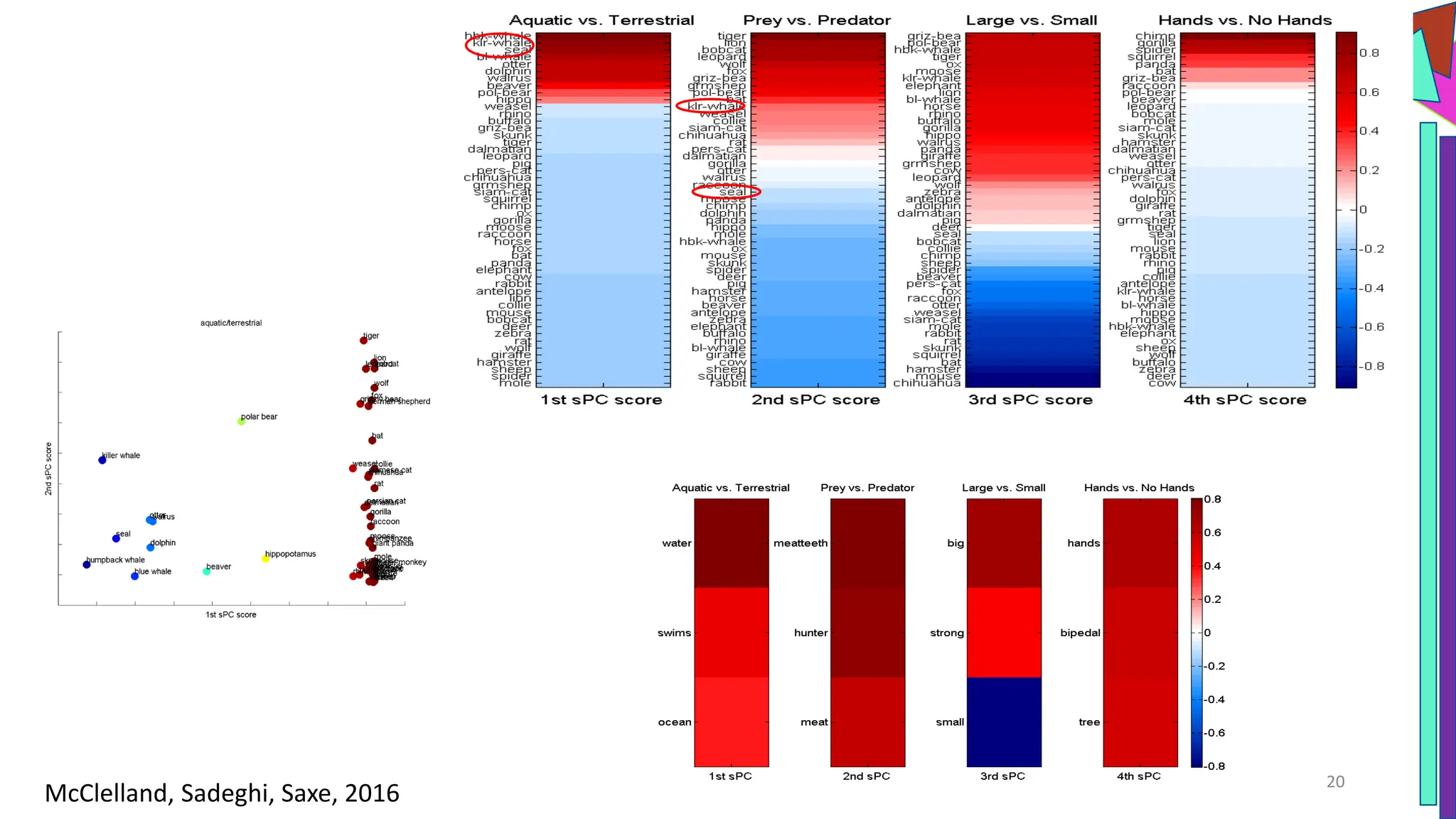
The document discusses a model of semantic category representation suggesting that semantic knowledge arises from interconnected processing units in a neural network. It highlights the limitations of traditional hierarchical structures in reflecting human categorization and proposes alternative connectionist models that capture a quasi-regular structure of knowledge. Additionally, it emphasizes the importance of using datasets that characterize human knowledge to enhance understanding of semantic representations.

1. Cross-cutting structure for
Semantic Category
Representation
Zahra Sadeghi

2. We will suggest that performance in semantic tasks arises through
the propagation of graded signals in a system of simple but
massively interconnected processing units.
We will argue that the representations we use in performing these
tasks are distributed, comprising patterns of activation across units
in a neural network; and that these patterns are governed by
weighted connections among the units.
We will further suggest that semantic knowledge is acquired
through the gradual adjustment of the strengths of these
connections, in the course of processing semantic information in
day to day experience.
2
• How do humans represent semantic knowledge of different types of
items and their properties?
Rogers & McClelland, 2003

3. Semantic Knowledge
• By semantic information, we refer to information that has not previously been
associated with the particular stimulus object itself and which is not available more-
or-less directly from the perceptual input provided by the object.
• semantic knowledge encompasses information about general category of
items from different modalities and their relationships.
• according to the research in cognitive sciences, people identify objects by utilizing
semantic knowledge which is stored in the part of their long-term memory called
semantic memory.

4. Semantic memory
• Semantic memory encompasses knowledge of objects, facts
meaning, concepts and words.
• associated with medial temporal lobe pathology
• episodic memory impairment is more severe in Alzheimer's disease
• semantic memory impairment is more severe in semantic dementia
4
Ranganath & Ritchey, 2012

5. Structure discovery
• Algorithms for finding structure in data are
important both as tools for scientific discovery
and as models of human learning.
• In both science and cognitive development, the
problem of structure discovery can be
addressed on at least two levels.
• At the first level, the form of the data is assumed
known and the task is to choose the instance of that
form that best explains the data.
• Biologists, for instance, have long agreed that tree
structures are useful for organizing living kinds but still
debate which tree is best.
• At the second, deeper level, the problem is to
discover the structural form of a domain:
• to discover, for example, that living kinds are tree
structured,
• or that the chemical elements have a periodic structure
5
Kemp and Tenenbaum, 2009

6. Categorization
• Semantic task performance is usually thought to depend upon a
mediating process of categorization.
• Under such approaches, there exists a representation in memory
(perhaps a node in a semantic network) corresponding to each of
many concepts or categories; and information about these concepts
is either stored in the representation itself, or is otherwise only
accessible from it.
• Hierarchical structure: The frequently invoked construct in categorization for
explaining empirical data
• class inclusion constraints can be described by a taxonomic hierarchy

7. taxonomic hierarchy
• Quillian, pointed out that the
taxonomic hierarchy can provide
an efficient mechanism for
storing and retrieving semantic
information.
• Economy of use (activation of the concept
cat spreads to the related concept animal,
and properties stored there are attributed
to the object.)
• Property Inheritance
• Generalization
• Semantic deficit
• Cognitive development
E. Rosch M. R. Quillian E. Warrington

8. Limitation of hierarchical representation
• Experimental studies found that a hierarchy both failed to fully
reflect the similarity structure in the data set and also missed
aspects of human similarity and property attribution judgments.
• Structured probabilistic models tend to rely on explicit, discrete
graphical structures.
• such models throw away important data, treating it as noise because it
does not fit the structure.
9

9. Connectionist model
• An alternative approach proposes
that our knowledge is represented
in the connections of a multi-layer
neural network – connections that
are potentially sensitive to many
kinds of structure at the same
time.
• Rumelhart’s initial goal was to
demonstrate that the
propositional content contained in
a traditional taxonomic hierarchy
could also be captured in the
distributed representations
acquired by a PDP network trained
with backpropagation.
10

10. Latent Hierarchies in Distributed Representations
• when a backpropagation
network is trained on a set
of training patterns with a
hierarchical similarity
structure, it will exhibit a
pattern of progressive
differentiation.

11. • a simple example
dataset with four items
(Canary, Salmon, Oak,
and Rose)
• Five properties
• The two animals share
the property that they
can Move, while the
two plants cannot.
• In addition each item
has a unique property:
can Fly, can Swim, has
Bark, and has Petals,
respectively.
12
By analytically calculating the SVD of a hierarchical dataset we can link hierarchical taxonomies of categories to
the dynamics of network learning.
Saxe et al, 2013

12. the relationship between the statistical structure of training
examples and the dynamics of learning
• Each input-output mode
is learned in time
inversely proportional to
its associated singular
value, yielding the
intuitive result that
stronger input-output
associations are learned
before weaker ones.
the strength of each
input-output mode is
given by:
൯
𝑠(𝑡) = (𝑆𝑒 Τ
2𝑆𝑡 𝜏 Τ
) ( 𝑆𝑒 Τ
𝑆𝑡 𝜏
− 1 + Τ
𝑆 𝑠0
13
Saxe et al, 2013

13. • Our effort is to bring broader awareness to the limitations of a
hierarchical structure of data.
• Our approach to overcoming these limitations reflects our interest in
exploring ways to characterize structure that may be quasi-regular,
and thus not fully consistent with any specific structure type
• Neural networks of the kinds we have often used in models are capable of
capturing quasi-regular structure, thereby reproducing patterns of human
behavior in several quasi-regular domains, such as single word reading and
knowledge of objects and their properties.
• A limitation of the approach, however, is that knowledge in this form is stored in
connection weights, and is often hard to interpret
14
Towards a flexible structure

14. Dataset
• Here we focus on human knowledge in the domain of animals
• The data set, here called the 50 mammal set
• This dataset is a characterization of human knowledge, so that the
effort to discover which sort of representation best characterizes this
data set is an exercise in modeling human knowledge, not simply an
exercise in modeling facts about objects in the world.
• The data set was obtained by asking participants to rate the
applicability of each of 85 different predicate terms to each of 50
different mammals
15

15. correlations matrix
hierarchical clustering captures many strong similarity
relations (reflected by dark blue color near the main
diagonal) but also misses many others (dark blue colors not
near the main diagonal).
16
The hierarchical tree is thus a Procrustean bed for this data
set, forcing items to fit into a structure that does not suit
them well.

16. 17
• A mammal and a bird were judged more similar if they were similar
in size and ferocity (Glick, 2010).
• This similarity cannot be captured in a hierarchical tree, given that all the birds are on
one branch of the tree and all of the mammals are on the other.

17. 18
T
X UDV

Z = UD Principal components(PCs)
V Loadings of PCs
1. principal components sequentially capture the maximum
variability among the columns of X, thus guaranteeing minimal
information loss;
2. principal components are uncorrelated, so we can talk about
one principal component without referring to others.
However, PCA also has an obvious drawback, that is, each PC is a
linear combination of all p variables and the loadings are typically
nonzero.
This makes it often difficult to interpret the derived PCs.
X be a n by p matrix
• We feel it is desirable not only to achieve the dimensionality
reduction but also to reduce the number of explicitly used
variables.
• An ad hocway to achieve this is to artificially set the
loadings with absolute values smaller than a threshold to zero.
• This informal thresholding approach is frequently used in
practice, but can be potentially misleading in various
respects (Cadima and Jolliffe 1995).

18. THE LASSO AND THE ELASTIC NET
2 2
1
K
k
k
B 

 
2 2
,
arg min ,
T T
A B
X XAB B A A I

  
• A particular disadvantage of ordinary PCA is that the principal components are
usually linear combinations of all input variables.
• Sparse PCA overcomes this disadvantage by finding linear combinations that
contain just a few input variables.

19. 20
McClelland, Sadeghi, Saxe, 2016

20. Highlights
• Our results highlight the fact that a tree structure may often provide
an imperfect guide to the full structure present in a data set.
• In particular, a hierarchical tree is bound to hide semantic distinctions
that cut across levels of the tree.
• the present work has focused on finding a way of projecting the
knowledge that is captured in a deep neural network onto dimensions
that may be more easily described.
21

21. A Critique of Pure Hierarchy: Uncovering Cross-
Cutting Structure in a Natural Dataset
JL McClelland, Z Sadeghi, AM Saxe
Neurocomputational Models of Cognitive Development and Processing:
Proceedings of the 14th Neural Computation and Psychology Workshop
https://www.worldscientific.com/doi/abs/10.1142/9789814699341_0004