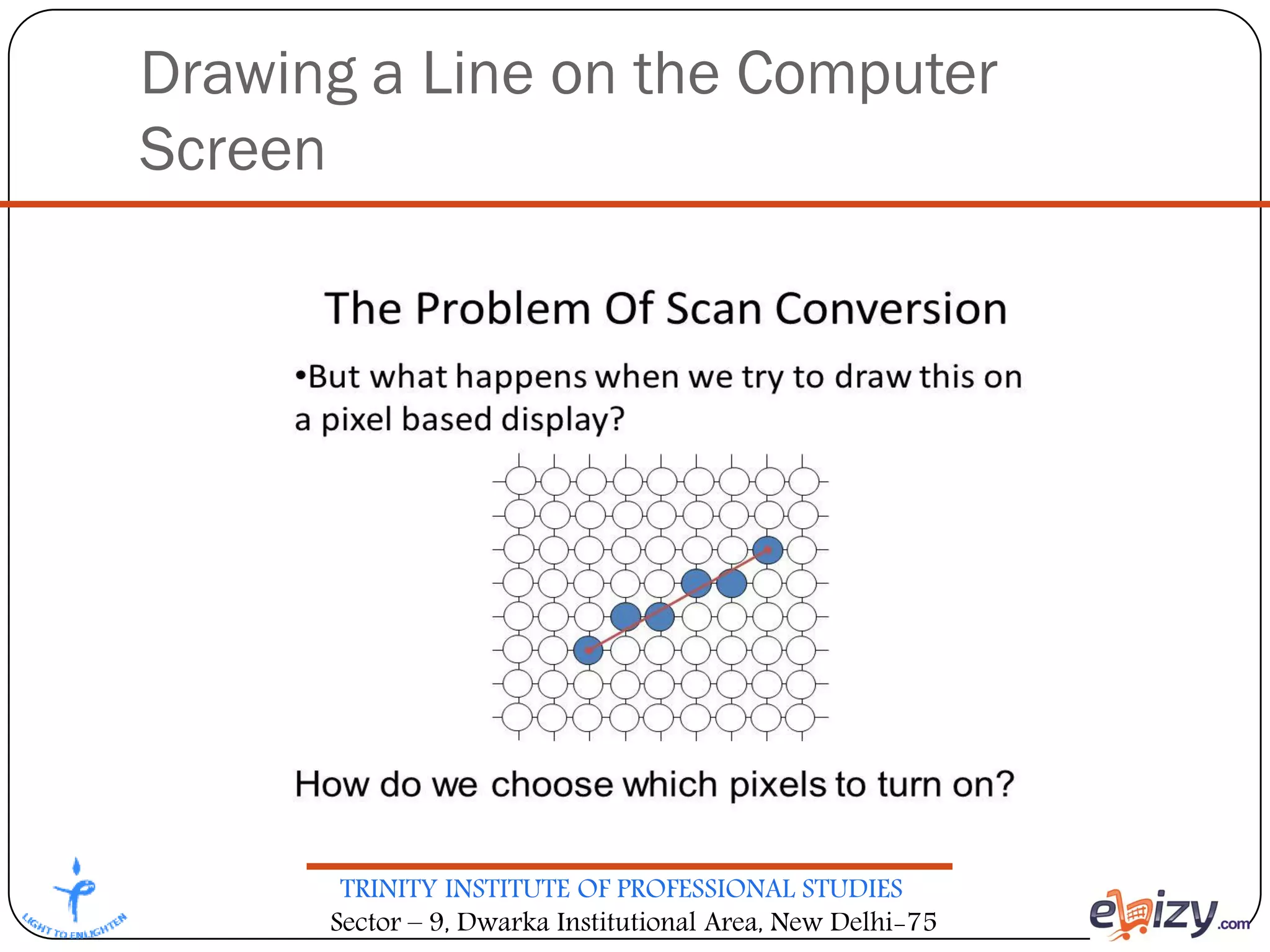
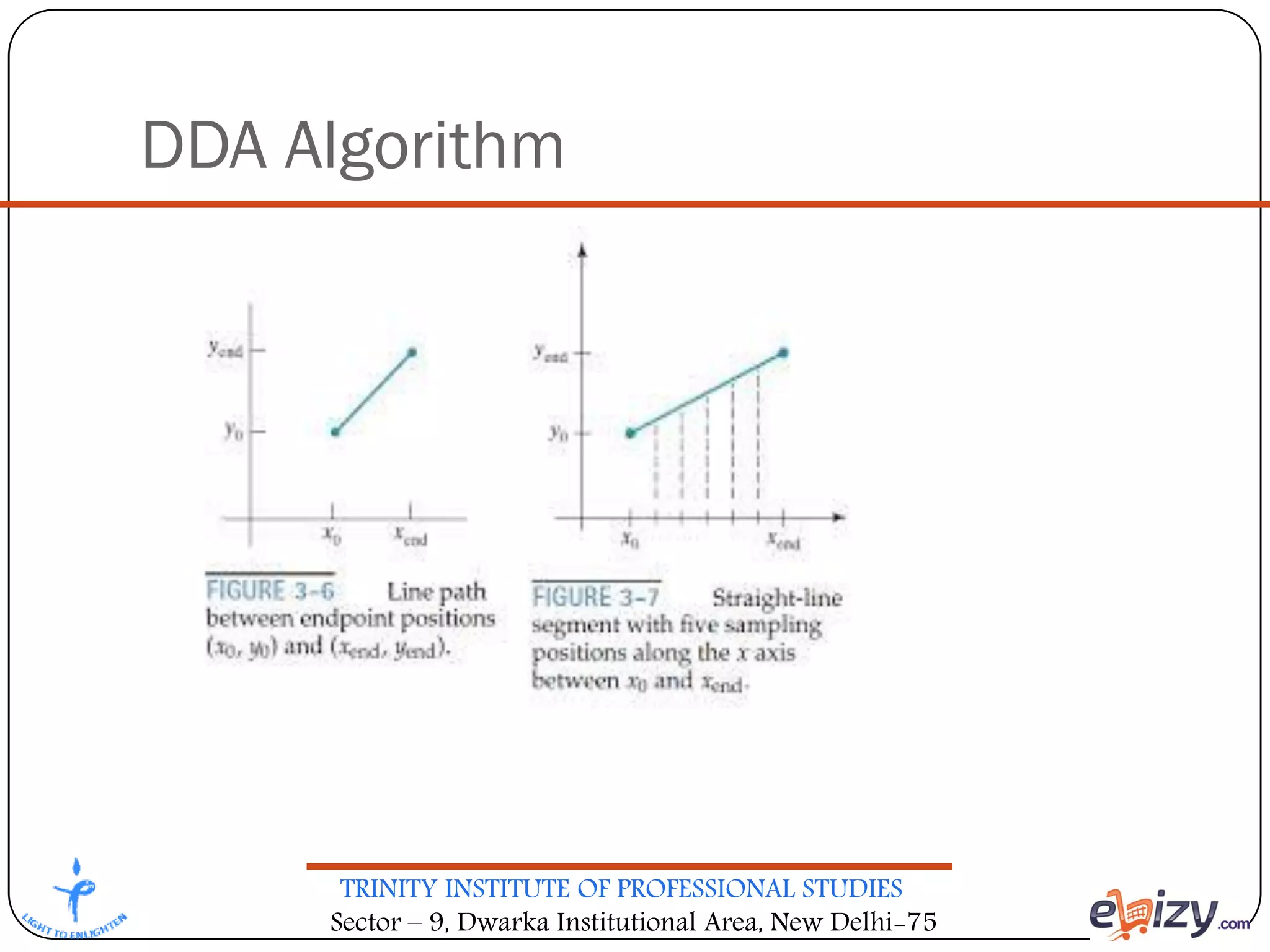
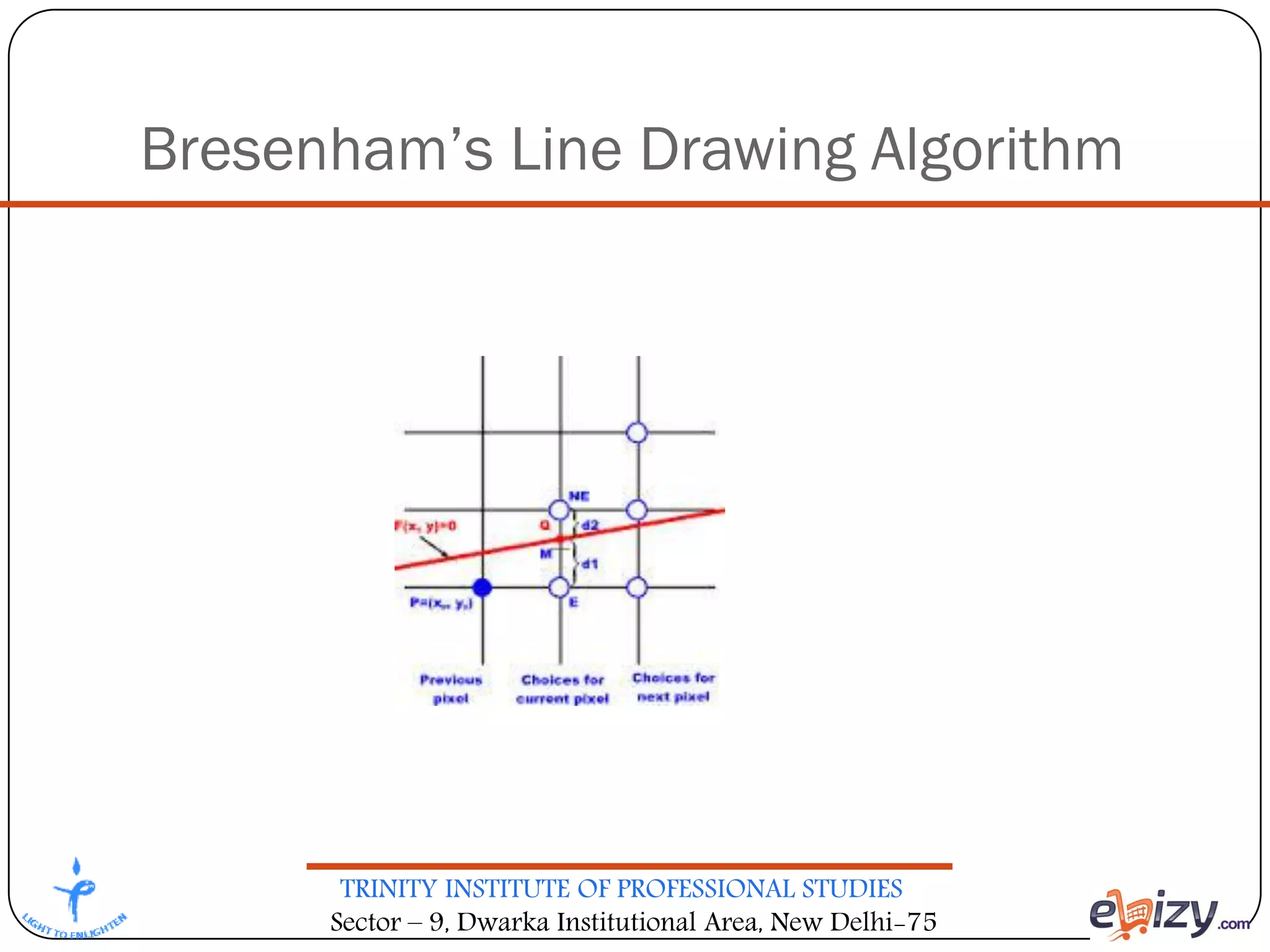
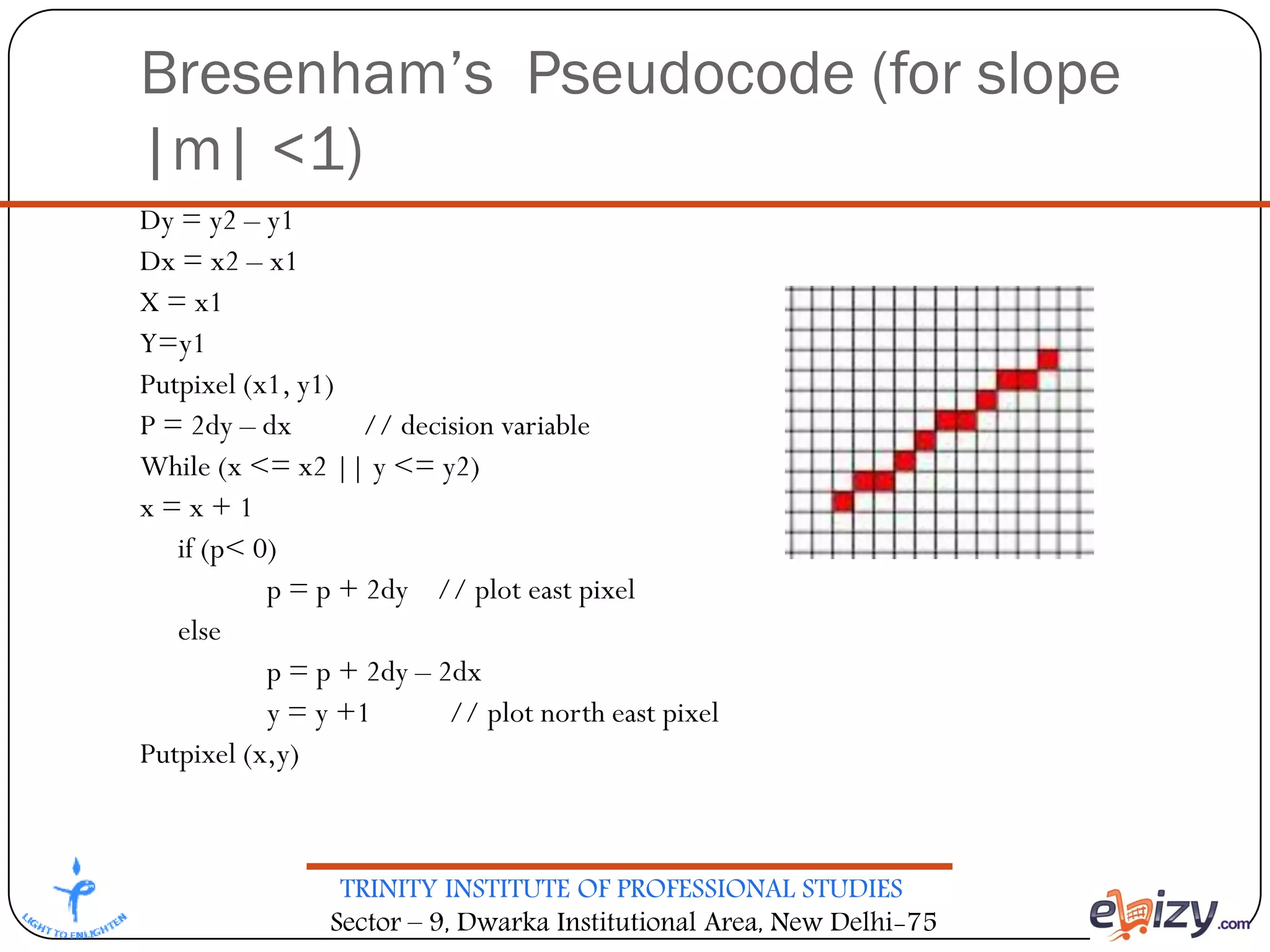
The document outlines the curriculum for a BCA course on computer graphics at Trinity Institute of Professional Studies, detailing topics like scan conversion algorithms, 2D and 3D transformations, and various graphics representations. It includes a breakdown of the marking scheme, textbooks, and references, as well as instructional strategies for answering exam questions. The course emphasizes raster graphics and algorithms such as DDA and Bresenham's for line drawing.

1. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Affiliated to Institution of G.G.S.IP.U, Delhi
Scan Conversion
Himja Sethi
Assistant Professor
Course BCA
Paper Title Computer Graphics
Paper Code BCA 303
Paper ID 20303

2. Quick Overview of Syllabus
Unit I Unit II
 Applications of computer graphics
 Video display technologies
 Raster scan systems
 Graphics related input and output
devices
 Computer graphics related
software
 Scan conversion of line, circle and
ellipse using algorithms, DDA,
Bresenham, mid-point
 2D and 3D geometric transformations
(Translation, Rotation, Scaling,
Shearing, Reflection)
 Composite transformations and its
practical application through numericals
 Homogenous coordinates
 Antialiasing
 Window to viewpoint transformation
 Clipping algorithms (Cohen Sutherland,
Cyrus Beck, Midpoint Subdivision)

3. Quick Overview of Syllabus
Unit III Unit IV
 Parametric Cubic Curve
Representation
 Solid modelling
 Types of surface representations
 Wireframe
 Sweep
 Spatial Partitioning
 Boundary
 Octree
 Comparison amongst all of the
above
 User interfaces for solid
modelling
 3D objects and related concepts
 Projection
 Types of projection
 Parallel
 Orthographic
 Oblique
 Perspective
 3D clipping
 Cohen Sutherland
 Hidden surface removal
 Depth buffer / z-buffer algo
 Depth sorting algo

4. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Course Books
TEXT BOOKS:
 Foley,Van Dam, Feiner, Hughes, Computer Graphics Principles &
Practice, 2000, Pearson
 Chennakesava R.Alavla “Computer Graphics”, PHI Learning Pvt.
Limited
REFERENCES BOOKS:
 D. Hearn & Baker: Computer Graphics with OpenGL, Pearson
Education,Third Edition,2009.
 Foley, J.D. &Van Dam,A: Fundamentals of Interactive Computer
Graphics.
 Rogers &Adams,“Mathematical Elements for Computer
Graphics”, McGraw Hill, 1989.

5. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
How to Attempt a Question?
 Introduction
 Definition
 Point-wise description
 Examples, if any
 Conclusion

6. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Marking Scheme
 Internal
25 marks (10 marks I minor +10 marks II
minor + 5 marks internal assessment)
 External
75 marks (Major semester exam)

7. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Affiliated to Institution of G.G.S.IP.U, Delhi
Lets begin with…

8. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Applications of Computer Graphics
around us

9. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Yes, that’s right…
 Gaming
 Animation Movies
 3D object simulation for engineering, manufacturing etc
 Virtual Reality Simulation for pilot training, surgical practice
etc
 ComputerAided Design
 And many more…

10. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Computer Graphics
Types Of Computer Graphics
 Raster Graphics
Primitive drawing using coordinate positions for each
pixel
 Vector graphics
Primitive drawing using pre-defined mathematical
functions
Main focus of the course is Raster Graphics

11. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Raster Graphics
Definition : Raster graphics, also called bitmap
graphics, are digital images that are composed of
tiny rectangular pixels that are arranged in a grid
(or raster) of x and y coordinates in such a way
that it forms an image.

12. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Drawing a Line on the Computer
Screen

13. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Solution
 Three approaches for solution are :
 Equation of line , y = mx + c
 DDA algorithm, step increments in x / y
 Bresenham’ s algorithm, using a decision variable to
find the right pixel

14. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Equation of line
y= mx + c, where m = (y2 – y1) / x2 – x1)
Through an example we can see that ,it is
 Quite expensive
 Involves floating point multiplication for each and
every pixel
 Requires large amount of memory space and
processing time.

15. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Scan Conversion Algorithms
Raster scan or scan conversion of a line involves finding the
right pixels to plot on the computer screen. Following
algorithms are used to achieve the solution
 Digital DifferentialAnalyzer Algorithm
 Bresenham’sAlgorithm

16. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
DDA Algorithm

17. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
DDA Pseudocode
m = (y2-y1)/(x2-x1)
dx = x2 – x1
dy = y2 – y1
Putpixel (x1, y1)
X = x1
Y = y1
If (dx > dy)
steps = dx
Else
steps = dy
While(x <= x2 || y <= y2)
xinc = x + dx/steps
yinc = y + dy/steps
putpixel (x,y)

18. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Analysis of DDA Algorithm
 Advantages
 Simple to understand
 Easy to implement
 Disadvantages
 Expensive computation
 Floating point division and addition
(i.e. slope m can be in decimal )

19. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Analysis of DDA Algorithm
 Advantages
 Simple to understand
 Easy to implement
 Disadvantages
 Expensive computation
 Floating point division and addition
(i.e. slope m can be in decimal )

20. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Bresenham’s Line Drawing Algorithm

21. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Bresenham’s Pseudocode (for slope
|m| <1)
Dy = y2 – y1
Dx = x2 – x1
X = x1
Y=y1
Putpixel (x1, y1)
P = 2dy – dx // decision variable
While (x <= x2 || y <= y2)
x = x + 1
if (p< 0)
p = p + 2dy // plot east pixel
else
p = p + 2dy – 2dx
y = y +1 // plot north east pixel
Putpixel (x,y)

22. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Analysis of Bresenham’s Algo
 Advantages
 Only integer computation
 Disadvantages
 Lacks precision
 Aliasing / staircasing

23. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Antialiasing
 Removing the jaggies or staircase effect caused due to under-
sampling of information due to rounding off coordinate
values to pixel positions, is called anti-aliasing.
 This can be achieved thorough super-sampling, area
sampling, higher resolution display systems and special
hardware configurations.

24. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Clipping
 Identifying portions of a picture that are inside or outside a
specified region of space is referred as clipping.
 Algorithms used for line clipping are:
 Cohen-Sutherland clipping
 Cyrus Beck clipping
 Midpoint subdivision algorithm

25. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
2D Transformations
 Translation – change of co-ordinate position along a straight
line
 Rotation – repositioning along a circular path w.r.t. origin or
a specific point
 Scaling – change in size of an object
 Shearing – distorts shape of an object along an axis
 Reflection – mirror image of an object

26. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
2D Transformations
 Translation – change of co-ordinate position along a straight
line
 Rotation – repositioning along a circular path w.r.t. origin or
a specific point
 Scaling – change in size of an object
 Shearing – distorts shape of an object along an axis
 Reflection – mirror image of an object

27. TRINITY INSTITUTE OF PROFESSIONAL STUDIES
Sector – 9, Dwarka Institutional Area, New Delhi-75
Thank You