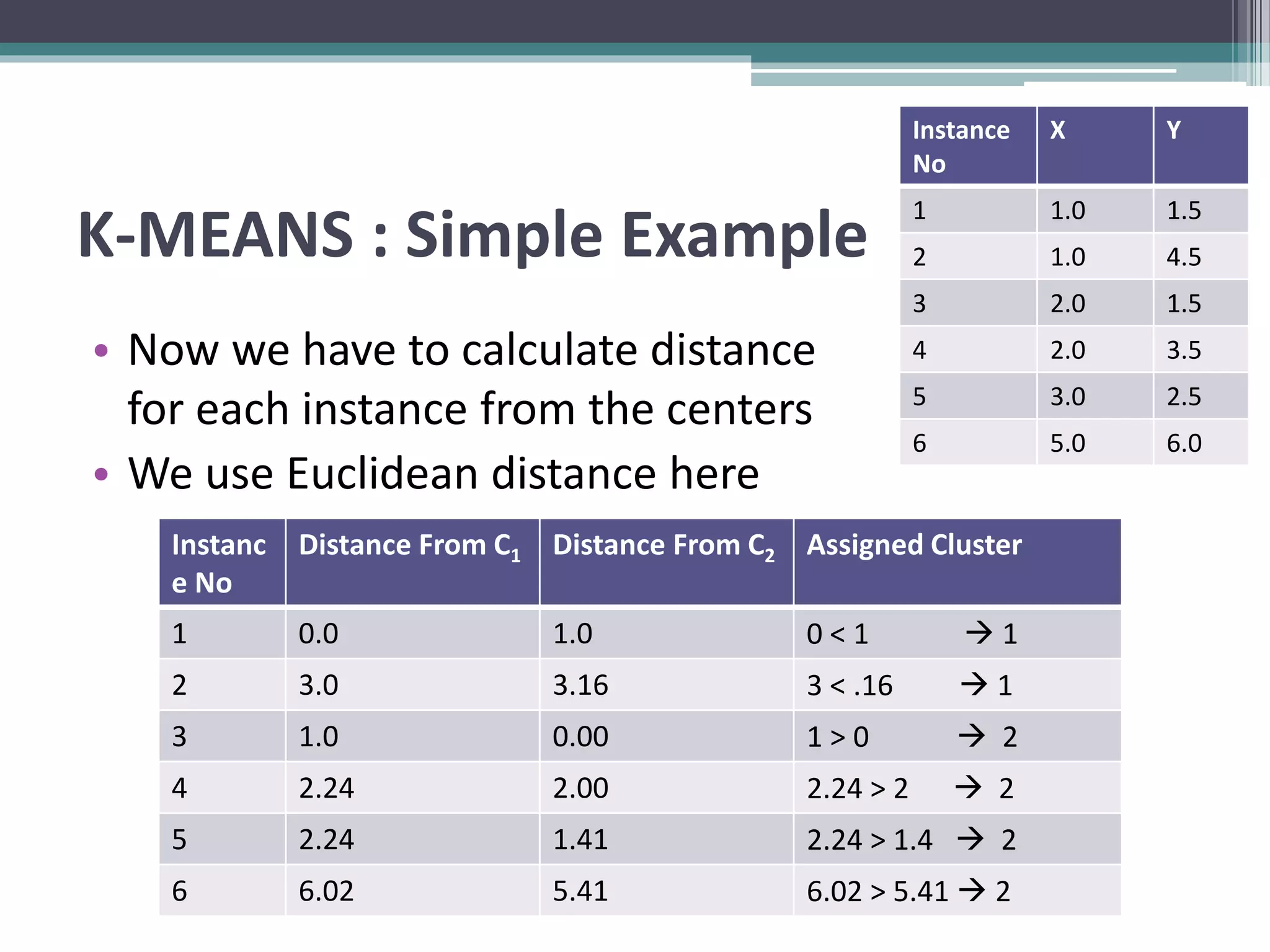
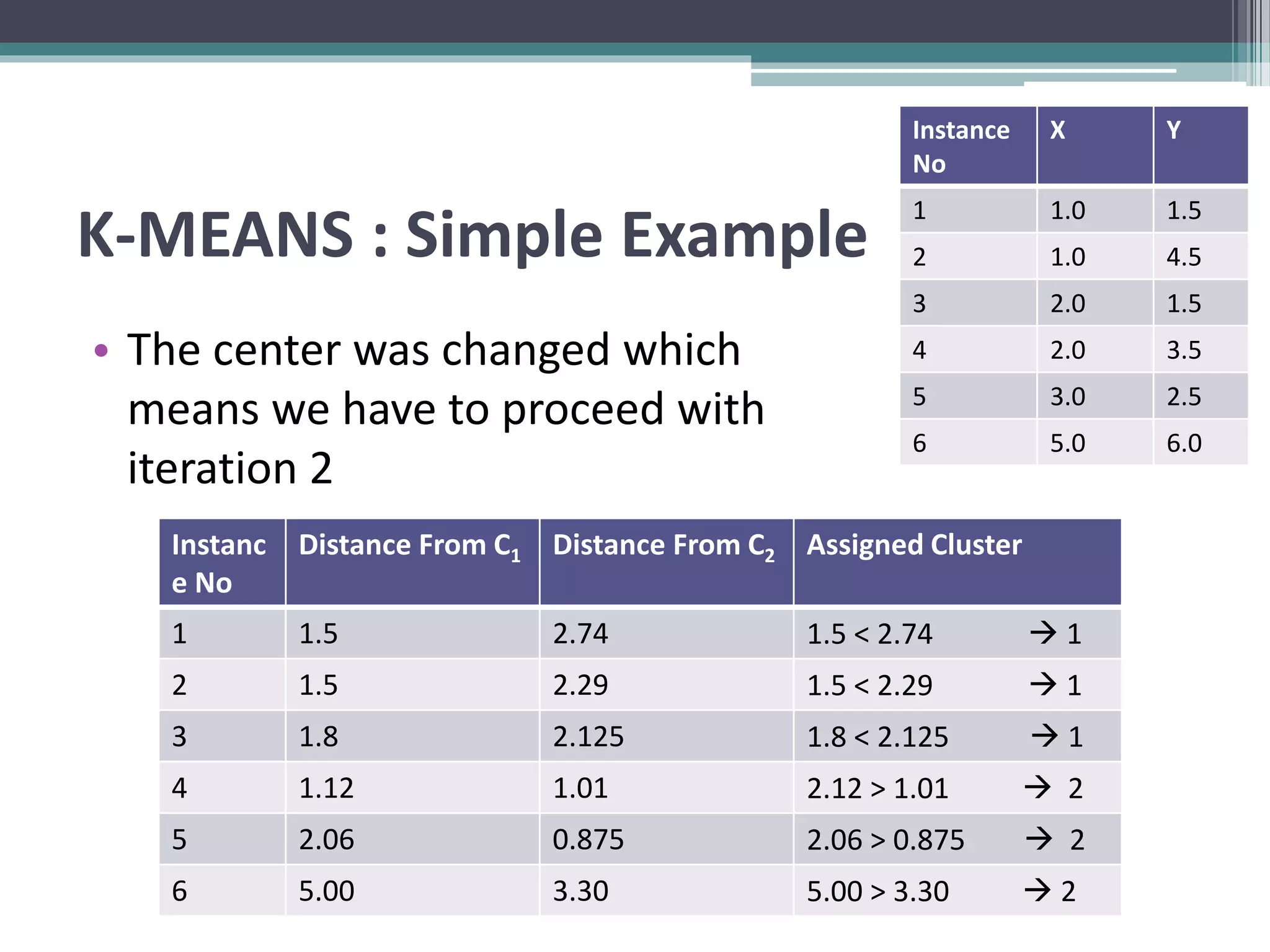
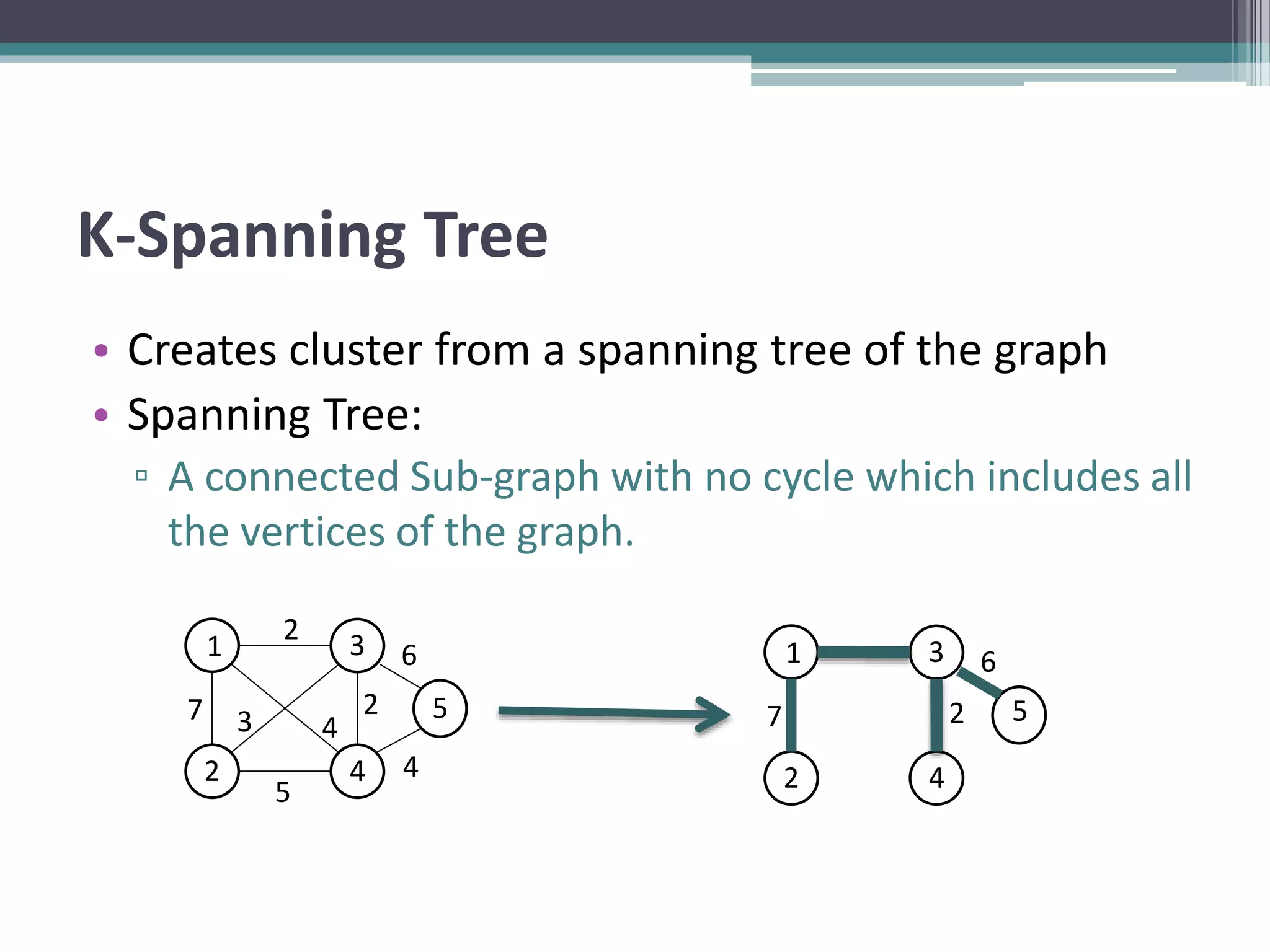
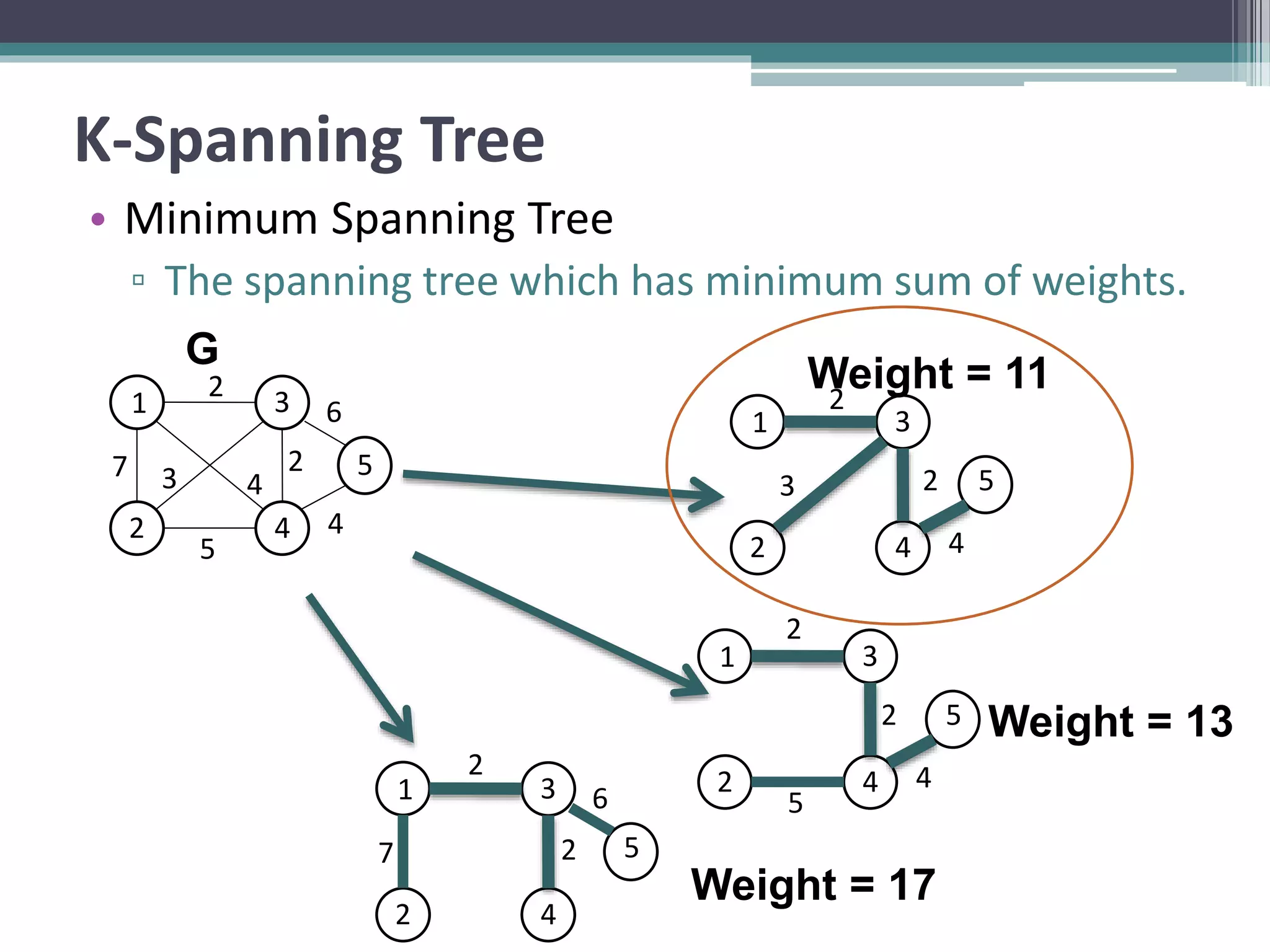
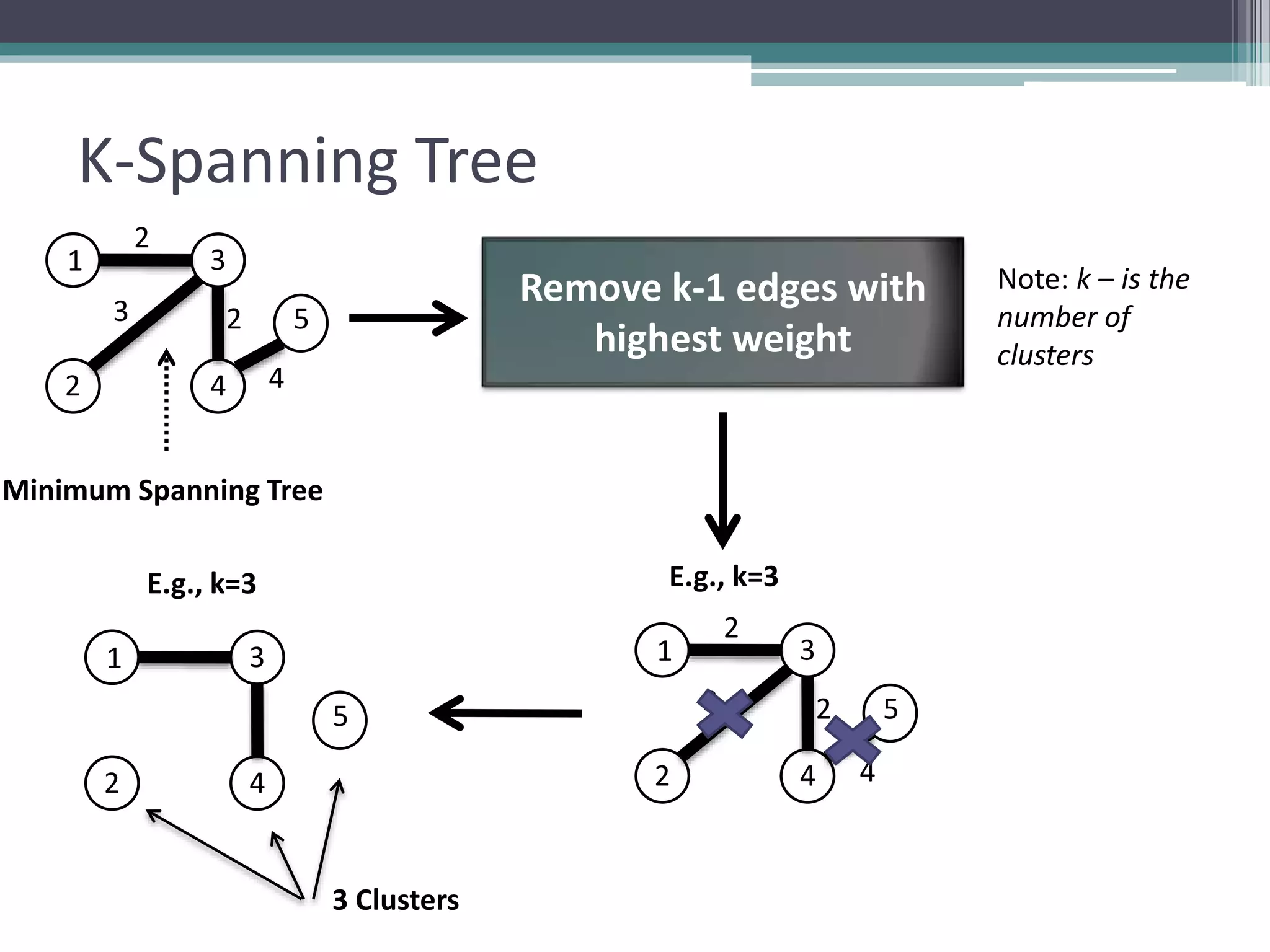
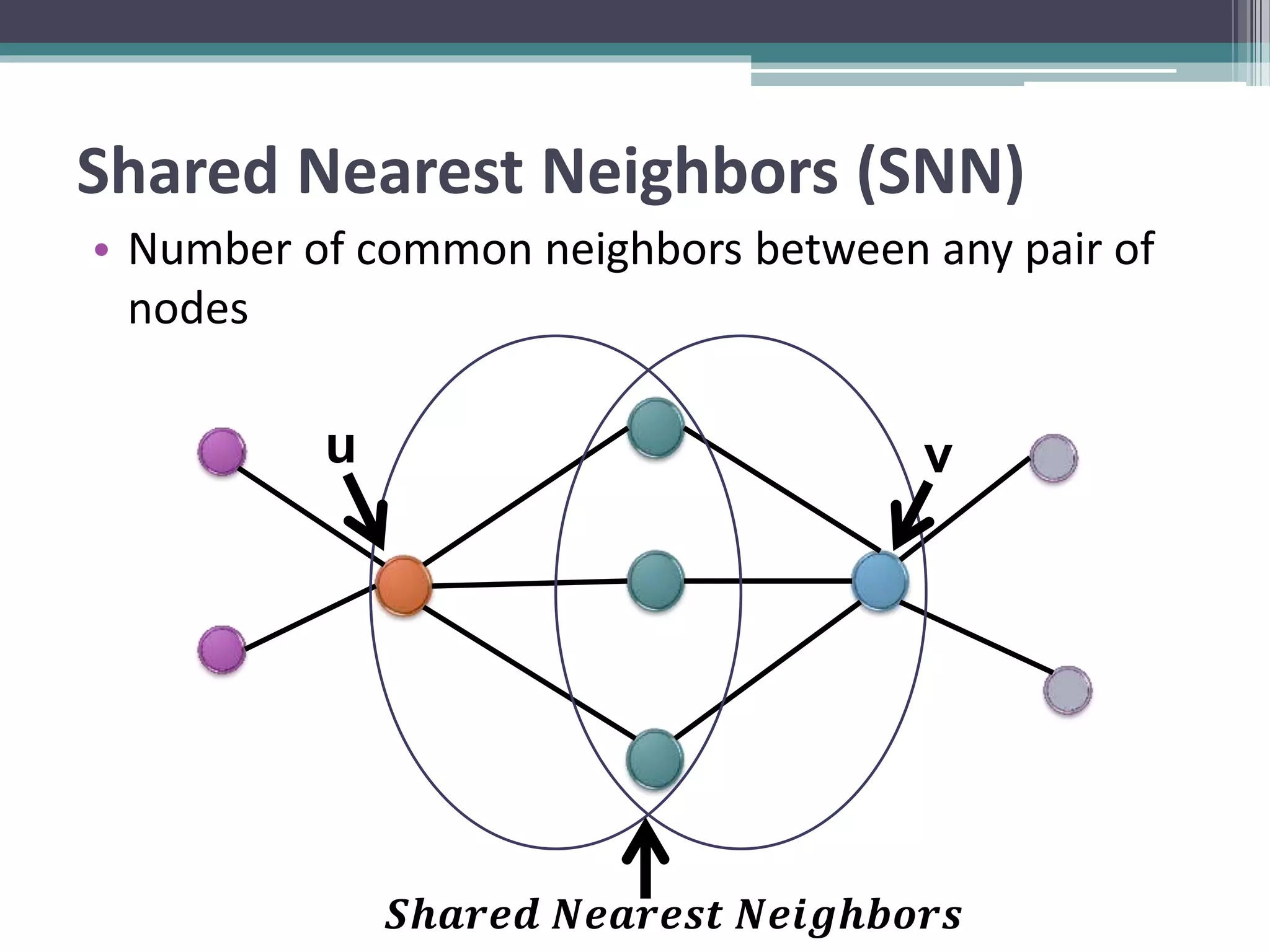
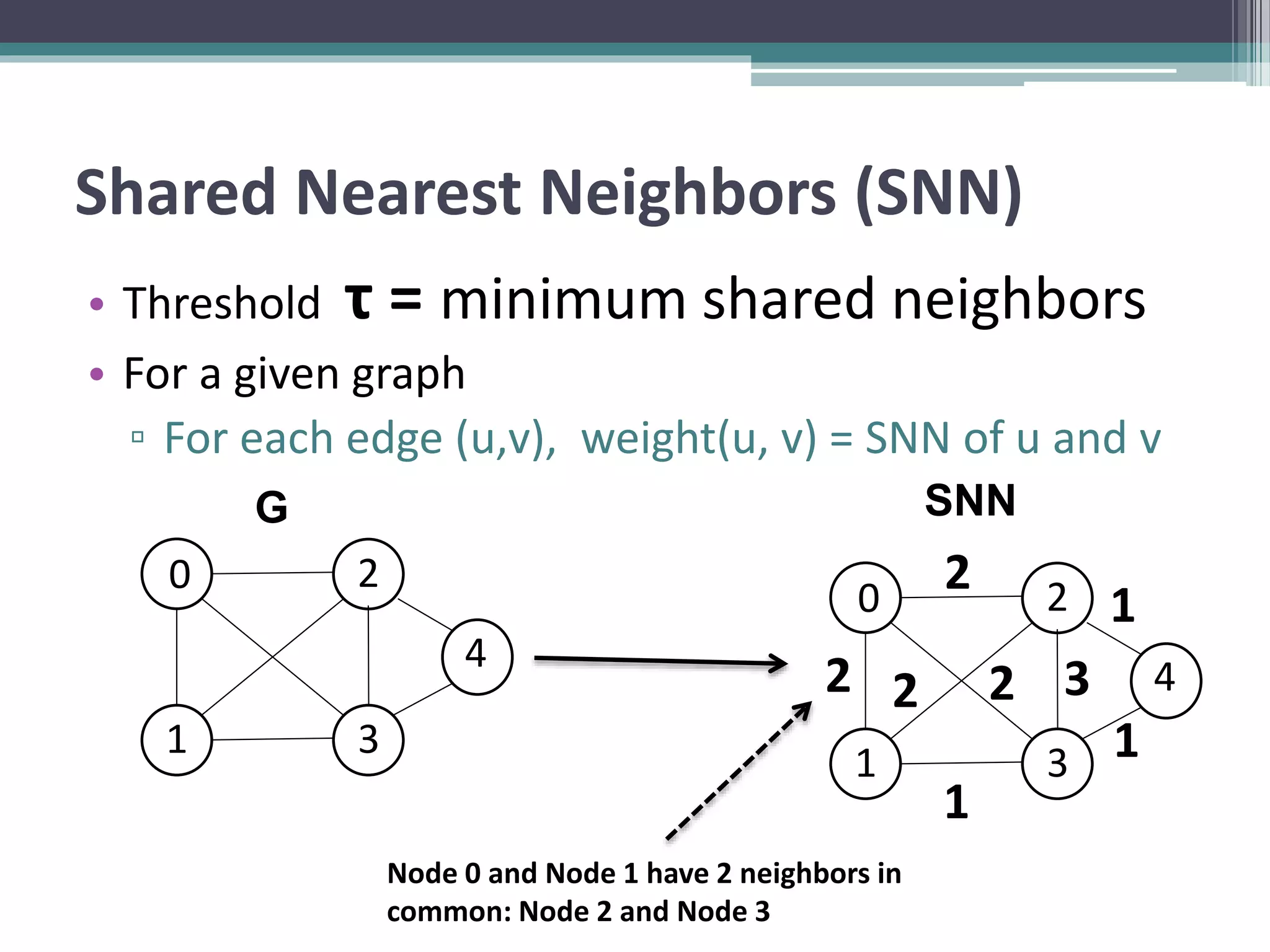
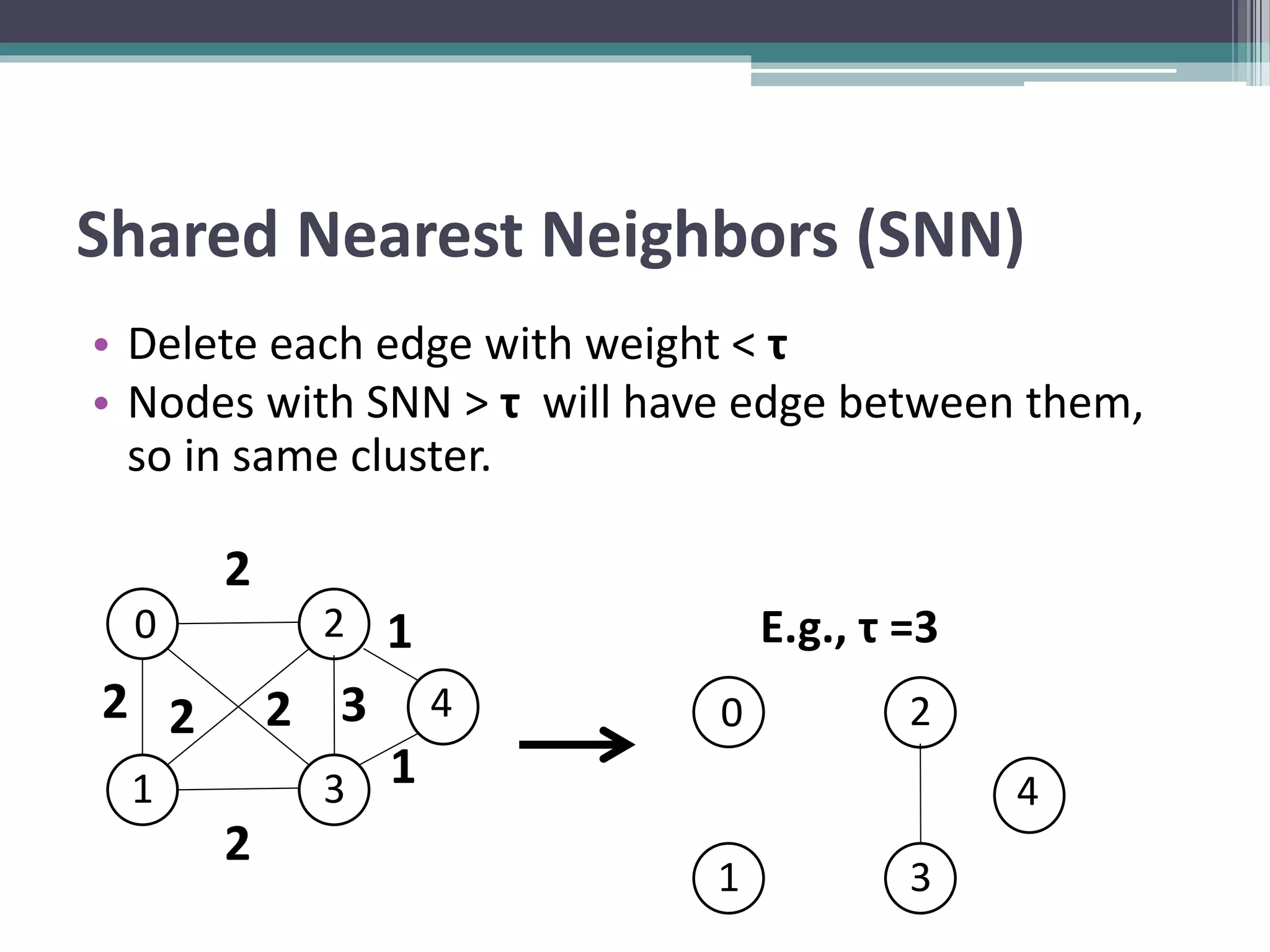
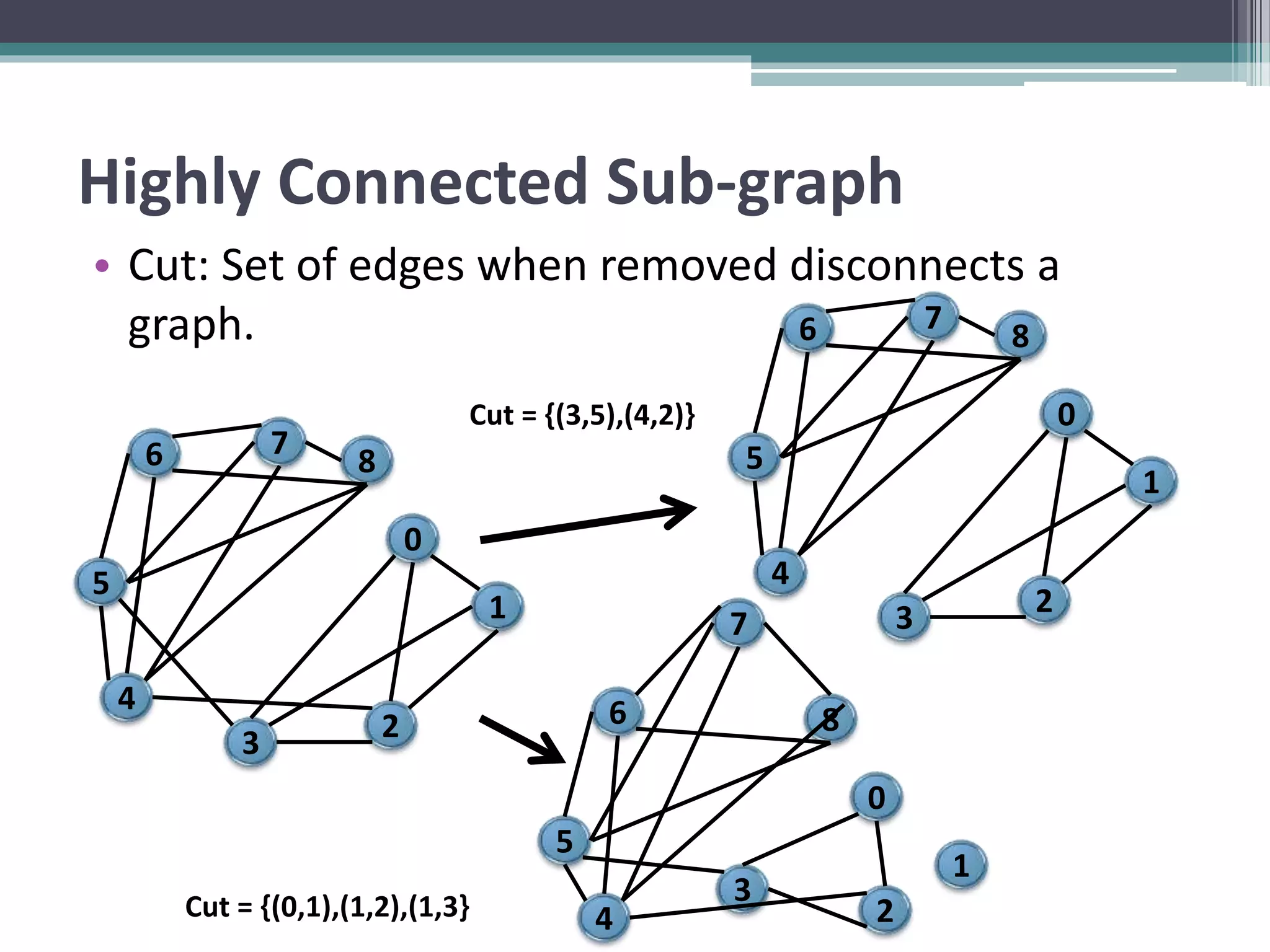
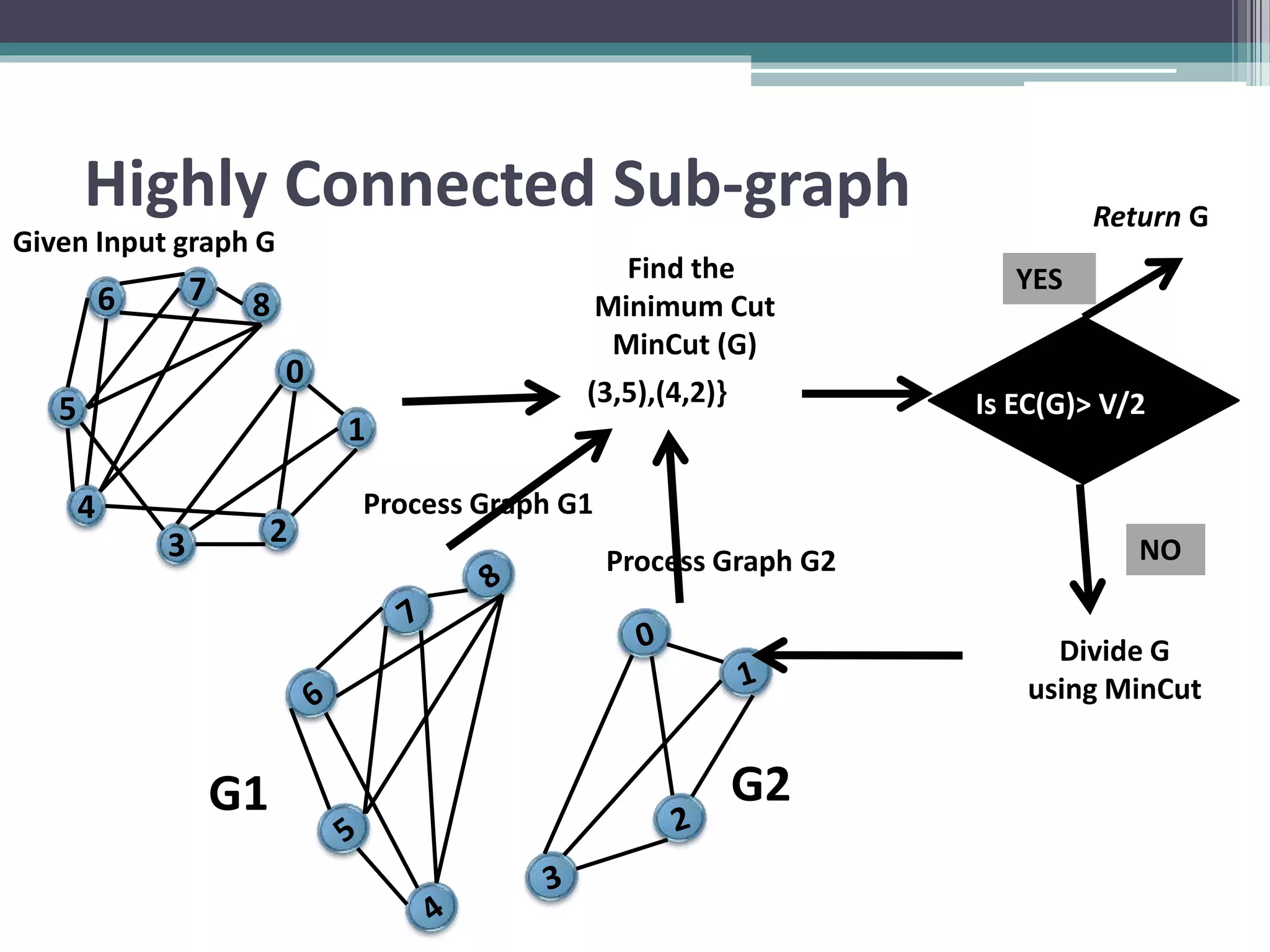
Clustering is an unsupervised machine learning technique used to group similar data points together. There are several common clustering algorithms such as K-means, hierarchical clustering, and density-based clustering. K-means clustering works by assigning data points to clusters based on their distance from initial cluster centers, then recalculating the cluster centers until cluster membership stabilizes. Graph clustering algorithms include approaches based on minimum spanning trees, shared nearest neighbors, and detecting highly connected subgraphs.

1. Data Mining Tools - Clustering
Presented By
Sayeed Mahmud

2. Data Mining
• The process of extracting meaningful knowledge
from raw data
▫ The knowledge which is not visible from raw data like
database tables.
• Useful in classifying, predicting, pattern identifying
• Example:
▫ Credit Card Theft Identification
 Data table for customers buying habits.
 Find a pattern for the buying habits.
 Irregular buying behavior – Alert Customer.

3. Common Tools Data Mining
• Decision Tree & Tables
• Association Rules
• Classification Rules
• Frequent Candidate Generation
• Clusters
• Outliers
• Linear Model
• Numeric Model

4. Cluster
• The act of grouping data based on some similarity
score
• Clustering - when no group is given
• Data with high similarity score belongs to same
cluster
• Common attributes are found for data in same
cluster
▫ Some common steps in processing
▫ Some common decisions to take

5. Clustering – Real life Example
• When collecting sea shells
▫ We don’t know how many types of shell we may find
▫ We look and judge which types of shells are similar
▫ We put different type of shells in separate bowls
▫ Similar type of shell goes to same bowl
▫ Finally we put the bowls on display for customers.

6. Clustering in Data Mining
• Clustering may apply to
▫ Numeric data
▫ Tabular data
▫ Graphs
• Several well known approaches
▫ Distance based
▫ Similarity score based
▫ Density based.
▫ Hierarchy Based.
▫ Partition Based

7. Algorithms
• Agglomerative
• K-Means
• NN (Nearest Neighbors)
• BIRCH
• DBSCAN
• OPTICS
• CURE
• CLIQUE
• PAM
• Other Tools :
▫ Neural Network
▫ Genetic Algorithm

8. Similarity Based Clustering : Simple
Example
Instance Income
Range
Magazine
Promotion
Watch
Promotion
Life Insurance
Promotion
Gender
I1 40 – 50K Yes No No Male
I2 25 – 35K Yes Yes Yes Female
I3 40 – 50K No No No Male
I4 25 – 35K Yes Yes Yes Male
I5 50 – 60K Yes No Yes Female
In this case Similarity Score : No of Matched Columns I1 and I3
4 matching Columns
Out of 5
Similarity Score = 4 / 5 = 0.80

9. Similarity Based Clustering : Simple
Example
I1 I2 I3 I4 I5
I1
I2
I3
I4
I5
I1 40 – 50K Y N N M
I2 25 – 35K Y Y Y F
I3 40 – 50K N N N M
I4 25 – 35K Y Y Y M
I5 50 – 60K Y N Y F
Lets say we consider similarity threshold 0.70
1.00
0.20
0.80
0.40
0.40
Cluster 1 – I1, I3
1.00
0.80
0.60
Cluster 2 – I2, I4
1.00
0.20
0.20
1.00
0.40 1.00
Cluster 3 – I5
0.00

10. Distance Based Clustering : K-MEANS
• K-Means:
▫ K cluster
▫ Means of each cluster doesn’t change then clustering
OK
• Initially K clusters are chosen with one member each
(called cluster center).
• Members or instances are chosen randomly or by
decision.
▫ Depending on this choosing – clustering may yield
different result.

11. K-MEANS : Simple Example
Instance
No
X Y
1 1.0 1.5
2 1.0 4.5
3 2.0 1.5
4 2.0 3.5
5 3.0 2.5
6 5.0 6.0
K = 2
Initial Cluster Centers I1, I3
C1 = I1, C2 = I2
I1 and I2 will be called center

12. K-MEANS : Simple Example
• Now we have to calculate distance
for each instance from the centers
• We use Euclidean distance here
Instance
No
X Y
1 1.0 1.5
2 1.0 4.5
3 2.0 1.5
4 2.0 3.5
5 3.0 2.5
6 5.0 6.0
Instanc
e No
Distance From C1 Distance From C2 Assigned Cluster
1 0.0 1.0 0 < 1  1
2 3.0 3.16 3 < .16  1
3 1.0 0.00 1 > 0  2
4 2.24 2.00 2.24 > 2  2
5 2.24 1.41 2.24 > 1.4  2
6 6.02 5.41 6.02 > 5.41  2

13. K-MEANS : Simple Example
C1: I1, I2
C2: I3, I4, I5, I6
Now we have to recalculate
center
of each cluster
For C1 :
X = (1.0 + 1.0) / 2 = 1.0
Y = (1.5 + 4.5) / 2 = 3.0
For C2 :
X = (2.0 + 2.0+3.0+5.0 ) / 4 =3.0
Y = (1.5 + 3.5 + 2.5 + 6.0) / 4 = 3.375
C1 (1.0, 3.0)
C2 (3.0, 3.375)
Centers Changes !!!

14. K-MEANS : Simple Example
• The center was changed which
means we have to proceed with
iteration 2
Instance
No
X Y
1 1.0 1.5
2 1.0 4.5
3 2.0 1.5
4 2.0 3.5
5 3.0 2.5
6 5.0 6.0
Instanc
e No
Distance From C1 Distance From C2 Assigned Cluster
1 1.5 2.74 1.5 < 2.74  1
2 1.5 2.29 1.5 < 2.29  1
3 1.8 2.125 1.8 < 2.125  1
4 1.12 1.01 2.12 > 1.01  2
5 2.06 0.875 2.06 > 0.875  2
6 5.00 3.30 5.00 > 3.30  2

15. K-MEANS : Simple Example
C1: I1, I2, I3
C2: I4, I5, I6
Now we have to recalculate
center
of each cluster
For C1 :
X = (1.0 + 1.0 + 2.0 ) / 3 = 1.33
Y = (1.5 + 4.5 + 1.5) / 3 = 2.50
For C2 :
X = (2.0 + 3.0 + 5.0 ) / 3 = 3.33
Y = (3.5 + 2.5 + 6.0) / 3 = 4.00
C1 (1.33, 2.50)
C2 (3.33, 4.00)
Centers Changes !!!

16. K-MEANS : Last Words
• This iteration goes on until center value is
unchanged.
• After the iteration is stopped we get a stable set of
clusters.
• K-Means is useful in situation where just a grouping
is important and the attributes are not significant.
• If we want to judge the significance of attributes
▫ Initial ordering based on various attributes
▫ Run K-Means on each order separately
▫ Judge by the obtained set of multiple clusters

17. Graph Clustering
• K Spanning Tree
• SNN (Shared Nearest Neighbors)
• Highly Connected Sub-graph
• Between-ness centrality
• Complete – Link
• CLIQUE
• Kernel K-Means

18. K-Spanning Tree
• Creates cluster from a spanning tree of the graph
• Spanning Tree:
▫ A connected Sub-graph with no cycle which includes all
the vertices of the graph.
1
2
3
4
5
2
3
2
4
6
5
7
4
1
2
3
4
52
6
7

19. K-Spanning Tree
• Minimum Spanning Tree
▫ The spanning tree which has minimum sum of weights.
1
2
3
4
5
2
3
2
4
6
5
7
4
G
1
2
3
4
5
2
3 2
4
Weight = 11
2
1
2
3
4
52
4
5
Weight = 13
1
2
3
4
52
6
7
Weight = 17
2

20. K-Spanning Tree
• We find out the Minimum Spanning Tree of a graph
using Prim or Kruskal’s algorithm.
• If K is the number of cluster, we remove K-1 edges
from the MST which have the most weight.
• This give us K Clusters.

21. K-Spanning Tree
1
2
3
4
5
2
3 2
Remove k-1 edges with
highest weight
4
Minimum Spanning Tree
Note: k – is the
number of
clusters
E.g., k=3
1
2
3
4
5
2
3 2
4
E.g., k=3
1
2
3
4
5
3 Clusters

22. Shared Nearest Neighbors (SNN)
• Number of common neighbors between any pair of
nodes
u v
𝑺𝒉𝒂𝒓𝒆𝒅 𝑵𝒆𝒂𝒓𝒆𝒔𝒕 𝑵𝒆𝒊𝒈𝒉𝒃𝒐𝒓𝒔

23. Shared Nearest Neighbors (SNN)
• Threshold τ = minimum shared neighbors
• For a given graph
▫ For each edge (u,v), weight(u, v) = SNN of u and v
0
1
2
3
4
G
0
1
2
3
4
SNN
2
2
22
1
1
3
1
Node 0 and Node 1 have 2 neighbors in
common: Node 2 and Node 3

24. Shared Nearest Neighbors (SNN)
• Delete each edge with weight < τ
• Nodes with SNN > τ will have edge between them,
so in same cluster.
24
0
1
2
3
42
2
22
1
1
3
2
0
1
2
3
4
E.g., τ =3

25. Highly Connected Sub-graph
• If a graph is highly-connected, sub-graph of it wont
be on different cluster
• If a graph is not highly connected, sub-graphs of it
may be on different clusters.

26. Highly Connected Sub-graph
• Cut: Set of edges when removed disconnects a
graph. 6
5
4
7
3 2
1
0
8
6
5
4
7
3
2
1
0
8
6
5
4
7
3 2
1
0
8
Cut = {(0,1),(1,2),(1,3}
Cut = {(3,5),(4,2)}

27. Highly Connected Sub-graph
• MinCut – Minimum Set of edges which when
removed disconnects the graph. {(3,5),(4,2)} in the
previous case.
• EC = |mincut|
• if EC > V/2 , the graph is highly connected hence
wont be divided.
• Else it may be divided by the cuts.

28. Highly Connected Sub-graph
6
5
4
7
3 2
1
0
8
Find the
Minimum Cut
MinCut (G)
Given Input graph G
(3,5),(4,2)}
YES
Return G
NO
G1 G2
Divide G
using MinCut
Is EC(G)> V/2
Process Graph G1
Process Graph G2

29. Thank You