Download to read offline
class 11 maths complex numbers ,logarithmic spirals in complex plane
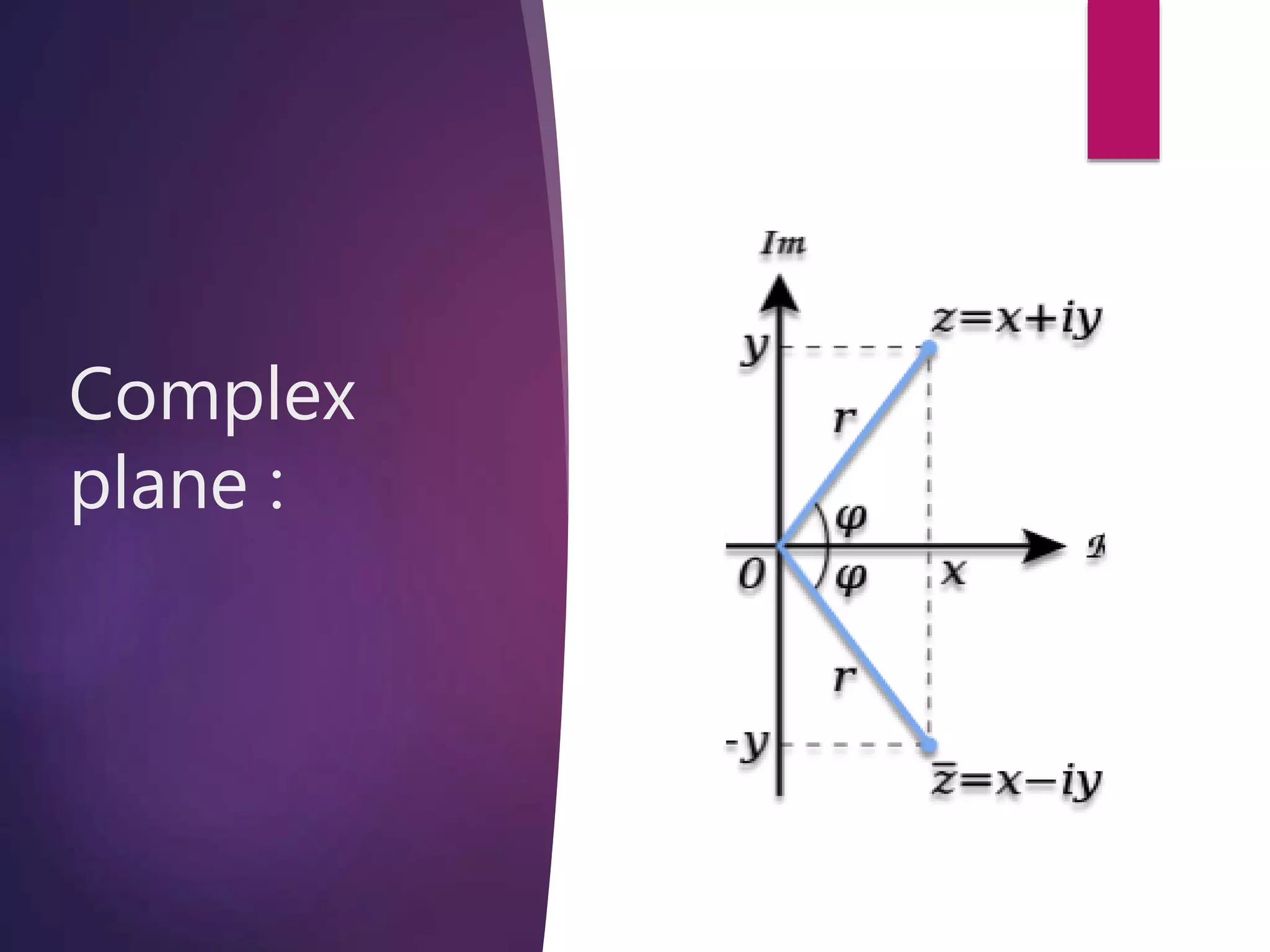
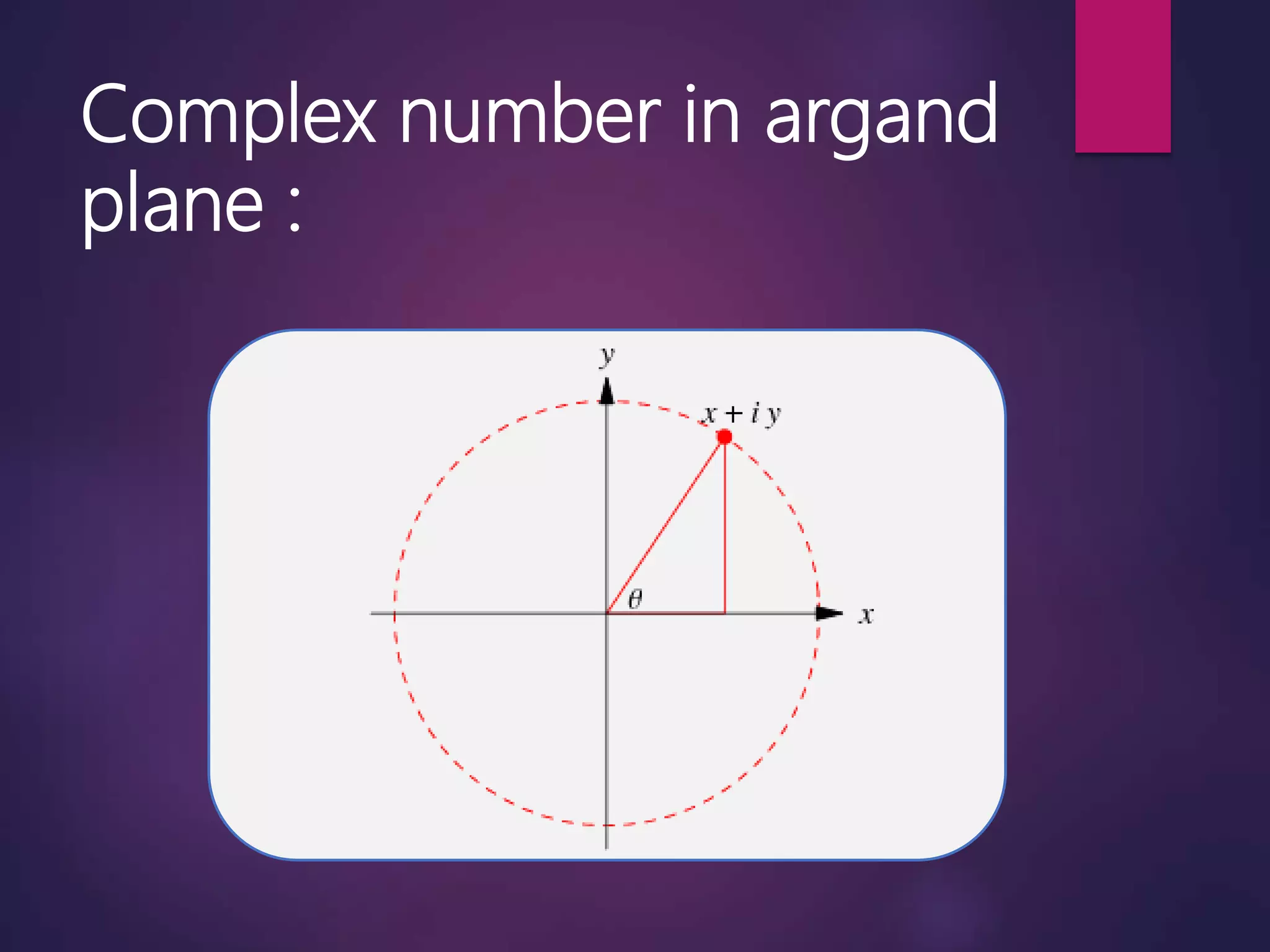
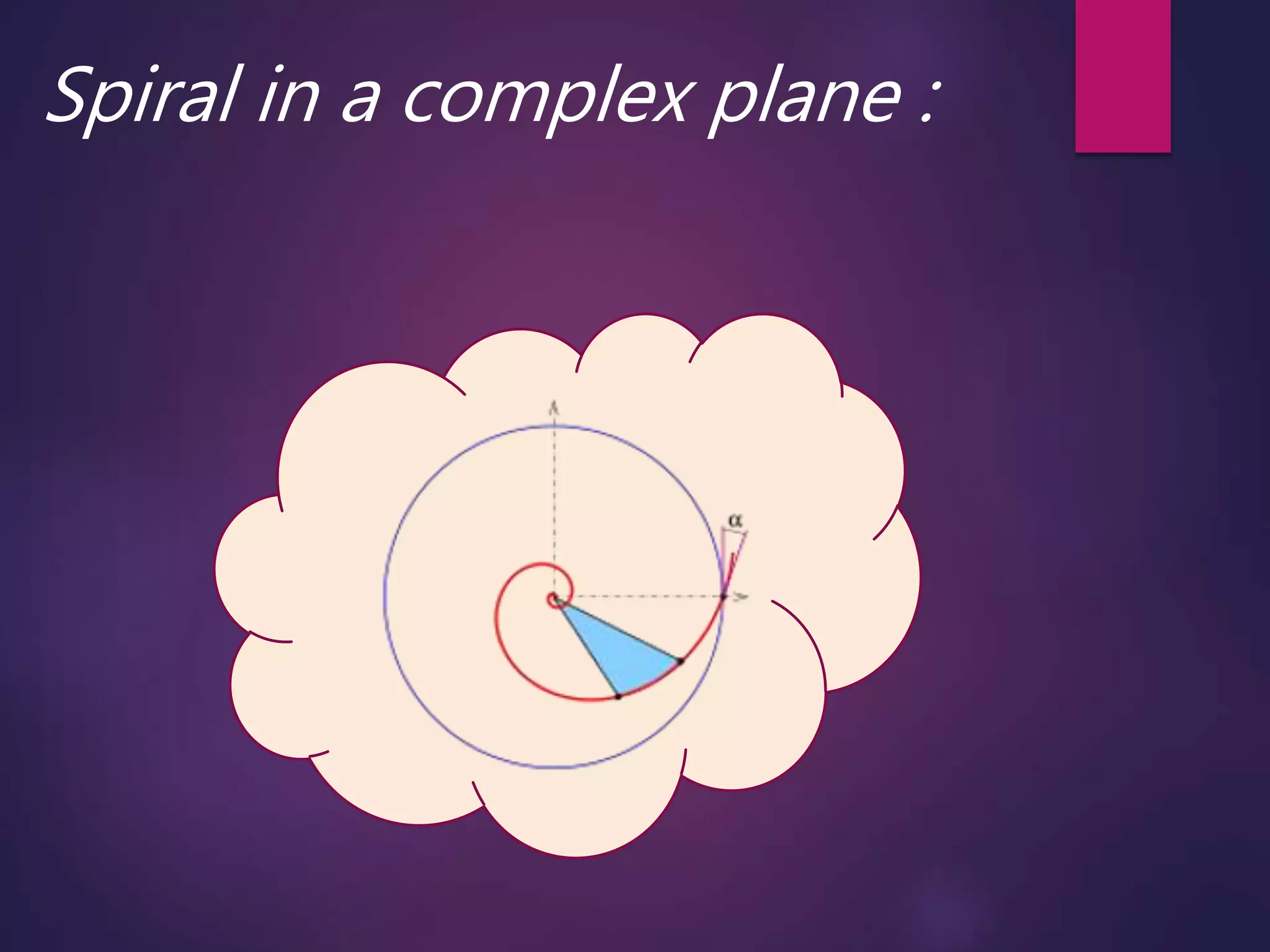
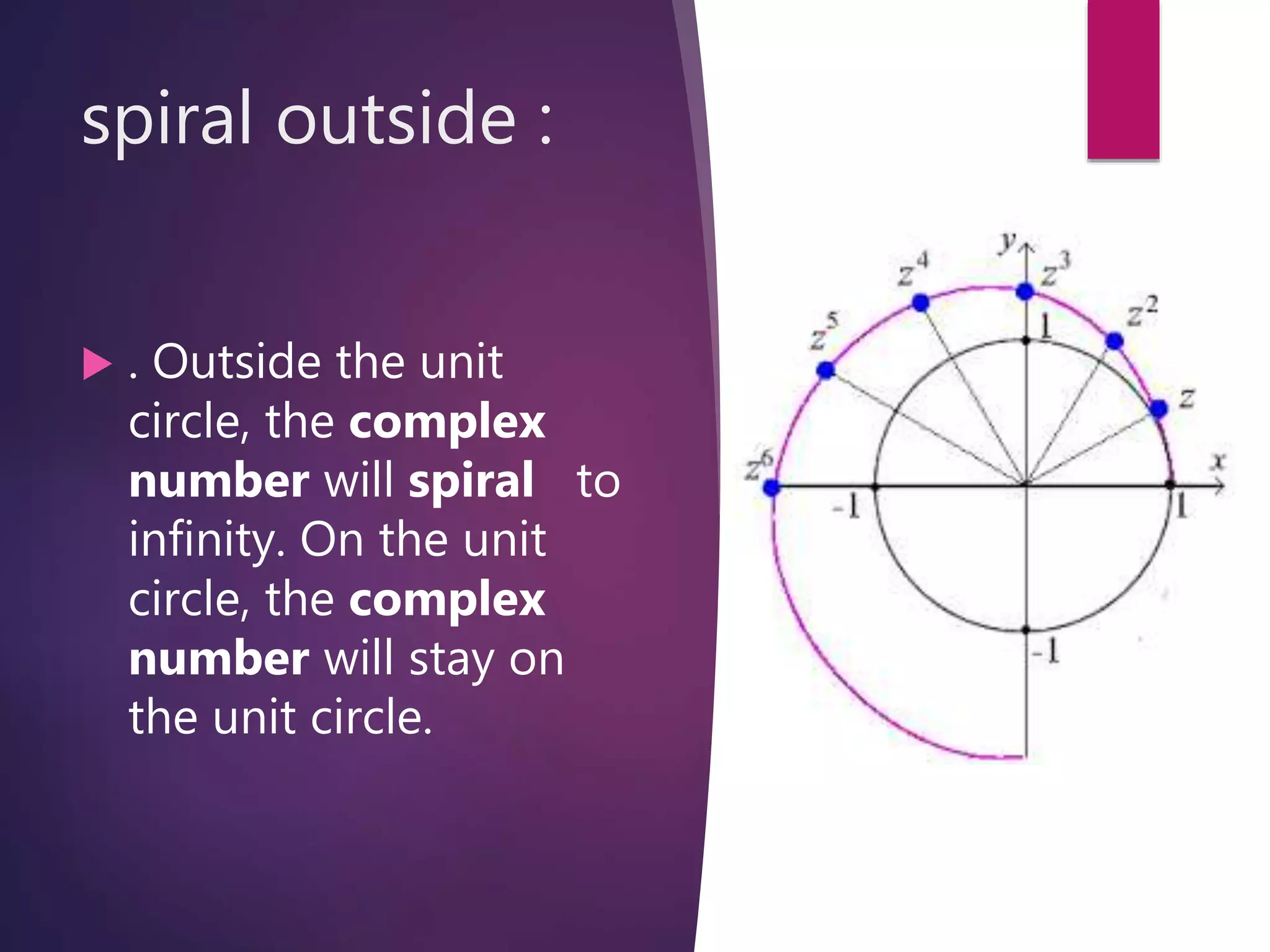
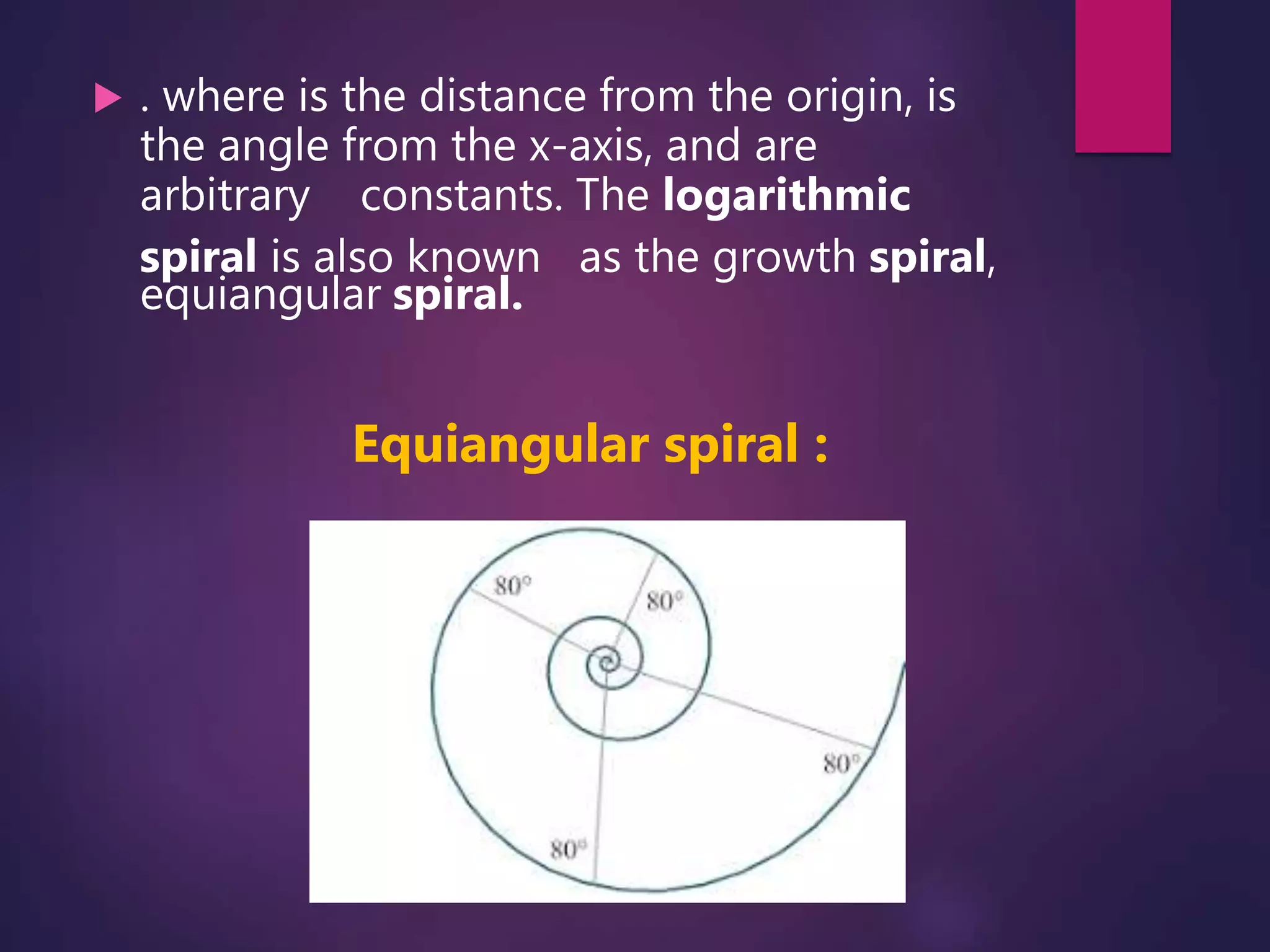
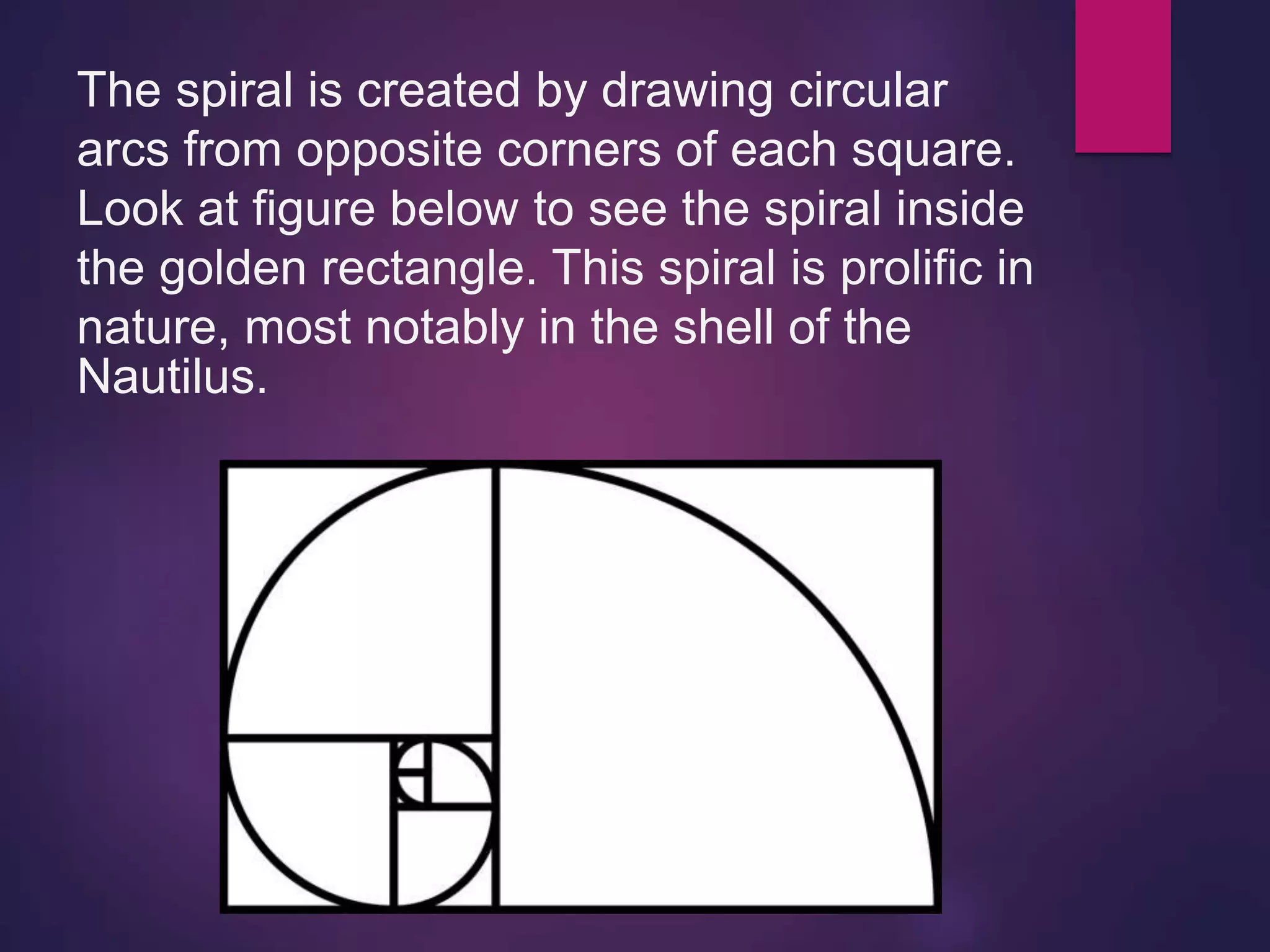
This document discusses complex numbers and logarithmic spirals in the complex plane. It begins by defining a complex number as a number that can be expressed as a + bi, where a and b are real numbers and i is the imaginary unit. The complex plane is then introduced as a way to represent complex numbers geometrically using the real and imaginary parts. Logarithmic spirals are discussed, with their polar equation given, and how they can be constructed from equally spaced rays. Examples of logarithmic spirals in nature and their use in photographic techniques are provided.
