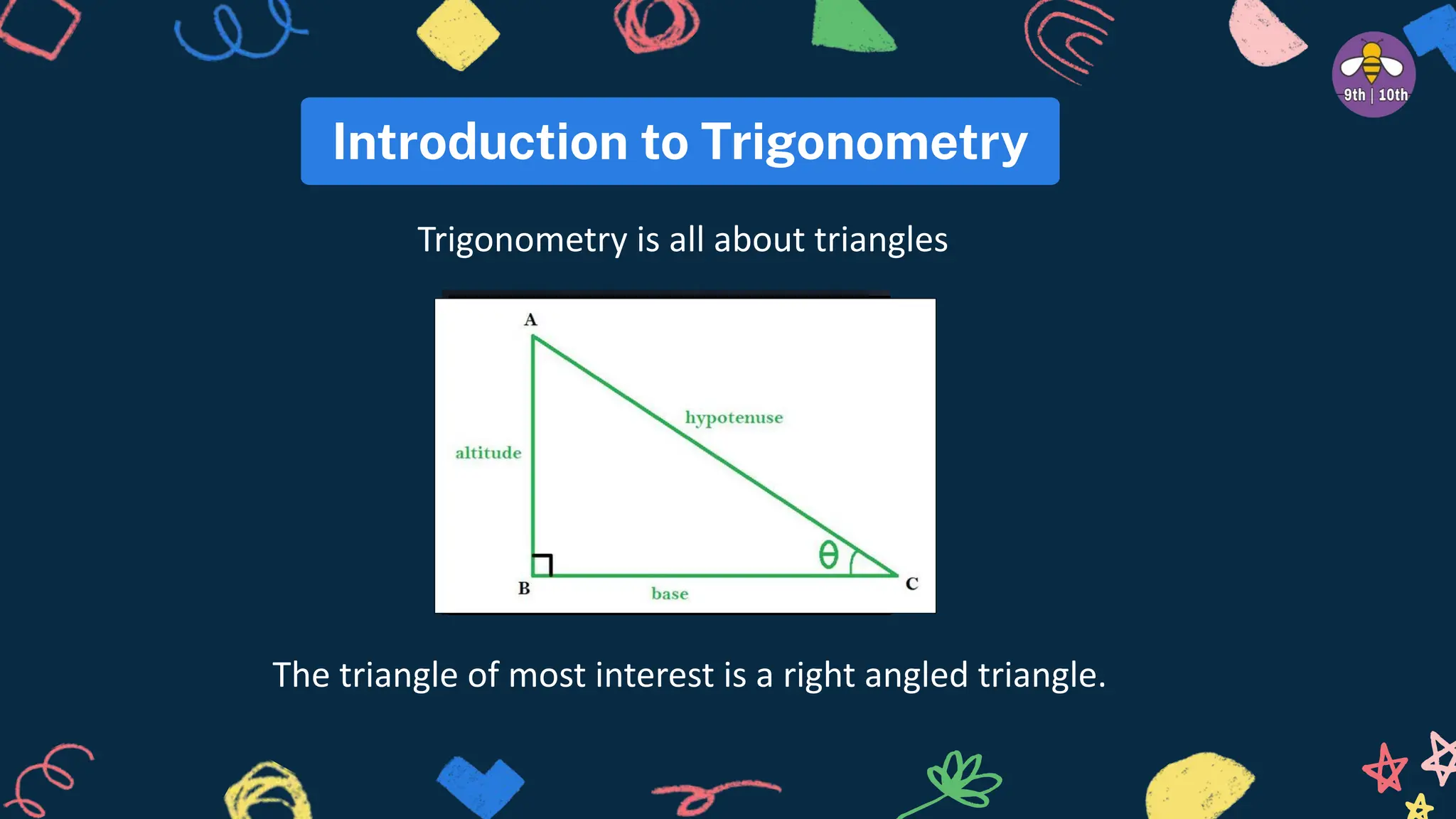
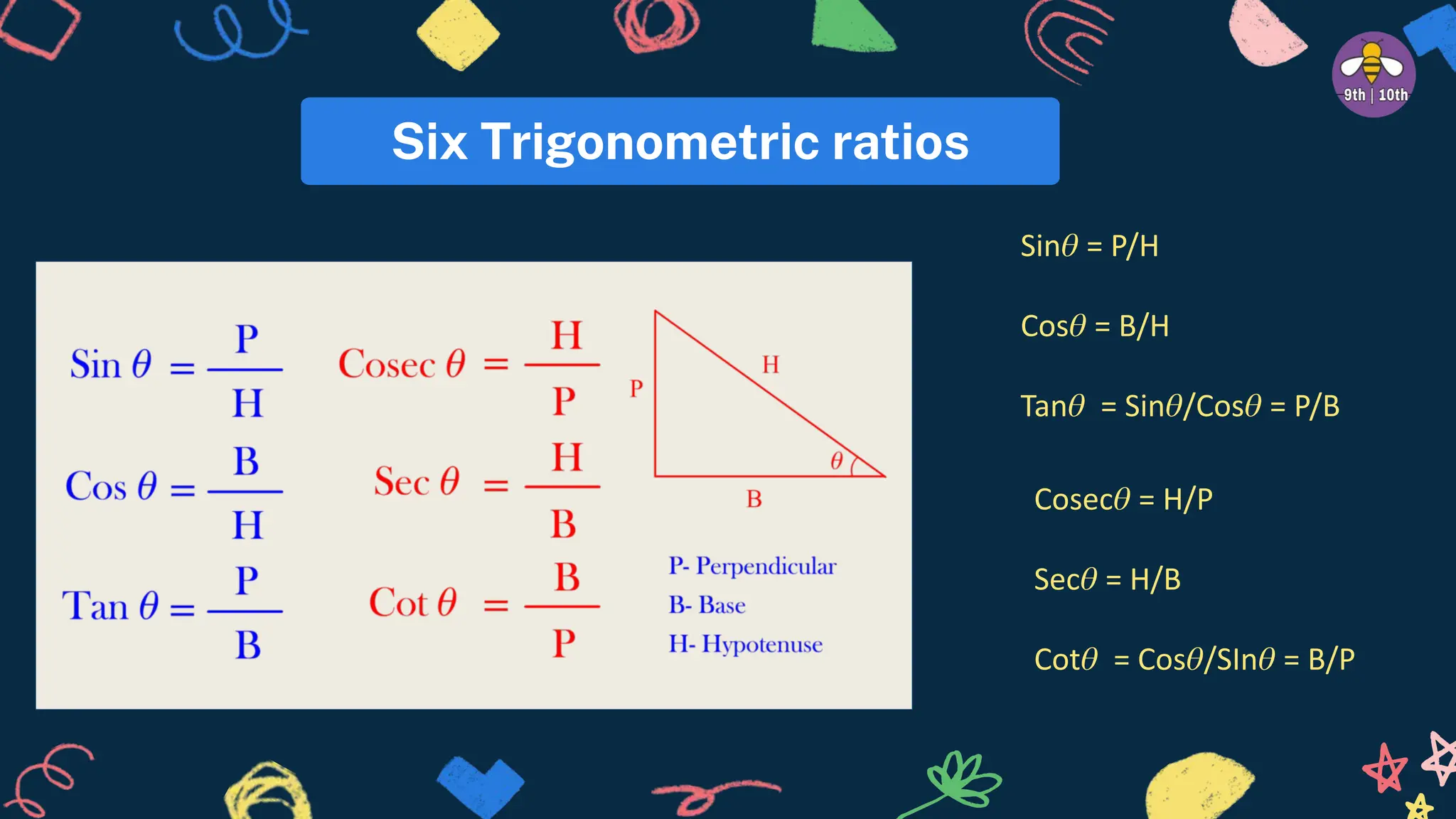
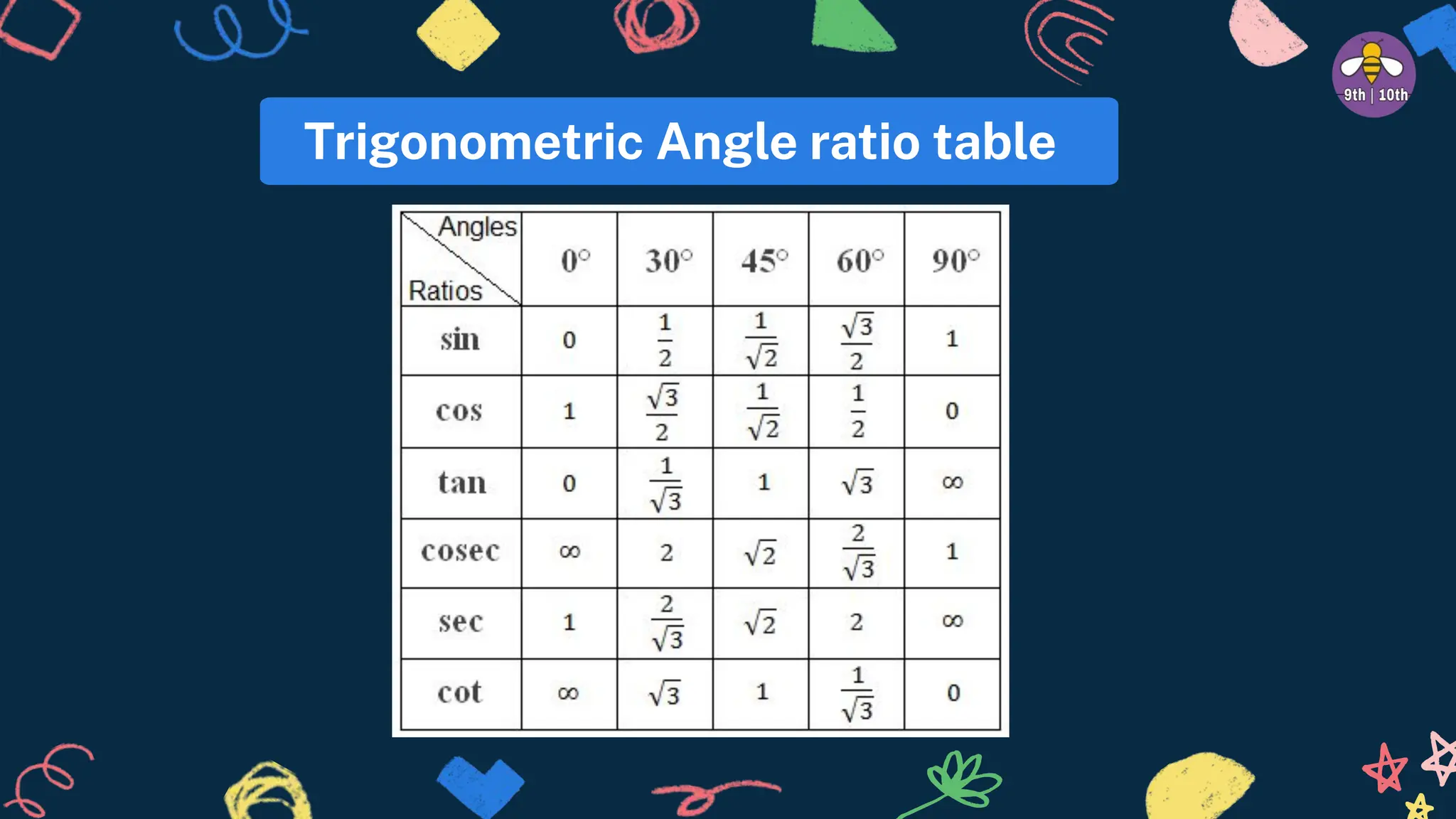
The document provides an introduction to trigonometry including definitions of six trigonometric ratios using a right angled triangle. It lists key trigonometric identities and then provides 14 practice questions involving trigonometric ratios, identities, and angle relationships to solve. The questions cover topics like solving for trigonometric functions given relationships between them, proving trigonometric identities, and evaluating expressions involving trigonometric functions.