This document describes Bloom filters, which provide an approximate and space-efficient way to check for set membership. A Bloom filter uses a bit array and k independent hash functions to represent a set S of m elements from a universe U. To check if an element x is in S, its k hash values are checked in the bit array - if any are 0, x is definitely not in S, but if all are 1, x is assumed to be in S, allowing for false positives. The probability of a false positive can be minimized by optimizing the number of hash functions k to be ln(2)*(n/m), where n is the size of the bit array. When optimized, a Bloom filter provides an efficient randomized

1. Bloom filters
From Probability and Computing
Randomized algorithms and probabilistic
analysis P109~P111
Michael Mitzenmacher Eli Upfal

2. Introduction
 Approximate set membership problem .
 Trade-off between the space and the
false positive probability .
 Generalize the hashing ideas.

3. Approximate set membership problem
 Suppose we have a set
S = {s1,s2,...,sm}  universe U
 Represent S in such a way we can
quickly answer “Is x an element of S ?”
 To take as little space as possible ,we
allow false positive (i.e. xS , but we
answer yes )
 If xS , we must answer yes .

4. Bloom filters
 Consist of an arrays A[n] of n bits (space) , and k
independent random hash functions
h1,…,hk : U --> {0,1,..,n-1}
1. Initially set the array to 0
2.  sS, A[hi(s)] = 1 for 1 i  k
(an entry can be set to 1 multiple times, only the first
times has an effect )
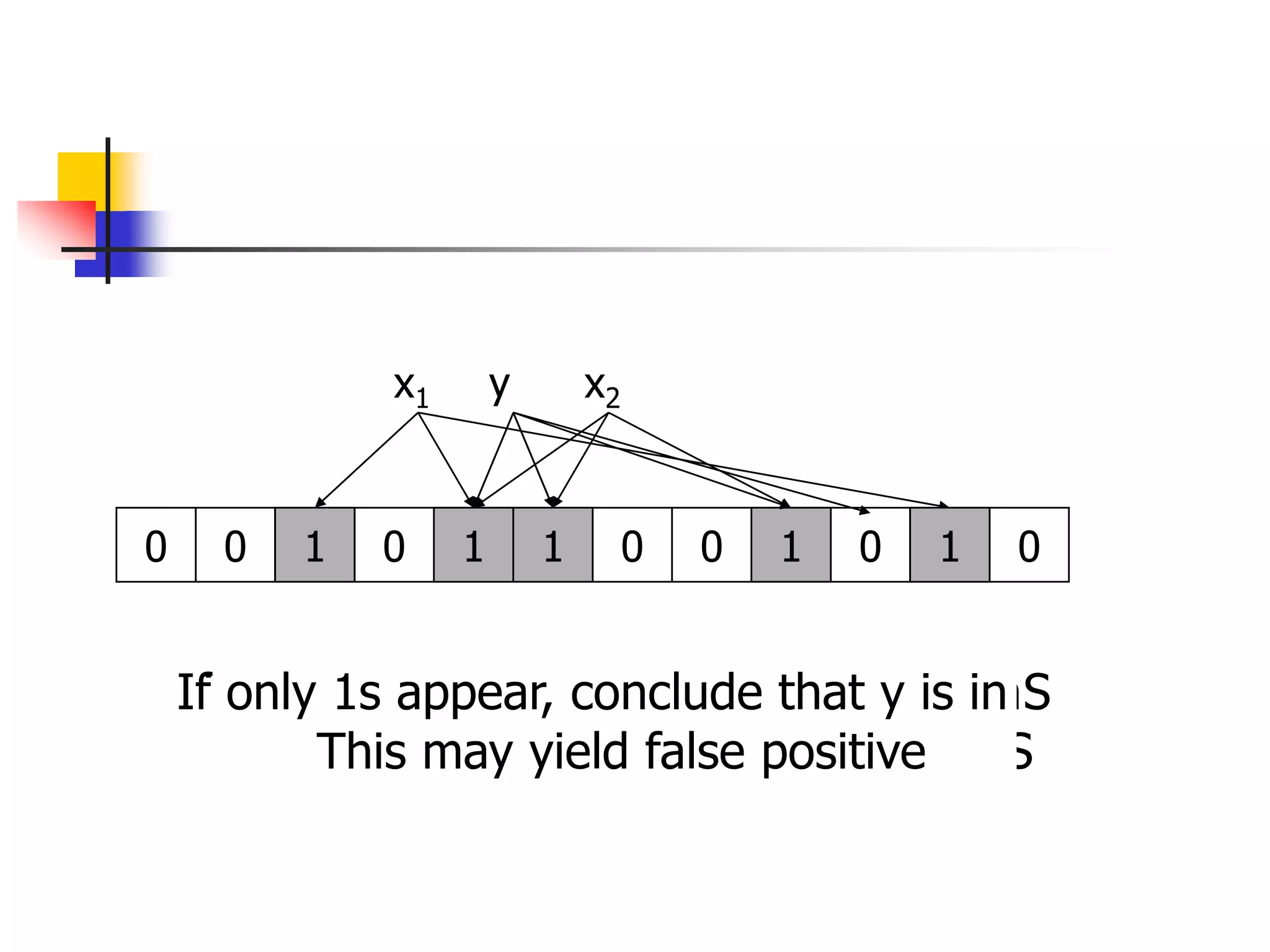
3. To check if xS , we check whether all location
A[hi(x)] for 1 i  k are set to 1
If not, clearly xS.
If all A[hi(x)] are set to 1 ,we assume xS

5. 0 0 0 0 0 0 0 0 0 0 0 0
Initial with all 0
1 1 1 1 1
x1 x2
Each element of S is hashed k times
Each hash location set to 1
1 1 1 1 1
y
To check if y is in S, check the k hash
location. If a 0 appears , y is not in S
1 1 1 1 1
y
If only 1s appear, conclude that y is in S
This may yield false positive

6. The probability of a false positive
 We assume the hash function are
random.
 After all the elements of S are hashed
into the bloom filters ,the probability
that a specific bit is still 0 is
/
1
(1 )km km n
p e
n

  

7.  To simplify the analysis ,we can assume a
fraction p of the entries are still 0 after all the
elements of S are hashed into bloom filters.
 In fact,let X be the random variable of
number of those 0 positions. By Chernoff
bound
It implies X/n will be very close to p with a very
high probability
2
/3
Pr( ) 2 n p
X np n e ne 
 
  

8.  The probability of a false positive f is
 To find the optimal k to minimize f .
Minimize f iff minimize g=ln(f)
 k=ln(2)*(n/m)
 f = (1/2)k = (0.6185..)n/m
The false positive probability falls exponentially
in n/m ,the number bits used per item !!
/
(1 ) (1 )
k km n k
f p e
   
/
/
/
ln(1 )
1
km n
km n
km n
dg km e
e
dk n e



  


9. Conclusion
 A Bloom filters is like a hash table ,and simply
uses one bit to keep track whether an item
hashed to the location.
 If k=1 , it’s equivalent to a hashing based
fingerprint system.
 If n=cm for small constant c,such as c=8 ,then
k=5 or 6 ,the false positive probability is just
over 2% .
 It’s interesting that when k is optimal
k=ln(2)*(n/m) , then p= 1/2.
An optimized Bloom filters looks like a random
bit-string