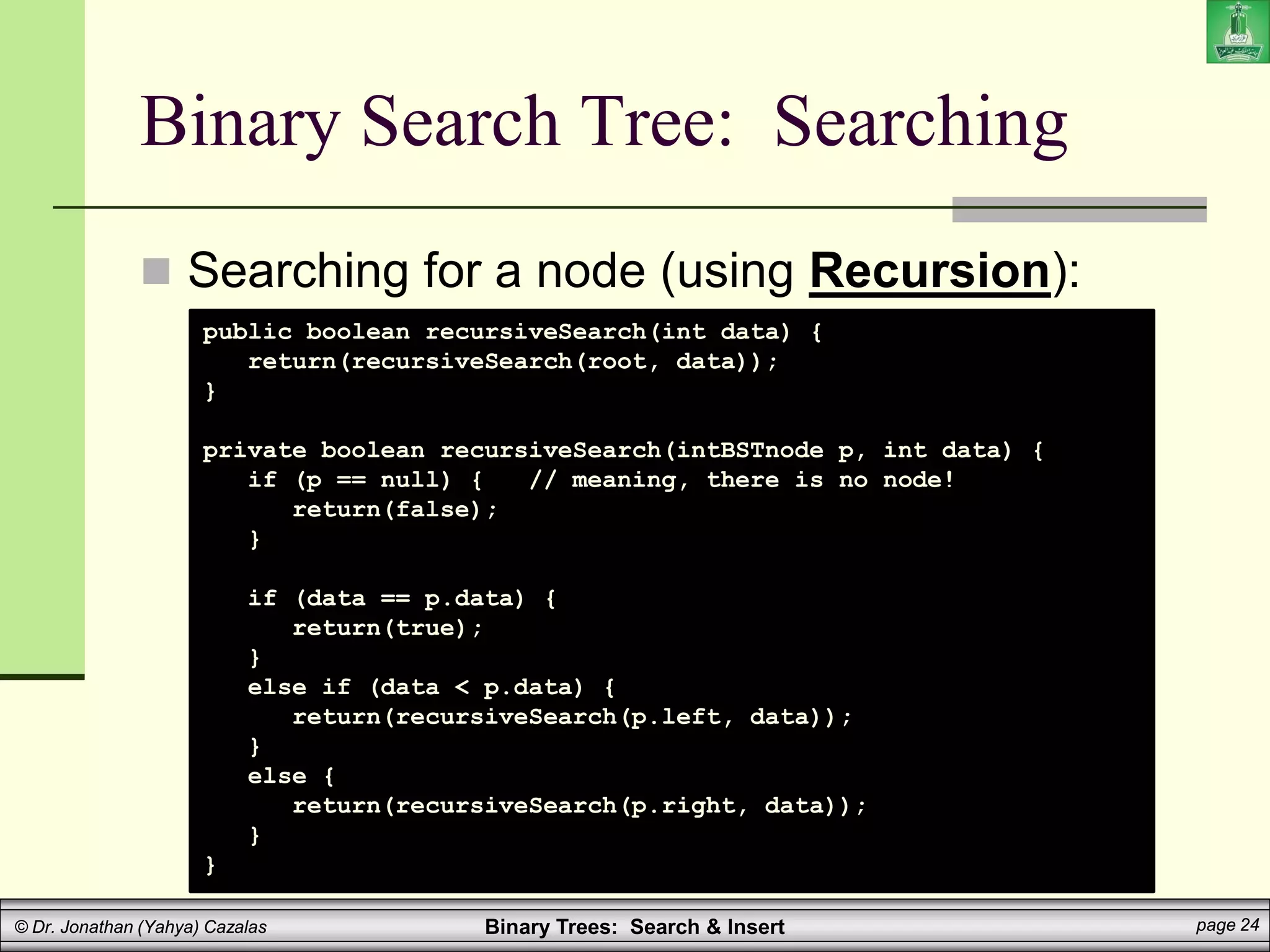
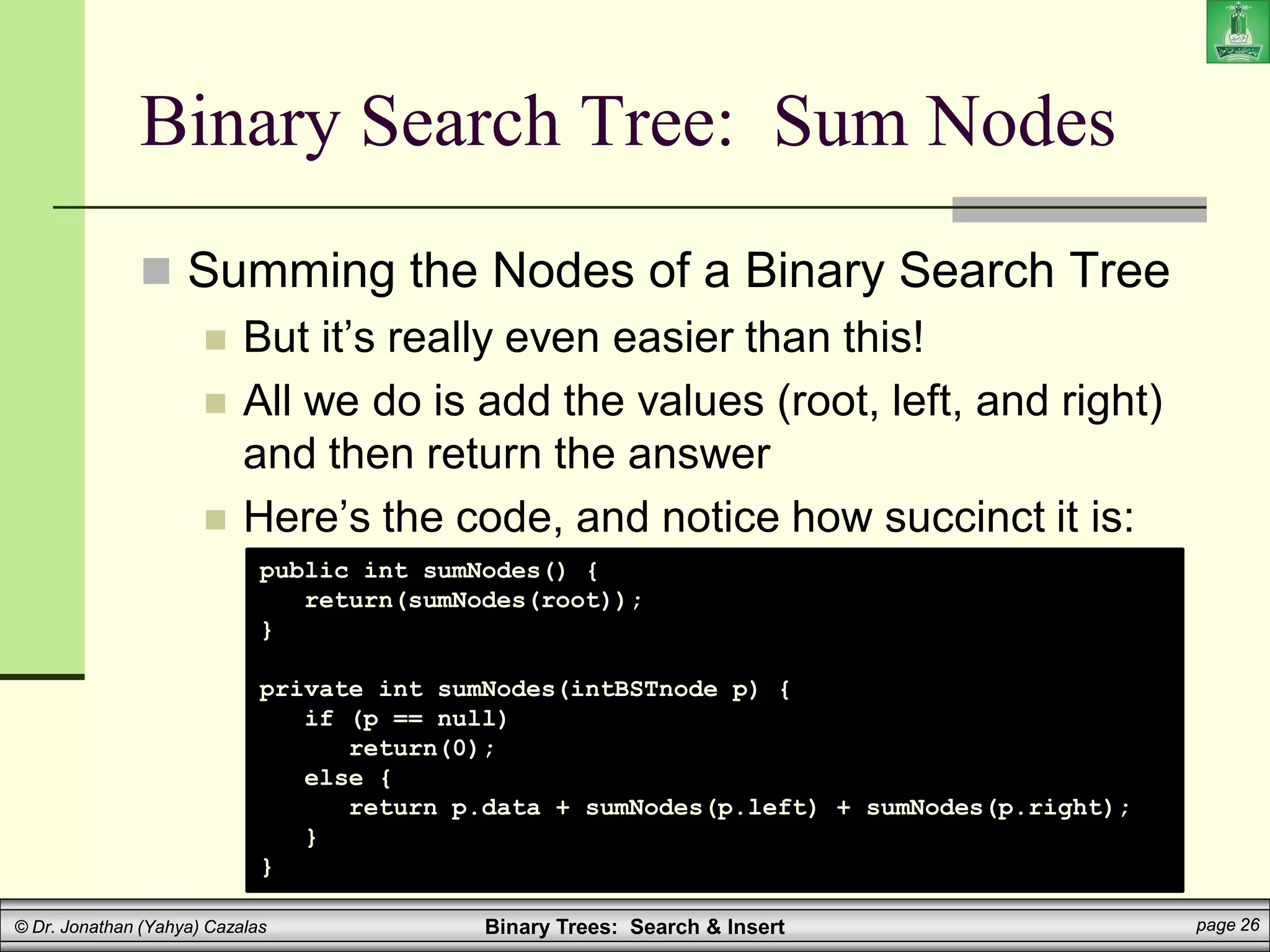
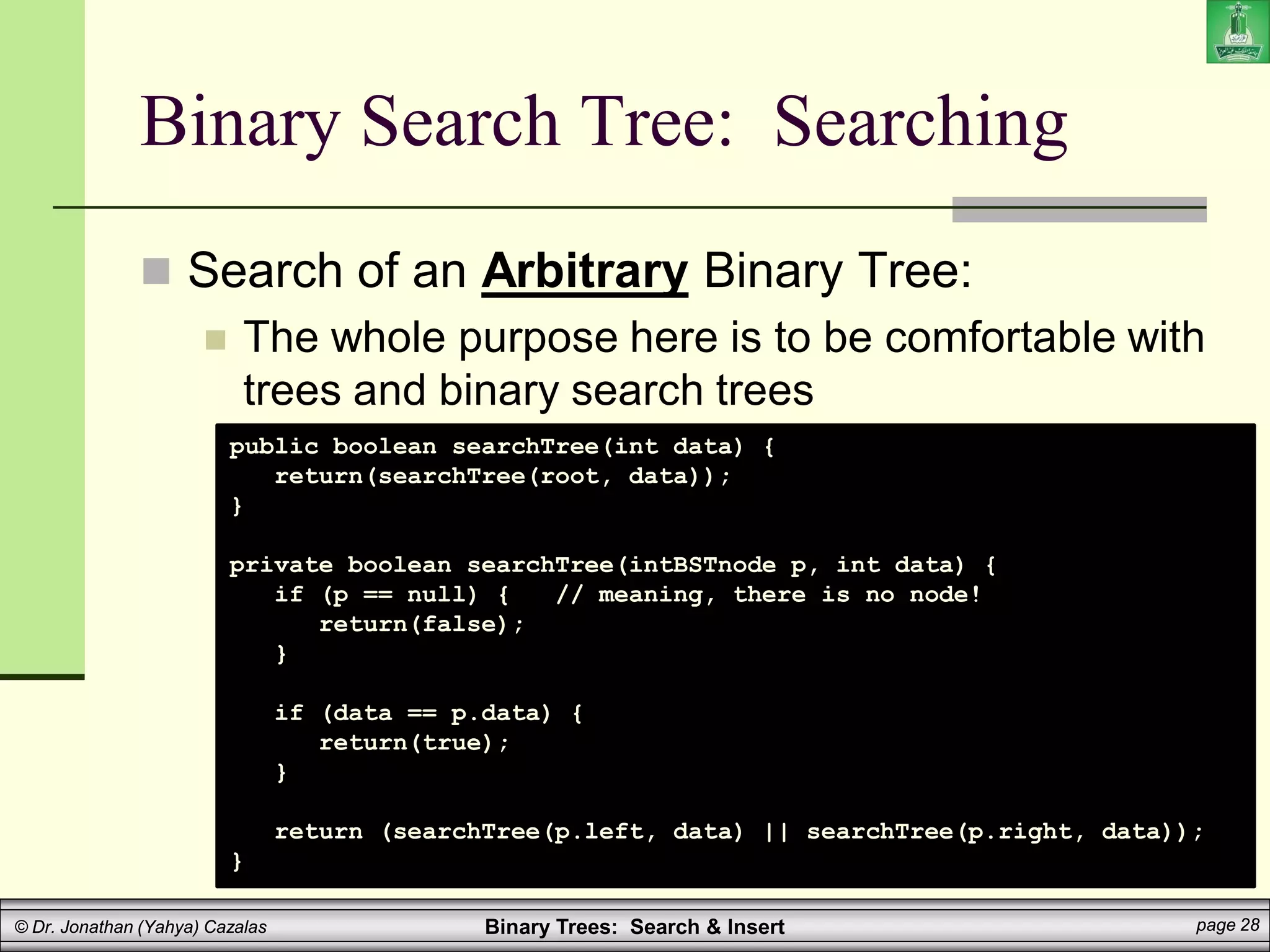
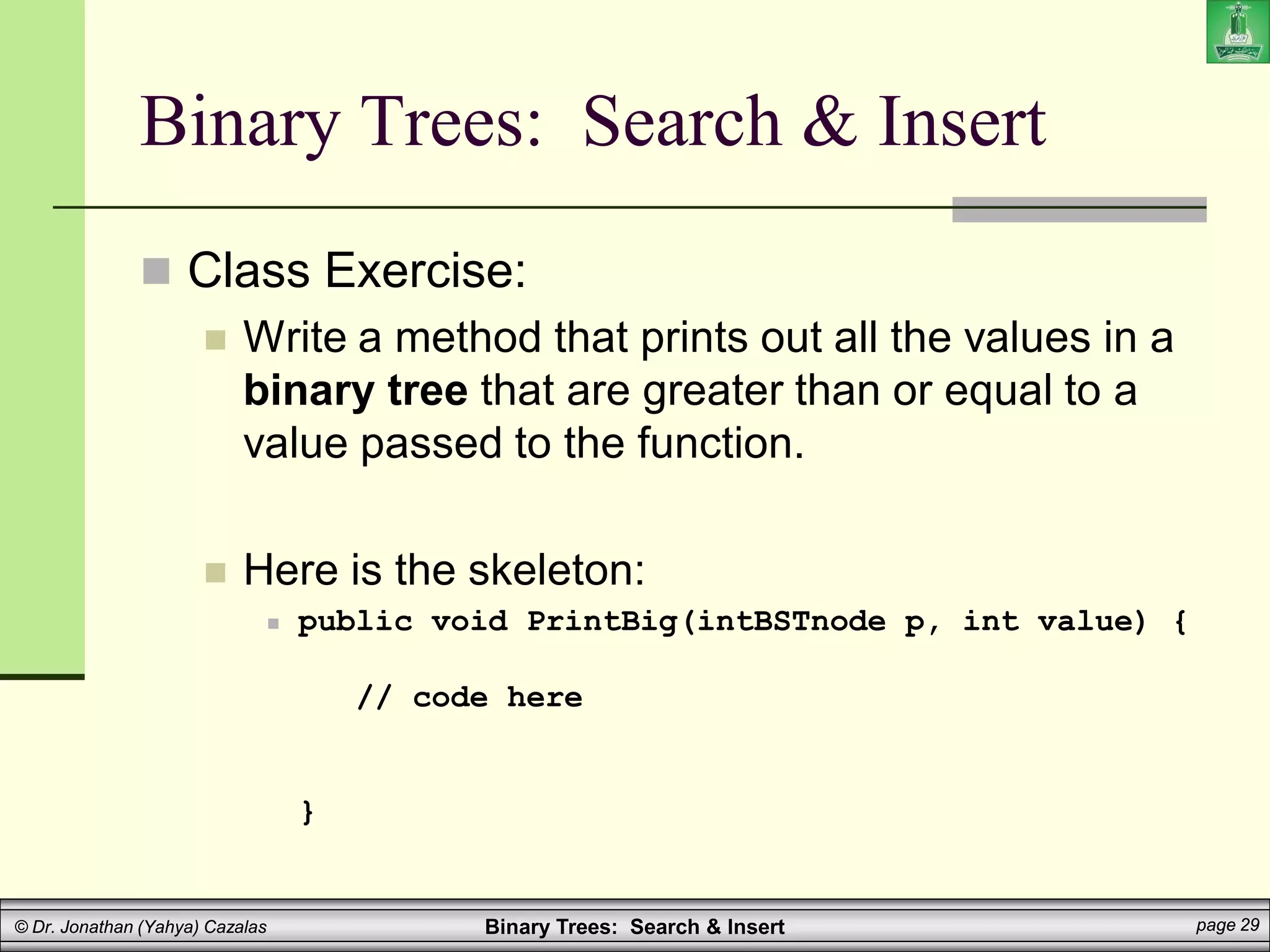
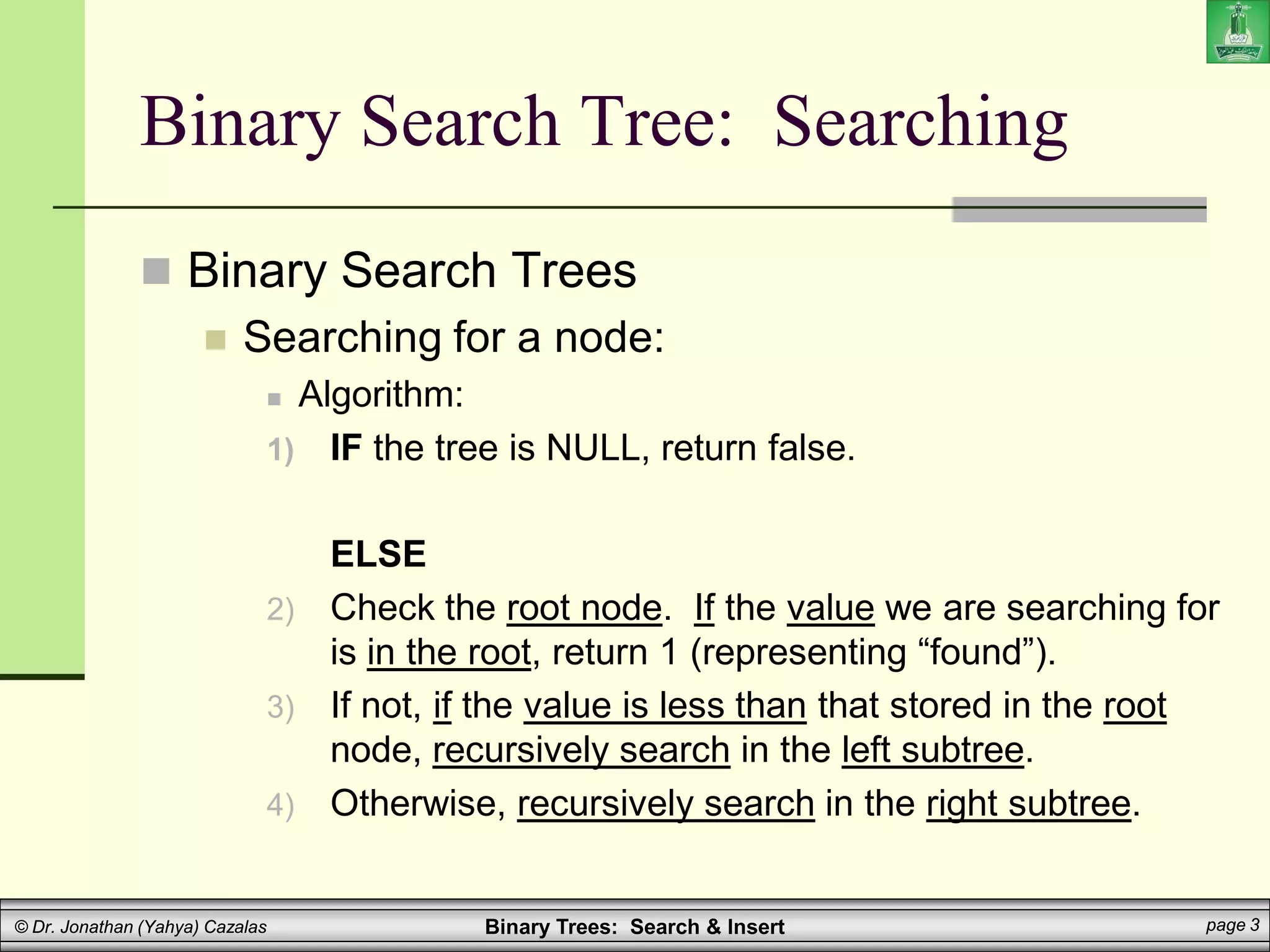
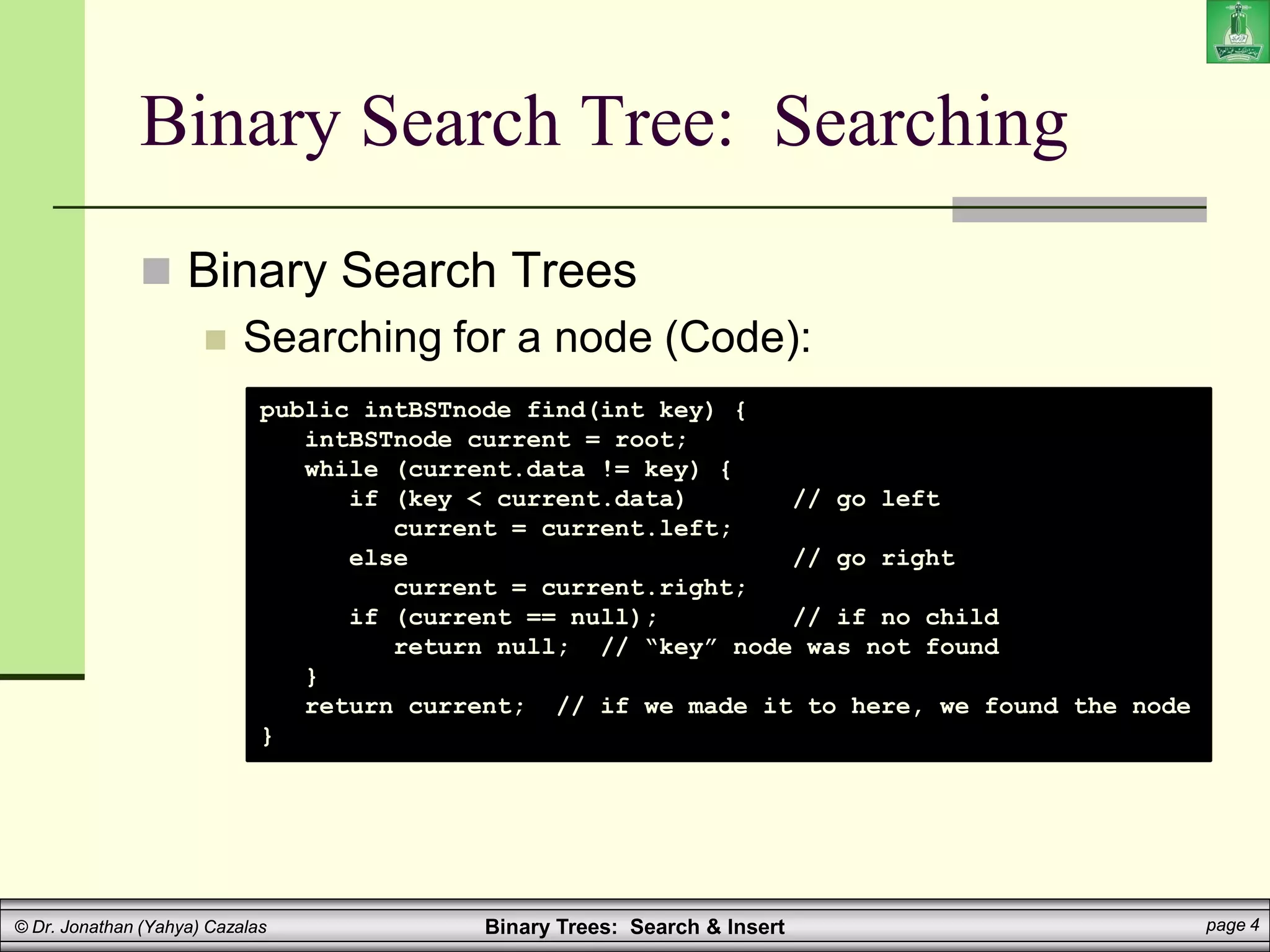
The document covers binary search trees, emphasizing their ordering property which ensures efficient searching (O(log n)). It details the algorithms for searching and inserting nodes, including code examples for implementation in a programming context. Additionally, it discusses the creation and traversal of binary search trees, as well as recursive methods for searching and summing values within the tree.












![Binary Trees: Search & Insert page 20
© Dr. Jonathan (Yahya) Cazalas
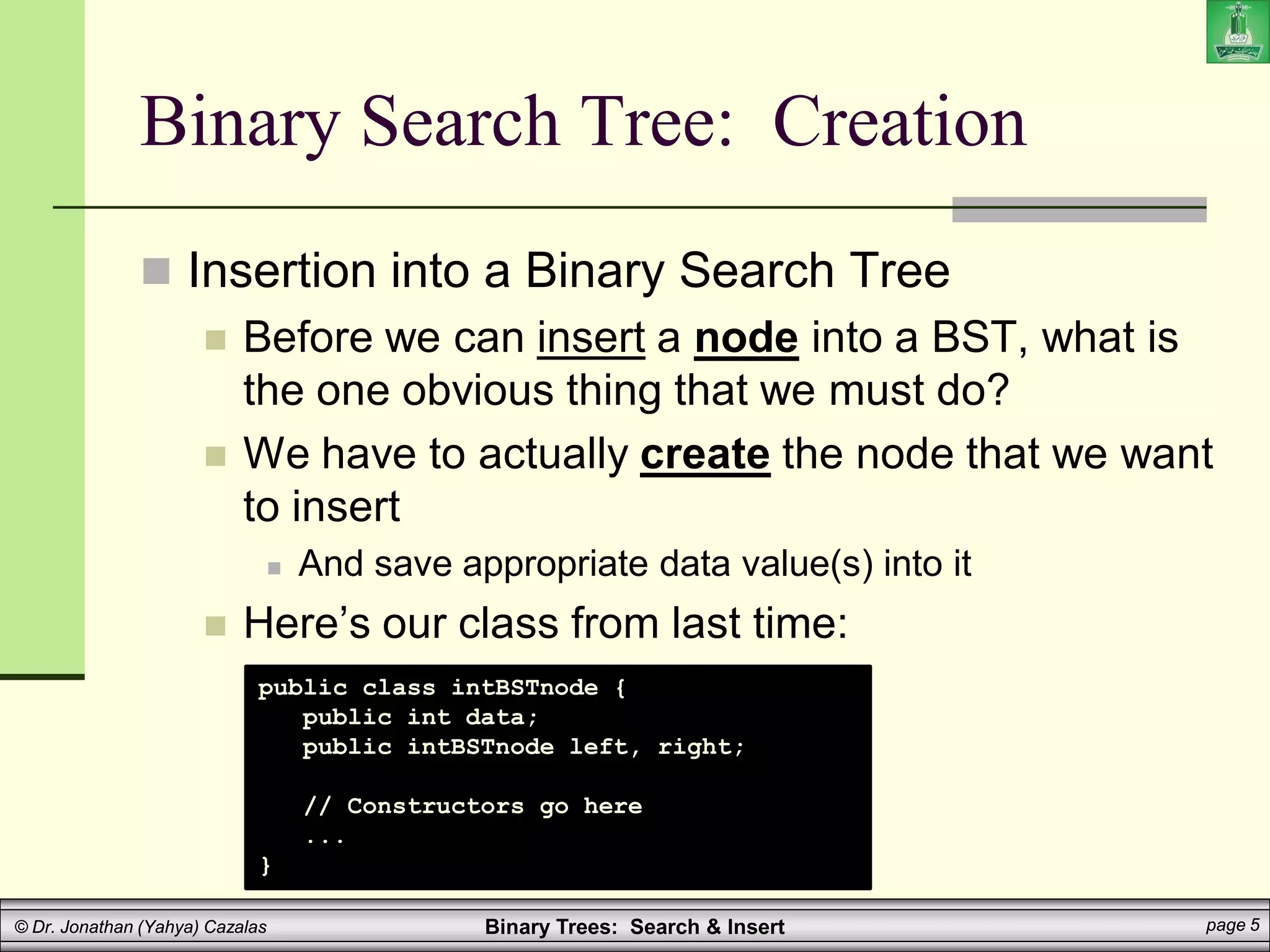
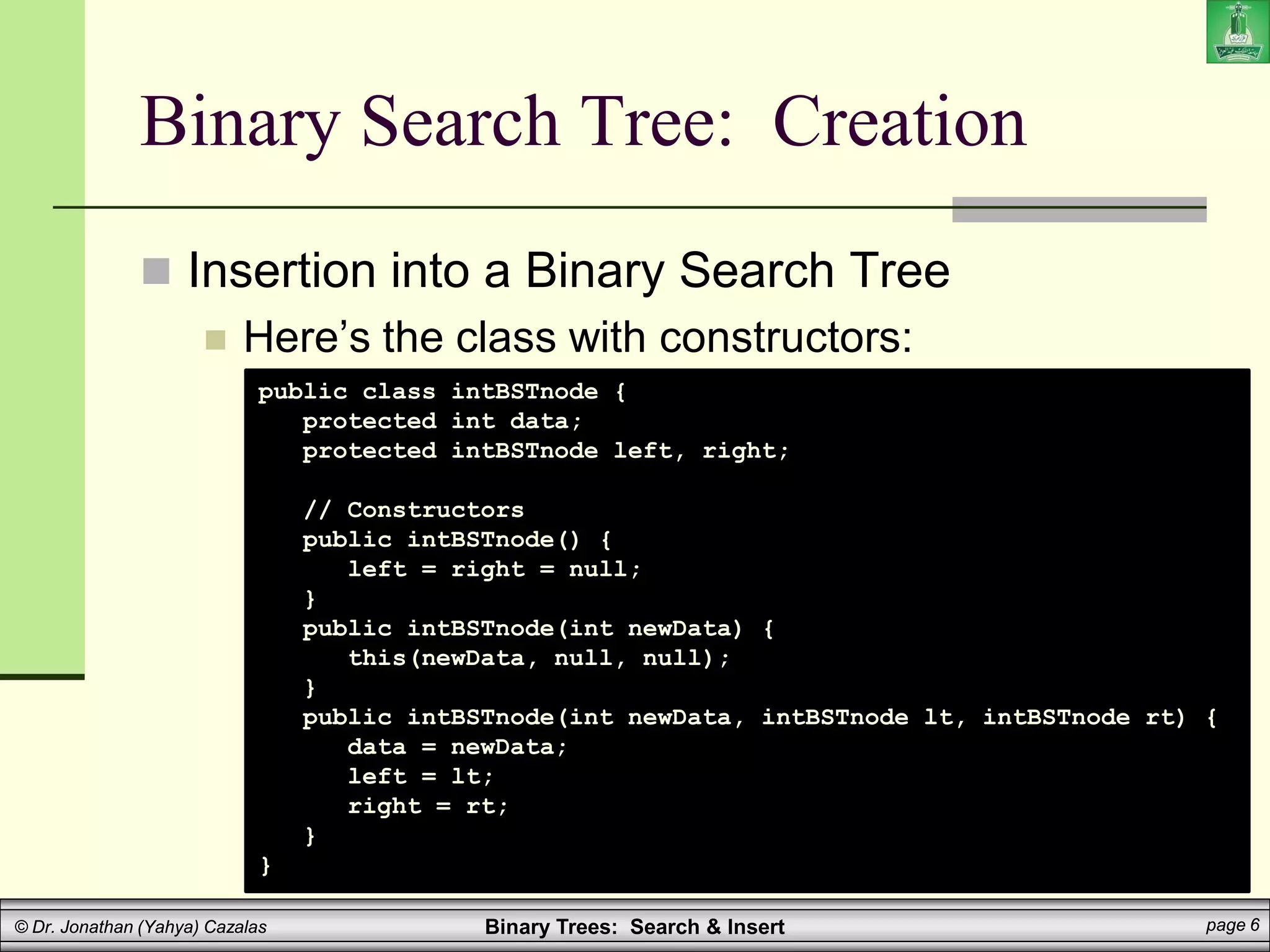
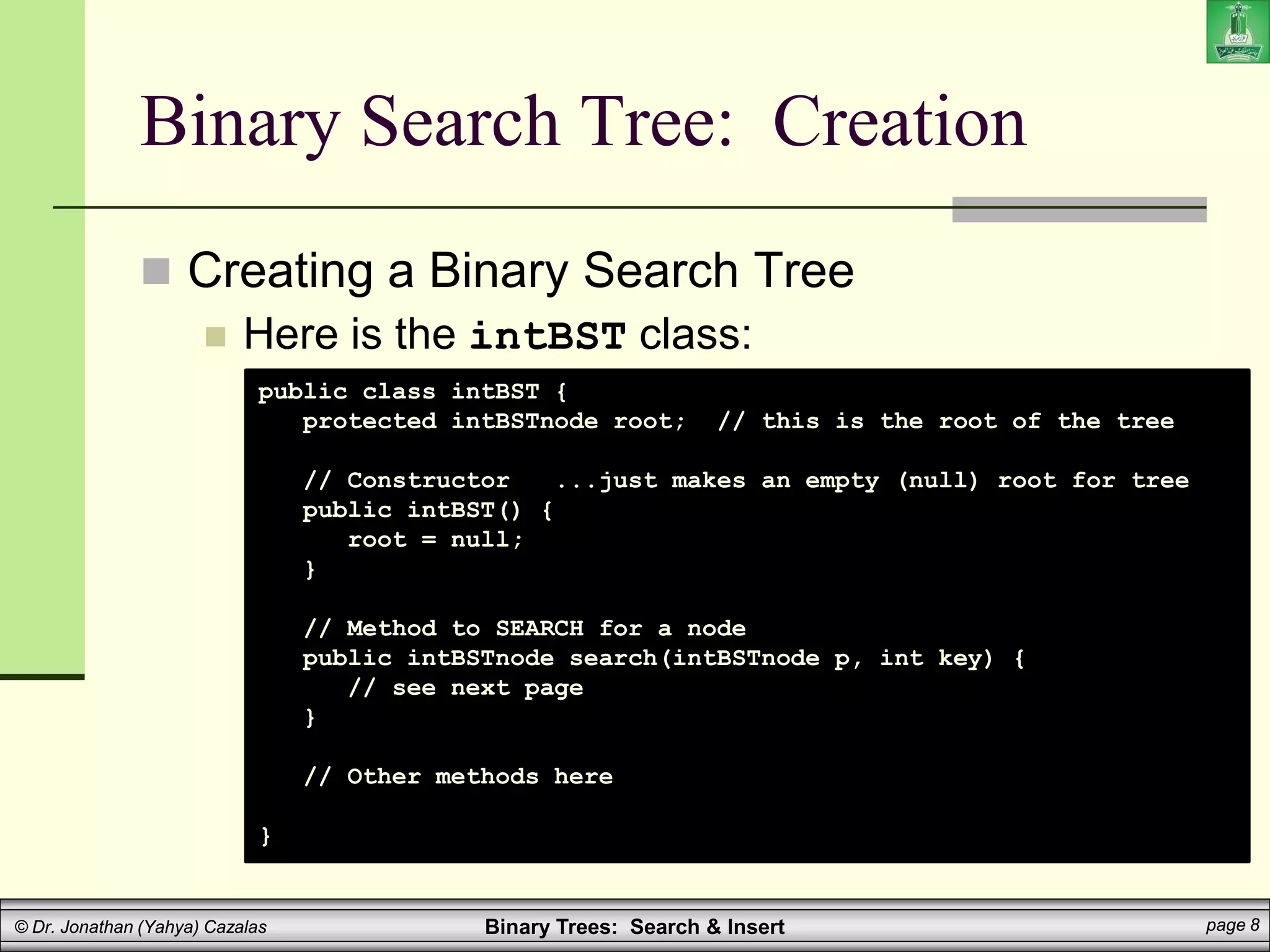
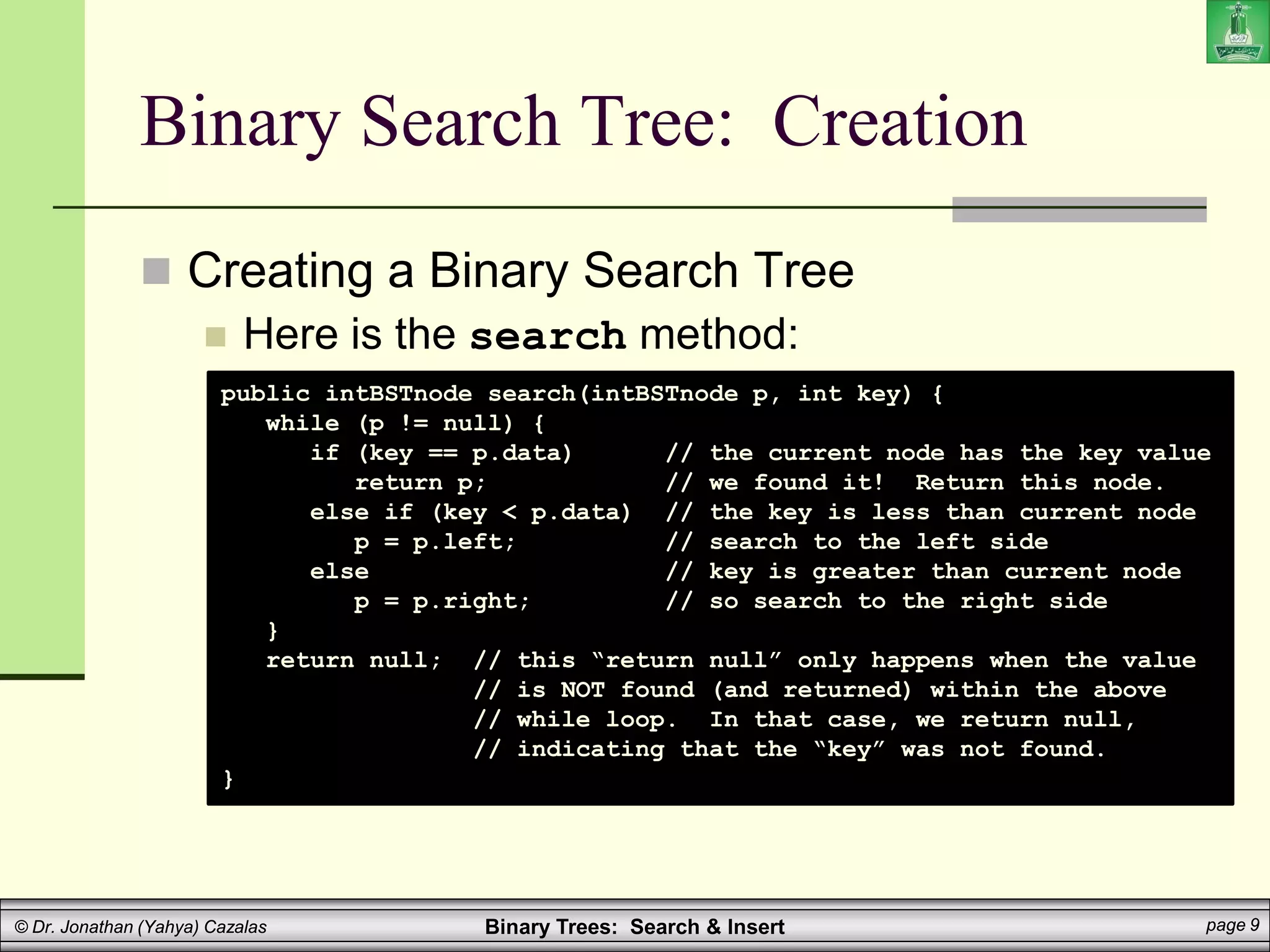
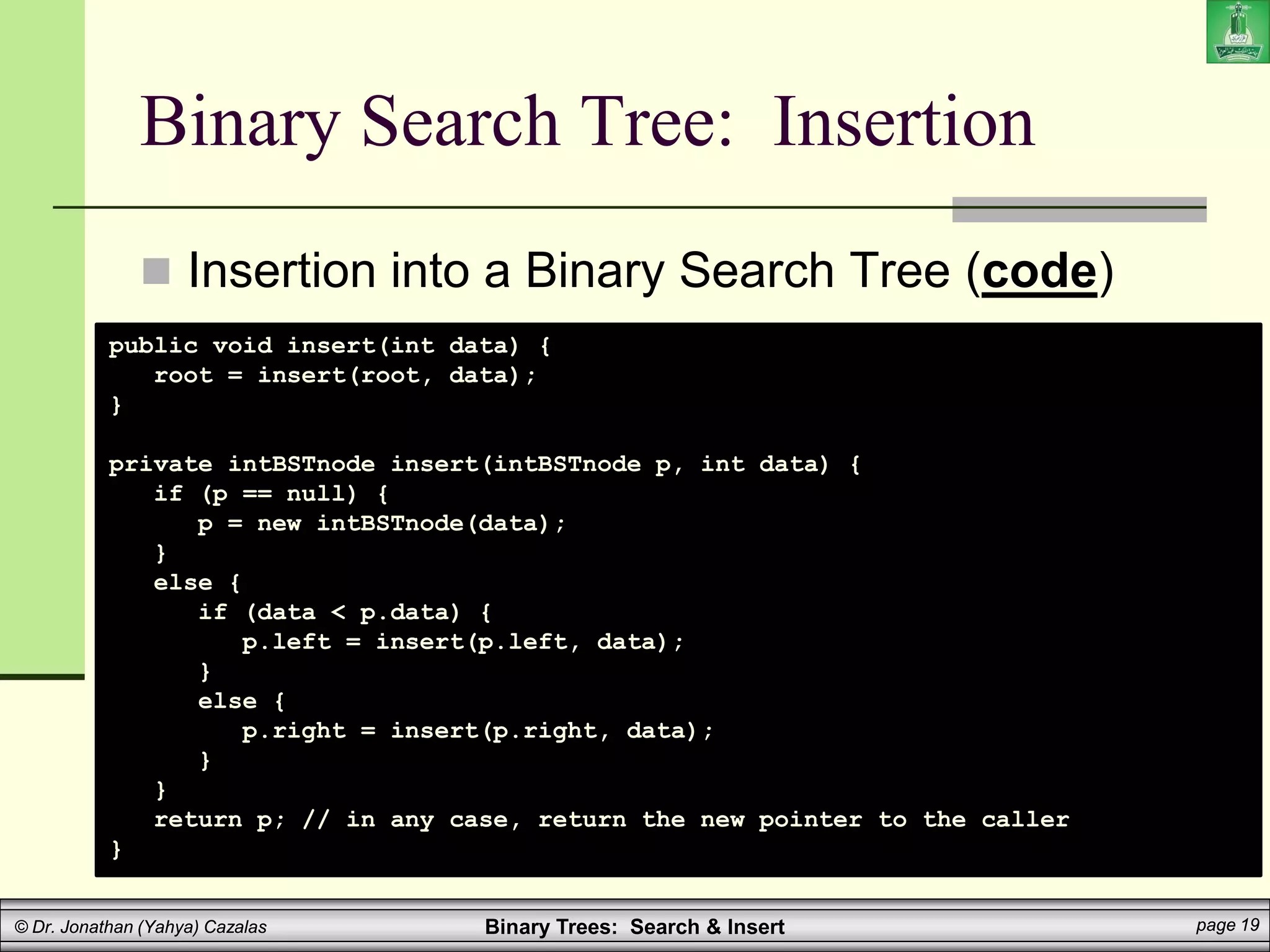
Binary Search Tree: Insertion
Insertion into a Binary Search Tree
Here is a sample main method:
public static void main(String[] args) throws IOException {
intBST myBST = new intBST();
myBST.insert(20);
myBST.insert(18);
myBST.insert(33);
}](https://image.slidesharecdn.com/cpcs20418binarytrees2-210408140723/75/binary_trees2-20-2048.jpg)