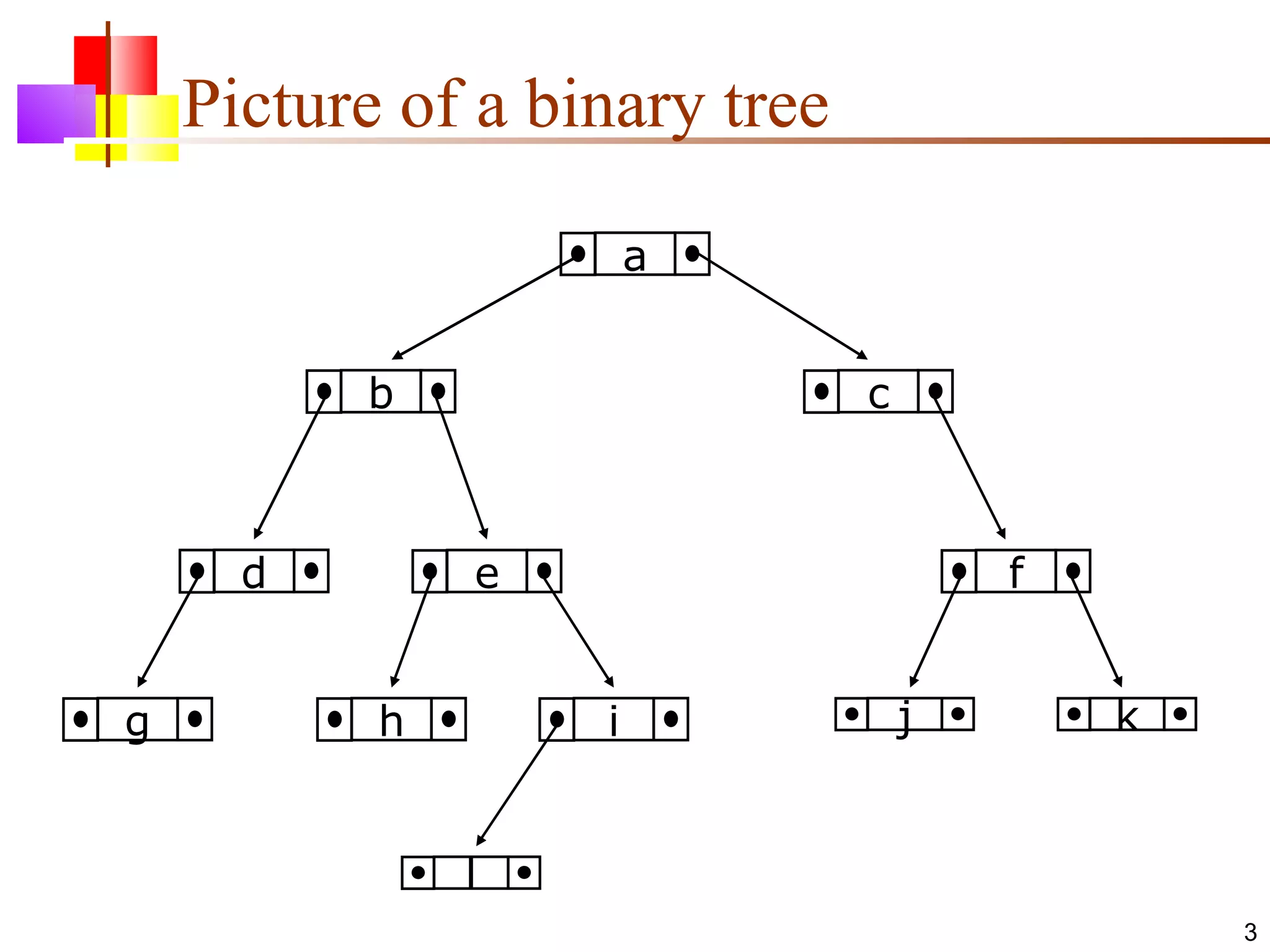
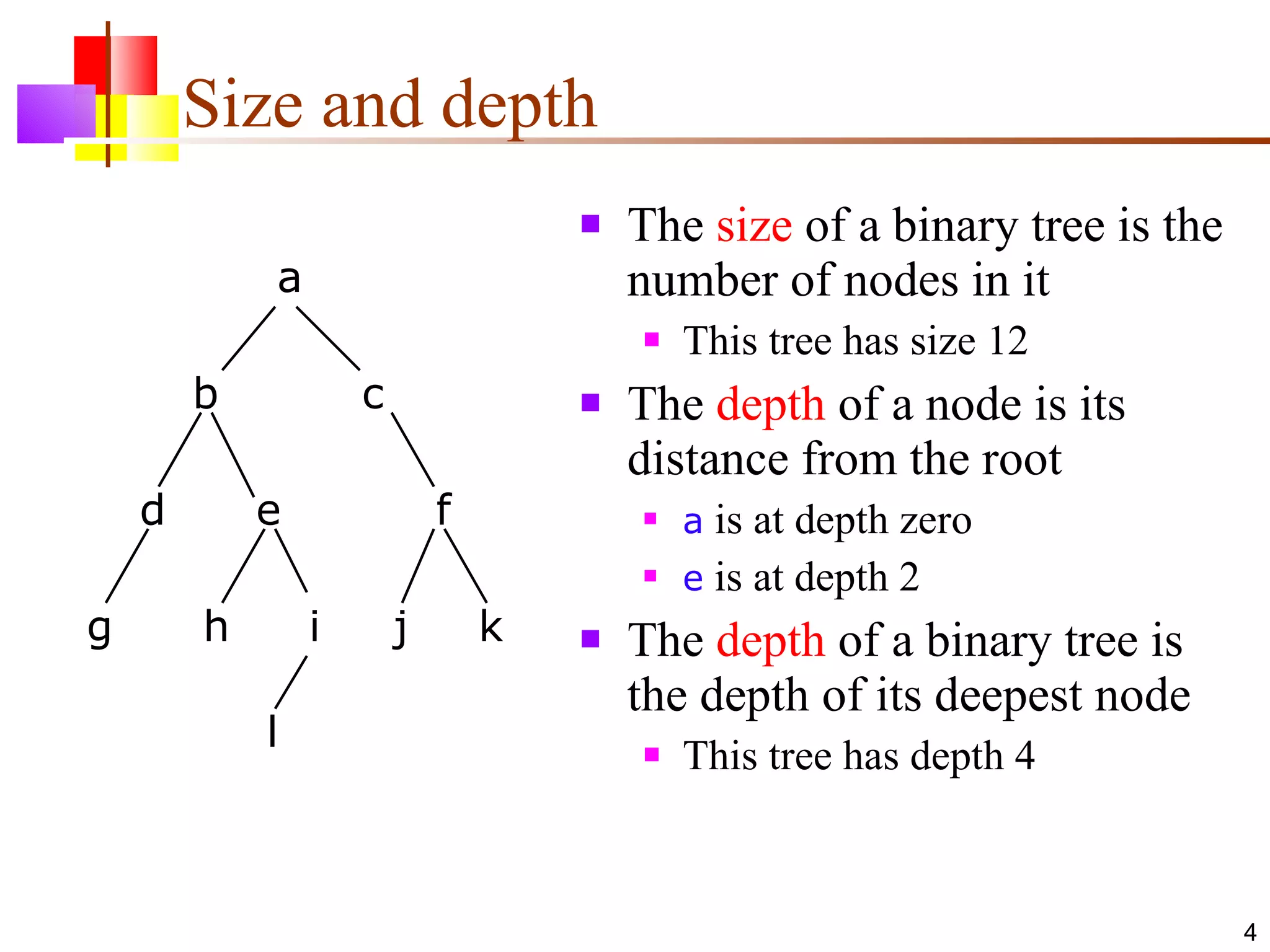
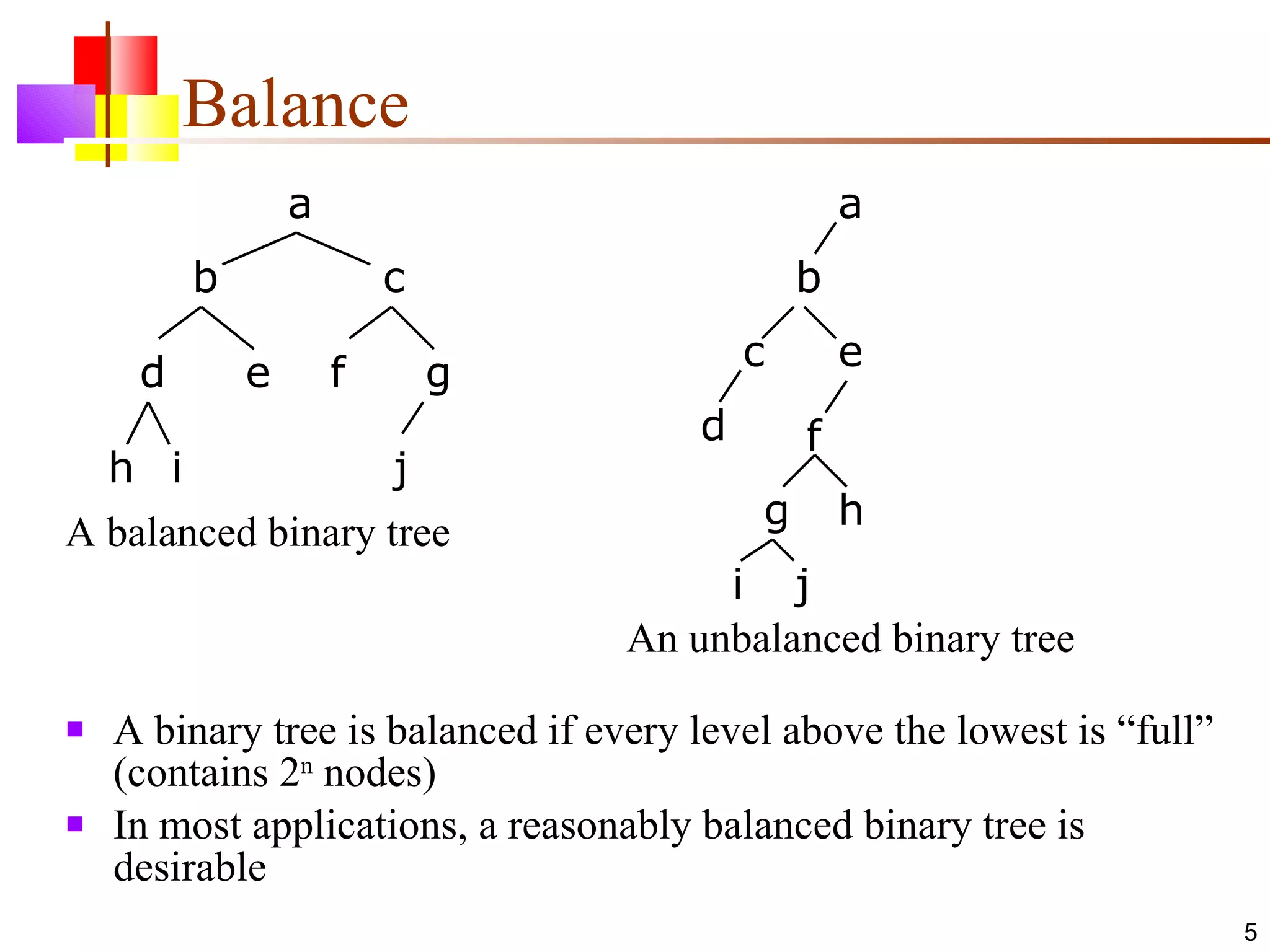
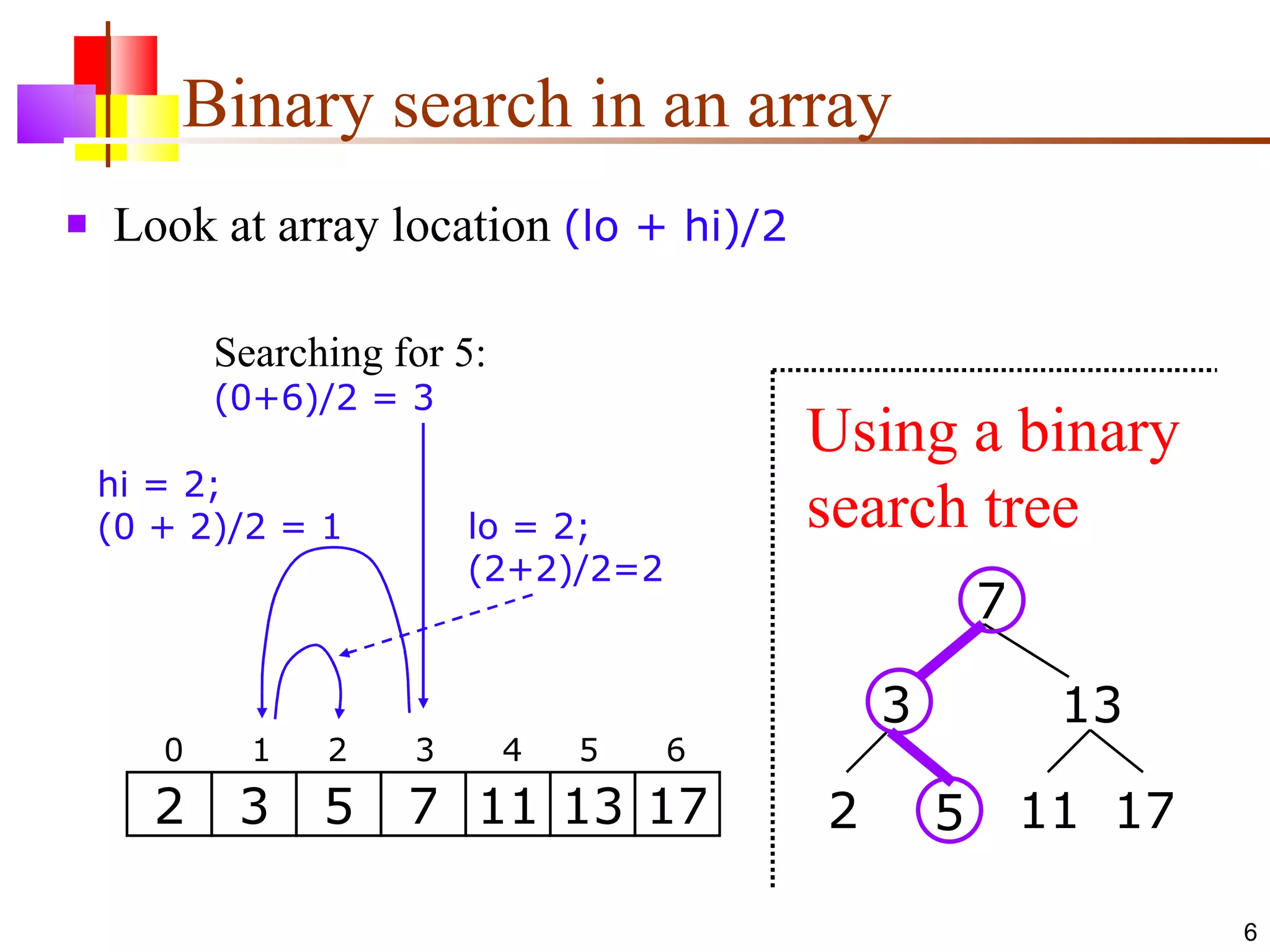
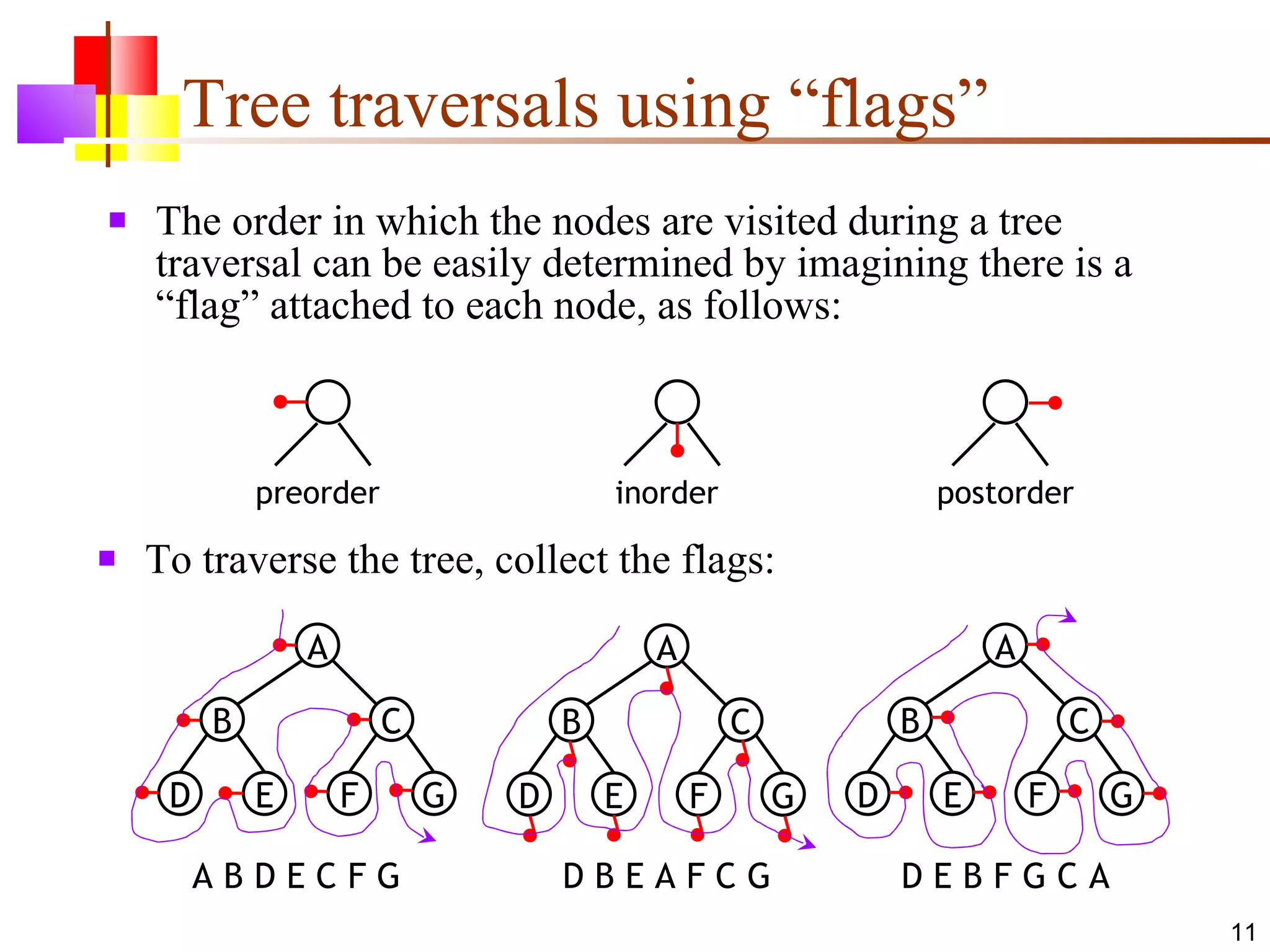
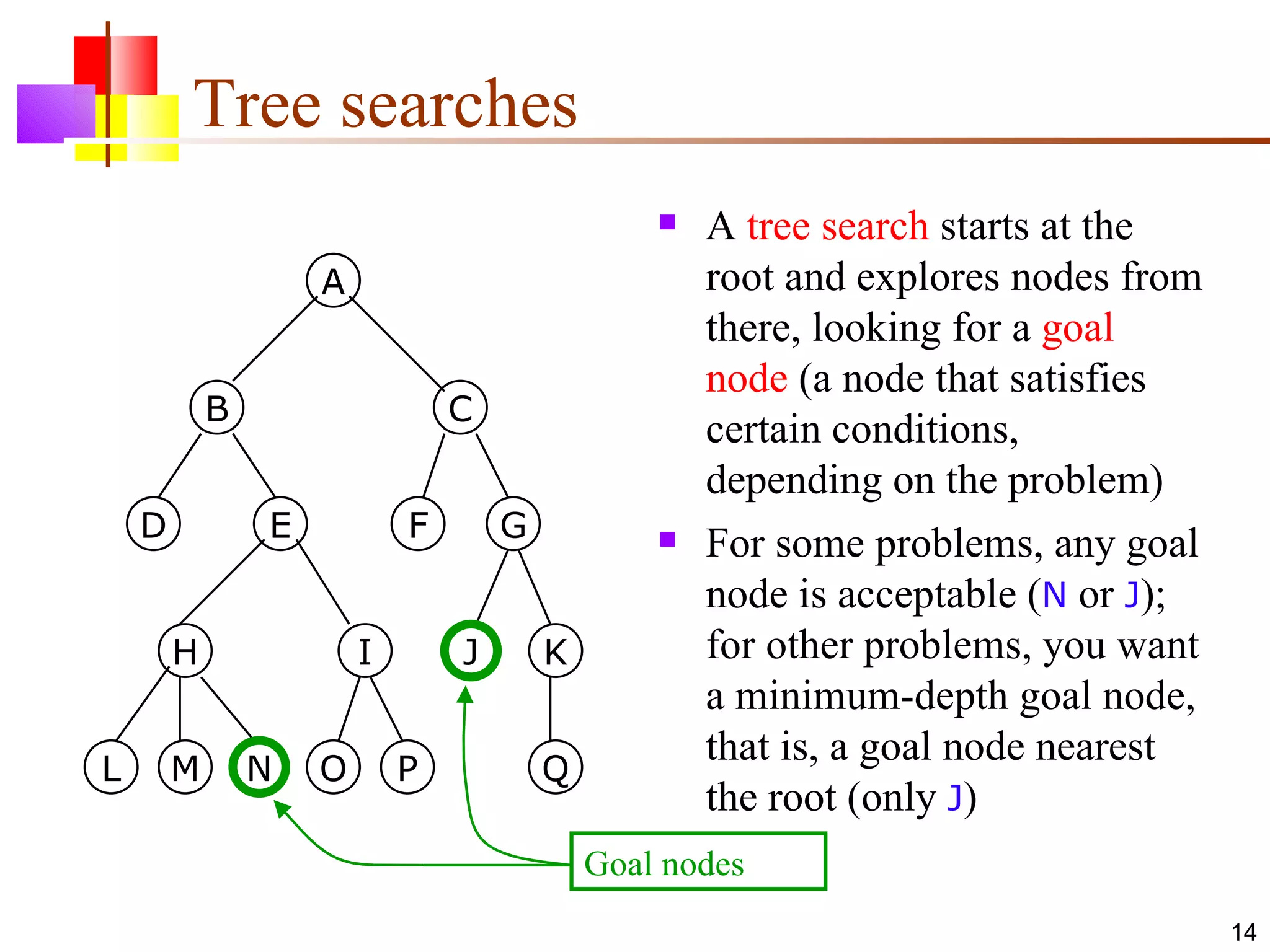
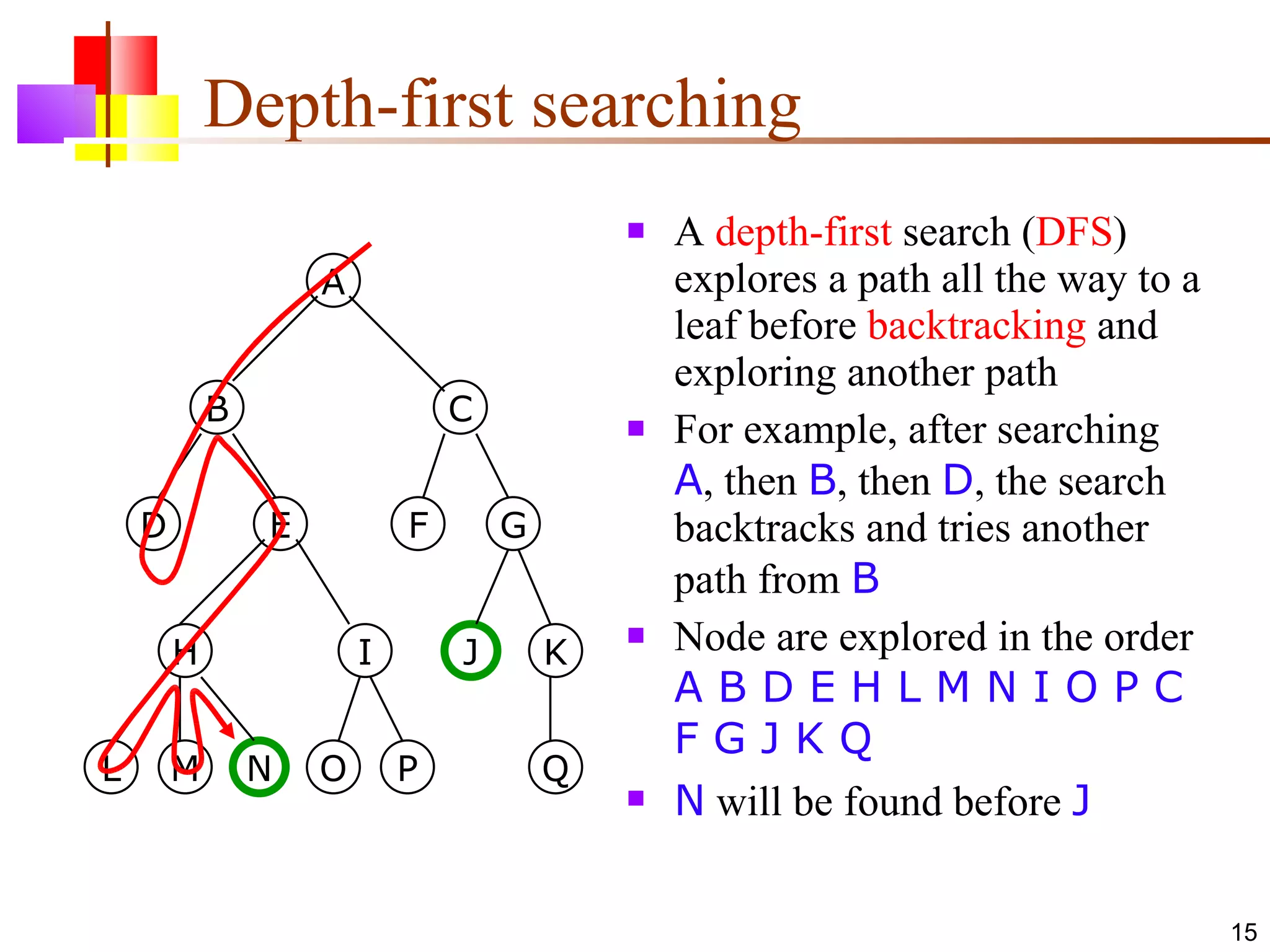
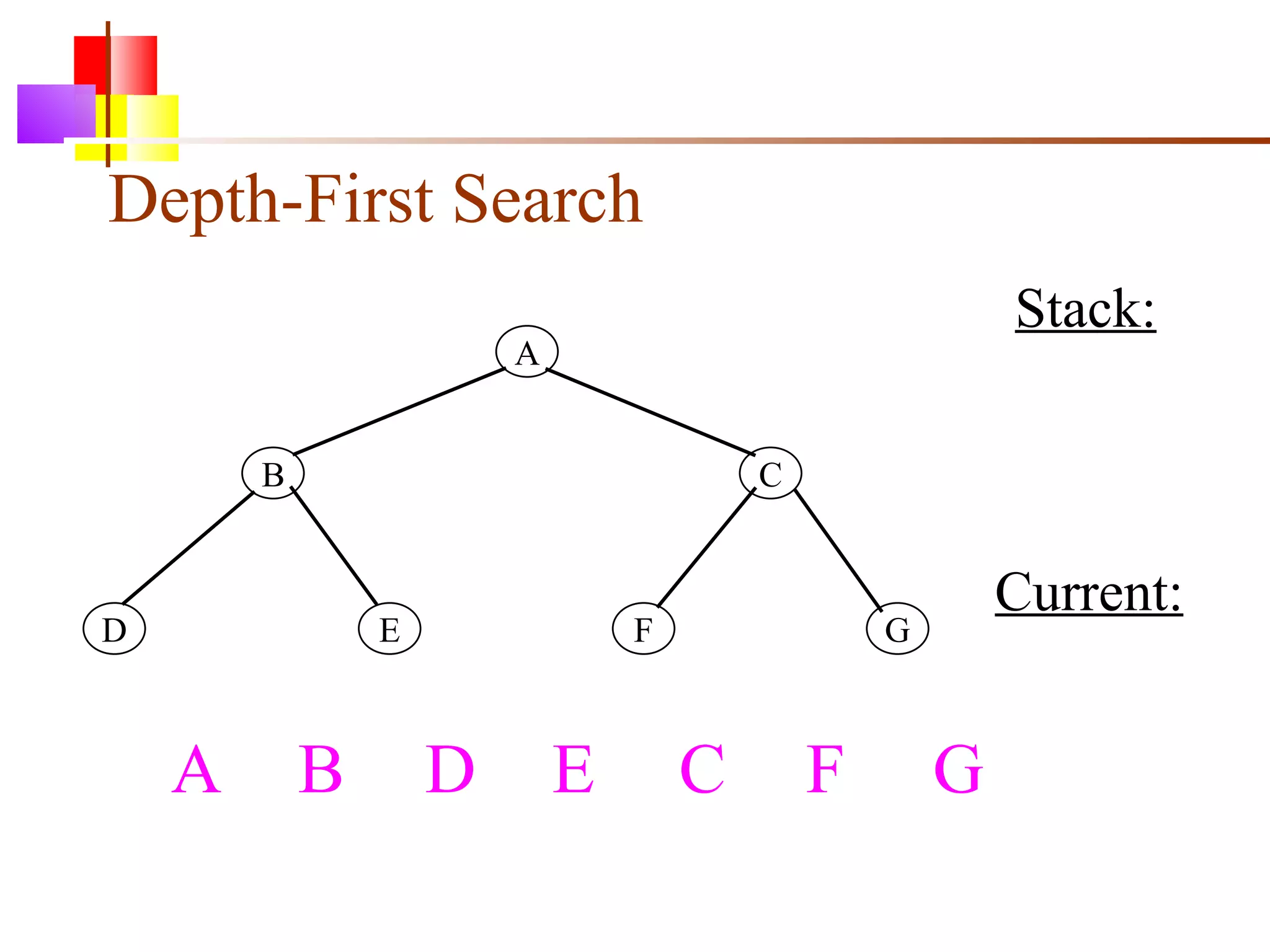
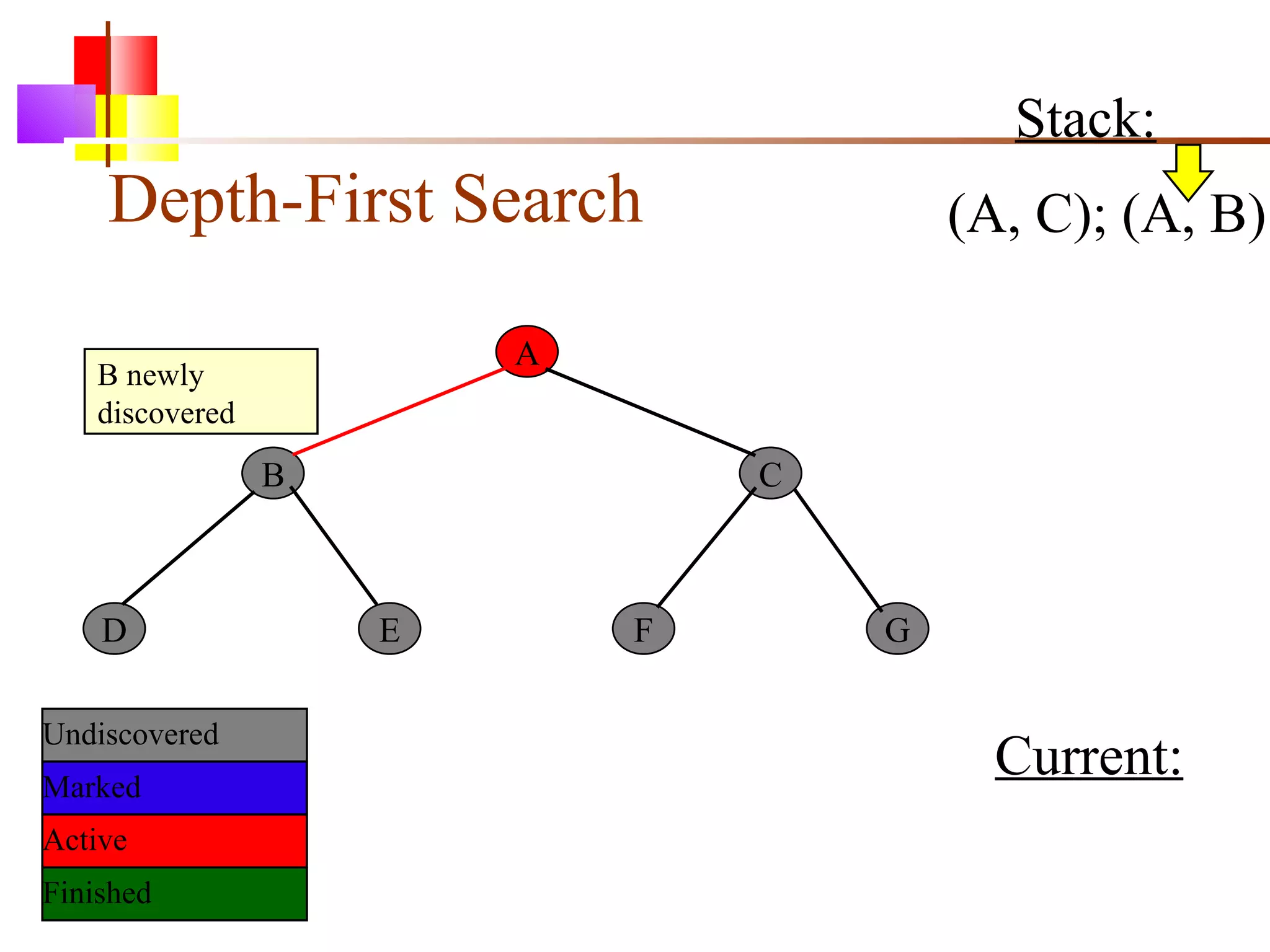
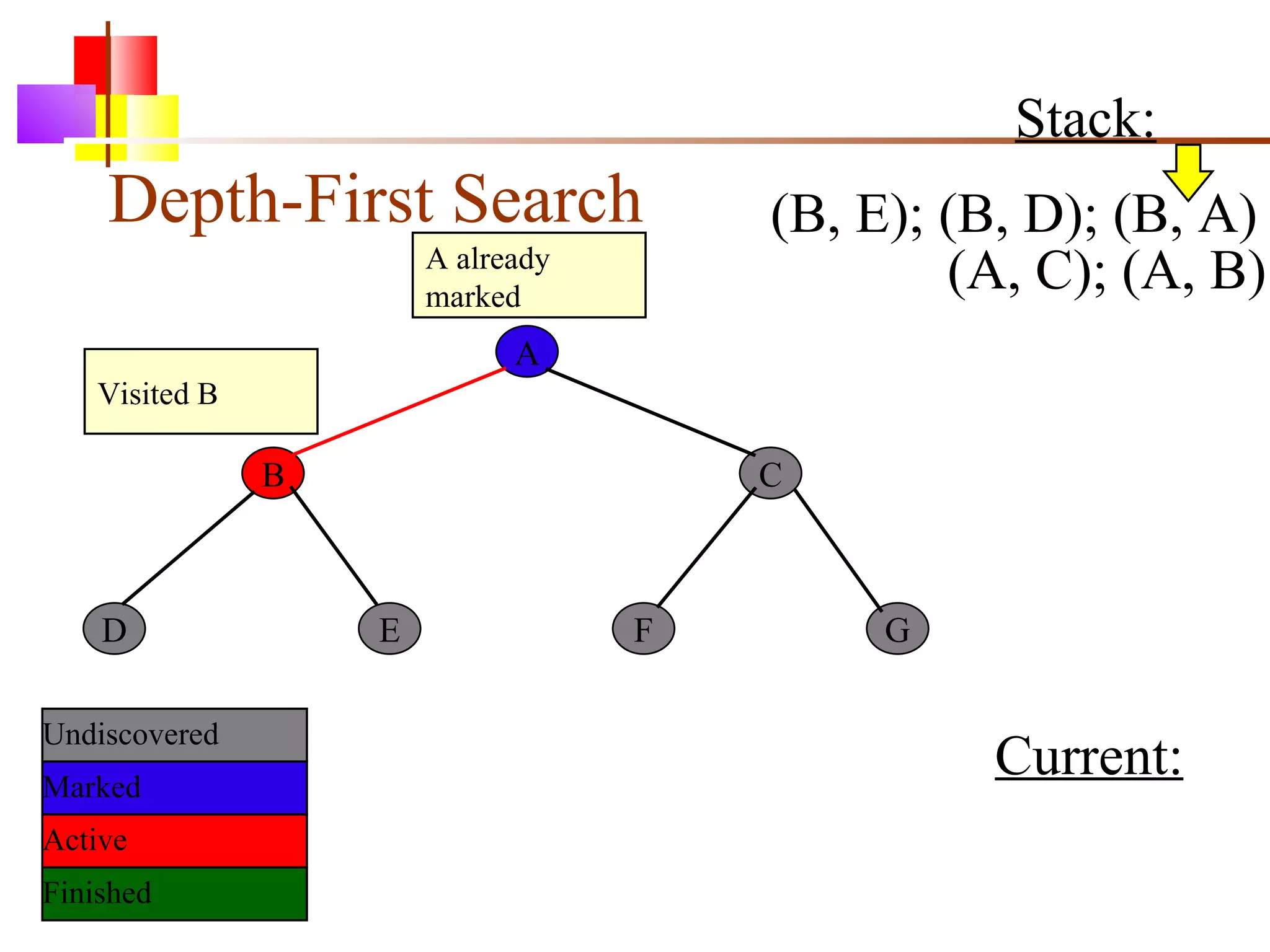
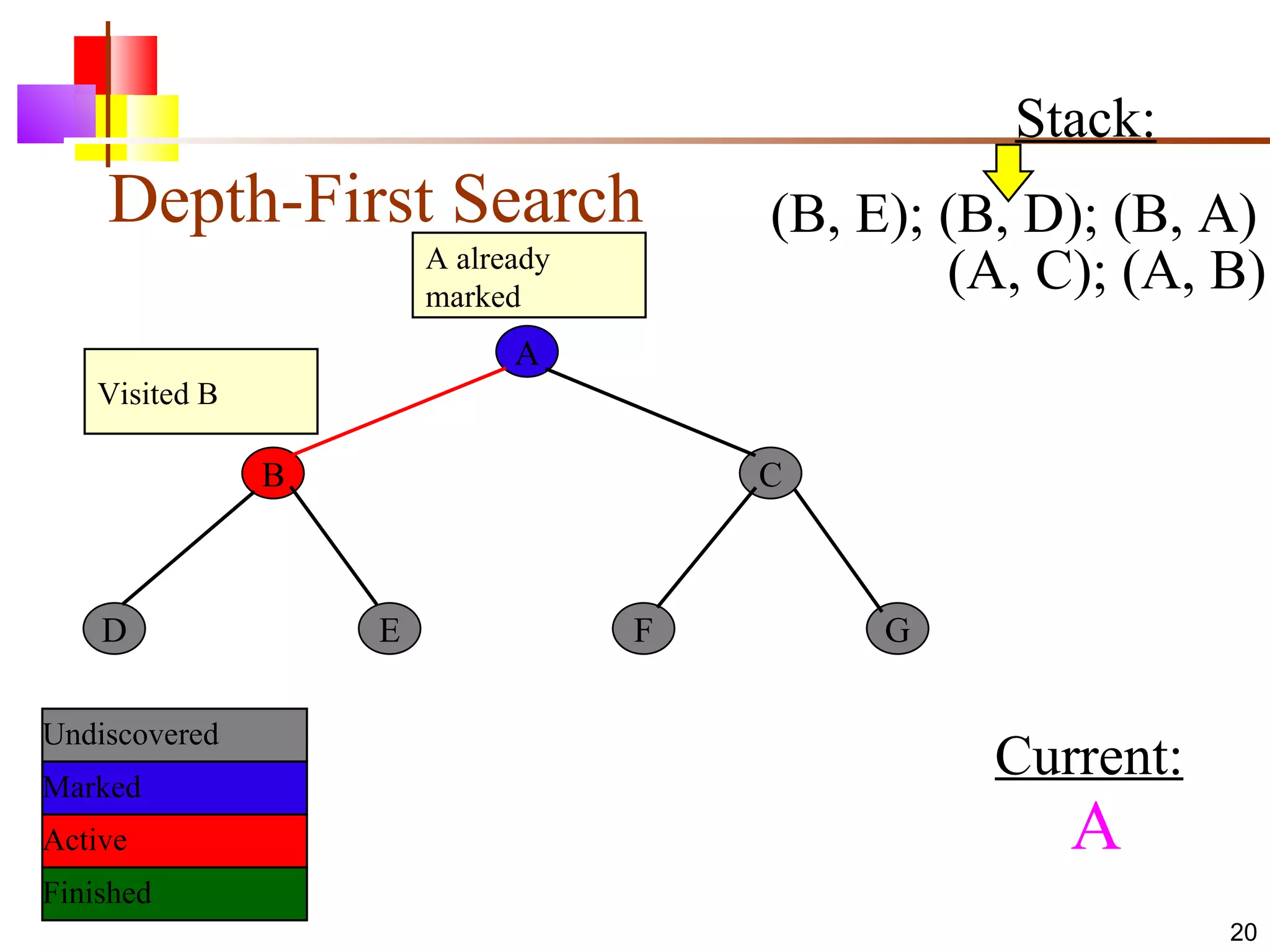
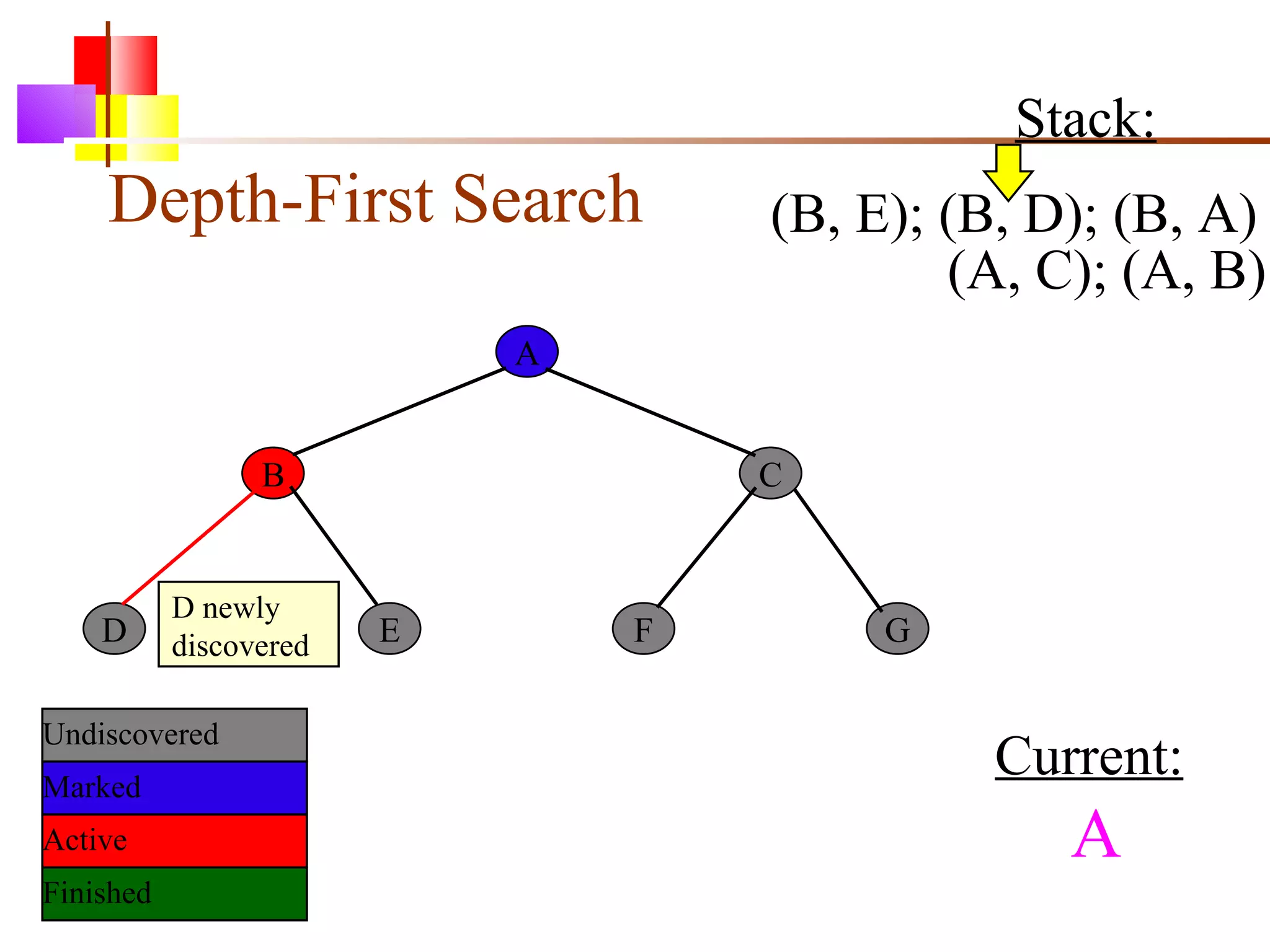
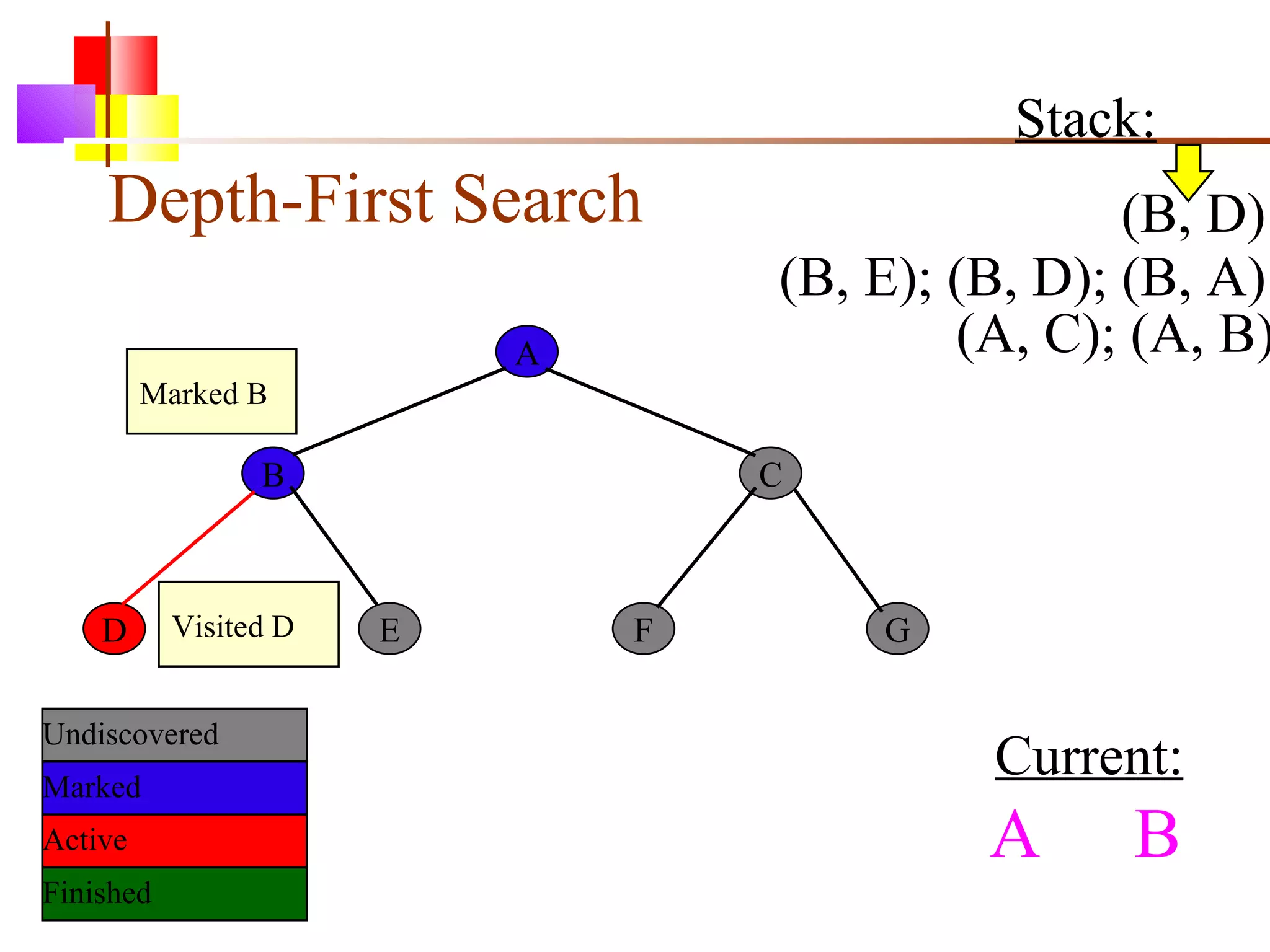
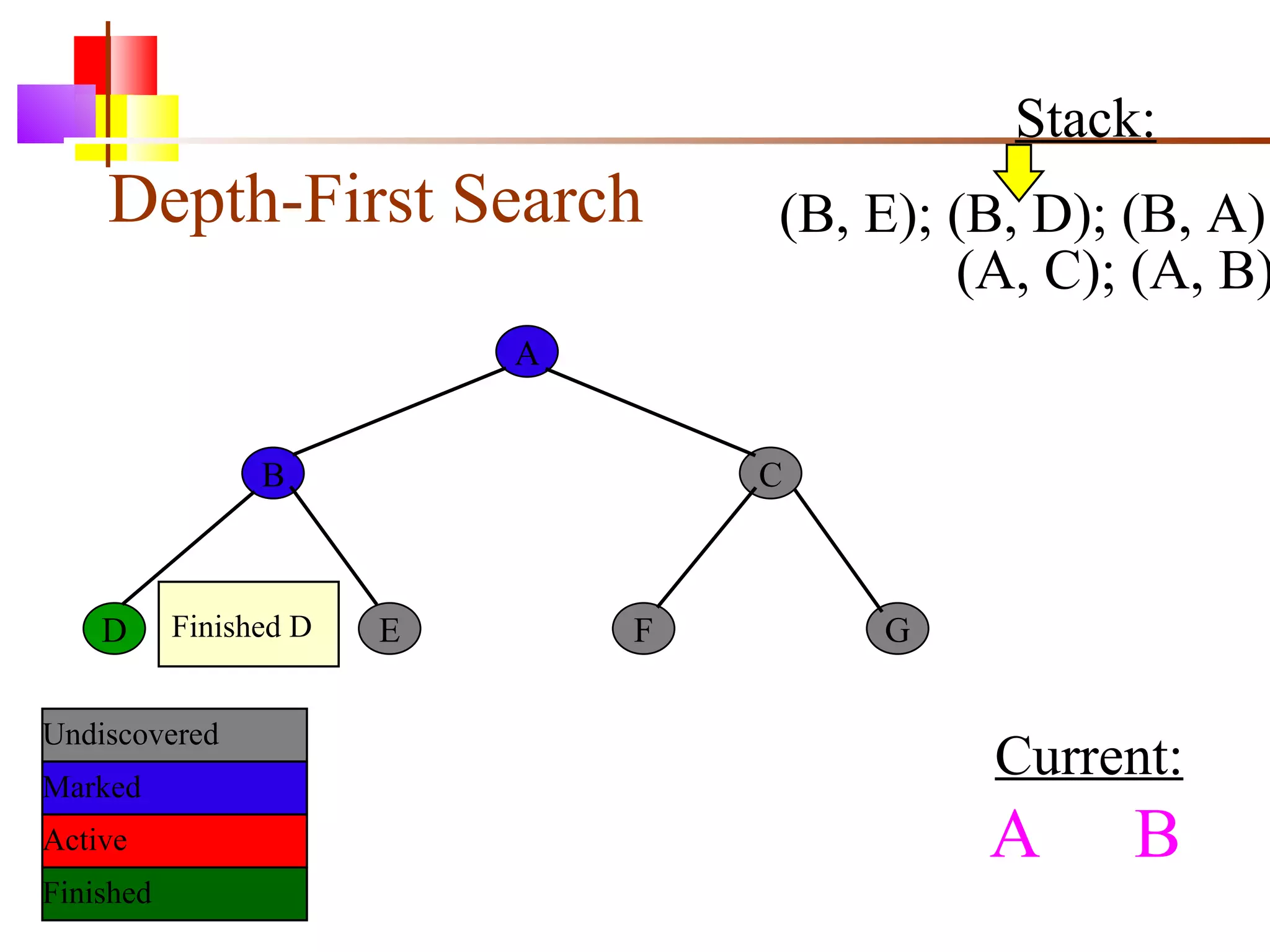
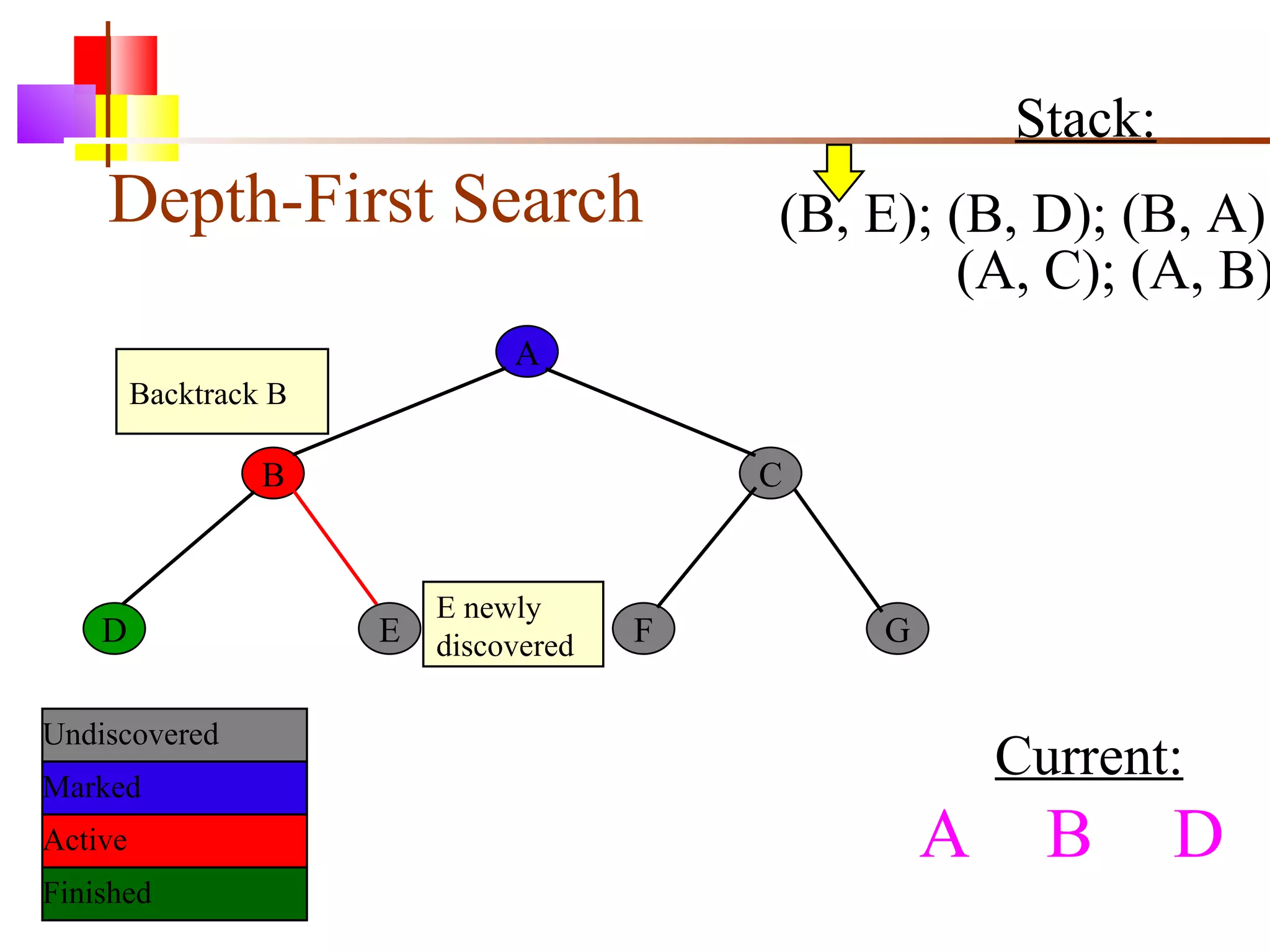
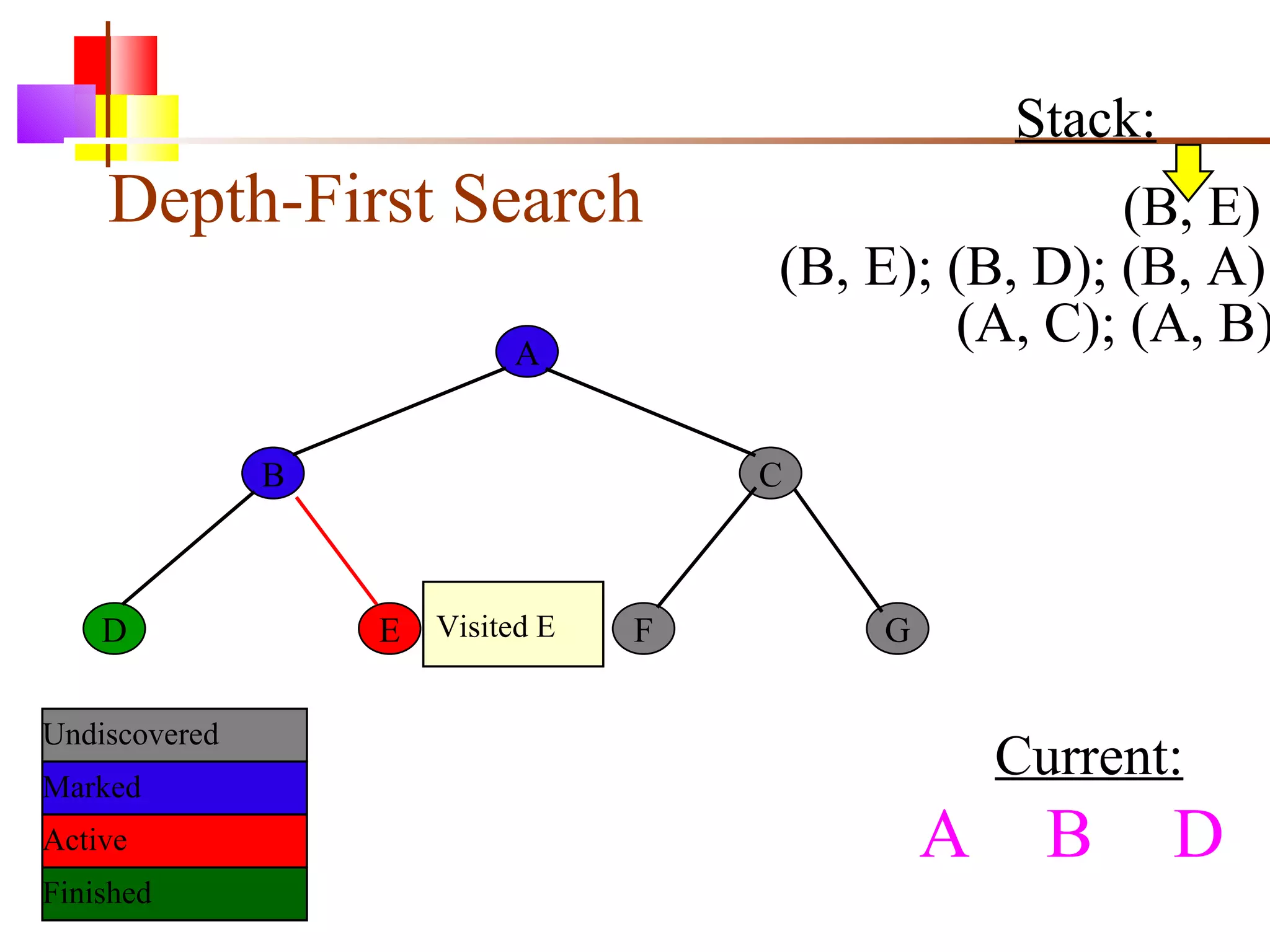
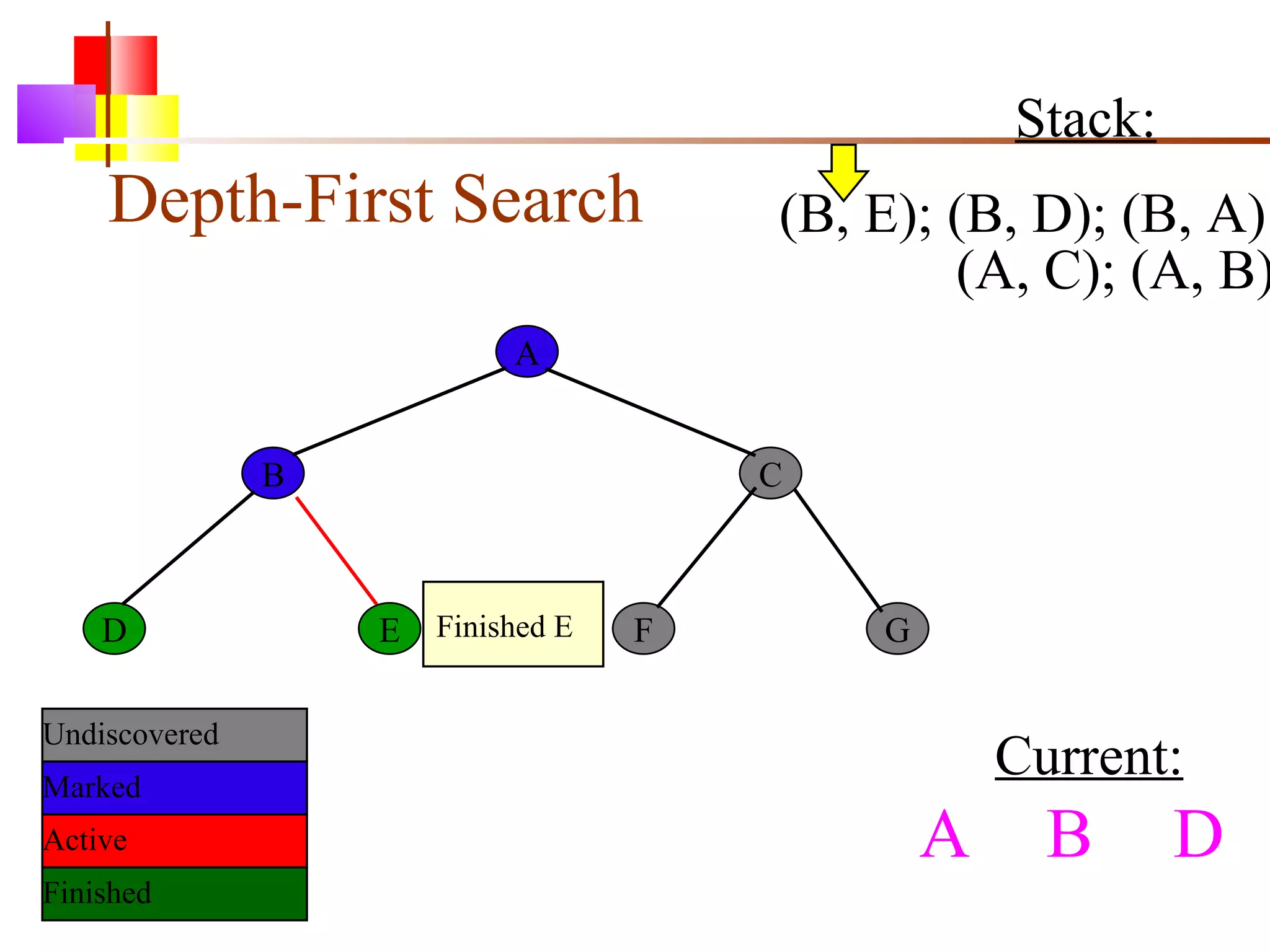
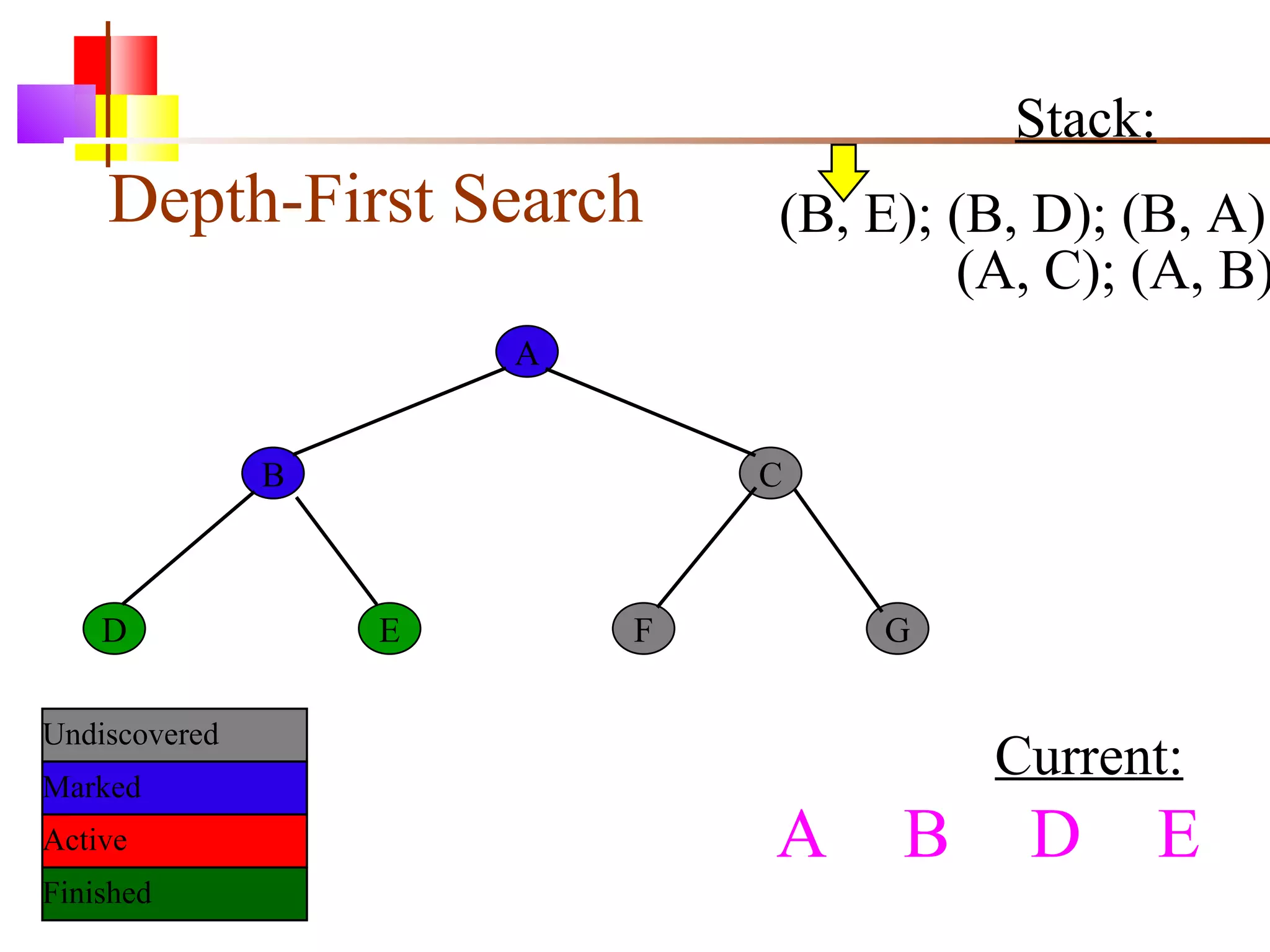
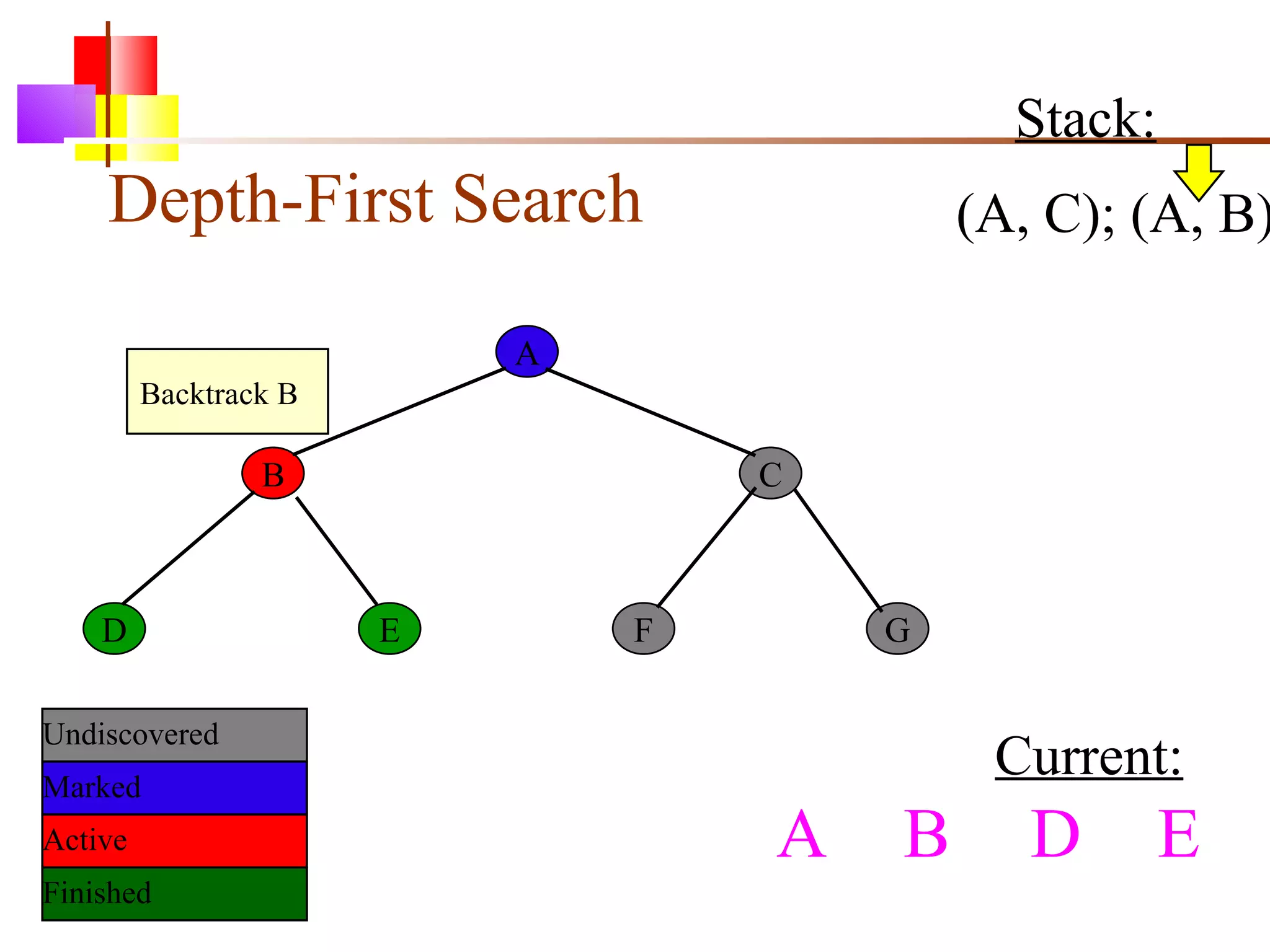
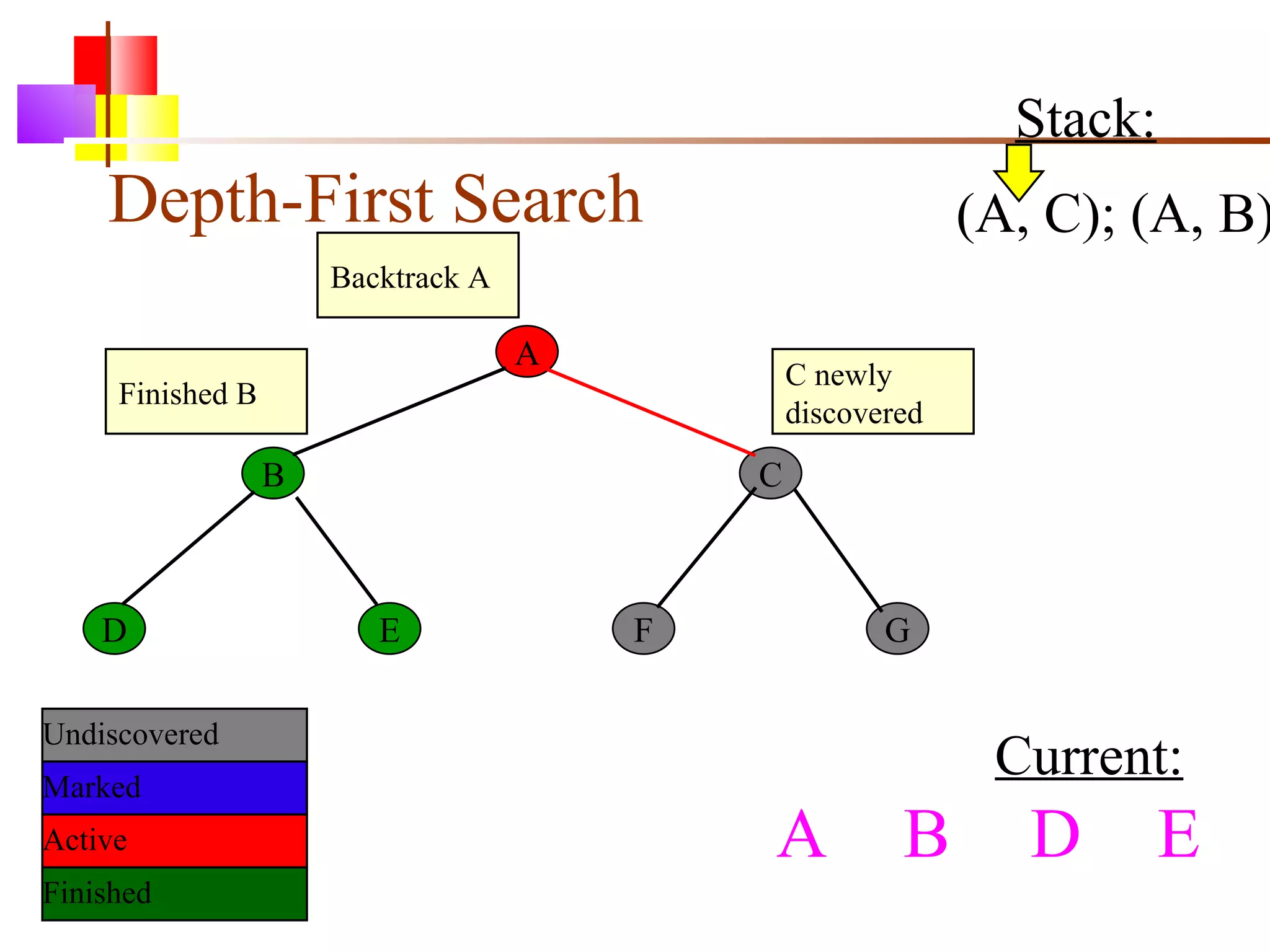
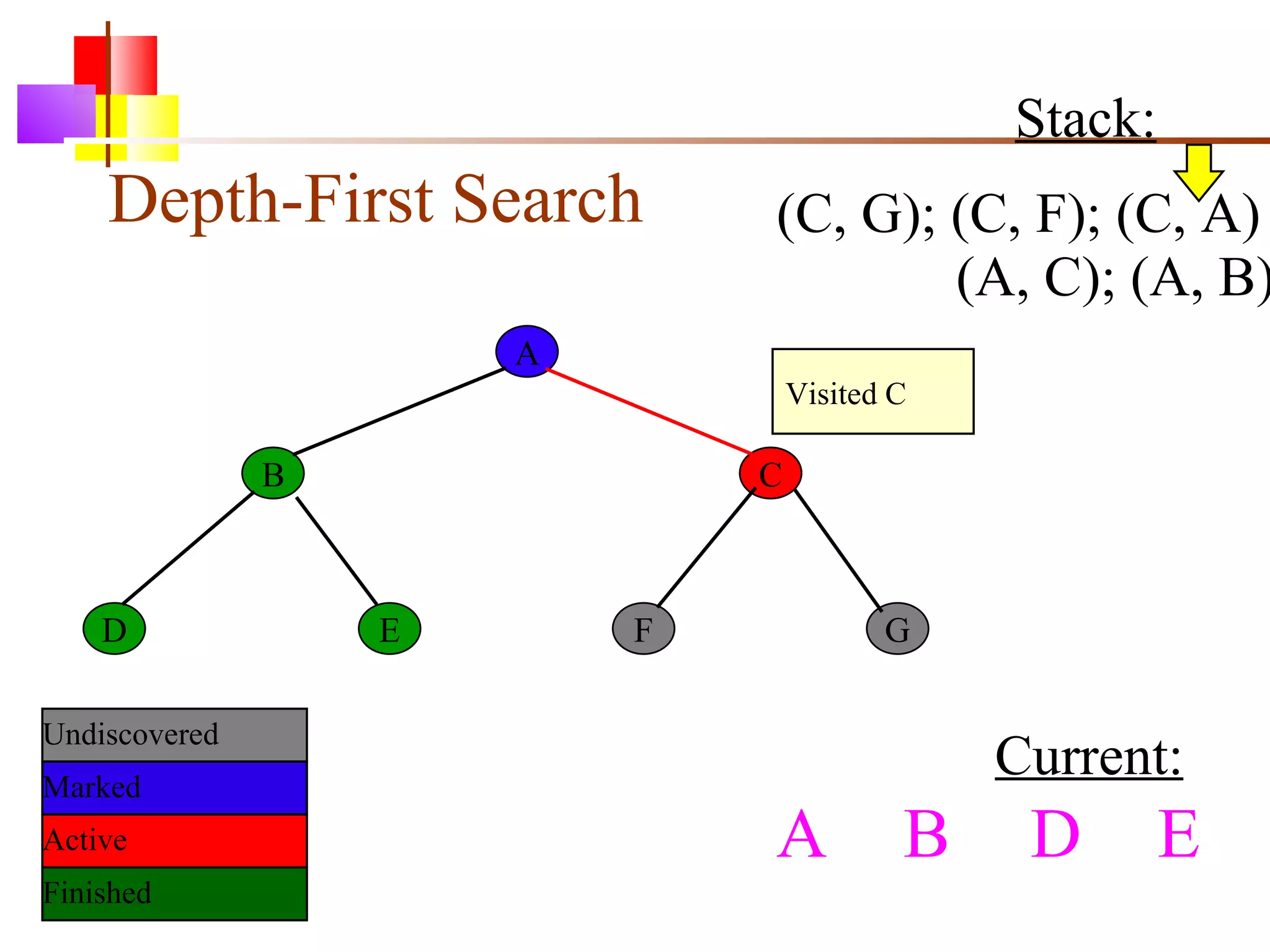
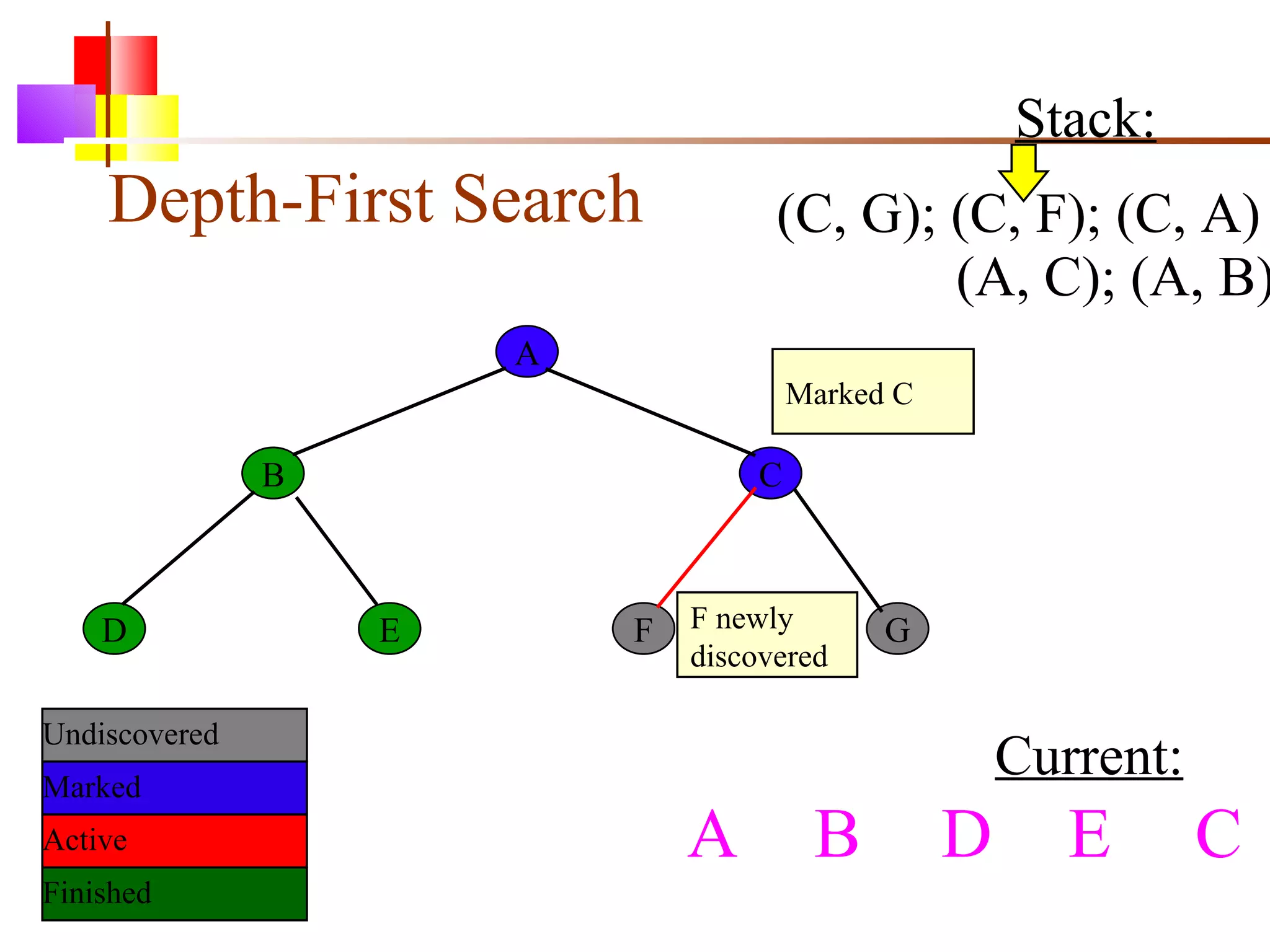
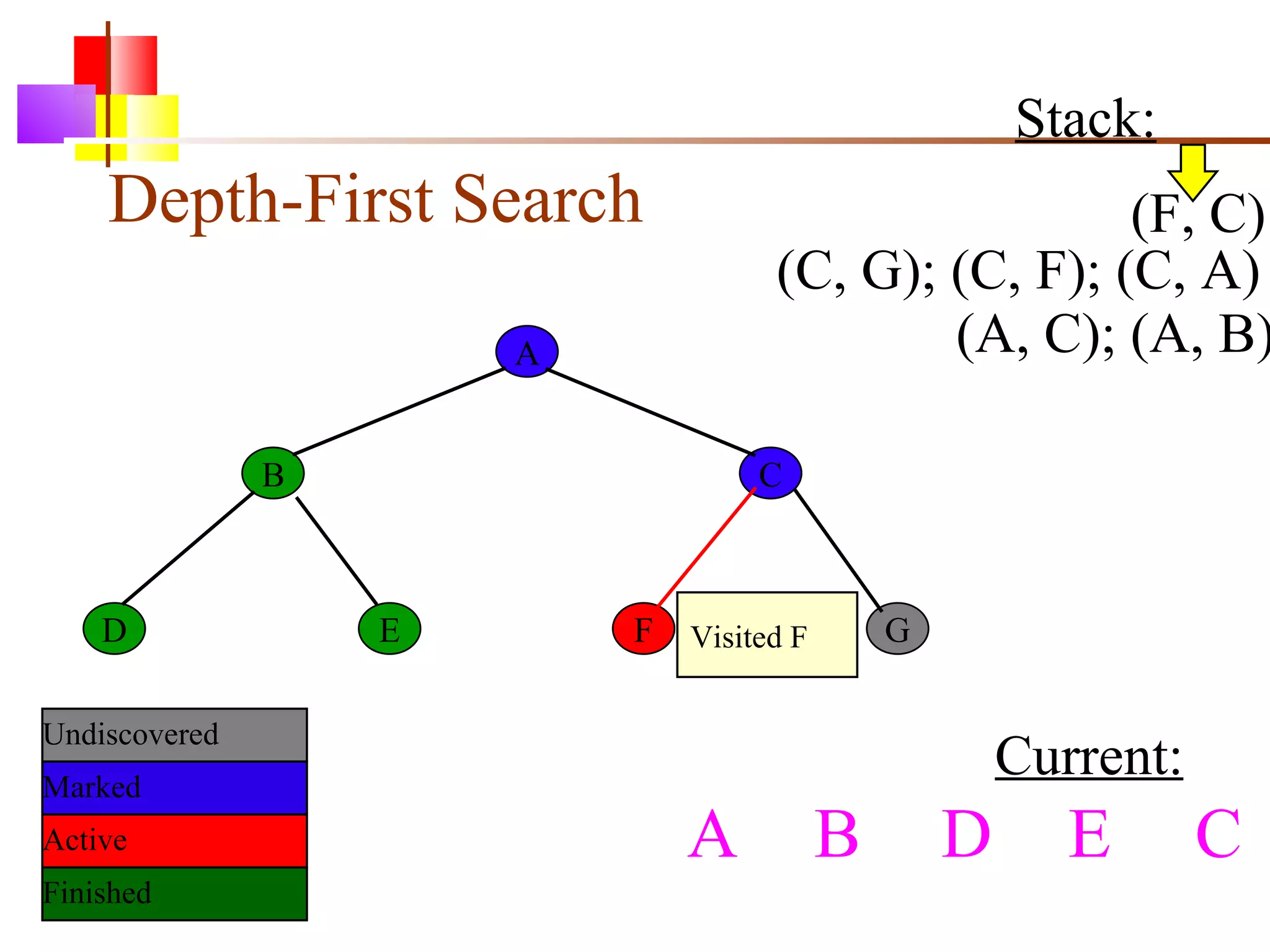
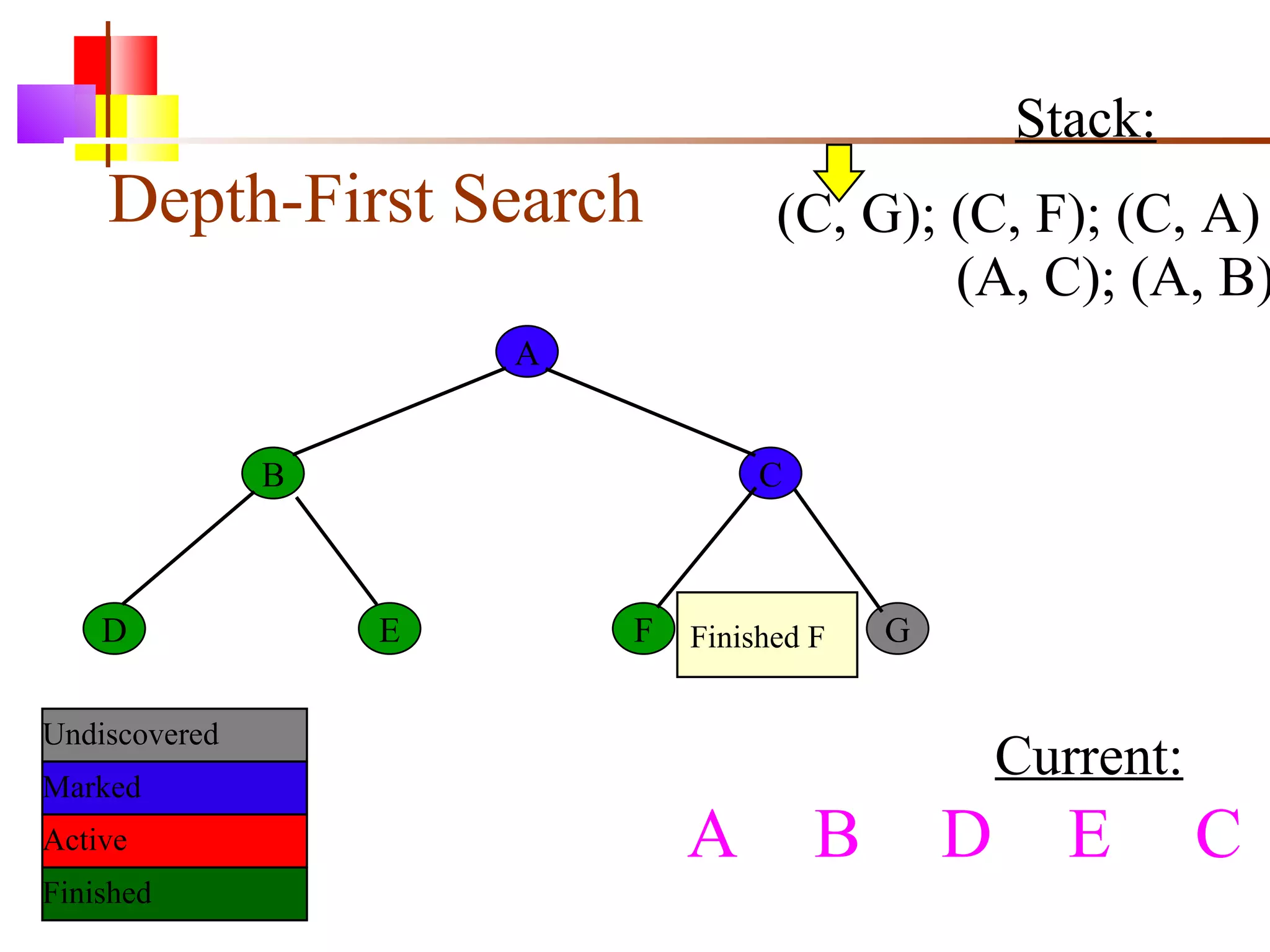
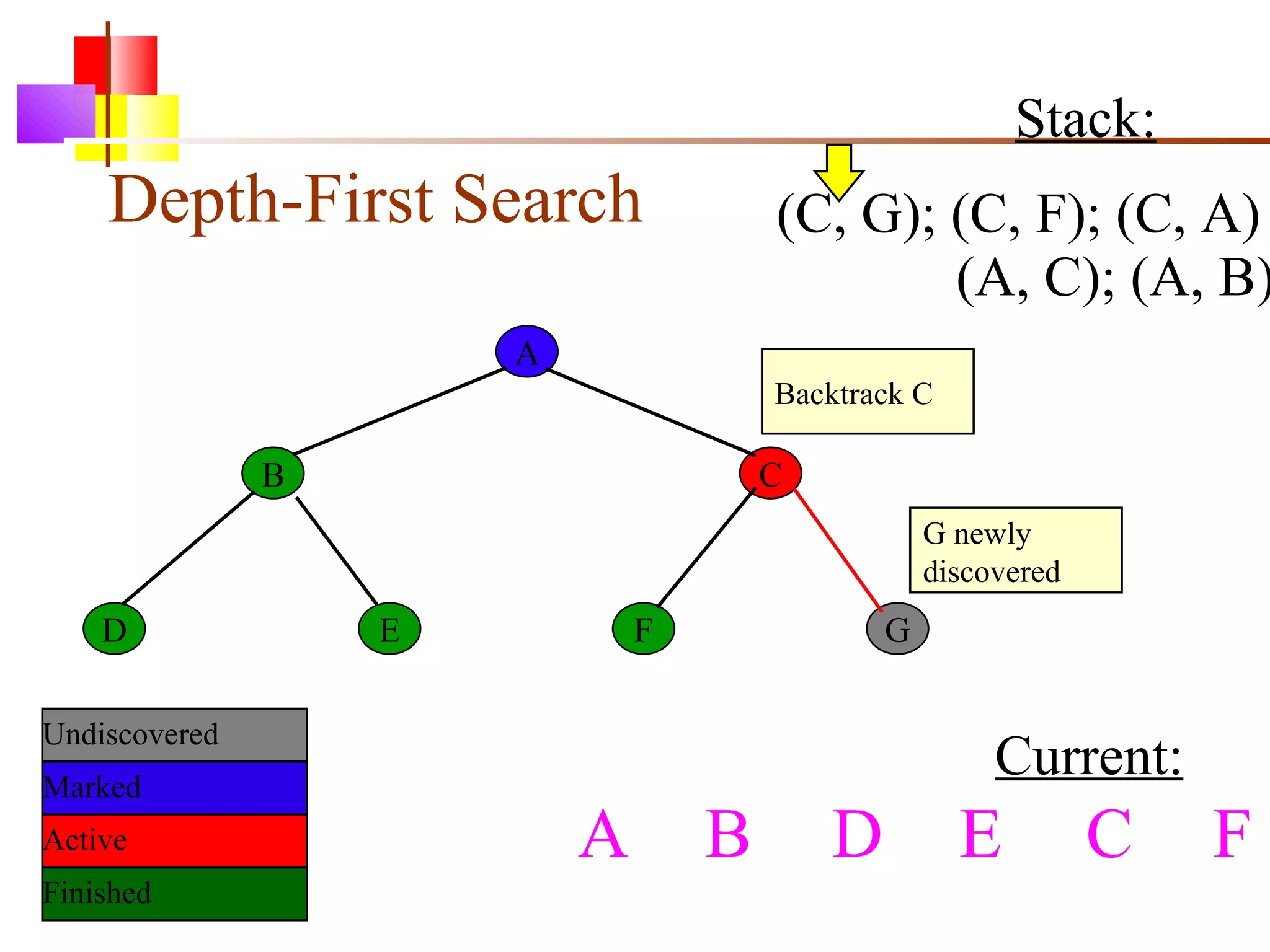
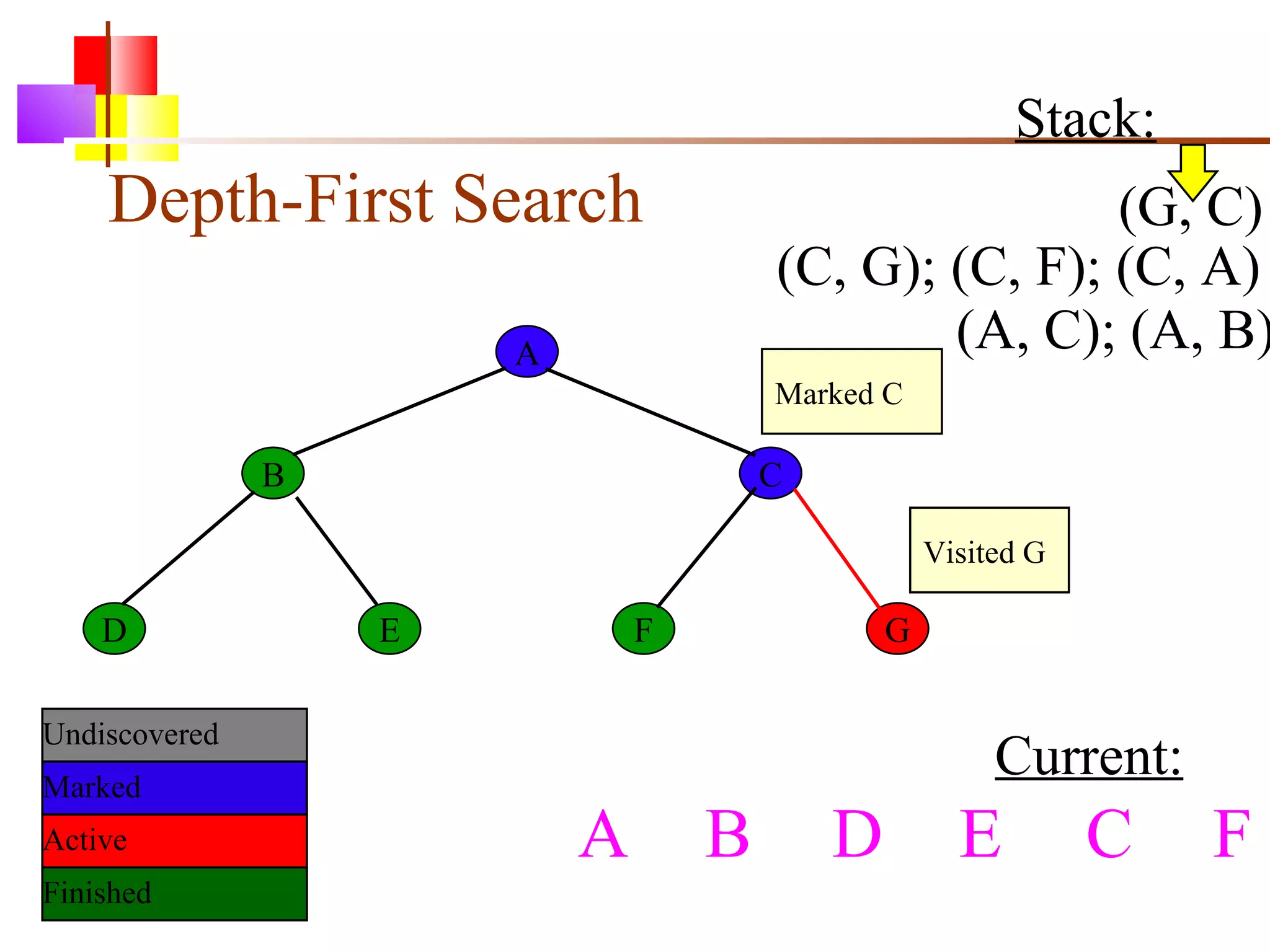
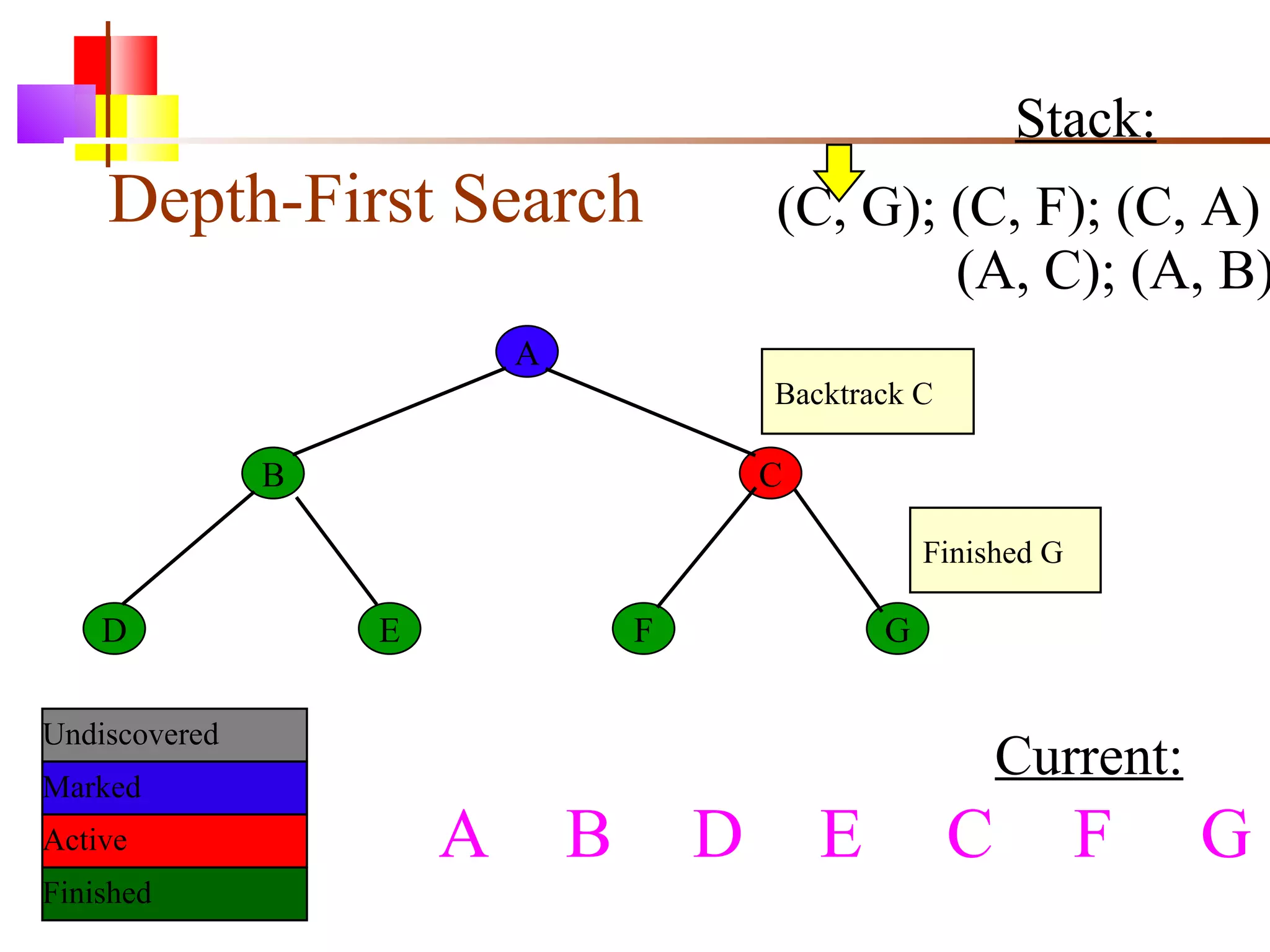
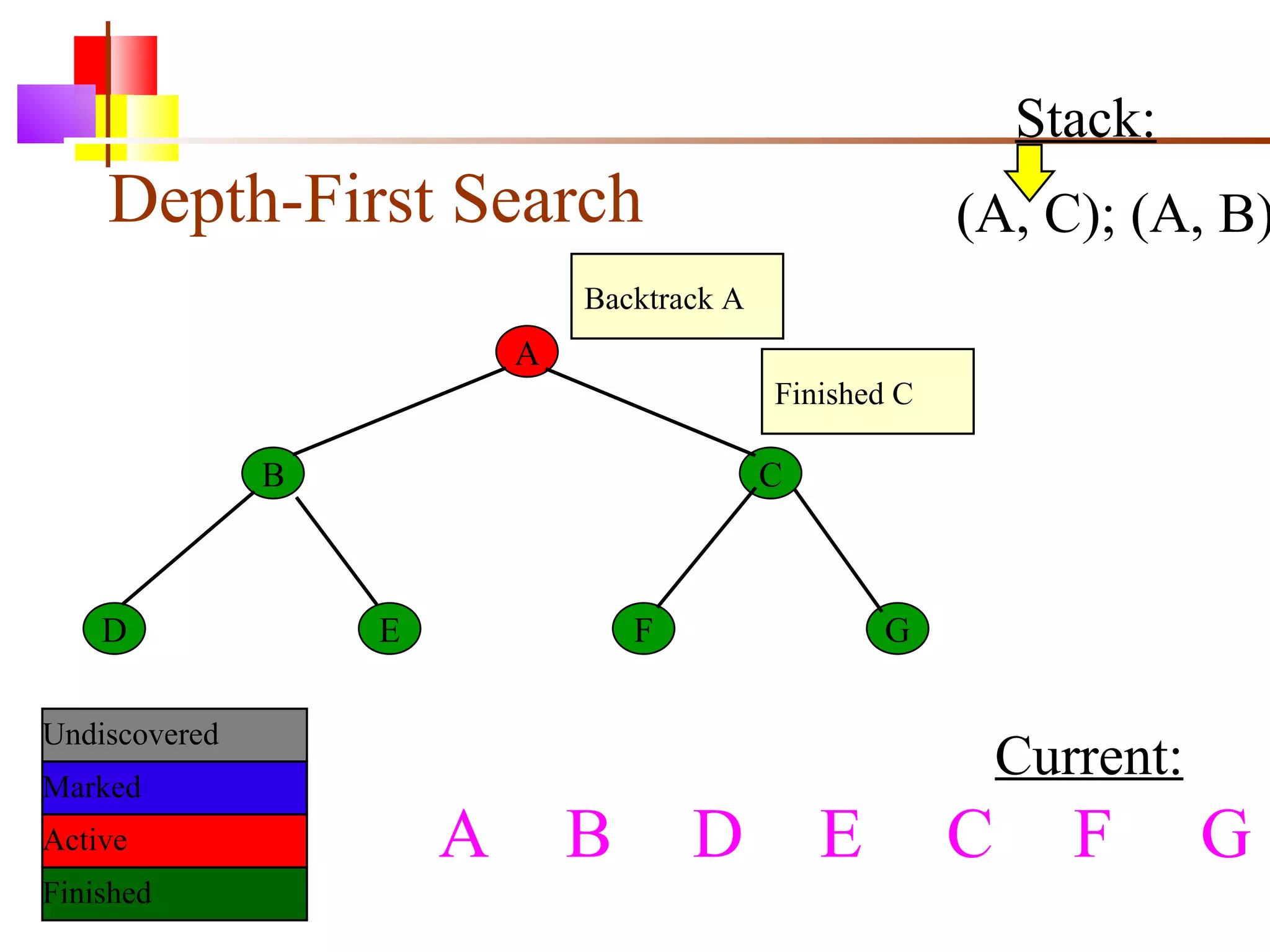
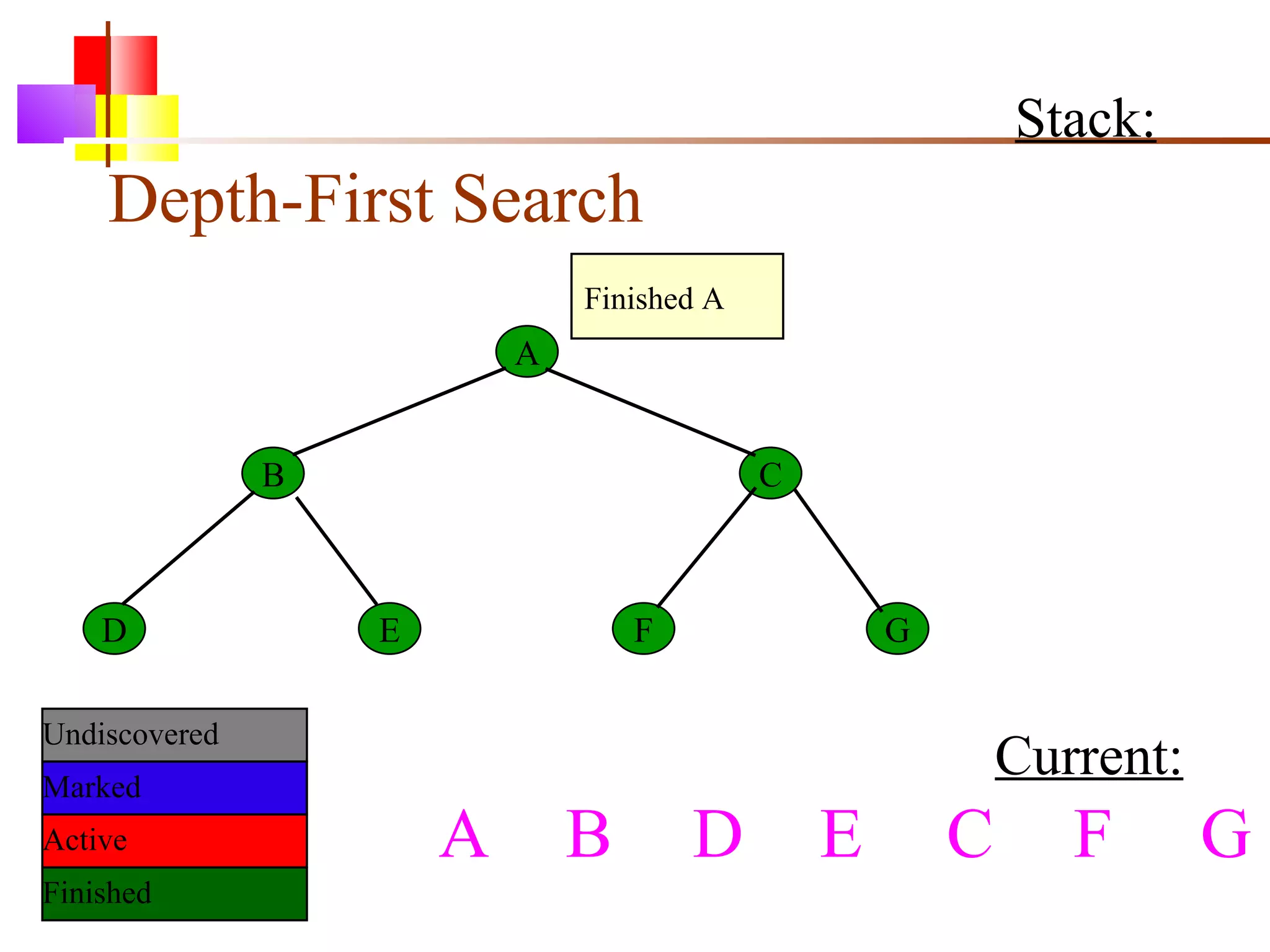
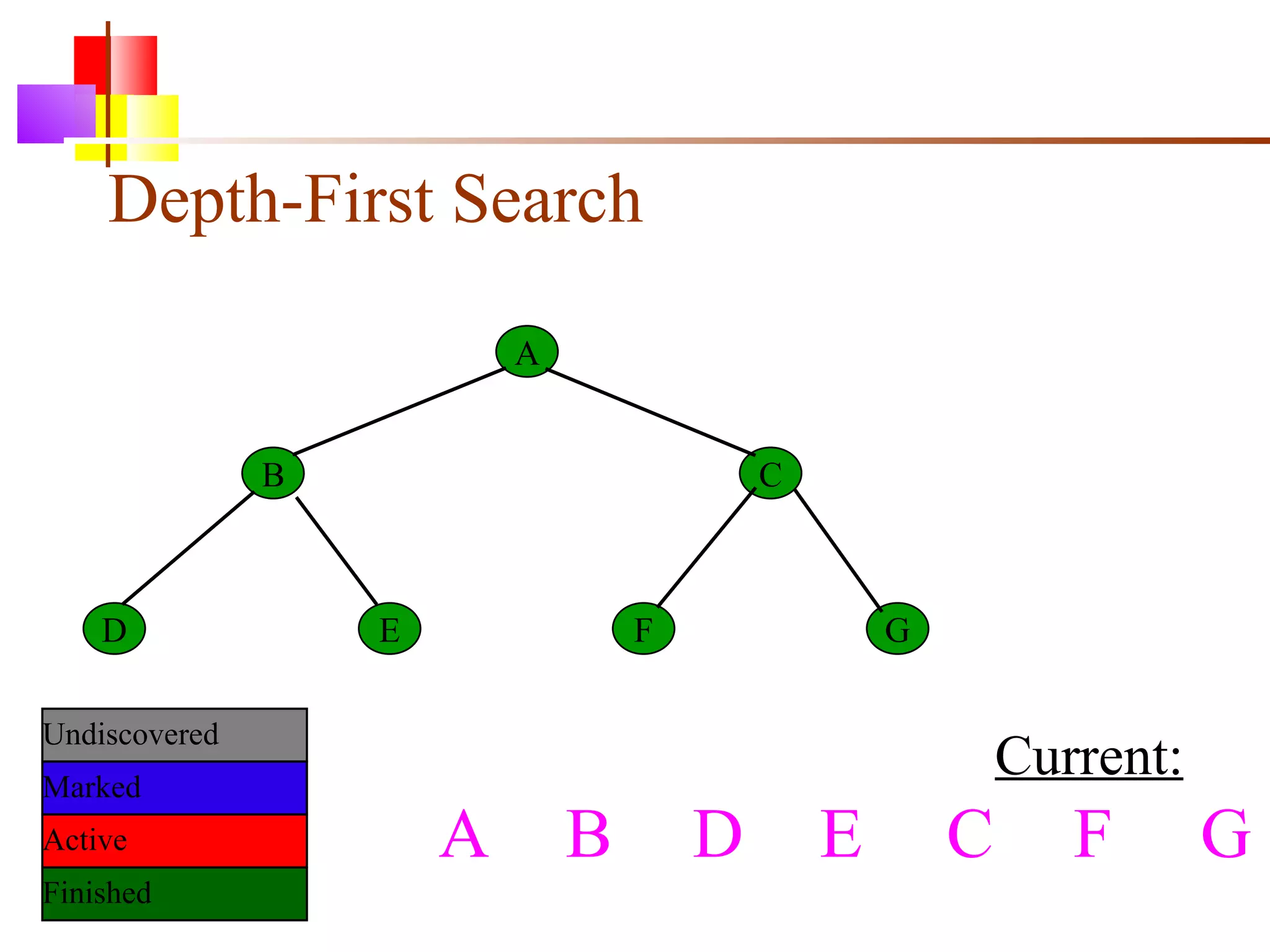
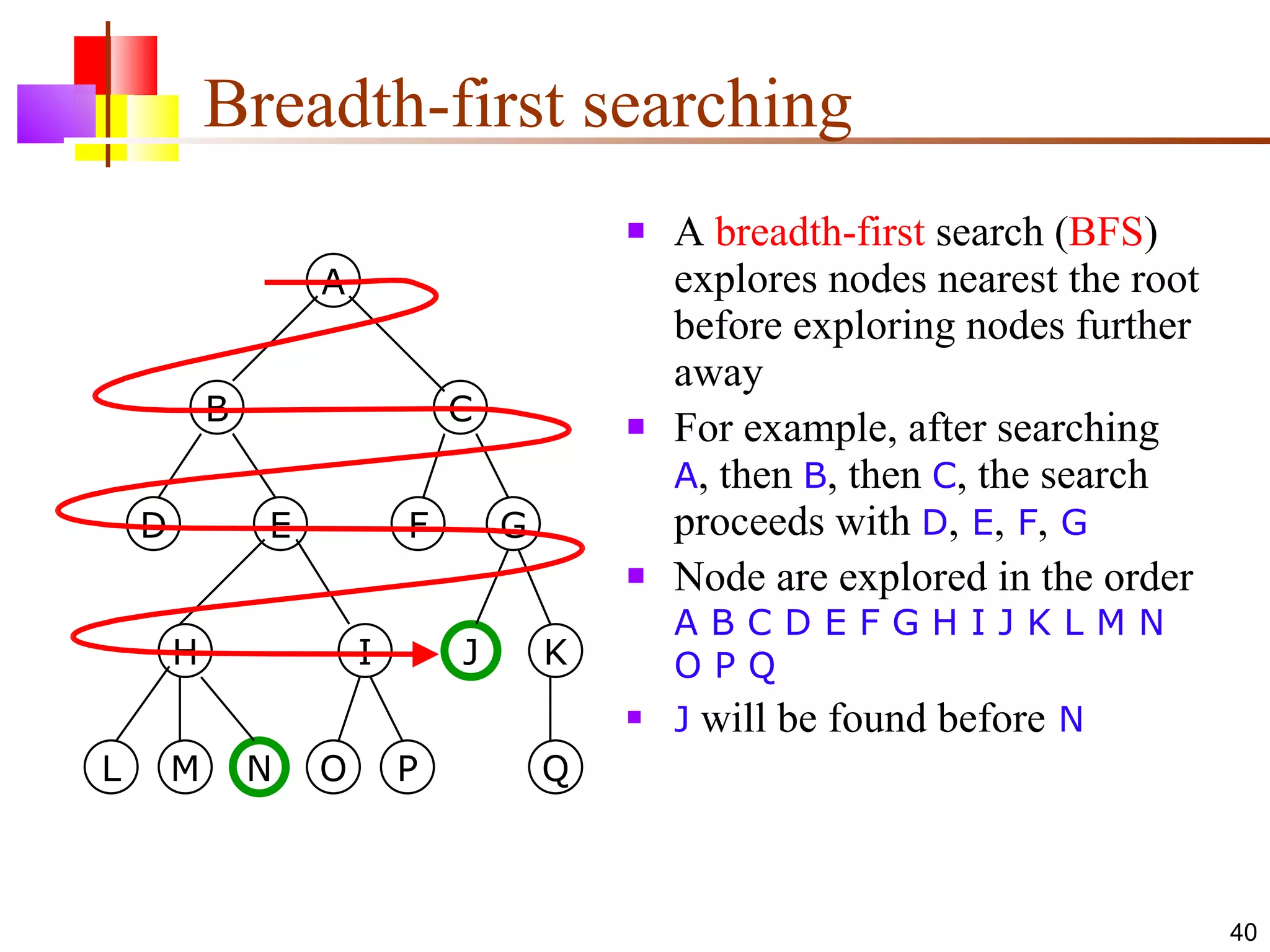
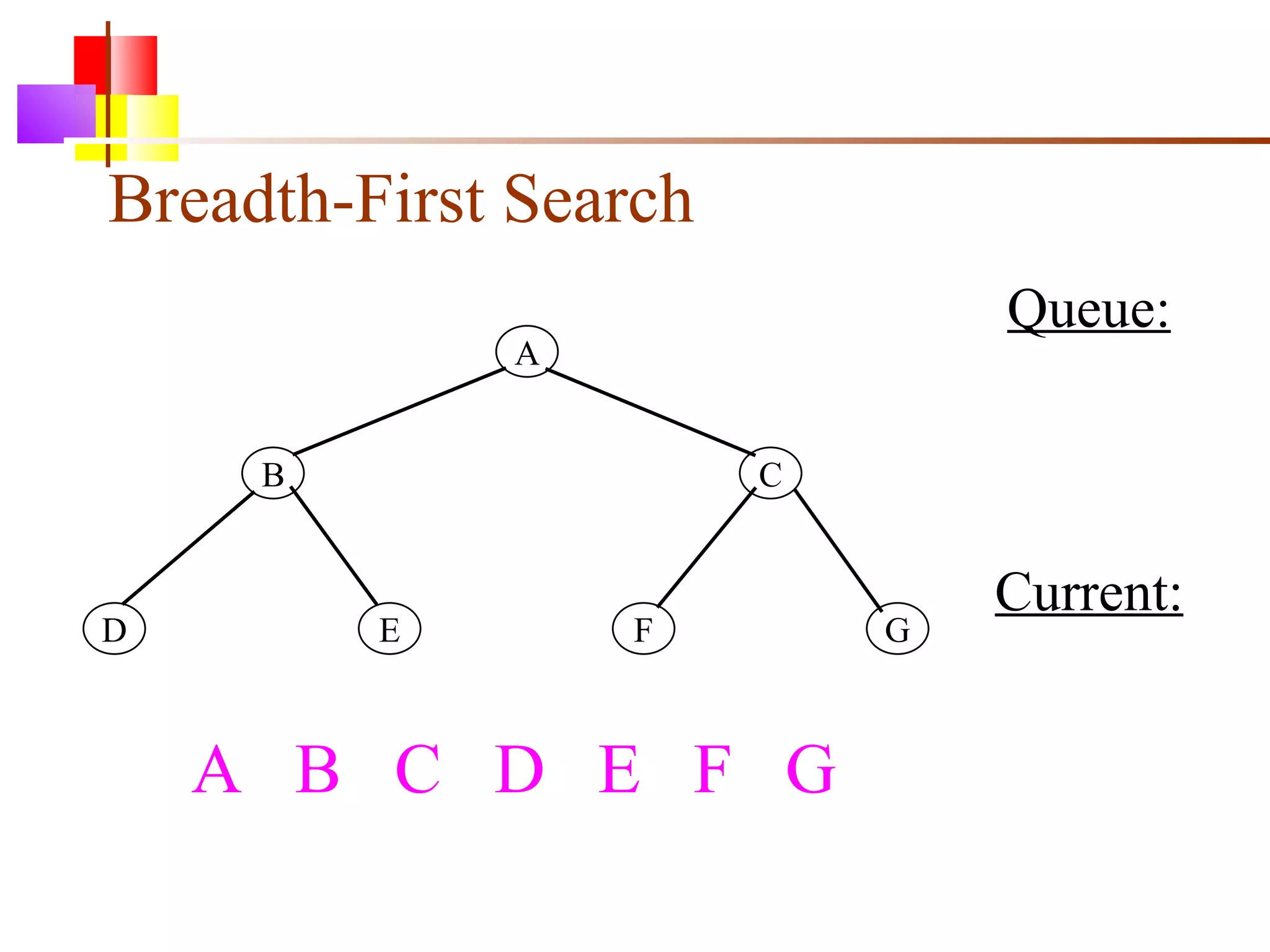
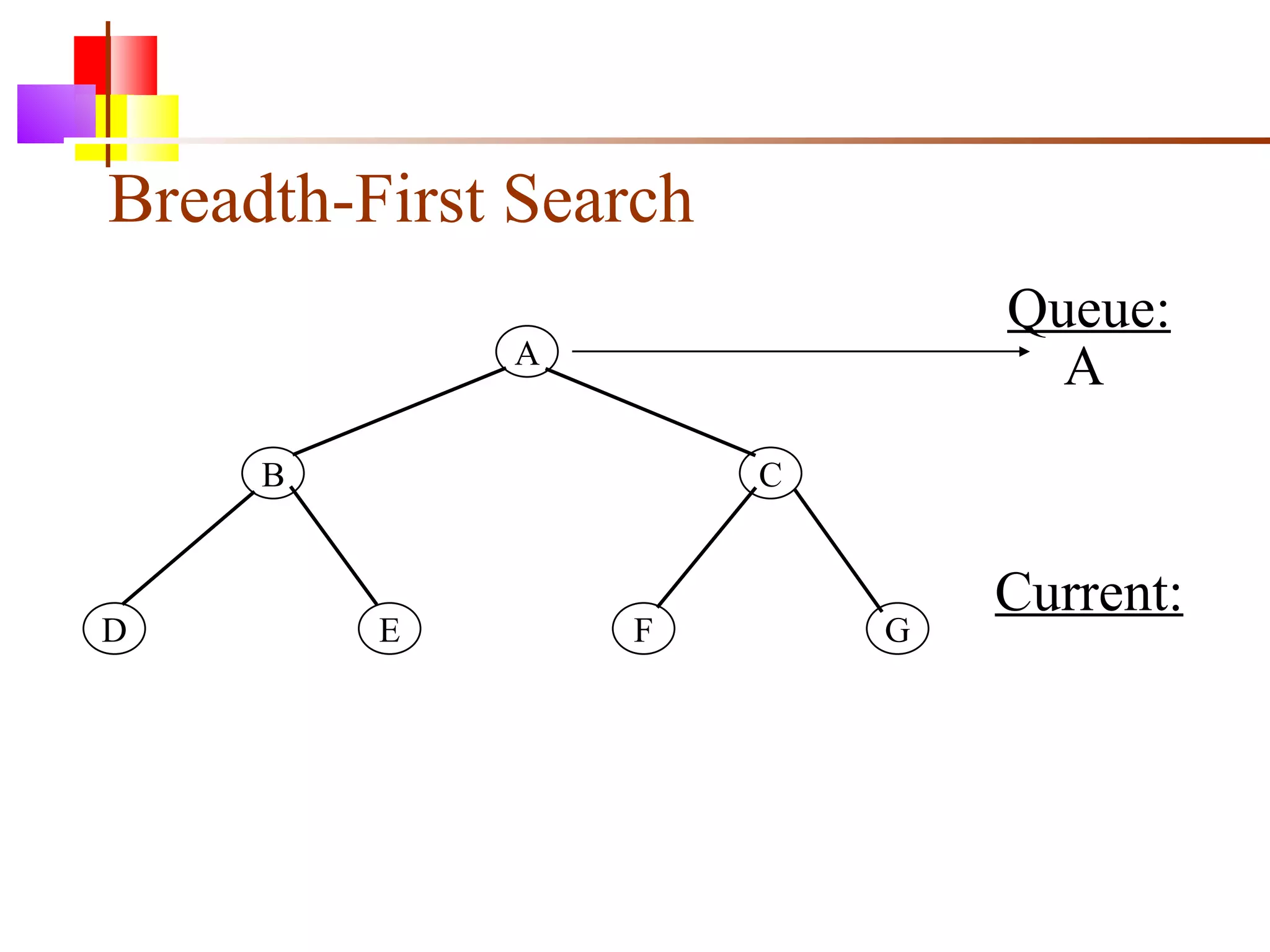
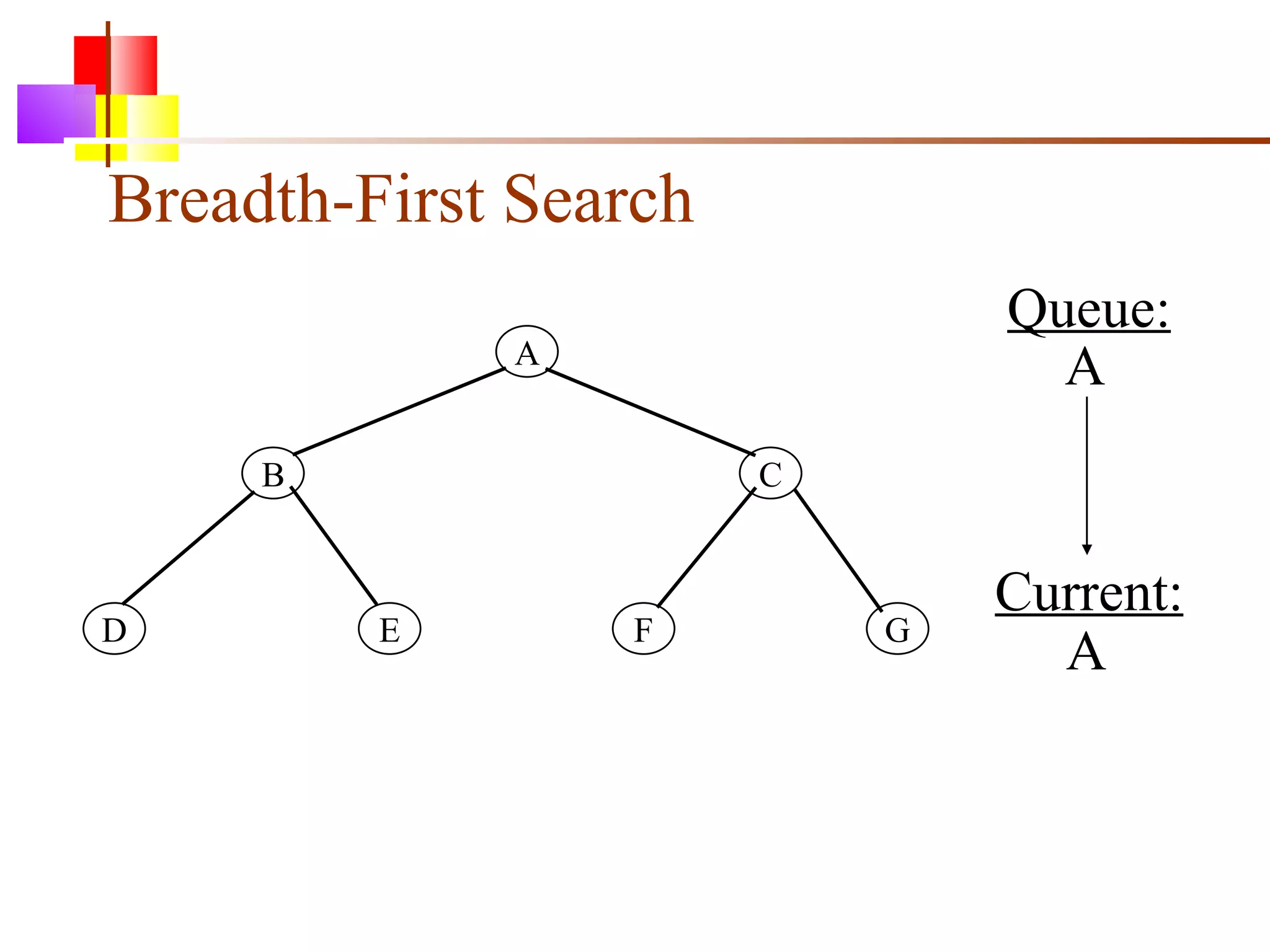
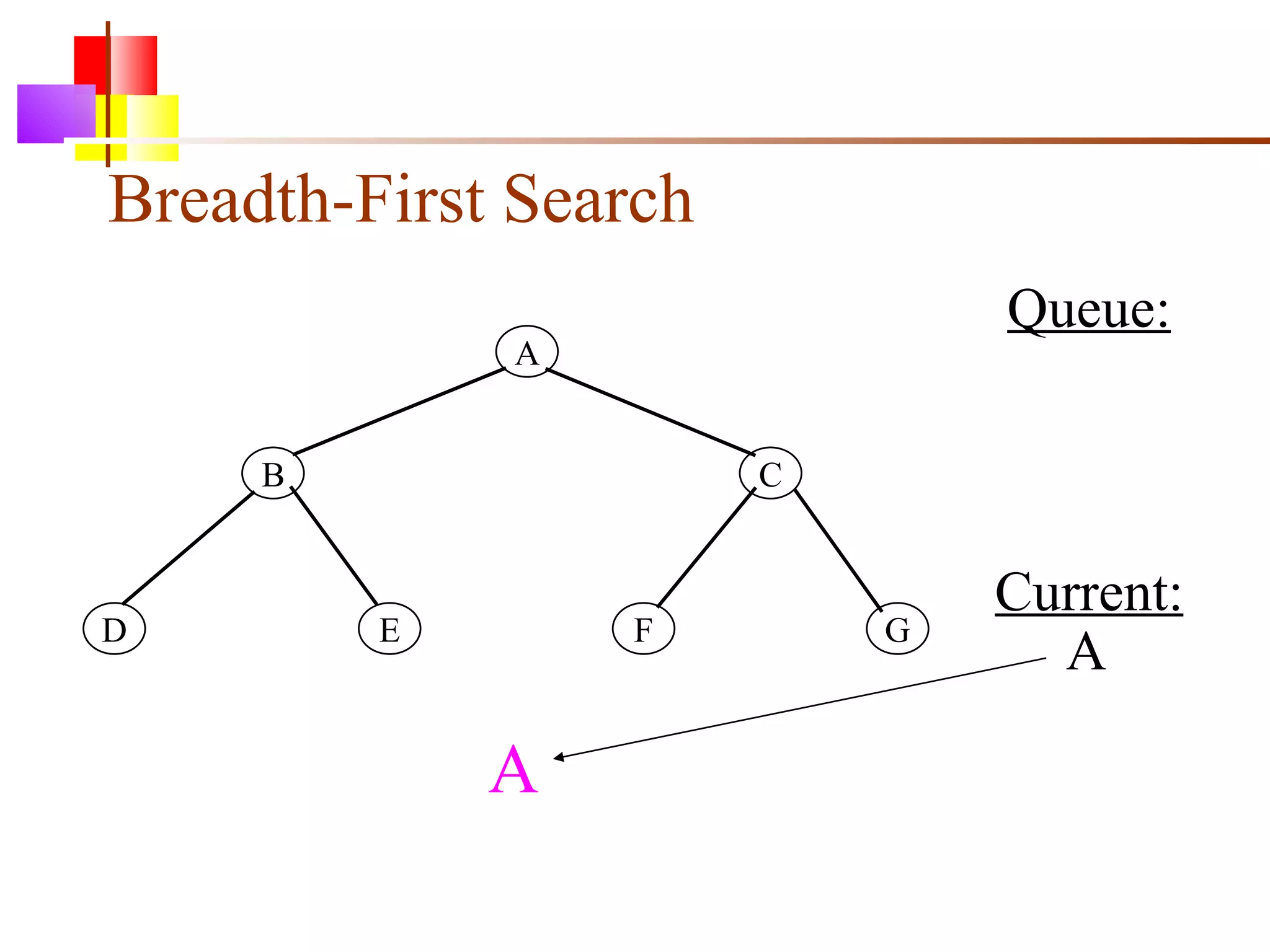
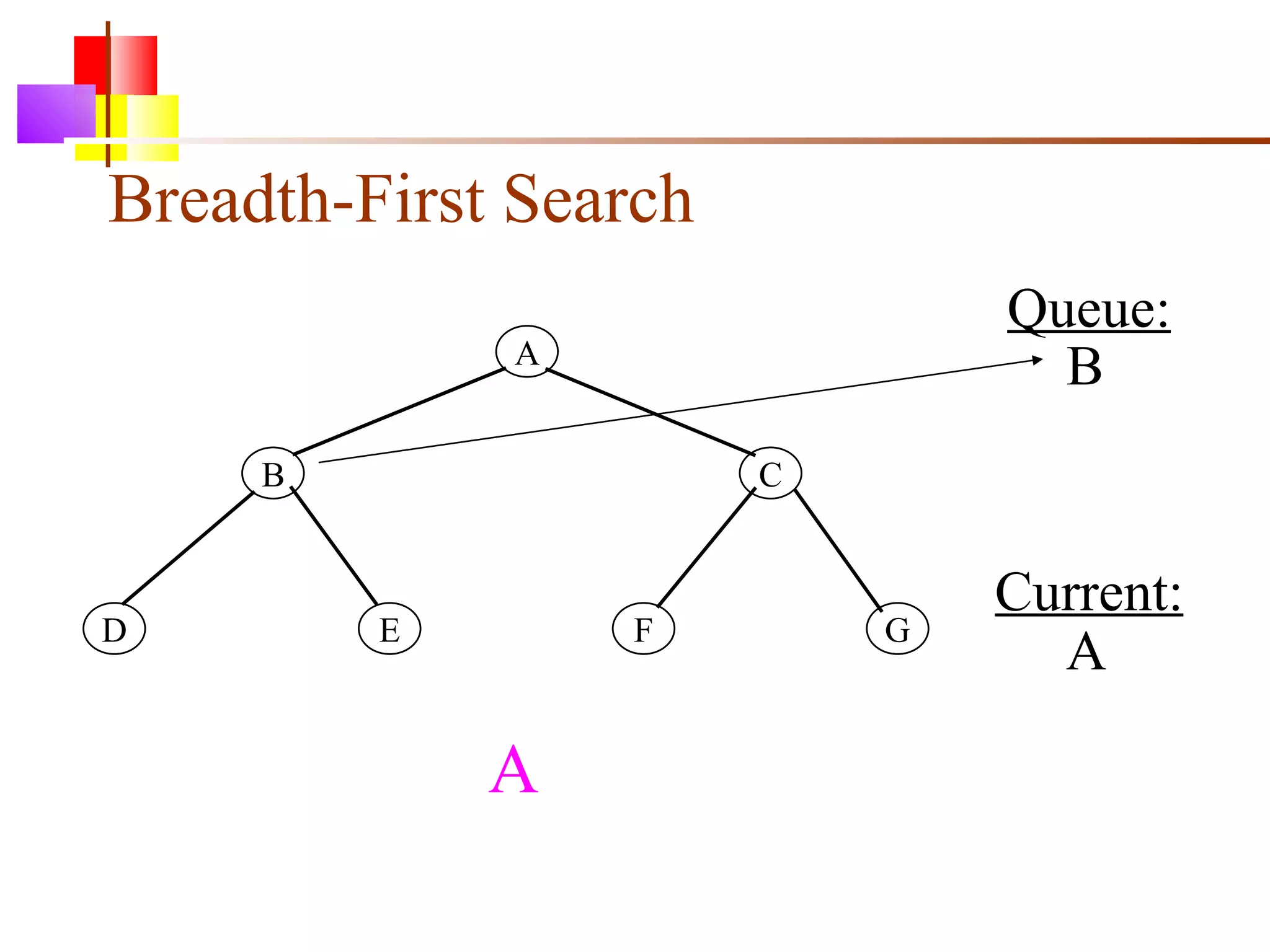
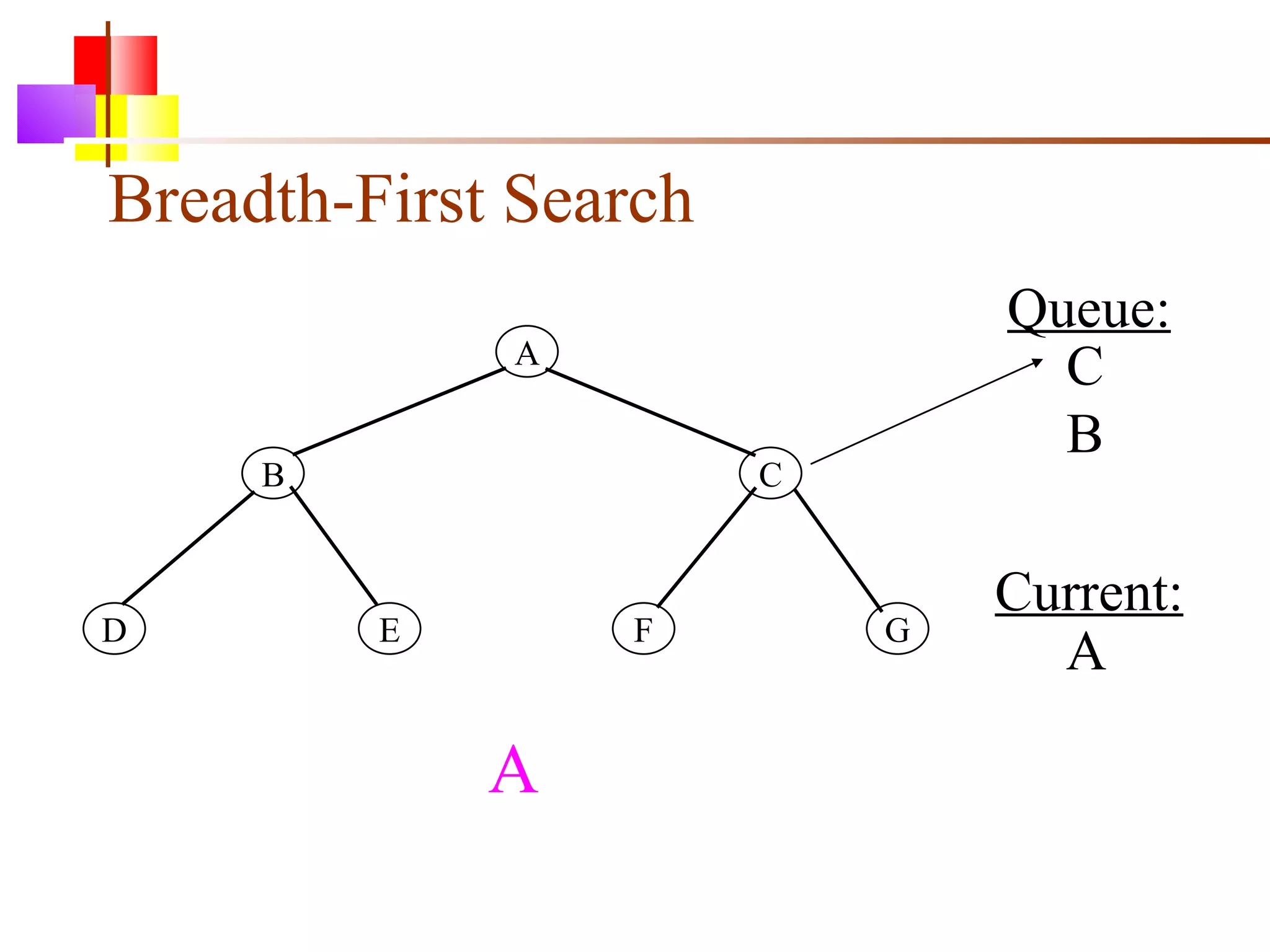
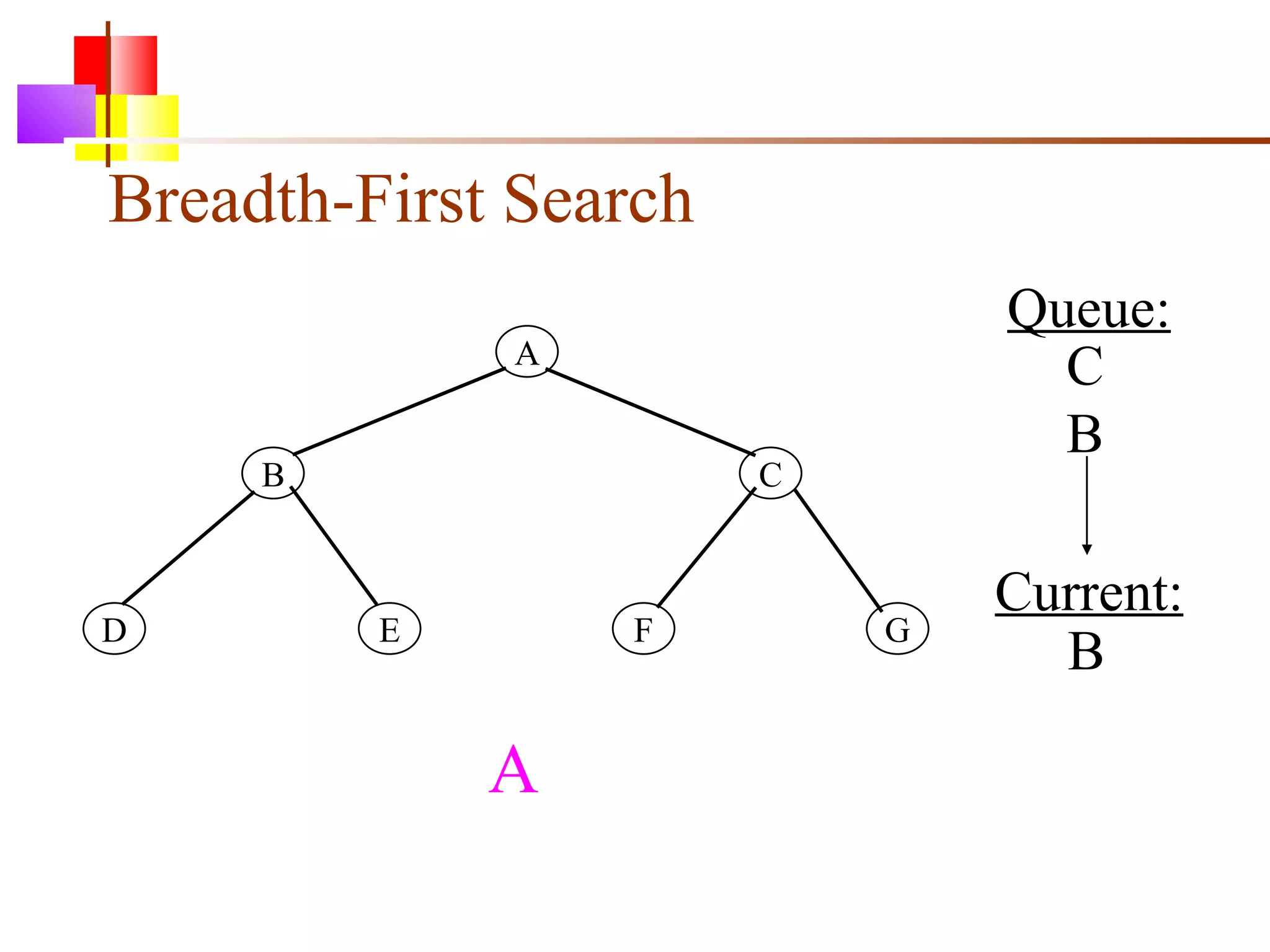
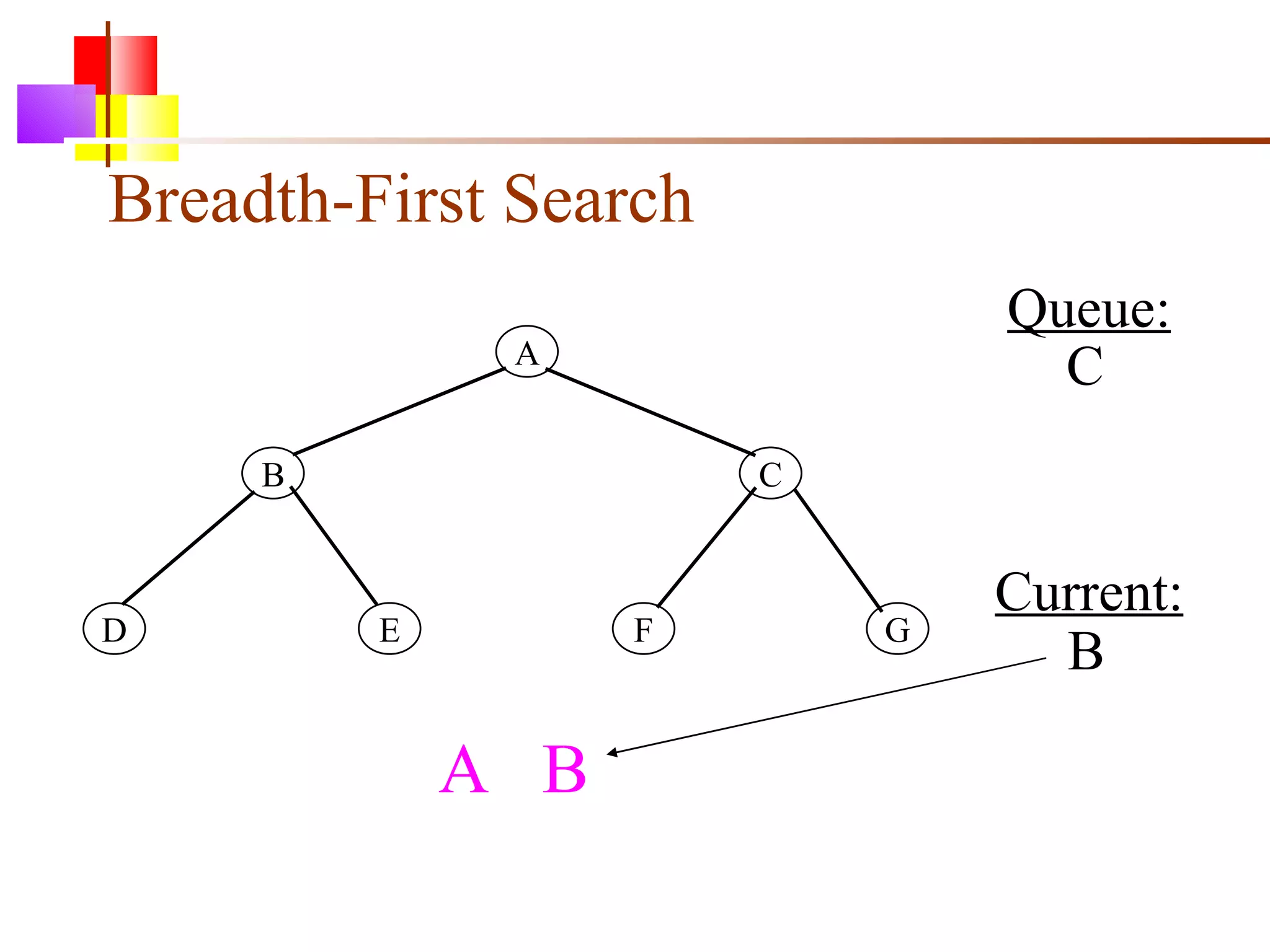
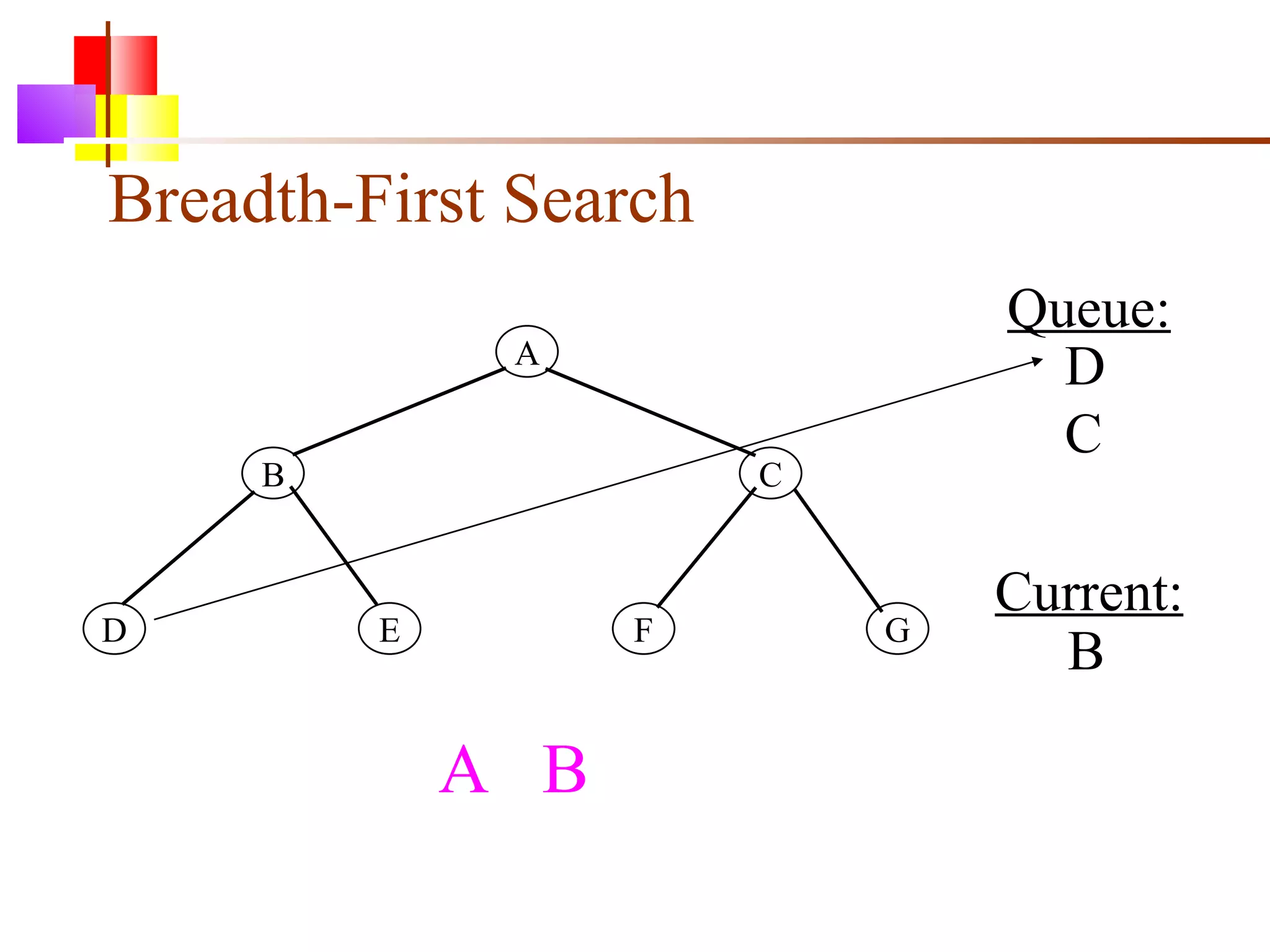
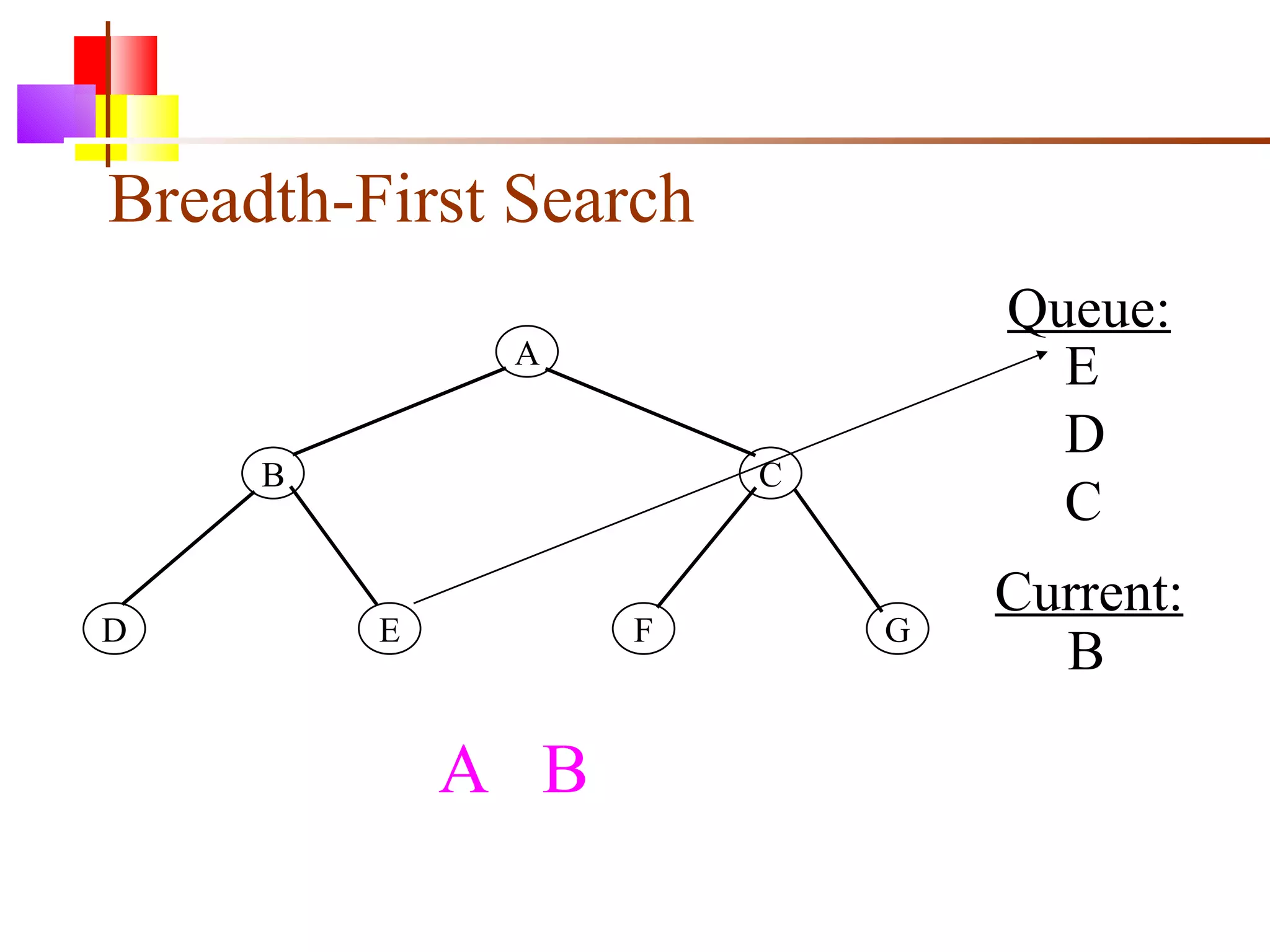
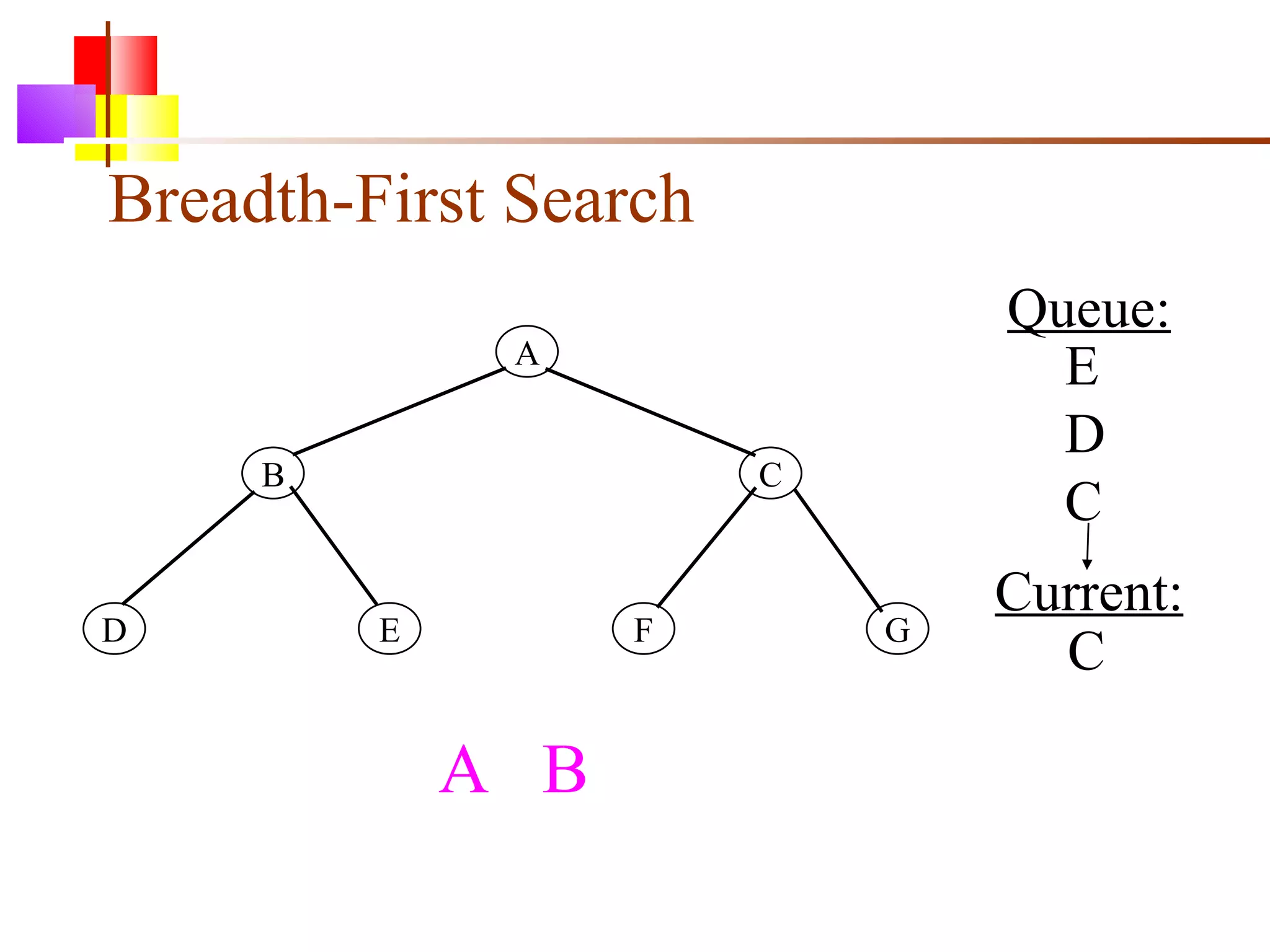
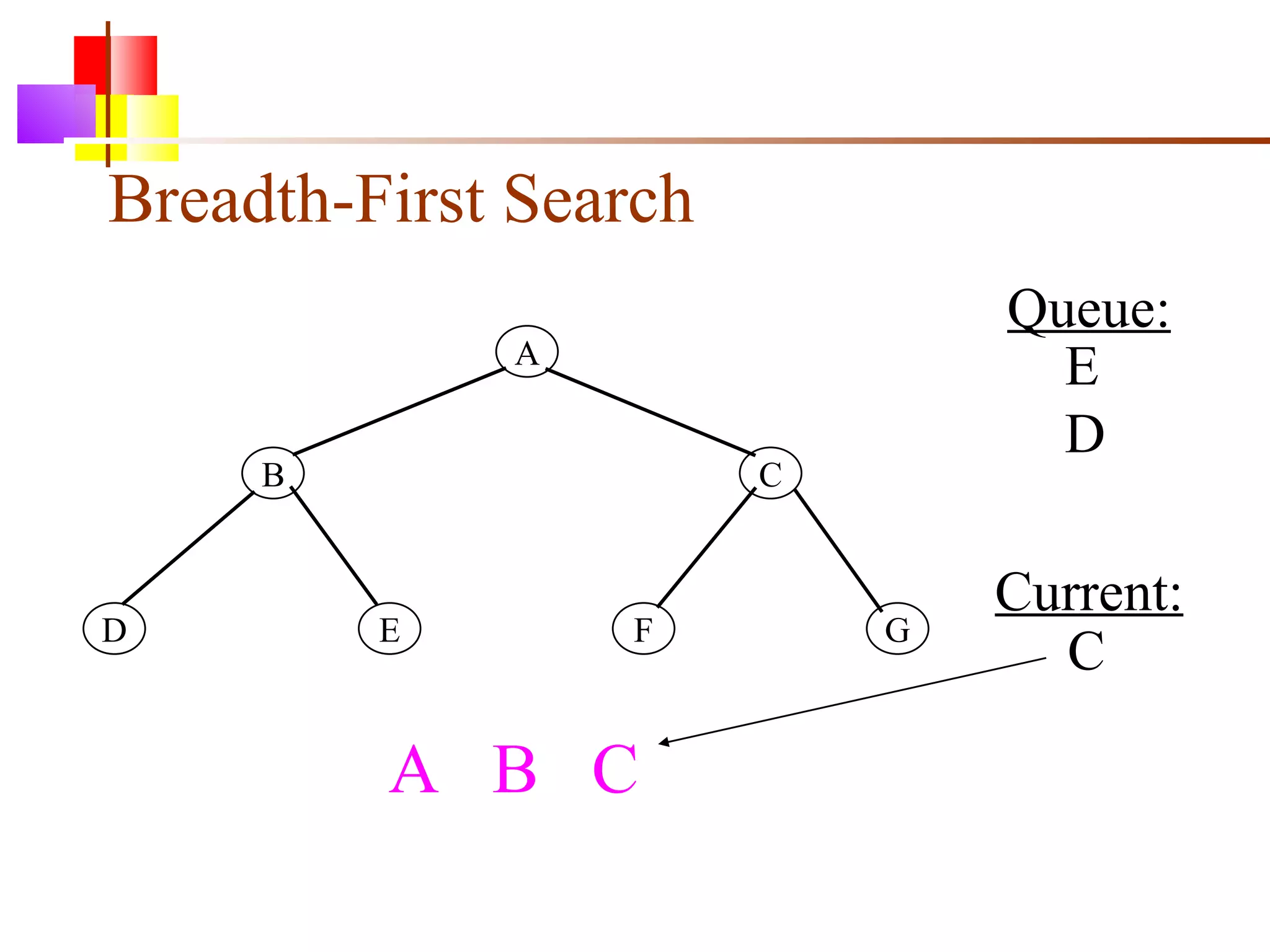
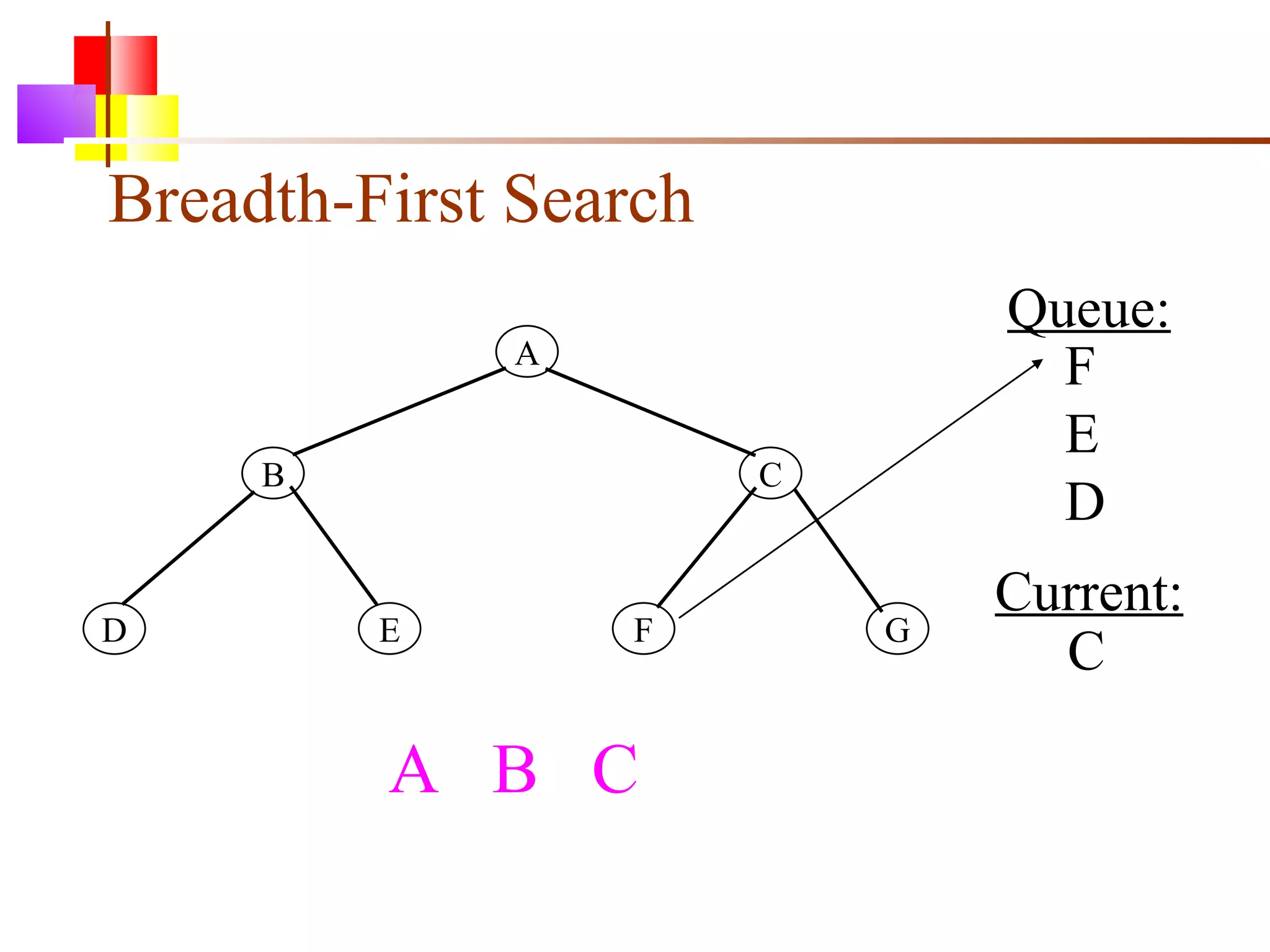
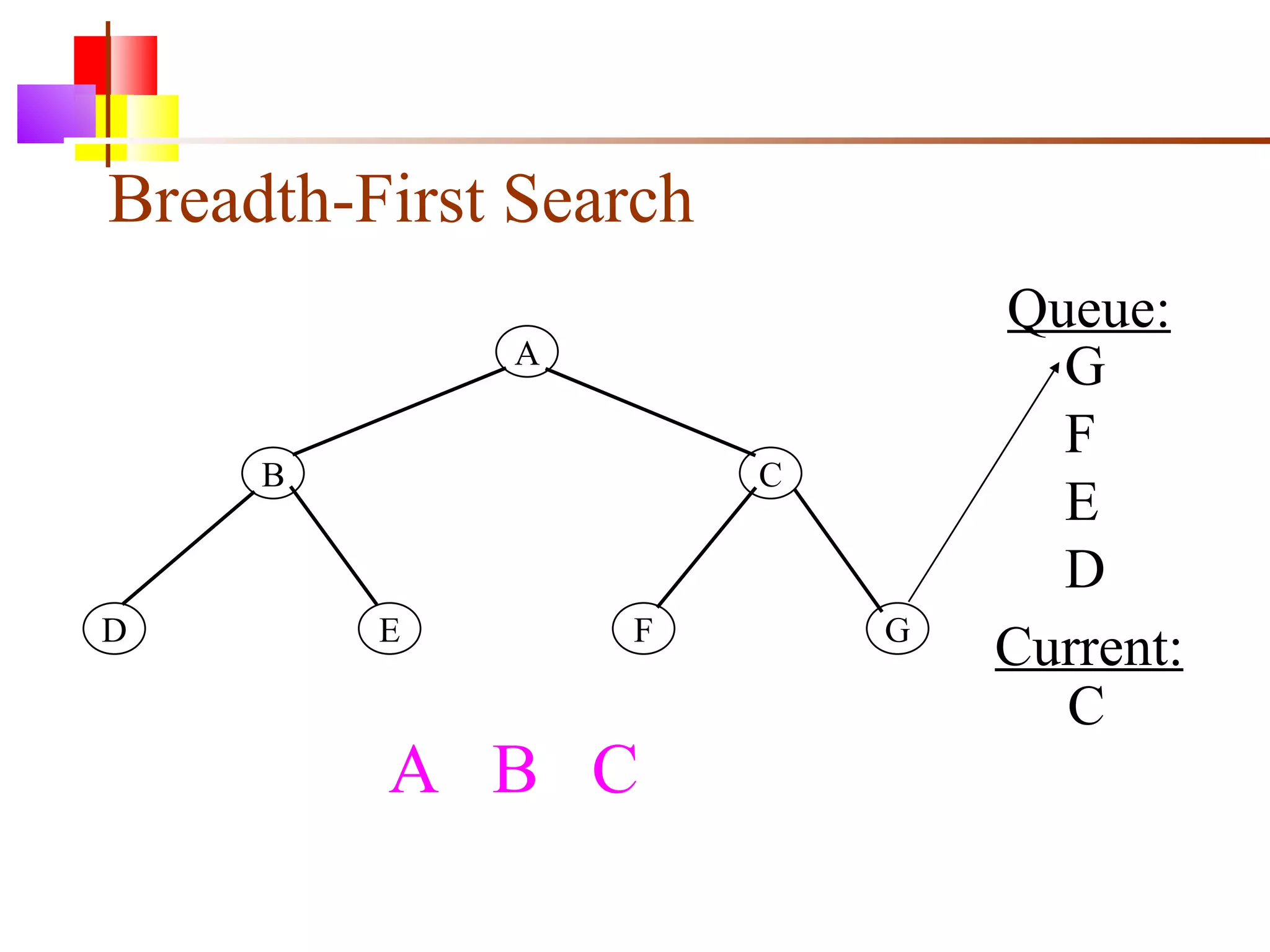
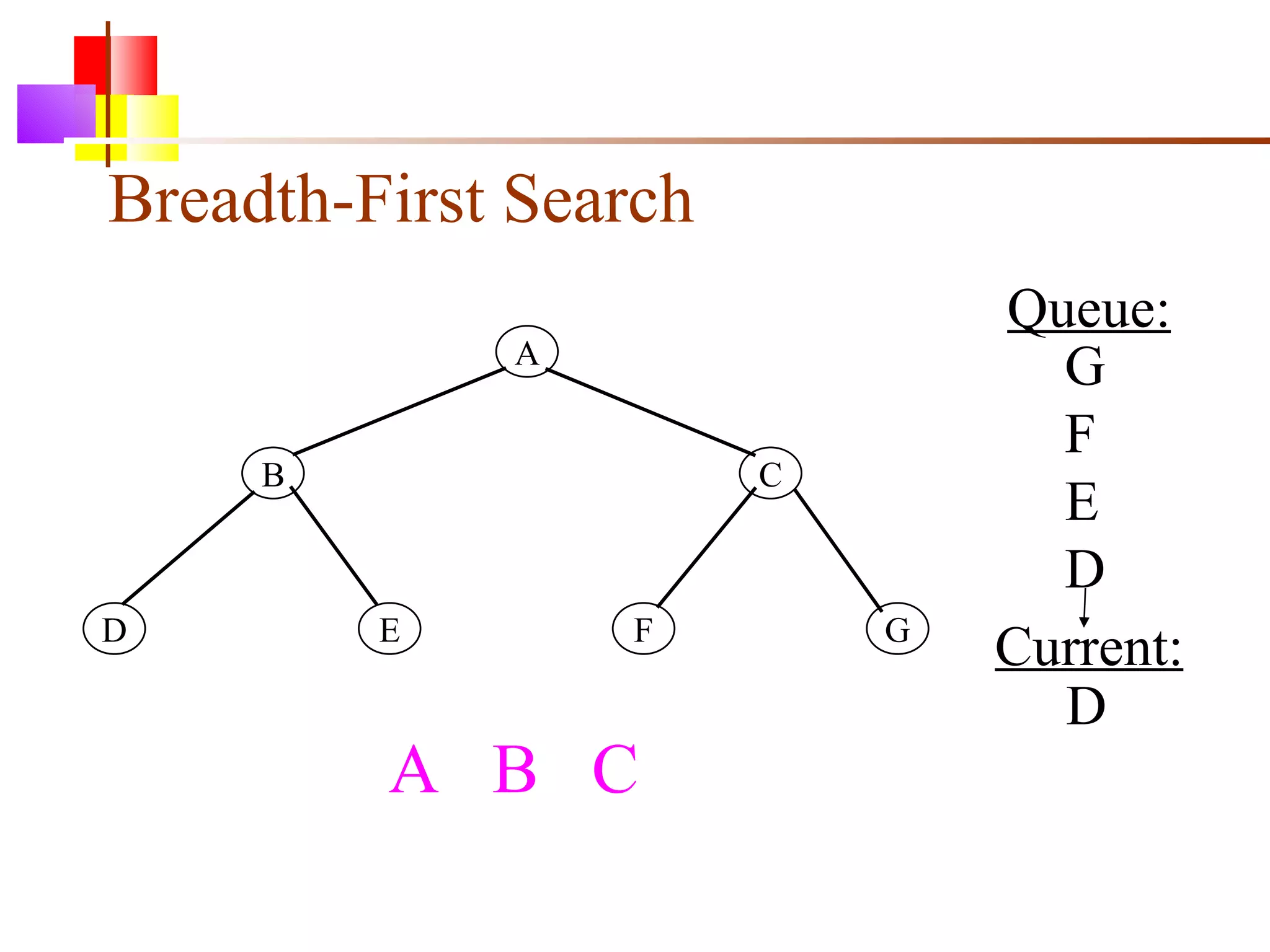
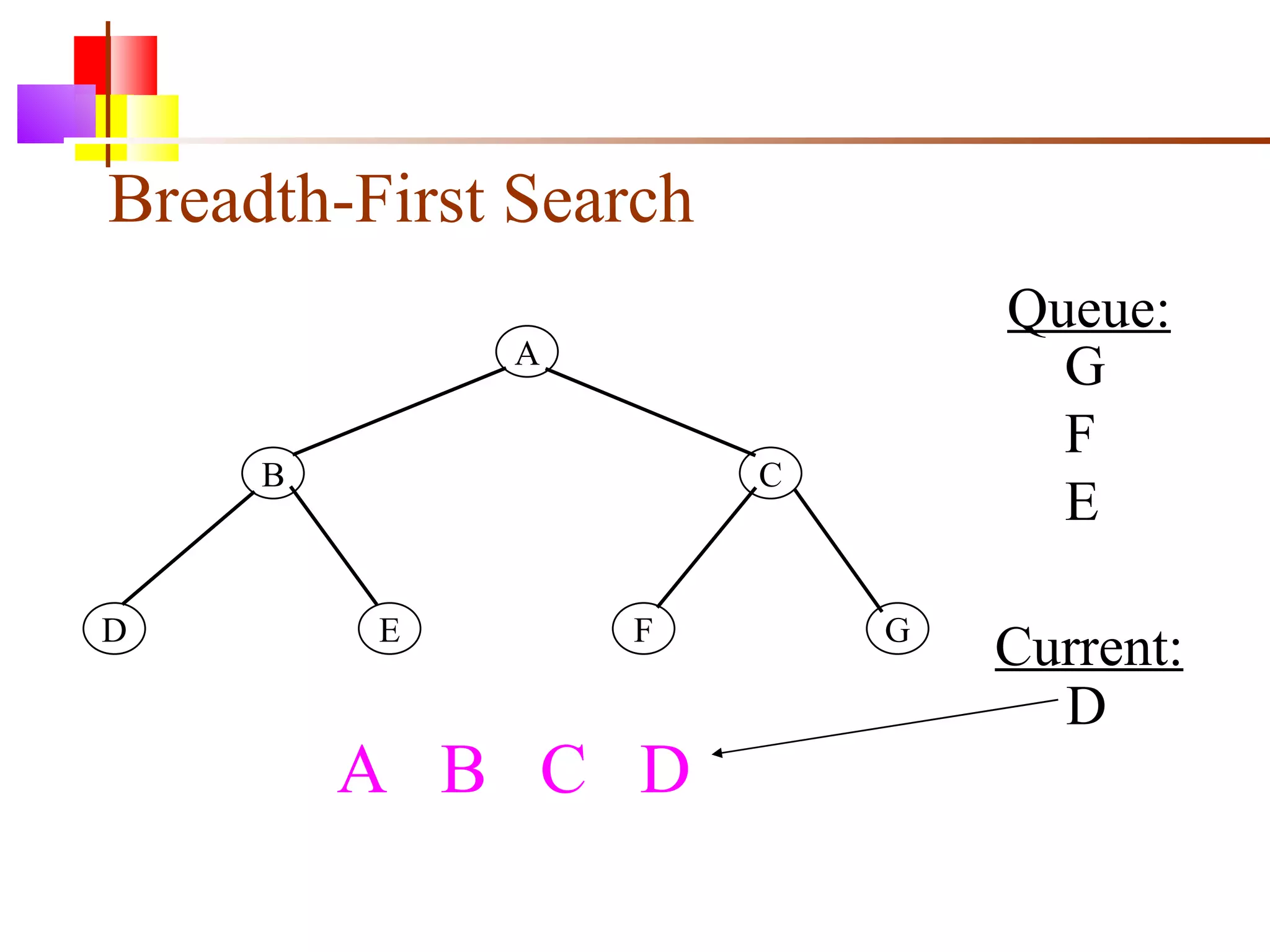
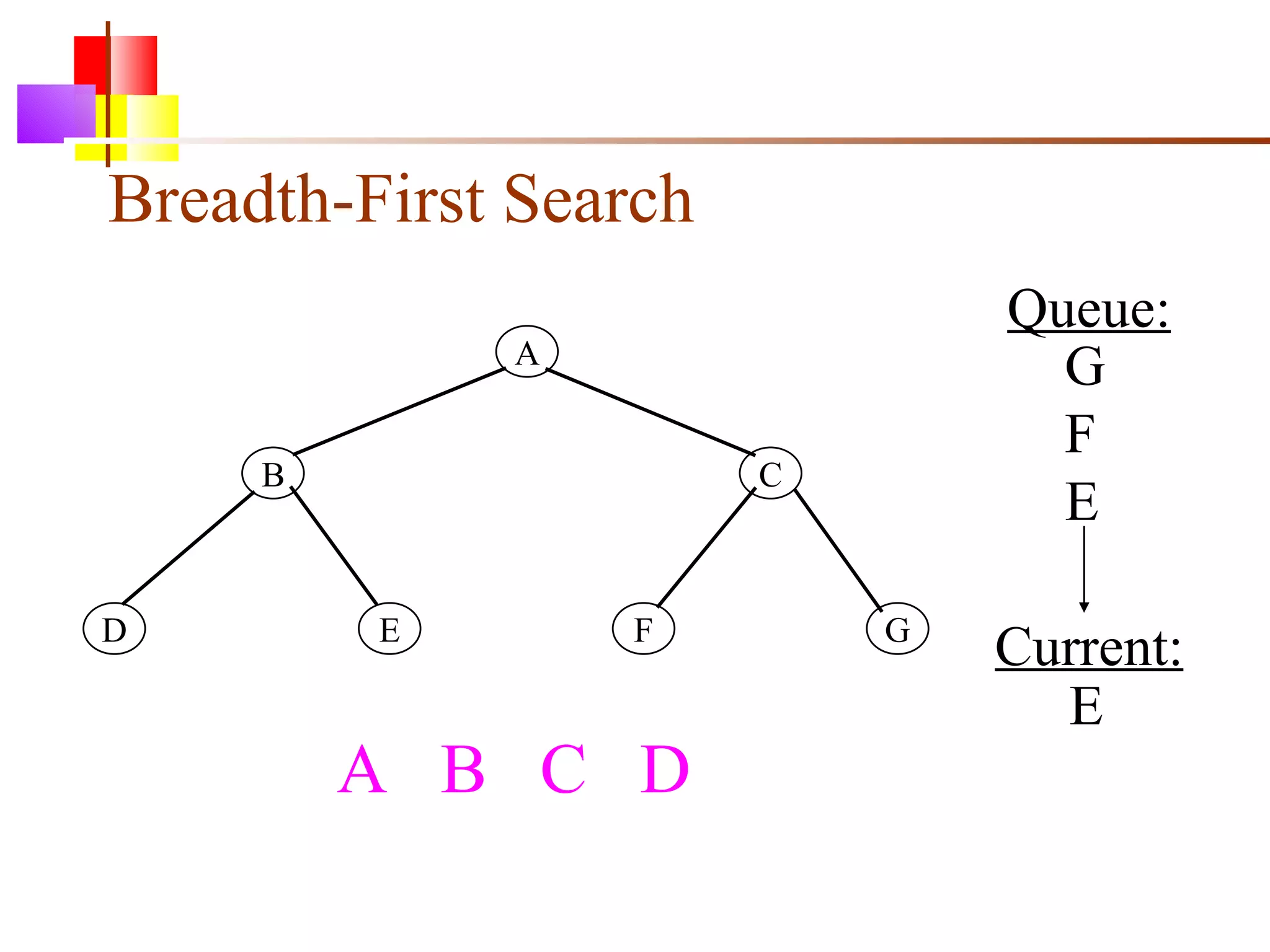
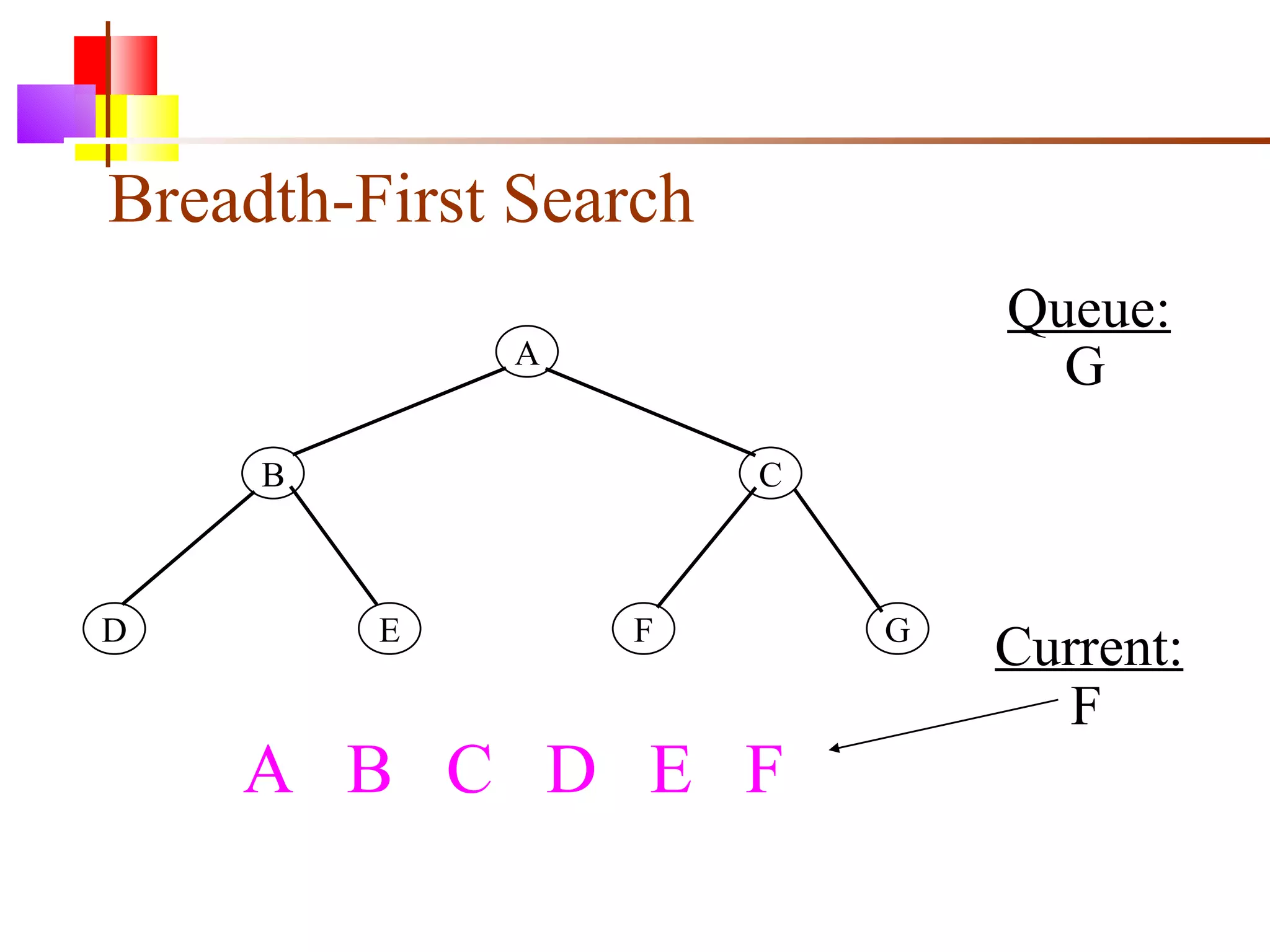
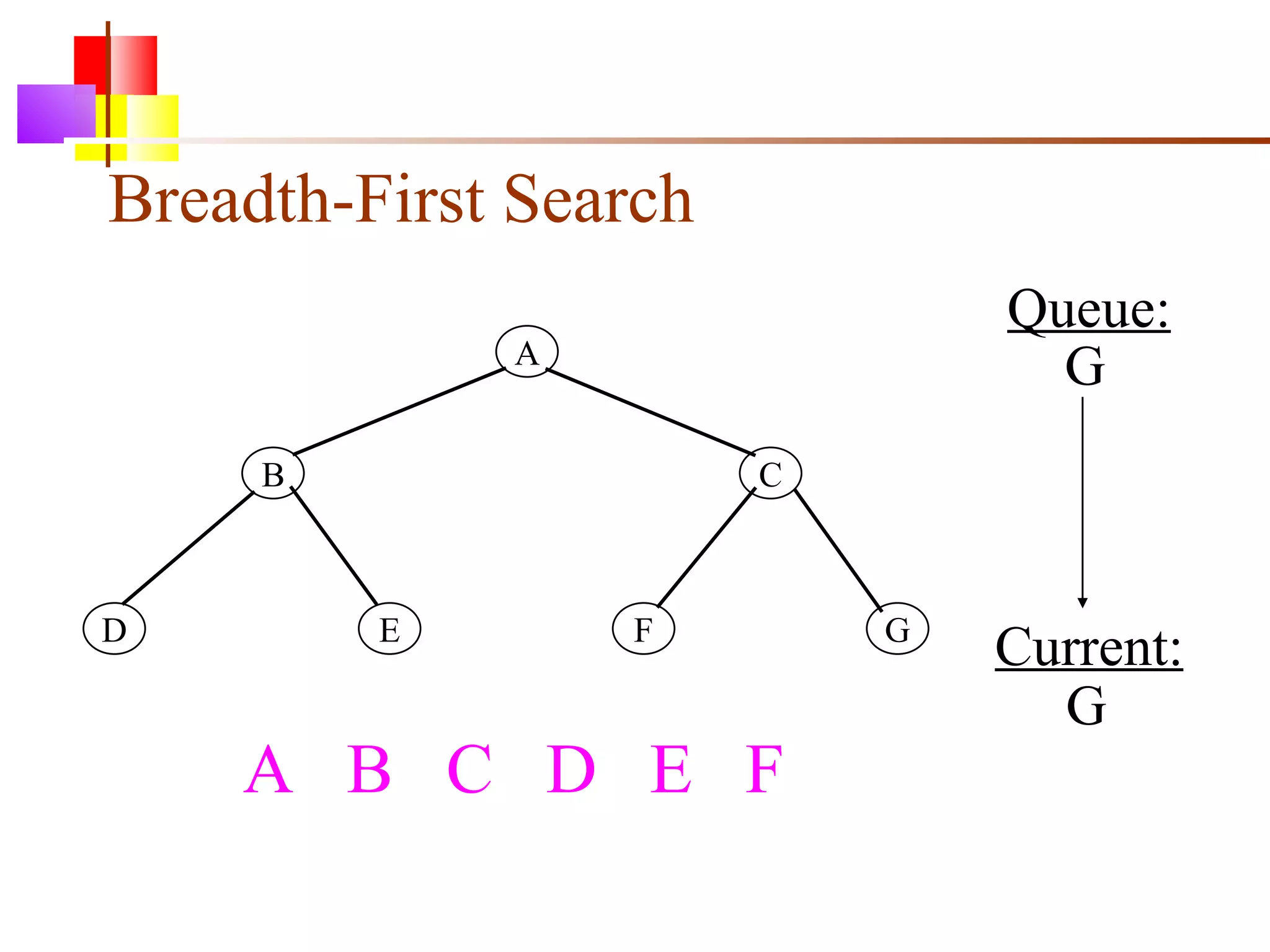
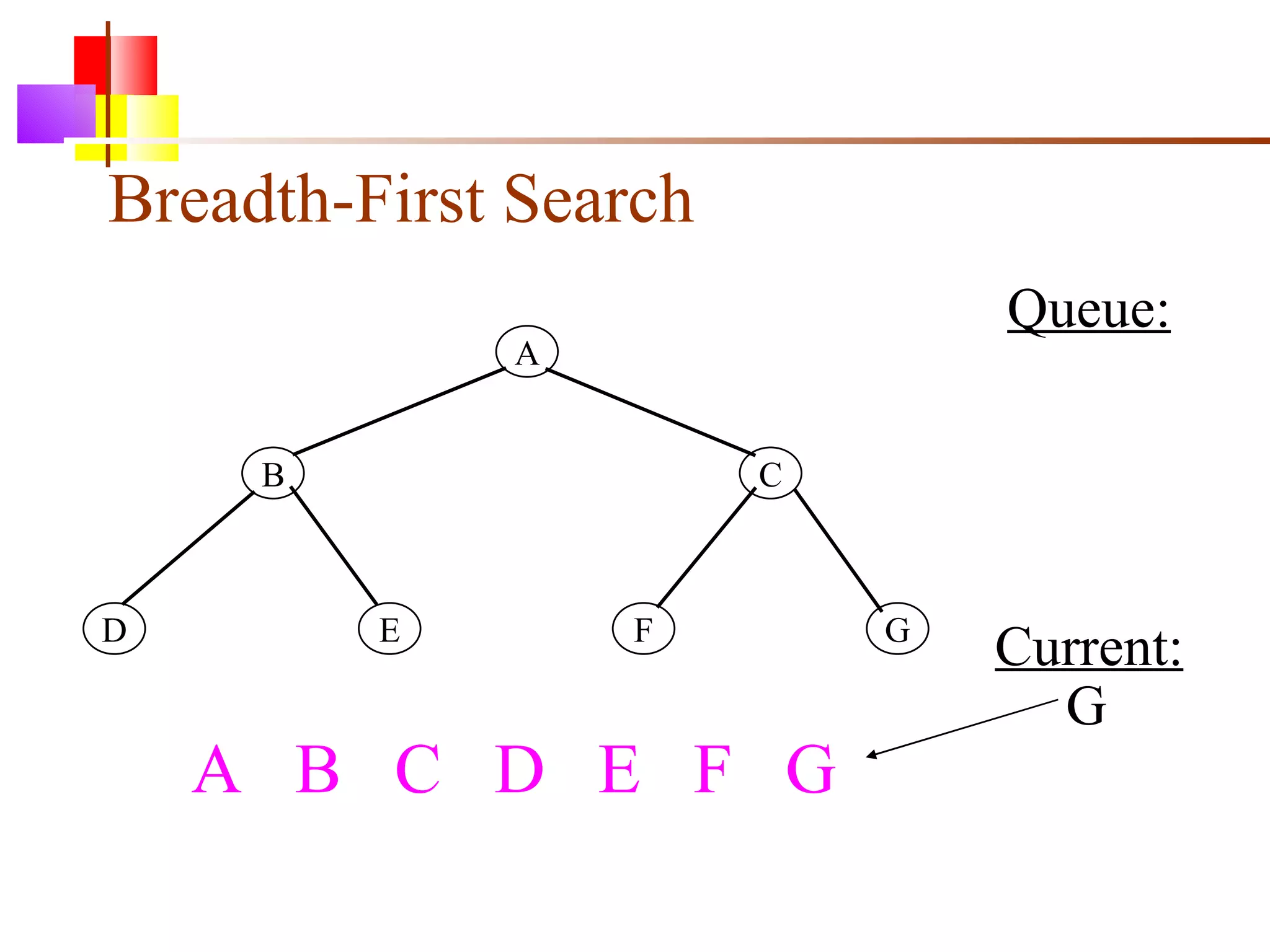
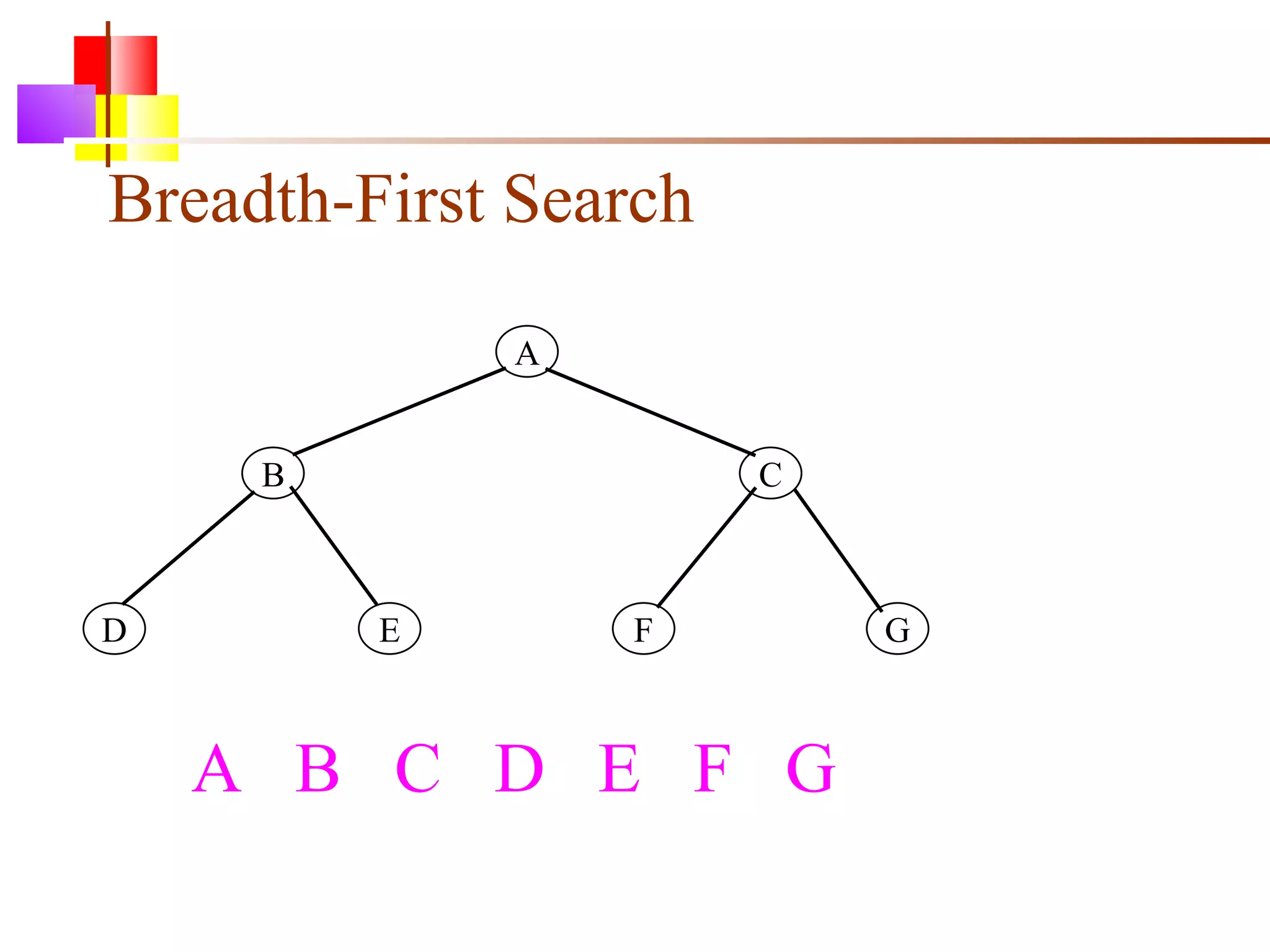
The document discusses binary trees and various operations on them. It defines what a binary tree is composed of (nodes with values and pointers to left and right children). It describes tree traversals like preorder, inorder and postorder that output the nodes in different orders. It explains two common search strategies - depth-first search (DFS) and breadth-first search (BFS) - and provides examples of how they traverse a sample tree. It also briefly discusses operations like finding the minimum/maximum element, inserting a new element, and deleting an existing element from the binary search tree.

1. Binary Trees

2. Parts of a binary tree A binary tree is composed of zero or more nodes Each node contains: A value (some sort of data item) A reference or pointer to a left child (may be null ), and A reference or pointer to a right child (may be null ) A binary tree may be empty (contain no nodes) If not empty, a binary tree has a root node Every node in the binary tree is reachable from the root node by a unique path A node with neither a left child nor a right child is called a leaf In some binary trees, only the leaves contain a value

3. Picture of a binary tree a b c d e g h i l f j k

4. Size and depth The size of a binary tree is the number of nodes in it This tree has size 12 The depth of a node is its distance from the root a is at depth zero e is at depth 2 The depth of a binary tree is the depth of its deepest node This tree has depth 4 a b c d e f g h i j k l

5. Balance A binary tree is balanced if every level above the lowest is “full” (contains 2 n nodes) In most applications, a reasonably balanced binary tree is desirable a b c d e f g h i j A balanced binary tree a b c d e f g h i j An unbalanced binary tree

6. Binary search in an array Look at array location (lo + hi)/2 2 3 5 7 11 13 17 0 1 2 3 4 5 6 Searching for 5: (0+6)/2 = 3 hi = 2; (0 + 2)/2 = 1 lo = 2; (2+2)/2=2 7 3 13 2 5 11 17 Using a binary search tree

7. Tree traversals A binary tree is defined recursively: it consists of a root , a left subtree , and a right subtree To traverse (or walk ) the binary tree is to visit each node in the binary tree exactly once Tree traversals are naturally recursive Since a binary tree has three “parts,” there are six possible ways to traverse the binary tree: root, left, right left, root, right left, right, root root, right, left right, root, left right, left, root

8. Preorder traversal In preorder , the root is visited first Here’s a preorder traversal to print out all the elements in the binary tree: public void preorderPrint(BinaryTree bt) { if (bt == null) return; System.out.println(bt.value); preorderPrint(bt.leftChild); preorderPrint(bt.rightChild); }

9. Inorder traversal In inorder , the root is visited in the middle Here’s an inorder traversal to print out all the elements in the binary tree: public void inorderPrint(BinaryTree bt) { if (bt == null) return; inorderPrint(bt.leftChild); System.out.println(bt.value); inorderPrint(bt.rightChild); }

10. Postorder traversal In postorder , the root is visited last Here’s a postorder traversal to print out all the elements in the binary tree: public void postorderPrint(BinaryTree bt) { if (bt == null) return; postorderPrint(bt.leftChild); postorderPrint(bt.rightChild); System.out.println(bt.value); }

11. Tree traversals using “flags” The order in which the nodes are visited during a tree traversal can be easily determined by imagining there is a “flag” attached to each node, as follows: To traverse the tree, collect the flags: preorder inorder postorder A B C D E F G A B C D E F G A B C D E F G A B D E C F G D B E A F C G D E B F G C A

12. Copying a binary tree In postorder , the root is visited last Here’s a postorder traversal to make a complete copy of a given binary tree: public BinaryTree copyTree(BinaryTree bt) { if (bt == null) return null; BinaryTree left = copyTree(bt.leftChild); BinaryTree right = copyTree(bt.rightChild); return new BinaryTree(bt.value, left, right); }

13. Other traversals The other traversals are the reverse of these three standard ones That is, the right subtree is traversed before the left subtree is traversed Reverse preorder: root, right subtree, left subtree Reverse inorder: right subtree, root, left subtree Reverse postorder: right subtree, left subtree, root

14. Tree searches A tree search starts at the root and explores nodes from there, looking for a goal node (a node that satisfies certain conditions, depending on the problem) For some problems, any goal node is acceptable ( N or J ); for other problems, you want a minimum-depth goal node, that is, a goal node nearest the root (only J ) L M N O P G Q H J I K F E D B C A Goal nodes

15. Depth-first searching A depth-first search ( DFS ) explores a path all the way to a leaf before backtracking and exploring another path For example, after searching A , then B , then D , the search backtracks and tries another path from B Node are explored in the order A B D E H L M N I O P C F G J K Q N will be found before J L M N O P G Q H J I K F E D B C A

16. How to do depth-first searching Put the root node on a stack; while (stack is not empty) { remove a node from the stack; if (node is a goal node) return success; put all children of node onto the stack; } return failure; At each step, the stack contains some nodes from each of a number of levels The size of stack that is required depends on the branching factor b While searching level n , the stack contains approximately b*n nodes When this method succeeds, it doesn’t give the path

17. Depth-First Search A B C D E F G A B D E C F G Stack: Current:

18. Depth-First Search A B C D E F G Undiscovered Marked Finished Active B newly discovered Stack: (A, C); (A, B) Current:

19. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active A already marked Visited B Stack: (B, E); (B, D); (B, A) (A, C); (A, B)

20. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active A already marked Visited B A Stack: (B, E); (B, D); (B, A) (A, C); (A, B)

21. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active D newly discovered A Stack: (B, E); (B, D); (B, A) (A, C); (A, B)

22. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Visited D A B Stack: (B, E); (B, D); (B, A) (A, C); (A, B) (B, D) Marked B

23. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Finished D A B Stack: (B, E); (B, D); (B, A) (A, C); (A, B)

24. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active E newly discovered Stack: (B, E); (B, D); (B, A) (A, C); (A, B) A B D Backtrack B

25. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Visited E Stack: (B, E); (B, D); (B, A) (A, C); (A, B) A B D (B, E)

26. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Finished E Stack: (B, E); (B, D); (B, A) (A, C); (A, B) A B D

27. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (B, E); (B, D); (B, A) (A, C); (A, B) A B D E

28. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (A, C); (A, B) A B D E Backtrack B

29. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (A, C); (A, B) A B D E Backtrack A Finished B C newly discovered

30. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (C, G); (C, F); (C, A) A B D E Visited C (A, C); (A, B)

31. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (C, G); (C, F); (C, A) Marked C (A, C); (A, B) F newly discovered A B D E C

32. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (C, G); (C, F); (C, A) (A, C); (A, B) Visited F A B D E C (F, C)

33. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (C, G); (C, F); (C, A) (A, C); (A, B) Finished F A B D E C

34. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (C, G); (C, F); (C, A) (A, C); (A, B) Backtrack C G newly discovered A B D E C F

35. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (C, G); (C, F); (C, A) (A, C); (A, B) Marked C Visited G A B D E C F (G, C)

36. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (C, G); (C, F); (C, A) (A, C); (A, B) Backtrack C Finished G A B D E C F G

37. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: (A, C); (A, B) Finished C A B D E C F G Backtrack A

38. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active Stack: A B D E C F G Finished A

39. Depth-First Search A B C D E F G Current: Undiscovered Marked Finished Active A B D E C F G

40. Breadth-first searching A breadth-first search ( BFS ) explores nodes nearest the root before exploring nodes further away For example, after searching A , then B , then C , the search proceeds with D , E , F , G Node are explored in the order A B C D E F G H I J K L M N O P Q J will be found before N L M N O P G Q H J I K F E D B C A

41. How to do breadth-first searching Put the root node on a queue; while (queue is not empty) { remove a node from the queue; if (node is a goal node) return success; put all children of node onto the queue; } return failure; Just before starting to explore level n , the queue holds all the nodes at level n-1 In a typical tree, the number of nodes at each level increases exponentially with the depth Memory requirements may be infeasible When this method succeeds, it doesn’t give the path There is no “recursive” breadth-first search equivalent to recursive depth-first search

42. Breadth-First Search A B C D E F G A B C D E F G Queue: Current:

43. Breadth-First Search A B C D E F G Queue: Current: A

44. Breadth-First Search A B C D E F G Queue: Current: A A

45. Breadth-First Search A B C D E F G Queue: Current: A A

46. Breadth-First Search A B C D E F G Queue: Current: B A A

47. Breadth-First Search A B C D E F G Queue: Current: C B A A

48. Breadth-First Search A B C D E F G Queue: Current: B A C B

49. Breadth-First Search A B C D E F G Queue: Current: B C A B

50. Breadth-First Search A B C D E F G Queue: Current: D C B A B

51. Breadth-First Search A B C D E F G Queue: Current: E D C B A B

52. Breadth-First Search A B C D E F G Queue: Current: C E D C A B

53. Breadth-First Search A B C D E F G Queue: Current: C A B C E D

54. Breadth-First Search A B C D E F G Queue: Current: C A B C F E D

55. Breadth-First Search A B C D E F G Queue: Current: C A B C G F E D

56. Breadth-First Search A B C D E F G Queue: Current: D A B C G F E D

57. Breadth-First Search A B C D A B C D E F G Queue: Current: D G F E

58. Breadth-First Search A B C D E F G A B C D Queue: Current: E G F E

59. Breadth-First Search A B C D E F G Queue: Current: F G A B C D E F

60. Breadth-First Search A B C D E F G Queue: Current: G G A B C D E F

61. Breadth-First Search A B C D E F G Queue: Current: G A B C D E F G

62. Breadth-First Search A B C D E F G A B C D E F G

63. Depth- vs. breadth-first searching When a breadth-first search succeeds, it finds a minimum-depth (nearest the root) goal node When a depth-first search succeeds, the found goal node is not necessarily minimum depth For a large tree, breadth-first search memory requirements may be excessive For a large tree, a depth-first search may take an excessively long time to find even a very nearby goal node How can we combine the advantages (and avoid the disadvantages) of these two search techniques?

64. findMin/ findMax Return the node containing the smallest element in the tree Start at the root and go left as long as there is a left child. The stopping point is the smallest element Similarly for findMax Time complexity = O(height of the tree)

65. insert Proceed down the tree as you would with a find If X is found, do nothing (or update something) Otherwise, insert X at the last spot on the path traversed Time complexity = O(height of the tree)

66. delete When we delete a node, we need to consider how we take care of the children of the deleted node. This has to be done such that the property of the search tree is maintained.

67. Delete cont… Three cases: (1) the node is a leaf Delete it immediately (2) the node has one child Adjust a pointer from the parent to bypass that node

68. Delete cont… (3) the node has 2 children replace the key of that node with the minimum element at the right subtree delete the minimum element Has either no child or only right child because if it has a left child, that left child would be smaller and would have been chosen. So invoke case 1 or 2. Time complexity = O(height of the tree)

69. Thank you for listening!