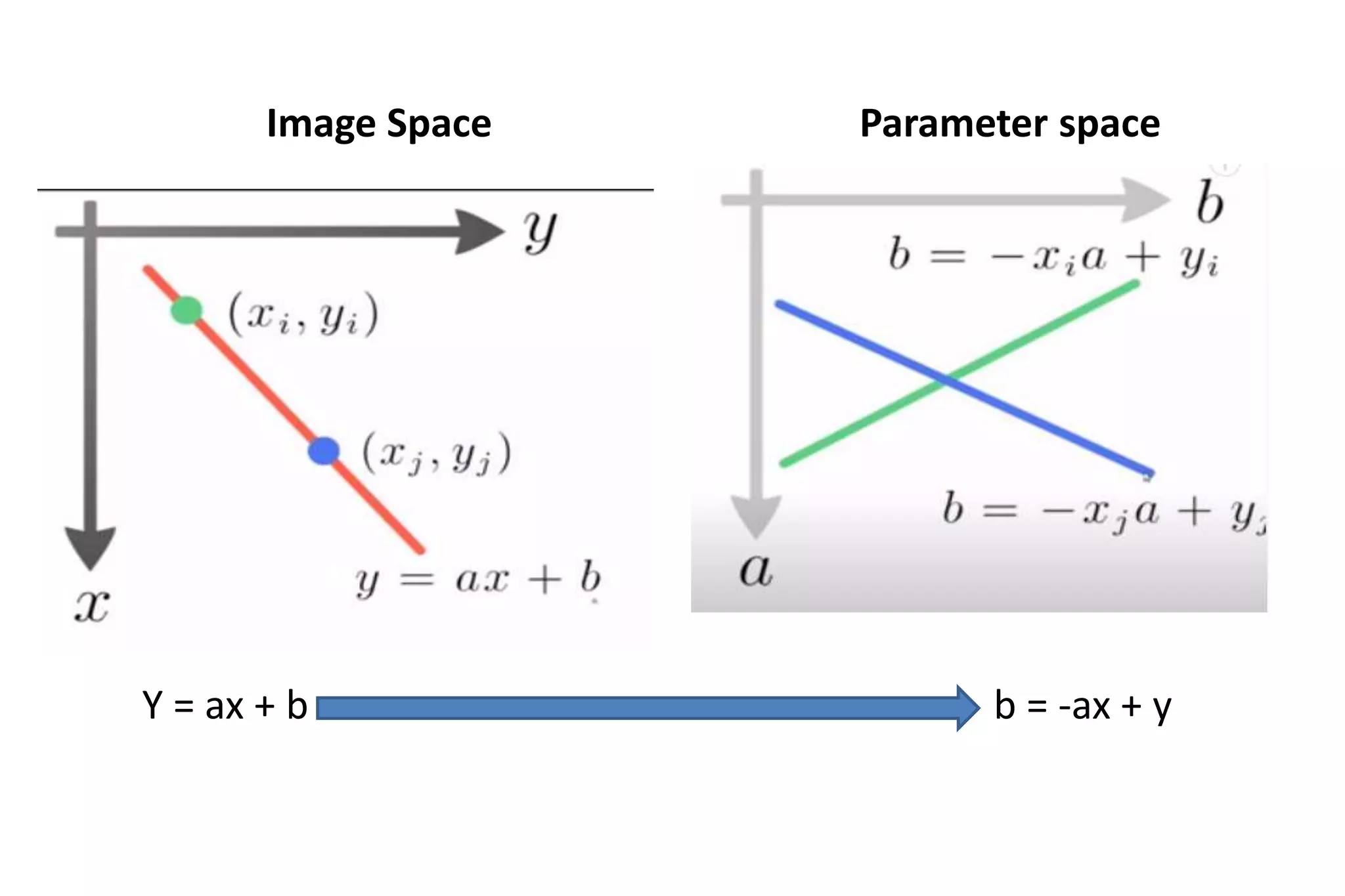
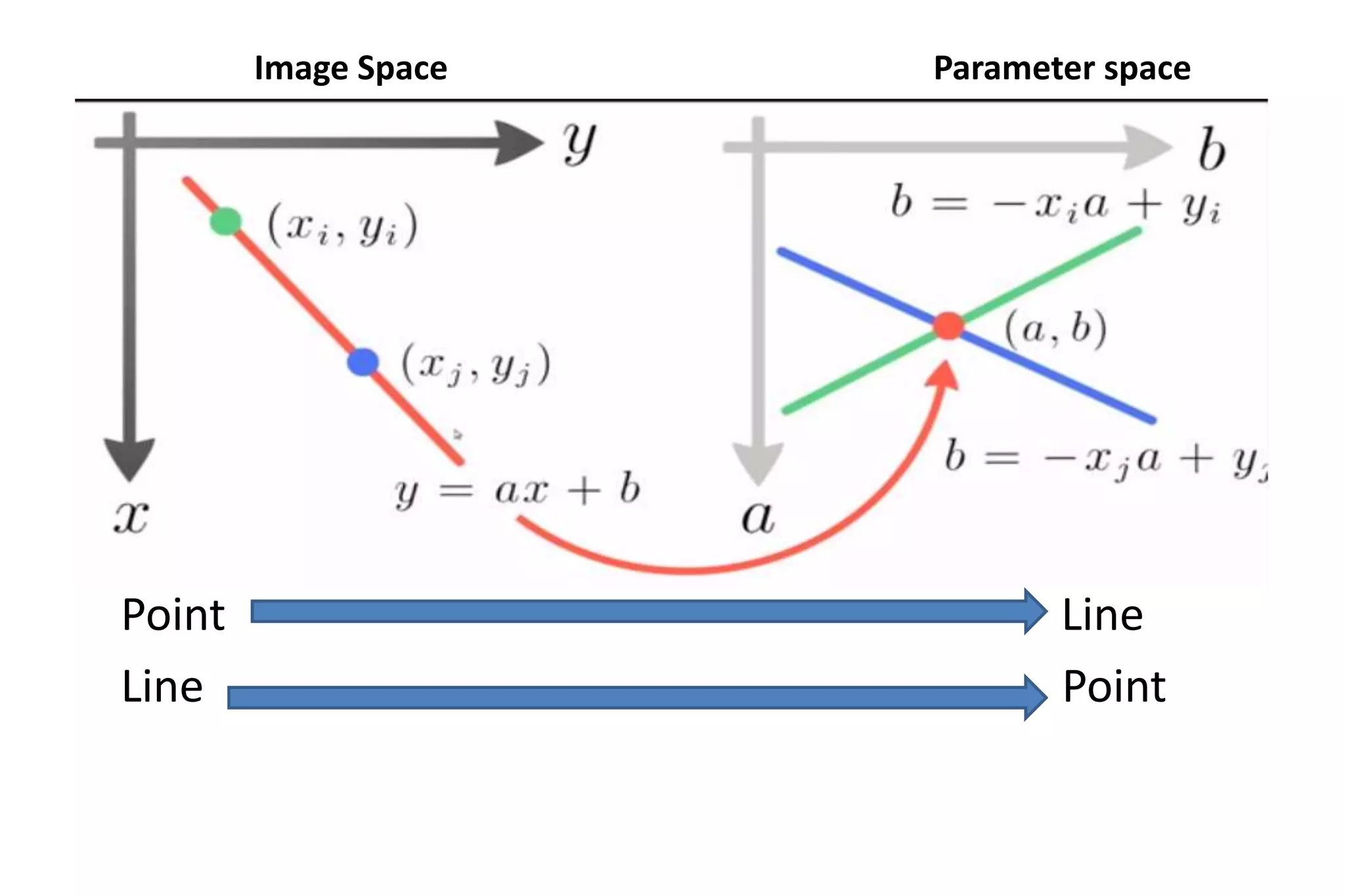
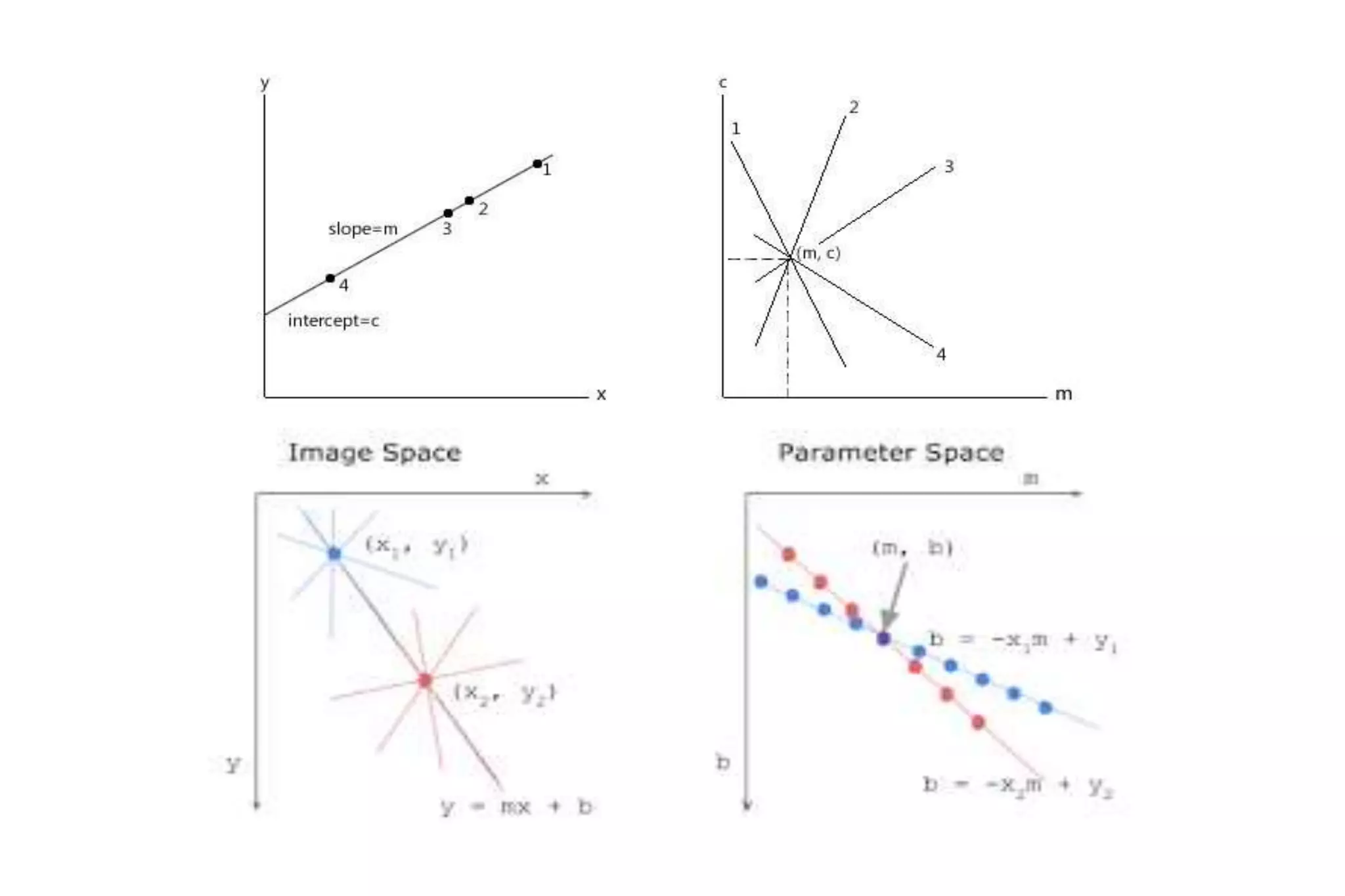
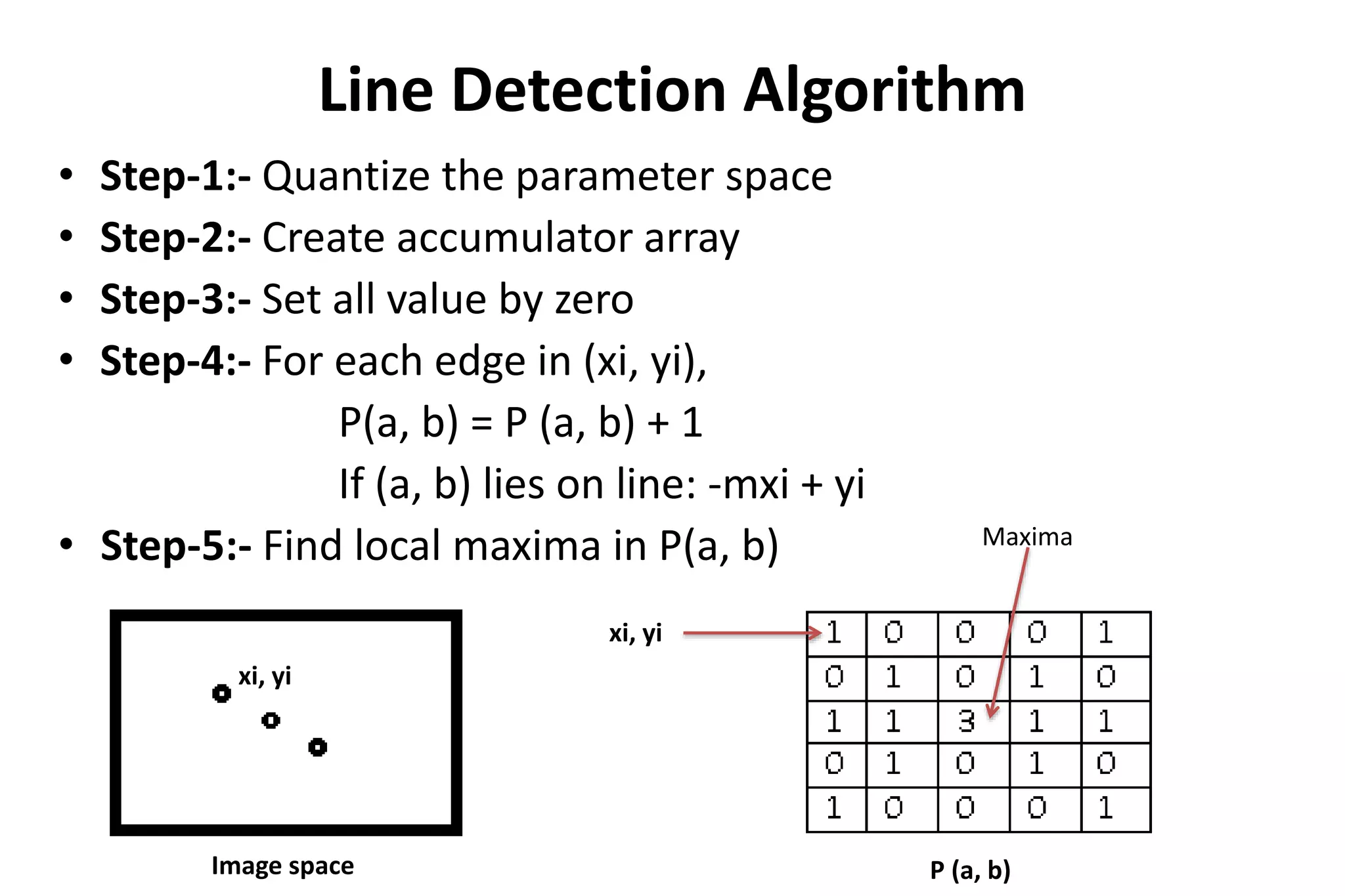
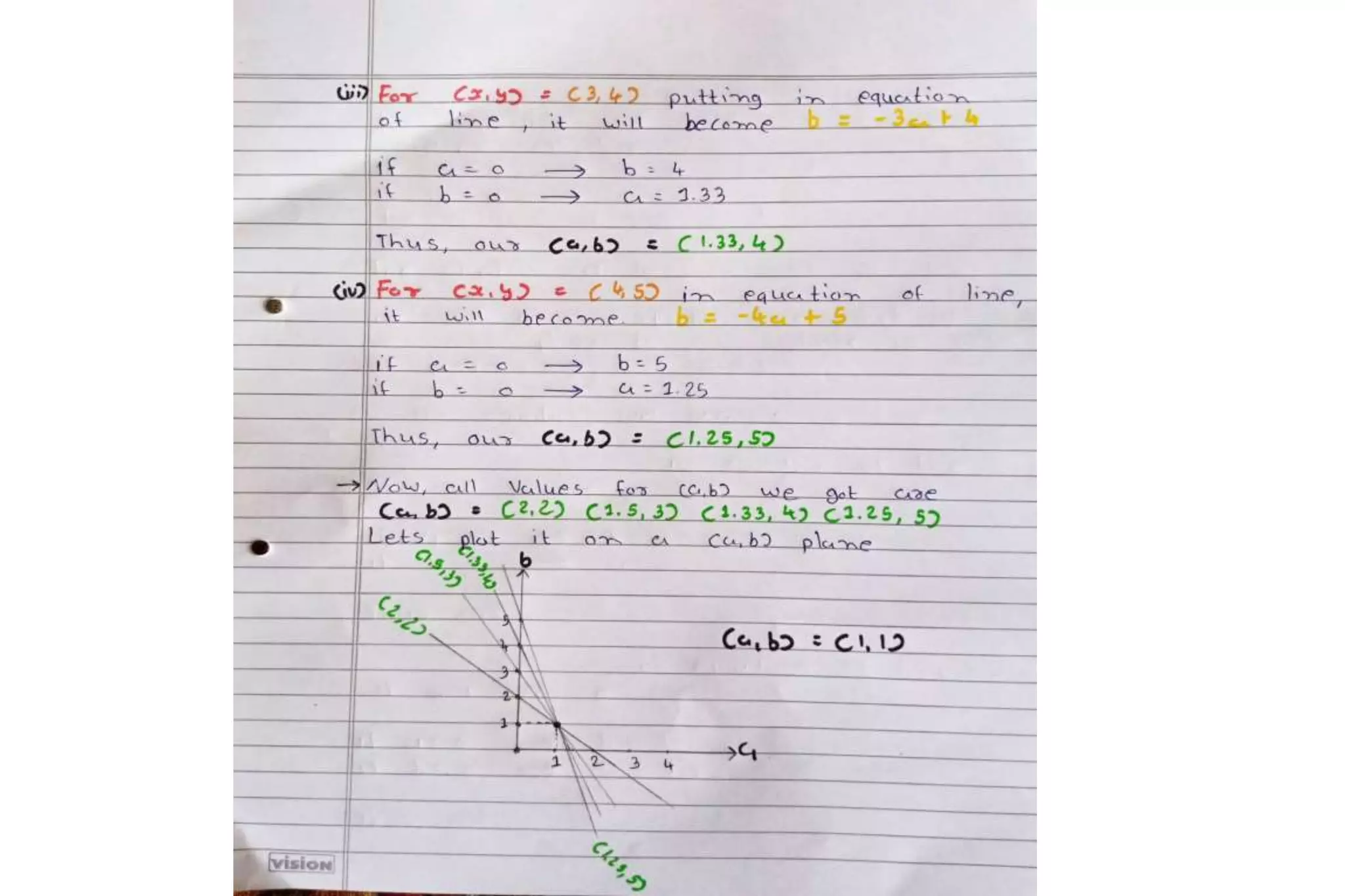
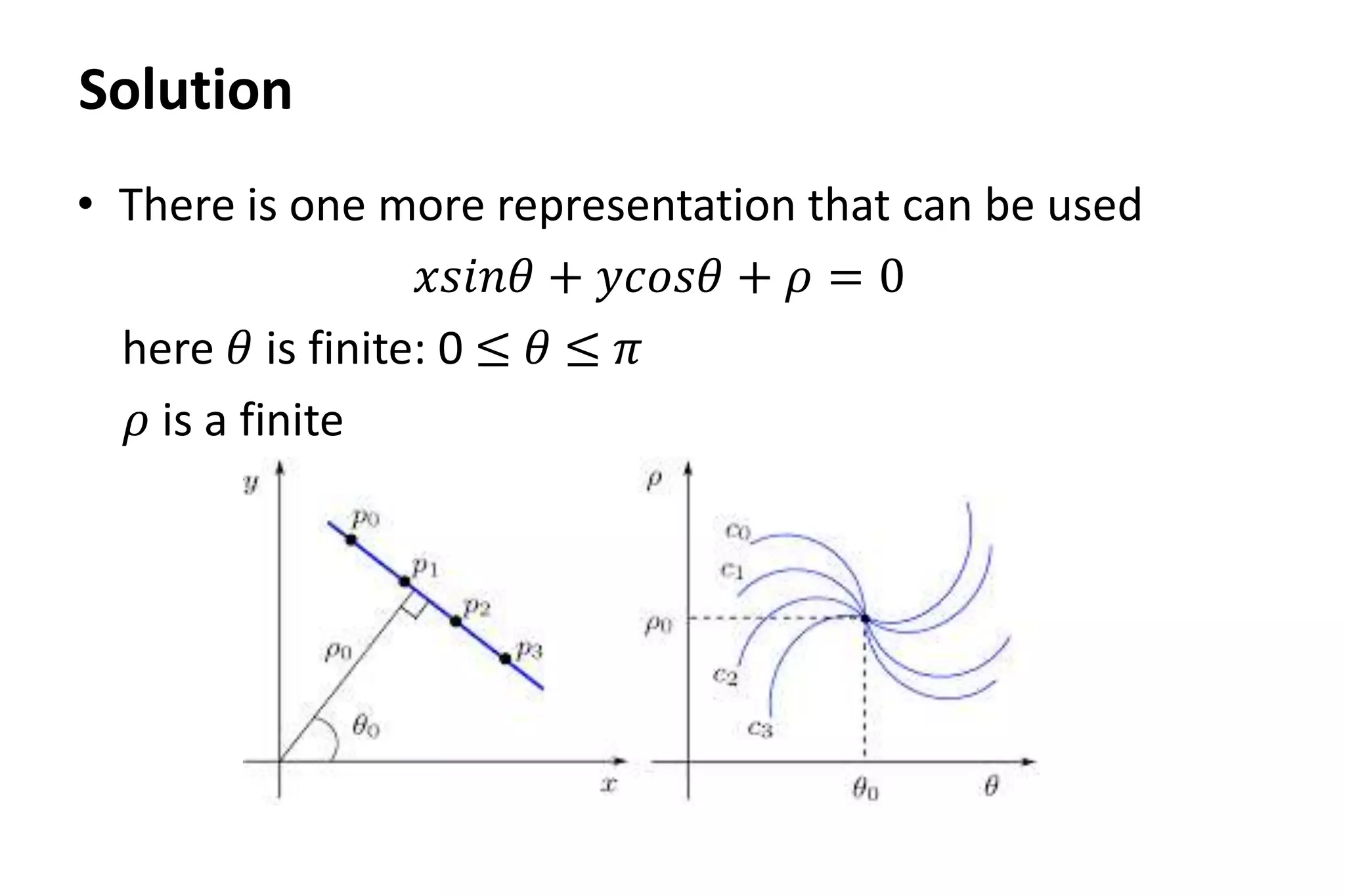
The Hough transform is a feature extraction technique used in image analysis and computer vision to detect shapes and patterns, like lines, circles, and curves. It works by having each edge point in an image vote for a set of possible shape parameters, which are then compiled into a histogram in a parameter space. Local maxima in this space correspond to the most likely shapes in the image. Specifically for line detection, the Hough transform represents a line using its slope (a) and intercept (b), with each edge point voting for all lines passing through it in the parameter space. The algorithm then finds local maxima in this space to detect the lines present in the image. The Hough transform is robust to noise, gaps,

1. Linear Hough Transform
190283103015
Raj Rana

2. Introduction
• The Hough transform is a feature Extraction technique
used in image analysis, computer vision and digital
image processing .
• It is a technique to isolate the curves of a given shapes
in a given image.
• Classical Hough Transform can locate regular curves like
straight lines, circles, parabolas, ellipses, etc.

3. • Every edge pixel Is a point that votes for all shapes that
passes through it.
• This voting procedure is carried out in a Parameter
space.
• Parameter space is a K-dimensional Histogram.

4. Hough Transform for Straight line
A straight line can be mathematically represented as:
Y = ax + b
Where, a is slope and b is a intercept

5. Image Space Parameter space
Y = ax + b b = -ax + y

6. Point Line
Line Point
Image Space Parameter space

8. Line Detection Algorithm
• Step-1:- Quantize the parameter space
• Step-2:- Create accumulator array
• Step-3:- Set all value by zero
• Step-4:- For each edge in (xi, yi),
P(a, b) = P (a, b) + 1
If (a, b) lies on line: -mxi + yi
• Step-5:- Find local maxima in P(a, b)
xi, yi
Image space P (a, b)
Maxima
xi, yi

9. Applications
• Detection of lines
• Fill the edges
• Linking the edge points
• To Find out Points are collinear
• Find aligned points in image that create lines

12. • We get our (a, b) = (1, 1)
• Our line of equation is y = ax + b
• By substitute values we will get,
y = x + 1
This line in collinear that has values (1,2), (2,3), (3,4), (4,5)
on it.
Hence all the points lies on the same line they are called
collinear.

13. Problem in Hough Transform
• For the line of equation
Y = ax + b
The slope a lies between – ∞ ≤ 𝑎 ≤ +∞
Which creates problem in the case of quantizing vertical
line.
It ends up with massive amount of data and large
accumulator to store it.
In that case this representation fails completely.

14. Solution
• There is one more representation that can be used
𝑥𝑠𝑖𝑛𝜃 + 𝑦𝑐𝑜𝑠𝜃 + 𝜌 = 0
here 𝜃 is finite: 0 ≤ 𝜃 ≤ 𝜋
𝜌 is a finite

15. Advantages of Hough Transform
• Tolerant to the gaps in the edges
• Not affected by noise
• Not affected by occlusion in image
Ending..