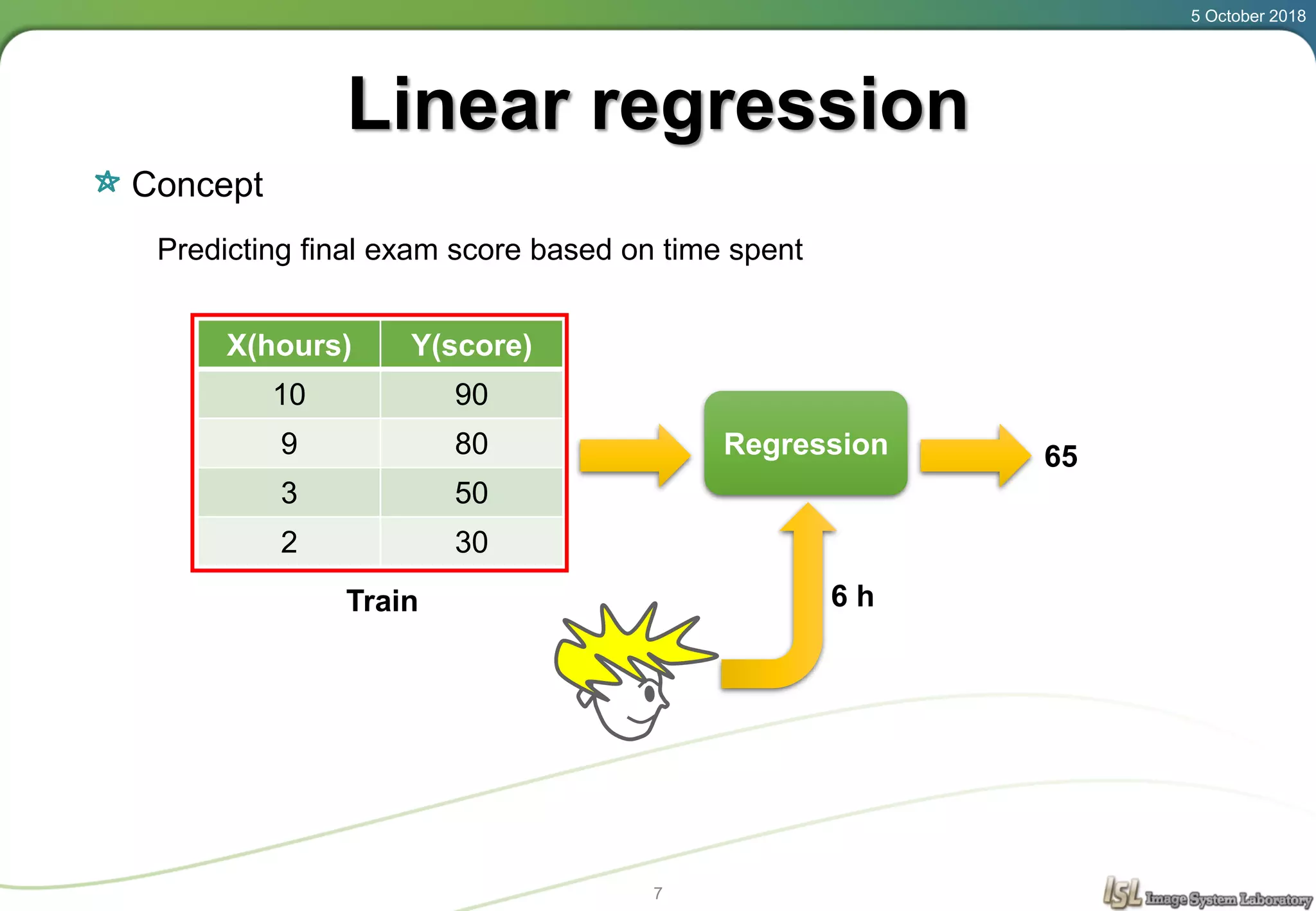
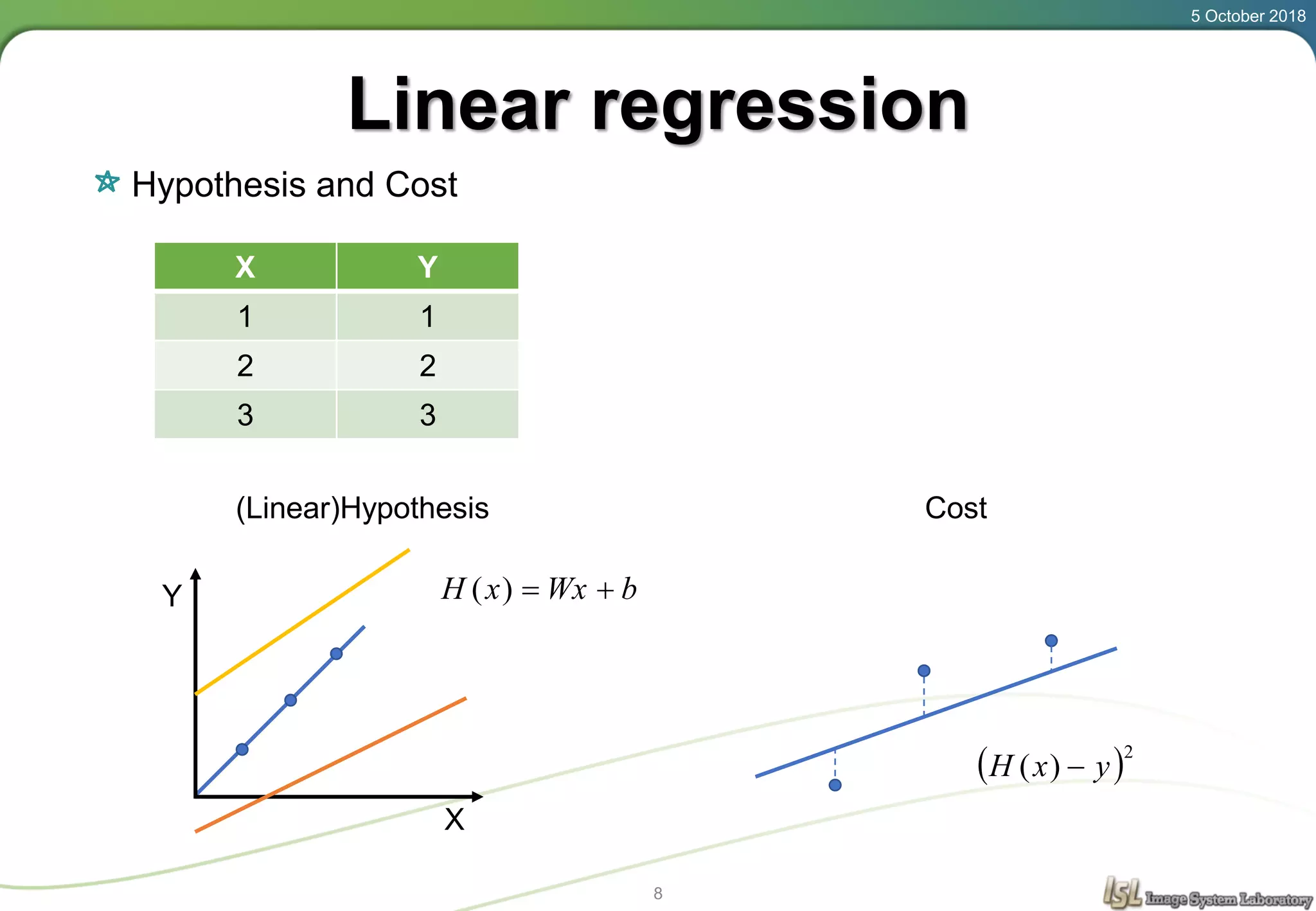
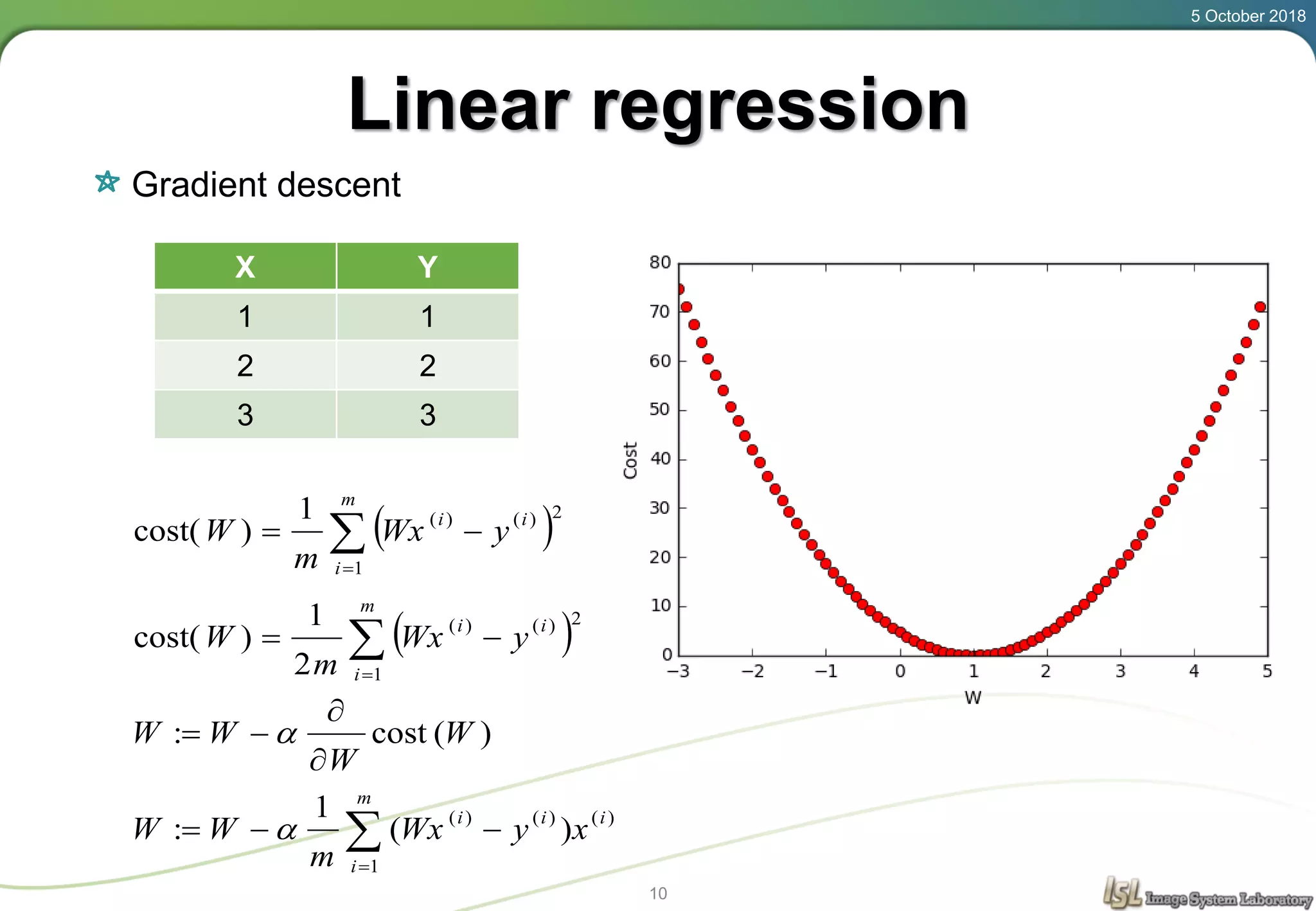
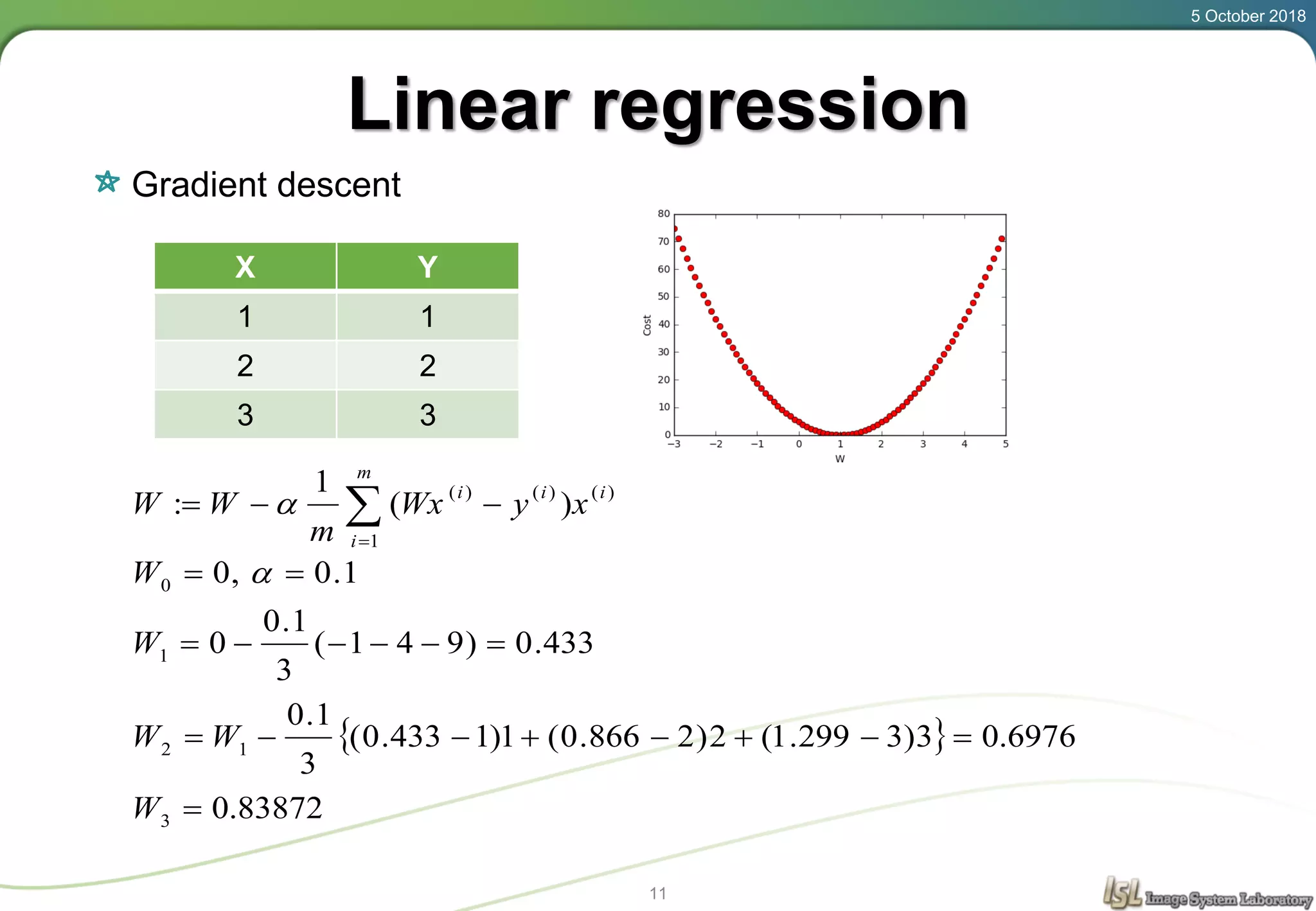
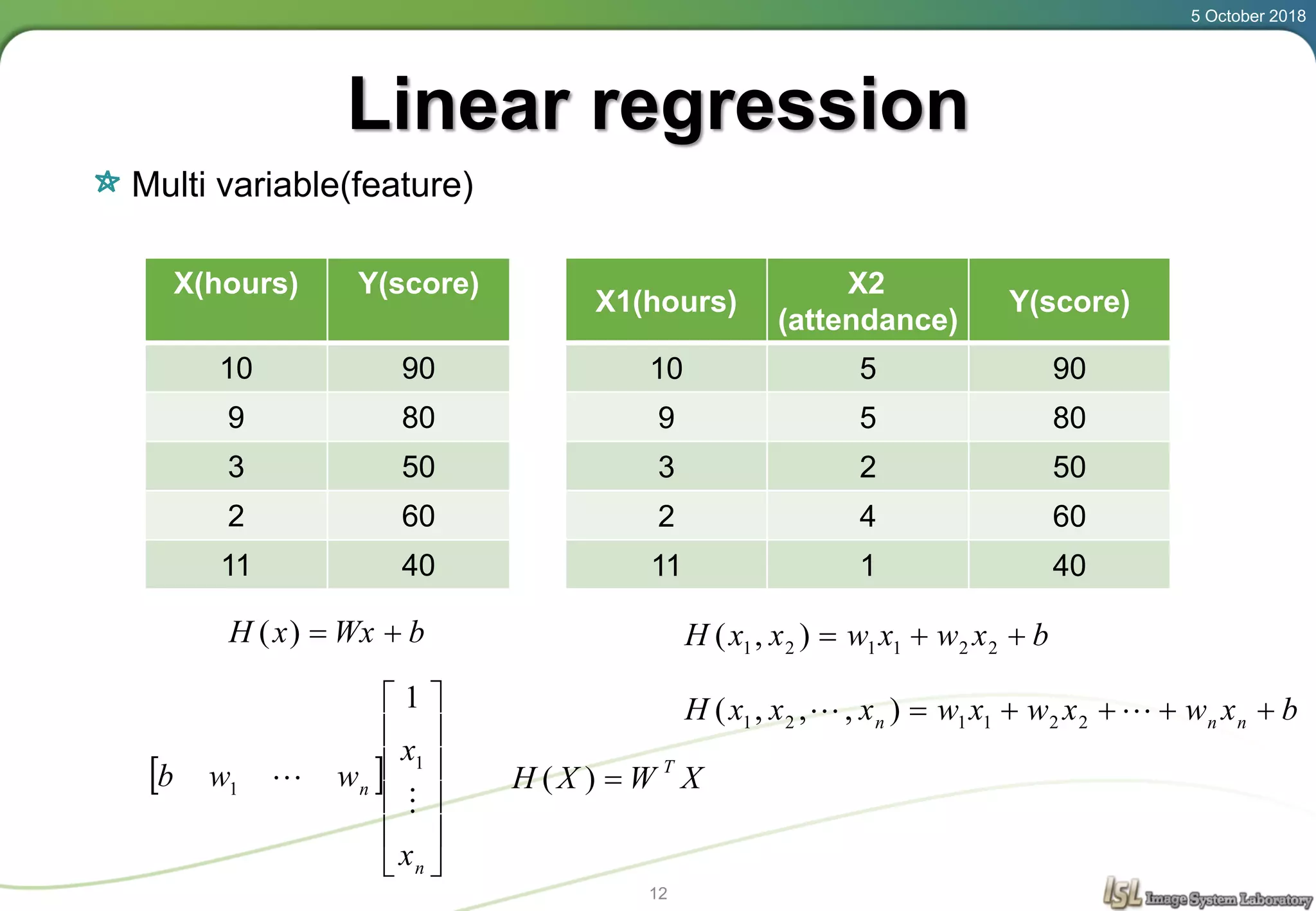
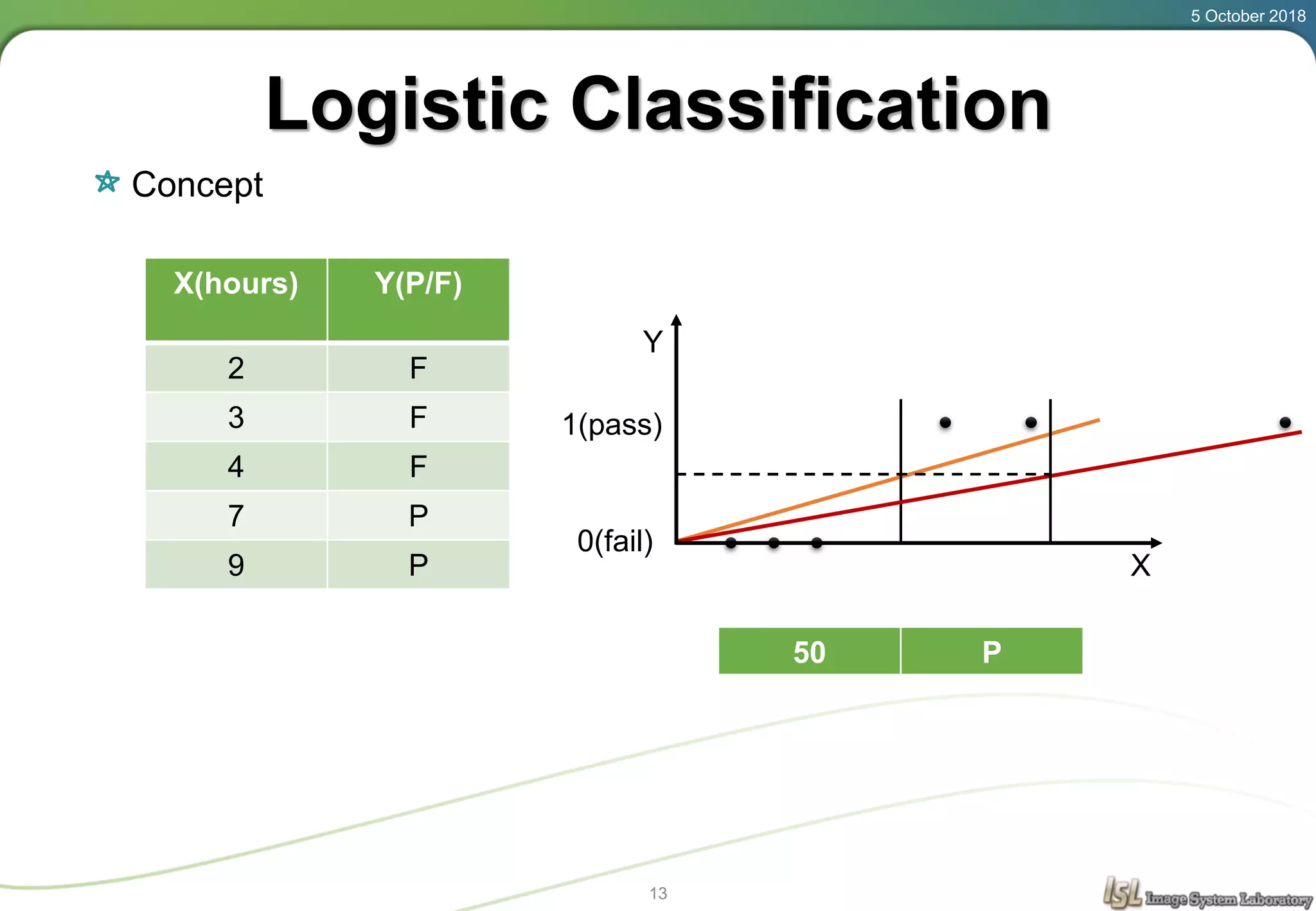
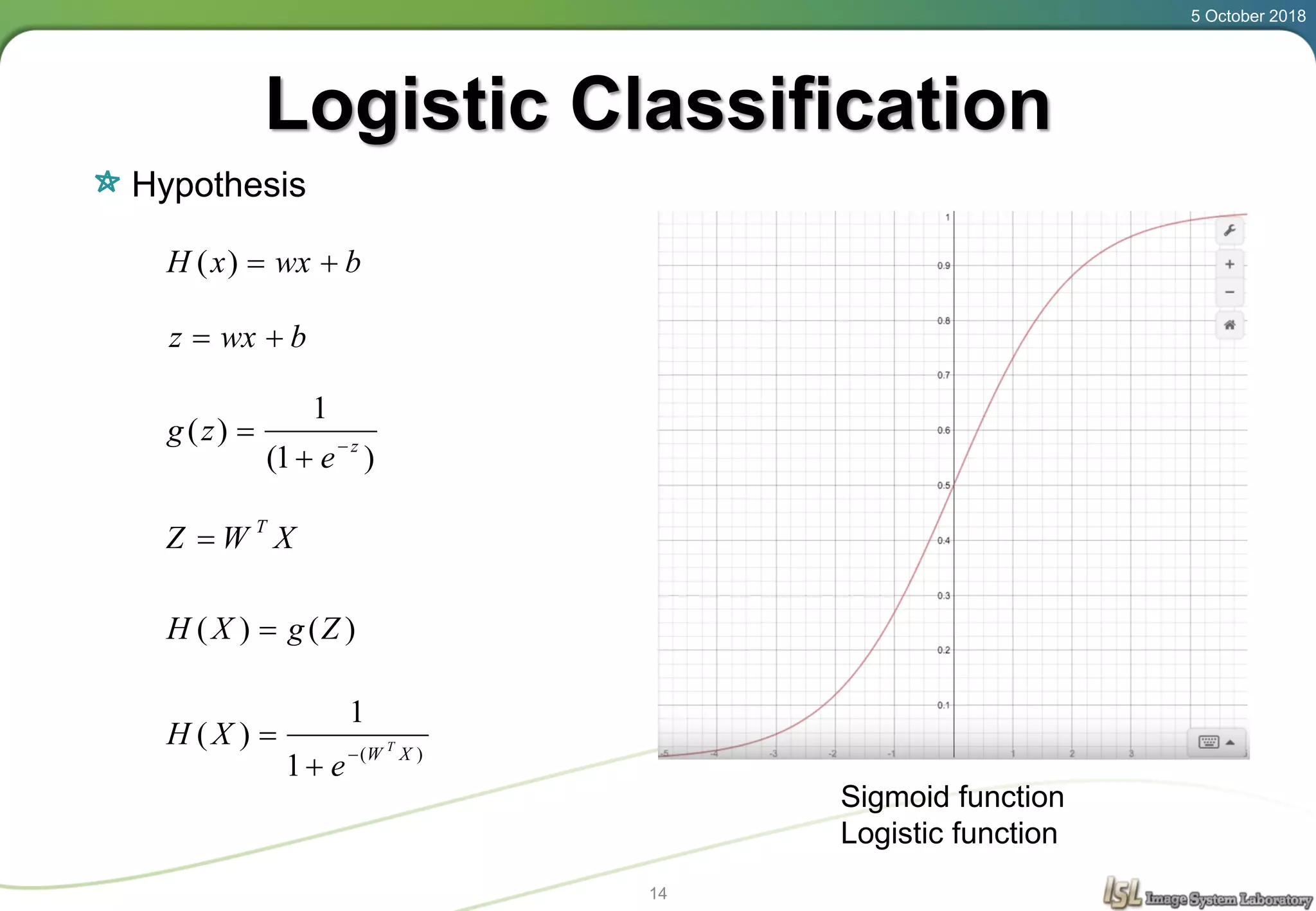
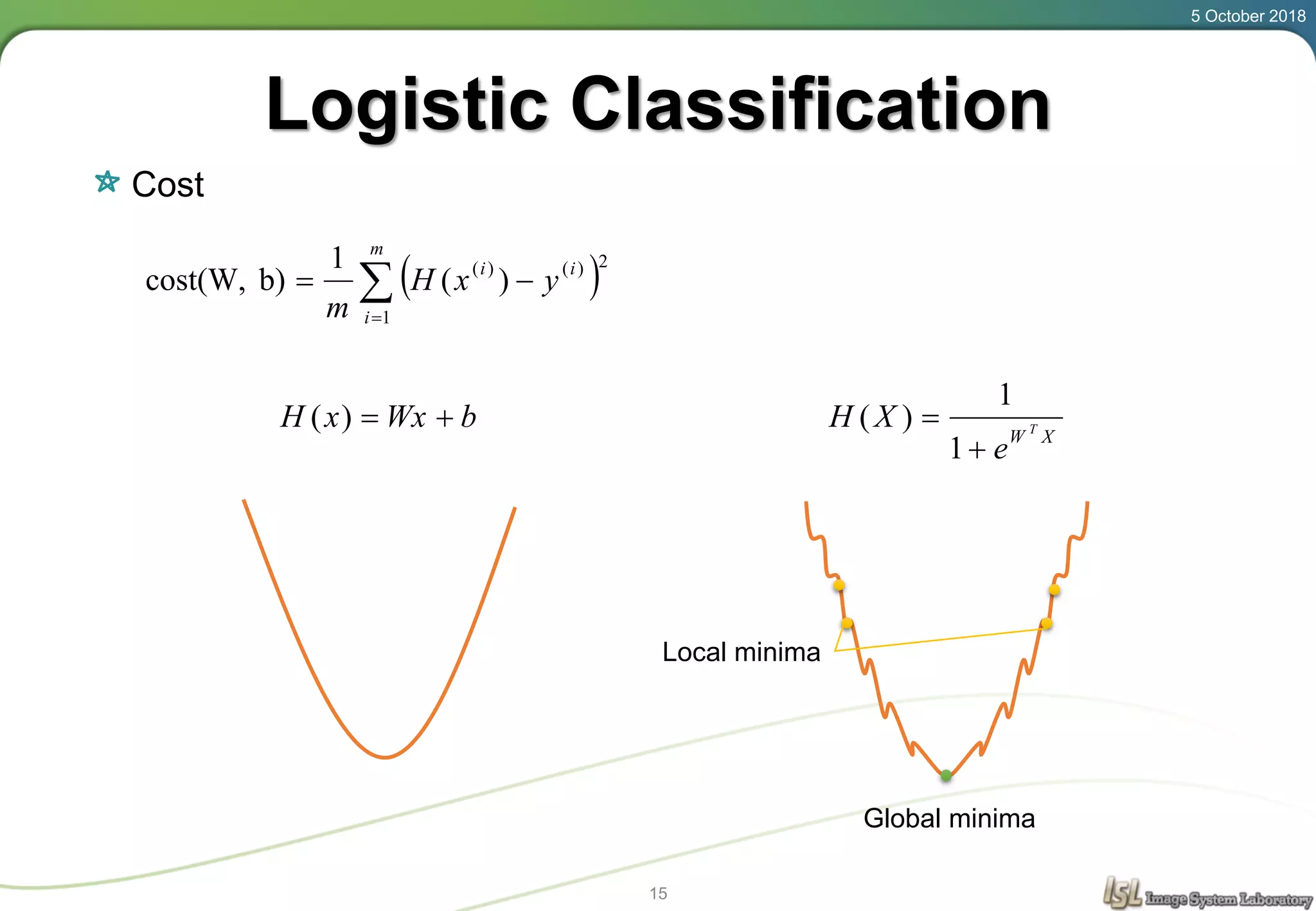
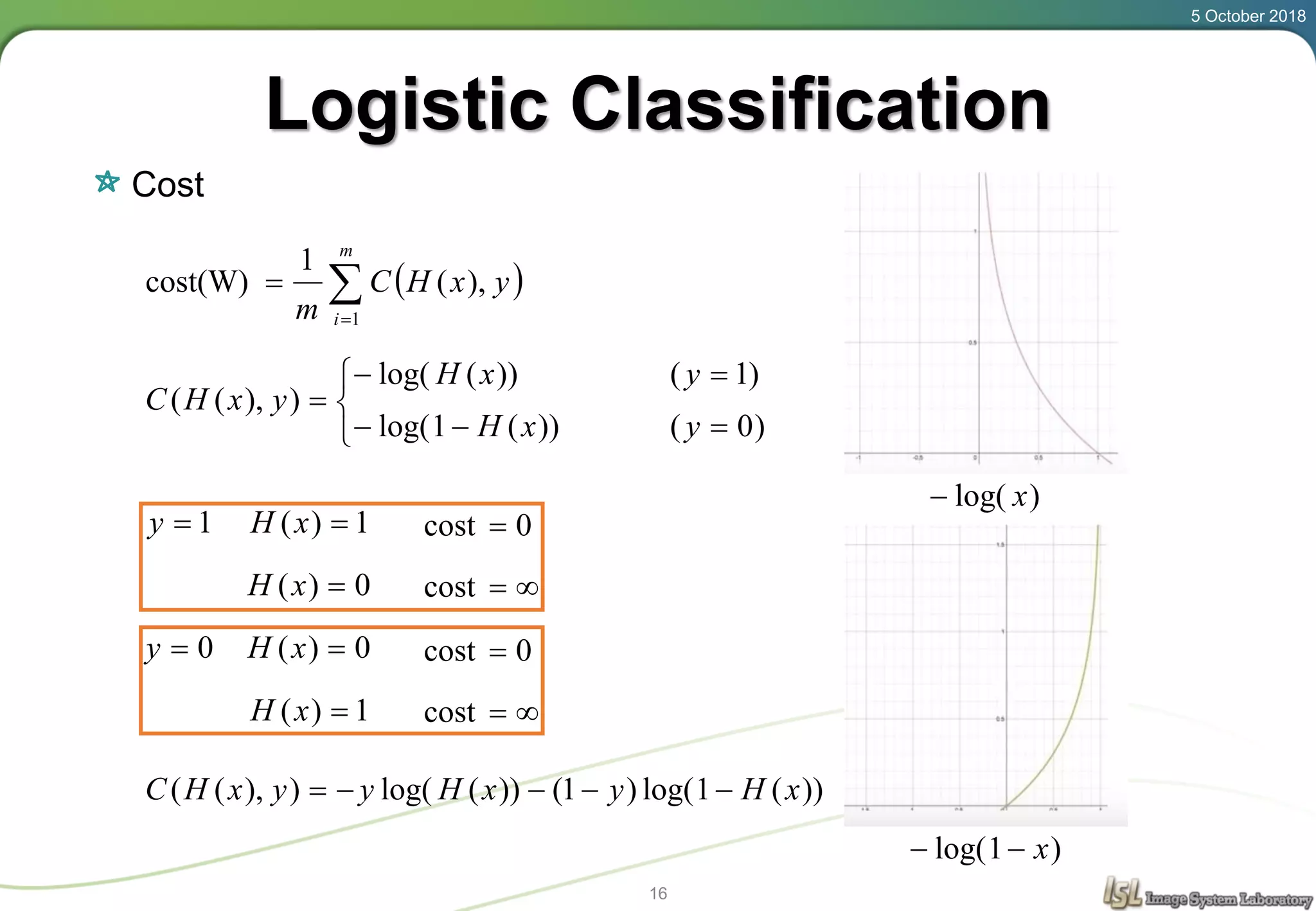
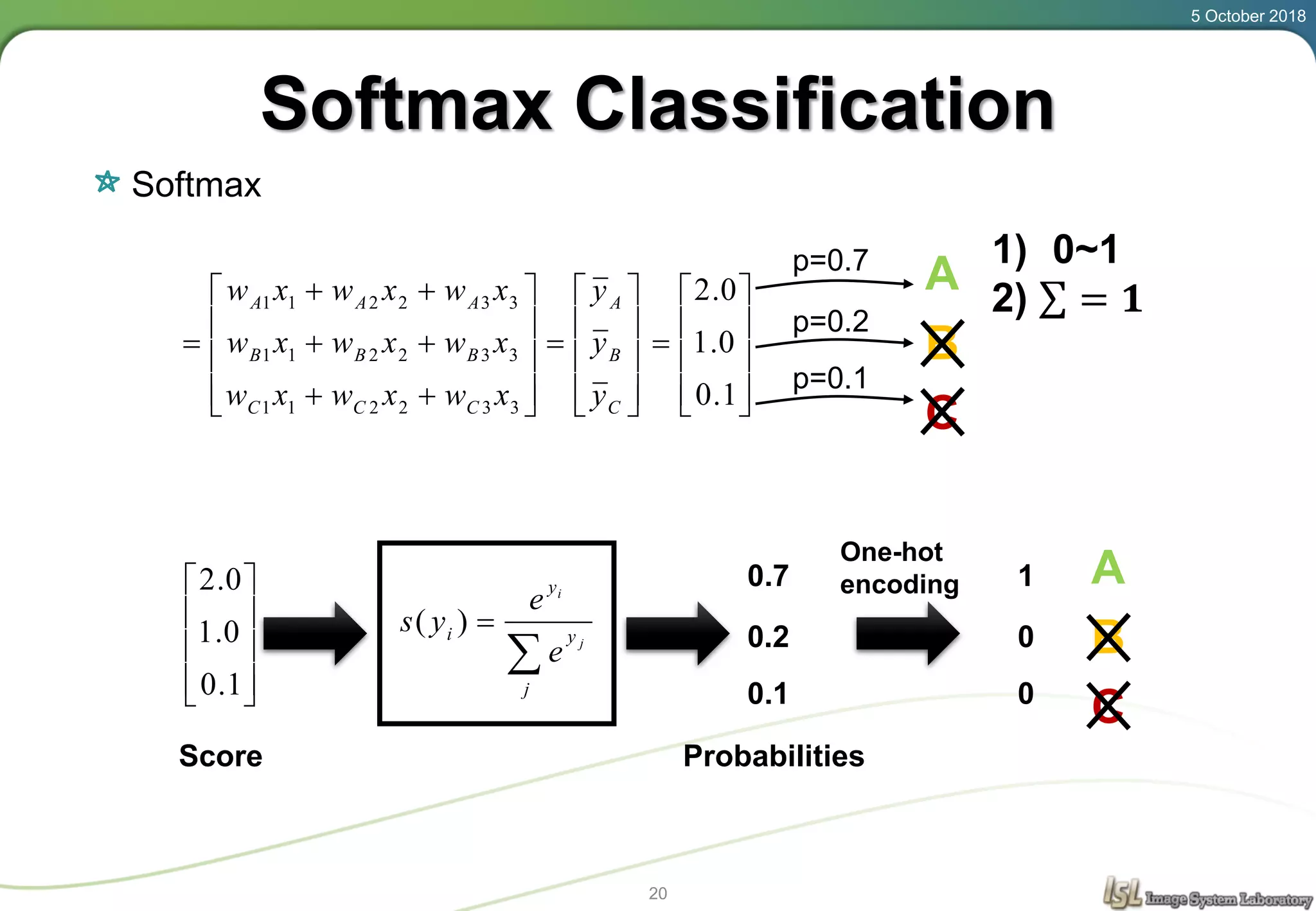
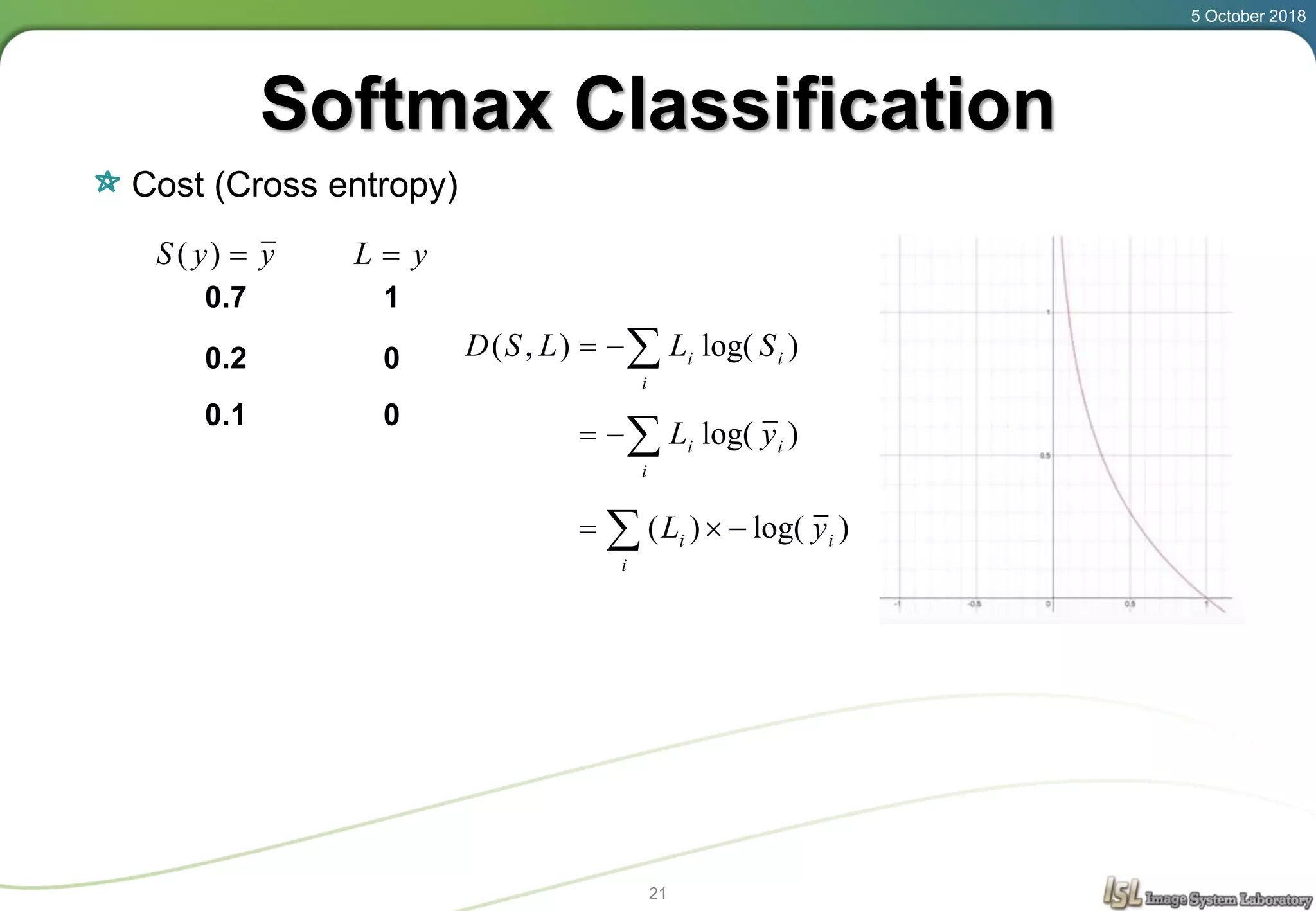
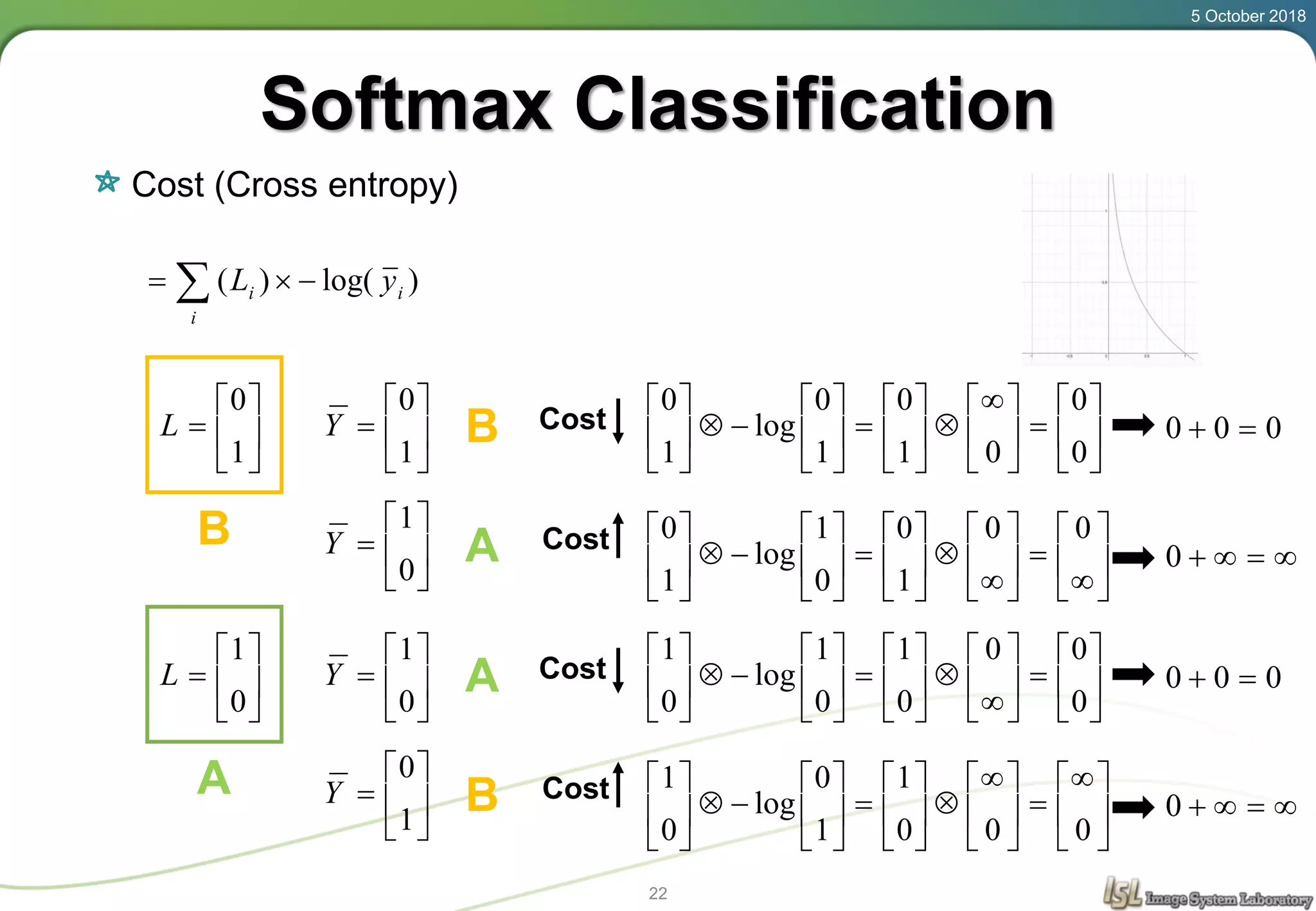
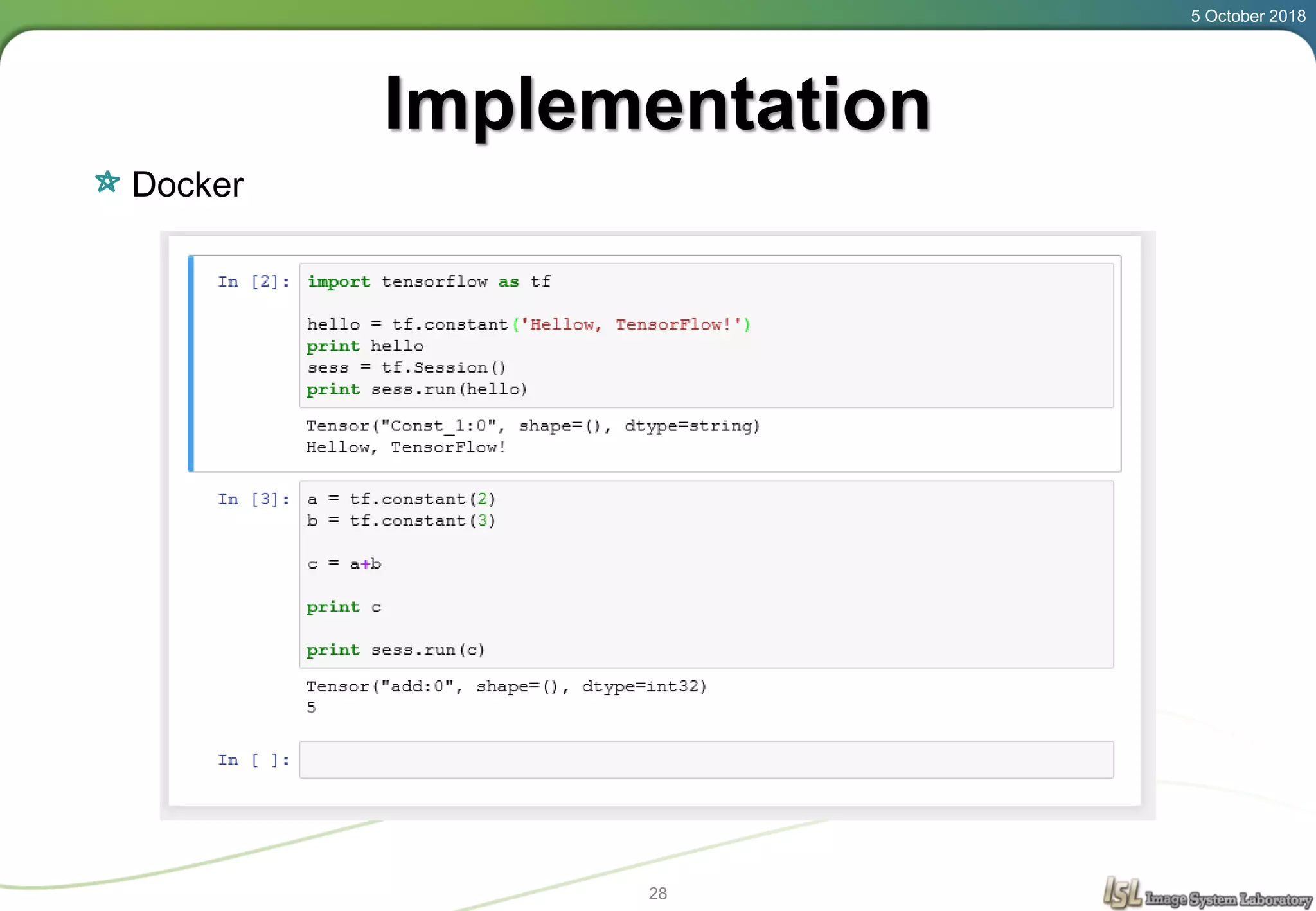
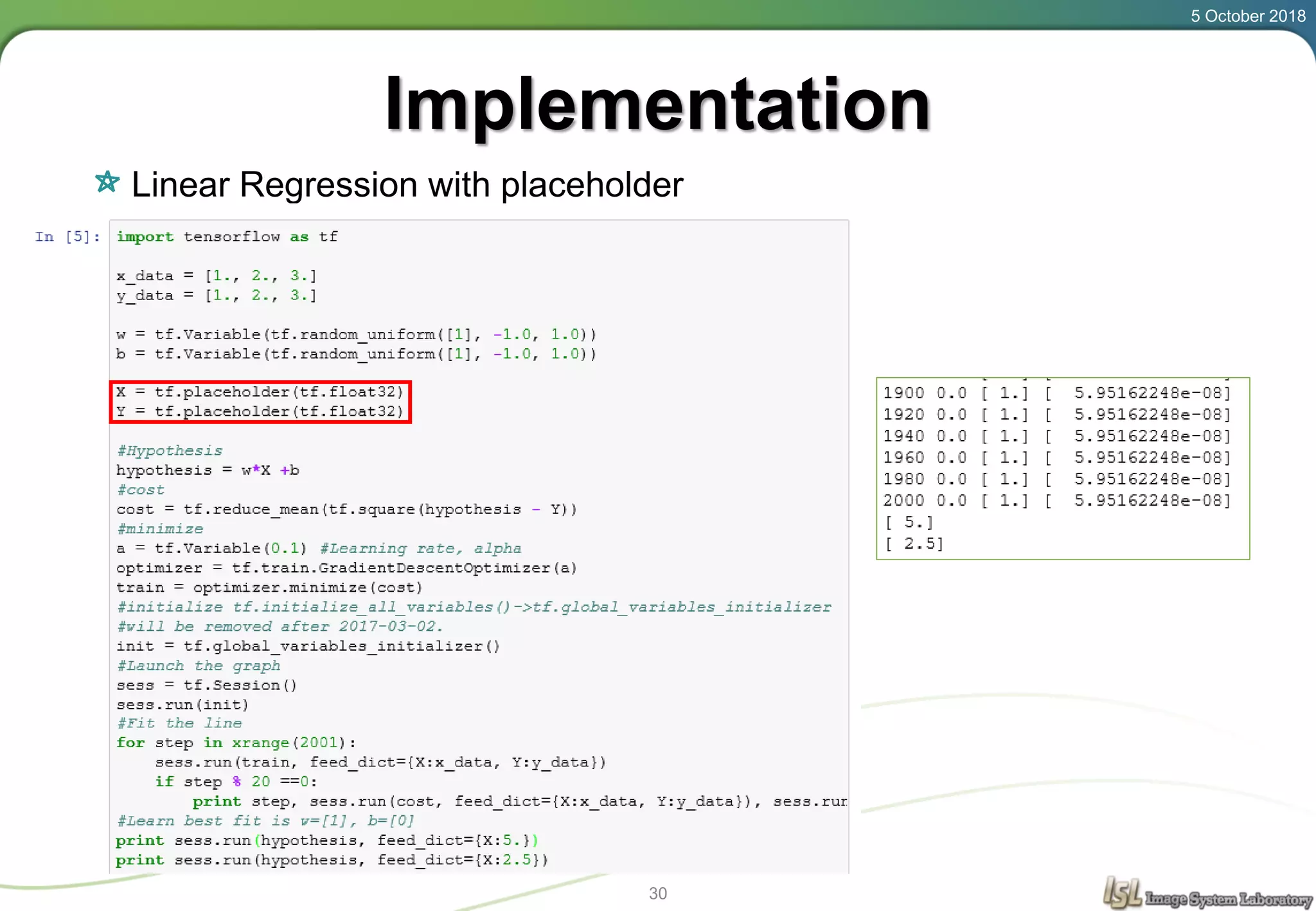
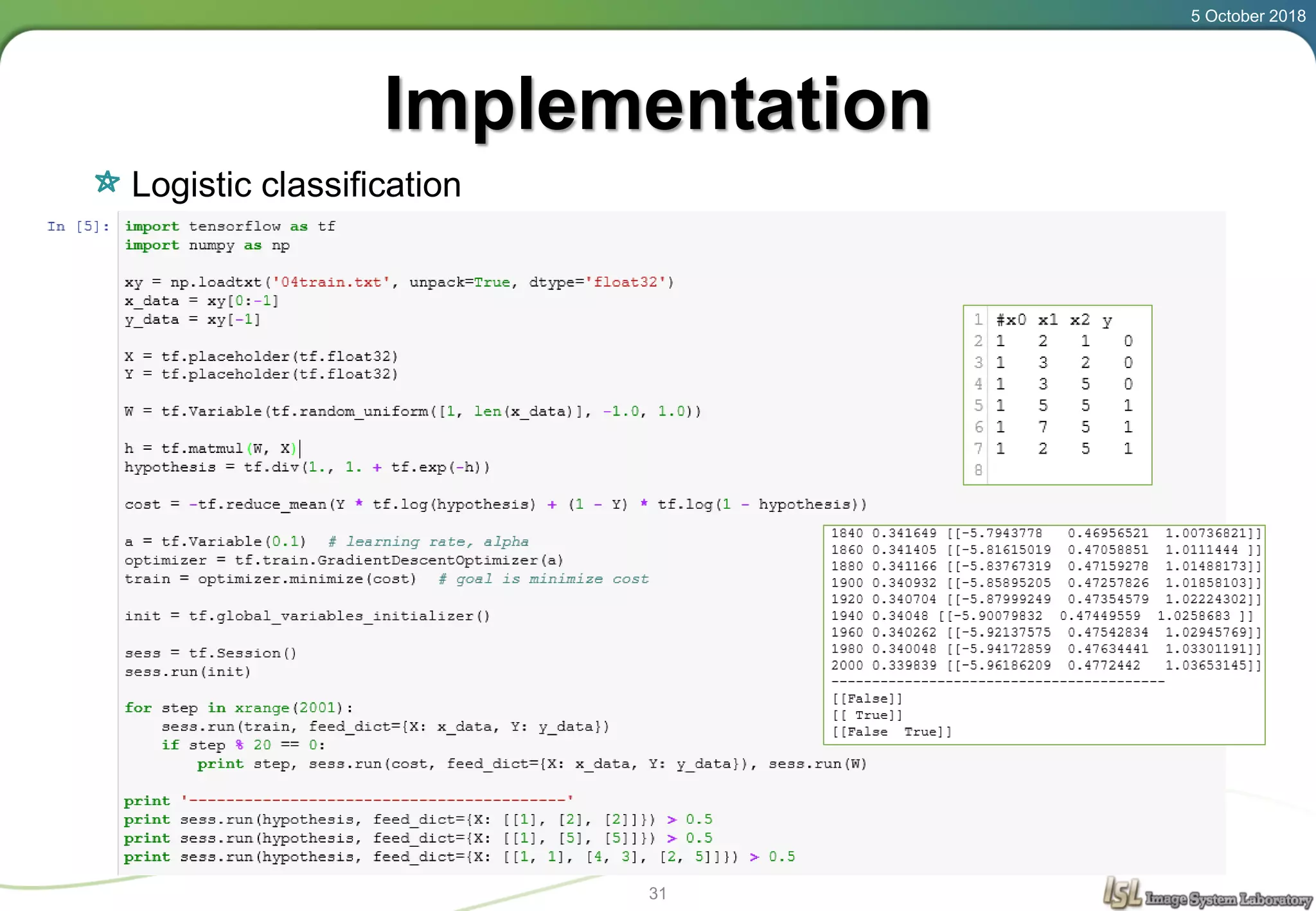
This document provides an overview of basic machine learning concepts including regression, logistic classification, and softmax classification. It introduces linear regression for predicting a continuous output variable, logistic regression for binary classification problems, and softmax classification for multi-class classification problems. Key aspects covered include the hypothesis, cost function, and using gradient descent to minimize the cost function for each of these machine learning algorithms.

1. Basic of ML : Regression and Classification
ISL lab Seminar
Han-Sol Kang
6 Feb 2017

2. 5 October 2018
2
Contents
Introduction
Linear
Regression
Logistic
Classification
Softmax
Classification
Impleme
ntation
* Reference : https://hunkim.github.io/ml/

3. Introduction
What is ML
5 October 2018
3
• Limitations of explicit programming
- Spam filter : many rules - Automatic driving : too many rules
• Machine learning : “Field of study that gives computers the ability to learn
without being explicitly programmed” - Arhur Samuel(1959)

4. Introduction
Supervised/Unsupervised learning
5 October 2018
4
• Supervised learning
- Learning with labeled examples (training set)
• Unsupervised learning : un-labeled data
- Google news grouping
- Word clustering

5. Introduction
Supervised learning
5 October 2018
5
• Most common problem type in ML
- Image labeling : learning from tagged images
- Email spam filter : learning from labeled (spam or ham) email
- Predicting exam score : learning from previous exam score and time spent

6. Introduction
Supervised learning
5 October 2018
6
• Type of supervised learning
- Predicting final exam score based on time spent
- Pass/non-pass based on time spent
- Letter grade (A, B, C, D and F) based on time spent
– Regression
– Binary classification
– Multi-label classification

7. Linear regression
Concept
5 October 2018
7
X(hours) Y(score)
10 90
9 80
3 50
2 30
Predicting final exam score based on time spent
Train
Regression
6 h
65

8. Linear regression
Hypothesis and Cost
5 October 2018
8
X Y
1 1
2 2
3 3
(Linear)Hypothesis
bWxxH )(
Cost
 2
)( yxH 
X
Y

9. Linear regression
Cost function(Loss function)
5 October 2018
9
X Y
1 1
2 2
3 3
3
))(())(())(( 2)3()3(2)2()2(2)1()1(
yxHyxHyxH 
 


m
i
ii
yxH
m 1
2)()(
)(
1
cost
 


m
i
ii
yxH
m 1
2)()(
)(
1
b)cost(W, Minimize

10. Linear regression
Gradient descent
5 October 2018
10
X Y
1 1
2 2
3 3
 


m
i
ii
yWx
m
W
1
2)()(1
)cost(
 


m
i
ii
yWx
m
W
1
2)()(
2
1
)cost(
)(cost: W
W
WW


 
)(
1
)()(
)(
1
: i
m
i
ii
xyWx
m
WW 

 

11. Linear regression
Gradient descent
5 October 2018
11
X Y
1 1
2 2
3 3
)(
1
)()(
)(
1
: i
m
i
ii
xyWx
m
WW 

 
1.0,00  W
 
0.83872
0.69763)3299.1(2)2866.0(1)1433.0(
3
1.0
433.0)941(
3
1.0
0
3
12
1



W
WW
W

12. Linear regression
Multi variable(feature)
5 October 2018
12
X(hours) Y(score)
10 90
9 80
3 50
2 60
11 40
X1(hours)
X2
(attendance)
Y(score)
10 5 90
9 5 80
3 2 50
2 4 60
11 1 40
bWxxH )( bxwxwxxH  221121 ),(
bxwxwxwxxxH nnn   221121 ),,,(
XWXH T
)( 












n
n
x
x
wwb


1
1
1

13. Logistic Classification
Concept
5 October 2018
13
X(hours) Y(P/F)
2 F
3 F
4 F
7 P
9 P X
Y
1(pass)
0(fail)
50 P

14. Logistic Classification
Hypothesis
5 October 2018
14
bwxxH )(
)1(
1
)( z
e
zg 


Sigmoid function
Logistic function
XWZ T

)()( ZgXH 
)(
1
1
)( XW T
e
XH 


bwxz 

15. Logistic Classification
Cost
5 October 2018
15
bWxxH )( XW T
e
XH


1
1
)(
 


m
i
ii
yxH
m 1
2)()(
)(
1
b)cost(W,
Local minima
Global minima

16. Logistic Classification
Cost
5 October 2018
16






)0())(1log(
)1())(log(
)),((
yxH
yxH
yxHC
))(1log()1())(log()),(( xHyxHyyxHC 
 


m
i
yxHC
m 1
),(
1
cost(W)
)log( x
)1log( x
1y 1)( xH
0)( xH
0cost 
cost
0y 0)( xH
1)( xH
0cost 
cost

17. Logistic Classification
Minimize cost
5 October 2018
17
)(cost: W
W
WW


 



m
i
xHyxHy
m 1
))(1log()1())(log(
1
cost(W)

18. Softmax Classification
Concept
5 October 2018
18
X1(hours)
X2
(attendance)
Y(grade)
10 5 A
9 5 A
3 2 B
2 4 B
11 1 C
X1
X2
B
B
C
AA

19. Softmax Classification
Concept
5 October 2018
19
ത𝑌
𝑊
𝑧
𝑋
ത𝑌
𝑊
𝑧
𝑋
ത𝑌
𝑊
𝑧
𝑋
 










3
2
1
321
x
x
x
www




















3
2
1
321
322
321
x
x
x
www
www
www
CCC
BBB
AAA
 










3
2
1
321
x
x
x
www
 










3
2
1
321
x
x
x
www

























C
B
A
CCC
BBB
AAA
y
y
y
xwxwxw
xwxwxw
xwxwxw
332211
332211
332211

20. Softmax Classification
Softmax
5 October 2018
20

























C
B
A
CCC
BBB
AAA
y
y
y
xwxwxw
xwxwxw
xwxwxw
332211
332211
332211











1.0
0.1
0.2
B
C
Ap=0.7
p=0.2
p=0.1


j
y
y
i j
i
e
e
ys )(










1.0
0.1
0.2
Score Probabilities
0.7
0.2
0.1
1) 0~1
2) σ = 𝟏
1
0
0
One-hot
encoding
B
C
A

21. Softmax Classification
Cost (Cross entropy)
5 October 2018
21
0.7
0.2
0.1
1
0
0
yyS )( yL 

i
ii SLLSD )log(),(
 
i
ii yL )log()(

i
ii yL )log(

22. Softmax Classification
Cost (Cross entropy)
5 October 2018
22
 
i
ii yL )log()(







1
0
L 






1
0
Y







0
1
YB
B
A
Cost
Cost






























0
0
01
0
1
0
log
1
0































 00
1
0
0
1
log
1
0
000 
0







0
1
L 






0
1
Y







1
0
YA
A
B
Cost
Cost































0
00
0
1
0
1
log
0
1






























000
1
1
0
log
0
1
000 
0

23. Softmax Classification
Cost(Loss) function & minimization
5 October 2018
23
 
i
ii LbwxSD
N
L )),((
1
Loss
Minimization->Gradient descent

24. Implementation
Docker
5 October 2018
24
Click

25. 5 October 2018
25
Implementation
Docker

26. 5 October 2018
26
Implementation
Docker

27. 5 October 2018
27
Implementation
Docker

28. 5 October 2018
28
Implementation
Docker

29. 5 October 2018
29
Implementation
Linear Regression

30. 5 October 2018
30
Implementation
Linear Regression with placeholder

31. 5 October 2018
31
Implementation
Logistic classification

32. 5 October 2018
32
Implementation
Softmax classification
 
i
ii LbwxSD
N
L )),((
1

33. Q & A