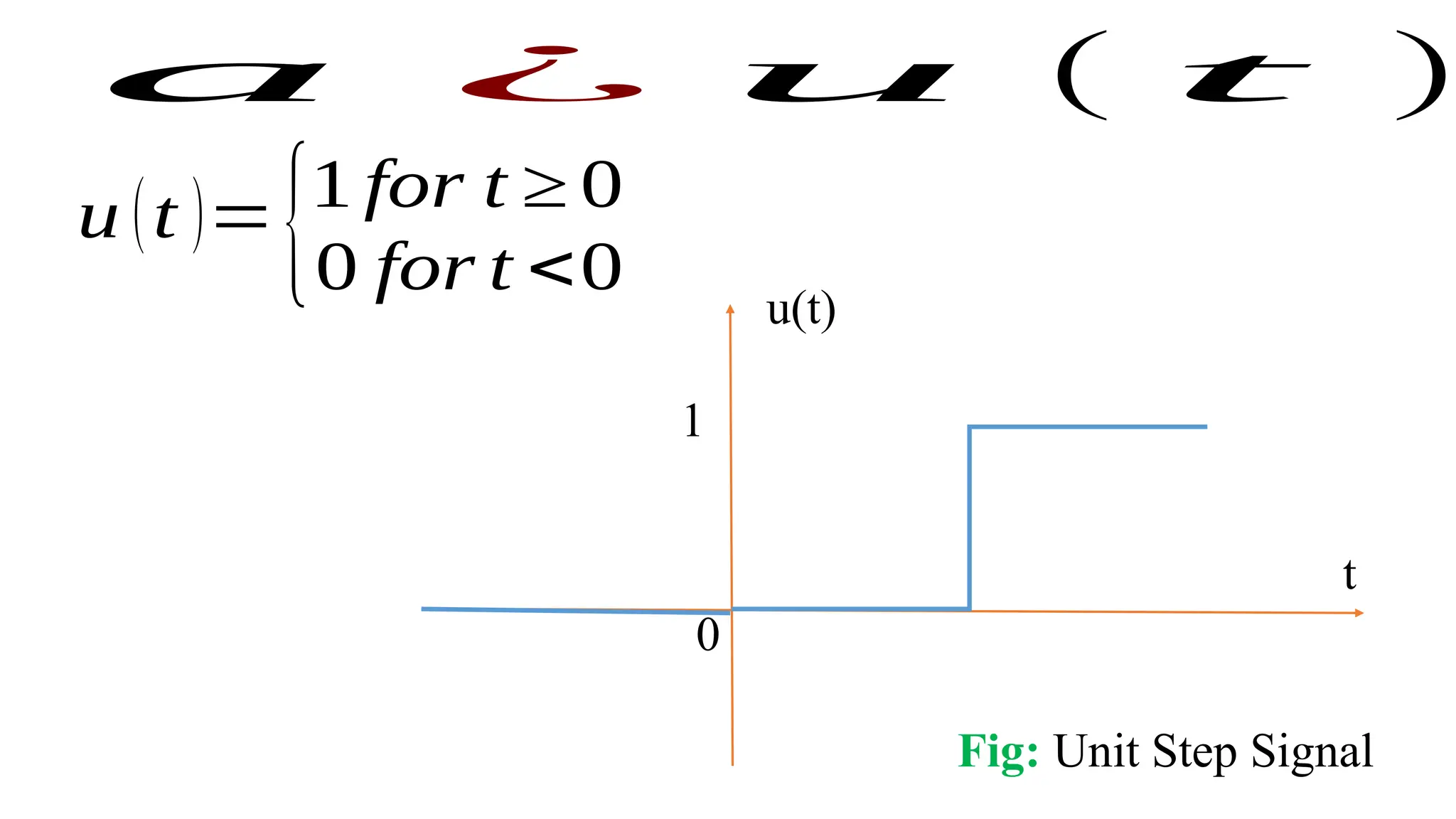
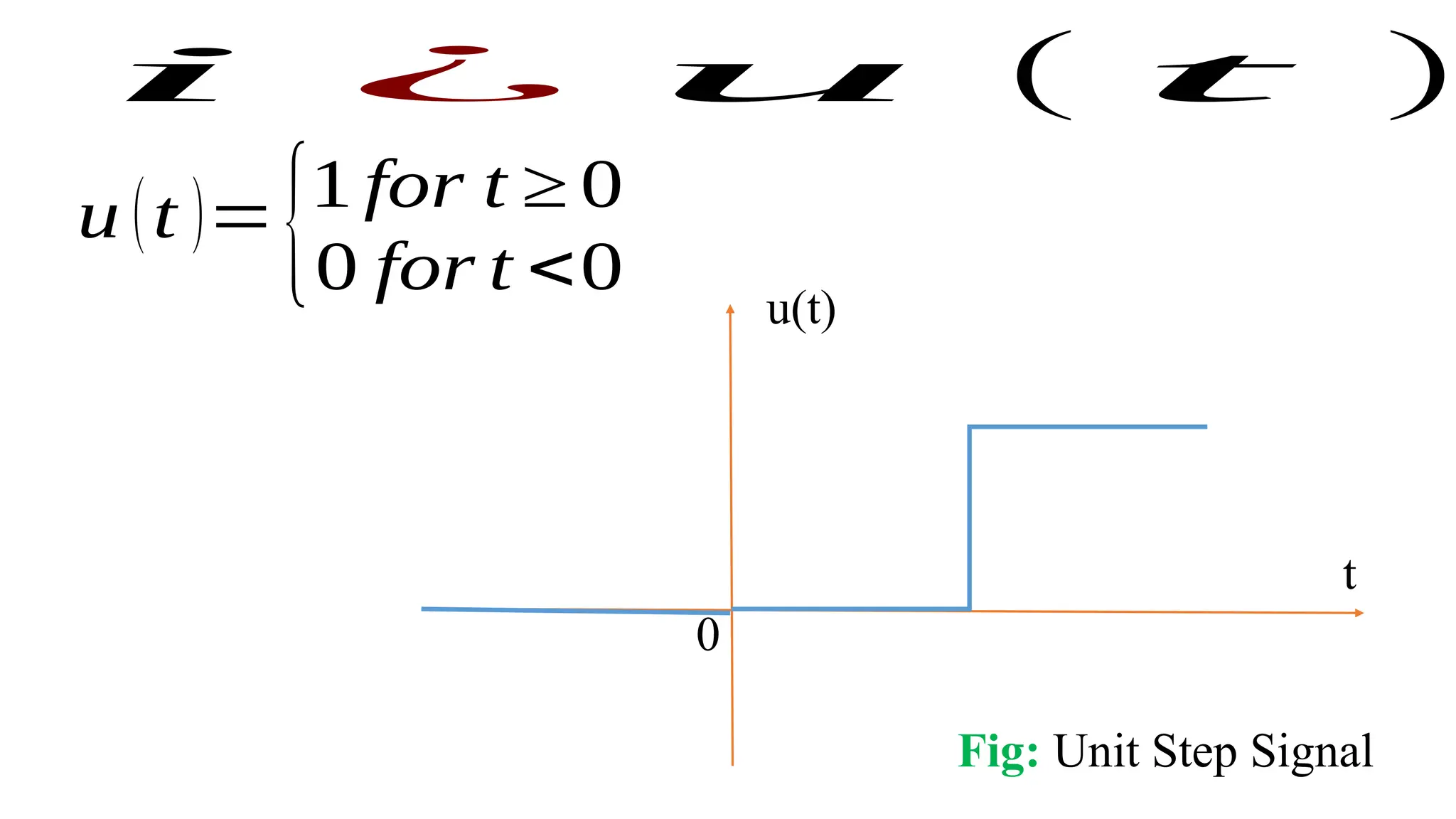
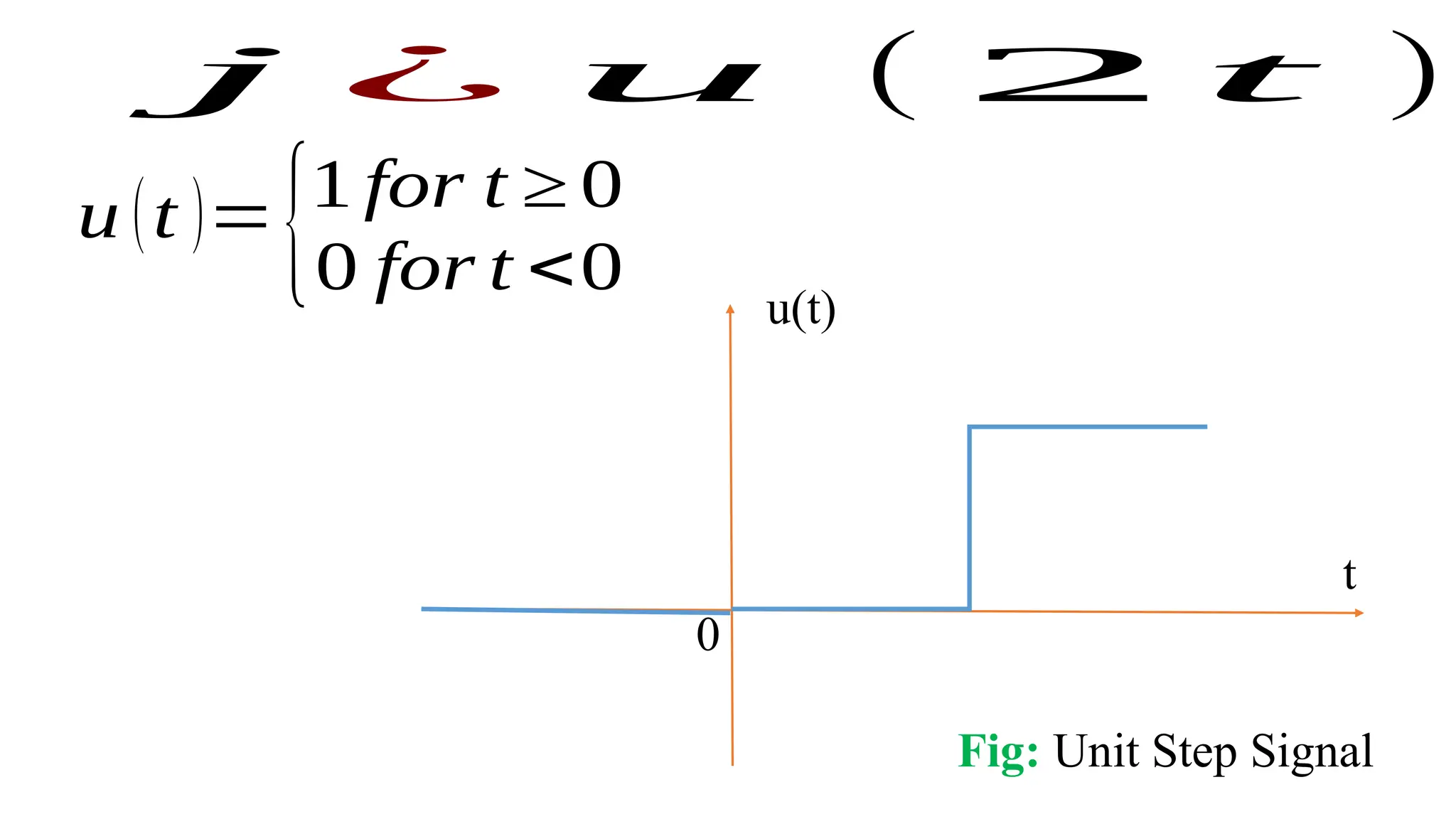
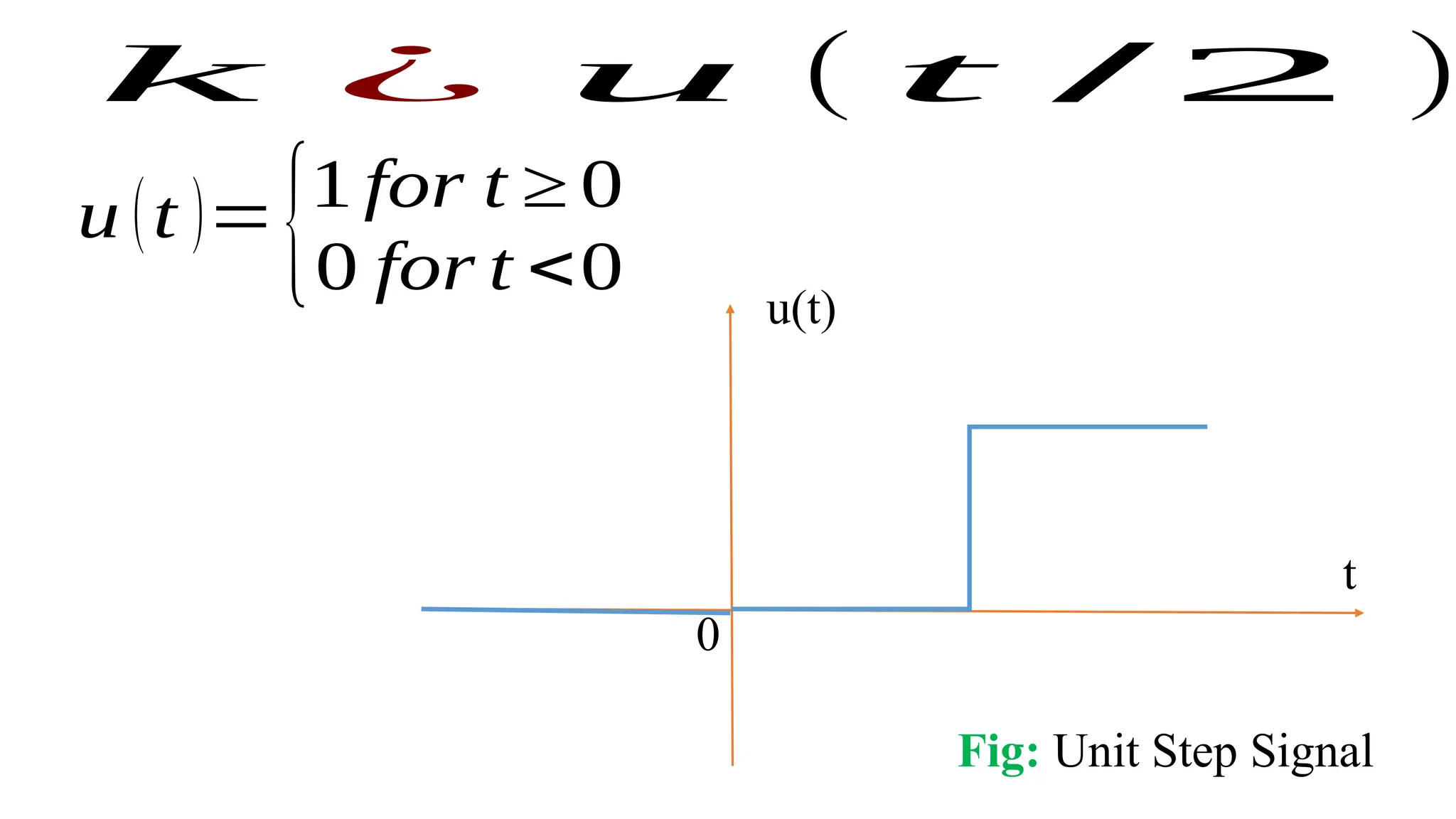
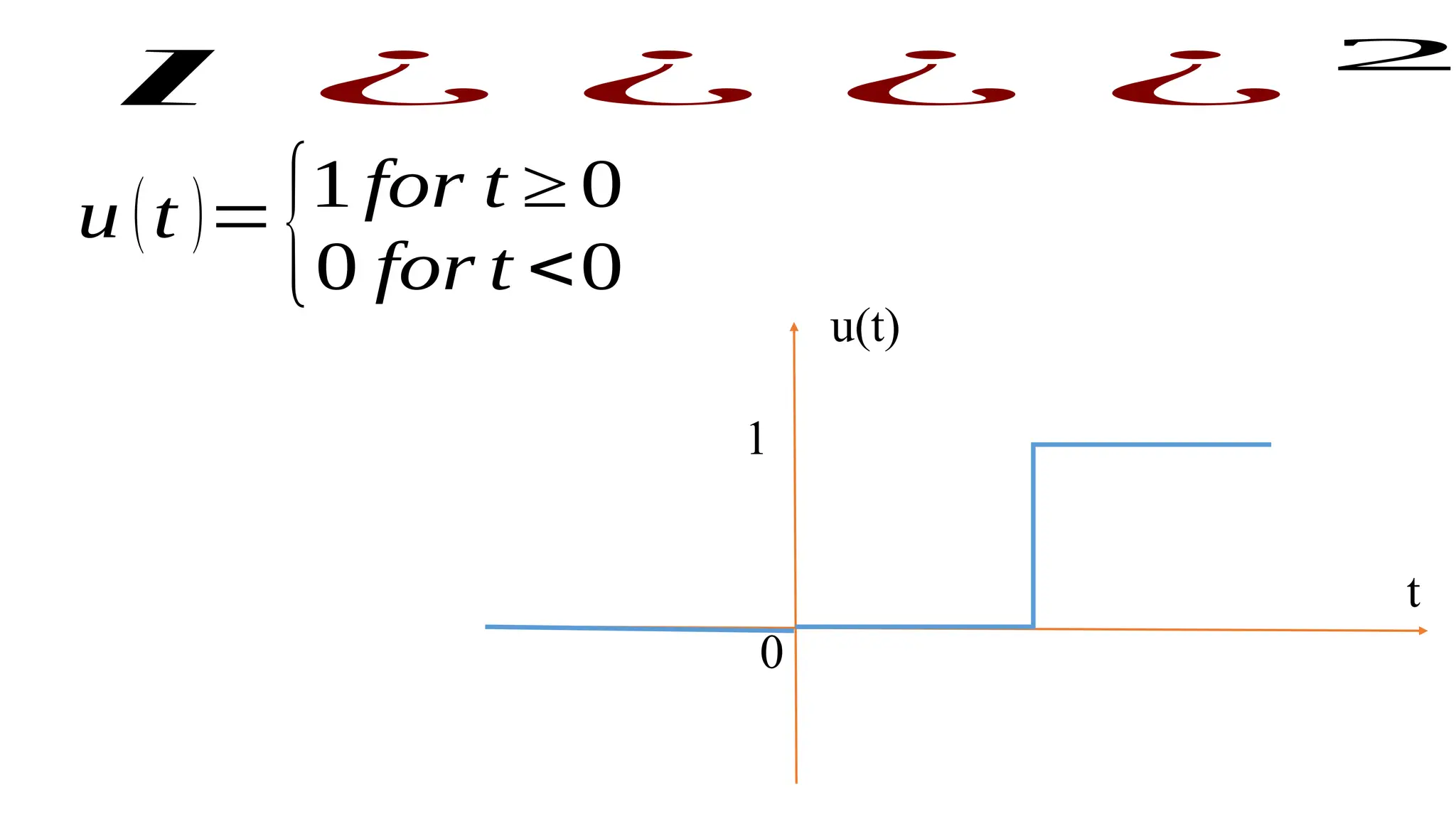
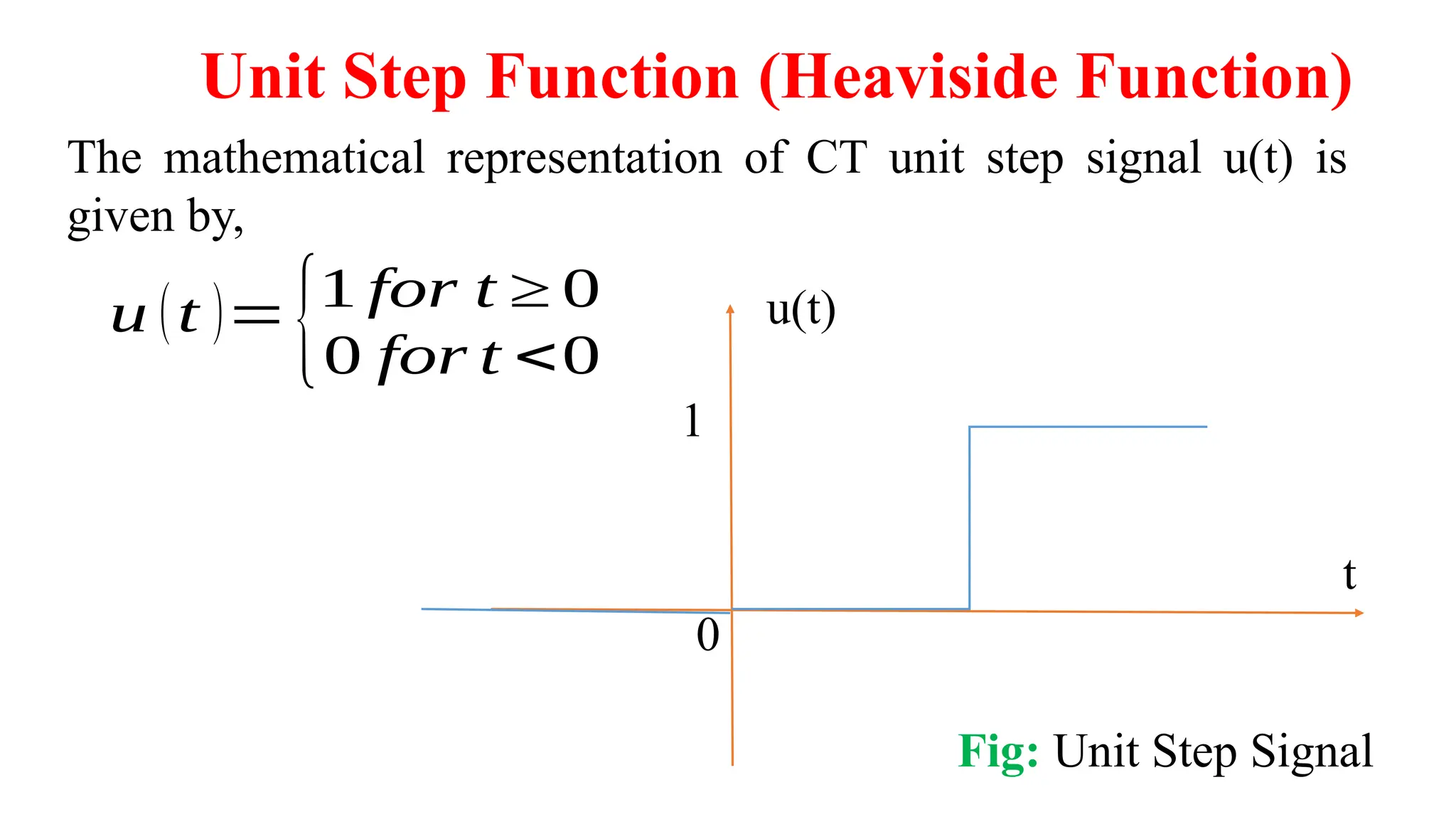
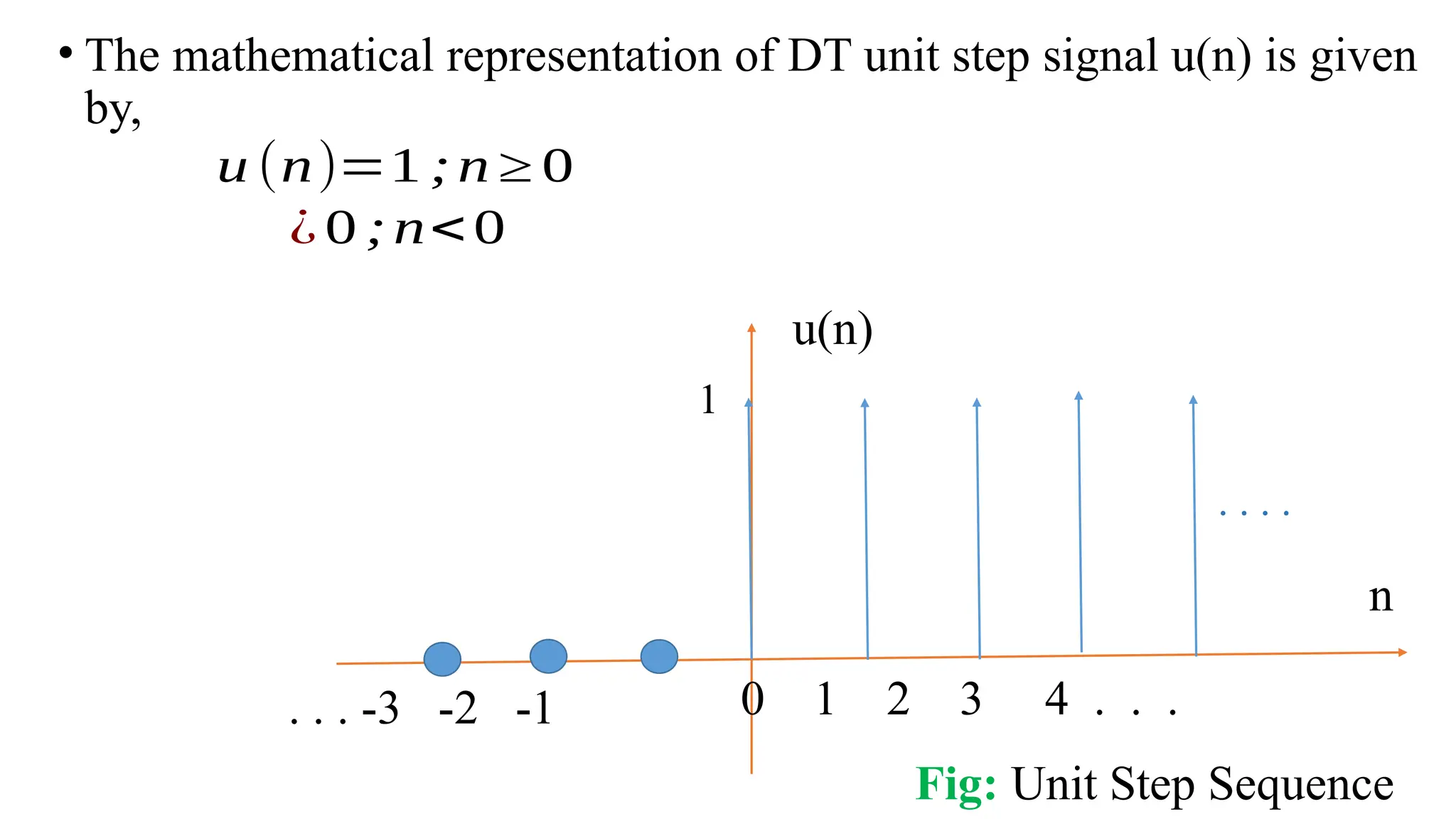
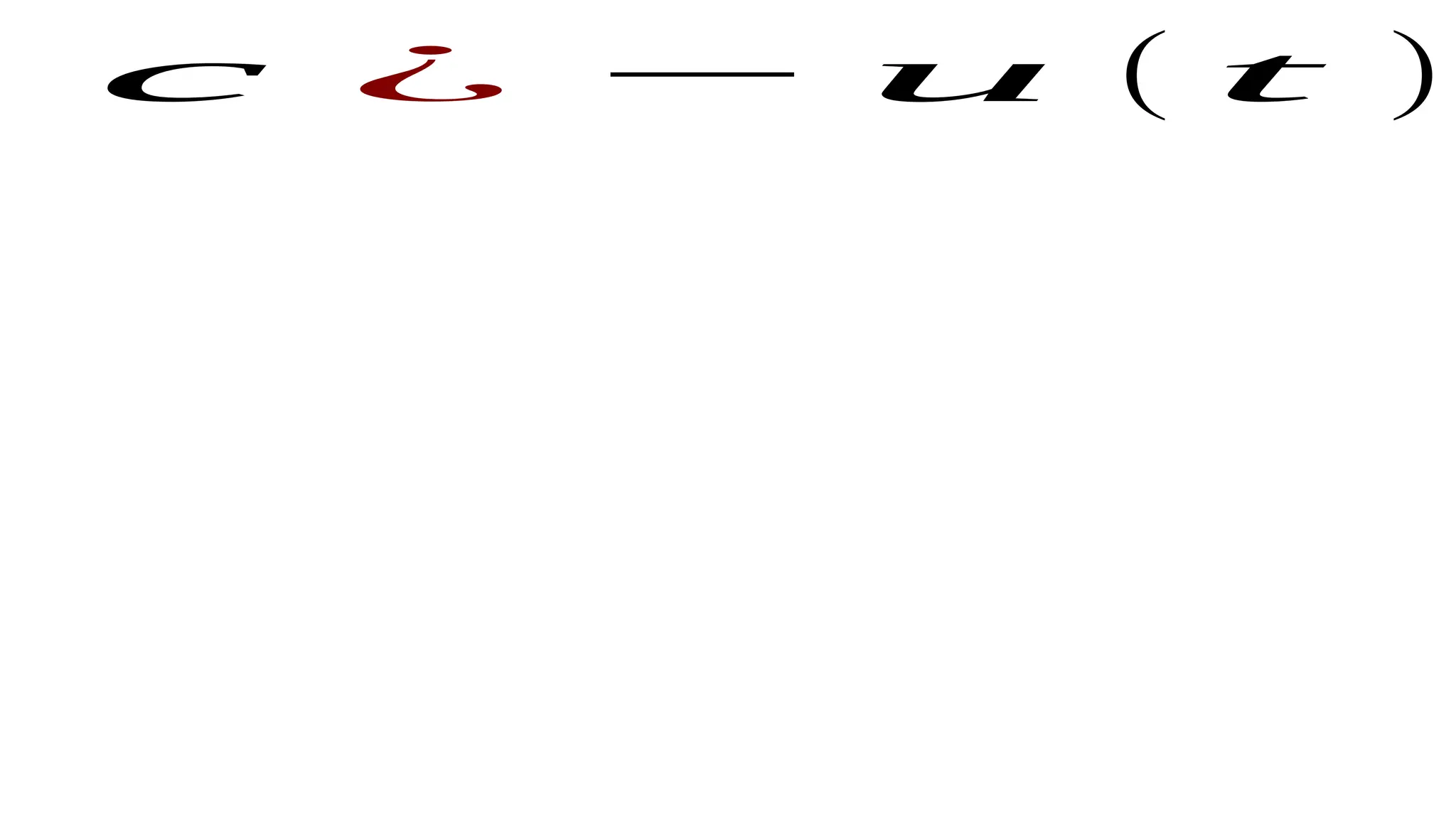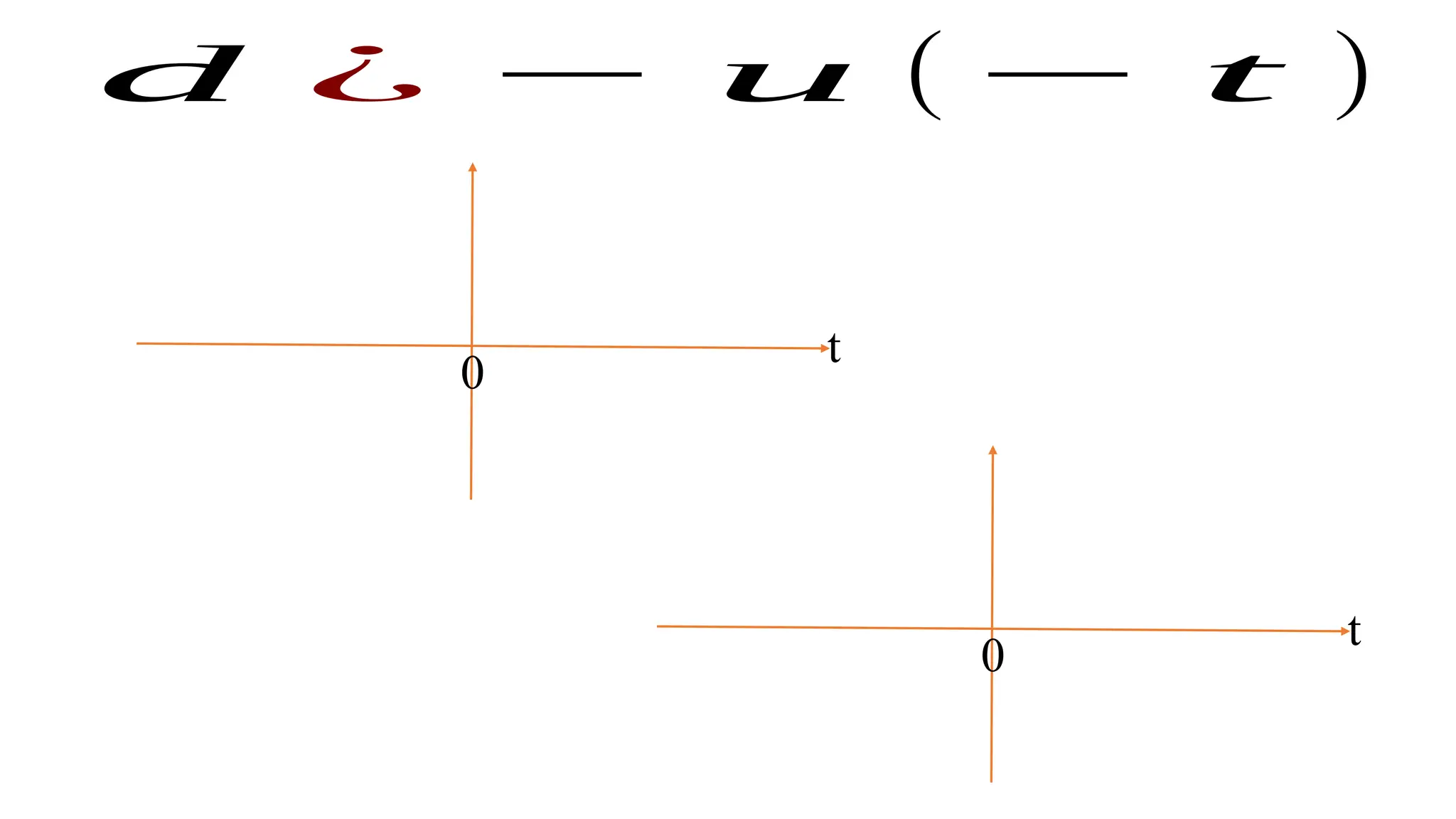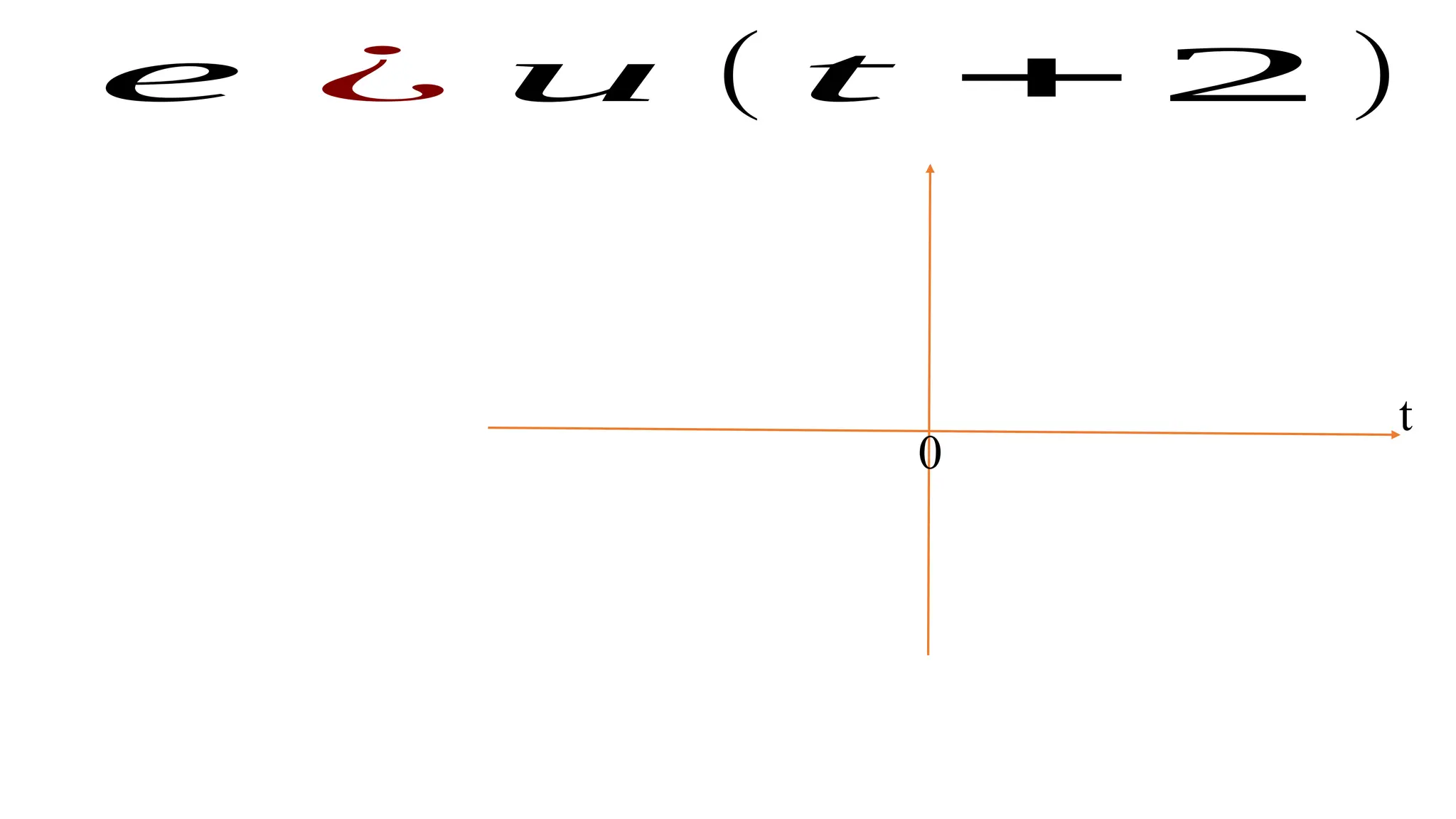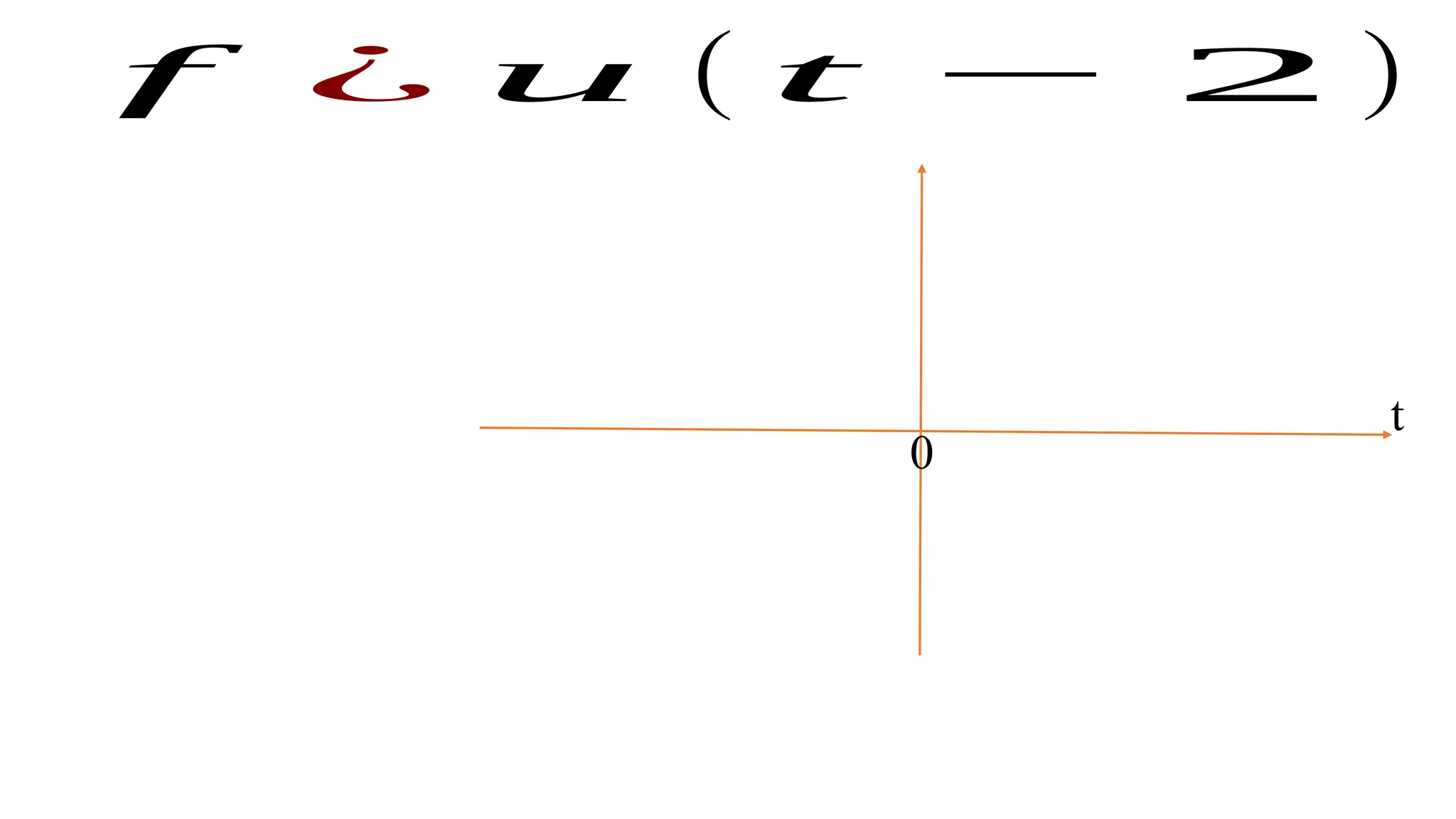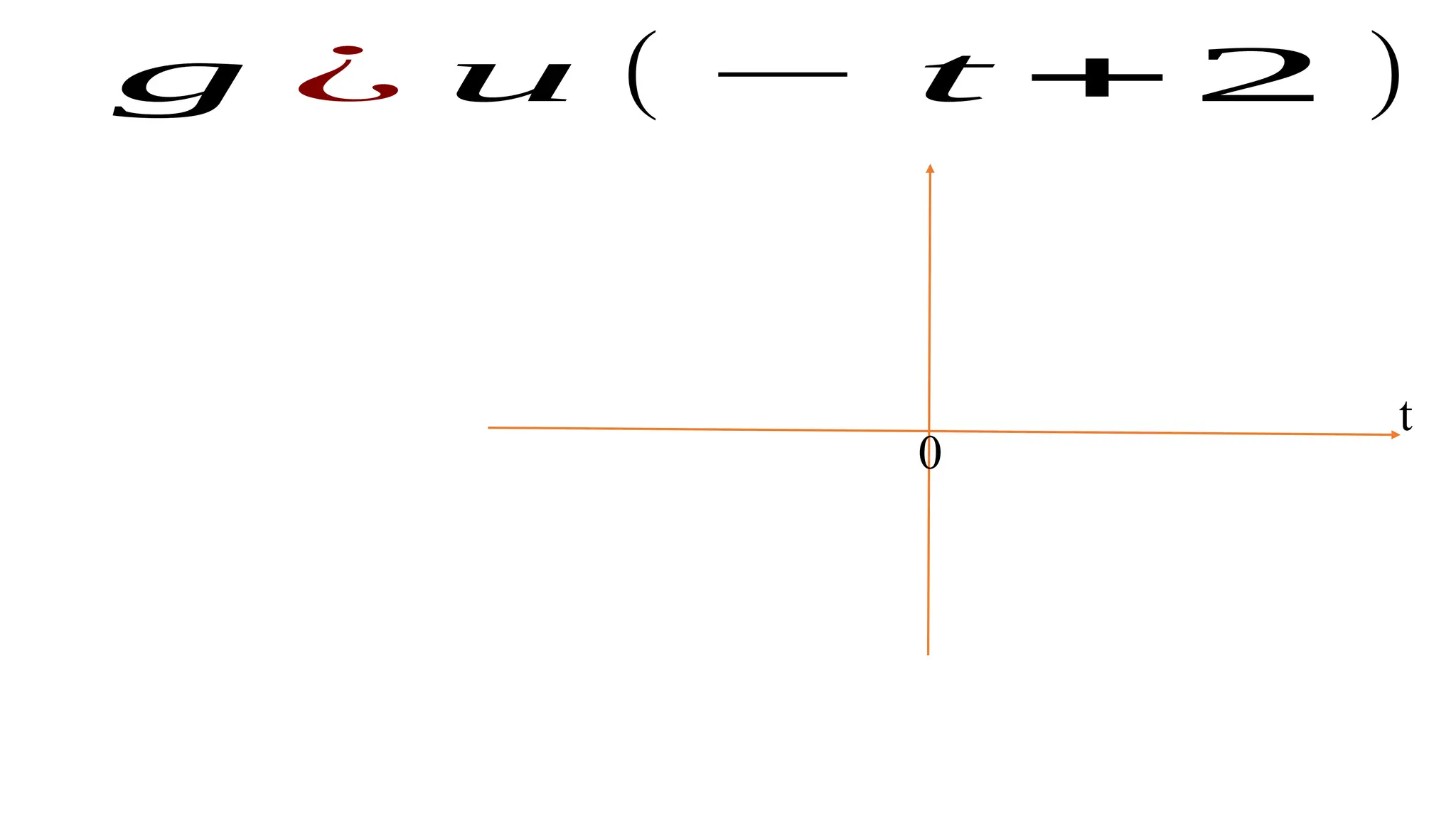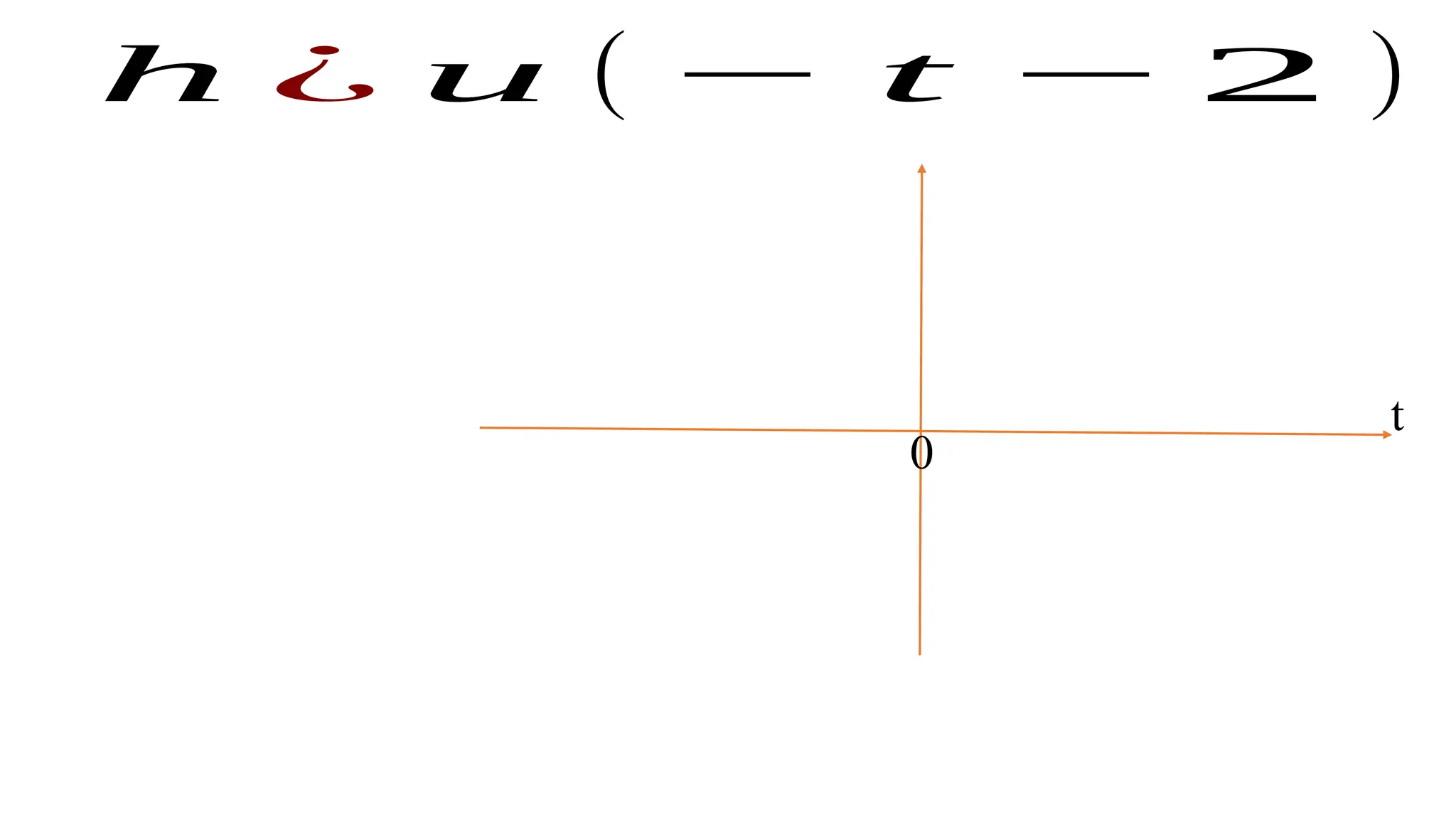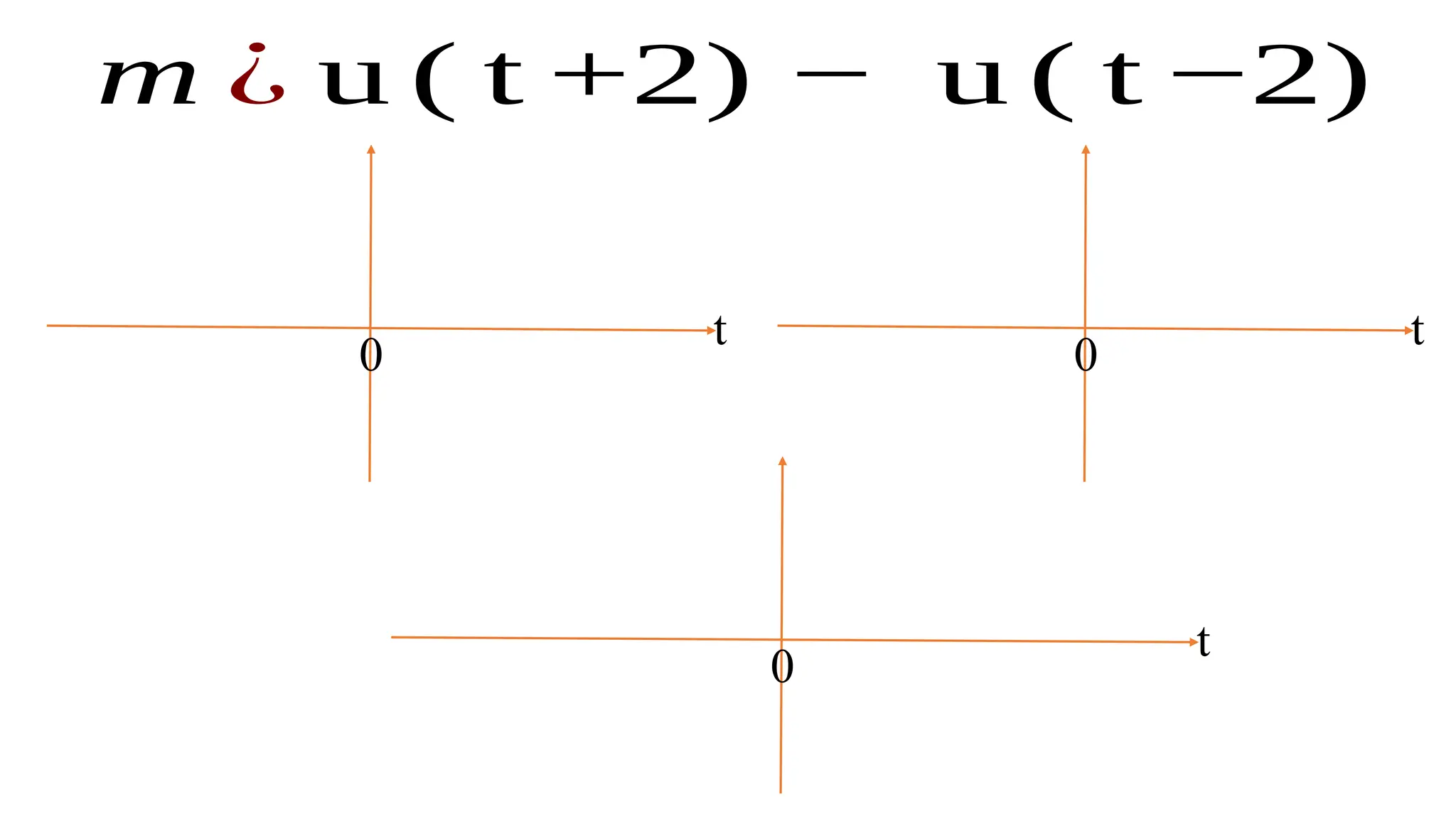The document discusses the mathematical representations of the unit step signal and unit impulse function, detailing their definitions and graphical representations. It includes MATLAB code snippets for generating these signals and sequences over specified time intervals. Additionally, it describes transformations of the unit step function through various operations.

1. t
u(t)
0
1
Fig: Unit Step Signal
The mathematical representation of CT unit step signal u(t) is
given by,
u (t )=
{1 for t ≥ 0
0 for t <0
Unit Step Function (Heaviside Function)

2. • The mathematical representation of DT unit step signal u(n) is given
by,
u (n)=1 ;n ≥ 0
¿ 0 ;n<0
n
u(n)
0 1 2 3 4 . . .
. . . .
1
. . . -3 -2 -1
Fig: Unit Step Sequence

3. • clc; clear all; close all
• % Generation of unit step signal
• t = -5:1:5
• x = (t >= 0)
• subplot(2, 1, 1)
• plot(t, x, "Color", 'r', "LineWidth", 3)
• xlabel("time")
• ylabel("Amplitude x(t)")
• title("Unit Step Signal")
• grid on
• clc; clear all; close all
• % Generation of unit step sequence
• n = -5:1:5
• x = (n >= 0)
• subplot(2, 1, 2)
• stem(t, x, "Color", 'g', "LineWidth", 3)
• xlabel("time")
• ylabel("Amplitude x(n)")
• title("Unit Step Sequence")
• grid on

4. • clc; clear all;
• t = input("Enter the value 't':")
• t1 = -t:1:t-1
• y1 = [zeros(1, t), ones(1, t)]
• subplot(2, 1, 1)
• plot(t1, y1, "LineWidth", 3, "Color", 'c')
• xlabel("time (t)")
• ylabel("Amplitude x(t)")
• title("Unit Step Signal")
• grid on
• clc; clear all;
• n = input("Enter 'n' value :")
• n1 = -n:1:n-1
• y1 = [zeros(1, n), ones(1, n)]
• subplot(2, 1, 2)
• stem(n1, y1, "LineWidth", 3, "Color", 'g')
• xlabel("time (n)")
• ylabel("Amplitude x(n)")
• title("Unit Step Sequence")
• grid on

5. Unit Impulse Function
• Impulse function is denoted by δ(t). and it is defined as
t
δ(t)
1
. . . . -2 -1 0 1 2 3 . . . . .
Fig: Unit Impulse Signal

6. • Discrete Time Unit Impulse Function or Unit Pulse Sequence.
δ (n)=
{1 for n=0
0 for n ≠ 0

7. • clc; clear all; close all
• % Generation of unit impulse signal
• t = -5:0.1:5
• x = (t == 0)
• subplot(2, 1, 1)
• plot(t, x, "LineWidth", 2, "Color", 'c')
• xlabel("Time (t)")
• ylabel("Amplitude x(t)")
• title("Unit Impulse Signal")
• grid on
• % Generation of unit impulse sequence
• n = -5:1:5
• x = (n == 0)
• subplot(2, 1, 2)
• stem(n, x, "LineWidth", 2, "Color", 'g')
• xlabel("Time (n)")
• ylabel("Amplitude x(n)")
• title("Unit Impulse Sequence")
• grid on

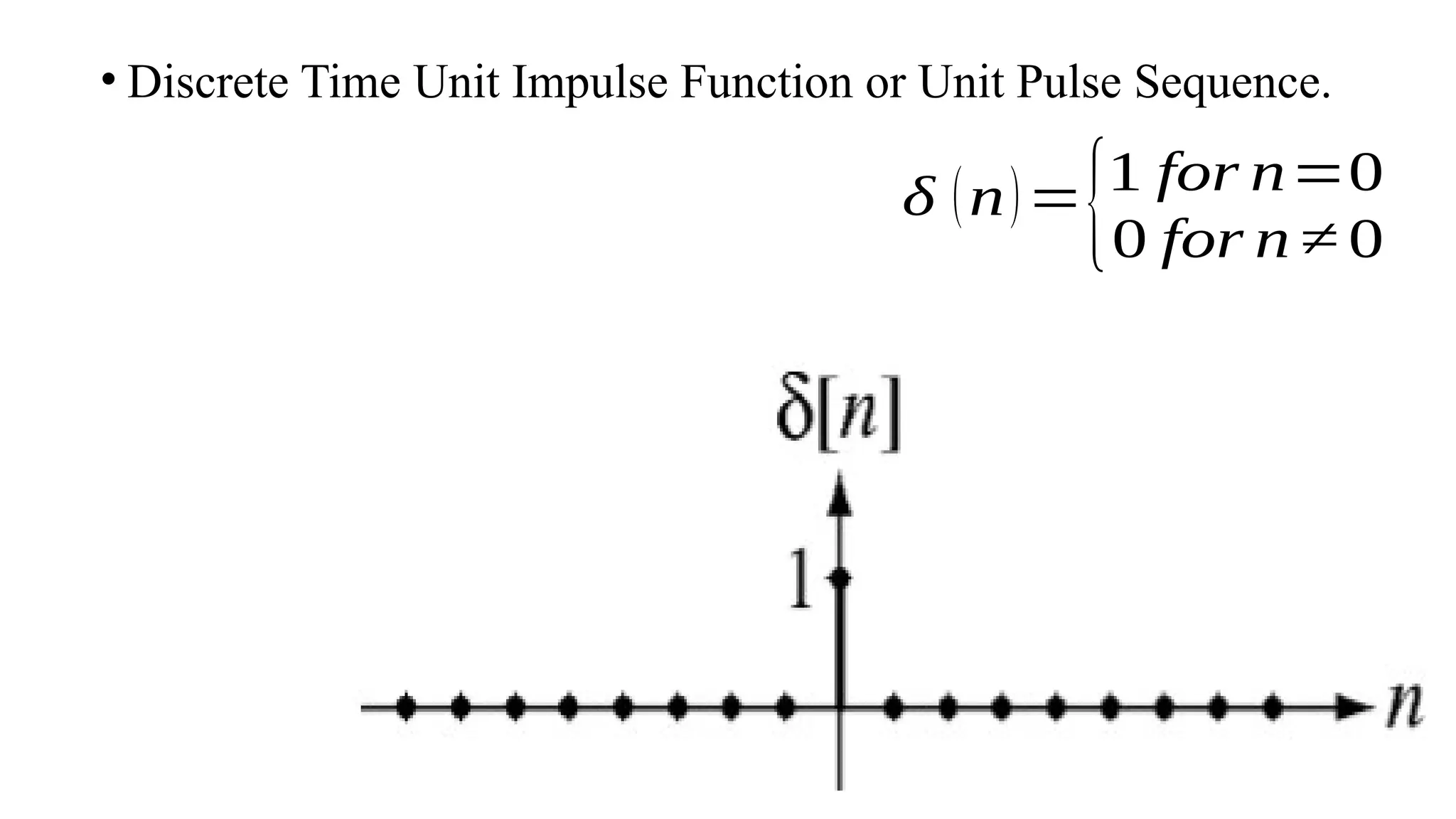
8. • clc; clear all; close all
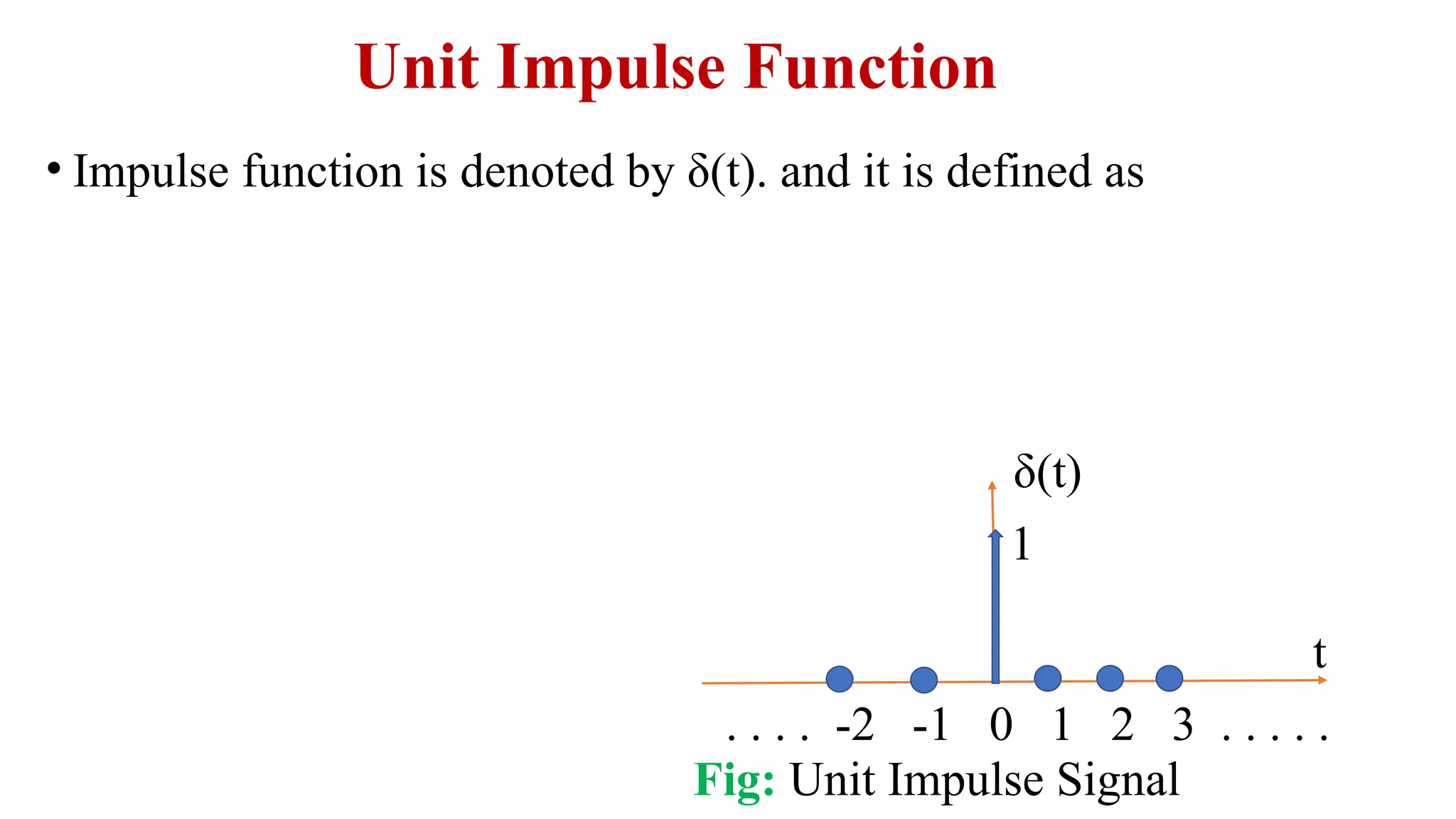
• % Generation of unit impulse signal
• t = input("Enter the value 't':")
• t1 = -t:1:t
• y1 = [zeros(1, t), ones(1,1), zeros(1, t)]
• subplot(2, 1, 1)
• plot(t1, y1,"LineWidth", 2, "Color", 'c')
• xlabel("Time (t)")
• ylabel("Amplitude, x(t)")
• title("Unit impulse signal")
• grid on
• % Generation of unit step sequence
• n = input("Enter the value 'n':")
• n1 = -n:1:n
• y1 = [zeros(1, n), ones(1, 1), zeros(1, n)]
• subplot(2, 1, 2)
• stem(n1, y1,"LineWidth", 2, "Color", 'r')
• xlabel("Time (n)")
• ylabel("Amplitude, x(n)")
• title("Unit impulse sequence")
• grid on

10. •Draw the graphical representation

11. t
u(t)
0
1
Fig: Unit Step Signal
u (t )=
{1 for t ≥ 0
0 for t <0
a ¿ u ( t )

12. t
u(-t)
0
1
Fig: Unit Step Signal
u (− t)=1 for − t ≥ 0=⇒ t ≤ 0
b ¿ u (− t )
𝐮 (𝐭)={𝟏𝐟𝐨𝐫 𝐭 ≥𝟎
𝟎𝐟𝐨𝐫 𝐭<𝟎

13. c ¿ − u ( t )

14. t
0
d ¿ − u (− t )
t
0

15. t
0
e ¿ u ( t + 2 )

16. t
0
f ¿ u ( t − 2 )

17. t
0
g ¿ u ( − t + 2 )

18. t
0
h ¿ u ( − t − 2 )

19. t
u(t)
0
Fig: Unit Step Signal
u (t )=
{1 for t ≥ 0
0 for t <0
i ¿ u ( t )

20. t
u(t)
0
Fig: Unit Step Signal
u (t )=
{1 for t ≥ 0
0 for t <0
j ¿ u ( 2 t )

21. t
u(t)
0
Fig: Unit Step Signal
u (t )=
{1 for t ≥ 0
0 for t <0
k ¿ u ( t / 2 )

22. t
u(t)
0
1
u (t )=
{1 for t ≥ 0
0 for t <0
l ¿ ¿ ¿ ¿ 2

23. t
0
m ¿ u ( t +2) − u ( t −2)
t
0
t
0

26. YAGI-UDA ANTENNA