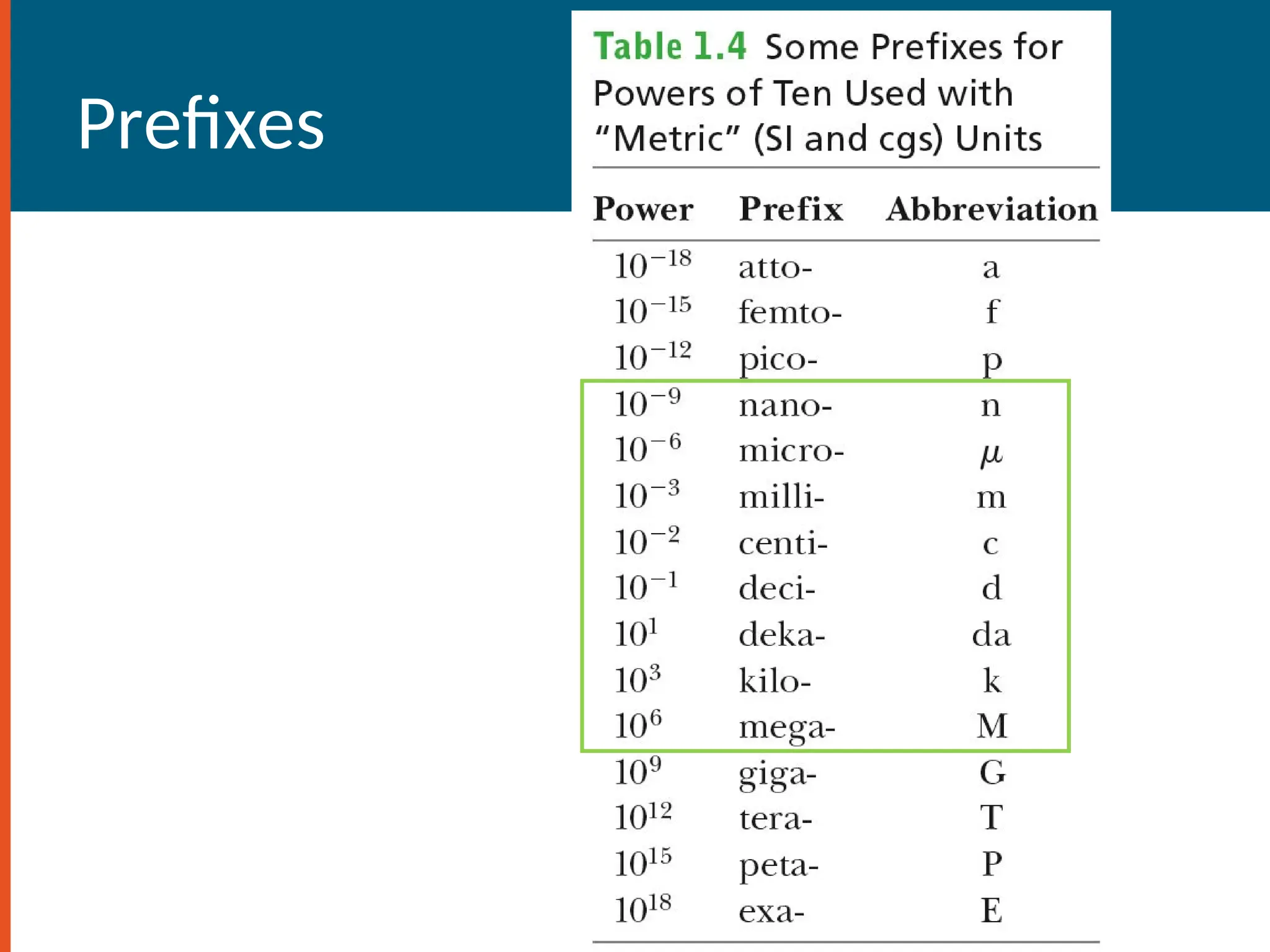
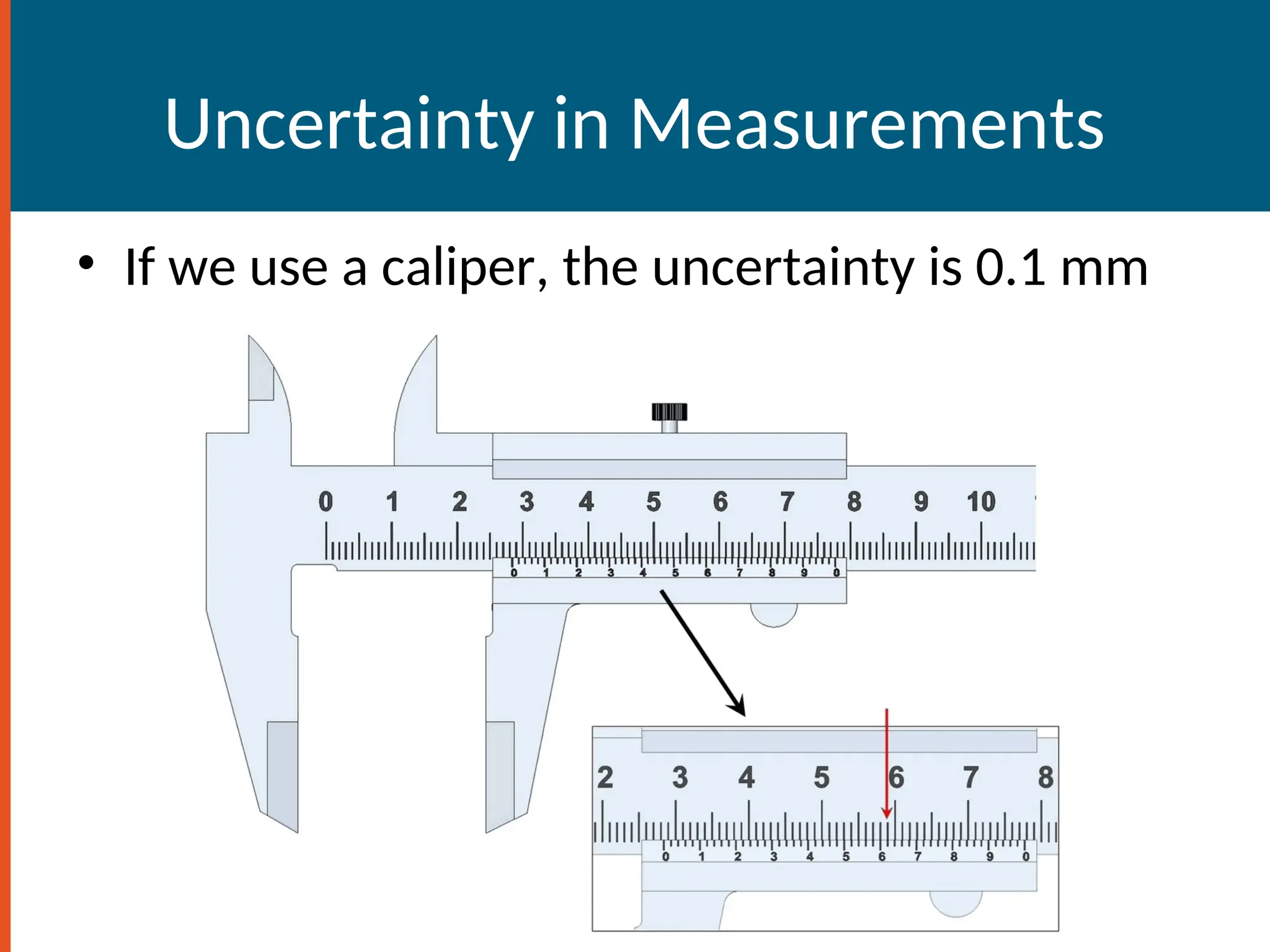
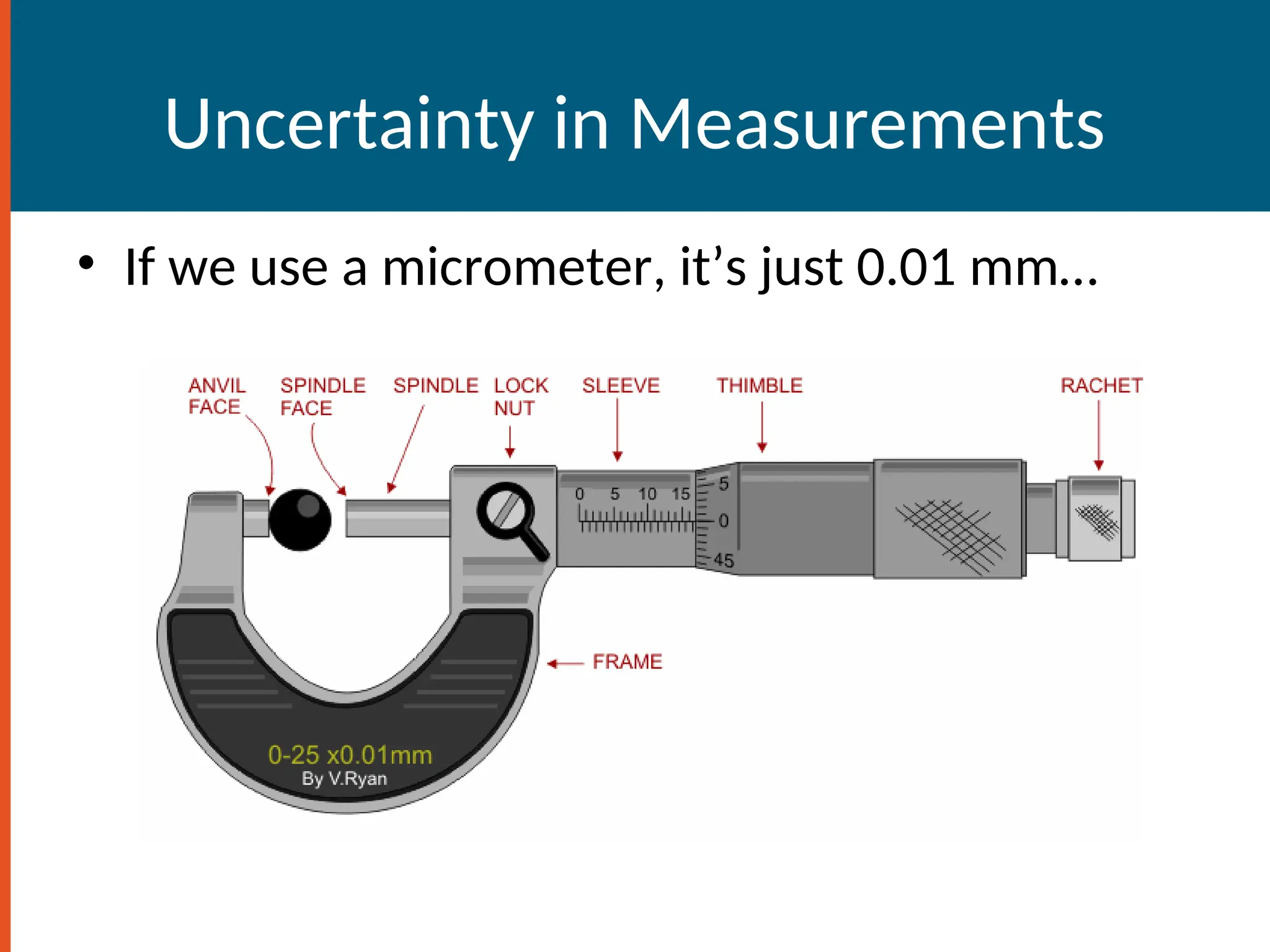
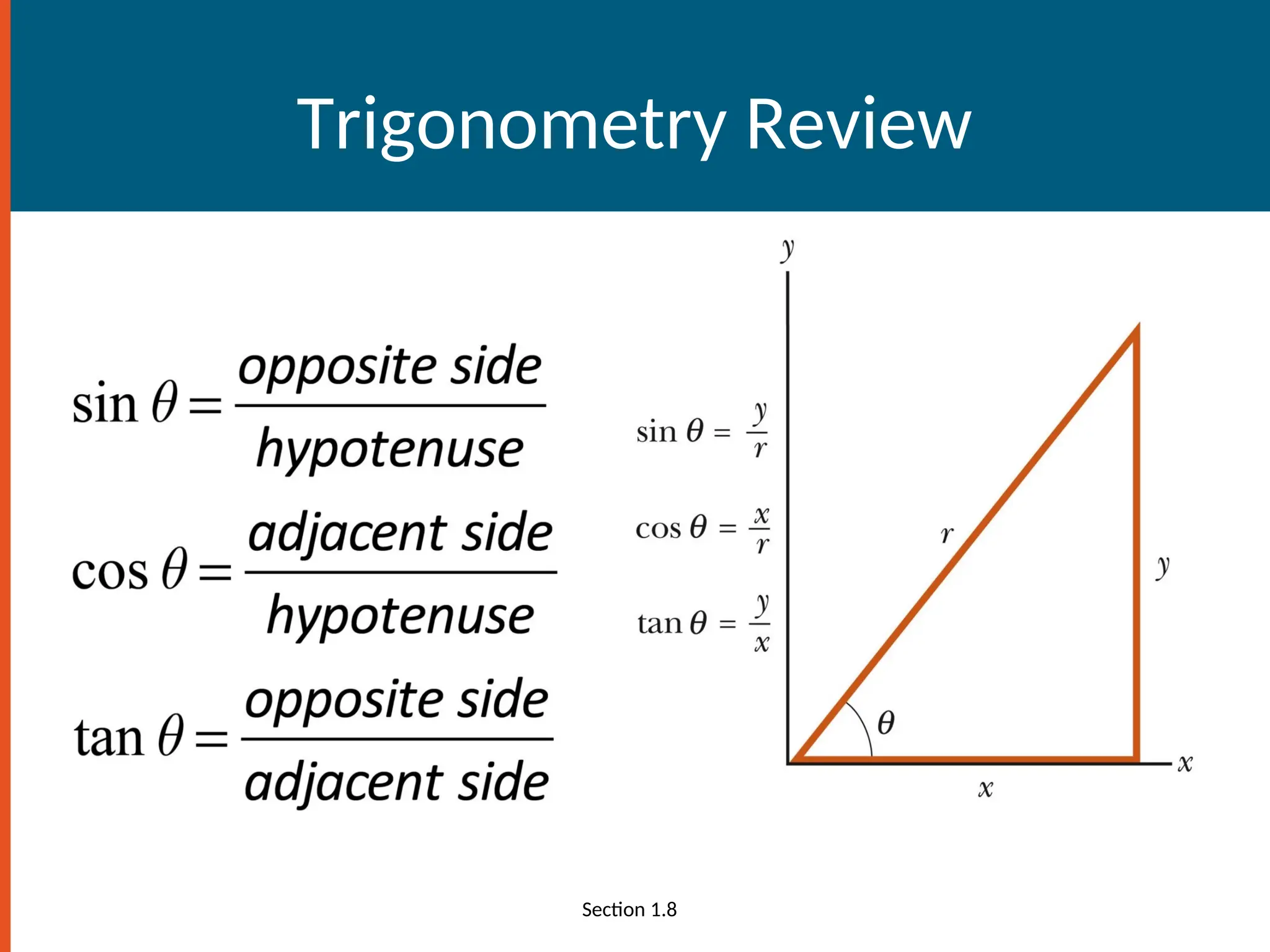
The document provides an introduction to physics, defining it as the study of nature through theories and experiments, focusing on matter and forces at both macroscopic and microscopic levels. It outlines fundamental concepts such as units of measurement, significant figures, and the importance of accuracy in measurements, along with methods for problem-solving in physics. Additionally, it covers coordinate systems, conversions, and the use of trigonometry in physical calculations.

1. Phy 101 - Castoldi
Chapter One
Introduction

2. Physics = Study of Nature

3. Theories and Experiments
• The goal of physics is to develop theories based on
experiments
• A physical theory, usually expressed mathematically,
describes how a given system works
• The theory makes predictions about how a system
should work
• Experiments check the theory’s predictions
• Every theory is a work in progress
Introduction

4. Physics studies Matter
• At the Macroscopic level:

5. Physics studies Matter
• At the Microscopic level:

6. Physics studies Forces
• Physics also studies the forces that rule nature
• Each fundamental force is predominant at a different level:
• Gravitational – glue that keeps the universe together
• Electric – glue that keeps atoms & molecules together
• Weak – responsible for radioactive decay
• Strong – glue that keeps nuclei together

7. Tools for our investigation: Units
• To communicate the result of a measurement
for a quantity, a unit must be defined
• Defining units allows everyone to relate to the
same fundamental amount
Section 1.1

8. Units
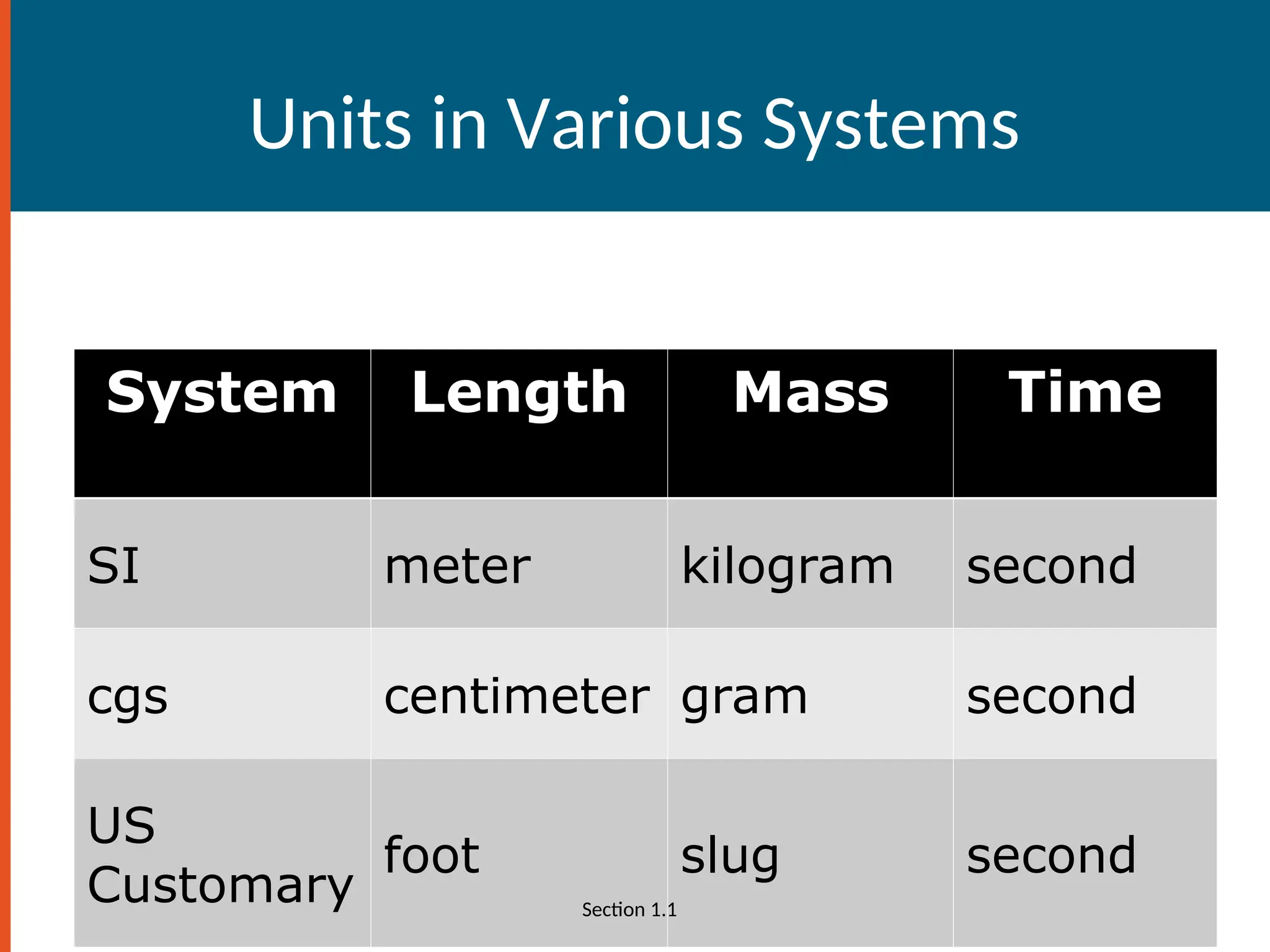
• Mechanics uses three fundamental quantities
– Length [L]
– Mass [M]
– Time [T]
• Other physical quantities can be constructed
from these three
e.g. Speed = Distance/Time [L/T]
Introduction

9. SI System of Measurement
• SI – Systéme International
– Agreed to in 1960 by an international committee
– Main system used in this text
Section 1.1

10. SI units
• Length
– meter, m
• Mass
– kilogram, kg
• Time
– seconds, s
Section 1.1

11. Other Systems of Measurements
• Gaussian system (cgs)
– cm, g, s
• US Customary (British)
– ft, sl(slugs), s
– Often uses weight, in pounds, instead of mass as a
fundamental quantity
Section 1.1

12. Units in Various Systems
System Length Mass Time
SI meter kilogram second
cgs centimeter gram second
US
Customary
foot slug second
Section 1.1

13. Conversion of Units
• Units can be treated like algebraic quantities that can
“cancel” each other
• Examples of conversion:
1 inch = 2.54 cm
1 mile = 1609 m
70 mi/hr x (1609 m/mi) x (1 hr/3600 s) = 31 m/s
Section 1.5

14. Check for Consistency
• It’s necessary to check the units for
consistency
• Example:
Area [A] = [L2
] = m2
Speed [v] = [L/T] = m/s

15. Powers of Ten
• 10 o
= 1
• 101
= 10
• 102
= 100
• …
• 10 -1
= 1/10 = 0.1
• 10 -2
= 1/100 = 0.01
• …

16. Prefixes
Section 1.1

19. Uncertainty in Measurements
• The accuracy of a measurement is related to the
sensitivity of the apparatus.
• For example, using a
metric ruler, we have
an uncertainty of 1 mm

20. Uncertainty in Measurements
• If we use a caliper, the uncertainty is 0.1 mm

21. Uncertainty in Measurements
• If we use a micrometer, it’s just 0.01 mm…

22. Uncertainty in Measurements
• As we just saw, every measurement has an
uncertainty related to the degree of accuracy of the
measuring device
• This uncertainty carries over through the calculations
• We will use rules for significant figures (sig. figs.) to
approximate the uncertainty in results of calculations
Section 1.4

23. Significant Figures
• A significant figure is a reliably known digit
• All non-zero digits are significant
• Zeros are not significant when they only locate the
decimal point
0.0175 cm has 3 sig. figs.
3500 cm is ambiguous
– better use the scientific notation:
3.5 x 103
if it has 2 sig. figs.
3.50 x 103
if it has 3 sig. figs.
Section 1.4

24. Significant Figures
• Example: measure the length of an object using a
meter stick. The accuracy is 1 mm or 0.1 cm
L = 2.2 cm ± 0.1 cm
This means that the actual
length of the object is
between 2.1 & 2.3 cm
• 16.2 cm is known to 3 significant figures
• 4.5 cm is known to 2 significant figures

25. Operations with Significant Figures
• When multiplying or dividing two or more quantities,
the number of significant figures in the final result is
the same as the number of significant figures in the
least accurate of the factors being combined
(16.2 cm) (4.4 cm) = 71.24 cm2
= 71 cm2
3 sig.fig. 2 sig.fig. 2 sig. fig.
Section 1.4

26. Operations with Significant Figures
• When adding or subtracting, we round the result to
the smallest number of decimal places of any term in
the sum (or difference)
123 kg + 5.35 kg = 128.35 kg = 128 kg
0 decimals 2 decimals 0 decimals
Problem solving:
for better precision, carry more digits in the calculations.
Only at the end, round the answer to the correct
number of significant figures.

27. Order of Magnitude calculations
• Necessary when details are not available
• Approximation based on a number of
assumptions
• Order of magnitude is the power of 10 that
applies
• Example: estimating the number of galaxies in
the universe
Section 1.6

28. No. of galaxies in the universe – 1
• What we know:
- astronomers can see ~ 10 billion light years
into space (the size of visible universe)
- our local group includes 14 galaxies
- the distance to the next local group of
galaxies is 2 million light years
1 light year = 1 ly =
= distance traveled by light in 1 year

29. No. of galaxies in the universe – 2
• Local group:
• r = 1 million ly d = 2 r = 2 million ly
Vol = 4/3 π r3
= (106
ly)3
= 1018
ly3
No. galaxies/Vol = 10/ 1018
ly3
= 10-17
galaxies/ly3
r

30. No. of galaxies in the universe – 3
• Universe:
R = 10 billion ly Vol’ = (1010
ly)3
= 1030
ly3
No. galaxies =
= (10-17
gal/ly3
) x Vol’ =
= (10-17
) x (1030
) = 1013
R

31. Coordinate Systems
• Used to describe the position of a point in
space
• Coordinate system consists of
– A fixed reference point called the origin, O
– Specified axes with scales and labels
– Instructions on how to label a point relative to the
origin and the axes
Section 1.7

32. Types of Coordinate Systems
Cartesian
Polar
Section 1.7

33. Cartesian coordinate system
• x- and y- axes
• Points are labeled (x,y)
• Positive x is usually
selected to be to the
right of the origin
• Positive y is usually
selected to be to
upward from the origin
Section 1.7

34. Polar coordinate system
• Origin and reference
line are noted
• Point is distance r from
the origin in the
direction of angle 
• Positive angles are
measured ccw from
reference line
• Points are labeled (r,)
• The standard reference
line is usually selected
to be the positive x axis
Section 1.7

35. Trigonometry Review
Section 1.8

36. Trigonometry Review
• Pythagorean Theorem
r2
= x2
+ y2
r = √ x2
+ y2
• To find an angle, you need the inverse trigon.
function
For example,  = sin-1
0.707 = 45°
Section 1.8

37. θ
The shadow of a tall building is 67.2 m (x),
θ = 50.0o
. Find the height of the building (y).
y = (tan θ) x =
= (tan 50.0o
) (67.2 m)
= 80.0 m
Example
y
x

38. Degrees vs. Radians
• Be sure your calculator is set for the
appropriate angular units for the problem
(we normally use degrees, but for the chapter
on rotations we will use radians)
• For example:
– tan -1
0.5774 = 30.0°
– tan -1
0.5774 = 0.5236 rad
Section 1.8

39. Rectangular  Polar
• Rectangular to polar
P = (x,y) = (-3.50 m, -2.50 m) find (r, θ)
_______
r = √(x2
+ y2
) =
________________
= √{(-3.50)2
+ (-2.50)2
}
= 4.30 m
θ = tan -1
(-2.50/-3.50) =
= 35.5o
+ 180o
= 216o
Section 1.8

40. Rectangular  Polar
• Polar to rectangular
P = (5.00 m, 37.0o
)
x = r cos  =
= (5.00 m) (cos 37.0o
)
= 3.99 m
y = r sin  =
= (5.00 m) (sin 37.0o
)
= 3.01 m
5.00 m
x
y

P

41. Problem Solving
Strategy

42. Problem Solving Strategy
• Problem
– Read the problem
• Read it at least twice
• Identify the nature of the problem
• Draw a sketch
– Draw a diagram
• Some types of problems require very specific types of
diagrams
• Label the physical quantities on the diagram
Section 1.9

43. Problem Solving cont.
• Strategy
– Identify the principles involved
– List the data (known quantities)
– List the unknown(s) (what you are looking for)
– Choose equation(s)
• Based on the principle, choose an equation or set of
equations to apply to the problem
Section 1.9

44. Problem Solving, cont.
• Solution
– Solve for the unknown quantity
– Substitute into the equation(s)
• Substitute the data into the equation
• Obtain a result
• Include units
Section 1.9

45. Problem Solving, final
• Final check
– Check the answer
• Do the units match?
– Are the units correct for the quantity being found?
• Does the answer seem reasonable?
– Check order of magnitude
• Are signs appropriate and meaningful?
Section 1.9

46. Problem Solving Summary
• Equations are the tools of physics
– Understand what the equations mean
and how to use them
• Carry through the algebra as far as possible
– Substitute numbers at the end
• Be organized
Section 1.9