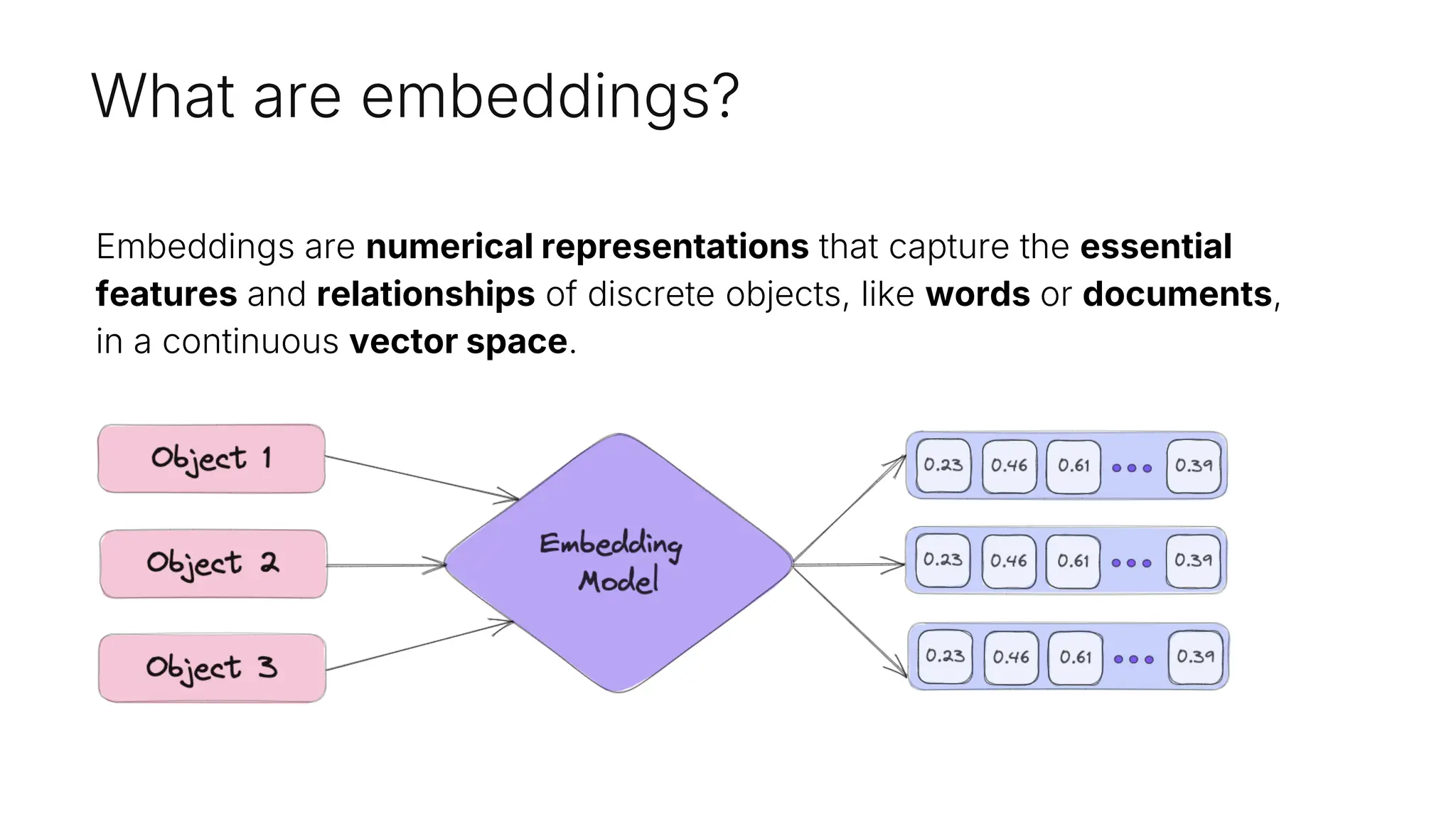
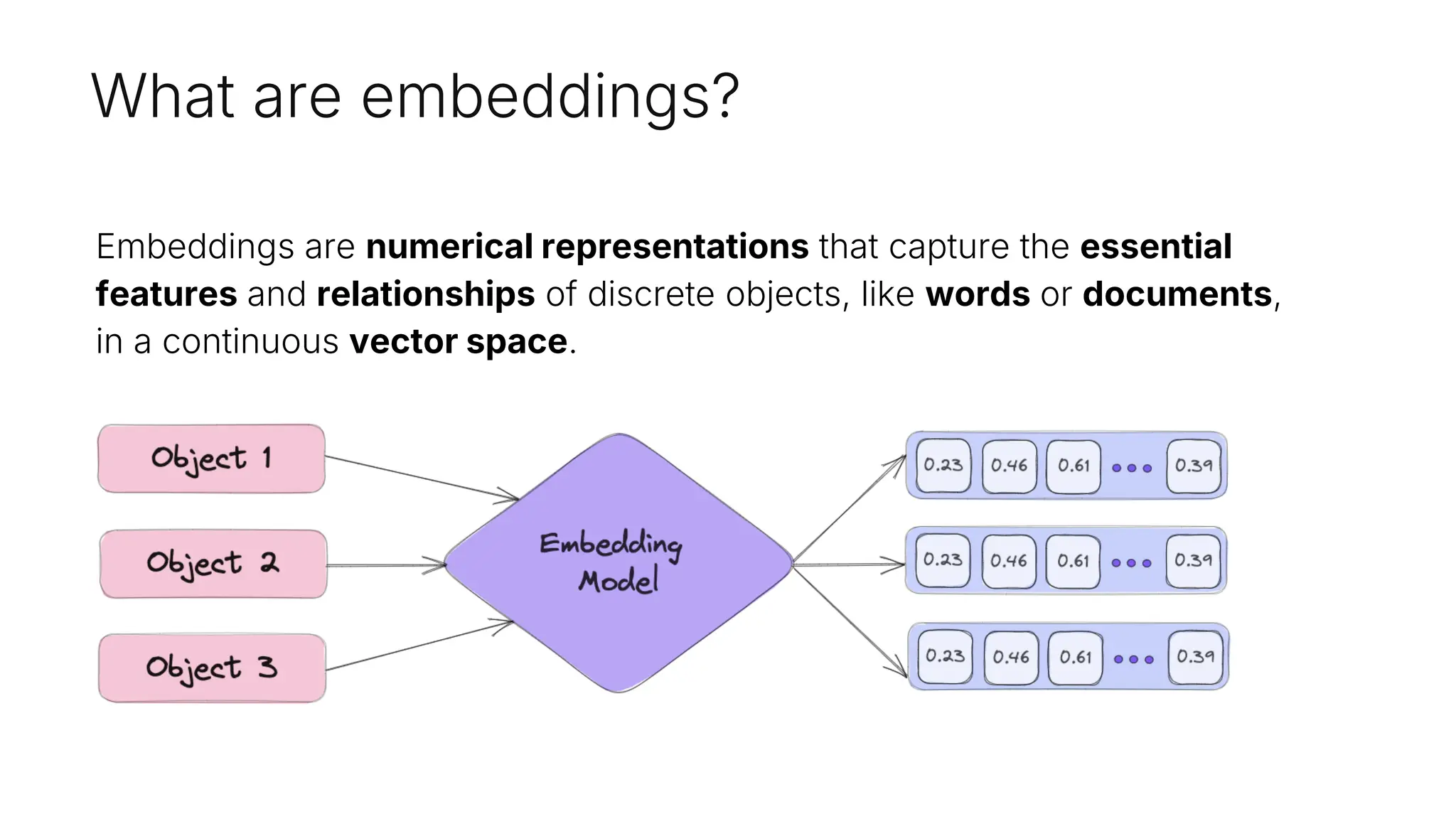
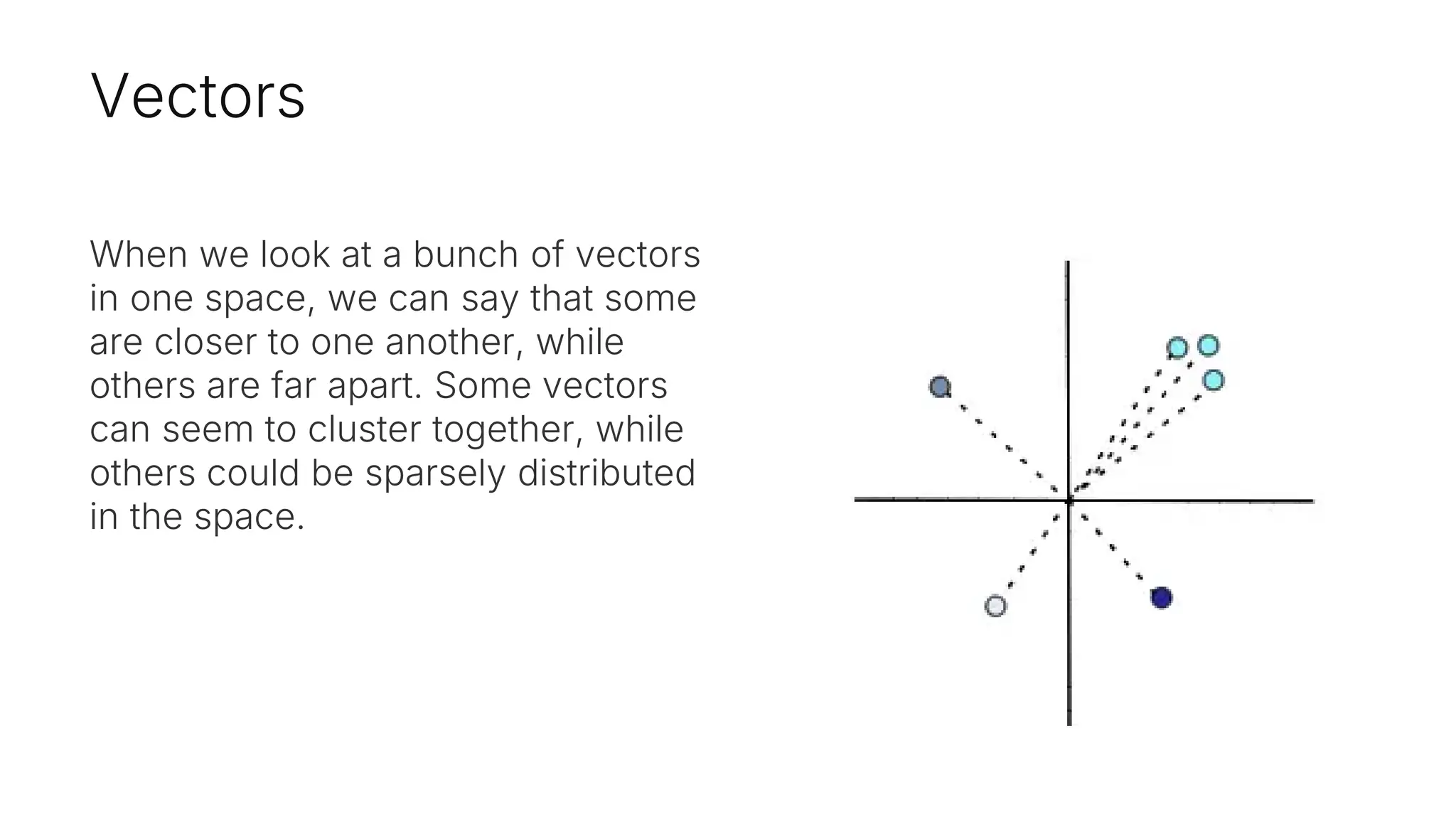
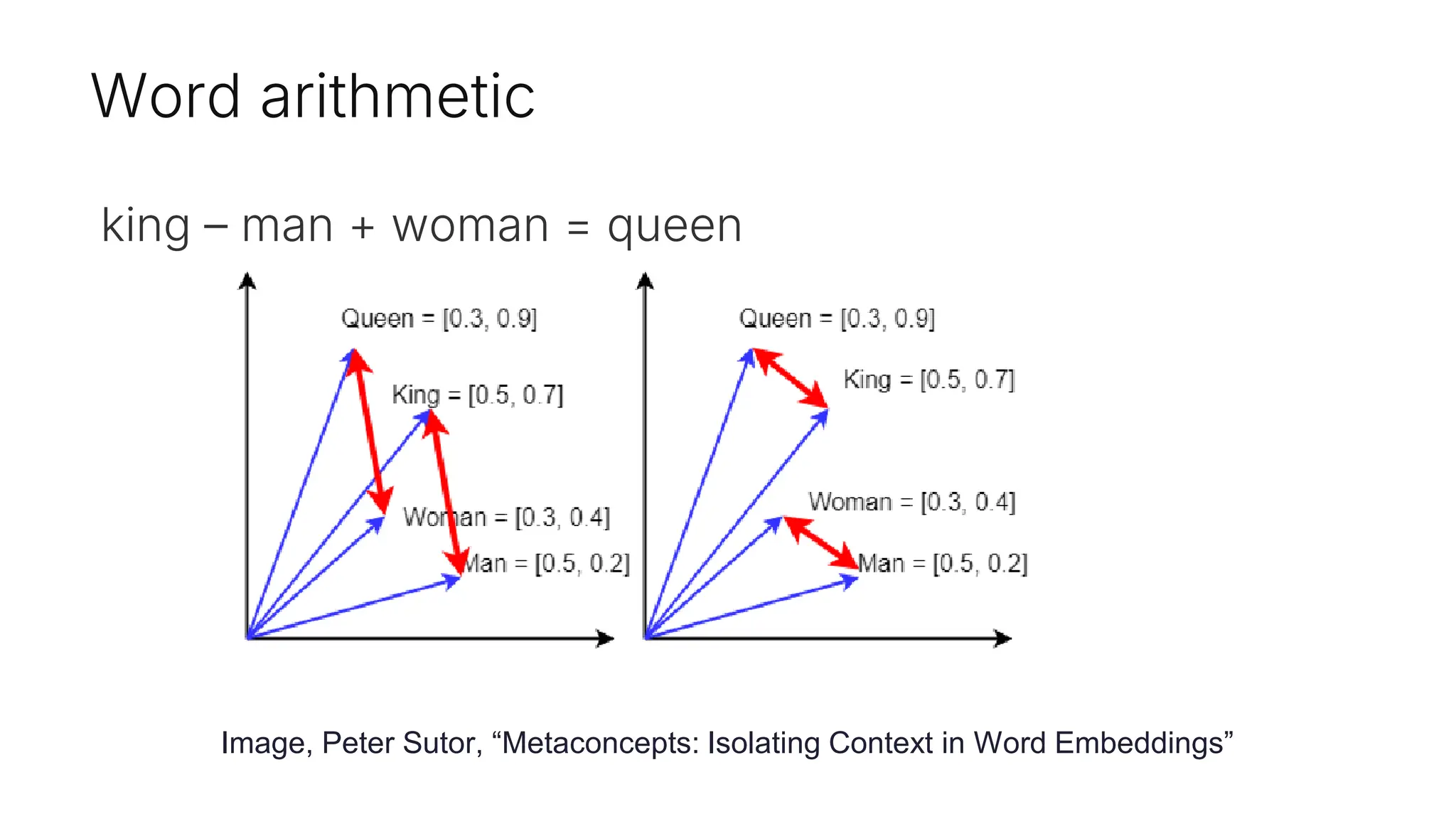
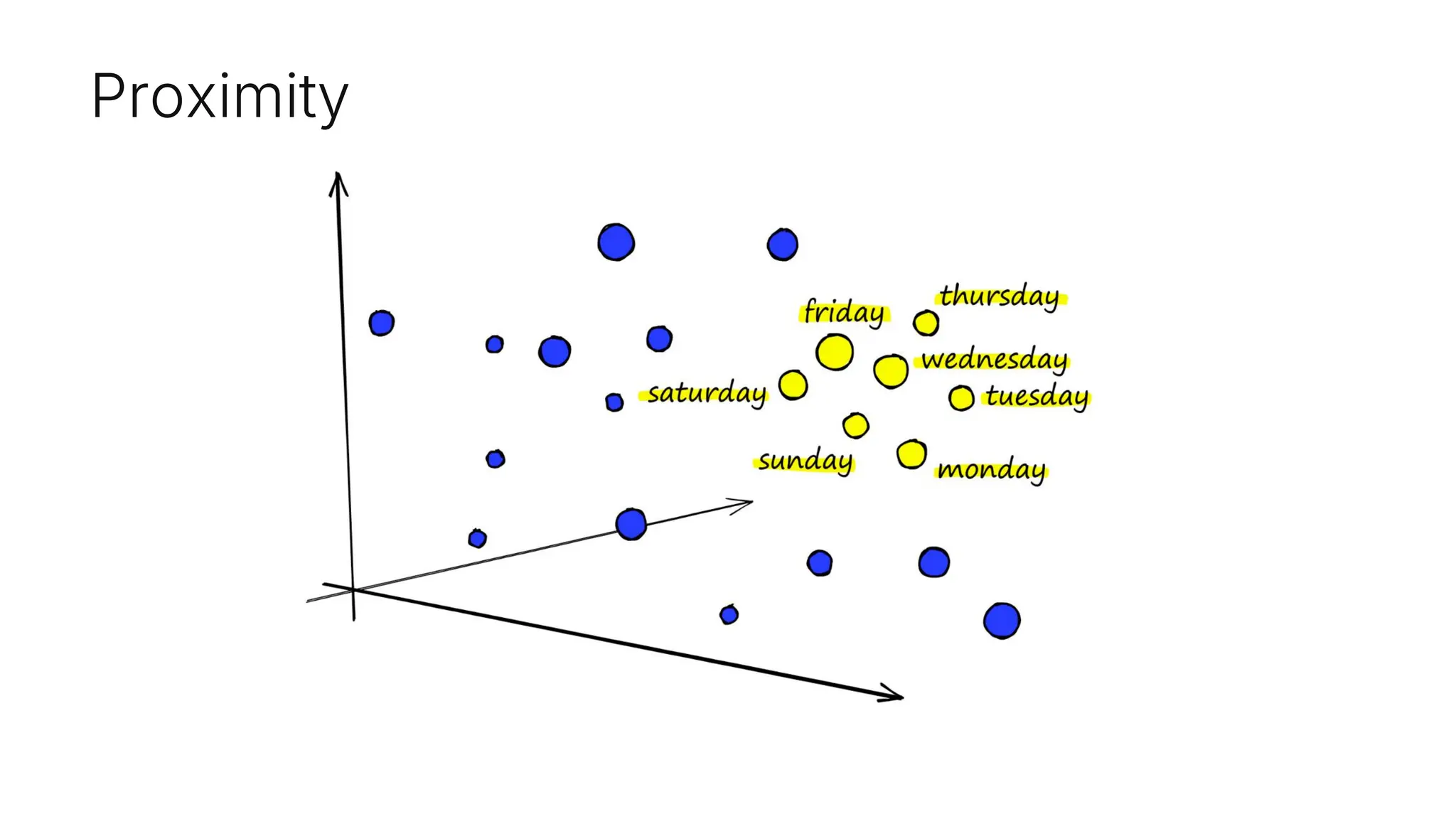
Embeddings are numerical representations that capture essential features and relationships of objects in a continuous vector space, influenced by their context. They offer semantic meaning and efficient comparison of similarities, applicable in various domains like semantic search and anomaly detection. Key points include adaptability, dimensionality, and context sensitivity affecting their interpretation.





![Vectors
As developers, it might be easier to
think of a vector as an array
containing numerical values. For
example:
vector = [0,-2,...4]](https://image.slidesharecdn.com/videoparislondonlegalpresentationembeddingsjocelyn-241227150655-0ac17fc6/75/apidays-Paris-2024-Embeddings-Core-Concepts-for-Developers-Jocelyn-Matthews-Pinecone-7-2048.jpg)
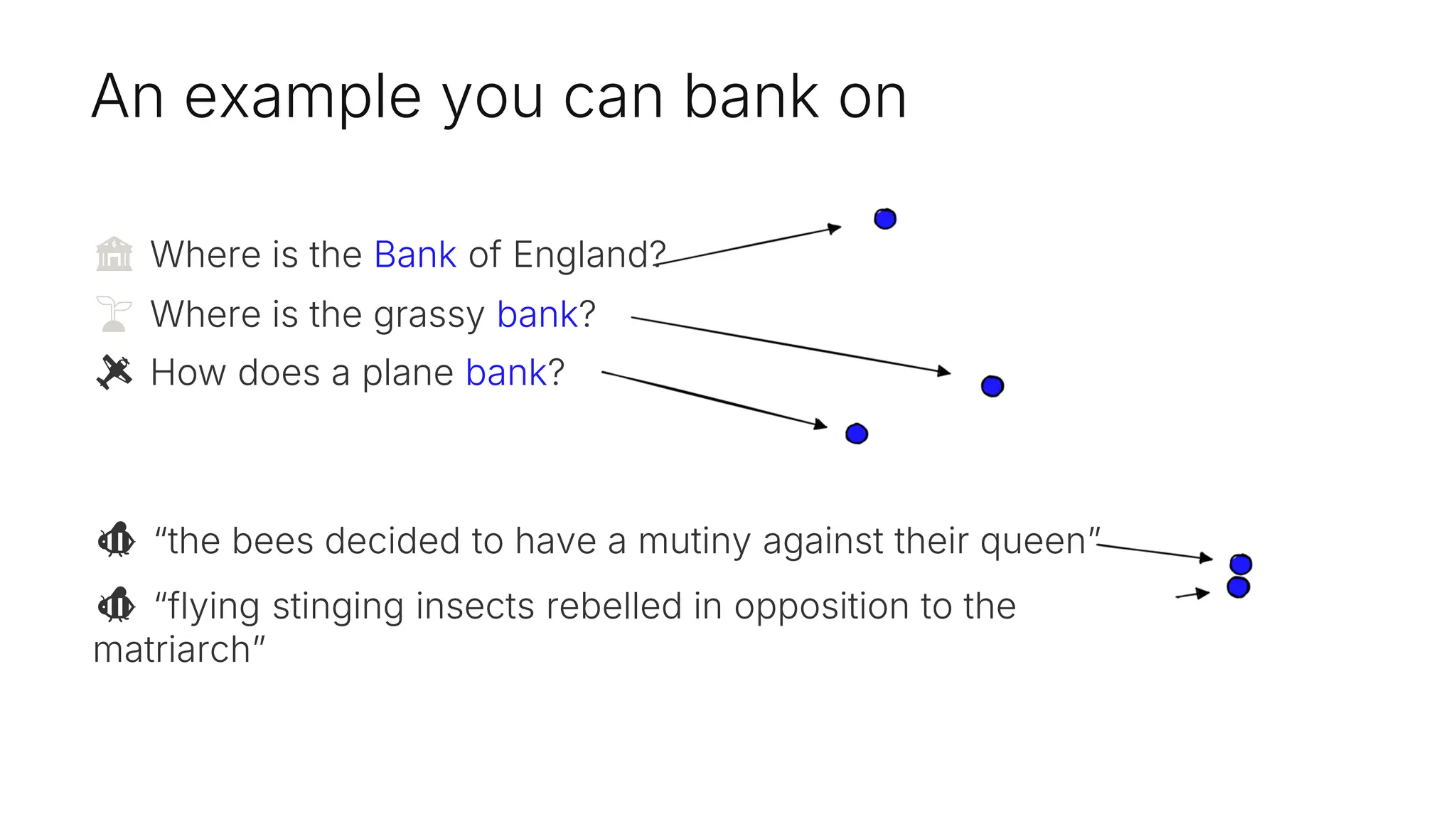

















![Check the vectors
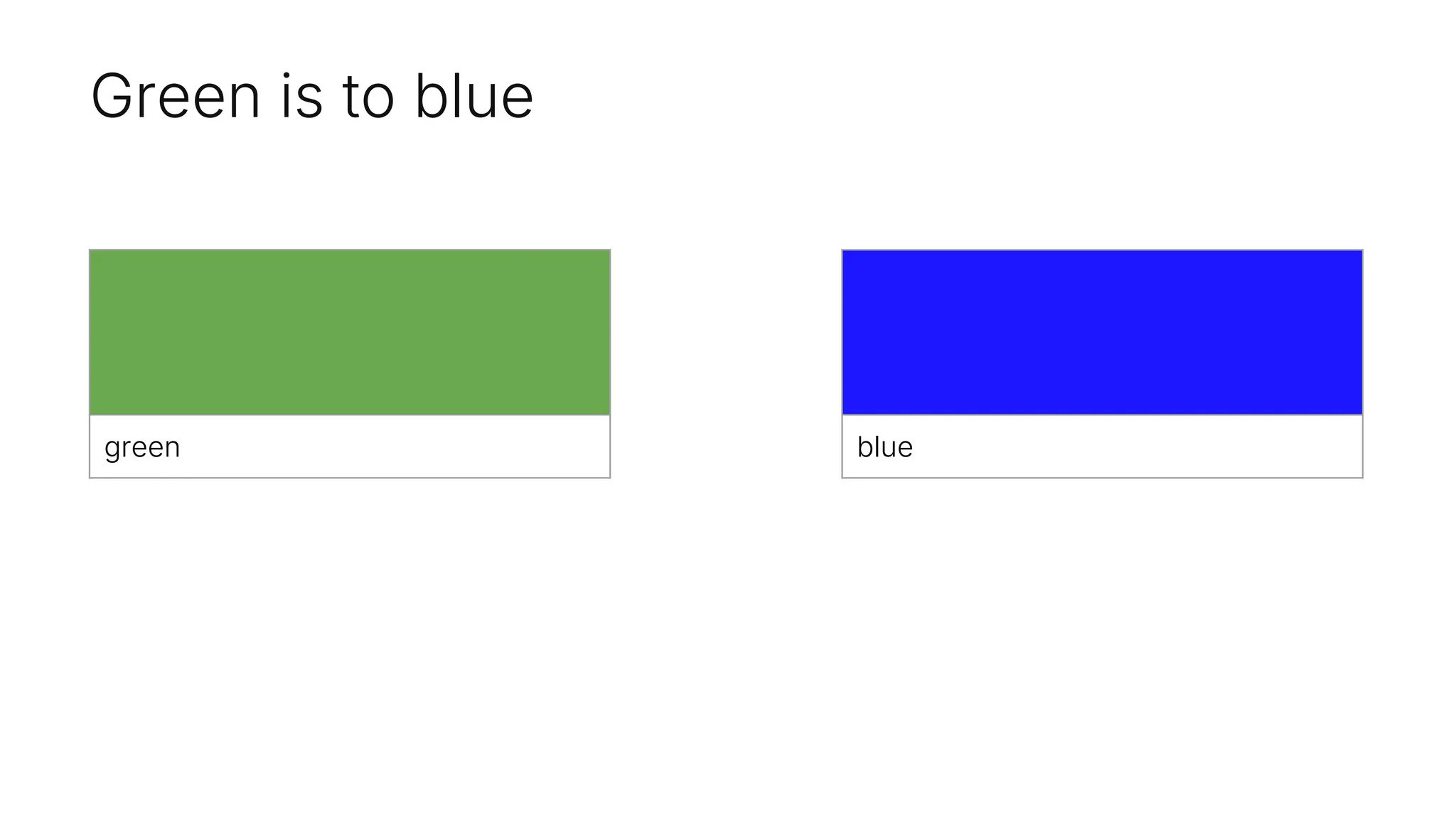
The distance between red and orange
is incredibly similar to blue and green…
But when we tested things trying to verify,
we got interesting results which show the
"understanding" of the relationship
This actually yields this
# Find a term that has the same distance and direction blue has from green, but starting from
blue
target_distance = distance_green_blue
target_direction = direction_green_blue
# Define a list of terms to compare
terms = ["red", "orange", "yellow", "green", "blue", "purple", "pink", "black", "white", "gray"]
# Get the embedding for each term
term_embeddings = {term: get_embedding(term) for term in terms}
# Find the term with the closest distance and same direction to the target distance and direction
closest_term = None
closest_distance = float('inf')
start_term = "red"
start_embedding = get_embedding(start_term)
for term, embedding in term_embeddings.items():
if term == start_term:
continue
distance, direction = cosine_distance_and_direction(start_embedding, embedding)
if direction == target_direction and abs(distance - target_distance) < closest_distance:
closest_distance = abs(distance - target_distance)
closest_term = term
closest_term, closest_distance](https://image.slidesharecdn.com/videoparislondonlegalpresentationembeddingsjocelyn-241227150655-0ac17fc6/75/apidays-Paris-2024-Embeddings-Core-Concepts-for-Developers-Jocelyn-Matthews-Pinecone-33-2048.jpg)
![Check the vectors
The distance between red and orange
is incredibly similar to blue and green…
But when we played around to verify, we
got interesting results revealing the
semantic "understanding" of the
relationship
This actually yields this
# Find a term that has the same distance and direction blue
has from green, but starting from blue
target_distance = distance_green_blue
target_direction = direction_green_blue
# Define a list of terms to compare
terms = ["red", "orange", "yellow", "green", "blue",
"purple", "pink", "black", "white", "gray"]
# Get the embedding for each term
term_embeddings = {term: get_embedding(term) for term in
terms}
# Find the term with the closest distance and same direction
to the target distance and direction
closest_term = None
closest_distance = float('inf')
start_term = "red"
start_embedding = get_embedding(start_term)
for term, embedding in term_embeddings.items():
if term == start_term:
continue
distance, direction =
cosine_distance_and_direction(start_embedding, embedding)
if direction == target_direction and abs(distance -
target_distance) < closest_distance:
closest_distance = abs(distance - target_distance)
closest_term = term
closest_term, closest_distance
('purple', np.float64(0.006596347059928065))
Purple](https://image.slidesharecdn.com/videoparislondonlegalpresentationembeddingsjocelyn-241227150655-0ac17fc6/75/apidays-Paris-2024-Embeddings-Core-Concepts-for-Developers-Jocelyn-Matthews-Pinecone-34-2048.jpg)
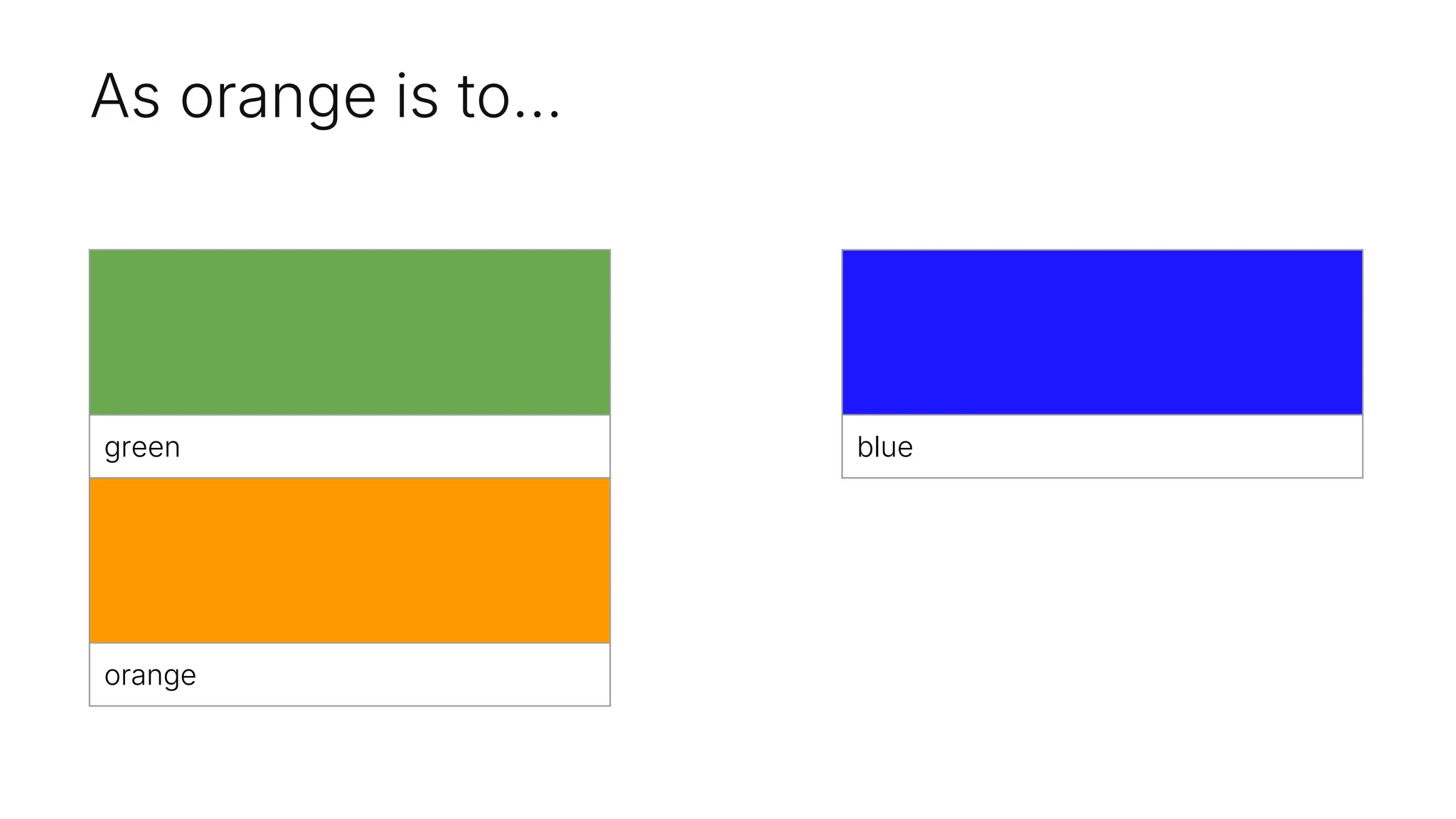
![Why not 'orange'?
The code's result of ('purple',
np.float64(0.006596347059928065))
suggests that, in the embedding space used by
the model, "red" and "purple" have a closer
semantic relationship than "red" and "orange".
The embedding model used in the code has
determined that "red" and "purple" are closer
semantically. This is likely due to the specific
contexts and relationships captured by the model
during training.
It yields 'purple' instead of orange because the
cosine distance and direction calculations
between the embeddings of "red" and other terms
result in "purple" being the closest match to the
target distance and direction from "green" to
"blue".
# Find a term that has the same distance and direction blue
has from green, but starting from blue
target_distance = distance_green_blue
target_direction = direction_green_blue
# Define a list of terms to compare
terms = ["red", "orange", "yellow", "green", "blue",
"purple", "pink", "black", "white", "gray"]
# Get the embedding for each term
term_embeddings = {term: get_embedding(term) for term in
terms}
# Find the term with the closest distance and same direction
to the target distance and direction
closest_term = None
closest_distance = float('inf')
start_term = "red"
start_embedding = get_embedding(start_term)
for term, embedding in term_embeddings.items():
if term == start_term:
continue
distance, direction =
cosine_distance_and_direction(start_embedding, embedding)
if direction == target_direction and abs(distance -
target_distance) < closest_distance:
closest_distance = abs(distance - target_distance)
closest_term = term
closest_term, closest_distance](https://image.slidesharecdn.com/videoparislondonlegalpresentationembeddingsjocelyn-241227150655-0ac17fc6/75/apidays-Paris-2024-Embeddings-Core-Concepts-for-Developers-Jocelyn-Matthews-Pinecone-35-2048.jpg)