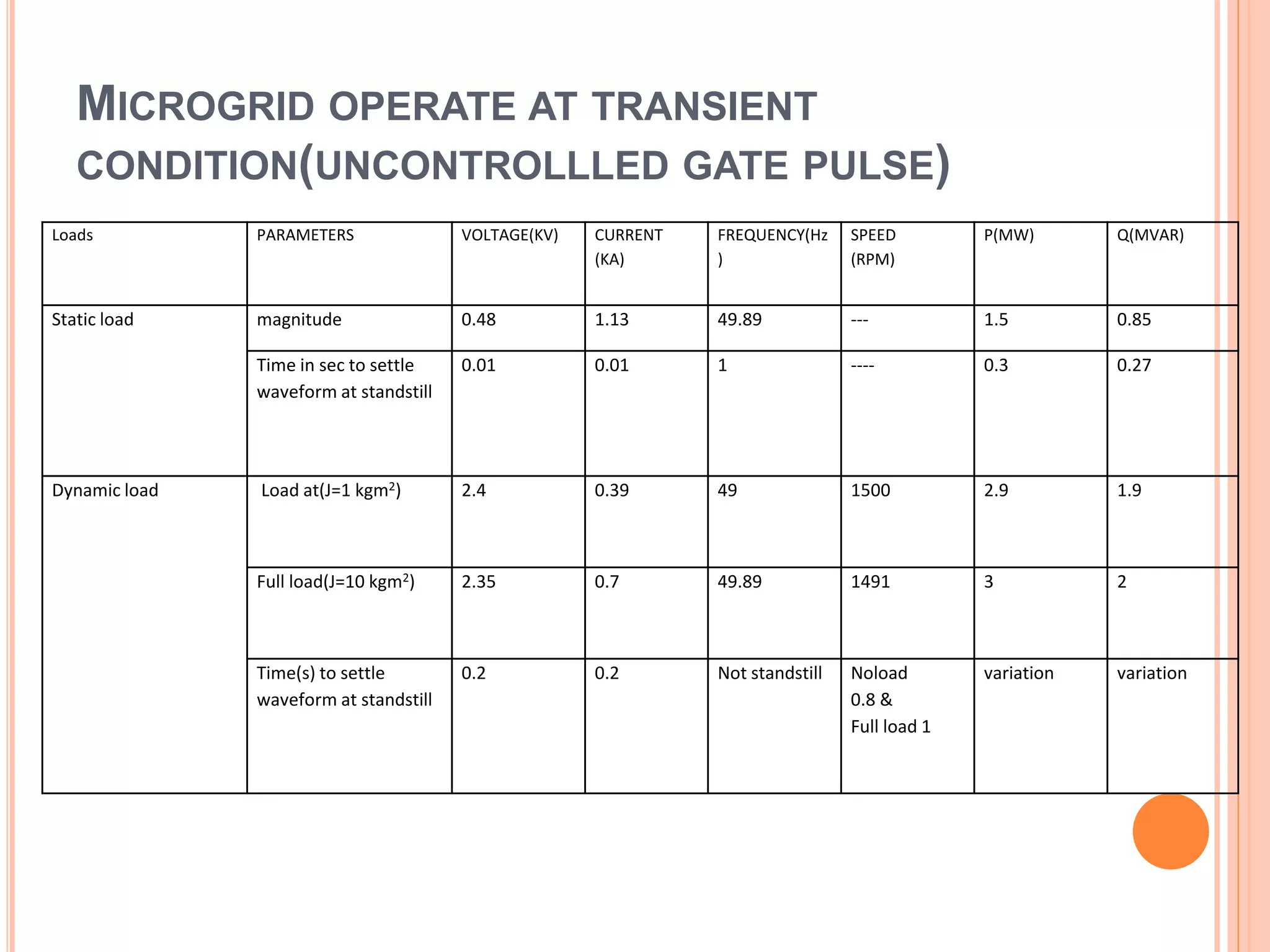
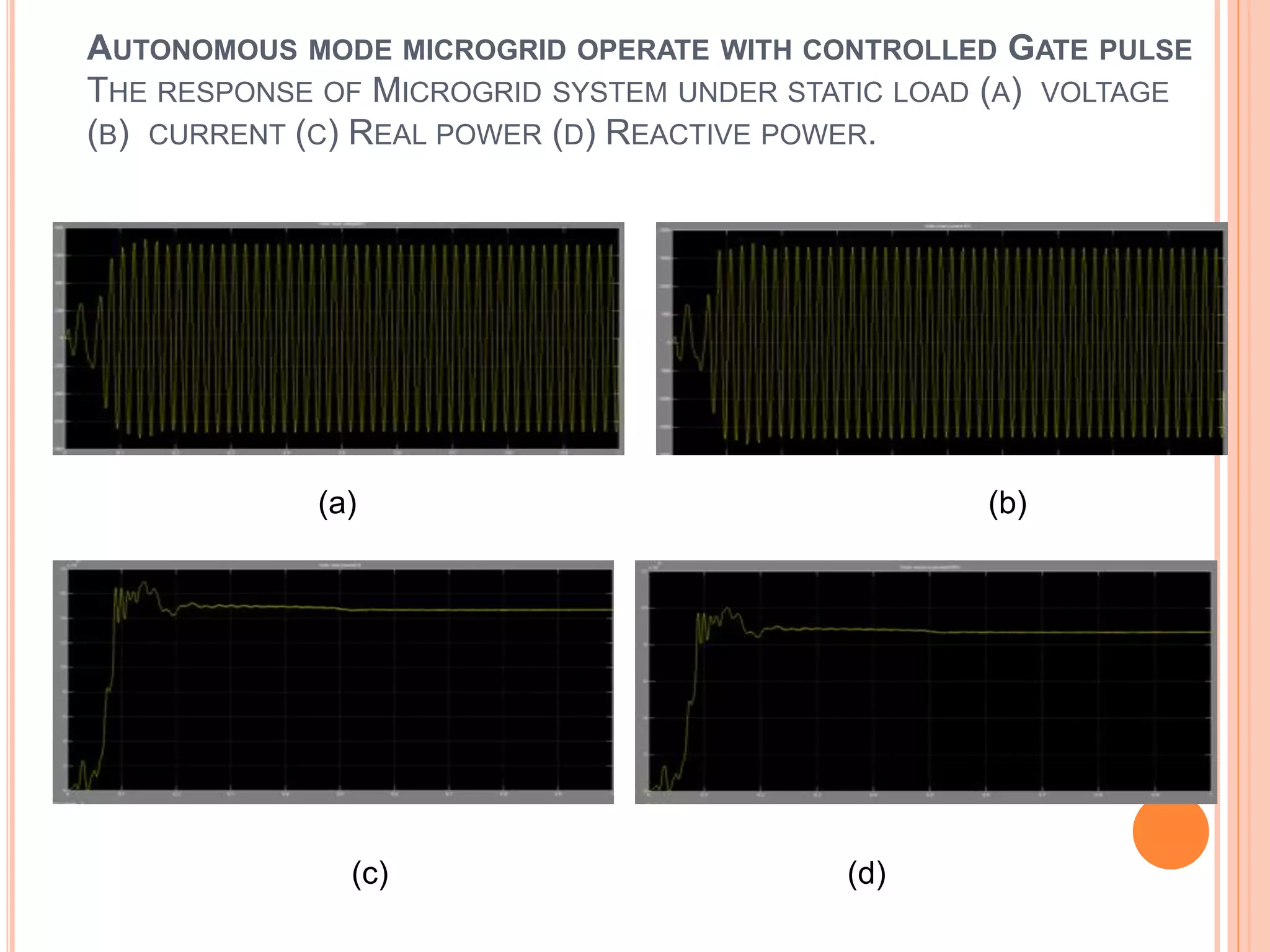
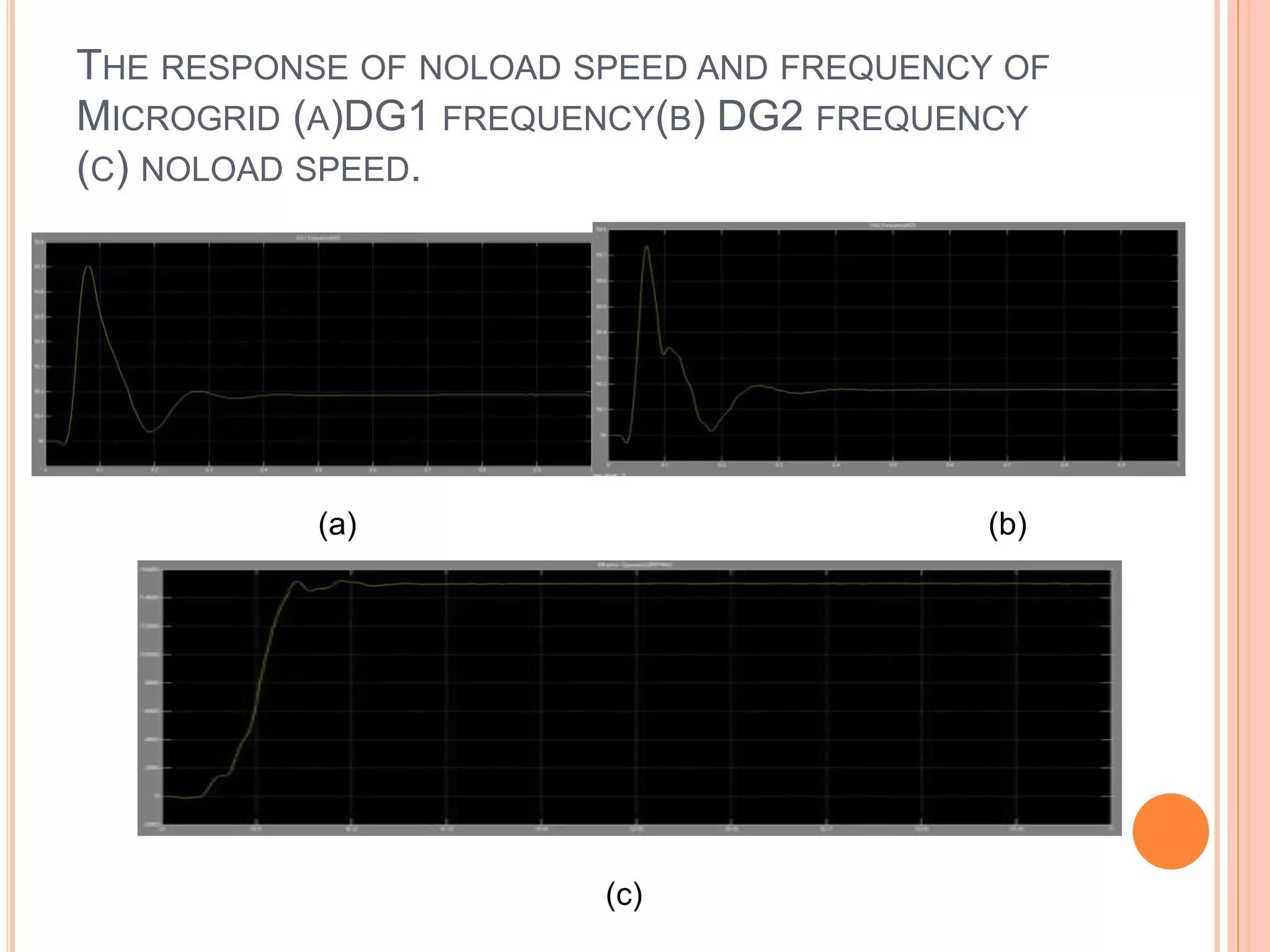
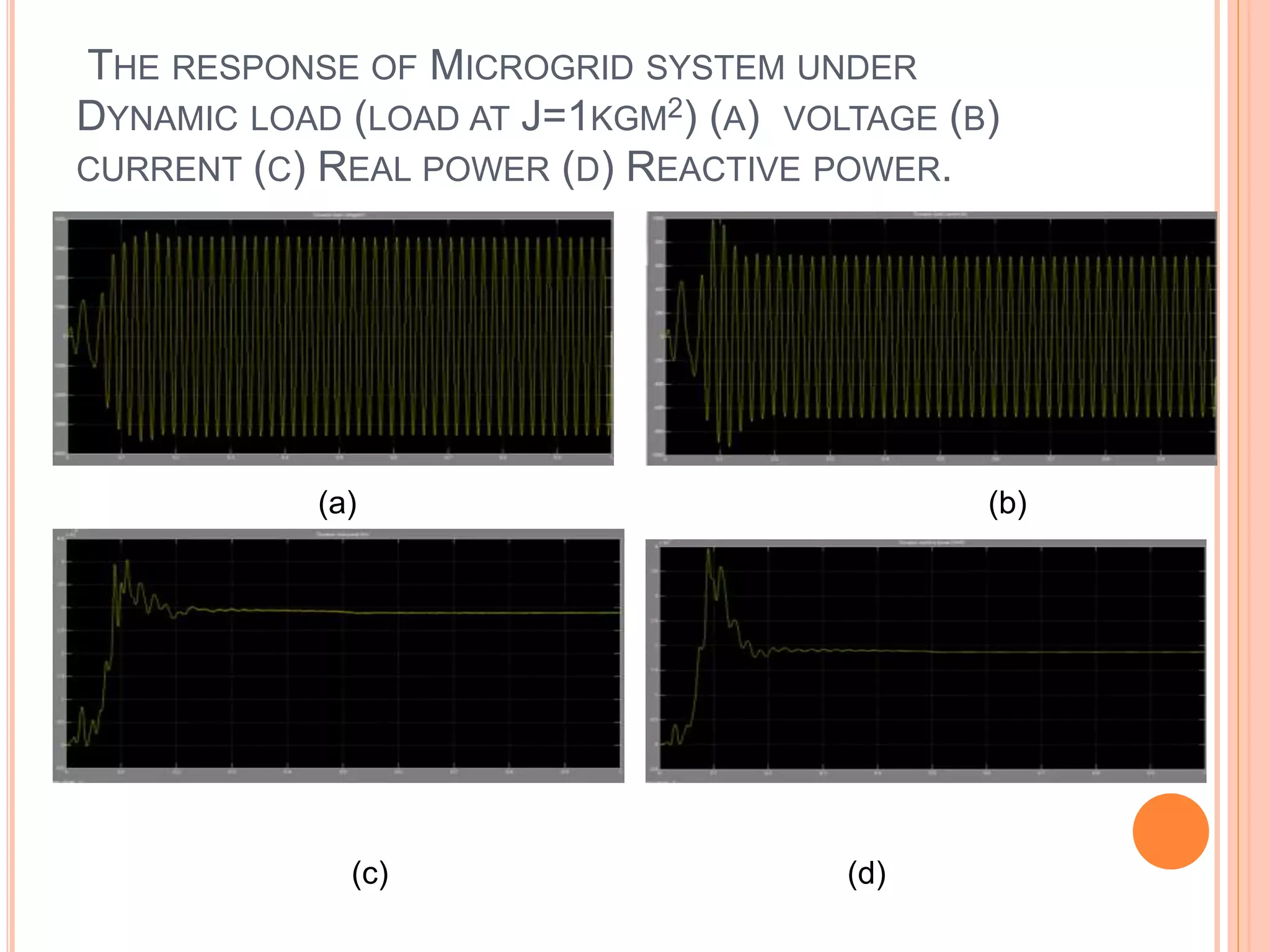
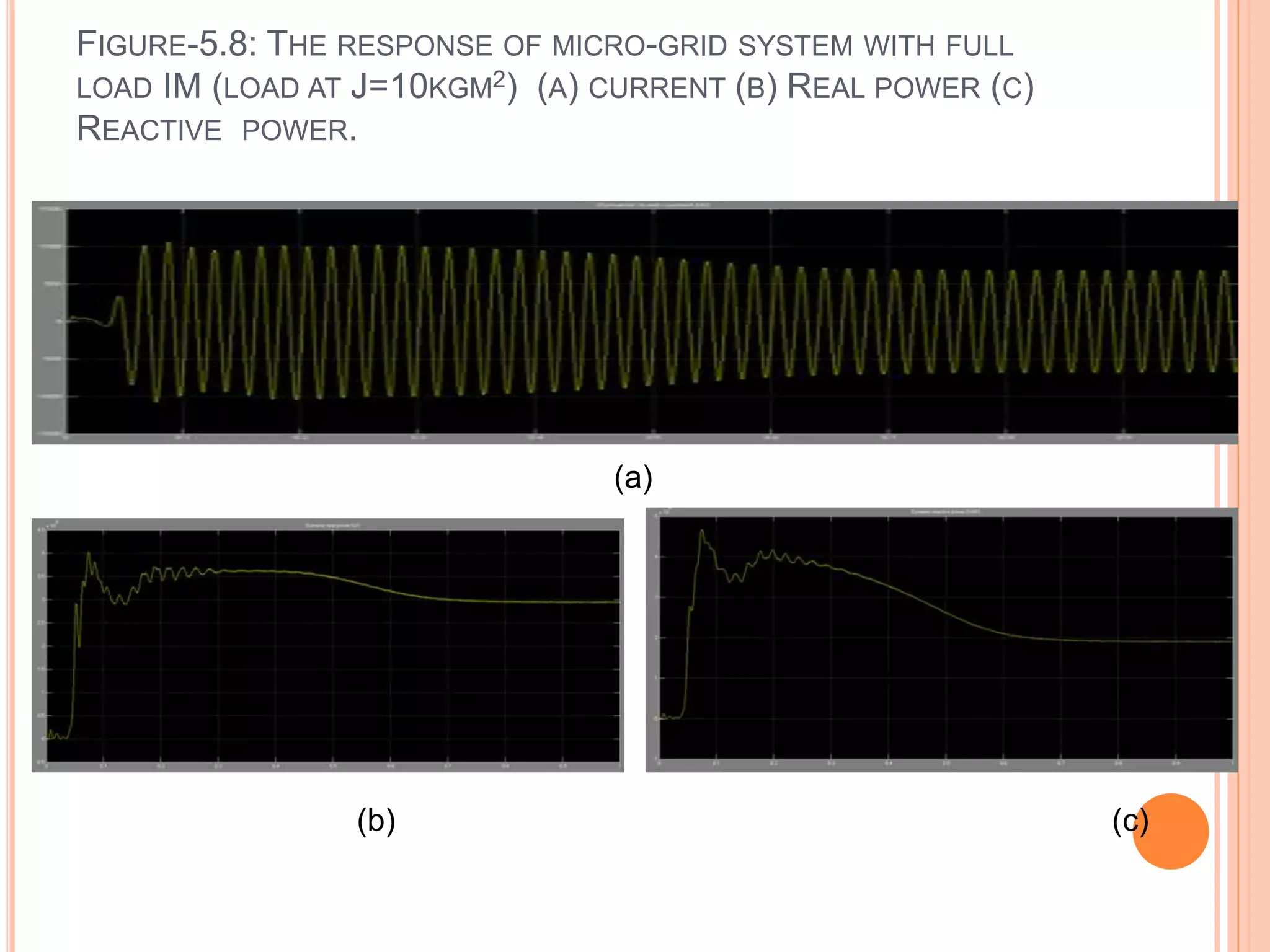
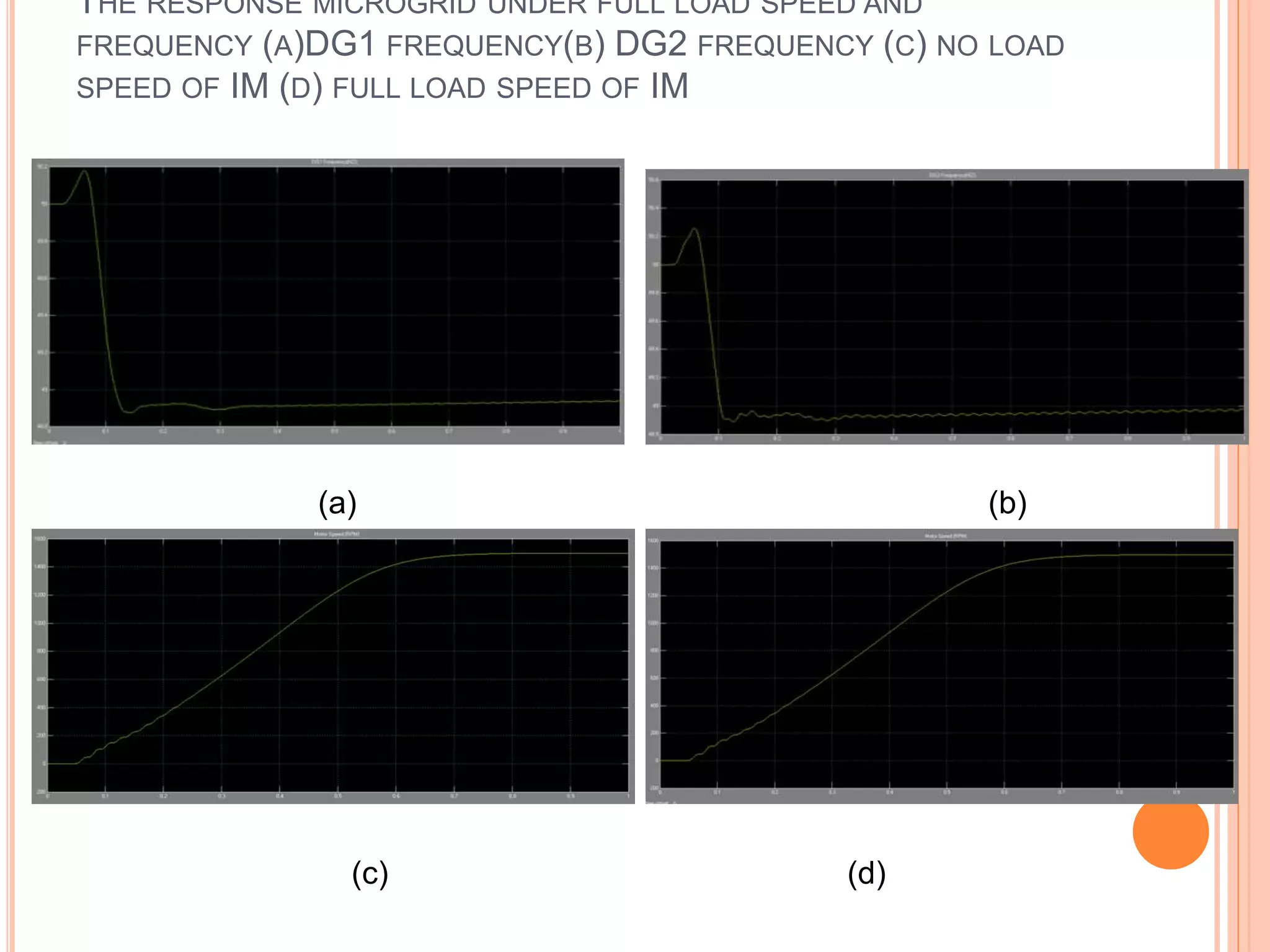
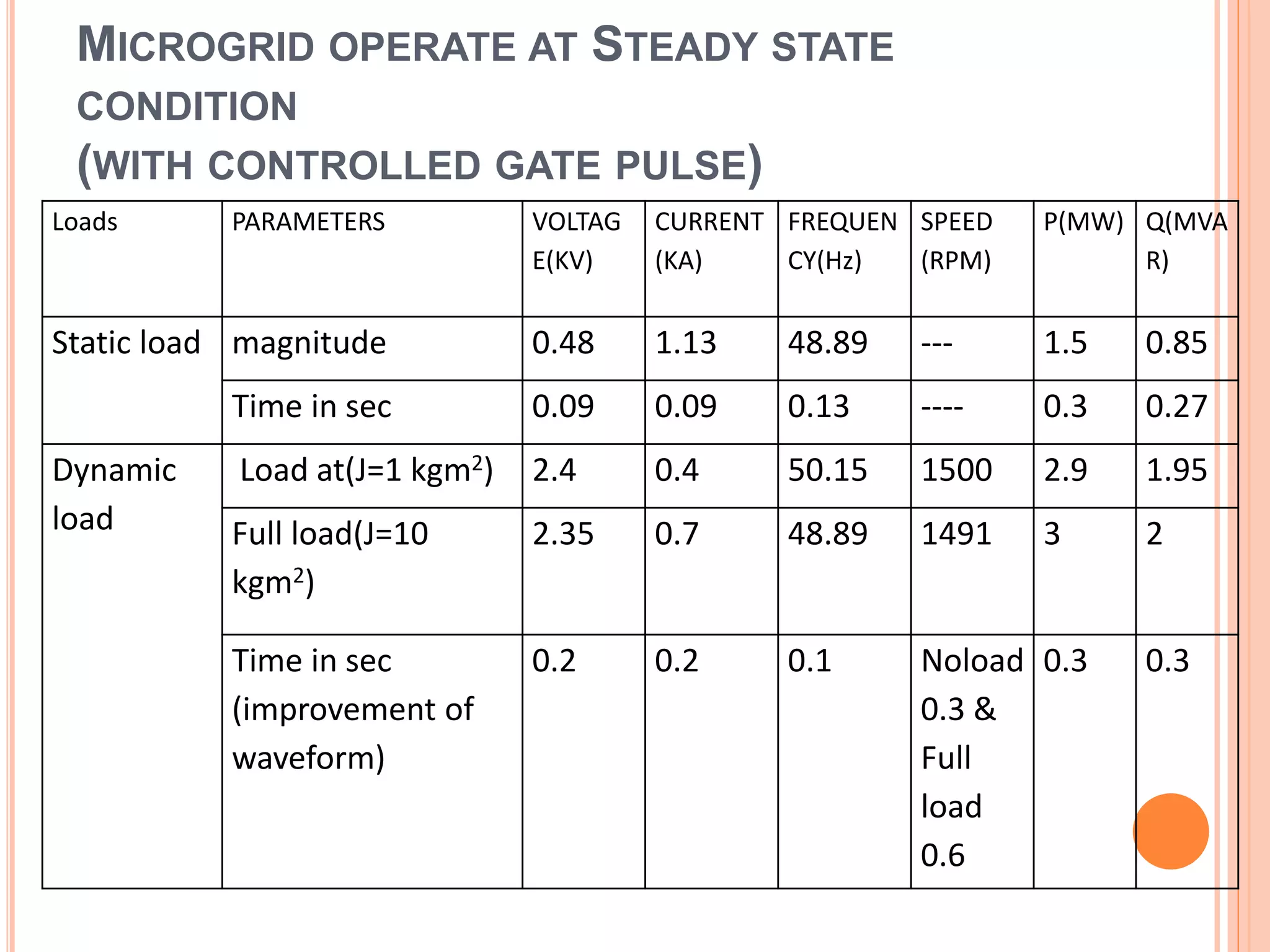
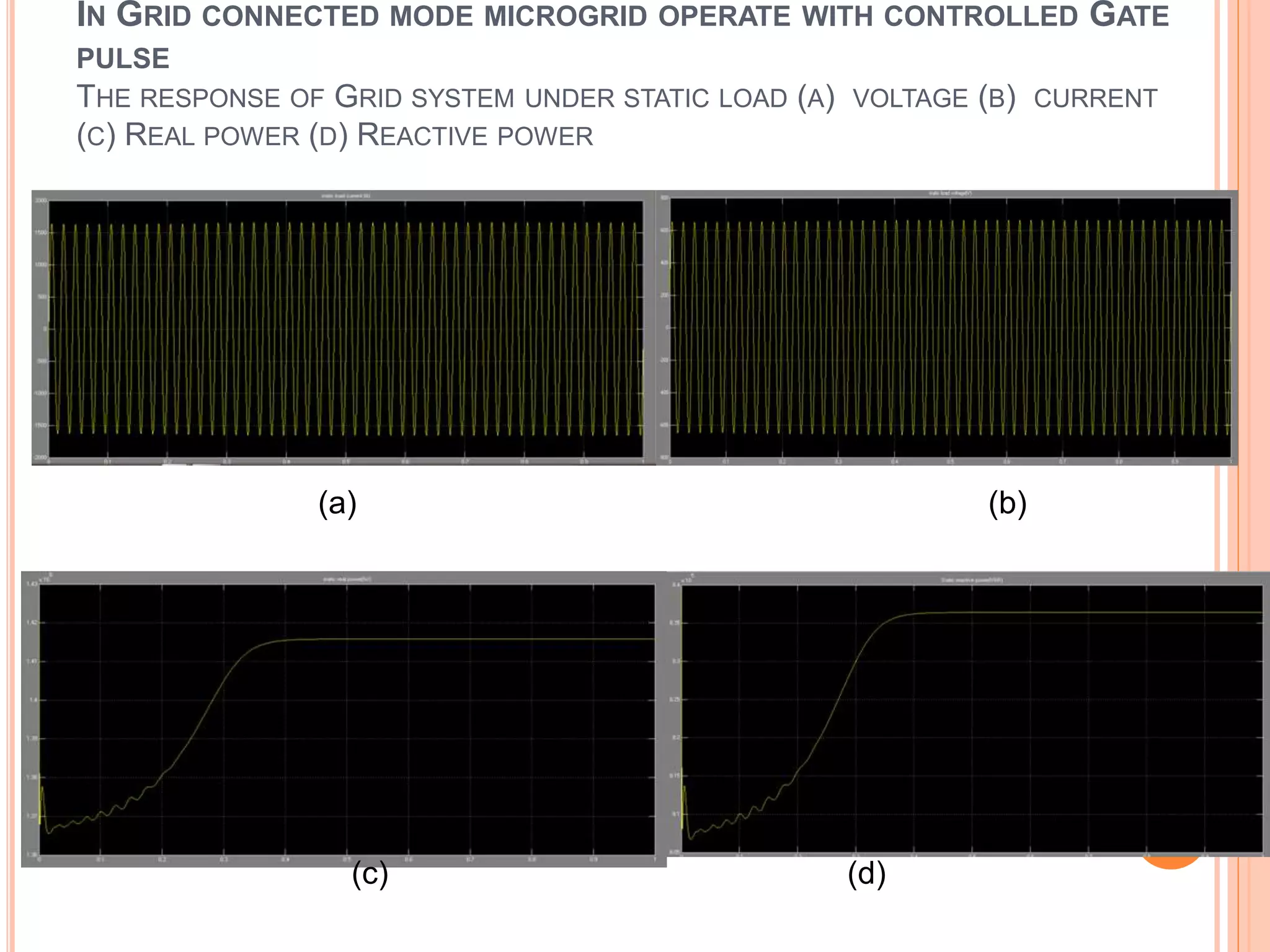
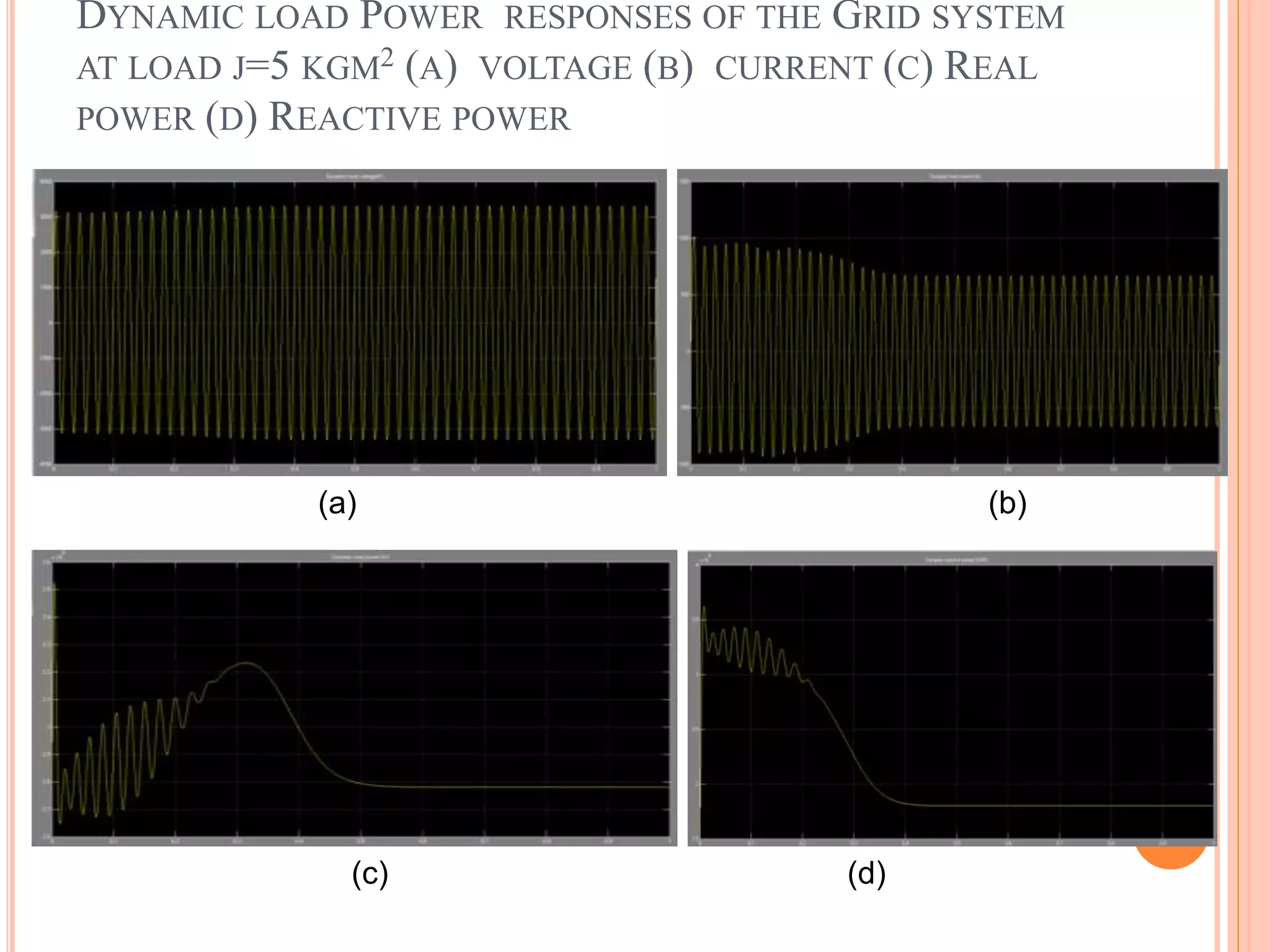
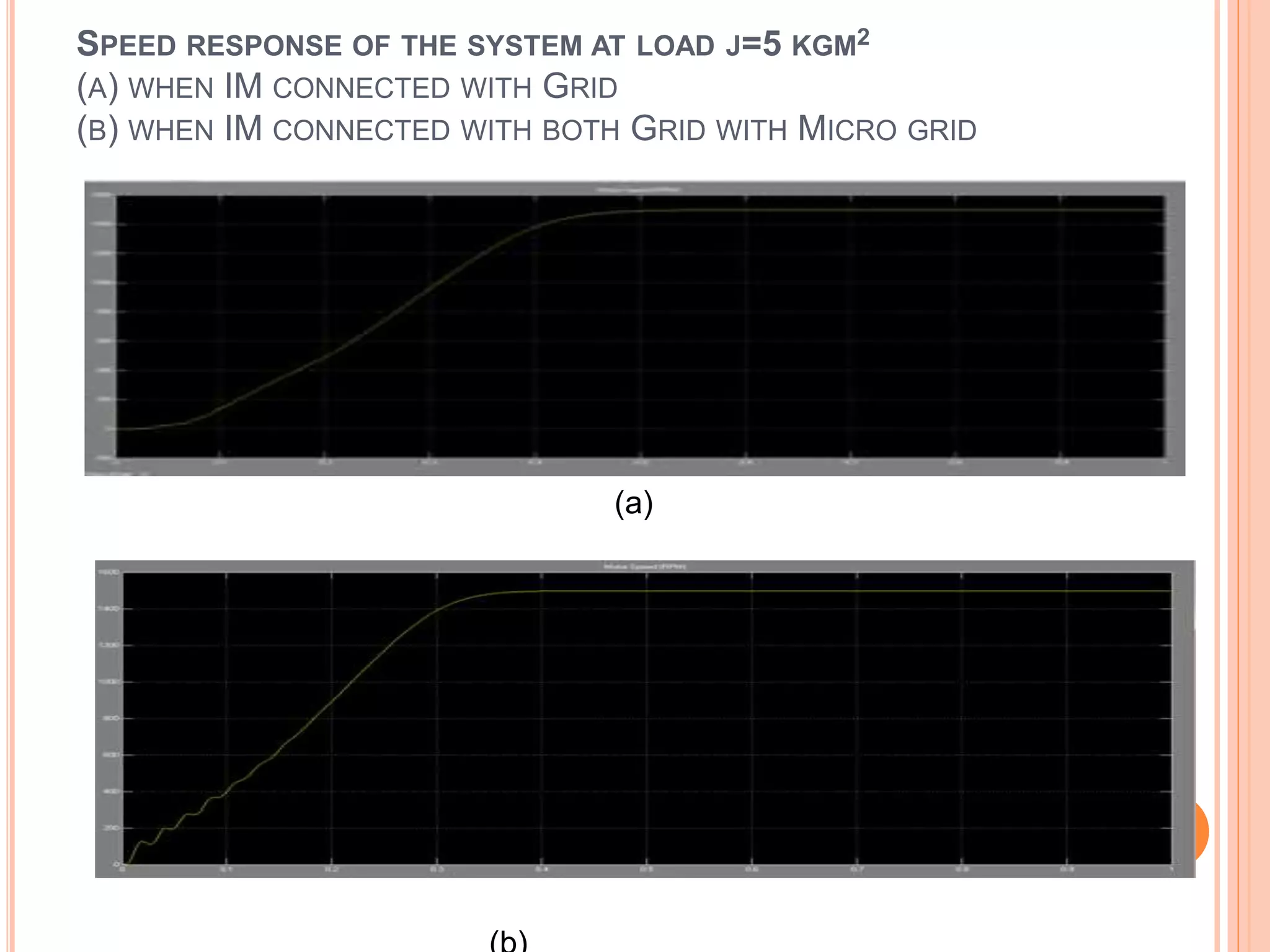
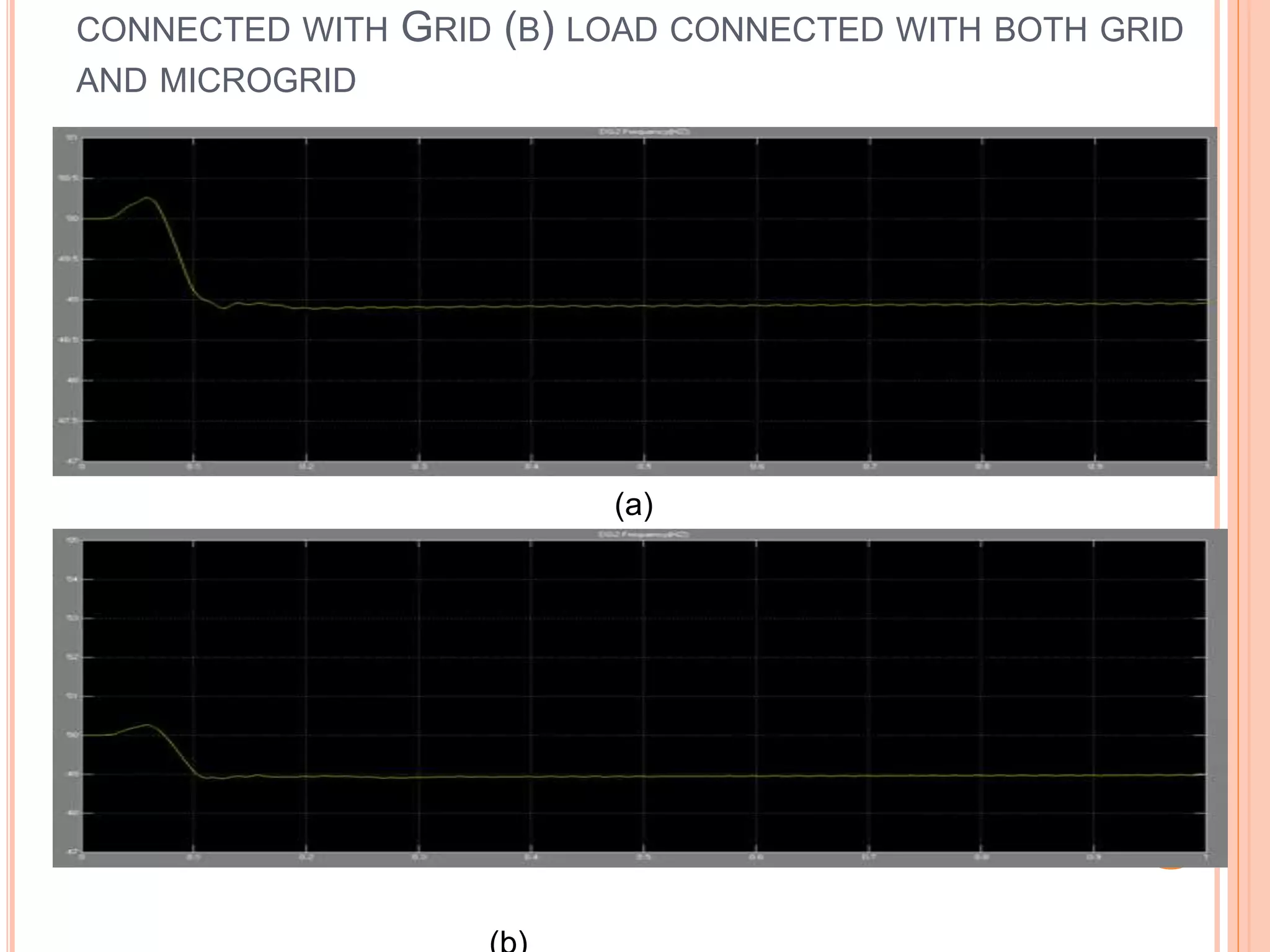
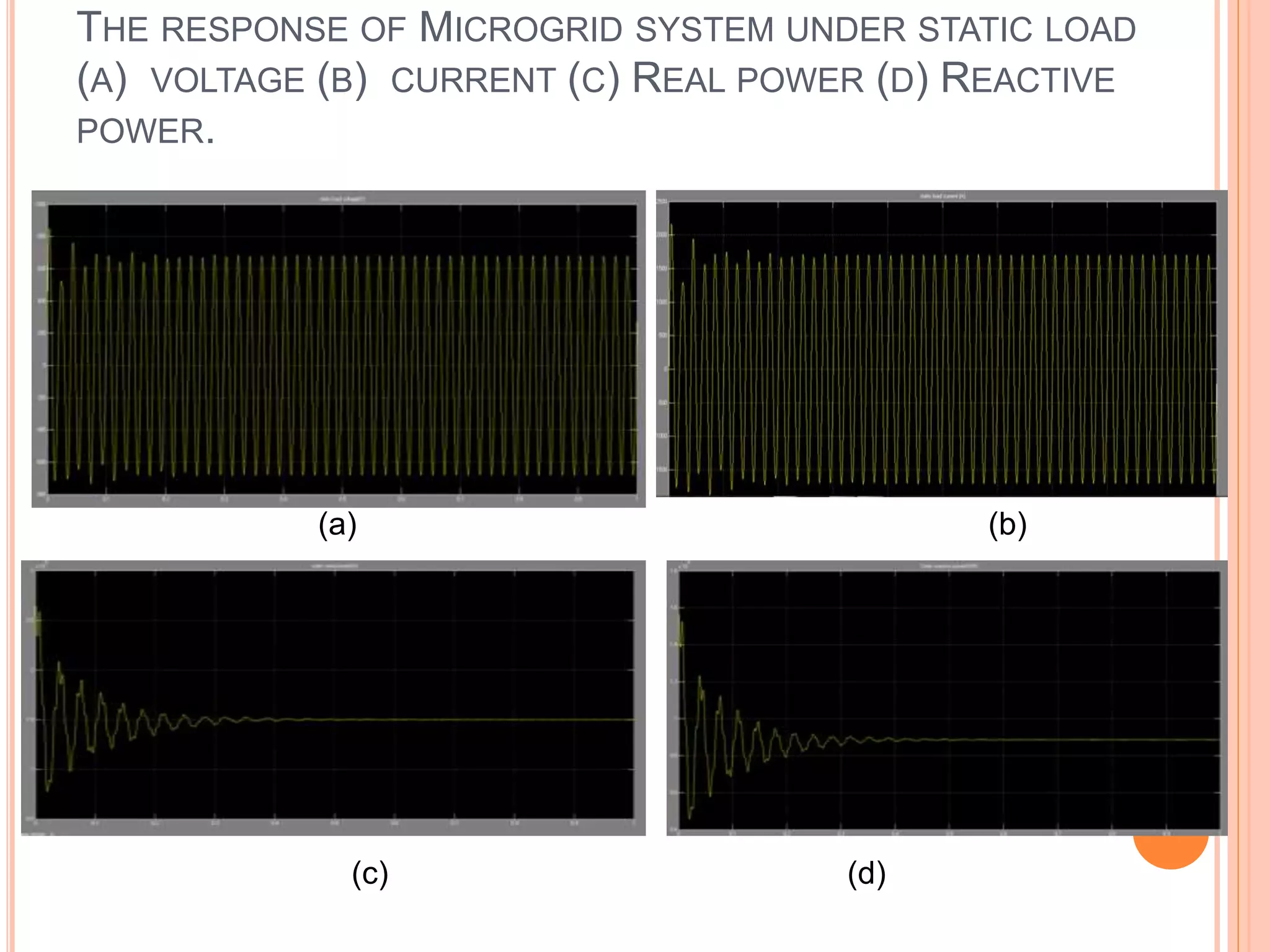
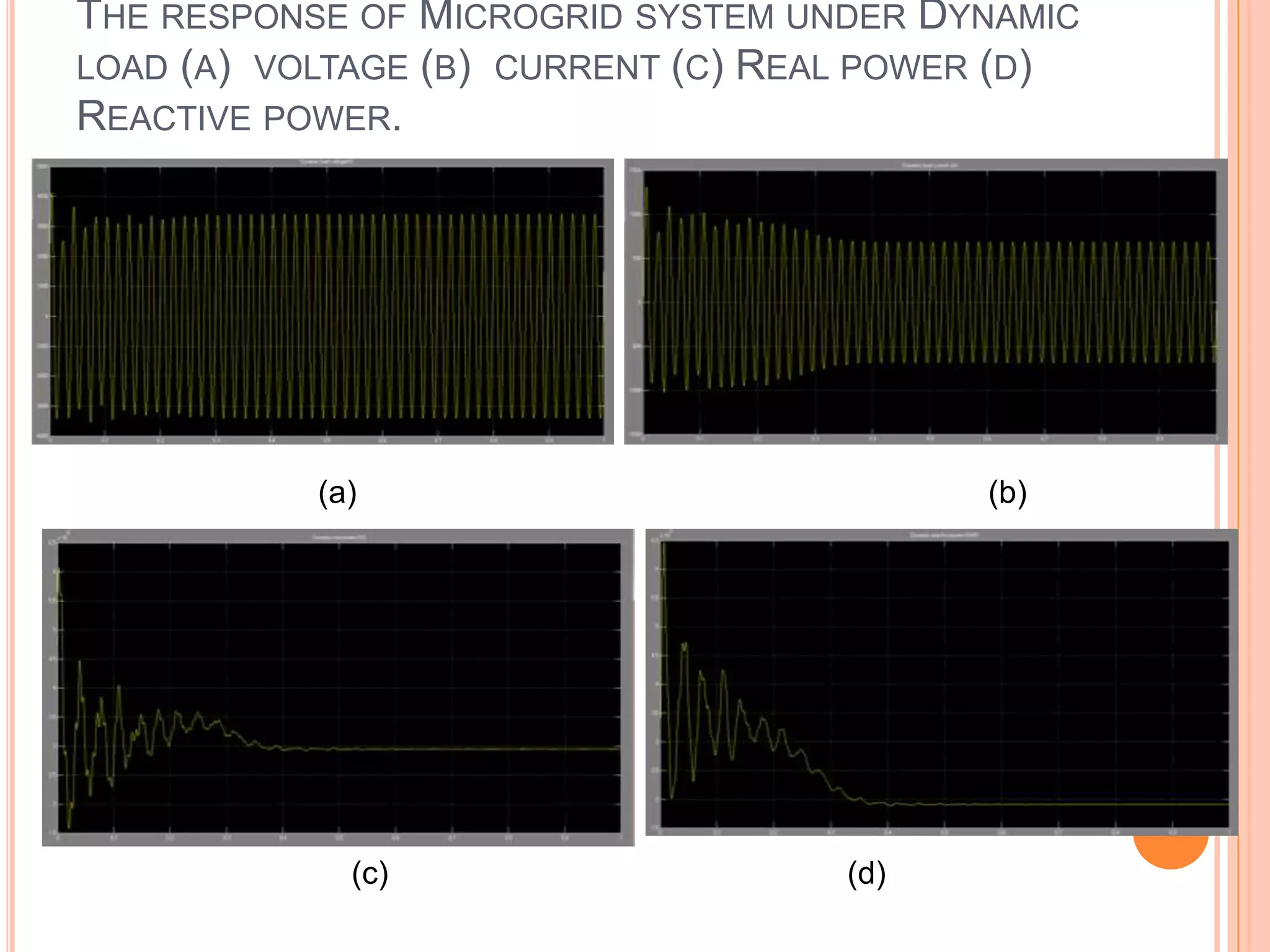
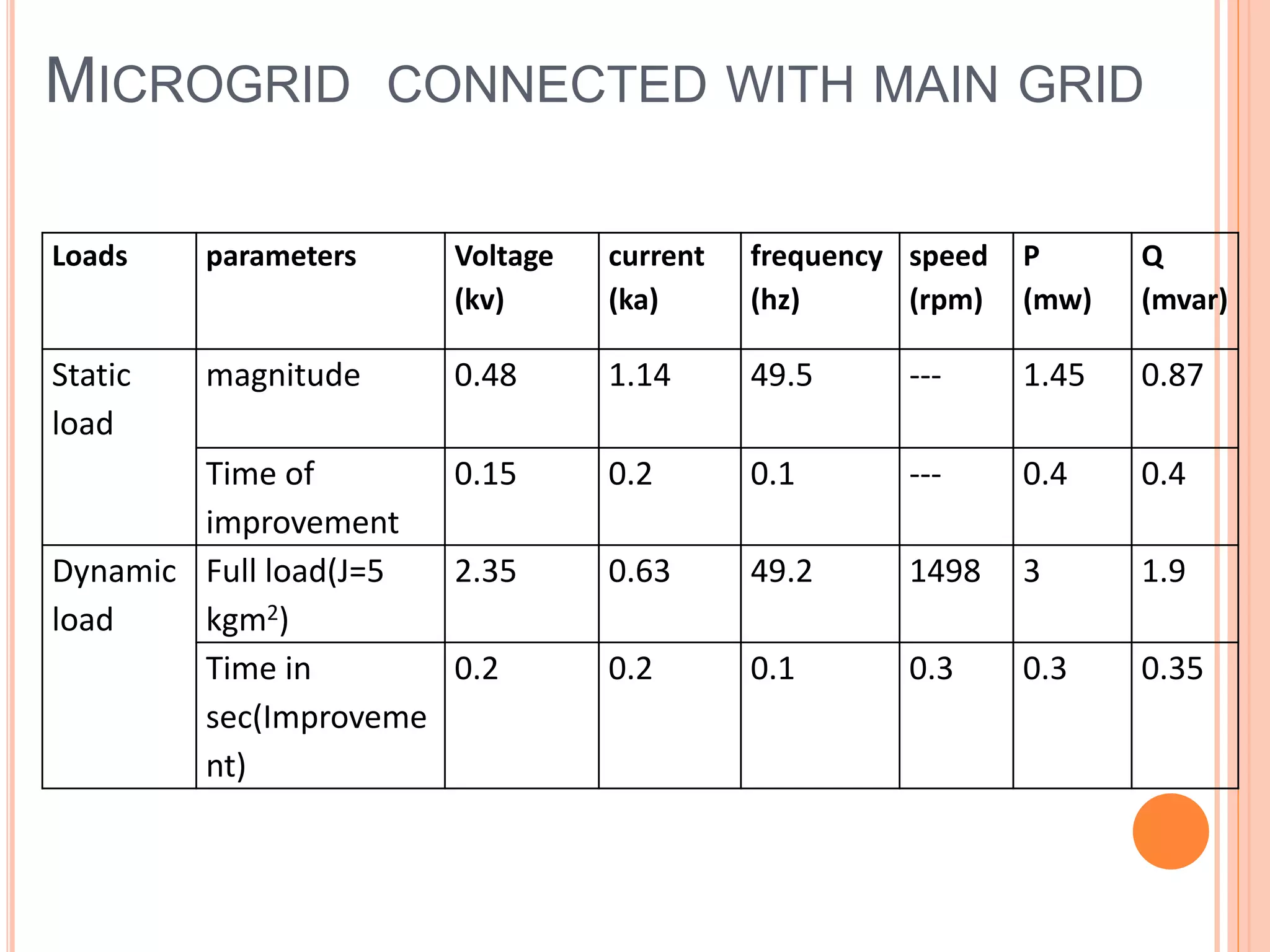
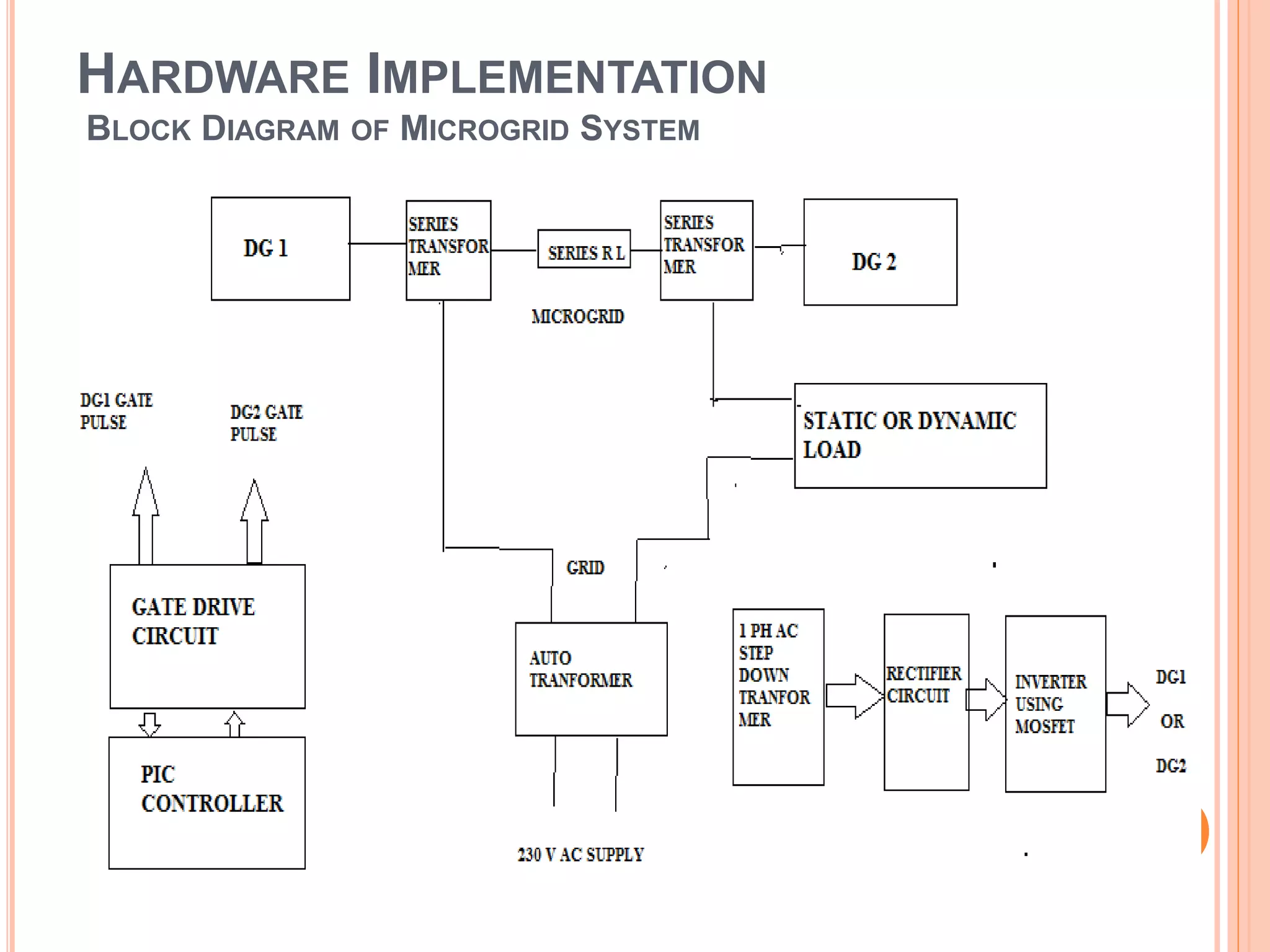
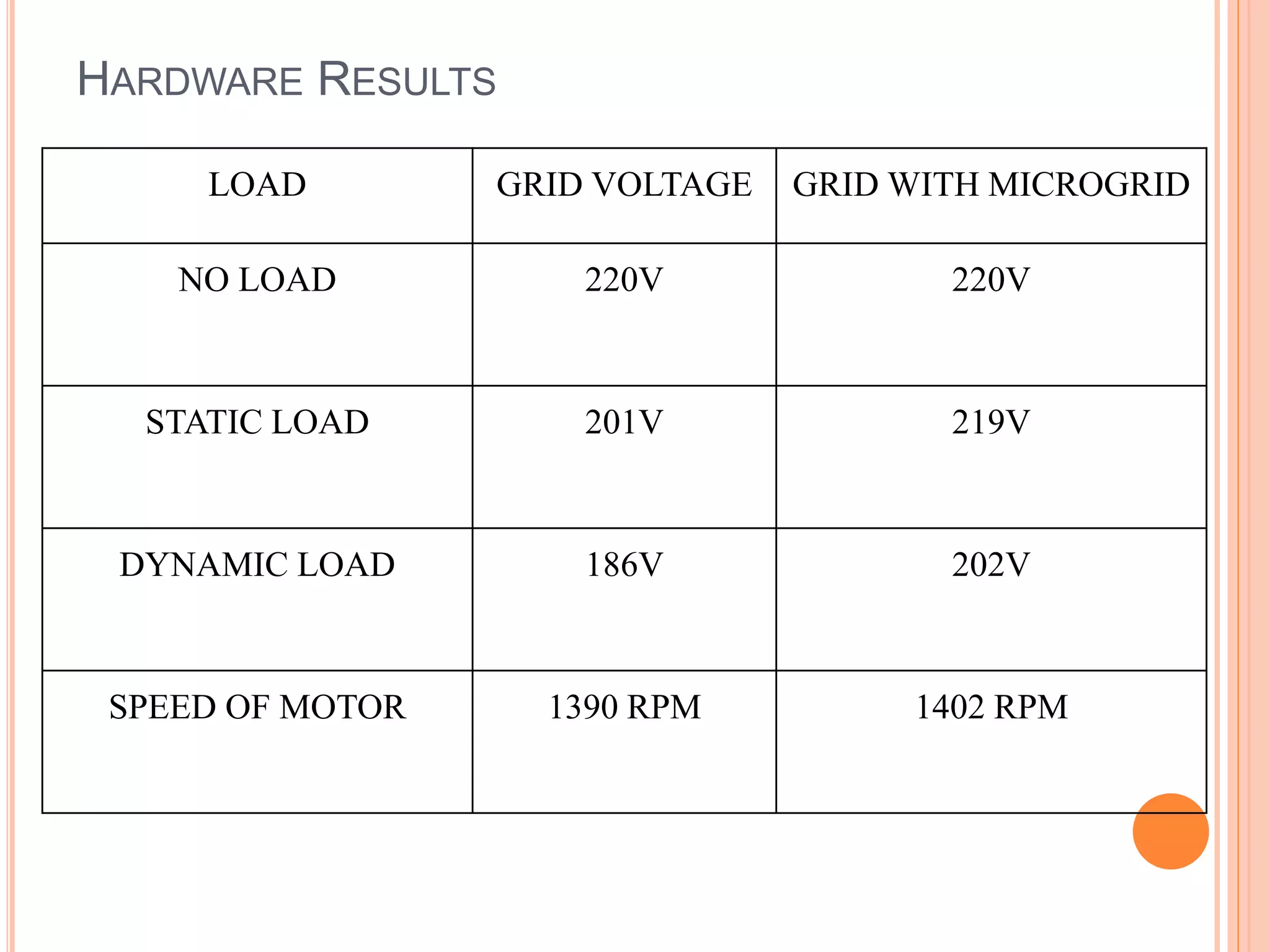
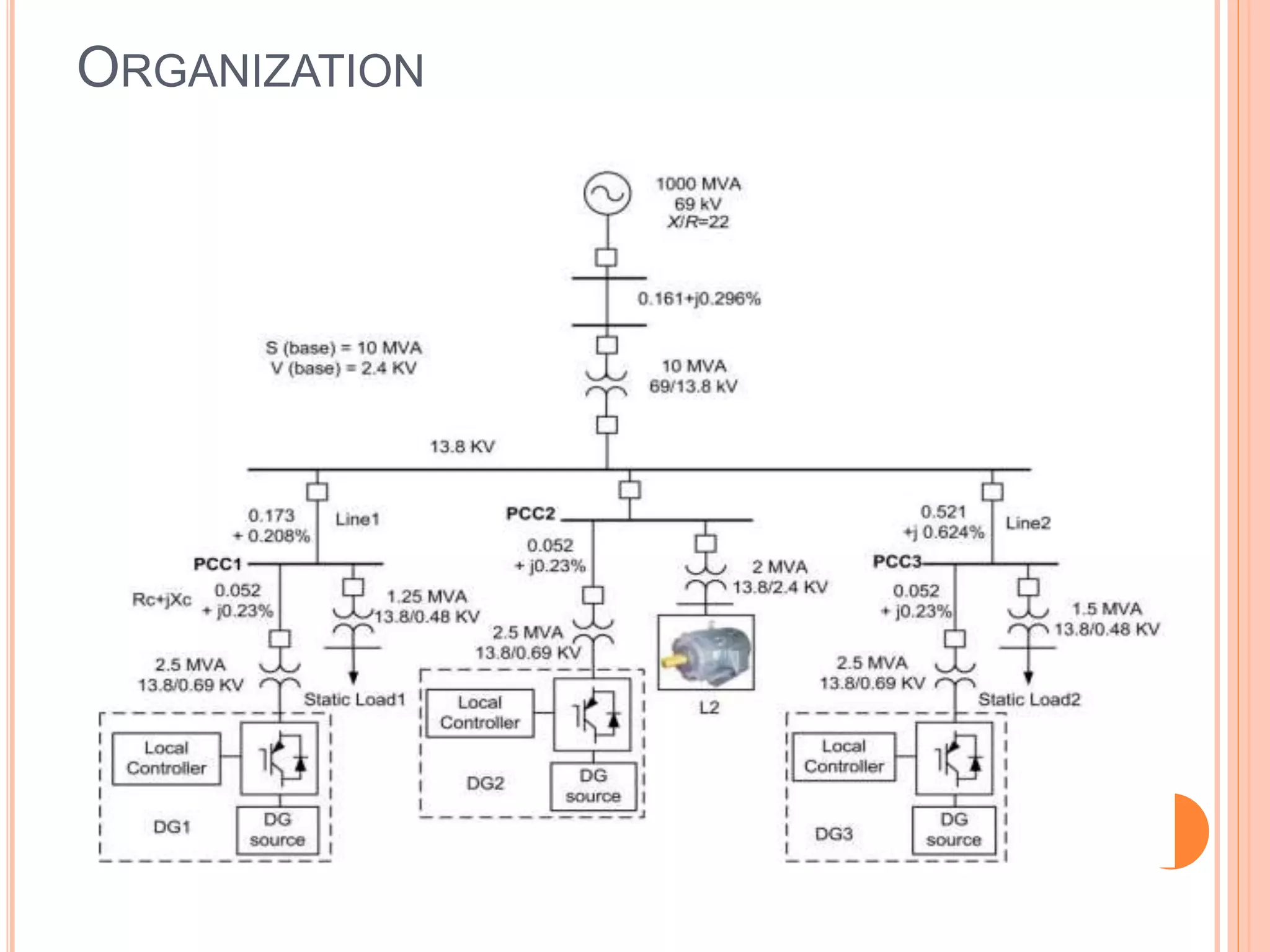
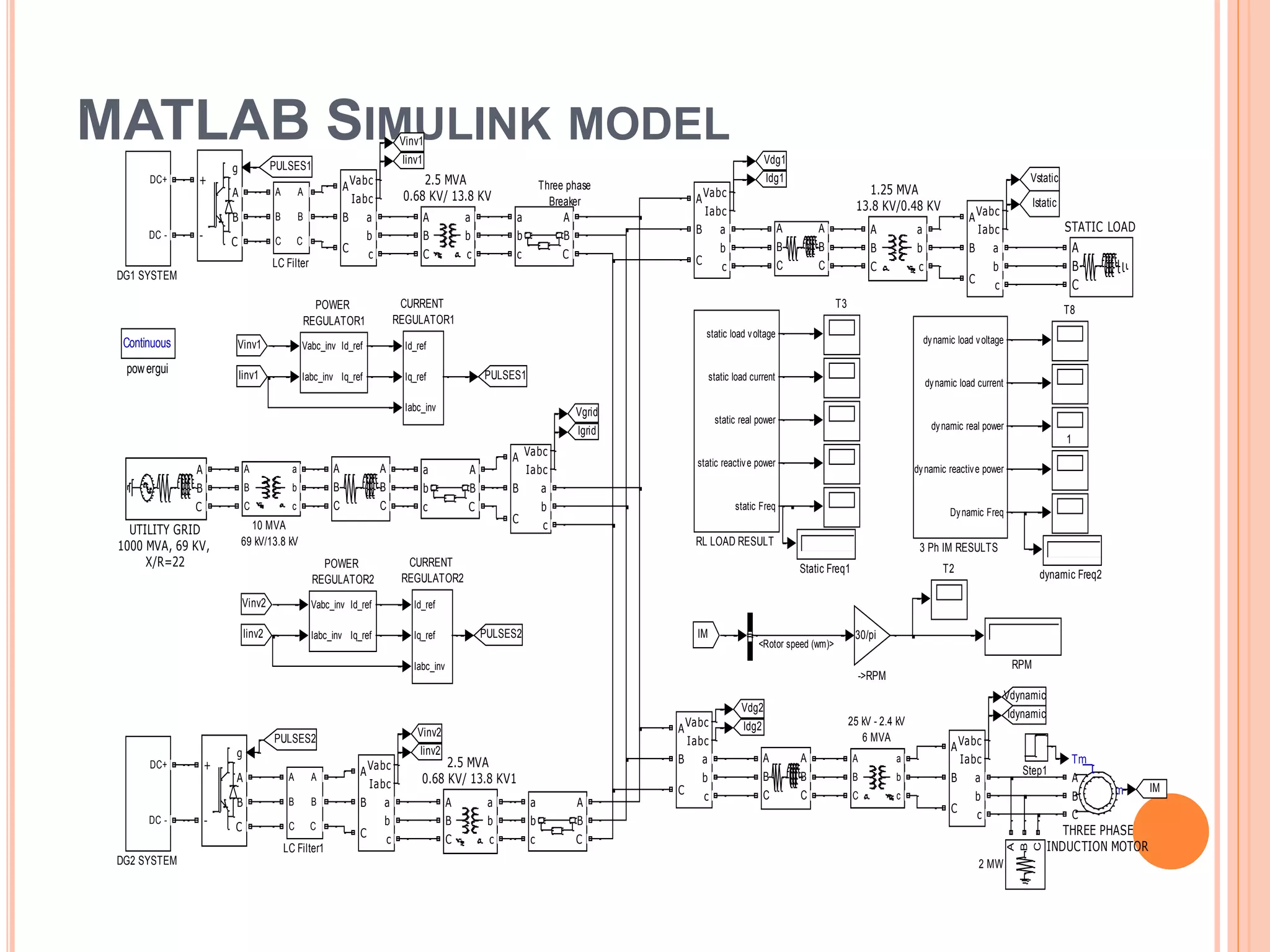
This document presents an analysis of low frequency oscillations in autonomous microgrids driven by dynamic loads, emphasizing the importance of effective control strategies to stabilize system performance. It introduces a two degree of freedom active damping controller designed to mitigate oscillatory dynamics while enhancing power quality and reliability. The findings highlight the significant impact of induction motor loads on microgrid stability and the proposed strategies improve operational efficiency across varying conditions.

1. ANALYSIS OF LOW FREQUENCY OSCILLATION IN
AUTONOMOUS MICROGRID WITH STATIC AND
DYNAMIC LOAD
Presented by-Godwin Lobo

2. INTRODUCTION
The concept of microgrid is gaining high momentum as enabling
structure to integrate renewable and distributed energy resources in
power networks. Moreover, the distinctive autonomous operational
capability of microgrids has brought in higher reliability measures in
supplying power demands when the utility grid is not available.
The majority of distributed/renewable generation (DG) units are
interfaced to the network by voltage source converter (VSCs). One well
established approach for autonomous microgrid operation is droop
control.

3. MOTIVATION OF MICROGRID
1. Accurate current control performance with a strong ability of
rejecting the grid distortion and voltage disturbances caused by
interfacing parameters mismatch and compensating for inverter
system delays.
2. Insensitivity to distribution system and ac side filter parameters.
3. Grid voltage sensorless operation with function fusion to reduce
system cost and increase the accuracy and reliability.
4. Fast voltage control performance with strong ability of mitigating
fast and dynamic voltage disturbances.
5. Stable and high power quality microgrid operation along the whole
loading trajectories of microgrid generators.

4. OBJECTIVES MICROGRID
1. To stabilize the microgrid system in the presence of IM loads, a two degree of freedom active
damping controller is proposed to stabilize the newly introduced oscillatory dynamics
2. Development of an interface monitoring unit along with a grid voltage sensorless interfacing
scheme for inverter based DG units.
3. Development of a voltage control system for the DG interface featuring fast load voltage
regulation and effective mitigation of fast and dynamic voltage disturbances.
4. Development of an autonomous control strategy of a microgrid system with effective damping
of low frequency modes.
5. Integration of the developed control algorithms to realize a robust DG interface for gird
connected and microgrid systems.
6. Improve reliability for mission-critical loads by connecting generators on a microgrid using
existing distribution networks.
7. Reduce reliance on fuel for diesel power by using renewable energy sources during outages.

5. NECESSITY OF MICROGRID
1. Utilization of Microgrid can help utilities defer investments in generation and
transmission capacity
2. Microgrid have the potential to offer increased total energy efficiency when used
with combined heat and power (CHP) or combined cooling heat and power, and can
therefore reduce energy costs
3. Appropriately integrated Microgrid can improve power availability and quality
4. Distributed systems offer potential security advantages over centralized systems
5. Microgrid promote fuel diversity (e.g., biomass, landfill gas, flare gas, wind, solar)
and therefore reduce overall energy price volatility
6. Renewable DG such as wind and solar photovoltaics provide emissions-free energy
7. Microgrid offer a quicker solution with regards to installation, lead time and siting
relative to centralized generation.

6. ORGANIZATION

7. PROBLEM STATEMENT
1. Electromechanical rotor oscillations in large IMs couple the rotor speed
oscillations, which are directly coupled to the supply frequency, and the rotor
flux dynamics
2. Unlike the idealized operation of an IM under an infinite-bus condition, in a
typical micro-grid system with IMs, active and reactive power oscillations will
be coupled.
3. The droop gains in a micro-grid system can vary over a considerable range to
optimize the cost and operation aspects of micro-grid via a higher-level
management controller. Therefore, system stability should be guaranteed over a
wide range of droop gain variation.
4.System stability should be also preserved under uncertainty in motor and system
parameters.

8. SYSTEM MODELING

9. The above figure shows the complete control system of a
typical VSC based DG unit, which consists of:
1) Power sharing control which sets the voltage phase and
magnitude for the inverter output voltage according to the
droop settings
2) Voltage control loop to yield close control characteristics of
the output voltage
3) Inner current loop to control the filter inductor current,
limiting the converter current during up normal conditions

11. STATE SPACE MODEL OF A VSC BASED DG UNIT:

12. MATLAB SIMULINK MODEL
Three phase
Breaker
Continuous
powergui
dynamic Freq2
g
A
B
C
+
-
g
A
B
C
+
-
A
B
C
UTILITY GRID
1000 MVA, 69 KV,
X/R=22
A
B
C
a
b
c
A
B
C
a
b
c
A
B
C
a
b
c
Vabc
Iabc
A
B
C
a
b
c
Vabc
Iabc
A
B
C
a
b
c
Vabc
Iabc
A
B
C
a
b
c
Vabc
Iabc
A
B
C
a
b
c
Vabc
Iabc
A
B
C
a
b
c
Vabc
Iabc
A
B
C
a
b
c
Vabc
Iabc
A
B
C
a
b
c
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
A
B
C
Tm
m
A
B
C
THREE PHASE
INDUCTION MOTOR
T9
T8
T7
T6
T5
T4
T3
T2
T13
T12
Step1
Static Freq1
A
B
C
STATIC LOAD
RPM
static load voltage
static load current
static real power
static reactive power
static Freq
RL LOAD RESULT
Vabc_inv
Iabc_inv
Id_ref
Iq_ref
POWER
REGULATOR2
Vabc_inv
Iabc_inv
Id_ref
Iq_ref
POWER
REGULATOR1
A
B
C
A
B
C
LC Filter1
A
B
C
A
B
C
LC Filter
Istatic
Vstatic
PULSES1
IM
PULSES2
Iinv2
Vinv2
Iinv1
Idg2
Vdg2
Idg1
Vdg1
Idynamic
Igrid
Vgrid
Vdynamic
Vinv1
Iinv2
Iinv1
IM
Vinv2
PULSES2
PULSES1
Vinv1
DC+
DC -
DG2 SYSTEM
DC+
DC -
DG1 SYSTEM
Id_ref
Iq_ref
Iabc_inv
CURRENT
REGULATOR2
Id_ref
Iq_ref
Iabc_inv
CURRENT
REGULATOR1
dynamic load voltage
dynamic load current
dynamic real power
dynamic reactive power
Dynamic Freq
3 Ph IM RESULTS
A
B
C
a
b
c
25 kV - 2.4 kV
6 MVA
A
B
C
2 MW
A
B
C
a
b
c
10 MVA
69 kV/13.8 kV
1
30/pi
->RPM
A
B
C
a
b
c
2.5 MVA
0.68 KV/ 13.8 KV1
A
B
C
a
b
c
2.5 MVA
0.68 KV/ 13.8 KV
A
B
C
a
b
c
1.25 MVA
13.8 KV/0.48 KV
<Rotor speed (wm)>

13. CONTROL STRATEGY
Vabc_inv
Iabc_inv
Id_ref
Iq_ref
POWER
REGULATOR1
PULSES1Iinv1
Vinv1 Id_ref
Iq_ref
Iabc_inv
CURRENT
REGULATOR1

14. POWER REGULATOR
2
Iq_ref
1
Id_ref
Vabc
Iabc
P & Q
Subsystem3
1
1
Vstatic In RMS
Discrete
RMS value3
PI
PI
-1 1/Base3
-K-
1/Base2
2
Iabc_inv
1
Vabc_inv

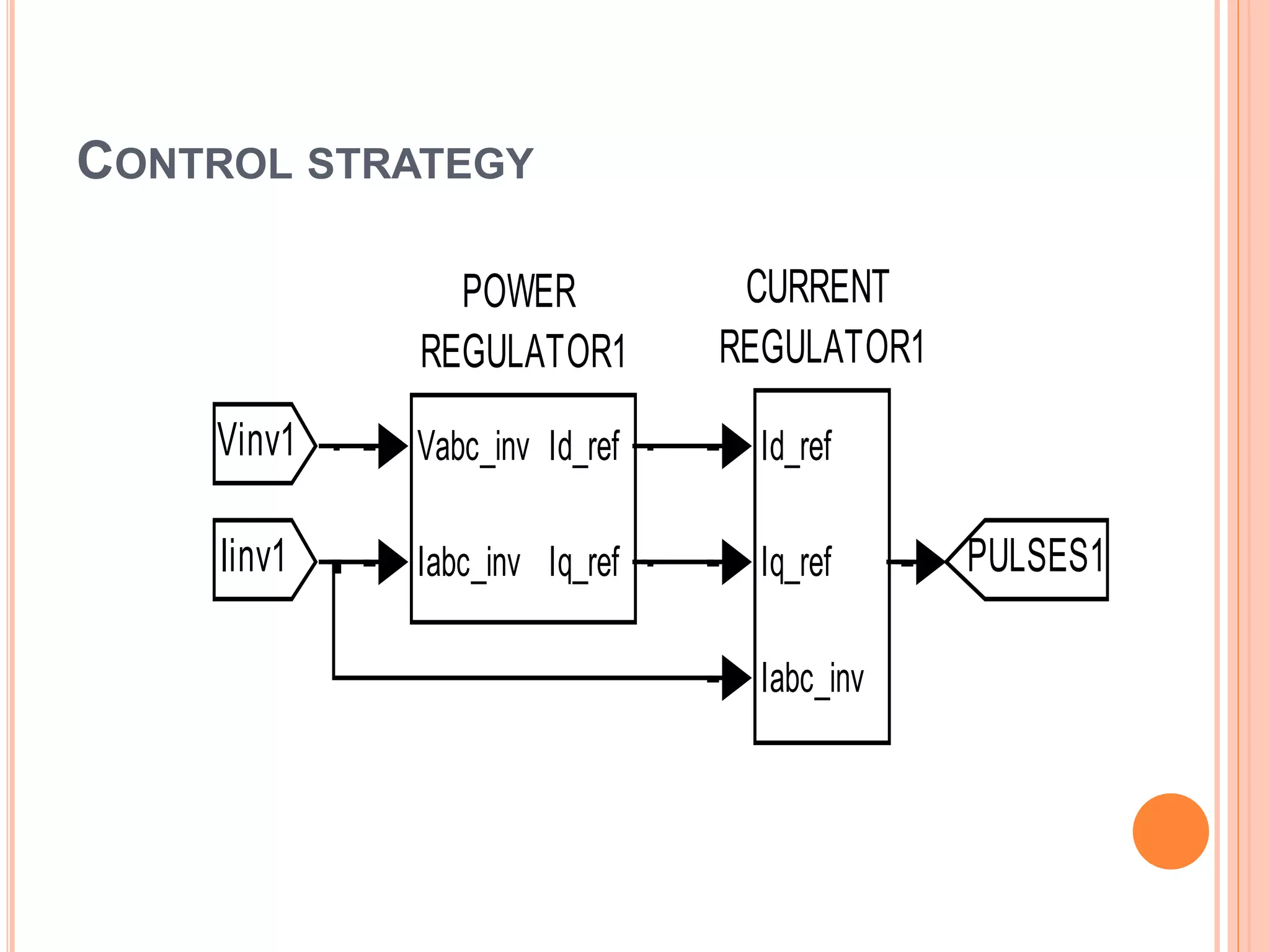
15. CURRENT REGULATOR
1
dq0
sin_cos
abc
abc
sin_cos
dq0
0
z
1
[Iq]
[Id]
[Id]
[Iq]
Freq
Sin_Cos
wt
Uref Pulses
PI
PI
3
Iabc_inv
2
Iq_ref
1
Id_ref

16. DG OUTPUT WITH AND WITHOUT FILTERS
OF INVERTERS
(a)
(b)

17. THE RESPONSE OF MICRO-GRID SYSTEM UNDER UNCONTROLLED
PULSE OPERATE WITH STATIC LOAD (A) VOLTAGE (B) CURRENT (C)
REAL POWER (D) REACTIVE POWER.
(a) (b)
(c) (d)

18. THE RESPONSE OF MICRO-GRID SYSTEM UNDER UNCONTROLLED
PULSE OPERATE WITH DYNAMIC LOAD (A) VOLTAGE (B) CURRENT (C)
REAL POWER (D) REACTIVE POWER..
(a) (b)
(c) (d)

19. THE FREQUENCY AND SPEED OF MICRO-GRID SYSTEM OPERATE
WITH UNCONTROLLED GATE PULSE (A) DG1 FREQUENCY (B) DG2
FREQUENCY (C) NOLOAD SPEED (D)FL SPEED.
(a) (b)
(c) (d)

20. MICROGRID OPERATE AT TRANSIENT
CONDITION(UNCONTROLLLED GATE PULSE)
Loads PARAMETERS VOLTAGE(KV) CURRENT
(KA)
FREQUENCY(Hz
)
SPEED
(RPM)
P(MW) Q(MVAR)
Static load magnitude 0.48 1.13 49.89 --- 1.5 0.85
Time in sec to settle
waveform at standstill
0.01 0.01 1 ---- 0.3 0.27
Dynamic load Load at(J=1 kgm2) 2.4 0.39 49 1500 2.9 1.9
Full load(J=10 kgm2) 2.35 0.7 49.89 1491 3 2
Time(s) to settle
waveform at standstill
0.2 0.2 Not standstill Noload
0.8 &
Full load 1
variation variation

21. AUTONOMOUS MODE MICROGRID OPERATE WITH CONTROLLED GATE PULSE
THE RESPONSE OF MICROGRID SYSTEM UNDER STATIC LOAD (A) VOLTAGE
(B) CURRENT (C) REAL POWER (D) REACTIVE POWER.
(a) (b)
(c) (d)

22. THE RESPONSE OF NOLOAD SPEED AND FREQUENCY OF
MICROGRID (A)DG1 FREQUENCY(B) DG2 FREQUENCY
(C) NOLOAD SPEED.
(a) (b)
(c)

23. THE RESPONSE OF MICROGRID SYSTEM UNDER
DYNAMIC LOAD (LOAD AT J=1KGM2) (A) VOLTAGE (B)
CURRENT (C) REAL POWER (D) REACTIVE POWER.
(a) (b)
(c) (d)

24. FIGURE-5.8: THE RESPONSE OF MICRO-GRID SYSTEM WITH FULL
LOAD IM (LOAD AT J=10KGM2) (A) CURRENT (B) REAL POWER (C)
REACTIVE POWER.
(a)
(b) (c)

25. THE RESPONSE MICROGRID UNDER FULL LOAD SPEED AND
FREQUENCY (A)DG1 FREQUENCY(B) DG2 FREQUENCY (C) NO LOAD
SPEED OF IM (D) FULL LOAD SPEED OF IM
(a) (b)
(c) (d)

26. MICROGRID OPERATE AT STEADY STATE
CONDITION
(WITH CONTROLLED GATE PULSE)
Loads PARAMETERS VOLTAG
E(KV)
CURRENT
(KA)
FREQUEN
CY(Hz)
SPEED
(RPM)
P(MW) Q(MVA
R)
Static load magnitude 0.48 1.13 48.89 --- 1.5 0.85
Time in sec 0.09 0.09 0.13 ---- 0.3 0.27
Dynamic
load
Load at(J=1 kgm2) 2.4 0.4 50.15 1500 2.9 1.95
Full load(J=10
kgm2)
2.35 0.7 48.89 1491 3 2
Time in sec
(improvement of
waveform)
0.2 0.2 0.1 Noload
0.3 &
Full
load
0.6
0.3 0.3

27. IN GRID CONNECTED MODE MICROGRID OPERATE WITH CONTROLLED GATE
PULSE
THE RESPONSE OF GRID SYSTEM UNDER STATIC LOAD (A) VOLTAGE (B) CURRENT
(C) REAL POWER (D) REACTIVE POWER
(a) (b)
(c) (d)

28. DYNAMIC LOAD POWER RESPONSES OF THE GRID SYSTEM
AT LOAD J=5 KGM2 (A) VOLTAGE (B) CURRENT (C) REAL
POWER (D) REACTIVE POWER
(a) (b)
(c) (d)

29. SPEED RESPONSE OF THE SYSTEM AT LOAD J=5 KGM2
(A) WHEN IM CONNECTED WITH GRID
(B) WHEN IM CONNECTED WITH BOTH GRID WITH MICRO GRID
(a)

30. CONNECTED WITH GRID (B) LOAD CONNECTED WITH BOTH GRID
AND MICROGRID
(a)

31. THE RESPONSE OF MICROGRID SYSTEM UNDER STATIC LOAD
(A) VOLTAGE (B) CURRENT (C) REAL POWER (D) REACTIVE
POWER.
(c) (d)
(a) (b)

32. THE RESPONSE OF MICROGRID SYSTEM UNDER DYNAMIC
LOAD (A) VOLTAGE (B) CURRENT (C) REAL POWER (D)
REACTIVE POWER.
(a) (b)
(c) (d)

33. MICROGRID CONNECTED WITH MAIN GRID
Loads parameters Voltage
(kv)
current
(ka)
frequency
(hz)
speed
(rpm)
P
(mw)
Q
(mvar)
Static
load
magnitude 0.48 1.14 49.5 --- 1.45 0.87
Time of
improvement
0.15 0.2 0.1 --- 0.4 0.4
Dynamic
load
Full load(J=5
kgm2)
2.35 0.63 49.2 1498 3 1.9
Time in
sec(Improveme
nt)
0.2 0.2 0.1 0.3 0.3 0.35

34. HARDWARE IMPLEMENTATION
BLOCK DIAGRAM OF MICROGRID SYSTEM

35. SCHEMATIC DIAGRAM OF LABORATORY HARDWARE
TEST SYSTEM

36. PIC MICROCONTROLLER

37. PIC CONTROLLER PIN DIAGRAM

38. DG’S INVERTER CIRCUIT USING MOSFET
DEVICE

39. DRIVER CIRCUIT FOR INVERTER

40. HARDWARE RESULTS
LOAD GRID VOLTAGE GRID WITH MICROGRID
NO LOAD 220V 220V
STATIC LOAD 201V 219V
DYNAMIC LOAD 186V 202V
SPEED OF MOTOR 1390 RPM 1402 RPM

41. CONCLUSION
This project addressed low frequency oscillations in converter based microgrids with dynamic
loads. A complete small-signal model of a typical MV microgrid with a typical dynamic load (IM load)
has been developed. Small-signal stability analysis has revealed that the electromechanical rotor
oscillations of large IM is source of lightly damped dynamics (low frequency modes) in MV microgrid
systems yielding to and oscillatory frequency and voltage performance even under conservatively
selected low droop gains.
The large motor type loads, the dominant low frequency microgrid are highly sensitive to the
motor dynamics and droop gains. It is shown that the active power drawn by the induction motor is
highly participating in shaping the lightly damped system. This finding has been used to design a
simple and effective two DOF active damping strategy which is based on remote compensation of the
power swings. The proposed active damping controller introduces transient supplementary power angle
and voltage magnitude signals to effectively damp microgrid frequency and voltage oscillations
without affecting the steady state power sharing characteristics.
The proposed active damping controller shows robust performance under large-signal
microgrid dynamics, such as large variation in motor slip during motor starting, full load torque
step disturbance, and large voltage dips associated with motor starting. Further, the proposed active
damping controller facilitates the use of an extended range of the static droop gains, which is essential
to optimize the economic and technical aspects of microgrid operation at different operating conditions.
A theoretical analysis, simulation and experimental results have been presented to validate the
effectiveness of the proposed scheme.