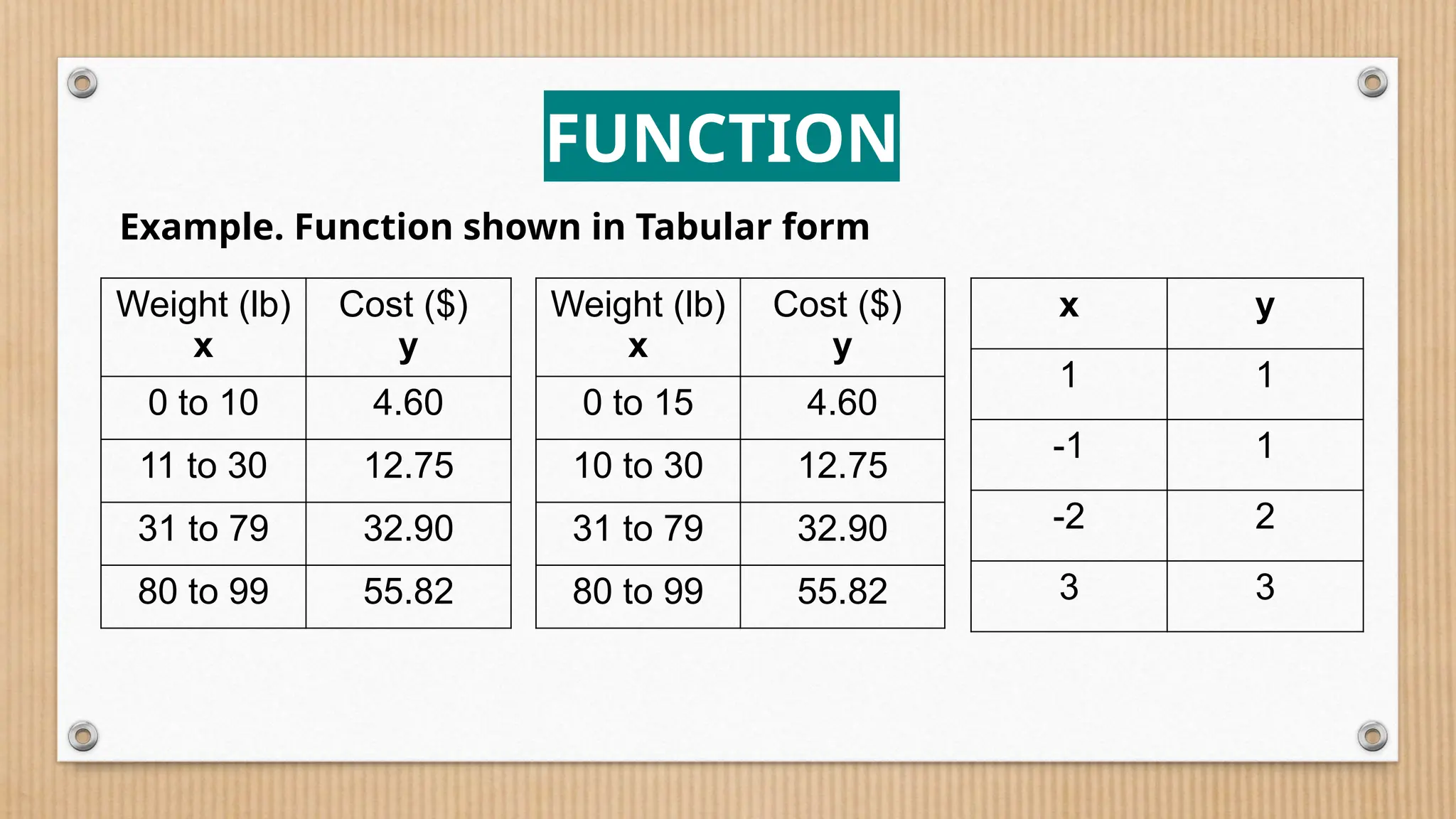
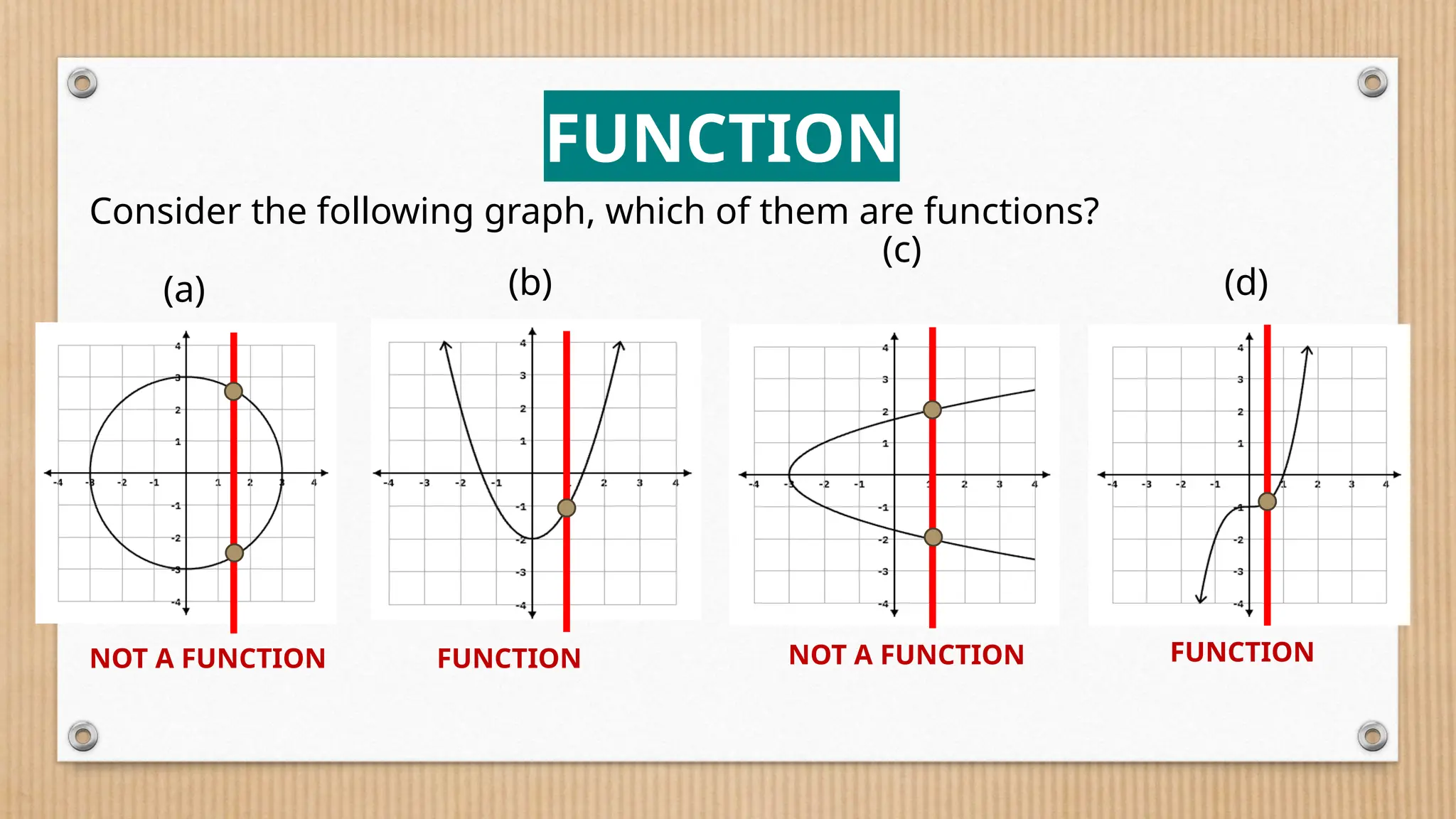
The document provides a comprehensive overview of functions, defining crucial components like domain, range, and types of functions including linear, absolute value, and quadratic functions. It explains the concept of functions as relations and describes how to determine if a relation is a function through examples and graphical representations. The document also emphasizes the importance of the vertical line test in identifying functions from their graphs.

1. Lesson 1:
Definition of Functions
Prepared by: Hannaniah S. Jimanga

2. Definition.
• A function from a set to a set is a relation with domain and range that
satisfies the following properties:
i. for every element , there is an element such that ; and
ii. for all elements and , if and , then .
• Notations: or
FUNCTION
A function is a relation in which for each value of the first
component of the ordered pairs, there is exactly one value of
the second component.

3. FUNCTION
Function as a Rule (expressed by formulas)
A function is a rule by which any allowed value of one variable ( the
independent variable) determines a unique value of a second variable (the
dependent variable).
A function is a relation between a dependent and independent variable/s
where in for every value of the independent variable, (x or input), there
exists a unique or a single value of the dependent variable, (y or output).

4. FUNCTION
Example. Function as Set of Ordered Pairs
The rule for obtaining the unique value of the dependent variable A
from the value of the dependent variable r.

5. FUNCTION
Function as Set of Ordered Pairs
A function is a set of ordered pair of real numbers such that no two
ordered pairs have the same first coordinate and different second
coordinate.
Any set of ordered pairs is called a relation. A function is a special relation.
Remark: NO two or more ordered pairs in must have the same domain.

6. FUNCTION
Example. Function as Set of Ordered Pairs
Consider the following relations from to , where and
Which of these relations are functions?
a.
Function
Not a Function
Not a Function
Function

7. FUNCTION
Function as an Equation
The solution set to an equation involving x and y is a set of
ordered pairs of the form
If there are two ordered pairs with the same first coordinates
and different second coordinates then the equation is not a
function.
Example:
1. 2. 3.
Not a Function Function Not a Function

8. FUNCTION
Function shown in Tabular form
Tables are used to provide a rule for pairing the value of one
variable with the value of another. Each value of the
independent variable must correspond to only one value of the
dependent variable.

9. FUNCTION
Example. Function shown in Tabular form
Weight (lb)
x
Cost ($)
y
0 to 10 4.60
11 to 30 12.75
31 to 79 32.90
80 to 99 55.82
Weight (lb)
x
Cost ($)
y
0 to 15 4.60
10 to 30 12.75
31 to 79 32.90
80 to 99 55.82
x y
1 1
-1 1
-2 2
3 3

10. FUNCTION
Function as a graph
Every function has a corresponding graph in the xy-plane.
NO two or more points must be intersected on the graph of a function upon
applying vertical line test.
The Vertical-Line Test
A graph is the graph of a function if and only if there is no vertical line that
crosses the graph more than once

11. (a) (b)
(c)
(d)
NOT A FUNCTION FUNCTION NOT A FUNCTION FUNCTION
FUNCTION
Consider the following graph, which of them are functions?

12. Domain and range of a Function
Domain is the set of all independent values
Range is the set of all the dependent values
Example: Give the domain and range of the relation and tell
whether it defines a function.
Not a Function
Domain: {3,4,6}
Range: {-1,2,5,8}

13. Domain and range of a Function
Domain is the set of all independent values
Range is the set of all the dependent values
Example: Give the domain and range of the relation and tell
whether it defines a function.
Function
Domain: {}
Range: {}

14. Domain and range of a Function
Domain is the set of all independent values
Range is the set of all the dependent values
Example: Give the domain and range of the relation and tell
whether it defines a function.
Not a Function
Domain: {}
Range: {}

15. Kinds of Functions and its graph
Linear Functions
A linear function is in the form
Where m and b are real numbers with .
• If then we get →constant function
• If , then we get →identity function

16. Kinds of Functions and its graph
Linear Functions
Example: Graph the following and state the domain and range.

17. Kinds of Functions and its graph
Absolute value functions
The absolute value function is the function defined by
Example: Graph the following and state its domain and range
x -2 -1 0 1 2 3
f(x) 2 1 0 1 2 3

18. Kinds of Functions and its graph
Absolute value functions
Example: Graph the following and state its domain and range
x -3 -2 -1 0 1 2 3
f(x)
x -3 -2 -1 0 1 2 3
f(x)

19. Graphs of functions and relations
Quadratic functions
A quadratic function is a function of the form
Where a, b and c are real numbers, with .
Example: Graph the function and state the domain and range.
1.
x -3 -2 -1 0 1 2 3
f(x)

20. Graphs of functions and relations
Quadratic functions
Example: Graph the function and state the domain and range.

21. Graphs of functions and relations
Square root functions
The square root function is the function defined by
Example: Graph and state its domain and range
Note: is a real number only when , then
x -3 -2 -1 0 1 2 3
f(x)

22. Graphs of functions and relations
Square root functions
Example: Graph the function and state the domain and range.

23. Graphs of functions and relations
Graphing Relations
Example: Graph the following and state its domain and range
Since the equations expresses x in terms of y, it is easier to choose the
white coordinate first.
x
y -3 -2 -1 0 1 2 3

24. Graphs of functions and relations
Graphing Relations
Example: Graph the following and state its domain and range