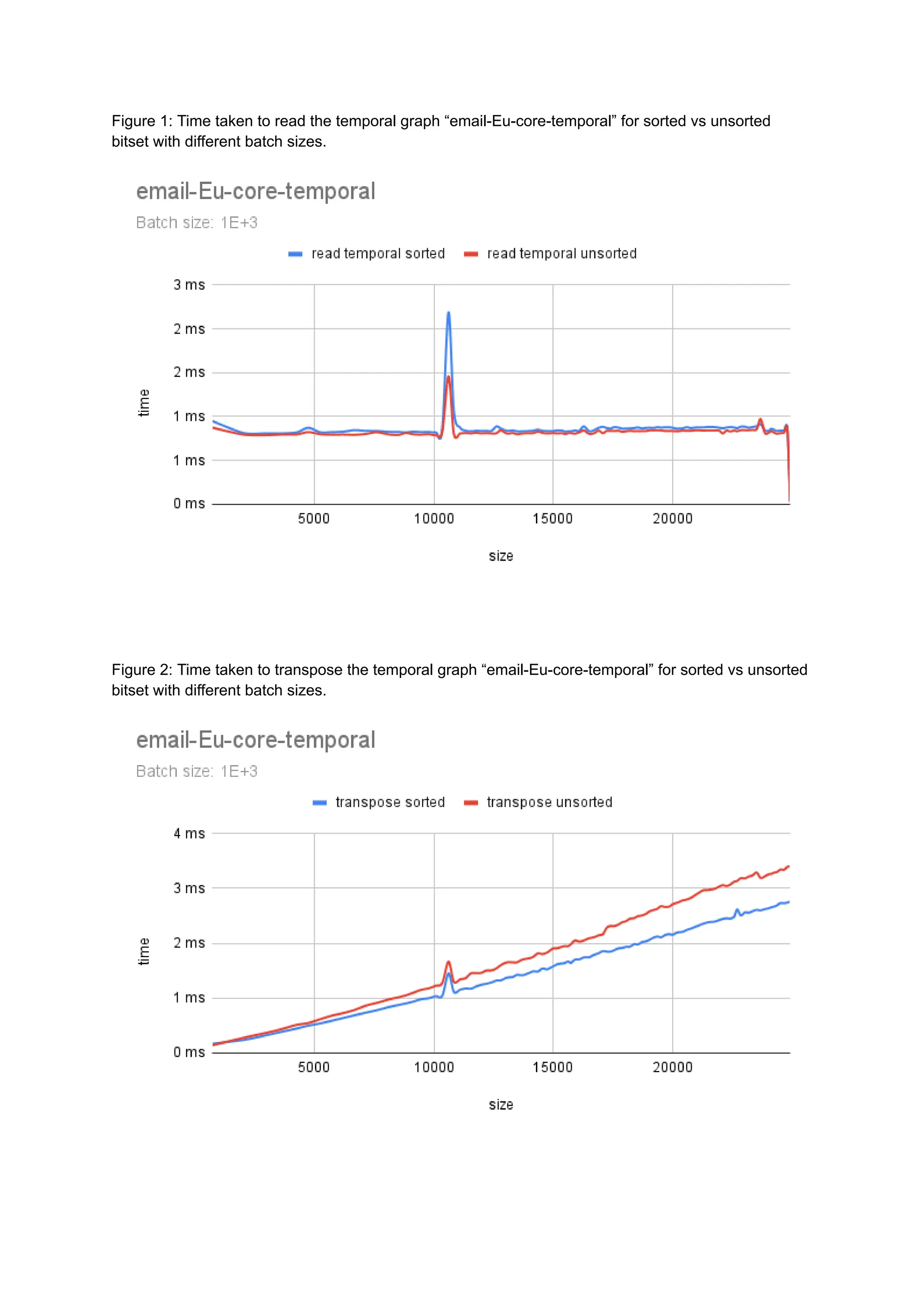
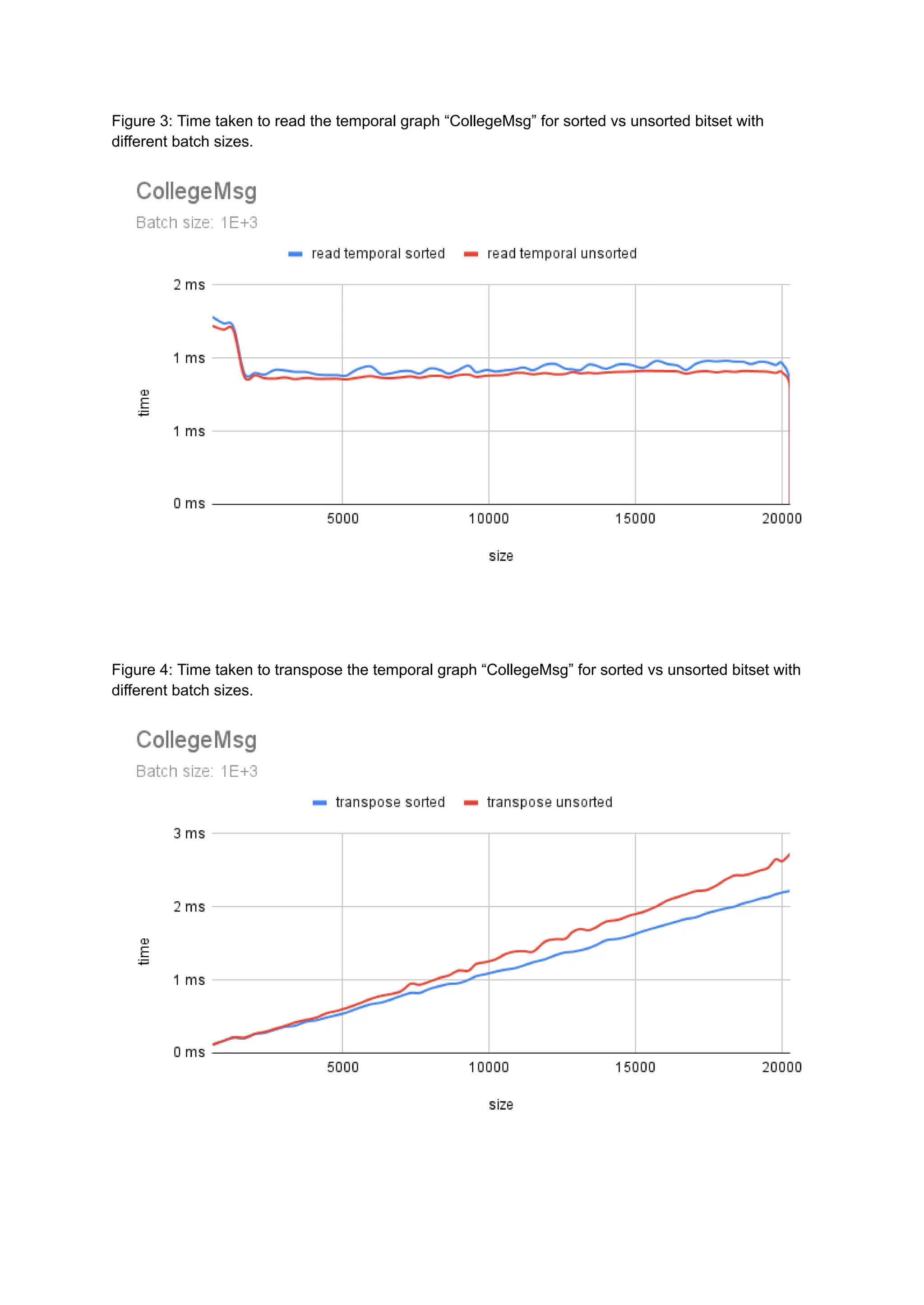
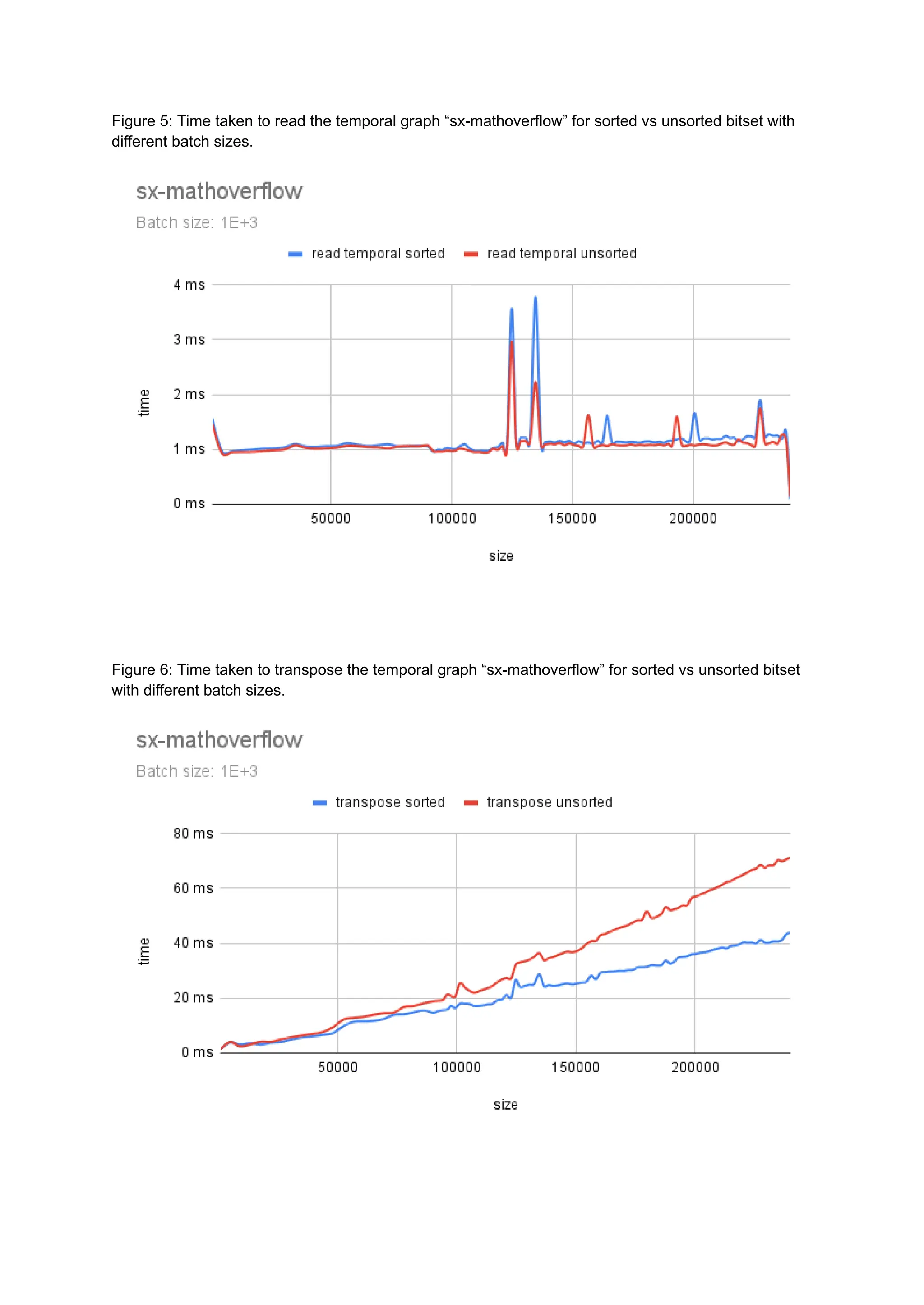
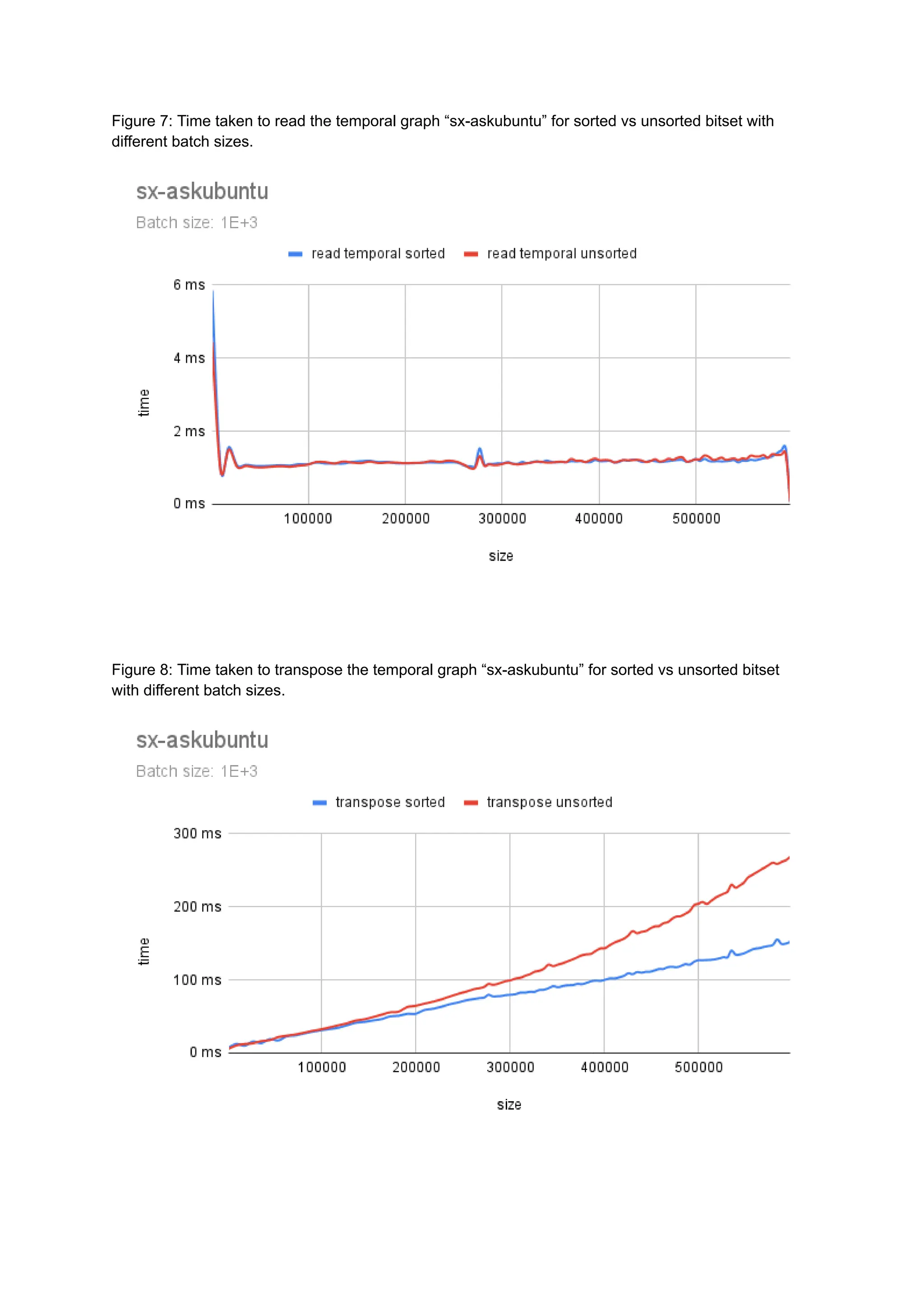
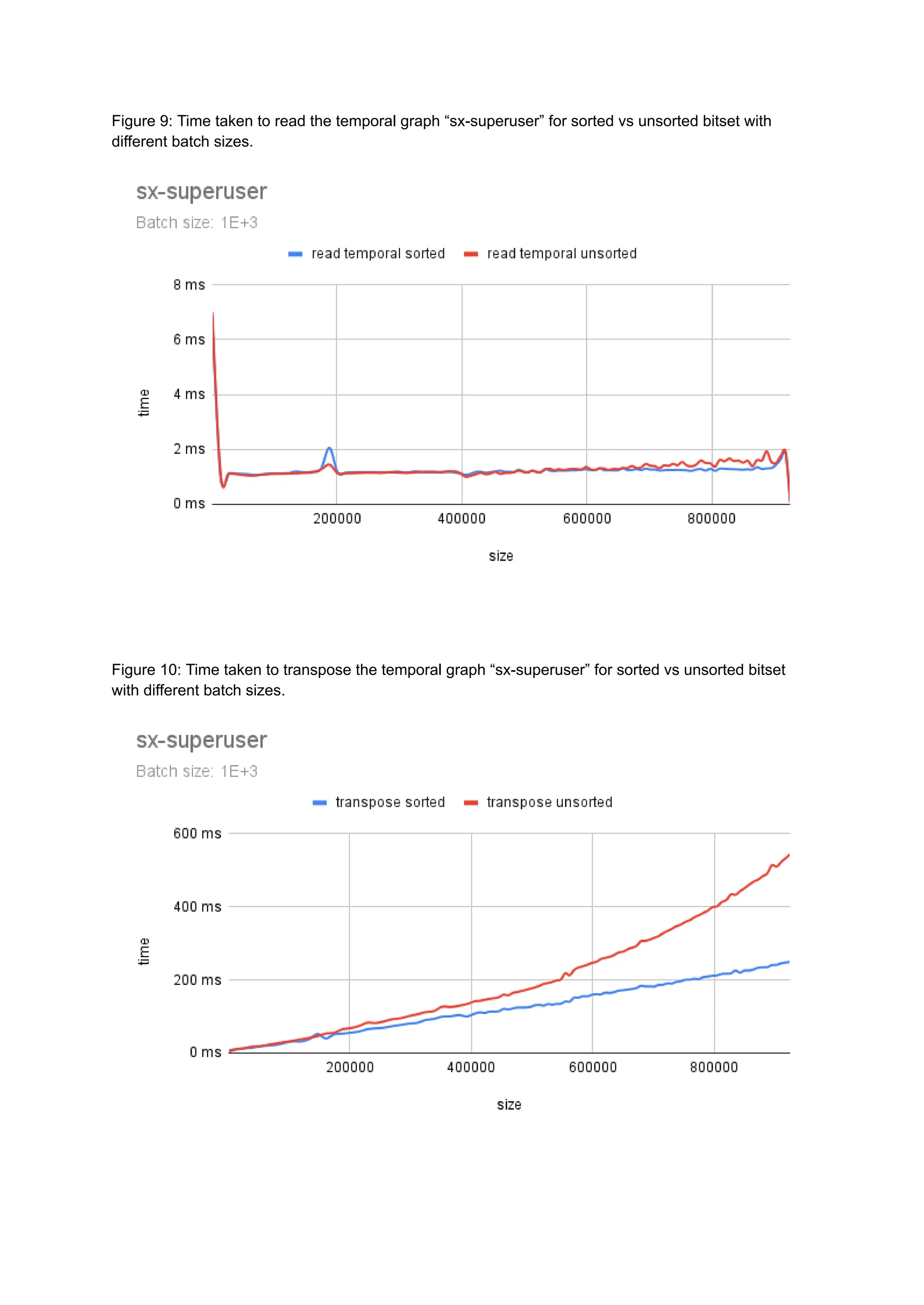
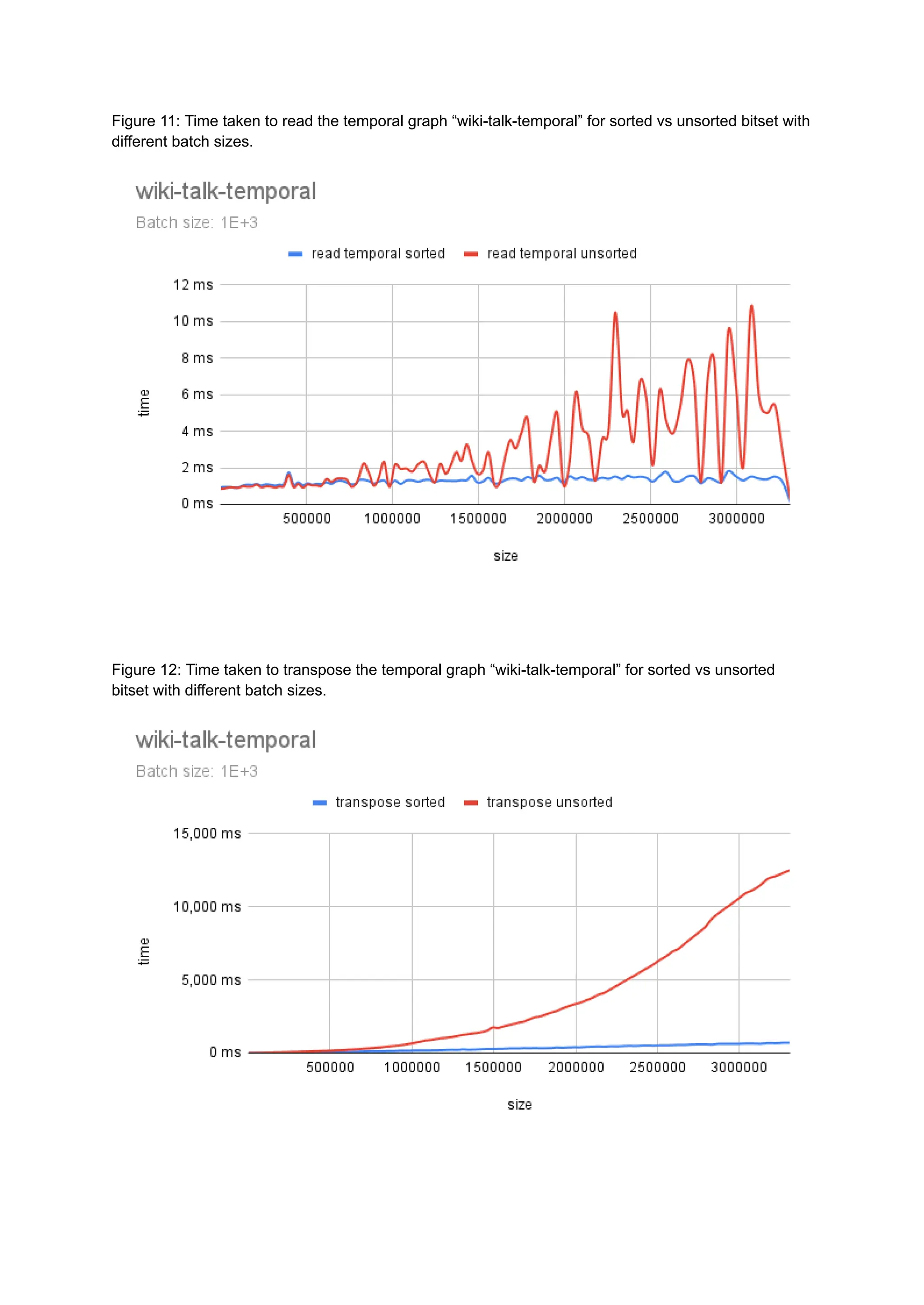
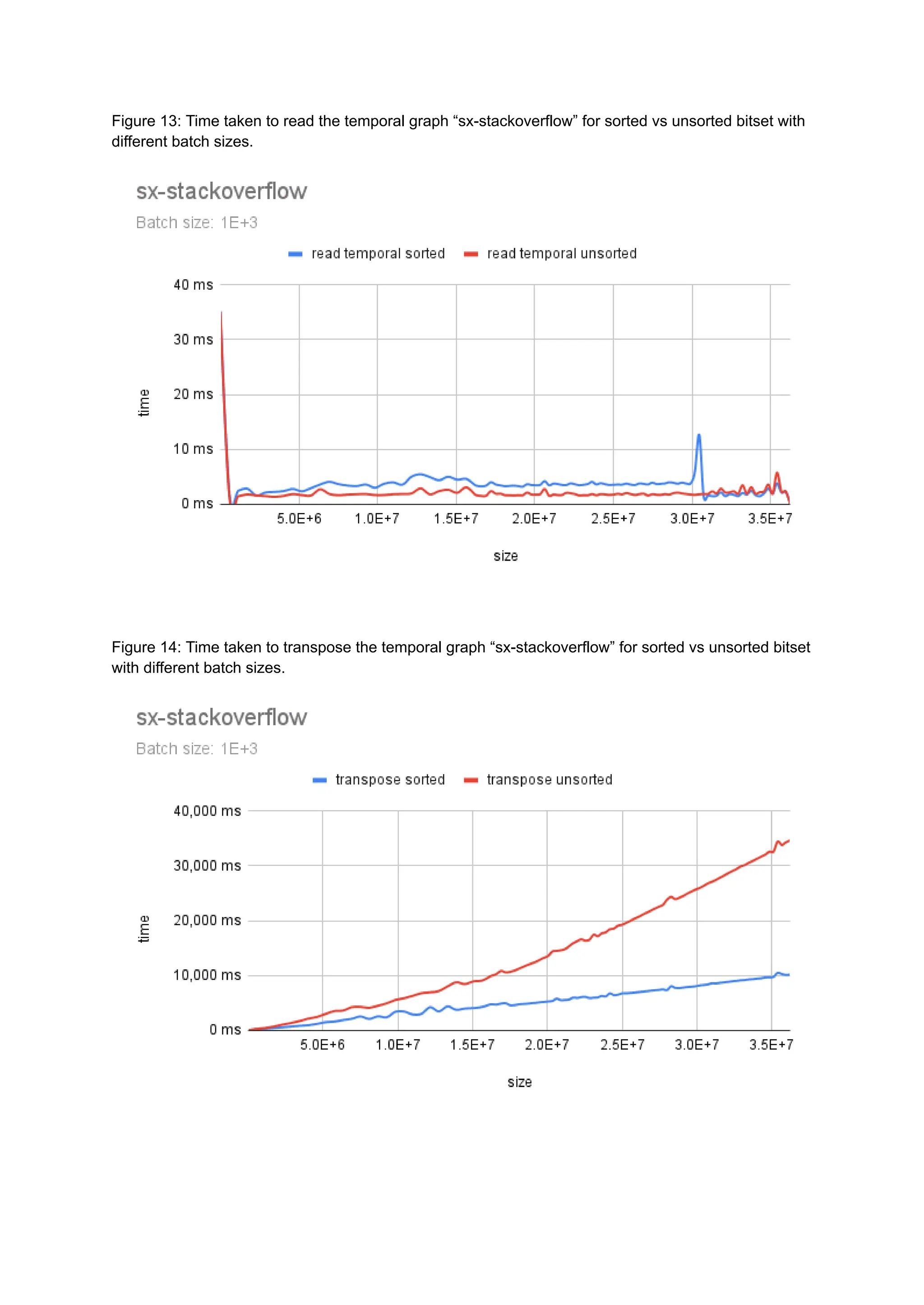
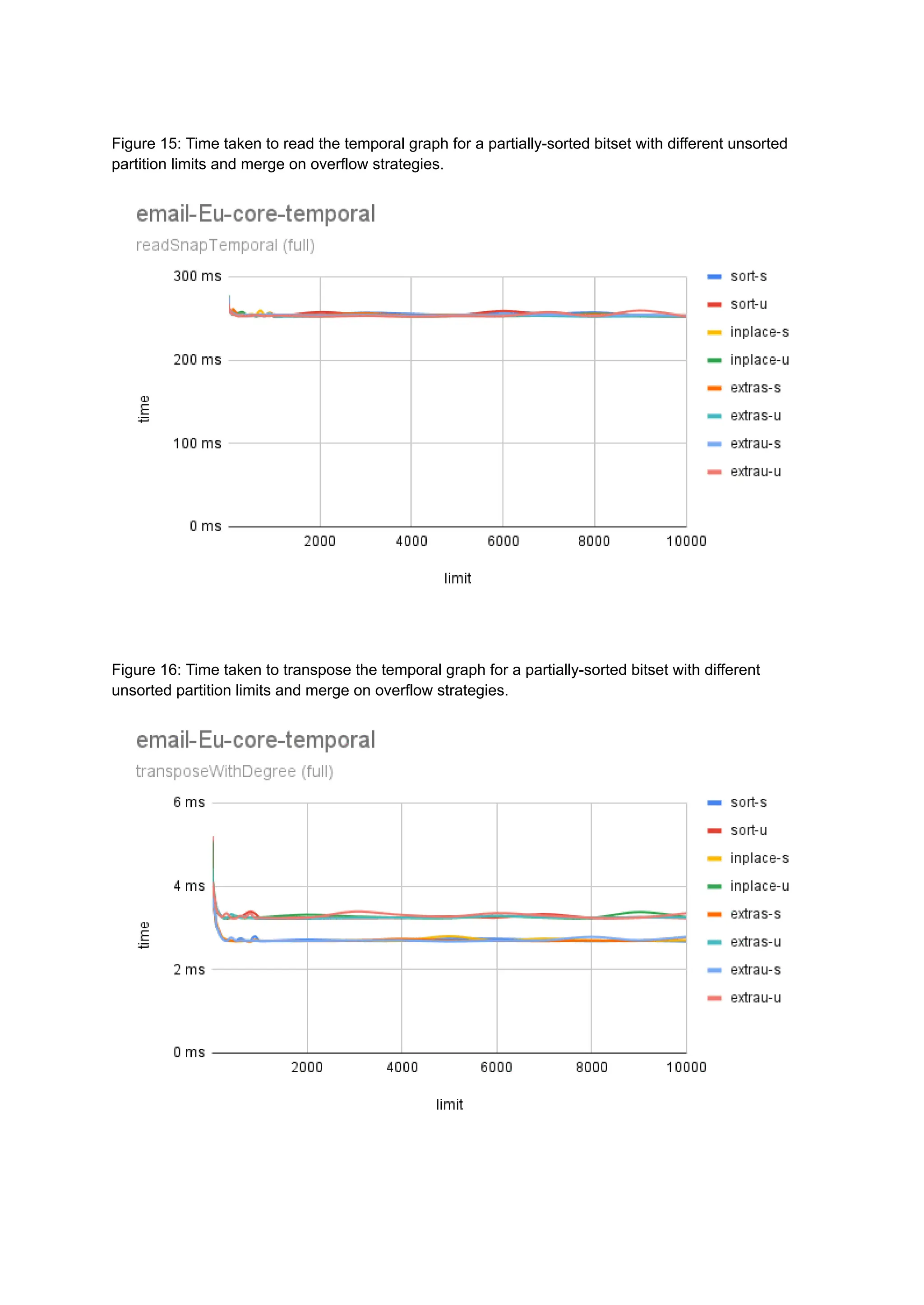
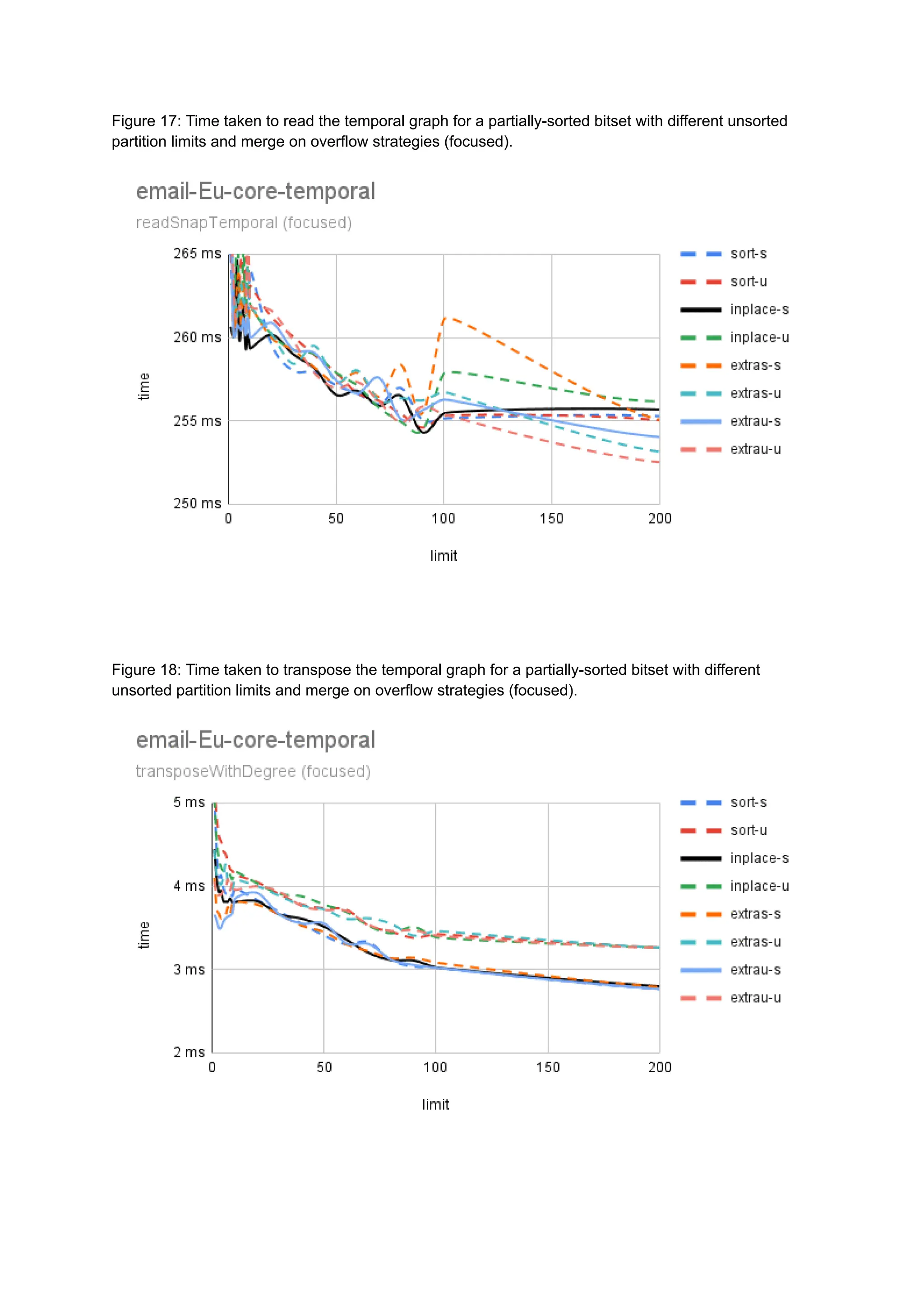
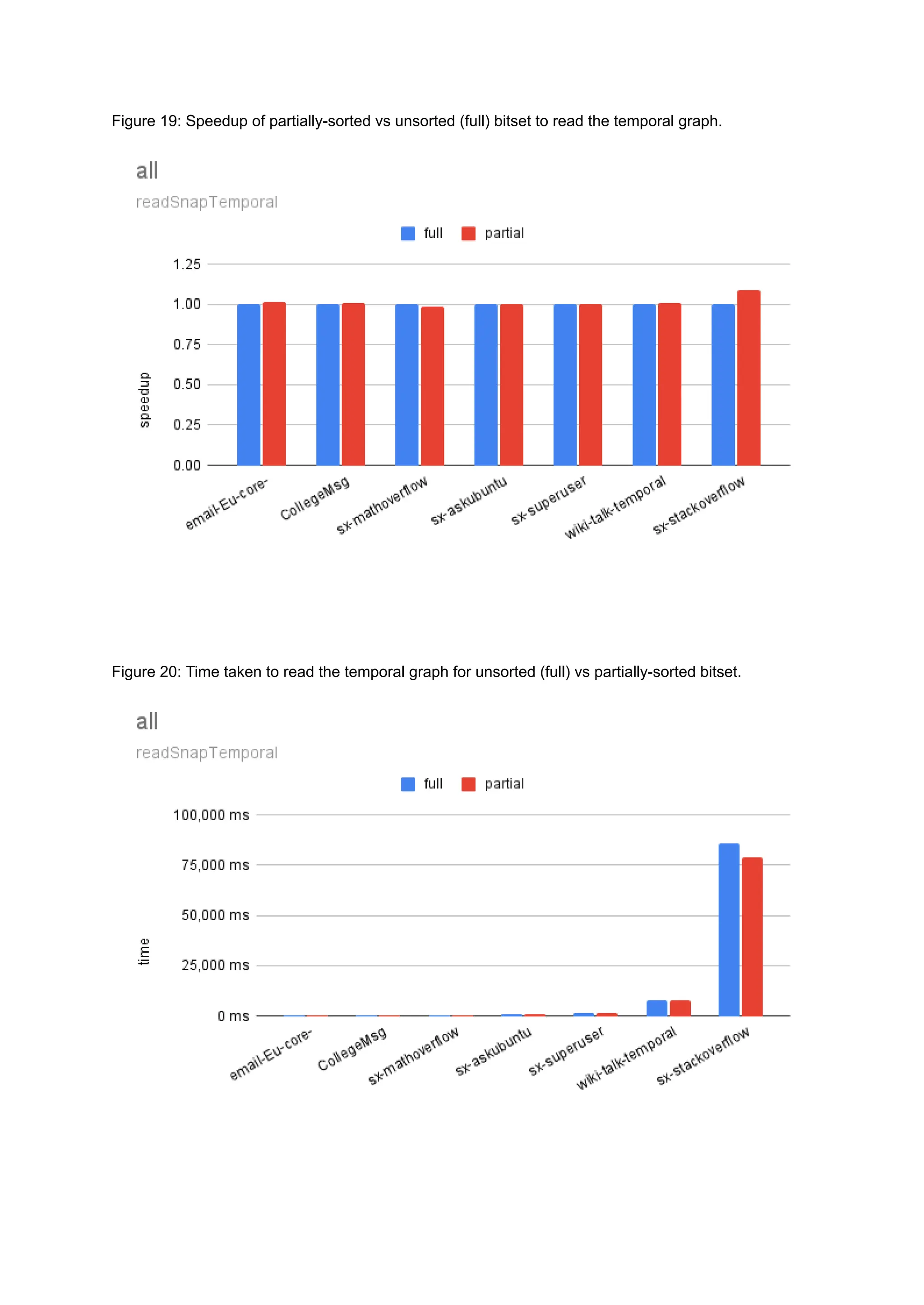
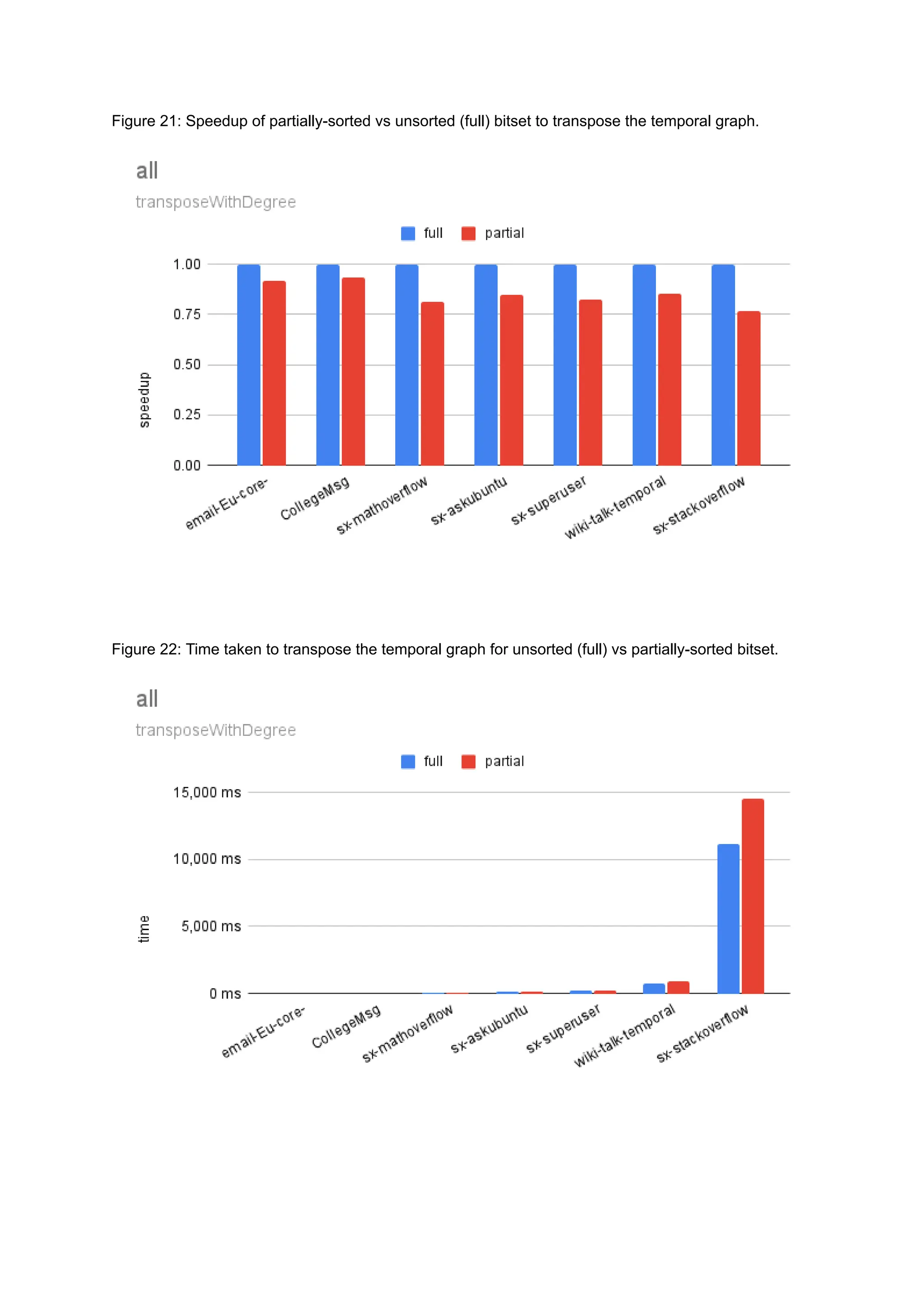
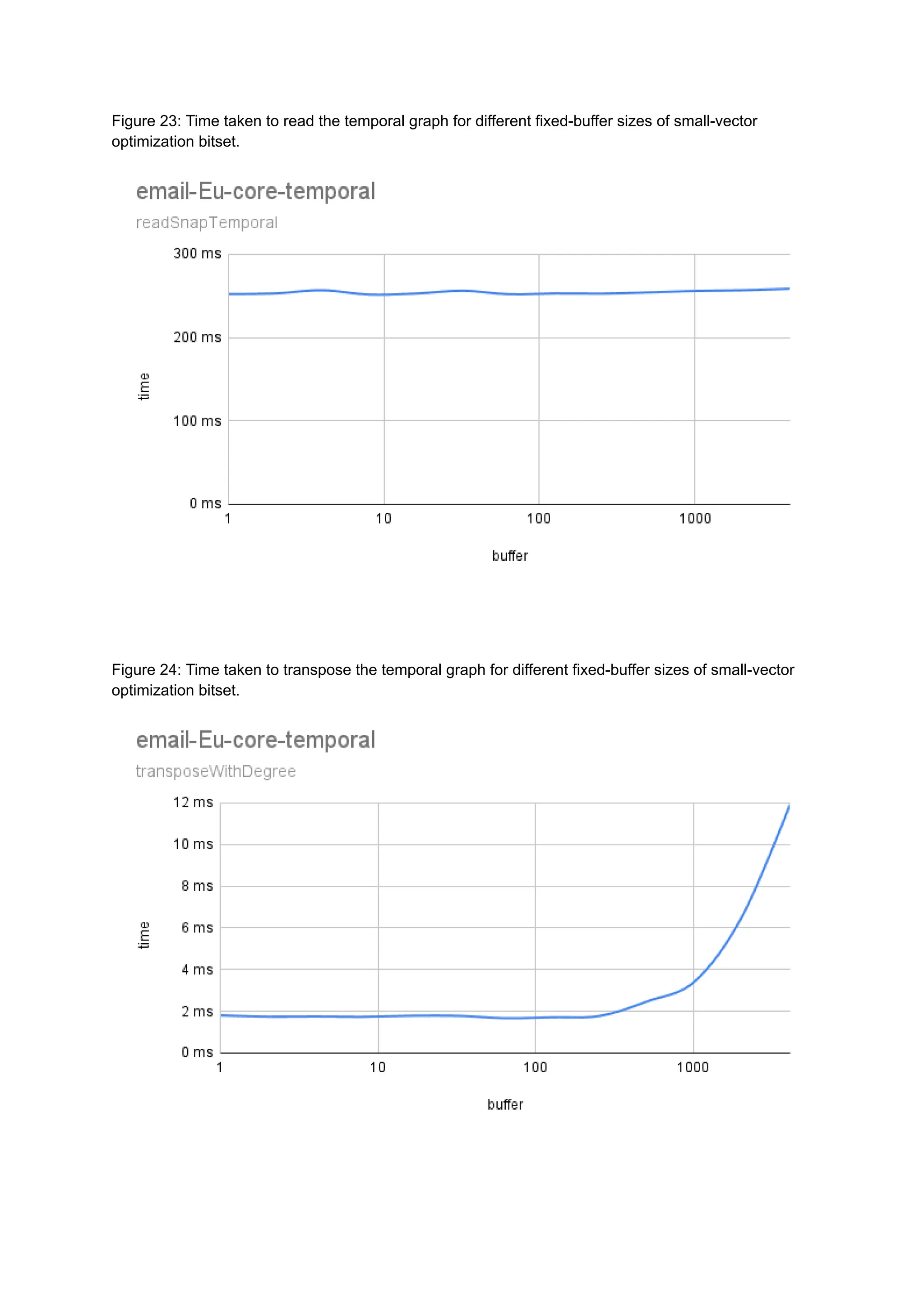
The document discusses the inefficiencies of using Compressed Sparse Row (CSR) representation for dynamic graphs, particularly in terms of memory access during edge addition and deletion. Different data structures for representing edge-lists, such as sorted and unsorted bitsets, were evaluated through experiments conducted on real-world temporal graphs, revealing performance variances depending on the structure and operations performed. The results indicate that sorted bitsets often outperform unsorted ones for specific tasks, while small-vector optimizations were found to provide minimal benefits due to memory allocation issues.

1. Adjusting Bitset for graph
Compressed Sparse Row (CSR) is an adjacency-list based graph representation that is
commonly used for efficient graph computations. Unfortunately, using CSR for dynamic
graphs is impractical since addition/deletion of a single edge can require on average
(N+M)/2 memory accesses, in order to update source-offsets and destination-indices. A
common approach is therefore to store edge-lists/destination-indices as an array of arrays,
where each edge-list is an array belonging to a vertex. While this is good enough for small
graphs, it quickly becomes a bottleneck for large graphs. What causes this bottleneck
depends on whether the edge-lists are sorted or unsorted. If they are sorted, checking for
an edge requires about log(E) memory accesses, but adding an edge on average requires
E/2 accesses, where E is the number of edges of a given vertex. Note that both addition and
deletion of edges in a dynamic graph require checking for an existing edge, before adding or
deleting it. If edge lists are unsorted, checking for an edge requires around E/2 memory
accesses, but adding an edge requires only 1 memory access.
An experiment was conducted in an attempt to find a suitable data structure for
representing bitset, which can be used to represent edge-lists of a graph. The data
structures under test include single-buffer ones like unsorted bitset, and sorted bitset;
single-buffer partitioned (by integers) like partially-sorted bitset; and multi-buffer ones like
small-vector optimization bitset (unsorted), and 16-bit subrange bitset (todo). An unsorted
bitset consists of a vector (in C++) that stores all the edge ids in the order they arrive. Edge
lookup consists of a simple linear search. Edge addition is a simple push-back (after lookup).
Edge deletion is a vector-delete, which requires all edge-ids after it to be moved back (after
lookup). A sorted bitset maintains edge ids sorted in ascending order of edge ids. Edge
lookup consists of a binary search. Edge addition is a vector-insert, which requires all
edge-ids after it to be shifted one step ahead. Edge deletion is a vector-delete, just like
unsorted bitset. A partially-sorted bitset tries to amortize the cost of sorting edge-ids by
keeping the recently added edges unsorted at the end (upto a limit) and maintains the old
edges as sorted. Edge lookup consists of binary search in the sorted partition, and then
linear search in the unsorted partition, or the other way around. Edge addition is usually a
simple push-back and updating of partition size. However, if the unsorted partition grows
beyond a certain limit, it is merged with the sorted partition in one of the following ways: sort
both partitions as a whole, merge partitions using in-place merge, merge partitions using
extra space for sorted partition, or merge partitions using extra space for unsorted partition
(this requires a merge from the back end). Edge deletion checks to see if the edge can be
brought into the unsorted partition (within limit). If so, it simply swaps it out with the last
unsorted edge id (and updates partition size). However, if it cannot be brought into the
unsorted partition a vector-delete is performed (again, updating partition size). A
small-vector optimization bitset (unsorted) makes use of an additional fixed-size buffer
(this size is adjusted to different values) to store edge-ids until this buffer overflows, when all
edge-ids are moved to a dynamic (heap-allocated) vector. Edge lookups, additions, and
deletions are similar to that of an unsorted bitset, except that count of edge-ids in the
fixed-size buffer and the selection of buffer or dynamic vector needs to be done with each
operation.

2. All variants of the data structures were tested with real-world temporal graphs. These are
stored in a plain text file in “u, v, t” format, where u is the source vertex, v is the destination
vertex, and t is the UNIX epoch time in seconds. All of them are obtained from the Stanford
Large Network Dataset Collection. The experiment is implemented in C++, and compiled
using GCC 9 with optimization level 3 (-O3). The system used is a Dell PowerEdge R740
Rack server with two Intel Xeon Silver 4116 CPUs @ 2.10GHz, 128GB DIMM DDR4
Synchronous Registered (Buffered) 2666 MHz (8x16GB) DRAM, and running CentOS Linux
release 7.9.2009 (Core). The execution time of each test case is measured using
std::chrono::high_performance_timer. This is done 5 times for each test case, and timings
are averaged. Statistics of each test case is printed to standard output (stdout), and
redirected to a log file, which is then processed with a script to generate a CSV file, with
each row representing the details of a single test case. This CSV file is imported into Google
Sheets, and necessary tables are set up with the help of the FILTER function to create the
charts. Similar charts are combined together into a single GIF (to help with interpretation of
results).
From the results, it appears that transpose of graphs based on sorted bitset is clearly faster
than the unsorted bitset. However, with reading graph edges there is no clear winner
(sometimes sorted is faster especially for large graphs, and sometimes unsorted). Maybe
when new edges have many duplicates, inserts are less, and hence sorted version is faster
(since sorted bitset has slow insert time). Transpose of a graph based on a fully-sorted bitset
is clearly faster than the partially-sorted bitset. This is possibly because partially sorted
bitset based graphs cause higher cache misses due to random accesses (while reversing
edges). However, with reading graph edges there is no clear winner (sometimes
partially-sorted is faster especially for large graphs, and sometimes fully-sorted). For
small-vector optimization bitset, on average, a buffer size of 4 seems to give small
improvement. Any further increase in buffer size slows down performance. This is possibly
because of unnecessarily large contiguous memory allocation needed by the buffer, and low
cache-hit percent due to widely separated edge data (due to the static buffer). In fact it even
crashes when 26 instances of graphs with varying buffer sizes can't all be held in memory.
Hence, small vector optimization is not so useful, at least when used for graphs.
Table 1: List of data structures for bitset attempted, followed by list of programs inc. results & figures.
single-buffer single-buffer partitioned multi-buffer
unsorted partially-sorted (vs) small-vector (optimization)
sorted subrange-16bit
1. Testing the effectiveness of sorted vs unsorted list of integers for BitSet.
2. Comparing various unsorted sizes for partially sorted BitSet.
3. Performance of fully sorted vs partially sorted BitSet (inplace-s128).
4. Comparing various buffer sizes for BitSet with small vector optimization.
5. Comparing various switch points for 16-bit subrange based BitSet.

3. Figure 1: Time taken to read the temporal graph “email-Eu-core-temporal” for sorted vs unsorted
bitset with different batch sizes.
Figure 2: Time taken to transpose the temporal graph “email-Eu-core-temporal” for sorted vs unsorted
bitset with different batch sizes.

4. Figure 3: Time taken to read the temporal graph “CollegeMsg” for sorted vs unsorted bitset with
different batch sizes.
Figure 4: Time taken to transpose the temporal graph “CollegeMsg” for sorted vs unsorted bitset with
different batch sizes.

5. Figure 5: Time taken to read the temporal graph “sx-mathoverflow” for sorted vs unsorted bitset with
different batch sizes.
Figure 6: Time taken to transpose the temporal graph “sx-mathoverflow” for sorted vs unsorted bitset
with different batch sizes.

6. Figure 7: Time taken to read the temporal graph “sx-askubuntu” for sorted vs unsorted bitset with
different batch sizes.
Figure 8: Time taken to transpose the temporal graph “sx-askubuntu” for sorted vs unsorted bitset
with different batch sizes.

7. Figure 9: Time taken to read the temporal graph “sx-superuser” for sorted vs unsorted bitset with
different batch sizes.
Figure 10: Time taken to transpose the temporal graph “sx-superuser” for sorted vs unsorted bitset
with different batch sizes.

8. Figure 11: Time taken to read the temporal graph “wiki-talk-temporal” for sorted vs unsorted bitset with
different batch sizes.
Figure 12: Time taken to transpose the temporal graph “wiki-talk-temporal” for sorted vs unsorted
bitset with different batch sizes.

9. Figure 13: Time taken to read the temporal graph “sx-stackoverflow” for sorted vs unsorted bitset with
different batch sizes.
Figure 14: Time taken to transpose the temporal graph “sx-stackoverflow” for sorted vs unsorted bitset
with different batch sizes.

10. Figure 15: Time taken to read the temporal graph for a partially-sorted bitset with different unsorted
partition limits and merge on overflow strategies.
Figure 16: Time taken to transpose the temporal graph for a partially-sorted bitset with different
unsorted partition limits and merge on overflow strategies.

11. Figure 17: Time taken to read the temporal graph for a partially-sorted bitset with different unsorted
partition limits and merge on overflow strategies (focused).
Figure 18: Time taken to transpose the temporal graph for a partially-sorted bitset with different
unsorted partition limits and merge on overflow strategies (focused).

12. Figure 19: Speedup of partially-sorted vs unsorted (full) bitset to read the temporal graph.
Figure 20: Time taken to read the temporal graph for unsorted (full) vs partially-sorted bitset.

13. Figure 21: Speedup of partially-sorted vs unsorted (full) bitset to transpose the temporal graph.
Figure 22: Time taken to transpose the temporal graph for unsorted (full) vs partially-sorted bitset.

14. Figure 23: Time taken to read the temporal graph for different fixed-buffer sizes of small-vector
optimization bitset.
Figure 24: Time taken to transpose the temporal graph for different fixed-buffer sizes of small-vector
optimization bitset.