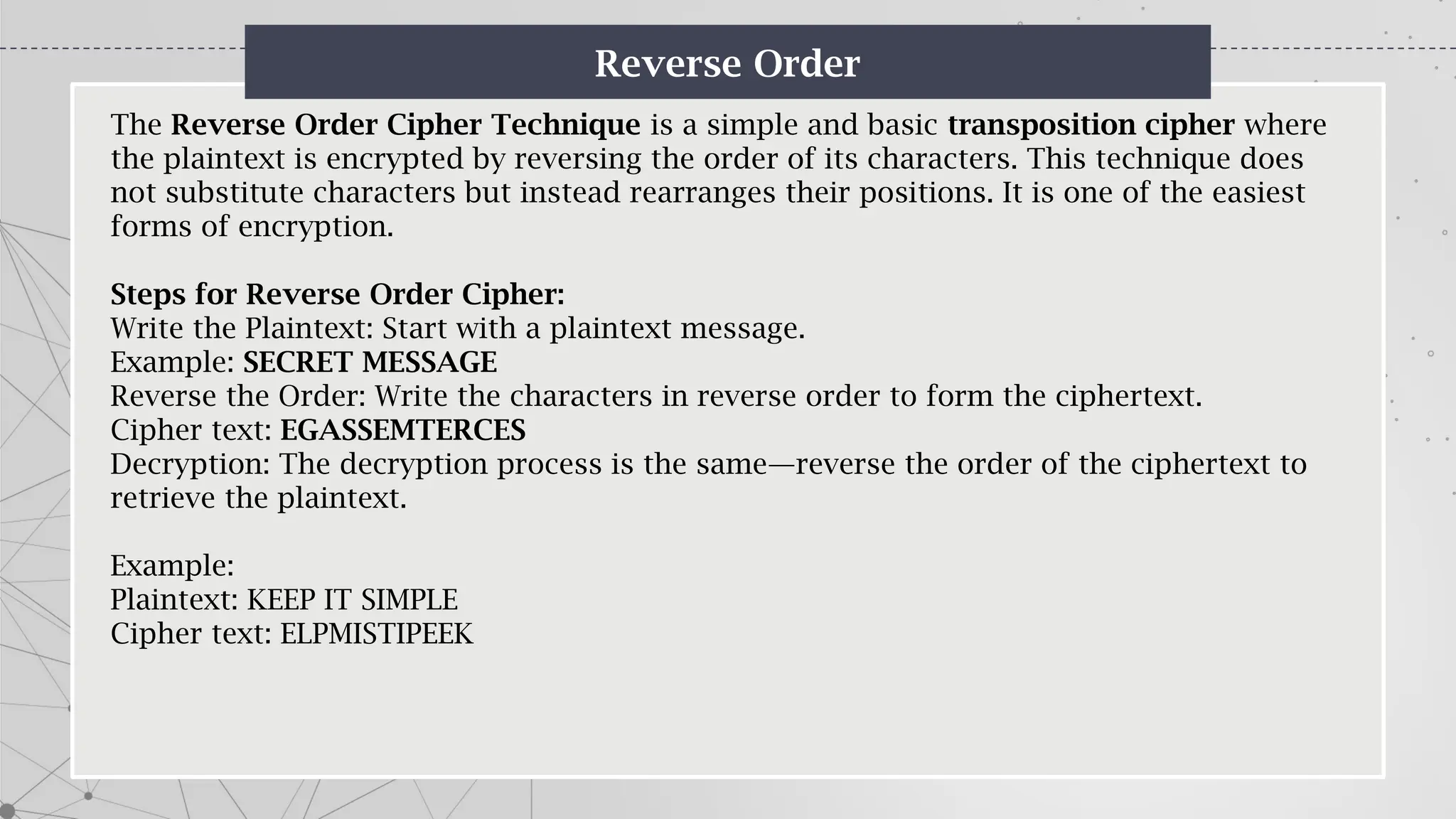
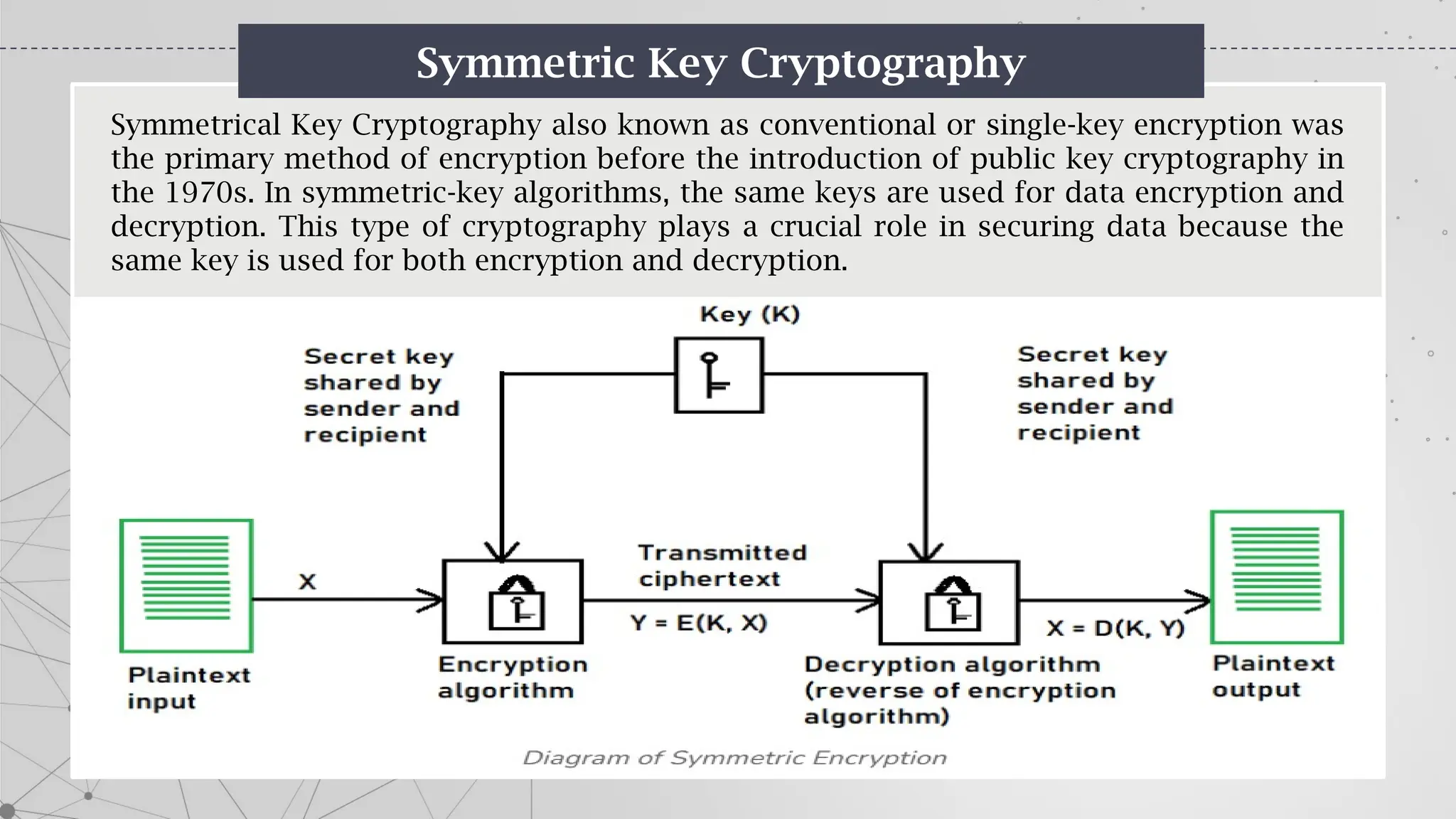
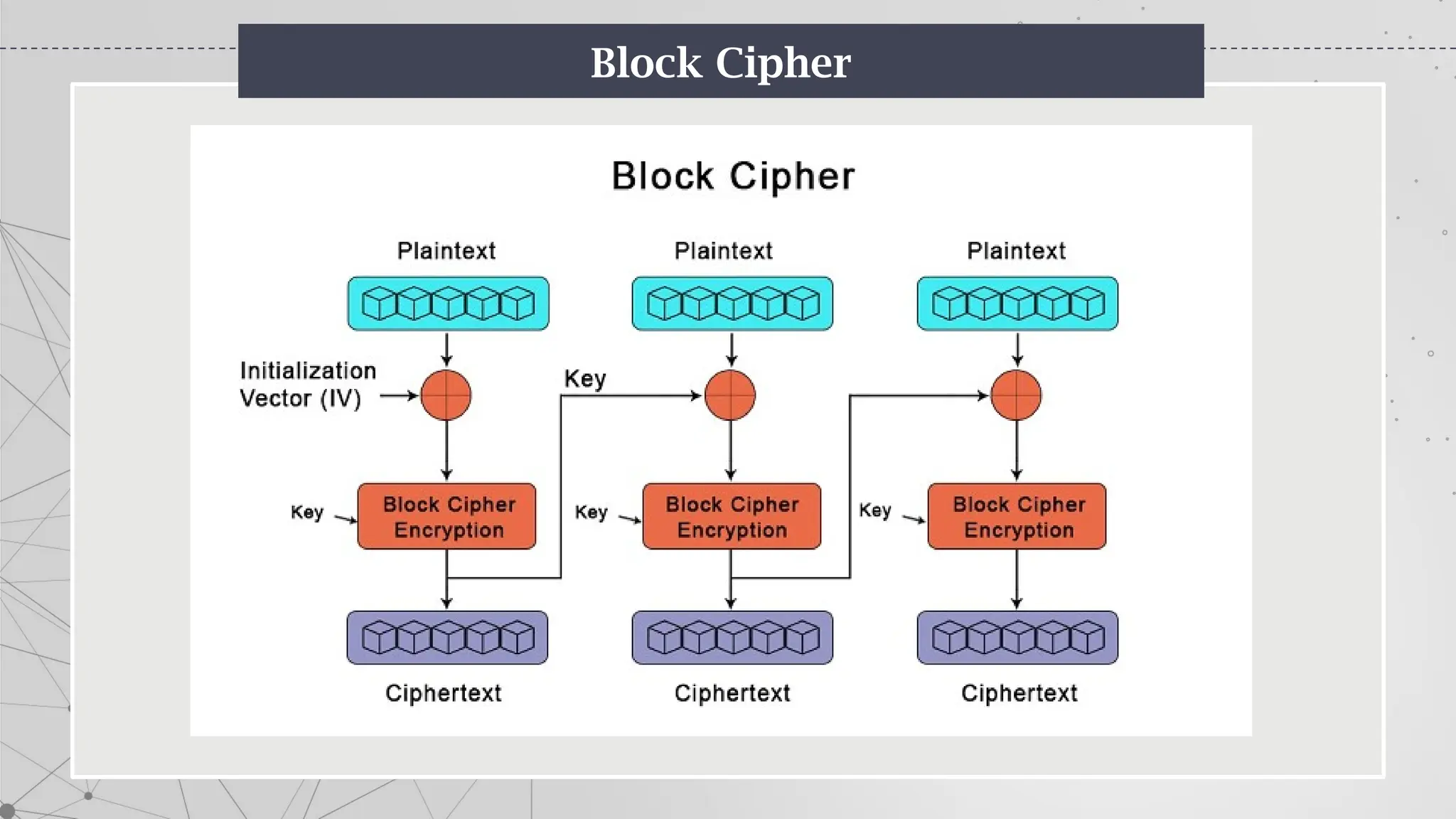
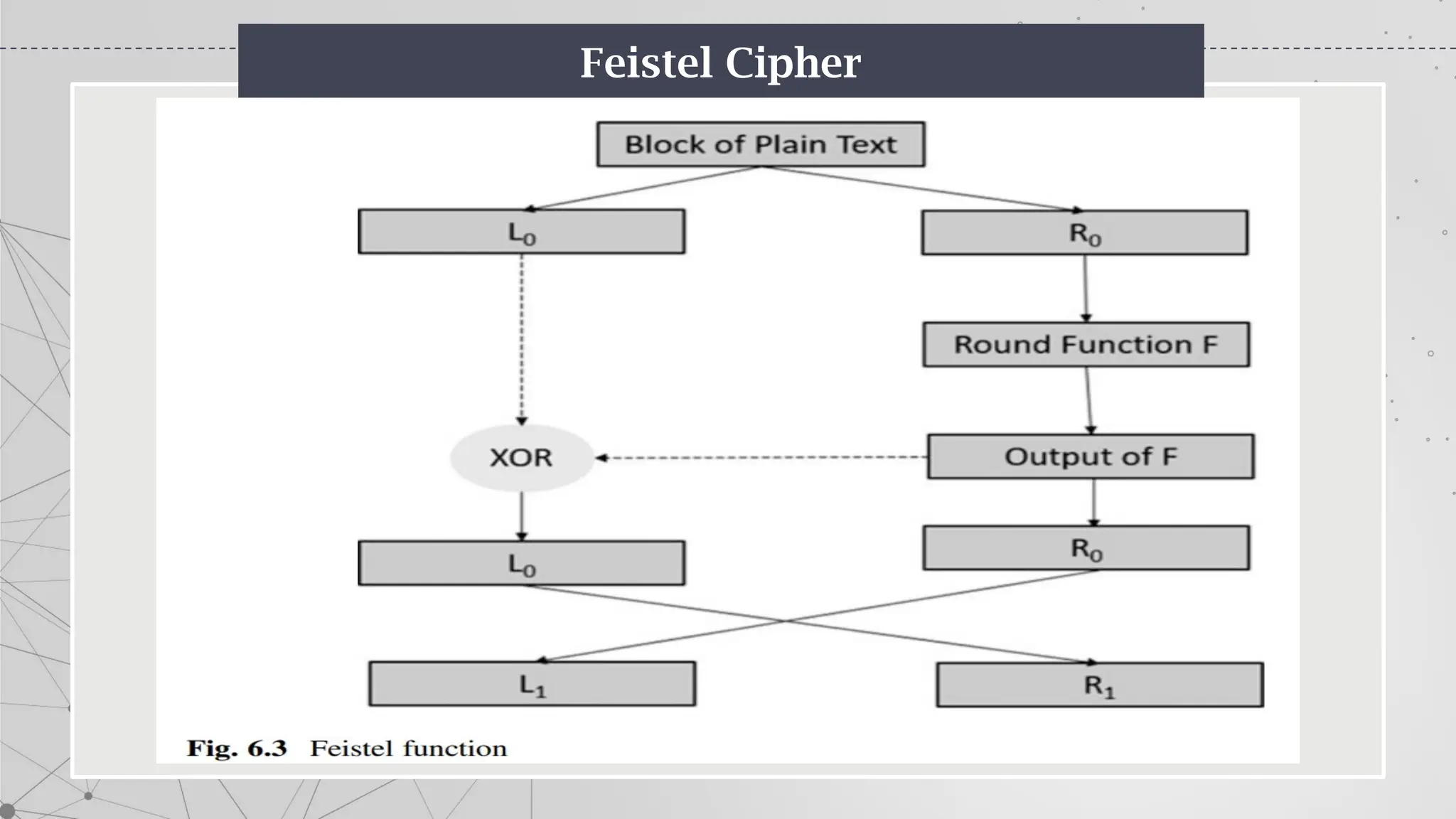
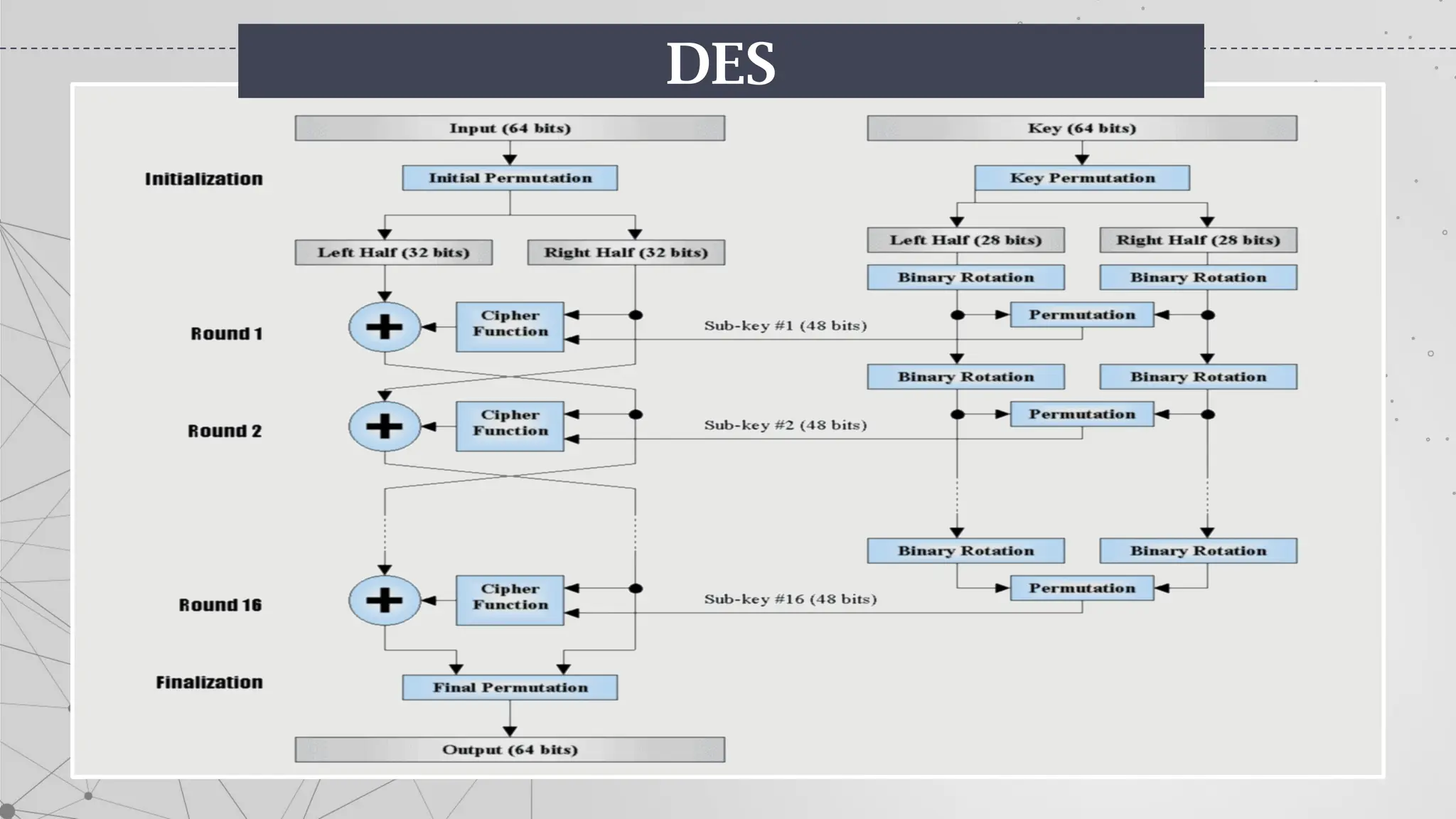
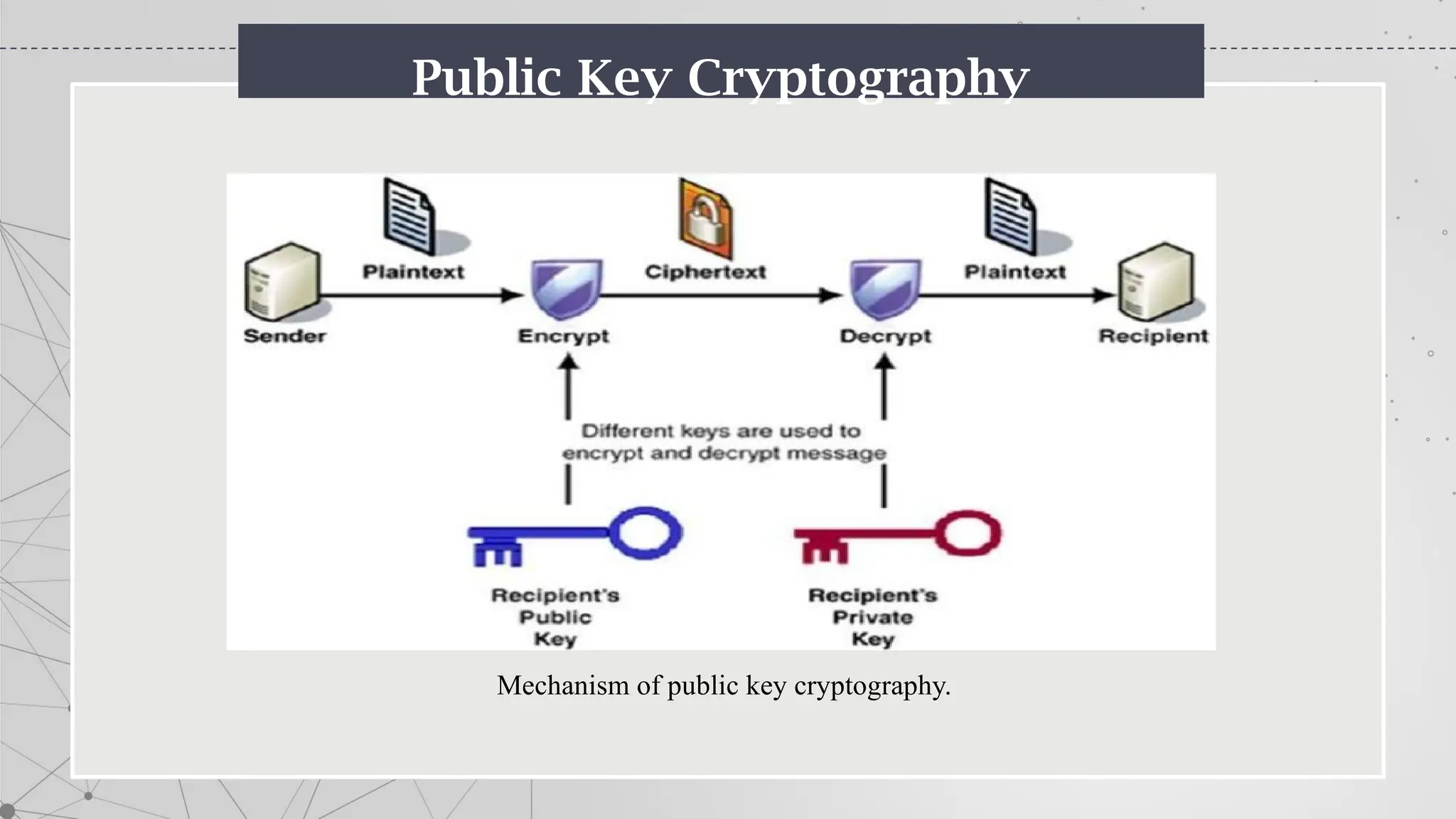
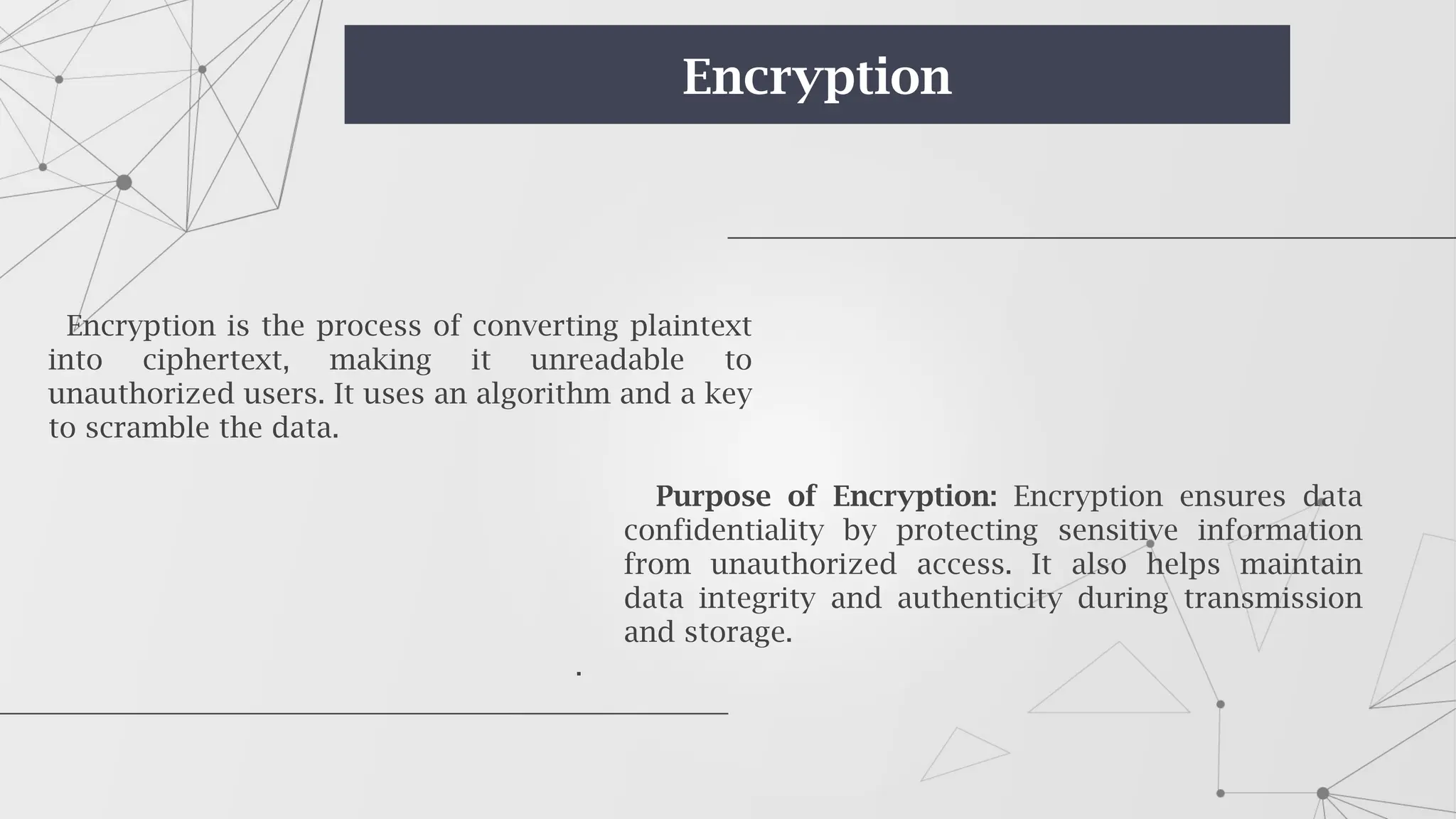
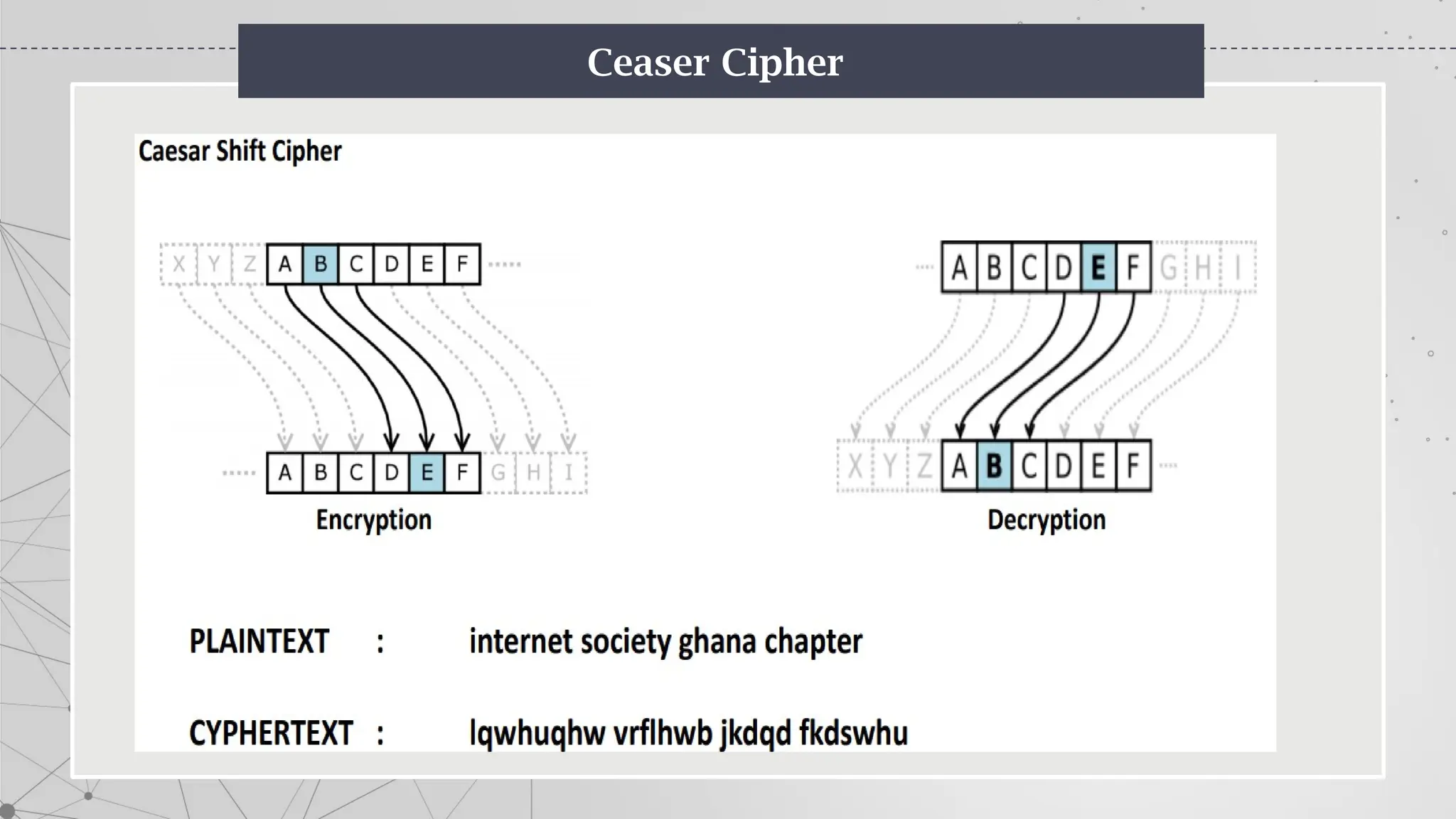
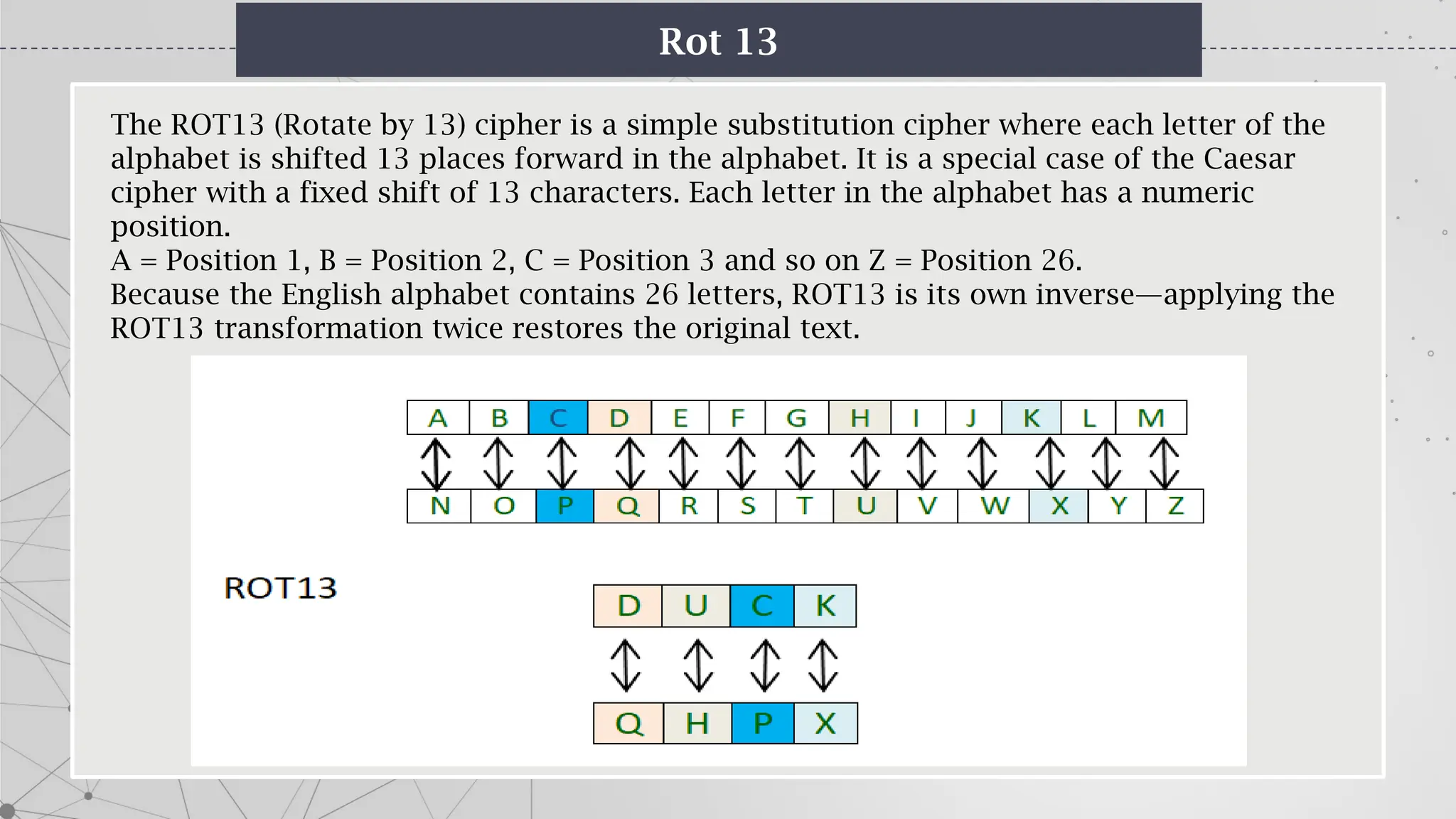
The document is an introduction to cryptography, covering basic terminologies, techniques, and historical background. It explains key concepts such as encryption and decryption, types of cryptography (symmetric and asymmetric), and various ciphers including the Caesar, Vigenère, and Playfair ciphers. Additionally, it outlines the role of cryptography in secure communication and the evolution of its methods throughout history.





































![Hill Cipher
Example:
1. Key Matrix (2×2):
2. K=[]
3. Plaintext (2-letter blocks): "HI“ (78)
Numerical equivalent: P=[
4. Encrypt:
C=(K P)mod 26
⋅
C= [ [ 26
⋅
C= mod 26
C=[
C=](https://image.slidesharecdn.com/4-250119144830-2fb991ad/75/4-IS-Mohsin-pptx-41-2048.jpg)