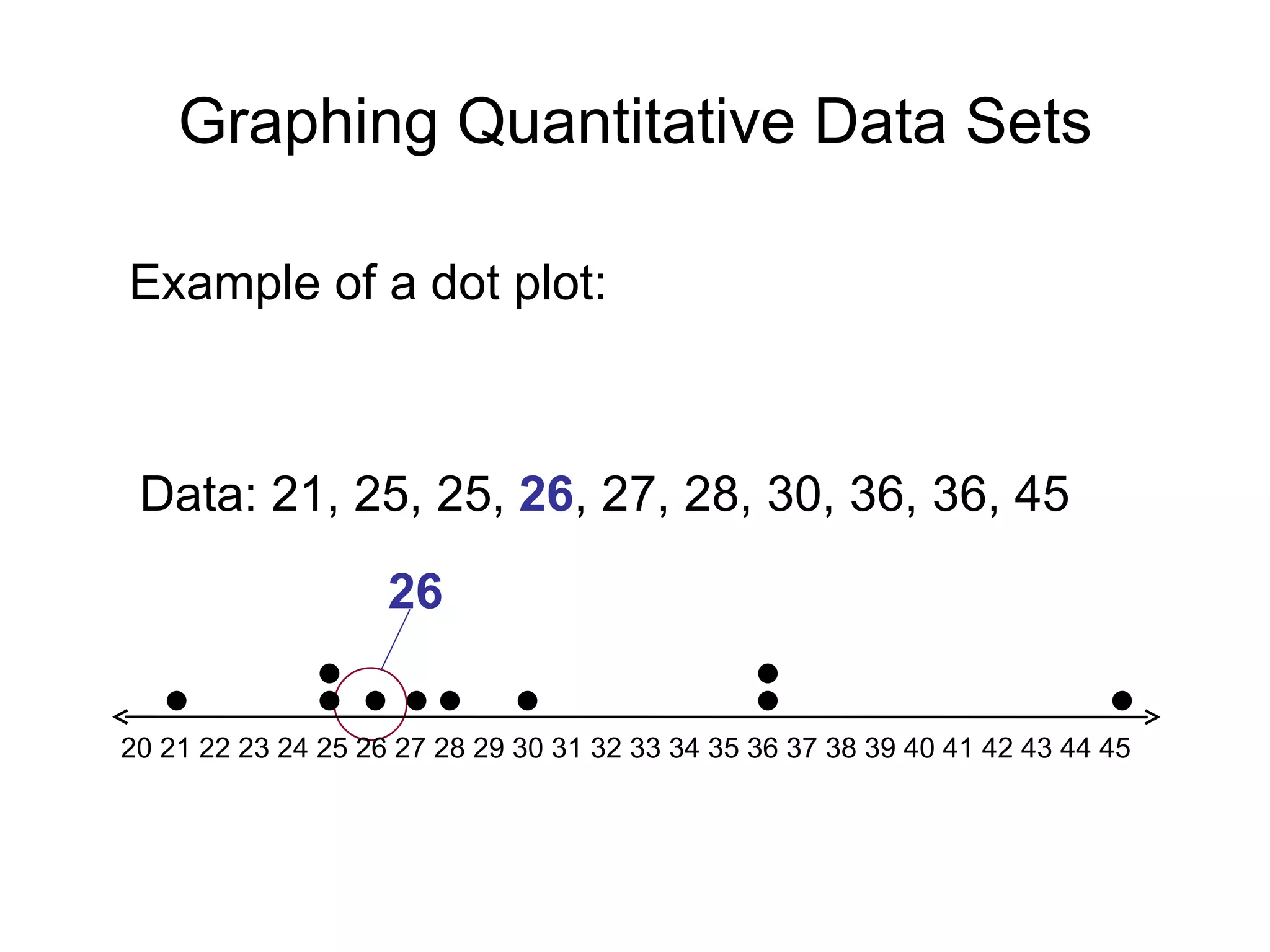
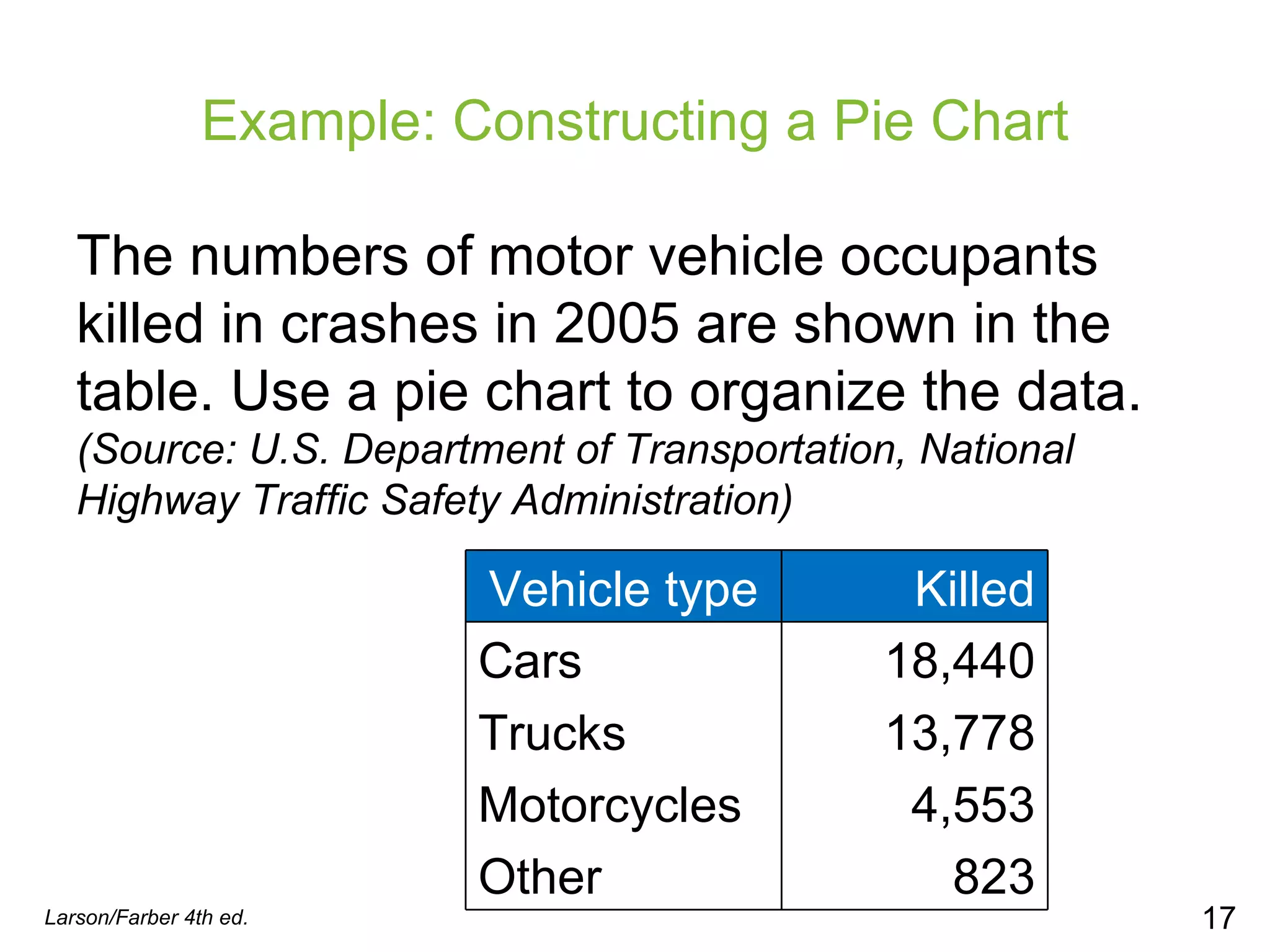
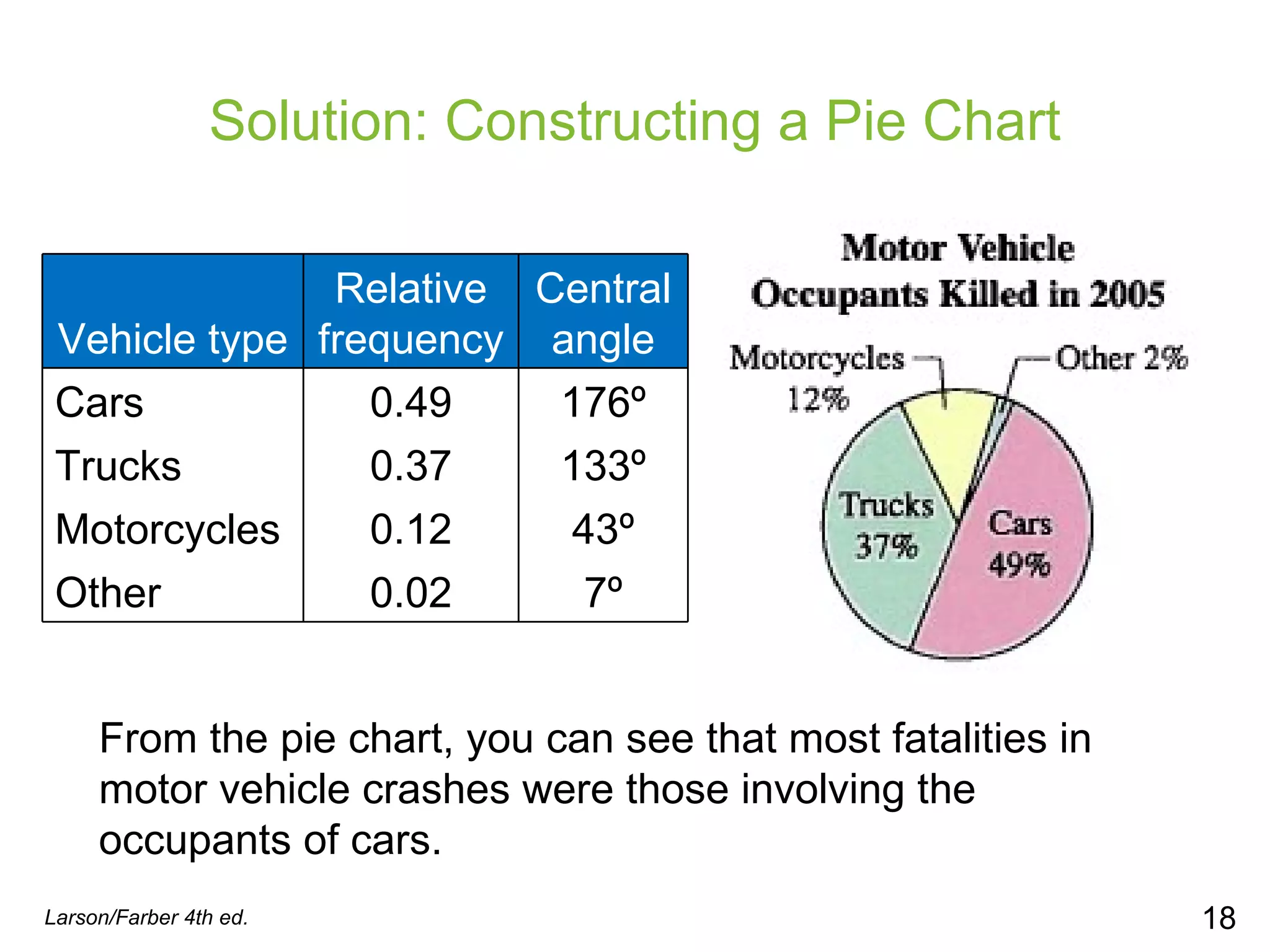
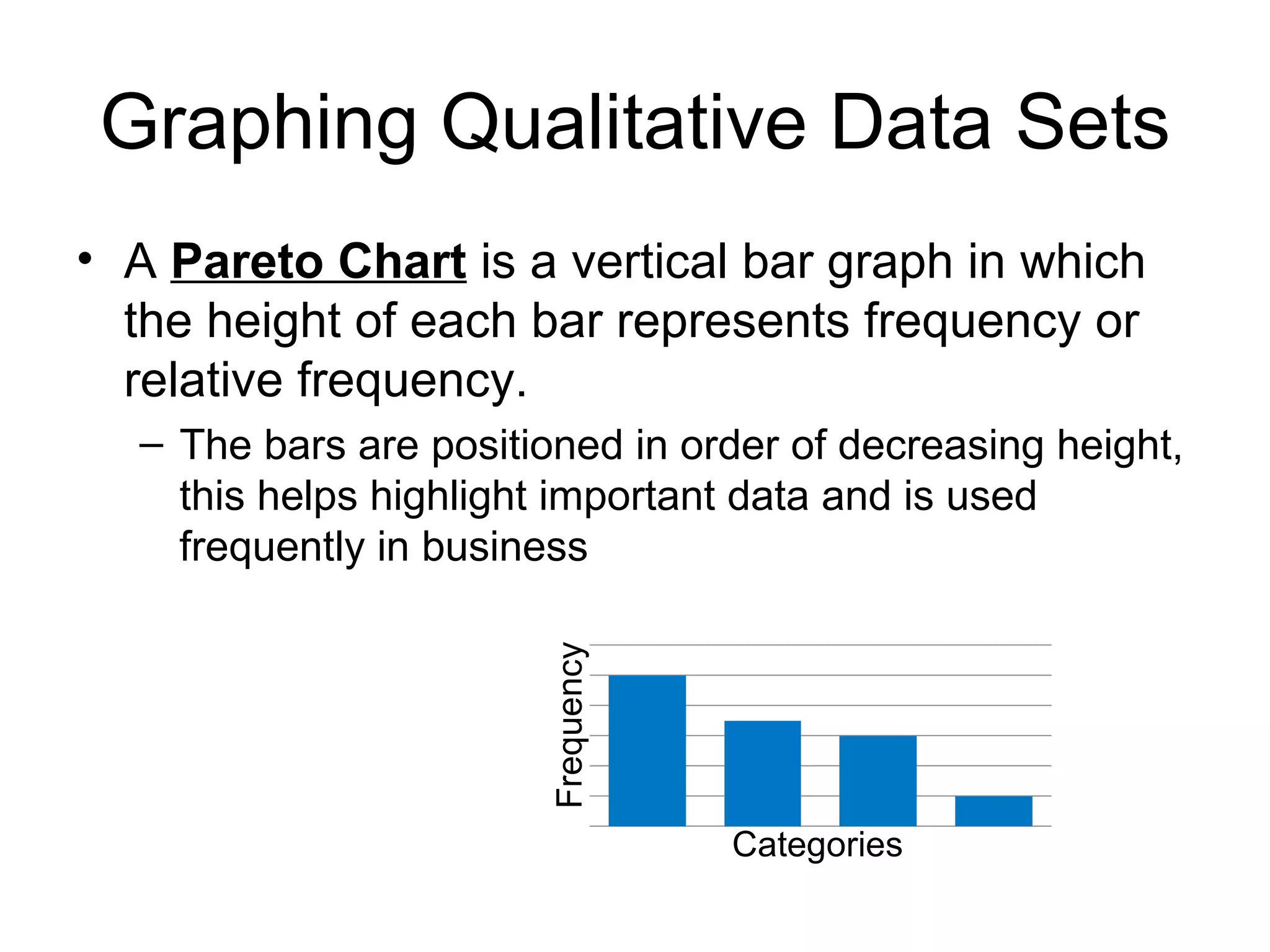
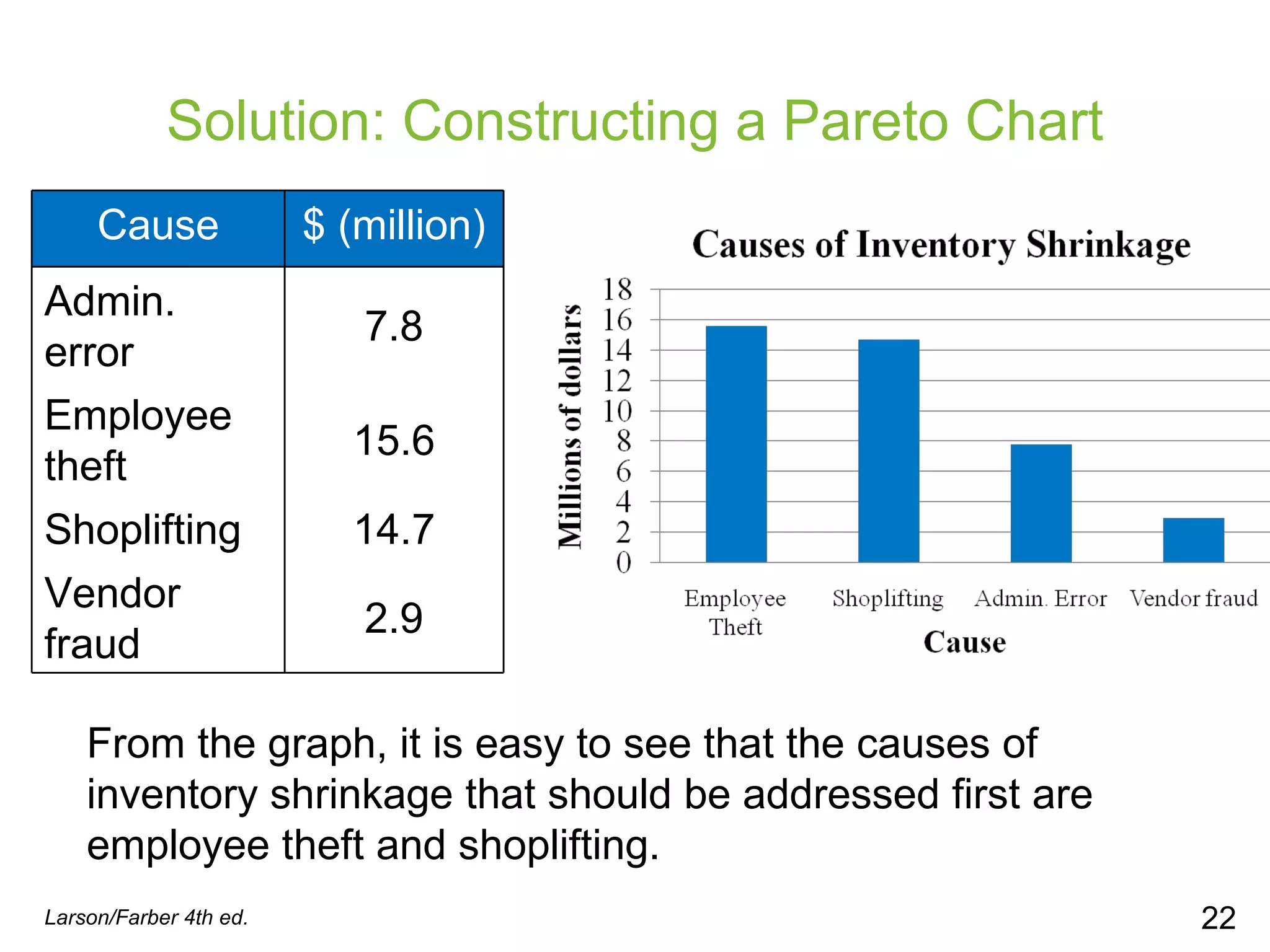
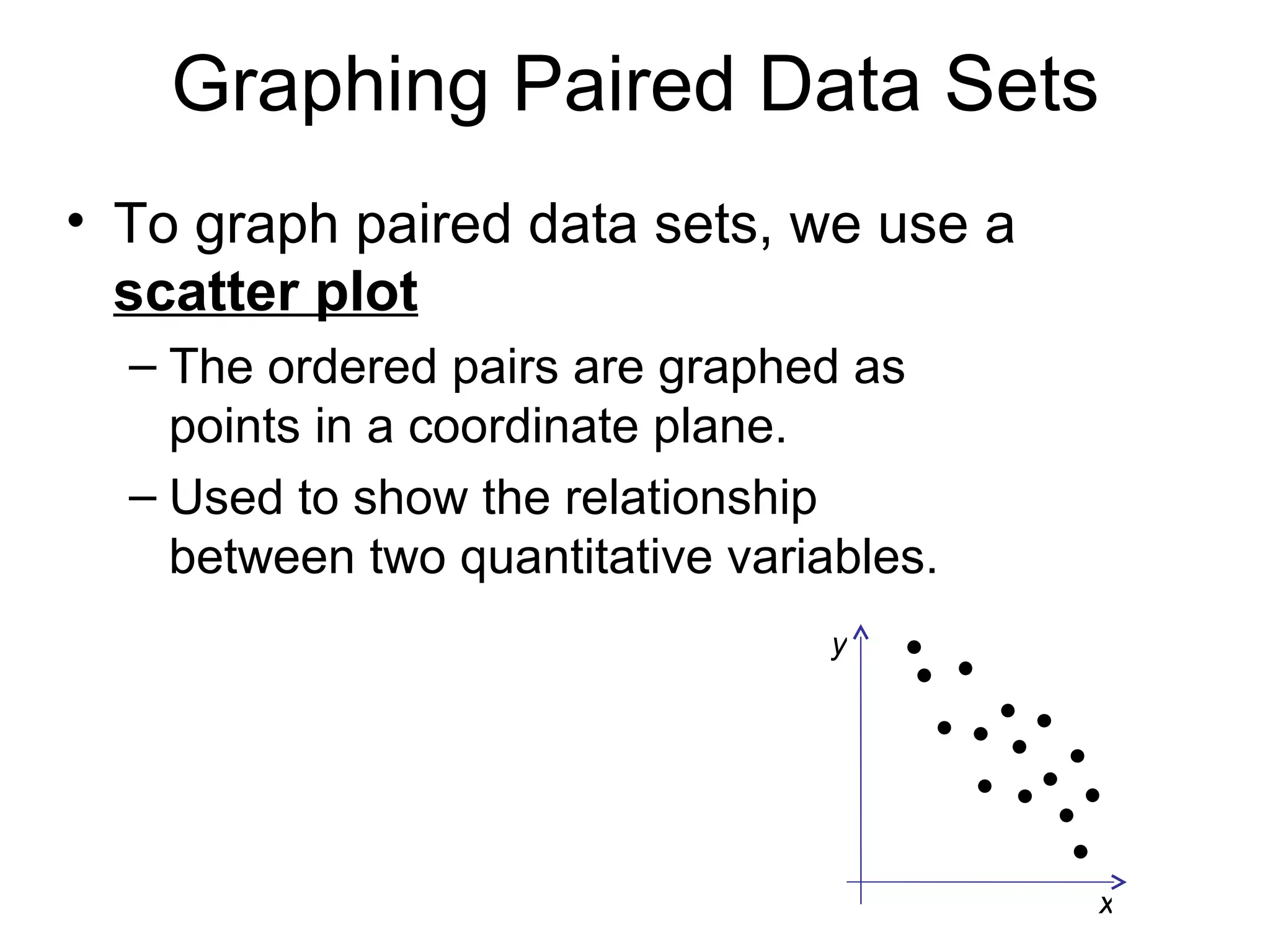
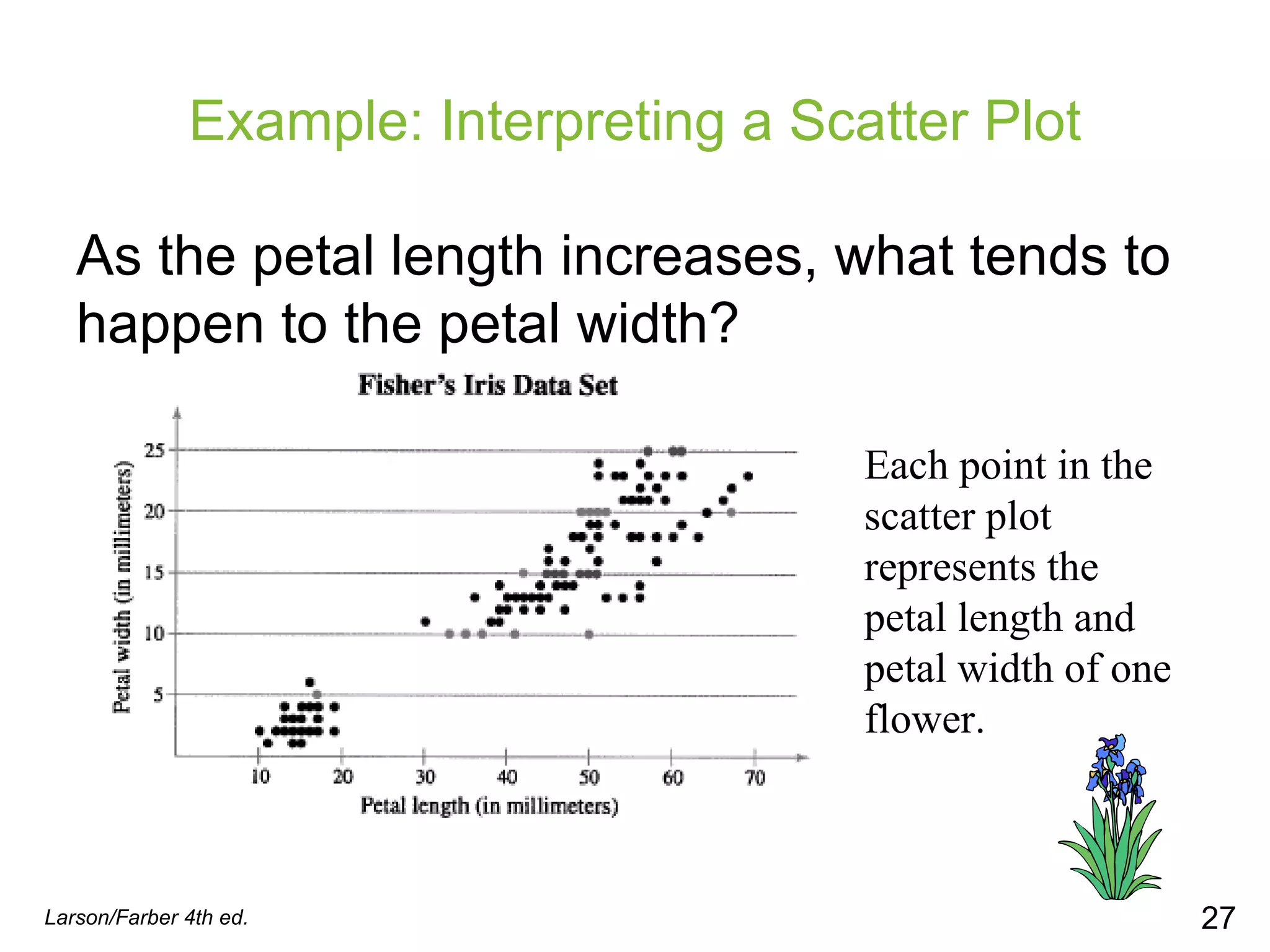
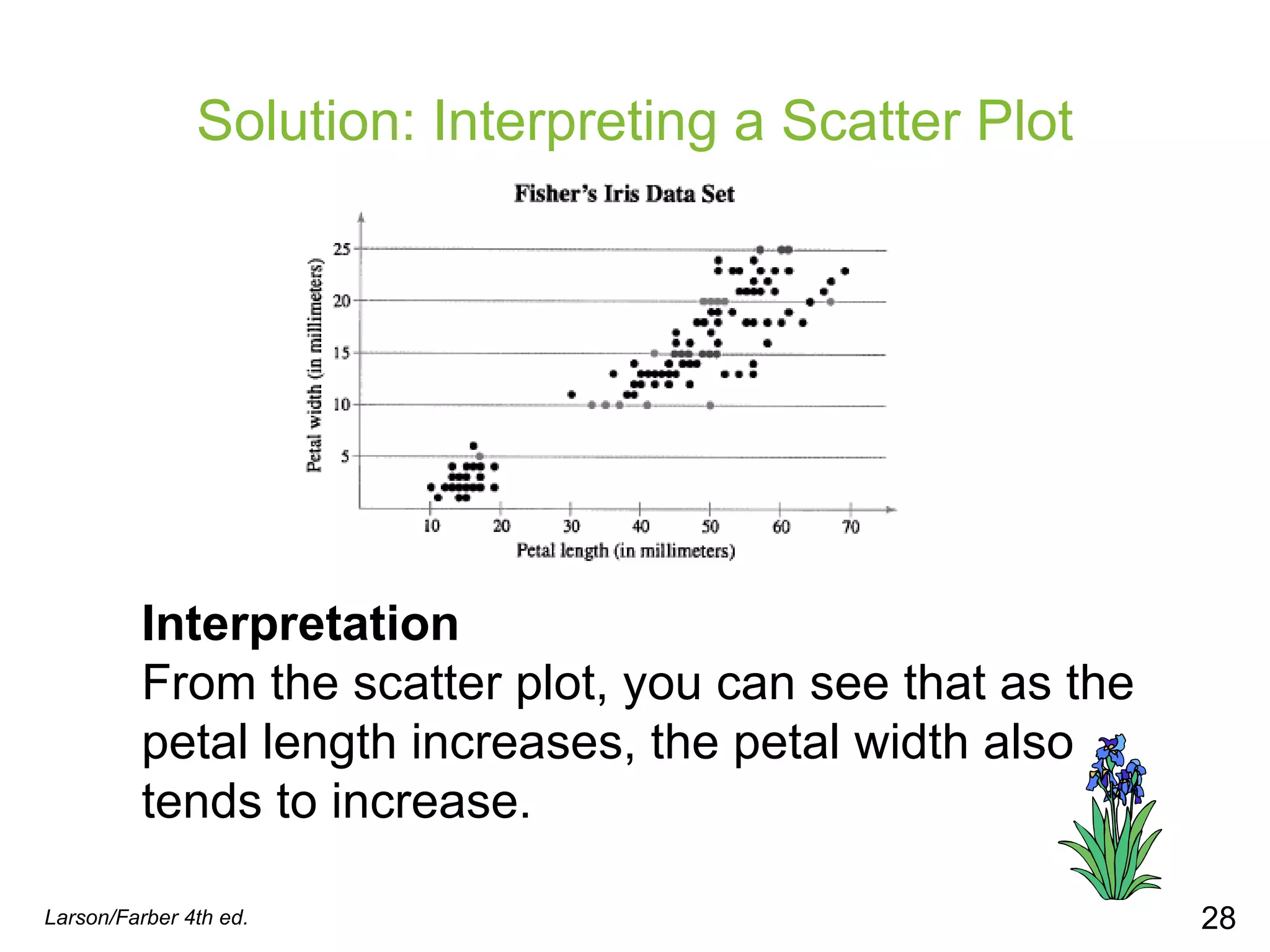
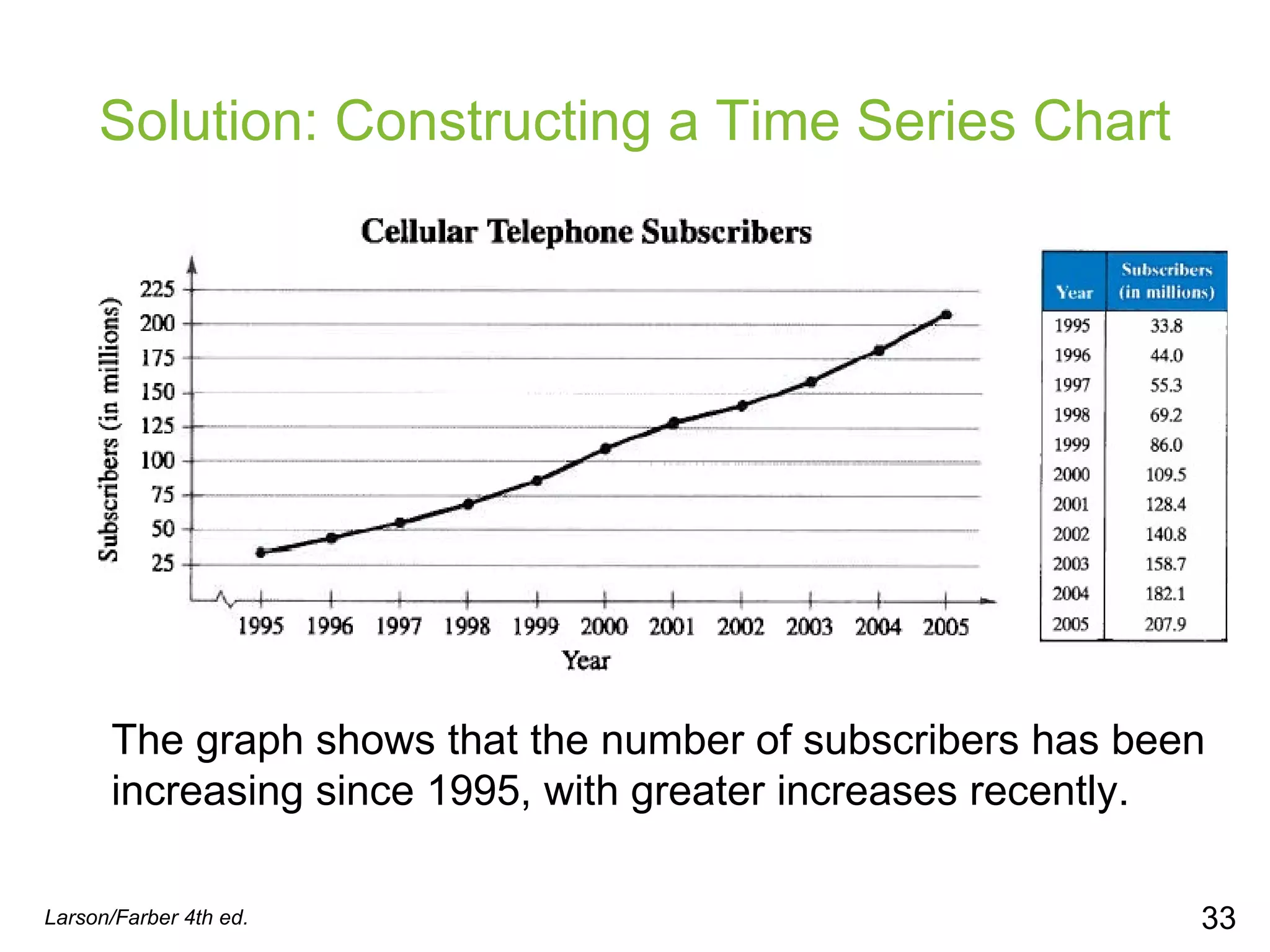
This document provides information on different types of graphs and displays that can be used to represent quantitative and qualitative data, including stem-and-leaf plots, dot plots, pie charts, Pareto charts, scatter plots, and time series charts. Examples are given for how to construct each type of graph or display using sample data sets. Key aspects like labeling axes, plotting data points, and interpreting trends are discussed.

1. Section 2.2 More Graphs and Displays Larson/Farber 4th ed.

2. Graphing Quantitative Data Sets A stem-and-leaf plot is another way to display quantitative data. Stem-and-leaf plots are part of exploratory data analysis (EDA) Each number is separated into a stem and a leaf . Similar to a histogram. Still contains original data values. Provides an easy way to sort data

3. Graphing Quantitative Data Sets Larson/Farber 4th ed. Data: 21, 25, 25, 26 , 27, 28, 30, 36, 36, 45 Example of a stem-and-leaf plot: Note: the leaf should always be a single digit. 26 2 1 5 5 6 7 8 3 0 6 6 4 5

4. Constructing a Stem-and-Leaf Plot Larson/Farber 4th ed. List all possible stems to the left of a vertical line List the leaf of each data entry to the right of its stem Make sure the leaves are ordered Use the plot to make a conclusion Include a key

5. Example1: Constructing a Stem-and-Leaf Plot The following are the numbers of league leading runs batted in (RBIs) for baseball’s American League during a recent 50-year period. Display the data in a stem-and-leaf plot. What can you conclude? Larson/Farber 4th ed. 155 159 144 129 105 145 126 116 130 114 122 112 126 118 118 108 122 121 109 140 126 119 113 117 118 119 139 139 122 78 133 126 123 145 121 134 124 119 124 129 112 126 148 147 112 109 132 142 109 133

6. Solution: Constructing a Stem-and-Leaf Plot Larson/Farber 4th ed. From the stem-and-leaf plot you can conclude that more than 50% of the RBI leaders had between 110 and 130 RBIs

7. Example2: Constructing Variations of Stem-and-Leaf Plots Using the same data from the first example, organize the data by using a stem-and-leaf plot that has two lines for each stem. What can you conclude? Larson/Farber 4th ed. 155 159 144 129 105 145 126 116 130 114 122 112 126 118 118 108 122 121 109 140 126 119 113 117 118 119 139 139 122 78 133 126 123 145 121 134 124 119 124 129 112 126 148 147 112 109 132 142 109 133 List two rows for each possible stem to the left of a vertical line Use the leaves 0, 1, 2, 3, and 4 for the first stem row and the leaves 5, 6, 7, 8, and 9 for the second stem row

8. Solution: Constructing a Stem-and-Leaf Plot From the display, you can conclude that most of the RBO leaders had between 105 and 135 RBIs

9. Constructing Variations of Stem-and-Leaf Plots Compare examples 1 and 2 Notice that by using two lines per stem, you obtain a more detailed picture of the data.

10. Graphing Quantitative Data Sets A dot plot is another way to plot quantitative data sets Each data entry is plotted, using a point, above a horizontal axis A dot plot allows you to see how data are distributed and to determine specific data entries

11. Graphing Quantitative Data Sets Data: 21, 25, 25, 26 , 27, 28, 30, 36, 36, 45 26 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 Example of a dot plot:

12. Constructing a Dot Plot Choose an appropriate scale for the horizontal axis. Be sure that each data entry will be included. Represent each data entry by plotting a point above the entry’s position on the axis. If an entry is repeated, plot another point above the previous point. Describe any patterns for the data.

13. Example3: Constructing a Dot Plot Use a dot plot to organize the RBI data given in example 1. 155 159 144 129 105 145 126 116 130 114 122 112 126 118 118 108 122 121 109 140 126 119 113 117 118 119 139 139 122 78 133 126 123 145 121 134 124 119 124 129 112 126 148 147 112 109 132 142 109 133

14. Solution: Constructing a Dot Plot From the dot plot, you can see that the most values cluster between 105 and 148 and 126 is the value that occurs the most.

15. Graphing Qualitative Data Sets A pie chart is a circle graph that shows relationships of part to whole. Pie charts provide a convenient way to present qualitative data graphically A circle is divided into sectors that represent categories. The area of each sector is proportional to the frequency of each category.

16. Constructing a Pie Chart Find the relative frequency, or percent, of each data entry Construct the pie chart using the central angle that corresponds to each category. To find the central angle, multiply 360º by the category's relative frequency. Draw/Sketch the pie chart

17. Example: Constructing a Pie Chart The numbers of motor vehicle occupants killed in crashes in 2005 are shown in the table. Use a pie chart to organize the data. (Source: U.S. Department of Transportation, National Highway Traffic Safety Administration) Larson/Farber 4th ed. Vehicle type Killed Cars 18,440 Trucks 13,778 Motorcycles 4,553 Other 823

18. Solution: Constructing a Pie Chart Larson/Farber 4th ed. From the pie chart, you can see that most fatalities in motor vehicle crashes were those involving the occupants of cars. Vehicle type Relative frequency Central angle Cars 0.49 176º Trucks 0.37 133º Motorcycles 0.12 43º Other 0.02 7º

19. Break

20. Graphing Qualitative Data Sets A Pareto Chart is a vertical bar graph in which the height of each bar represents frequency or relative frequency. The bars are positioned in order of decreasing height, this helps highlight important data and is used frequently in business Categories Frequency

21. Example: Constructing a Pareto Chart In a recent year, the retail industry lost $41.0 million in inventory shrinkage. Inventory shrinkage is the loss of inventory through breakage, pilferage, shoplifting, and so on. The causes of the inventory shrinkage are administrative error ($7.8 million), employee theft ($15.6 million), shoplifting ($14.7 million), and vendor fraud ($2.9 million). Use a Pareto chart to organize this data. (Source: National Retail Federation and Center for Retailing Education, University of Florida) Larson/Farber 4th ed.

22. Solution: Constructing a Pareto Chart Larson/Farber 4th ed. From the graph, it is easy to see that the causes of inventory shrinkage that should be addressed first are employee theft and shoplifting. Cause $ (million) Admin. error 7.8 Employee theft 15.6 Shoplifting 14.7 Vendor fraud 2.9

23. Paired Data Sets If two data sets have the same number of entries, and each entry in the first data set corresponds to one entry in the second data set, the sets are called paired data sets Example: Suppose a data set contains the costs of an item and a second data set contains sales amounts for the item at each cost. Because each cost corresponds to a sales amount, the data sets are paired.

24. Graphing Paired Data Sets To graph paired data sets, we use a scatter plot The ordered pairs are graphed as points in a coordinate plane. Used to show the relationship between two quantitative variables. x y

25. Constructing a Scatter Plot Label the Horizontal and Vertical axes Plot the paired data Describe any trends

26. Example: Interpreting a Scatter Plot The British statistician Ronald Fisher introduced a famous data set called Fisher's Iris data set. This data set describes various physical characteristics, such as petal length and petal width (in millimeters), for three species of iris. The petal lengths form the first data set and the petal widths form the second data set. (Source: Fisher, R. A., 1936) Larson/Farber 4th ed.

27. Example: Interpreting a Scatter Plot As the petal length increases, what tends to happen to the petal width? Larson/Farber 4th ed. Each point in the scatter plot represents the petal length and petal width of one flower.

28. Solution: Interpreting a Scatter Plot Larson/Farber 4th ed. Interpretation From the scatter plot, you can see that as the petal length increases, the petal width also tends to increase.

29. Graphing Paired Data Sets A data set that is composed of quantitative entries taken at regular intervals over a period of time is a time series . Example: The amount of precipitation measured each day for one month. Use a time series chart to graph. Larson/Farber 4th ed. time Quantitative data

30. Constructing a Time Series Chart Label the Horizontal and Vertical axes Plot the paired data and connect them with line segments Describe any patterns you see

31. Example: Constructing a Time Series Chart The table lists the number of cellular telephone subscribers (in millions) for the years 1995 through 2005. Construct a time series chart for the number of cellular subscribers. (Source: Cellular Telecommunication & Internet Association) Larson/Farber 4th ed.

32. Solution: Constructing a Time Series Chart Let the horizontal axis represent the years. Let the vertical axis represent the number of subscribers (in millions). Larson/Farber 4th ed.

33. Solution: Constructing a Time Series Chart Larson/Farber 4th ed. The graph shows that the number of subscribers has been increasing since 1995, with greater increases recently.

34. Homework P55 #1 – 29 odd and 30