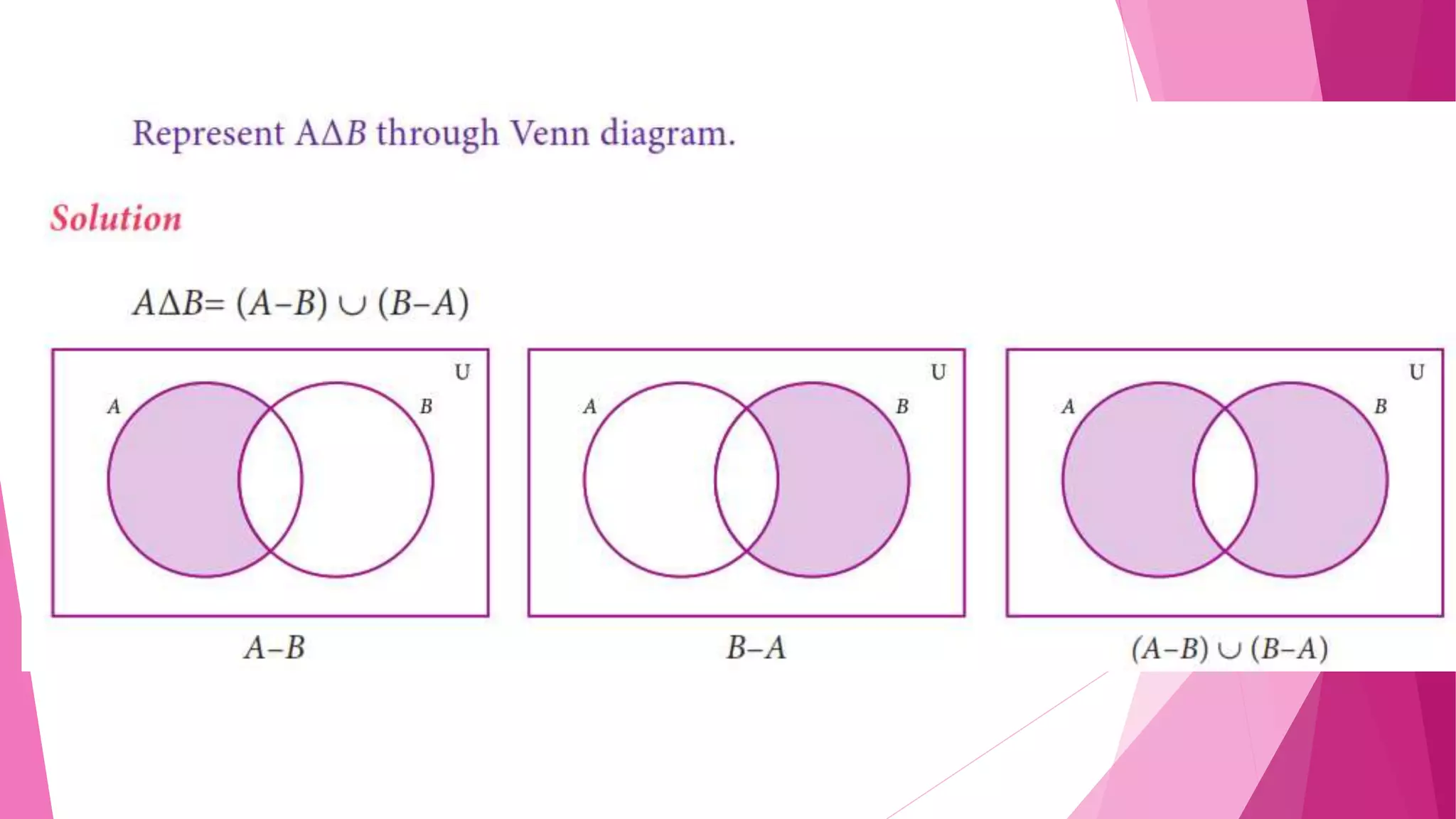
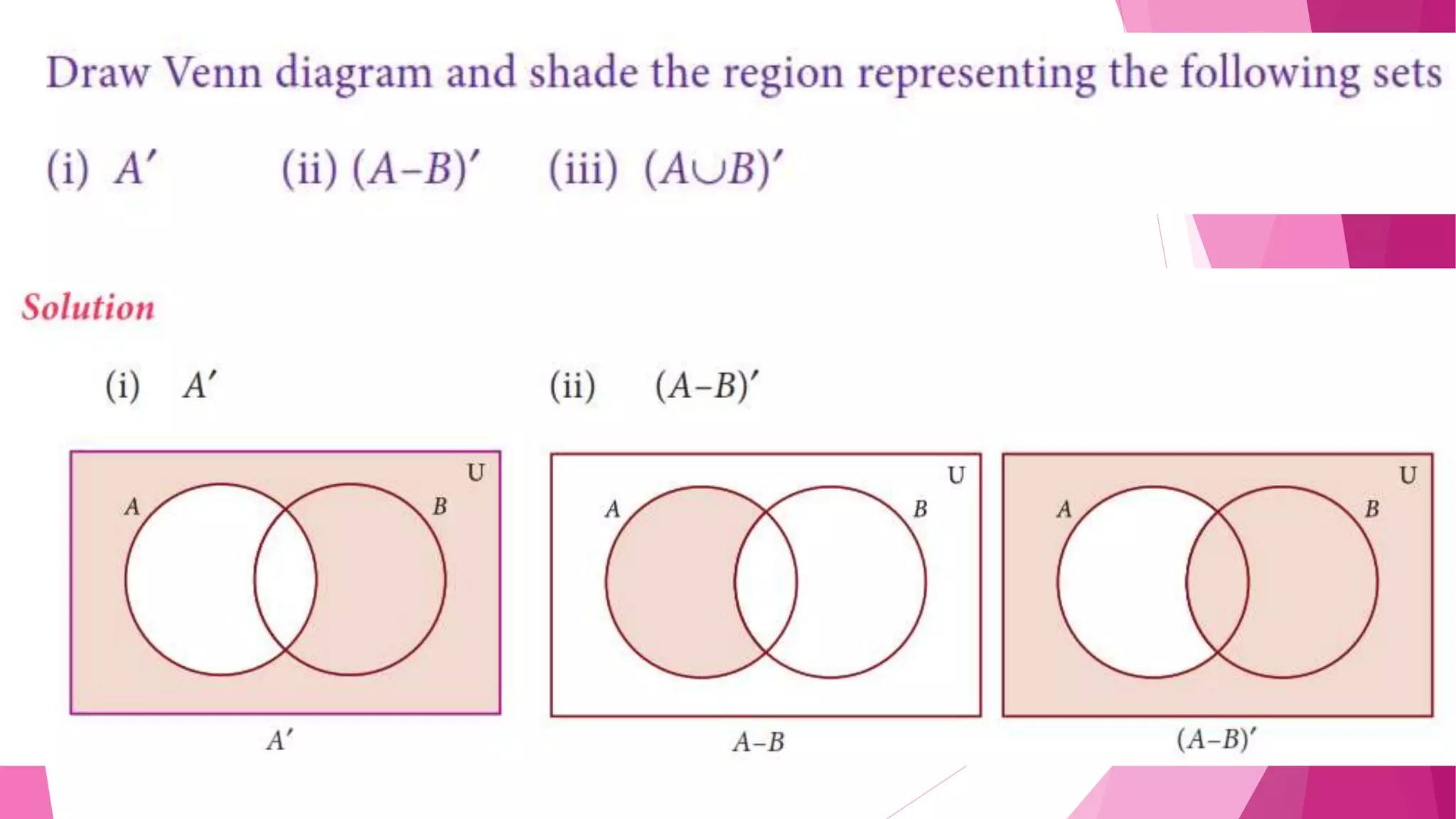
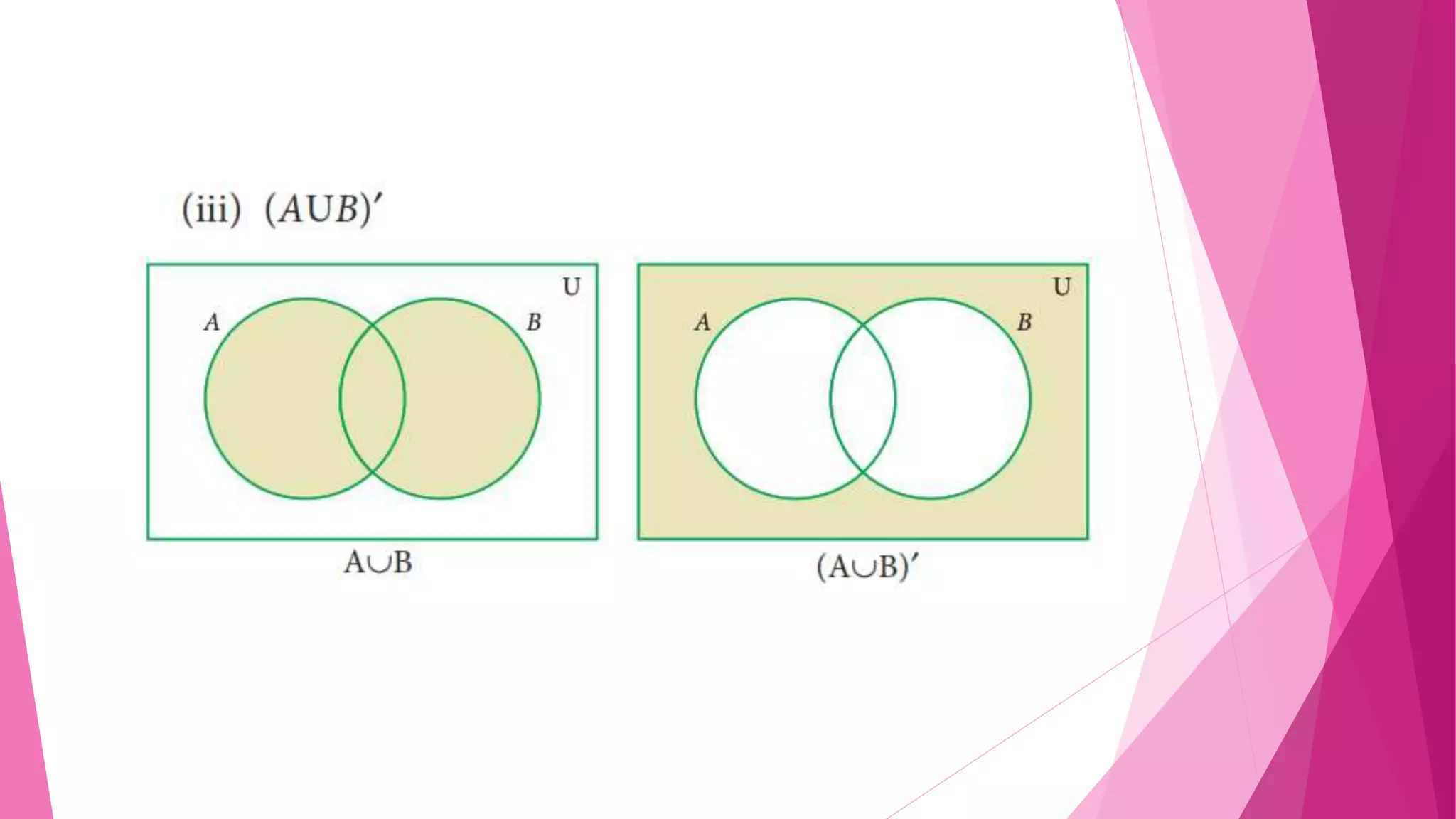
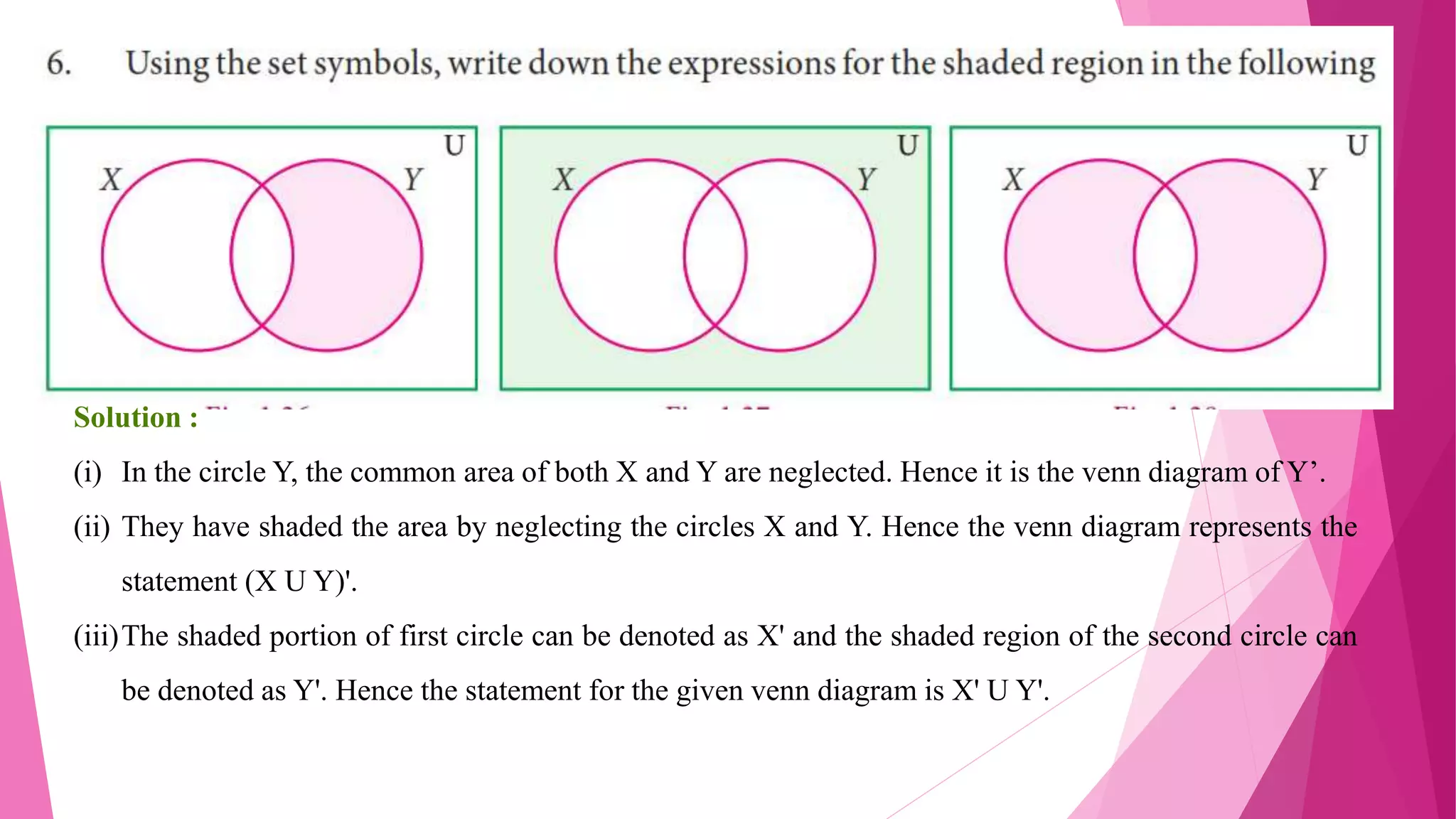
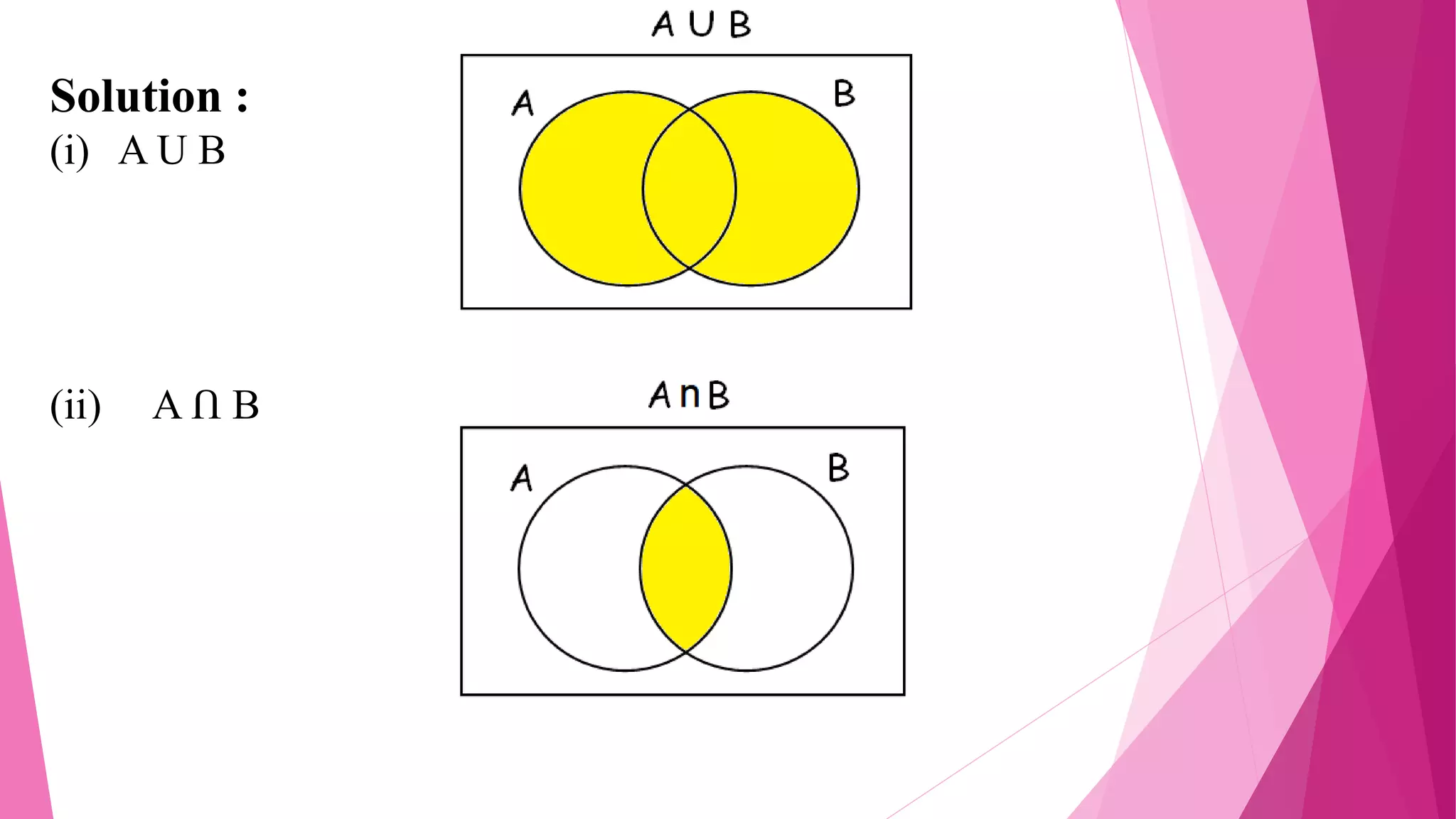
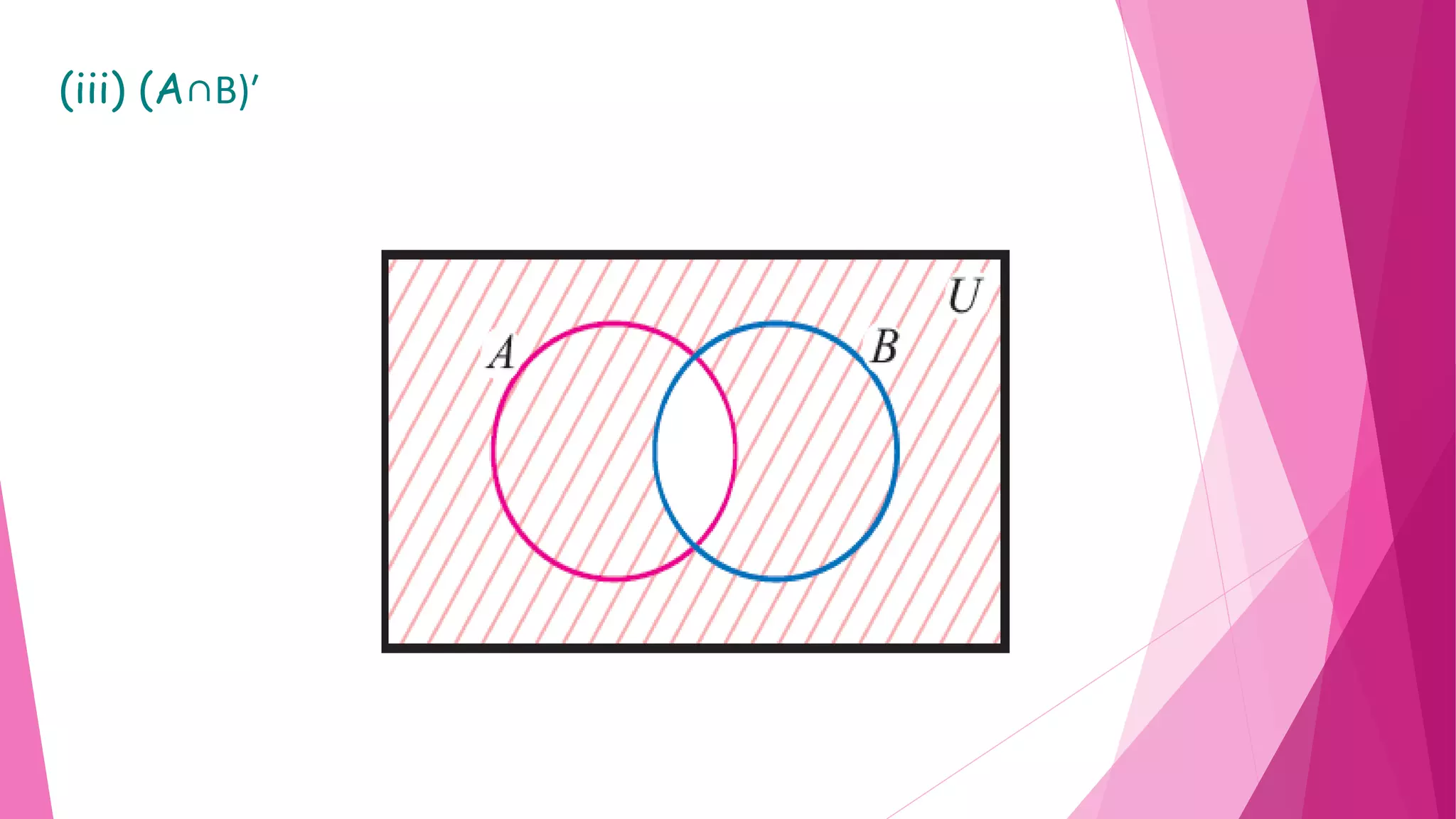
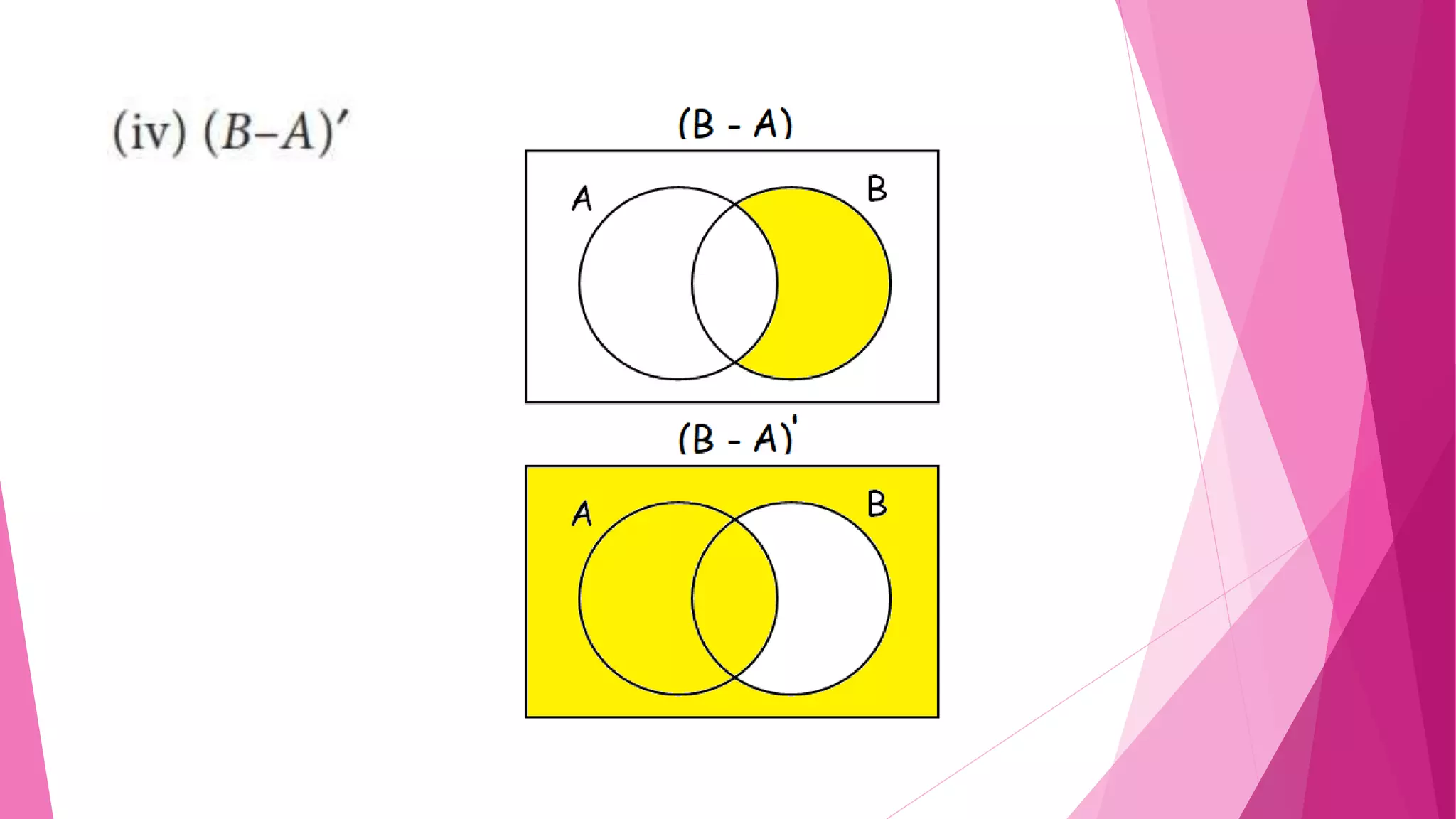
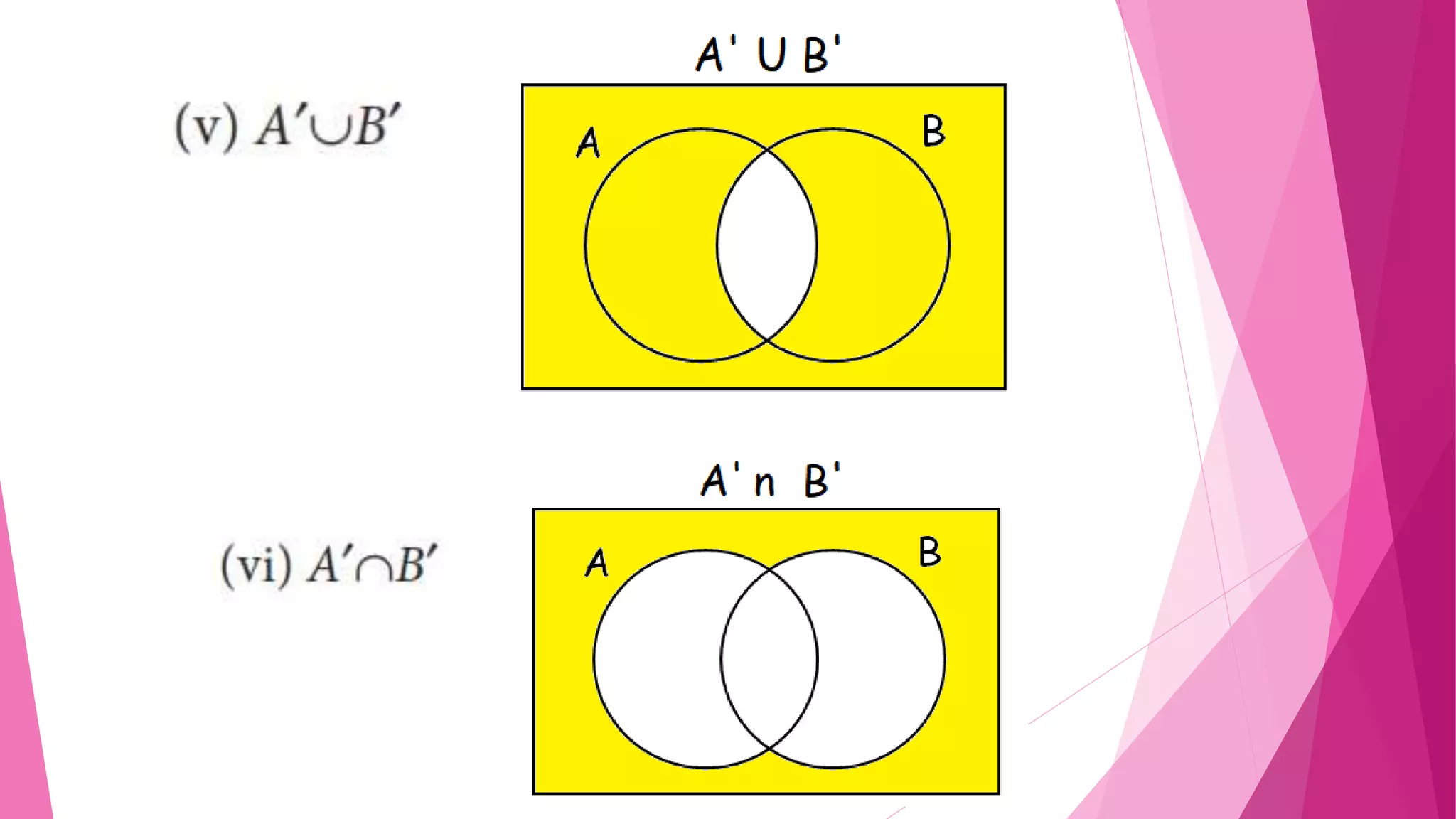
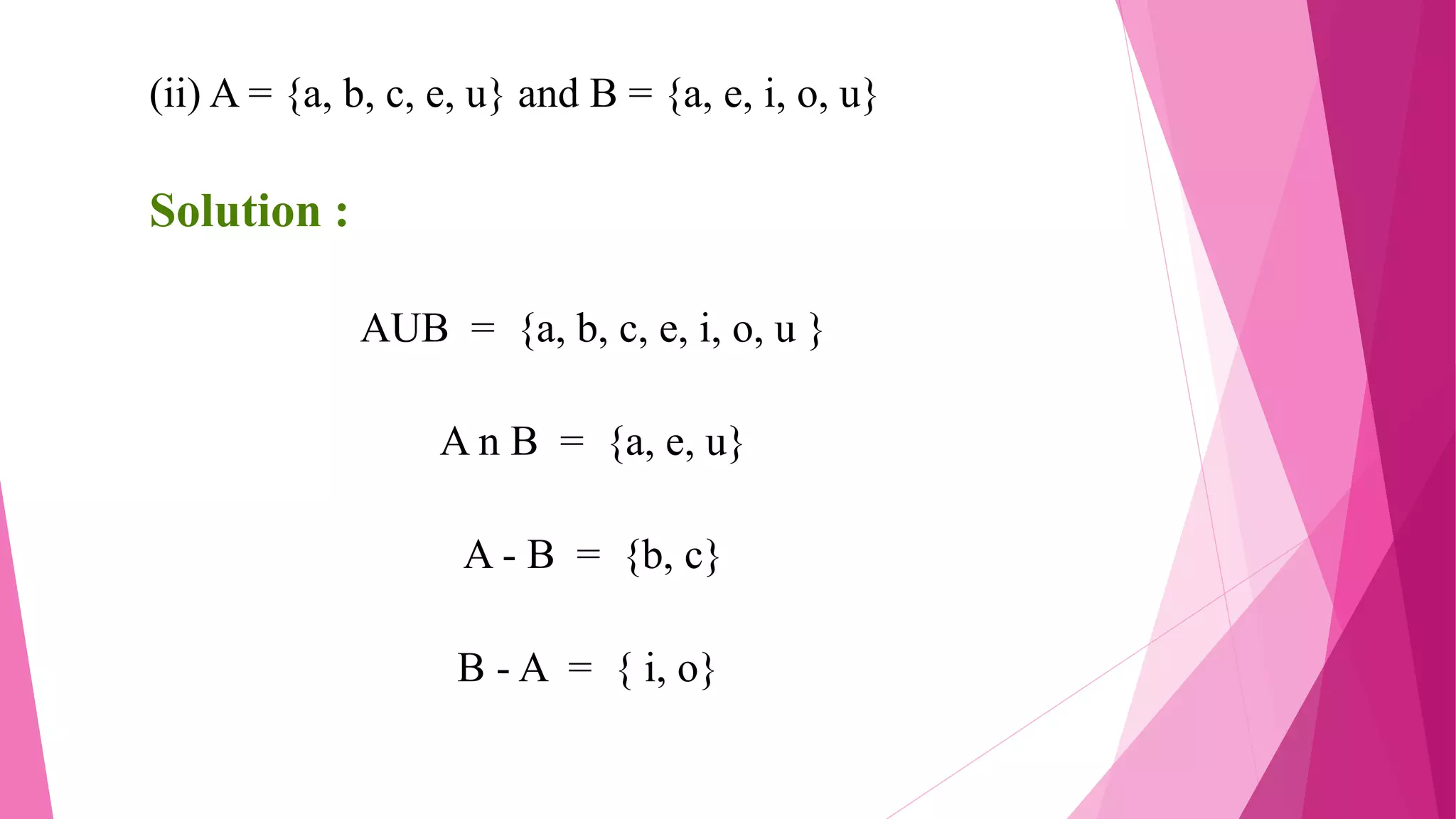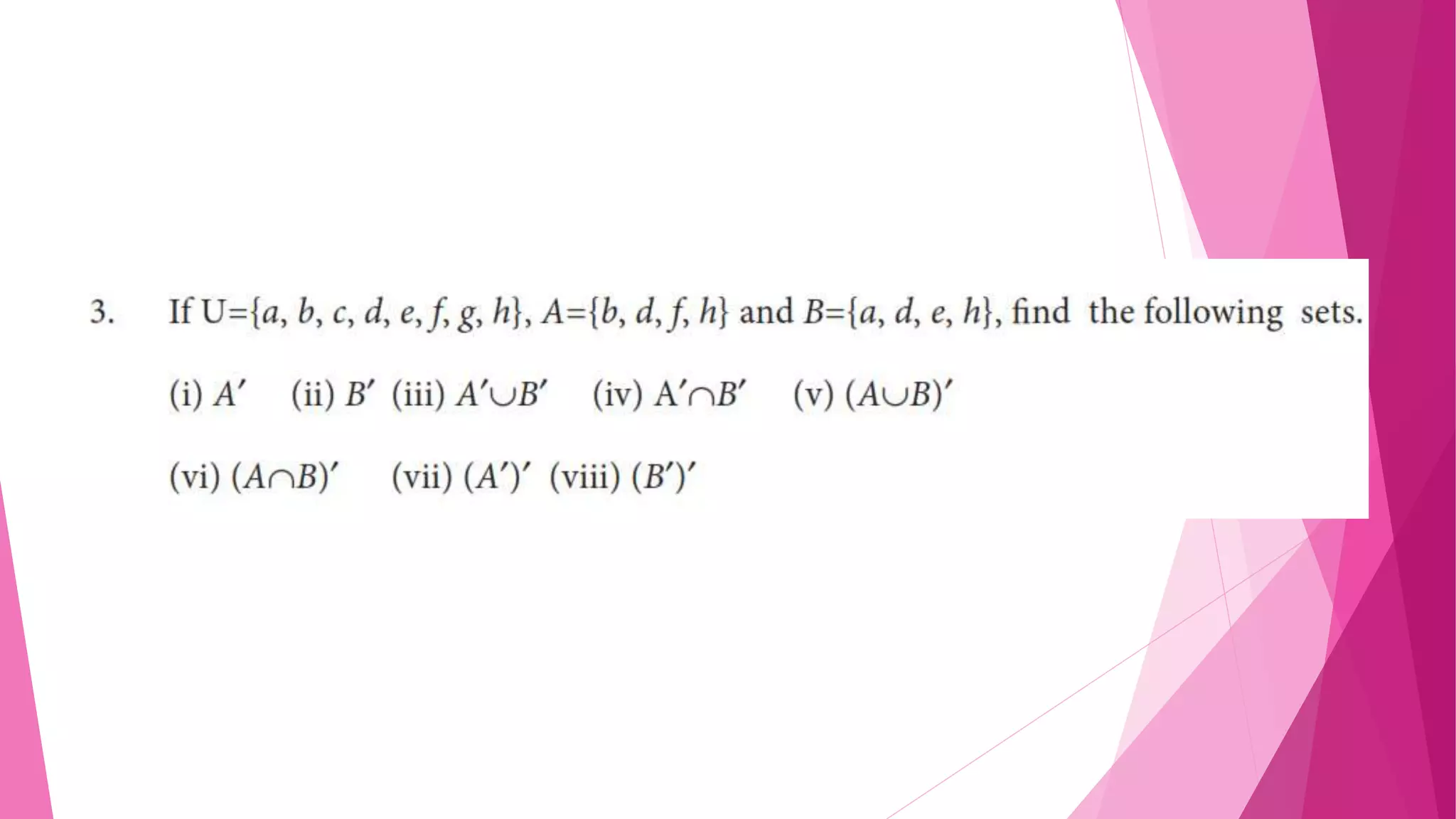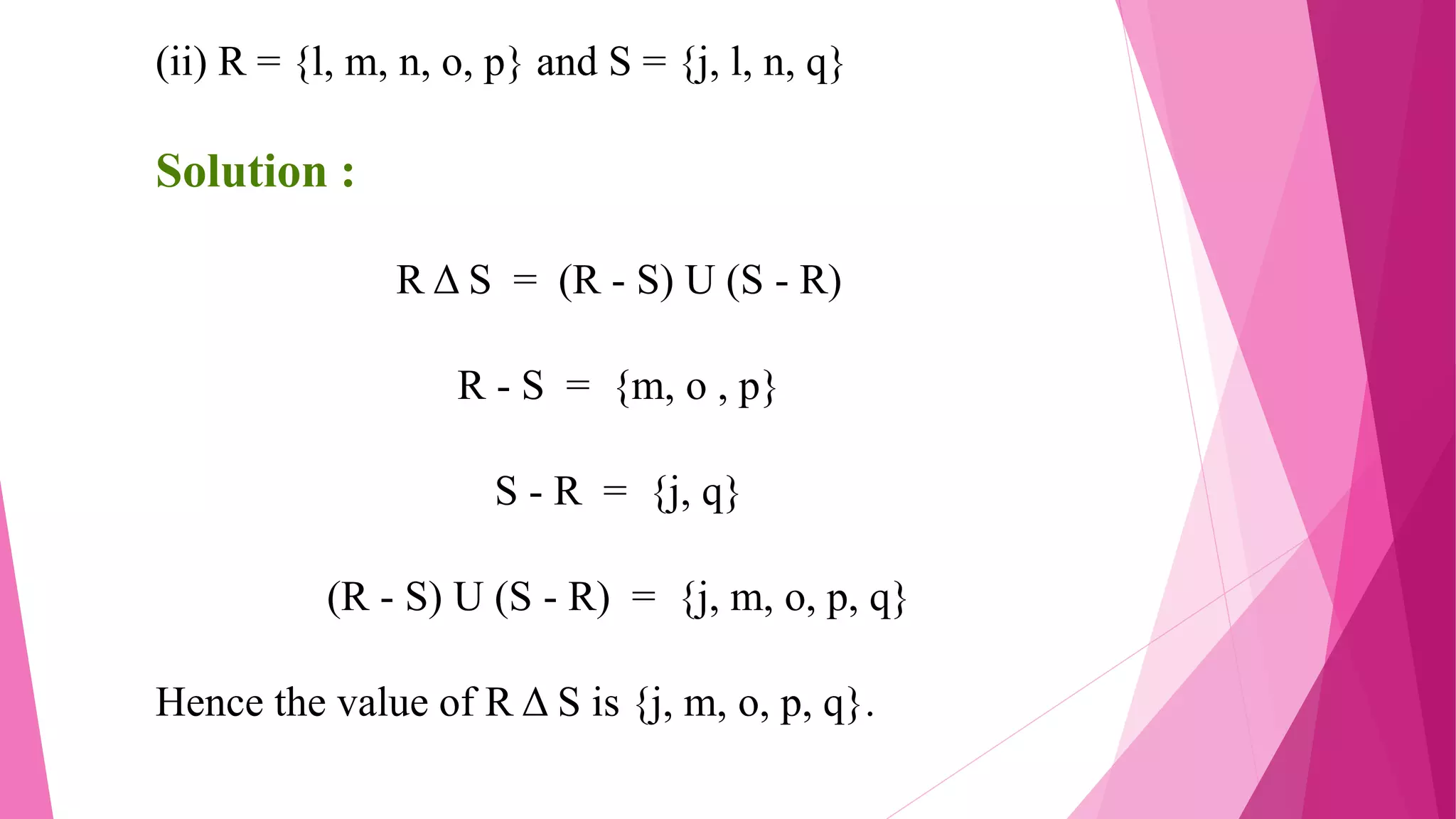The document provides detailed solutions to various mathematical set operations, including union, intersection, and set differences, using examples from both numerical and alphabetical sets. It includes explanations and results for operations with different sets, expressed through equations and Venn diagrams. The document serves as a pedagogical resource for understanding set theory concepts in mathematics.

1. Pedagogy of Mathematics – Part II (Ex1.3)
By
Dr. I. Uma Maheswari
Principal
Peniel Rural College of Education, Vemparali, Dindigul District
iuma_maheswari@yahoo.co.in

2. Std IX
Chapter 1 – Set Language
Ex - 1.3

24. Solution :
(i) We have to write the elements in the circle A.
A = {2, 4, 7, 8, 10}
(ii) We have to write the elements in the circle B.
B = {3, 4, 6, 7, 9, 11}
(iii) A U B means the elements in both circles.
A U B = {2, 3, 4, 6, 7, 8, 9, 10, 11}
(iv) A ∩ B means the common elements of both sets A and B.
A∩B = {4, 7}

25. (v) A – B
A - B = {2, 8, 10}
(vi) B – A
B - A = {3, 6, 9, 11}
(vii) A' = {1, 3, 6, 9, 11, 12}
(viii) B′ = {1, 2, 8, 10, 12}
(ix) U = {1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12}

27. (i) A = {2, 6, 10, 14} and B = {2, 5, 14, 16}
Solution :
AUB = {2, 4, 5, 6, 10, 14, 16}
A n B = {2, 14}
A - B = {6, 10}
B - A = {5, 16}

28. (ii) A = {a, b, c, e, u} and B = {a, e, i, o, u}
Solution :
AUB = {a, b, c, e, i, o, u }
A n B = {a, e, u}
A - B = {b, c}
B - A = { i, o}

29. (iii) A = {x : x ∈N, x ≤ 10} and B = {x : x ∈W, x < 6}
Solution :
A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
B = {0, 1, 2, 3, 4, 5}
AUB = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A n B = { 1, 2, 3, 4, 5}
A - B = {6, 7, 8, 9, 10}
B - A = {0}

30. (iv) A= Set of all letters in the word “mathematics” and
B = Set of all letters in the word “geometry”
Solution :
A = {m, a, t, h, e, i, c, s }
B = {g, e, o, m, e, t, r, y}
AUB = {m, a, t, h, e, i, c, s, g, o, r, y}
A n B = { m, t, e}
A - B = {a, h, i, c , s}
B - A = {g, o, r, y}

32. (i) A' = {a, c, e, g}
(ii) B' = {b, c, f, g}
(iii) A′∪B′ = { a, b, c, e, g }
(iv) A′∩B′ = { c, g }
(v) (A∪B)′
To find (A∪B)′, first we have to find A U B
A U B = {a, b, d, e, f, h}
(A U B)' = {c, g}

33. (v) (A∪B)′
To find (A∪B)′, first we have to find A U B
A U B = {a, b, d, e, f, h}
(A U B)' = {c, g}

35. Solution :
(i) A' = {0, 2, 4, 6}
(ii) B' = {1, 4, 6}
(iii) A′∪B′ = {0, 1, 2, 4, 6 }
(iv) A′∩B′ = {4, 6}

36. (v) (A∪B)′
To find (A∪B)′, first we have to find A U B
A U B = {0, 1, 2, 3, 5, 7}
(A U B)' = {4, 6}
(vi) (A∩B)′ = {0, 1, 2, 4, 6 }
(vii) (A′)′
{1, 3, 5, 7}
(viii) (B′)′
B = {0, 2, 3, 5, 7}

38. (i) P = {2, 3, 5, 7, 11} and Q = {1, 3, 5, 11}
Solution :
P Δ Q = (P - Q) U (Q - P)
P - Q = {2, 7}
Q - P = {1, 11}
(P - Q) U (Q - P) = {1, 2, 7, 11}
Hence the value of P Δ Q is {1, 2, 7, 11}

39. (ii) R = {l, m, n, o, p} and S = {j, l, n, q}
Solution :
R Δ S = (R - S) U (S - R)
R - S = {m, o , p}
S - R = {j, q}
(R - S) U (S - R) = {j, m, o, p, q}
Hence the value of R Δ S is {j, m, o, p, q}.

40. (iii) X = {5, 6, 7} and Y = {5, 7, 9, 10}
Solution :
X Δ Y = (X - Y) U (Y - X)
X - Y = {6}
Y - X = {9, 10}
(X - Y) U (Y - X) = {6, 9, 10}
Hence the value of X Δ Y is {6, 9, 10}.

41. Solution :
(i) In the circle Y, the common area of both X and Y are neglected. Hence it is the venn diagram of Y’.
(ii) They have shaded the area by neglecting the circles X and Y. Hence the venn diagram represents the
statement (X U Y)'.
(iii)The shaded portion of first circle can be denoted as X' and the shaded region of the second circle can
be denoted as Y'. Hence the statement for the given venn diagram is X' U Y'.

43. Solution :
(i) A U B
(ii) A Ո B

44. (iii) (A∩B)′

47. (vii) What do you observe from the Venn diagram (iii)
and (v)?
(iii) and (v) are equal.