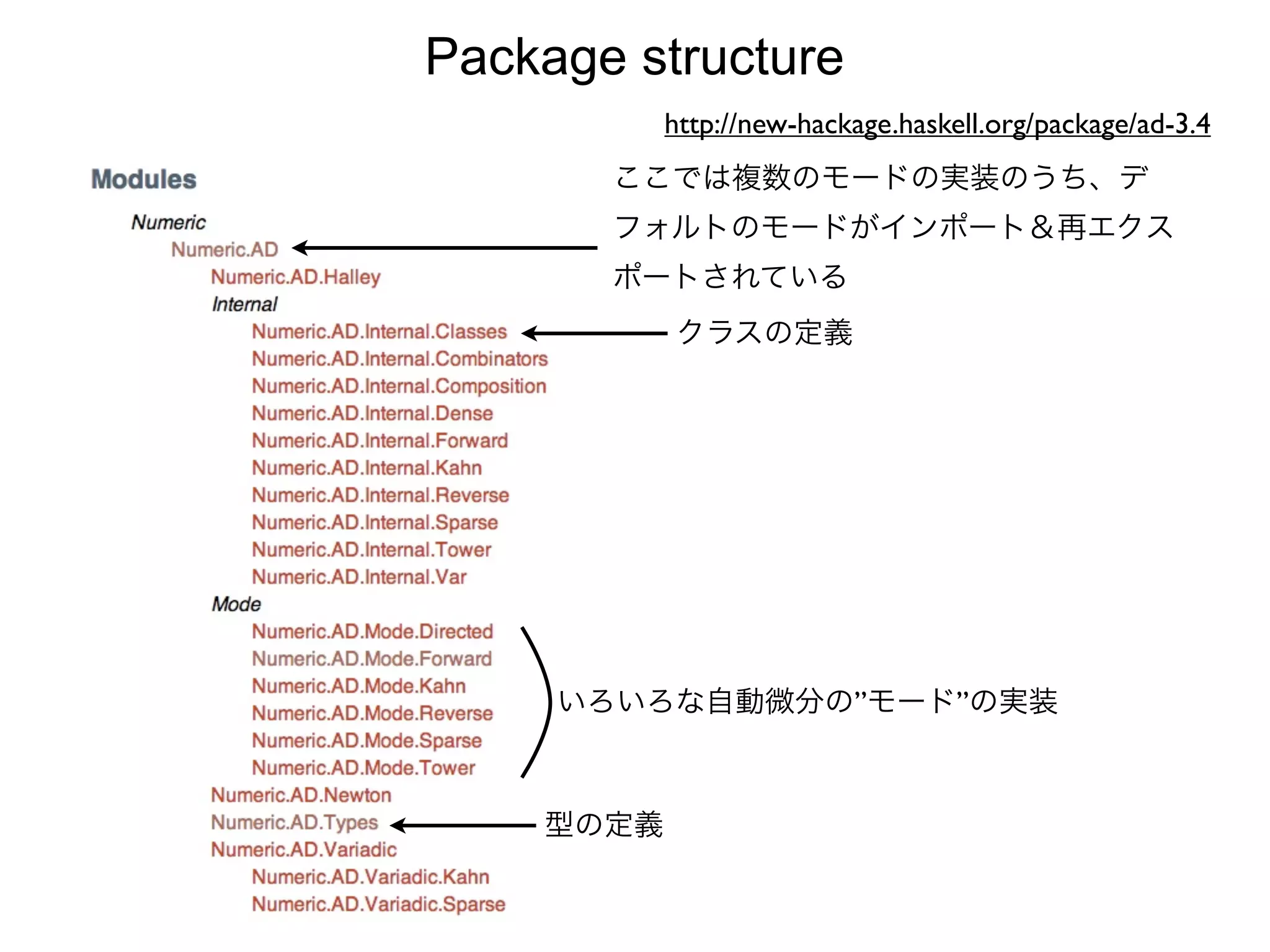
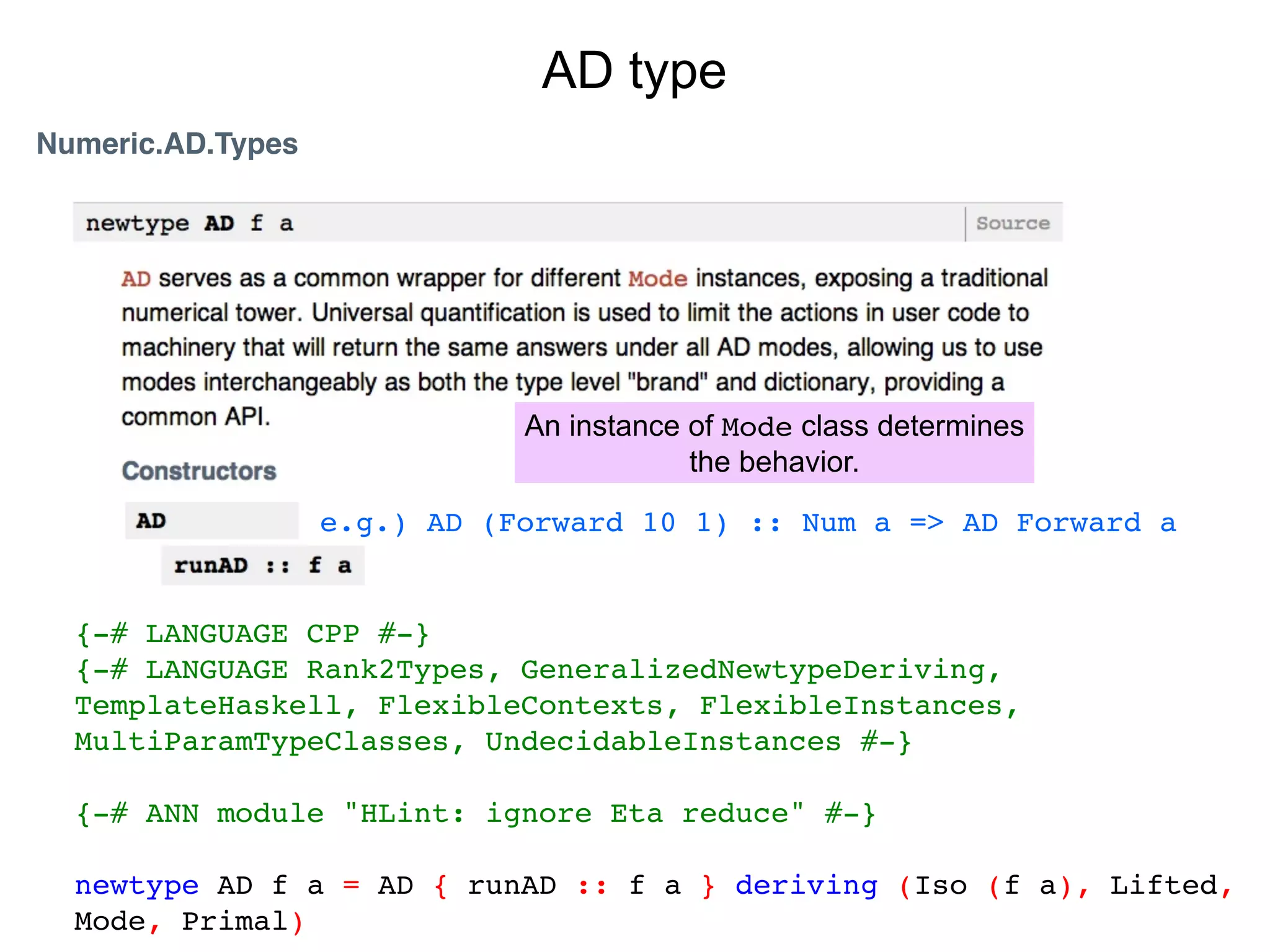
This document provides an introduction to the ad-3.4 automatic differentiation library in Haskell. It summarizes the key capabilities of the library including differentiating arbitrary mathematical functions, calculating gradients, Jacobians and Hessians. It also provides examples of how to use the library to differentiate single variable scalar functions, calculate gradients, perform Taylor expansions, and check equality of functions. The document discusses some of the core classes and types in the library like Mode, Lifted and AD that enable automatic differentiation. It points to resources that explain the mechanism of automatic differentiation and package structure.

1. (An attempt of)
Introduction to ad-3.4,
an automatic differentiation library in Haskell
3/31/2013
Ekmett study meeting
in Shibuya, Tokyo
by Nebuta
Any comments or correction to the material are welcome

2. About myself
Nebuta (@nebutalab) https://github.com/nebuta
My interest in softwares:
Programming languages (Haskell, Scala, Ruby, etc)
Image processing, data visualization, web design
Brainstorming and lifehack methods that take advantage of IT, etc.
My research areas:
A graduate student, studying biophysical chemistry and quantitative
biology (2010−)
Imaging live cells, analyzing microscopy images by Scala on ImageJ
Where my interest in Haskell came from:
MATLAB、ImageJで細胞の顕微鏡画像の解析 (2010年) → MATLAB,
Javaはいまいち使いづらい → Scalaっていうイケてる言語がある
（2011年）
→ 関数型？ → Haskell 面白い！（2011年）

3. ad-3.4, an automatic differentiation library
What you can do
Differentiation of arbitrary mathematical functions
Taylor expansion
Calculation of gradient, Jacobian, and Hessian, etc.
Dependencies
array (≥0.2 & <0.5), base (4.*), comonad (≥3),
containers (≥0.2 & <0.6), data-reify (0.6.*), erf (2.0.*),
free (≥3), mtl (≥2), reflection (≥1.1.6),
tagged (≥0.4.2.1), template-haskell (≥2.5 & <2.9)
Installation
$ sudo cabal install ad simple-reflect
記号で微分するのに使う
For symbolic differentiation

4. How to use ad-3.4
https://github.com/ekmett/ad/blob/master/README.markdown#examples
Differentiation of a single-variable scalar function
>> :m + Numeric.AD ※Derivative of a
>> diff sin 0 trigonometric function
1.0
>> :m + Debug.SimpleReflect
>> diff sin x -- x :: Expr is defined in Debug.SimpleReflect
cos x * 1 Derivative with a symbol!
>> diff (x -> if x >= 0 then 1 else 0) 0
0.0 Not delta function nor undefined.
Gradient
>> grad ([x,y] -> exp (x * y)) [x,y]
[0 + (0 + y * (0 + exp (x * y) * 1)),0 + (0 + x * (0 + exp (x
* y) * 1))]
>> grad ([x,y] -> exp (x * y)) [1,1]
[2.718281828459045,2.718281828459045]

5. How to use (continued)
Taylor expansion
Prelude Numeric.AD Debug.SimpleReflect> take 3 $ taylor exp 0 d
[exp 0 * 1,1 * exp 0 * (1 * d / 1),(0 * exp 0 + 1 * exp 0 * 1) *
(1 * d / 1 * d / (1 + 1))]
Prelude Numeric.AD Debug.SimpleReflect> take 3 $ taylor exp x d
[exp x * 1,1 * exp x * (1 * d / 1),(0 * exp x + 1 * exp x * 1) *
(1 * d / 1 * d / (1 + 1))]
Prelude Numeric.AD Debug.SimpleReflect> take 3 $ taylor exp x 0
[exp x * 1,1 * exp x * (1 * 0 / 1),(0 * exp x + 1 * exp x * 1) *
(1 * 0 / 1 * 0 / (1 + 1))]
•Taylor expansion is an infinite list! Taylor expansion (general)
•No simplification, and slow in higher order terms
Exponential function

6. How to use (continued)
Equality of functions
>> sin x == sin x
True
>> diff sin x
cos x * 1
>> diff sin x == cos x * 1
True
>> diff sin x == cos x * 0.5 * 2
False
Cool! (no simplification, though...)
And so on.

7. Cf. Mechanism of automatic differentiation
Read a Wikipedia article http://en.wikipedia.org/wiki/Automatic_differentiation
I don’t understand it yet.
（What’s the difference from symbolic differentiation?）
？？
要は、合成関数の微分を
機械的に順次適用していく、
(f + g)’ = f’ + g’
という認識で良いかと思われる
It seems to be mechanical, successive
application of rules of differentiation for
composite functions.

8. I’ll try to appreciate the type and class organization
注意：
Githubに上がっている最新バージョン
（https://github.com/ekmett/ad）は4.0で、
Hackage(http://hackage.haskell.org/package/ad-3.4)とは違います。
ライブラリの構造が若干違うようです。
cabal unpack ad-3.4 でver. 3.4のソースをダウンロードする
か、Hackageを見て下さい。
I’ll use ad-3.4 on Hackage, not ad-4.0 on Github

9. Package structure
http://new-hackage.haskell.org/package/ad-3.4
ここでは複数のモードの実装のうち、デ
フォルトのモードがインポート＆再エクス
ポートされている
クラスの定義
いろいろな自動微分の”モード”の実装
型の定義

10. The starting point for exploration: diff function
Numeric.AD.Mode.Forward １変数スカラー関数の微分
{-# LANGUAGE Rank2Types #-}
diff :: Num a => (forall s. Mode s => AD s a -> AD s a) -> a -> a
diff f a = tangent $ apply f a
微分対象の関数fは(AD s a->AD s a)型として表される
Numeric.AD.Internal.Forward
{-# LANGUAGE Rank2Types, TypeFamilies, DeriveDataTypeable,
TemplateHaskell, UndecidableInstances, BangPatterns #-}
tangent :: Num a => AD Forward a -> a
tangent (AD (Forward _ da)) = da
tangent _ = 0
bundle :: a -> a -> AD Forward a
bundle a da = AD (Forward a da)
apply :: Num a => (AD Forward a -> b) -> a -> b
apply f a = f (bundle a 1)
この部分の型：
AD Forward a
どうやらAD型が になるようだ。

11. AD type
Numeric.AD.Types
An instance of Mode class determines
the behavior.
e.g.) AD (Forward 10 1) :: Num a => AD Forward a
{-# LANGUAGE CPP #-}
{-# LANGUAGE Rank2Types, GeneralizedNewtypeDeriving,
TemplateHaskell, FlexibleContexts, FlexibleInstances,
MultiParamTypeClasses, UndecidableInstances #-}
{-# ANN module "HLint: ignore Eta reduce" #-}
newtype AD f a = AD { runAD :: f a } deriving (Iso (f a), Lifted,
Mode, Primal)

12. Classes that have AD type as an instance
Numeric.AD.Types http://hackage.haskell.org/packages/archive/ad/3.4/doc/
html/Numeric-AD-Types.html#t:AD
例：１変数実数スカラー関数 y = f(x)
（fがLiftedのインスタンス &&
aがFloatingのインスタンス）のとき、
AD f a
はFloatingのインスタンス。
diffの第一引数の型
AD s a -> AD s a
は、以下の型に適合する＊
Floating a => a -> a
＊こういう言い方が正確か分からないが。

13. Let’s look at some examples of values with AD type
adtest.hs
import Numeric.AD
import Numeric.AD.Types
import Numeric.AD.Internal.Classes
import Numeric.AD.Internal.Forward
f x = x + 3
g x | x > 0 = x
| otherwise = 0
d = diff (g . f)
GHCi
*Main> :t (g . f)
(g . f) :: (Num c, Ord c) => c -> c
*Main> :t (g . f) :: (Num a, Ord a, Mode s) => AD s a -> AD s a
(g . f) :: (Num a, Ord a, Mode s) => AD s a -> AD s a
:: (Num a, Ord a, Mode s) => AD s a -> AD s a
*Main> :t f
f :: Num a => a -> a
*Main> :t f :: (Num a, Lifted s) => AD s a -> AD s a
f :: (Num a, Lifted s) => AD s a -> AD s a
:: (Num a, Lifted s) => AD s a -> AD s a
*Main> :t g
g :: (Num a, Ord a) => a -> a
*Main> :t d
d :: Integer -> Integer

14. Let’s play around with apply and tangent
GHCi
> :l adtest.hs
[1 of 1] Compiling Main ( adtest.hs, interpreted )
Ok, modules loaded: Main.
[*Main]
> :t apply
apply :: Num a => (AD Forward a -> b) -> a -> b
[*Main]
> :t apply f
apply f :: Num a => a -> AD Forward a Since f :: Num t0 => t0 -> t0,
[*Main] b in the type of apply is restricted to
> :t apply f 0 AD Forward a
apply f 0 :: Num a => AD Forward a
[*Main]
> apply f 0
3
[*Main]
> :t tangent
tangent :: Num a => AD Forward a -> a
[*Main]
> :t tangent $ apply f 0
tangent $ apply f 0 :: Num a => a
[*Main]
> tangent $ apply f 0
1

15. Lifted class and Mode class
Chain rule of differentiation
http://hackage.haskell.org/packages/archive/ad/3.4/doc/
Wrap a (Num a => a) value into t html/Numeric-AD-Internal-Classes.html#t:Mode
Definition of different modes.
Mode is a subclass of Lifted http://hackage.haskell.org/packages/archive/ad/3.4/doc/
html/Numeric-AD-Internal-Classes.html#t:Lifted
e.g.) Forward is an instance of Lifted and Mode

16. Lifted class defines chain rules of differentiation
http://hackage.haskell.org/packages/archive/ad/3.4/doc/html/
src/Numeric-AD-Internal-Classes.html#deriveLifted
deriveLifted (in Numeric.AD.Internal.Classes)というTemplate
Haskellの関数がLiftedのインスタンスを作ってくれる。
A part of deriveLifted
exp1 = lift1_ exp const
log1 = lift1 log recip1
sin1 = lift1 sin cos1
cos1 = lift1 cos $ negate1 . sin1
tan1 = lift1 tan $ recip1 . square1 . cos1

17. deriveNumeric generates instances of Num, etc.
http://hackage.haskell.org/packages/archive/ad/3.4/doc/html/
src/Numeric-AD-Internal-Classes.html#deriveNumeric
deriveNumeric (in Numeric.AD.Internal.Classes)
-- | @'deriveNumeric' f g@ provides the following instances:
--
-- > instance ('Lifted' $f, 'Num' a, 'Enum' a) => 'Enum' ($g a)
-- > instance ('Lifted' $f, 'Num' a, 'Eq' a) => 'Eq' ($g a)
-- > instance ('Lifted' $f, 'Num' a, 'Ord' a) => 'Ord' ($g a)
-- > instance ('Lifted' $f, 'Num' a, 'Bounded' a) => 'Bounded' ($g a)
--
-- > instance ('Lifted' $f, 'Show' a) => 'Show' ($g a)
-- > instance ('Lifted' $f, 'Num' a) => 'Num' ($g a)
-- > instance ('Lifted' $f, 'Fractional' a) => 'Fractional' ($g a)
-- > instance ('Lifted' $f, 'Floating' a) => 'Floating' ($g a)
-- > instance ('Lifted' $f, 'RealFloat' a) => 'RealFloat' ($g a)
-- > instance ('Lifted' $f, 'RealFrac' a) => 'RealFrac' ($g a)
-- > instance ('Lifted' $f, 'Real' a) => 'Real' ($g a)

18. Definition of deriveNumeric
deriveNumeric :: ([Q Pred] -> [Q Pred]) -> Q Type -> Q [Dec]
deriveNumeric f t = do
members <- liftedMembers
let keep n = nameBase n `elem` members
xs <- lowerInstance keep ((classP ''Num [varA]:) . f) t `mapM` [''Enum, ''Eq,
''Ord, ''Bounded, ''Show]
ys <- lowerInstance keep f t `mapM` [''Num,
''Fractional, ''Floating, ''RealFloat,''RealFrac, ''Real, ''Erf, ''InvErf]
return (xs ++ ys)
lowerInstance :: (Name -> Bool) -> ([Q Pred] -> [Q Pred]) -> Q Type -> Name -> Q Dec
lowerInstance p f t n = do
#ifdef OldClassI
ClassI (ClassD _ _ _ _ ds) <- reify n
#else
ClassI (ClassD _ _ _ _ ds) _ <- reify n
#endif
instanceD (cxt (f [classP n [varA]]))
(conT n `appT` (t `appT` varA))
(concatMap lower1 ds)
where
lower1 :: Dec -> [Q Dec]
lower1 (SigD n' _) | p n'' = [valD (varP n') (normalB (varE n'')) []] where
n'' = primed n'
lower1 _ = []
primed n' = mkName $ base ++ [prime] This looks an important part,
where but a bit difficult....
base = nameBase n'
h = head base
prime | isSymbol h || h `elem` "/*-<>" = '!'
| otherwise = '1'

19. A pitfall?
>> :t diff ((**2) :: Floating a => a -> a)
diff ((**2) :: Floating a => a -> a) :: Floating a => a -> a
>> :t diff ((**2) :: Double -> Double)
<interactive>:1:7:
Couldn't match expected type `ad-3.4:Numeric.AD.Internal.Types.AD
s a0'
with actual type `Double'
Expected type: ad-3.4:Numeric.AD.Internal.Types.AD s a0
-> ad-3.4:Numeric.AD.Internal.Types.AD s a0
Actual type: Double -> Double
In the first argument of `diff', namely
`((** 2) :: Double -> Double)'
In the expression: diff ((** 2) :: Double -> Double)
You need to keep functions polymorphic for differentiation.
import Numeric.AD
func x = x ** 2
func2 x = x ** 3
fs = [func, func2]
test = map (f -> diff f 1.0) fs
So, this does not compile. (there is a GHC extension to accept this, isn’t there..?)

20. Summary
An interesting library that shows how to use types and
typeclasses effectively and beautifully.
Sorry, but I’m still unclear about how Lifted actually
executes differentiation
It seems to be done by Num instance of AD f a, via
instance (Lifted f, Num a) => Num (AD f a)...
Things that might be improved for application
• Simplification of terms
• Improving the performance of higher order taylor expansion.
• Is automatic integration possible, maybe?
These might be a good practice for seasoned Haskellers (I’m not...)

21. 感想
• Haskellならではのコードの簡潔さのおかげで、ソースの
どこを追っていけば良いかはわりと明確。
• 他のEkmett氏のライブラリよりは具体的な対象がはっき
りしている分、少しは分かりやすい。
• とはいっても、私には若干（相当？）手に余る感じで、
深いところまでは解説出来ませんでした。知らないGHC
拡張も多し。ただ、人に説明しようとすることで少しは
理解が進んで、嬉しい。