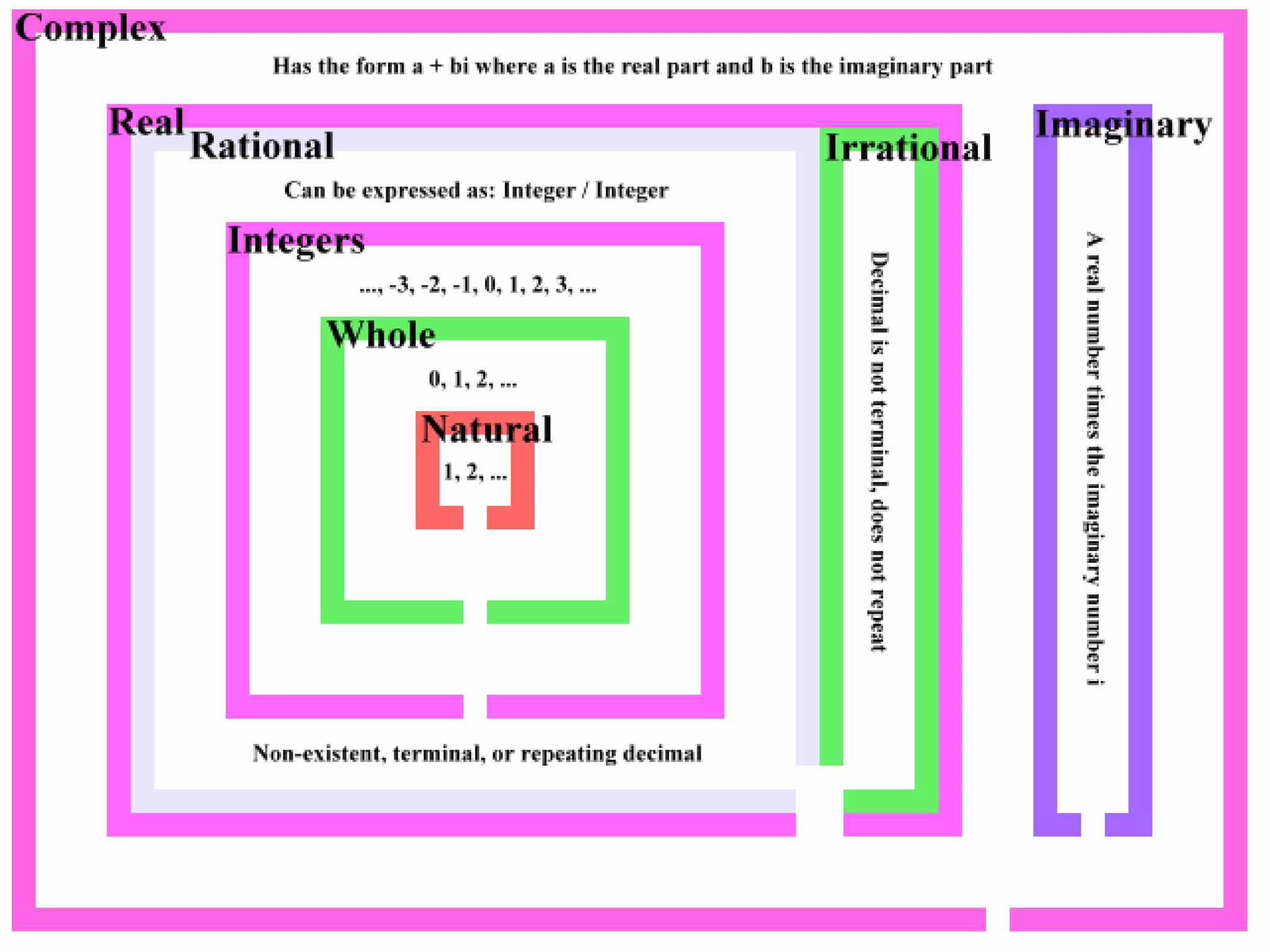
The document provides an overview of the history and types of number systems. It discusses how ancient civilizations like the Egyptians, Babylonians, and Mayans developed different base number systems based on counting fingers and toes. It then explains the modern decimal number system and provides examples of different types of numbers like rational, irrational, integer, natural numbers. The document also briefly touches on concepts like terminating and recurring decimals as well as scientists who contributed to the study of number systems.

1. The mysterious world of numbers…
22

2. Contents
 Acknowledgment
 I nt roduct ion
 Brief I nt roduct ion about
number s
 Hist ory of Number Syst em
 Number Syst em according
t o dif f erent civilizat ions
 Types of Numbers
 Decimal Expansion Of
Number Syst em
 Scient ist s relat ed t o
Number Syst em
 What is a number line?
 What is t he dif f erence
bet ween numeral and
number ?
 Word Alt ernat ives

3. We would like to thank Teema madam for
giving us an opportunity to express ourselves
via mathematical projects.We are also
thankful to Bharti madam, our computer
teacher for letting us use the school
computers for presentation and providing us
with an e-mail ID. Also, we thank our friends
for their ideas and co-operation they
provided to us. We are grateful to all of them.

4. A number system defines a set of values used to
represent a quantity. We talk about the number of
people attending school, number of modules taken
per student etc.
Quantifying items and values in relation to each
other is helpful for us to make sense of our
environment.
The study of numbers is not only related to
computers. We apply numbers everyday, and
knowing how numbers work, will give us an
insight of how computers manipulate and store
numbers.

5. Brief Introduction About
NumbersA number is a mathematical object used in counting
and measuring. It is used in counting and measuring.
Numerals are often used for labels, for ordering serial
numbers, and for codes like ISBNs. In mathematics,
the definition of number has been extended over the
years to include such numbers as zero, negative
numbers, rational numbers, irrational numbers, and
complex numbers.

6. Brief Introduction About
Numbers
Numbers were probably first used many thousands of
years ago in commerce, and initially only whole
numbers and perhaps rational numbers were needed.
But already in Babylonian times, practical problems of
geometry began to require square roots.
Certain procedures which take one or more numbers as
input and produce a number as output are called
numerical operation.

7. The History Of Number System
The number system with which we are
most familiar is the decimal (base-10)
system , but over time our ancestor have
experimented with a wide range of
alternatives, including duo-decimal (base-
12), vigesimal (base-20), and sexagesimal
(base-60)…

8. The Ancient Egyptians
The Ancient Egyptians experimented with duo-decimal (base-
12) system in which they counted finger-joints instead of
finger . Each of our finger has three joints. In addition to their
base-twelve system, the Egyptians also experimented with a sort
–of-base-ten system. In this system , the number 1 through 9
were drawn using the appropriate number of vertical lines.
A human hand palm was the way
of counting used by the
Egyptians…

9. The Ancient Babylonians
Babylonians, were famous for their astrological observations
and calculations, and used a sexagesimal (base-60)
numbering system. In addition to using base sixty, the
babylonians also made use of six and ten as sub-bases. The
babylonians sexagesimal system which first appeared
around 1900 to 1800 BC, is also credited with being the first
known place-value of a particular digit depends on both the
digit itself and its position within the number . This as an
extremely important development, because – prior to place-
value system – people were obliged to use different symbol
to represent different power of a base.

10. Aztecs, Eskimos, And Indian
Merchants.Other cultures such as the Aztecs, developed vigesimal (base-
20) systems because they counted using both finger and toes.
The Ainu of Japan and the Eskimos of Greenland are two of
the peoples who make use of vigesimal systems of present
day . Another system that is relatively easy to understand is
quinary (base-5), which uses five digit : 0, 1, 2, 3, and 4. The
system is particularly interesting , in that a quinary finger-
counting scheme is still in use today by Indian merchant
near Bombay . This allow them to perform calculations on
one hand while serving their customers with the other.
Aztecs were the ethnic
group of Mexico

12. The number system we use on day-to-day basis in the
decimal system , which is based on ten digits: zero
through nine. As the decimal system is based on ten
digits, it is said to be base -10 or radix-10. Outside of
specialized requirement such as computing , base-10
numbering system have been adopted almost
universally.The decimal system with which we are
fated is a place-value system, which means that the
value of a particular digit depends both on the itself
and on its position within the number.

13. This system is unique to our current decimal
system, as our current decimal system uses
base -10 whereas, the Mayan Number
System uses base- 20.
The Mayan system used a combination of
two symbols. A dot (.) was used to represent
the units and a dash (-) was used to
represent five.The Mayan's wrote their
numbers vertically as opposed to
horizontally with the lowest denomination
on the bottom. Several numbers according to Mayan
Number System

14. The binary numeral system, or base-2 number
system, represents numeric values using two symbols, 0
and 1. More specifically, the usual base-2 system is a
positional notation with a radix of 2. Owing to its
straight forward implementation in digital electronic
circuitry using logic gates, the binary system is used
internally by all modern computers. Counting in binary
is similar to counting in any other number system.
Beginning with a single digit, counting proceeds through
each symbol, in increasing order. Decimal counting uses
the symbols 0 through 9, while binary only uses the
symbols 0 and 1.

15. Ancient Egyptians had an understanding of fractions,
however they did not write simple fractions as 3/5 or 4/9
because of restrictions in notation.The Egyptian scribe
wrote fractions with the numerator of 1.They used the
hieroglyph “an open mouth" above the number to
indicate its reciprocal.The number 5, written , as a fraction
1/5 would be written as . . .There are some exceptions.
There was a special hieroglyph for 2/3, , and some
evidence that 3/4 also had a special hieroglyph. All other
fractions were written as the sum of unit fractions. For
example 3/8 was written as 1/4 + 1/8.

16. Types of numbers

18. The real numbers include all of the measuring numbers .
Real numbers are usually written using decimal numerals ,
in which a decimal point is placed to the right of the digit
with place value one.
 It includes all types of numbers such as Integers,Whole
numbers, Natural numbers, Rational number, Irrational
numbers and etc… Let us see them in detail…

19. A rational number is a number that can be
expressed as a fraction with an integer
numerator and a non-zero natural number
denominator.The symbol of the rational
number is ‘Q’. It includes all types of
numbers other than irrational numbers, i.e.
it includes integers, whole number, natural
numbers etc…

20. This is a type of a rational number. Fractions are written
as two numbers, the numerator and the denominator
,with a dividing bar between them.
 In the fraction m/n ‘m’ represents equal parts, where ‘n’
equal parts of that size make up one whole.
 If the absolute value of m is greater than n ,then the
absolute value of the fraction is greater than 1.Fractions
can be greater than ,less than ,or equal to1 and can
also be positive ,negative , or zero.

21. If a real number cannot be written as a fraction of two
integers, i.e. it is not rational, it is called irrational
numbers . A decimal that can be written as a fraction
either ends(terminates)or forever repeats about which
we will see in detail further.
Real number pi (π) is an example of irrational.
π=3.14159365358979……the number neither start
repeating themselves or come in a specific pattern.

22.  Integers are the number which includes
positive and negative numbers.
 Negative numbers are numbers that are less
than zero.They are opposite of positive
numbers . Negative numbers are usually
written with a negative sign(also called a
minus sign)in front of the number they are
opposite of .When the set of negative
numbers is combined with the natural
numbers zero, the result is the set of integer
numbers , also called ‘Z’.

23.  The most familiar numbers are the
natural numbers or counting numbers:
One,Two,Three and so on….
 Traditionally, the sequence of natural
numbers started with 1.However in the
19th
century, mathematicians started
including 0 in the set of natural numbers.
 The mathematical symbol for the set of
all natural numbers is ‘N’.

24. Moving to a greater level of abstraction, the real numbers can
be extended to the complex numbers. This set of number
arose historically, from trying to find closed formulas for the
roots of cubic and quadratic polynomials. This led to
expressions involving the square roots of negative numbers,
eventually to the definition of a new number: the square root
of negative one denoted by “I”. The complex numbers consist
of all numbers of the form (a+bi) ; Where a and b are real
numbers.

25. Other Types
There are different kind of other numbers too. It includes
 hyper-real numbers,
 hyper-complex numbers,
 p-adic numbers,
 surreal numbers etc.
These numbers are rarely used in our day-to-day life.
Therefore, we need not know about them in detail.

26. A decimal expansion of a number can be
either,
 Terminating
 Non-terminating, non recurring
 Non terminating, recurring
Let us see each of the following
briefly…

27. A decimal expansion in which the remainder
becomes zero. For example, 54 9 =
Terminating decimal is always a rational number.
It can be written in p/q form.
549
6
54
0
As the remainder is zero, this
is a terminating decimal

28. “Recurring” means “repeating”. In this form, when we
divide a number by another, remainder never becomes
zero, and also the number does not repeat themselves in
any specific pattern. If a number is non terminating and
non repeating, they are always classified as irrational
number. For example,
0.10100100010000100000100.... does have a pattern, but
it is not a fixed-length recurring pattern, so the number
is irrational.

29. In this form, when a number is divided by the other, the
remainder never becomes zero, instead the numbers of the
quotient start repeating themselves. Such numbers are
classified as rational numbers. For example,
3.7250725072507250…
In this example, “7250” have started repeating itself.
Hence, it is a rational number. It can be expressed in p/q
form.

30. Euclid :
Euclid was an ancient mathematician from
Alexandria, who is best known for his major work,
Elements. He told about the division lemma,
according to which,
A prime number that divides a product of two
integers must divide one of the two integer.
Euclid – The father of geometry

31. R. Dedekind And G. Cantor :
In 1870s two German mathematicians; Cantor and
Dedekind, showed that :
Corresponding to every real number, there is a point
on the number line, and corresponding to every
point on the number line, there exists a unique real
number.
R. DedekindG. Cantor

32. Archimedes :
He was a Greek mathematician. He was the first to
compute the digits in the decimal expansion of π (pi).
He showed that -
3.140845 < π < 3.142857
Archimedes

33. What is a number line?
A number line is a line with marks on it that are
placed at equal distance apart. One mark on the
number line is usually labeled zero and then each
successive mark to the left or to the write of the zero
represents a particular unit such as 1, or 0.5. It is a
picture of a straight line.
A number line

34. No, number and numerals are not same. Numerals
are used to make numbers. It is a symbol used to
represent a number.
For example, the NUMERAL 4 is the name of
NUMBER four.
Numeral “7”
Number 7

35. Some numbers traditionally have words to express
them, including the following:
 Pair, couple, brace: 2
 Dozen: 12
 Bakers dozen: 13
 Score: 20
 Gross: 144
 Ream(new measure): 500
 Great gross: 1728

37. Project made and Compiled
by ~
Murugesh
Subash
Sethuarvind