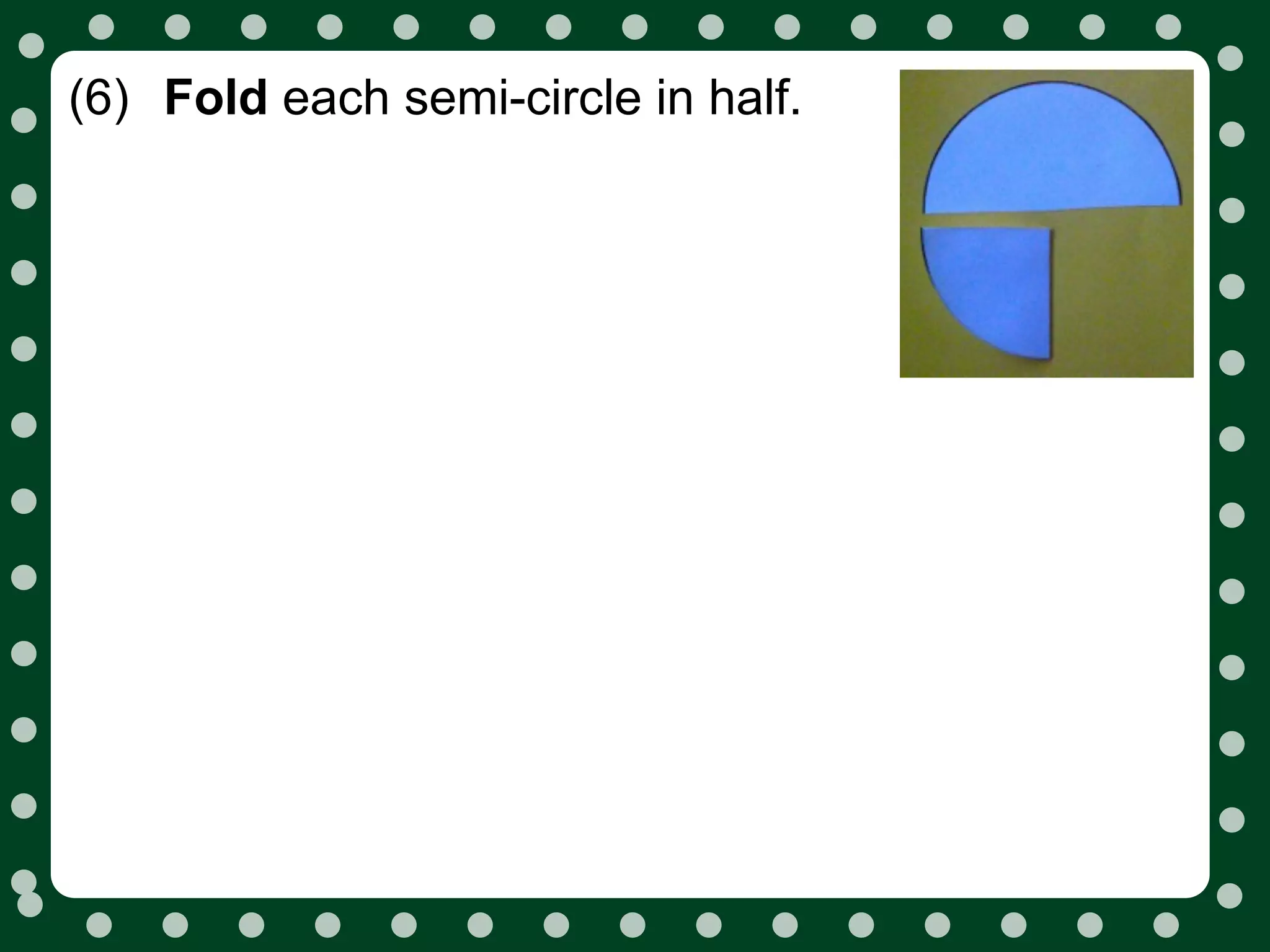
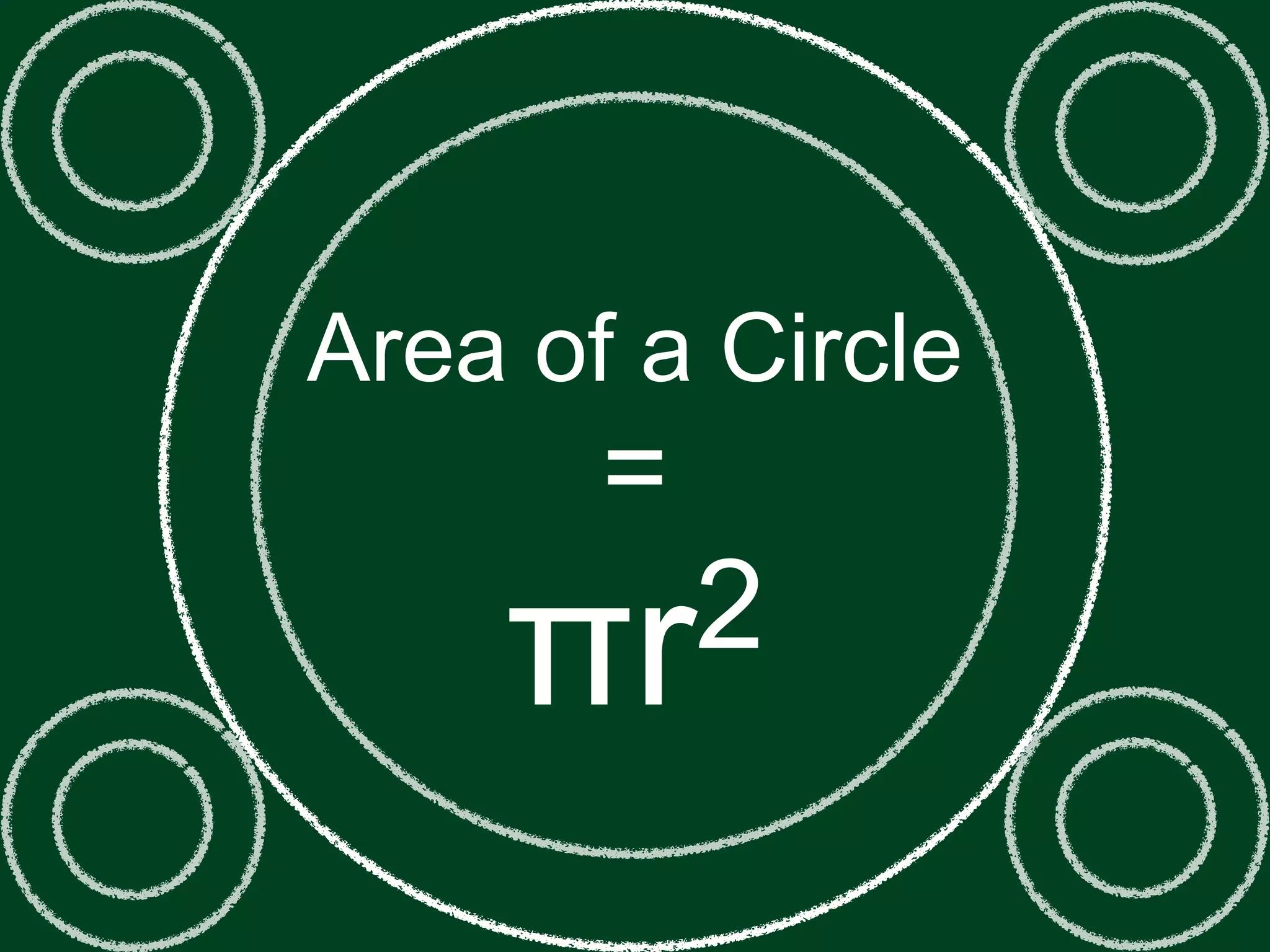
The document describes how ancient mathematicians derived the formula for the area of a circle by cutting a circle into pieces and rearranging them to form a rectangle. They determined that the height of the rectangle is equal to the radius of the circle, and the base is equal to half the circumference. Substituting these relationships into the area formula for a rectangle produces the area of a circle formula: A = πr2.

1. How did they
come up with the
formula for the
area of a circle?

2. Gather the following
• Print Circle.pdf

3. Gather the following
• Print Circle.pdf
• If no access to a printer, get a circular object
such as a cup or can, and piece of paper. Trace
the circle onto the paper.

4. Gather the following
• Print Circle.pdf
• If no access to a printer, get a circular object
such as a cup or can, and piece of paper. Trace
the circle onto the paper.
• Scissors

5. Gather the following
• Print Circle.pdf
• If no access to a printer, get a circular object
such as a cup or can, and piece of paper. Trace
the circle onto the paper.
• Scissors
• Ruler

6. Do the following
• Use your scissors to cut out the circle.

7. Do the following
• Use your scissors to cut out the circle.
• Keep your scissors handy as you will
need them.

8. Do the following
• Use your scissors to cut out the circle.
• Keep your scissors handy as you will
need them.
• Work through the steps on the next several
pages using your cut out circle.

9. Do the following
• Use your scissors to cut out the circle.
• Keep your scissors handy as you will
need them.
• Work through the steps on the next several
pages using your cut out circle.
• When you see record, write the answer on your
Learning Guide.

10. (1) Fold the circle in half.

11. (1) Fold the circle in half.
(2) What does this fold represent?

12. (1) Fold the circle in half.
(2) What does this fold represent?
✓ The diameter.

13. (1) Fold the circle in half.
(2) What does this fold represent?
✓ The diameter.
(3) Use the ruler to measure the fold.
Record the measure of the fold.

14. (1) Fold the circle in half.
(2) What does this fold represent?
✓ The diameter.
(3) Use the ruler to measure the fold.
Record the measure of the fold.
(4) Using the diameter, find the circumference of
the circle and record the result.

15. (1) Fold the circle in half.
(2) What does this fold represent?
✓ The diameter.
(3) Use the ruler to measure the fold.
Record the measure of the fold.
(4) Using the diameter, find the circumference of
the circle and record the result.
(5) Cut the circle on the fold to
create 2 semi-circles.

16. (6) Fold each semi-circle in half.

17. (6) Fold each semi-circle in half.
(7) What does this fold represent?

18. (6) Fold each semi-circle in half.
(7) What does this fold represent?
✓ The radius.

19. (6) Fold each semi-circle in half.
(7) What does this fold represent?
✓ The radius.
(8) Record the measure of the fold.

20. (6) Fold each semi-circle in half.
(7) What does this fold represent?
✓ The radius.
(8) Record the measure of the fold.
(9) Cut the semi-circles on the folds. You should
have 4 pieces now.

21. (6) Fold each semi-circle in half.
(7) What does this fold represent?
✓ The radius.
(8) Record the measure of the fold.
(9) Cut the semi-circles on the folds. You should
have 4 pieces now.
(10) Each piece represents what
fraction of the circle?

22. (6) Fold each semi-circle in half.
(7) What does this fold represent?
✓ The radius.
(8) Record the measure of the fold.
(9) Cut the semi-circles on the folds. You should
have 4 pieces now.
(10) Each piece represents what
fraction of the circle?
✓ 1/4

23. (11)Fold each of the 4 pieces in half.

24. (11)Fold each of the 4 pieces in half.
(12)Record the measure of the fold.

25. (11)Fold each of the 4 pieces in half.
(12)Record the measure of the fold.
(13)Record your observation
between this fold to the other 2 folds.

26. (11)Fold each of the 4 pieces in half.
(12)Record the measure of the fold.
(13)Record your observation
between this fold to the other 2 folds.
(14)What does this fold represent?

27. (11)Fold each of the 4 pieces in half.
(12)Record the measure of the fold.
(13)Record your observation
between this fold to the other 2 folds.
(14)What does this fold represent?
✓ The radius.

28. (11)Fold each of the 4 pieces in half.
(12)Record the measure of the fold.
(13)Record your observation
between this fold to the other 2 folds.
(14)What does this fold represent?
✓ The radius.
(15)Cut the 4 pieces on the folds.
You should now have 8 pieces.

29. (16)Each piece represents what fraction of the
circle?

30. (16)Each piece represents what fraction of the
circle?
✓ 1/8

31. (16)Each piece represents what fraction of the
circle?
✓ 1/8
(17)Fold each of the 8 pieces in
half.

32. (16)Each piece represents what fraction of the
circle?
✓ 1/8
(17)Fold each of the 8 pieces in
half.
(18)Record the measure of the fold.

33. (16)Each piece represents what fraction of the
circle?
✓ 1/8
(17)Fold each of the 8 pieces in
half.
(18)Record the measure of the fold.
(19)Record your observation between this fold to
the other 3 folds.

34. (20)What does this fold represent?

35. (20)What does this fold represent?
✓ The radius.

36. (20)What does this fold represent?
✓ The radius.
(21)Cut the 8 pieces on the folds. You should
have 16 pieces.

37. (20)What does this fold represent?
✓ The radius.
(21)Cut the 8 pieces on the folds. You should
have 16 pieces.
(22)Each piece represents what fraction of the
circle?

38. (20)What does this fold represent?
✓ The radius.
(21)Cut the 8 pieces on the folds. You should
have 16 pieces.
(22)Each piece represents what fraction of the
circle?
✓ 1/16

39. (23)Arrange the pieces of the circle to make a
rectangle best you can.

40. (23)Arrange the pieces of the circle to make a
rectangle best you can.
(24)Record the measure of the base and height
of the rectangle created.

41. (25) Record your observations between the
measure of the base and height of the
rectangle and previous measures recorded or
calculated.

42. (25) Record your observations between the
measure of the base and height of the
rectangle and previous measures recorded or
calculated.
(26)How do you find the area of a rectangle?

43. (25) Record your observations between the
measure of the base and height of the
rectangle and previous measures recorded or
calculated.
(26)How do you find the area of a rectangle?
✓ Area = base * height

44. (25) Record your observations between the
measure of the base and height of the
rectangle and previous measures recorded or
calculated.
(26)How do you find the area of a rectangle?
✓ Area = base * height
(27)Notice the height of the rectangle is one of
the cuts made. What is the relationship
between the cut and the circle?

45. ✓ The radius.

46. ✓ The radius.
(28)What part of the circle makes up the longer
sides of the rectangle?

47. ✓ The radius.
(28)What part of the circle makes up the longer
sides of the rectangle?
✓ The circumference.

48. ✓ The radius.
(28)What part of the circle makes up the longer
sides of the rectangle?
✓ The circumference.
(29)How do you find the circumference of a
circle?

49. ✓ The radius.
(28)What part of the circle makes up the longer
sides of the rectangle?
✓ The circumference.
(29)How do you find the circumference of a
circle?
✓ C = 2πr or

50. ✓ The radius.
(28)What part of the circle makes up the longer
sides of the rectangle?
✓ The circumference.
(29)How do you find the circumference of a
circle?
✓ C = 2πr or
✓ C = πd

51. (30)To find the area of a rectangle, only one of
the 2 bases (or longer sides) is needed.

52. (30)To find the area of a rectangle, only one of
the 2 bases (or longer sides) is needed.
(31)If C = 2πr is used to find the circumference
of the whole circle, how can you find the
length of one base?

53. (30)To find the area of a rectangle, only one of
the 2 bases (or longer sides) is needed.
(31)If C = 2πr is used to find the circumference
of the whole circle, how can you find the
length of one base?
✓ Divide the circumference by 2 to represent
half the diameter.

54. Recap what we have
✓ The height of the rectangle is the radius of the
original circle.

55. Recap what we have
✓ The height of the rectangle is the radius of the
original circle.
✓ The base of the rectangle is half the
circumference of the original circle.

56. Recap what we have
✓ The height of the rectangle is the radius of the
original circle.
✓ The base of the rectangle is half the
circumference of the original circle.
✓ The area of a rectangle is found by multiplying
the base times the height of the rectangle.

57. Recap what we have
✓ The height of the rectangle is the radius of the
original circle.
✓ The base of the rectangle is half the
circumference of the original circle.
✓ The area of a rectangle is found by multiplying
the base times the height of the rectangle.
✓ Substitute what was found for the base and
height to find the formula for the area of a circle.

58. Area of a Circle Formula
A = b⋅h • Start with the formula
for the area of a
rectangle.

59. Area of a Circle Formula
A = b⋅h • Start with the formula
for the area of a
rectangle.
• Substitute the base as
half the circumference.

60. Area of a Circle Formula
A = b⋅h • Start with the formula
1 for the area of a
A = ⋅ 2π r ⋅ h rectangle.
2
• Substitute the base as
half the circumference.

61. Area of a Circle Formula
A = b⋅h • Start with the formula
1 for the area of a
A = ⋅ 2π r ⋅ h rectangle.
2
• Substitute the base as
half the circumference.
• Substitute the radius
for the height.

62. Area of a Circle Formula
A = b⋅h • Start with the formula
1 for the area of a
A = ⋅ 2π r ⋅ h rectangle.
2
1 • Substitute the base as
A = ⋅ 2π r ⋅ r
2 half the circumference.
• Substitute the radius
for the height.

63. Area of a Circle Formula
A = b⋅h • Start with the formula
1 for the area of a
A = ⋅ 2π r ⋅ h rectangle.
2
1 • Substitute the base as
A = ⋅ 2π r ⋅ r
2 half the circumference.
• Substitute the radius
for the height.
• Simplify.

64. Area of a Circle Formula
A = b⋅h • Start with the formula
1 for the area of a
A = ⋅ 2π r ⋅ h rectangle.
2
1 • Substitute the base as
A = ⋅ 2π r ⋅ r
2 half the circumference.
1 1+1
• Substitute the radius
A = ⋅ 2π r
2
for the height.
• Simplify.

65. Area of a Circle Formula
A = b⋅h • Start with the formula
1 for the area of a
A = ⋅ 2π r ⋅ h rectangle.
2
1 • Substitute the base as
A = ⋅ 2π r ⋅ r
2 half the circumference.
1 1+1
• Substitute the radius
A = ⋅ 2π r
2
for the height.
2
A = πr • Simplify.

66. Area of a Circle
=
πr 2