1. 時系列データ分析 4
ホワイトノイズから分散不均一構造へ
-ARCH,GARCH モデルの活用 -

2. これまでの流れ１
・全ての時点でのデータの確率分布は、同一分布と仮定
・同一の確率分布から独立にデータを抽出したと仮定
本当に同一分布なのか？
時間依存していないのか？
◎ 自己相関性（自己相関係数）を
調べる
・コレログラムの作成
→ acf( 【対象データ】 .plot=T)
・ Ljung-Box 検定
→ 自己相関関係の有無を判定
全ての時点の確率分布が
同一分布だと考えて良いのか？
① （弱）定常性の検討
・平均が一定
・分散が一定
・自己共分散がラグにのみ依存
②ホワイトノイズの検討
・平均が０
・分散が一定
・自己共分散が０
◎ 誤差項が定常性（ホワイトノイズ）を満たすと仮定した１次自己回帰
モデルの導入

3. これまでの流れ２
◎ 誤差項が定常性（ホワイトノイズ）を満たすと仮定した１次自己回帰
モデルの導入
AR(1) は、モデルとして妥当なのか？評価が必要。
◎ 自己回帰係数 Φ の大きさによる特徴で分類
① |Φ|<1 の場合：定常性を満たす。
② Φ=1 の場合 ：単位根を持つ非定常時系列。
③それ以外の場合：非定常。
だけど、自己回帰係数は事前には分からないのでは？
◎ 単位根検定を実施する！これにより、モデルが定常であるかを判定す
る！
・ Dickey-Fuller 検定 （ DF 検定）
・拡張 Dickey-Fuller 検定 （ ADF 検定）
・ Phillips-Perron 検定 （ PP 検定）
・ McKinnons's 検定

4. ここから考える事
◎ 単位根検定だけ？
◎ 誤差平均（残差系列）と誤差分散（残差の２乗系列）を調べる
・コレログラム acf( 【対象データ】 ,plot=T)
・ AIC による次数選択 ar(ar.fit$ データ )$order
・ Lung-Box 検定 Box.test(ar.fit$ データ , type=“L”)
残差に自己相関が現れた。どうするか？
分散不均一性を説明するモデルを検討する。
・ ARCH モデル
・ GARCH モデル

5. ARCH モデルと GARCH モデル
分散不均一性を説明するモデル。
・ ARCH モデル
・ GARCH モデル

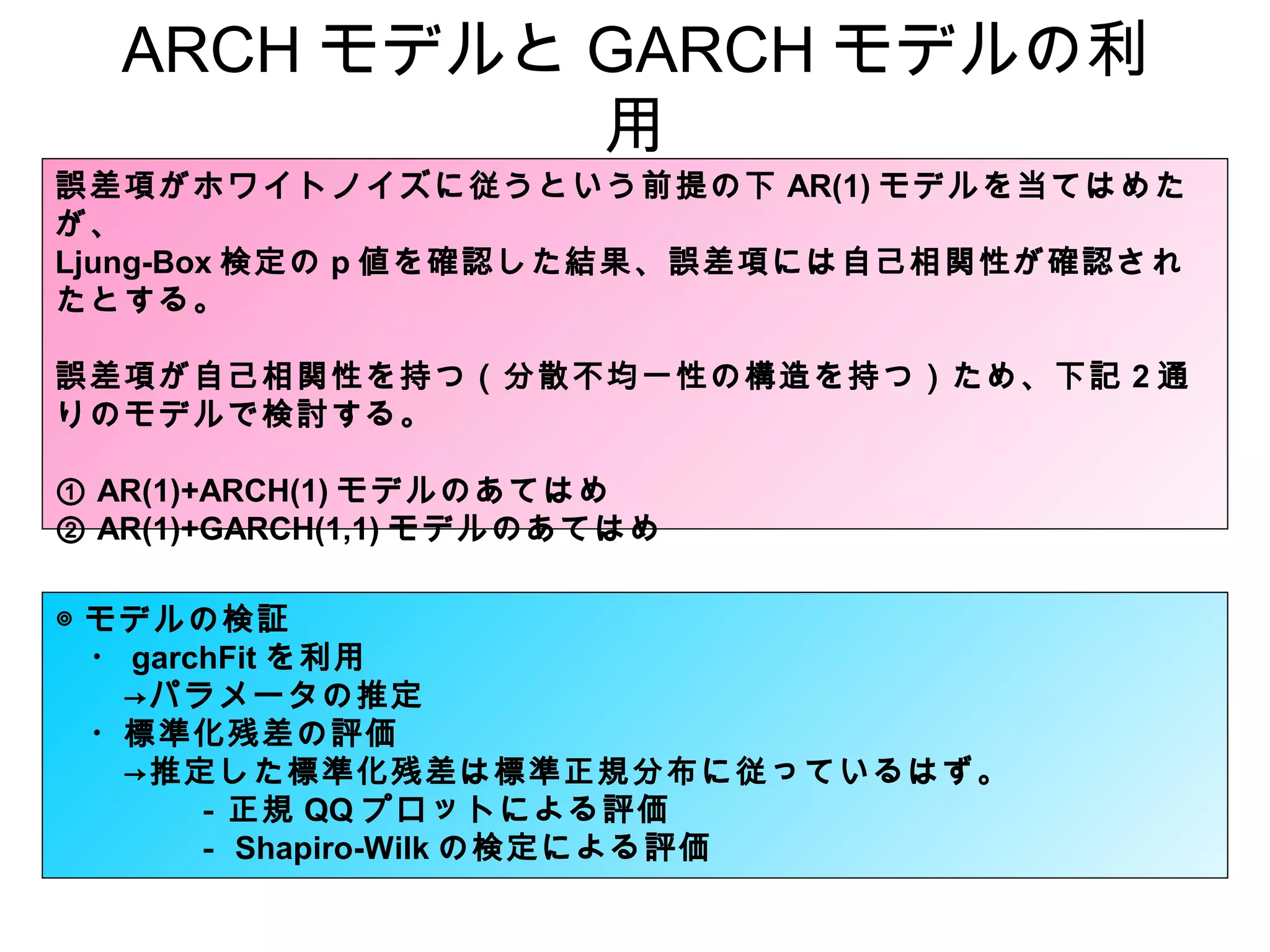
6. ARCH モデルと GARCH モデルの利
用
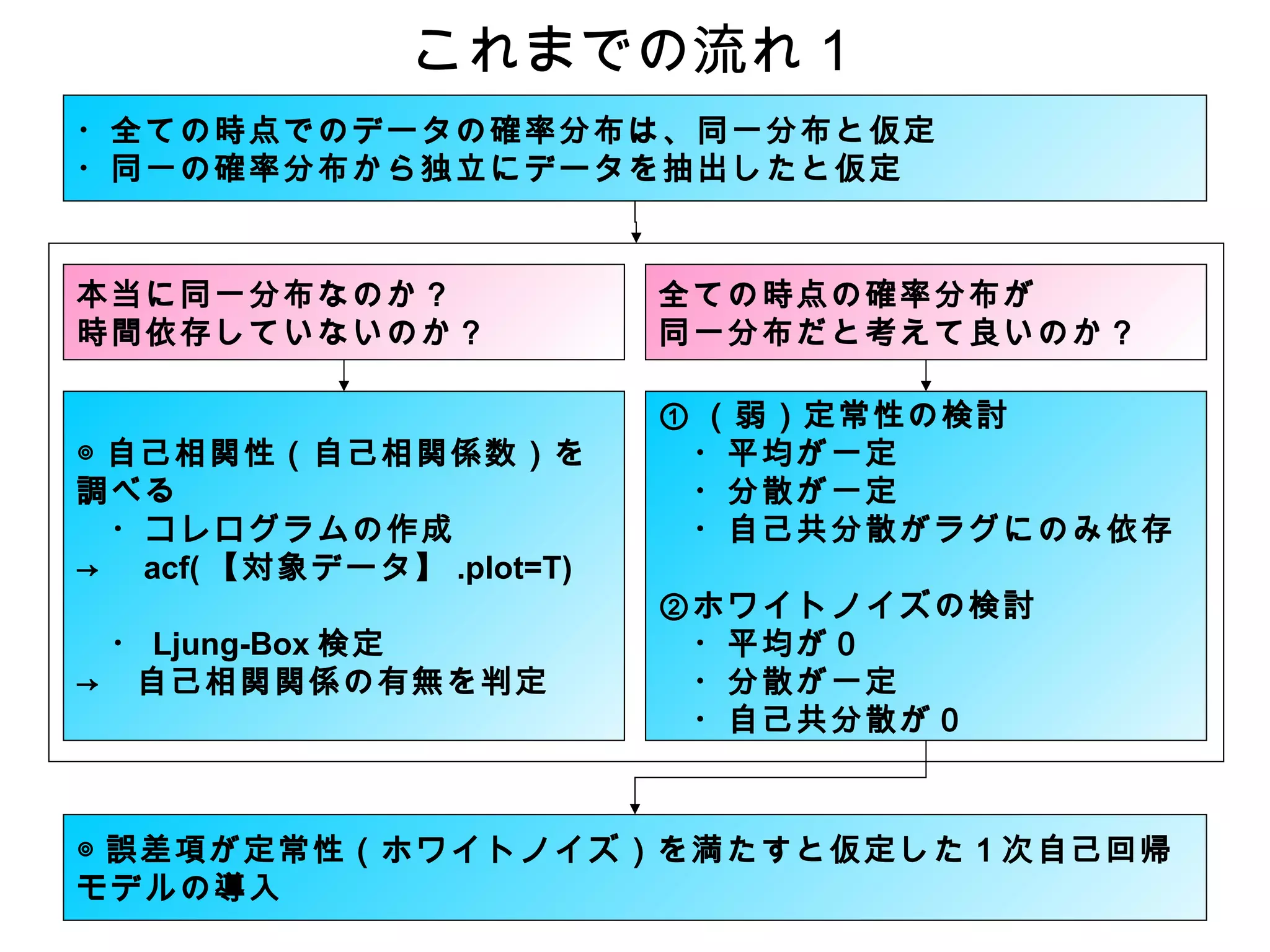
誤差項がホワイトノイズに従うという前提の下 AR(1) モデルを当てはめた
が、
Ljung-Box 検定の p 値を確認した結果、誤差項には自己相関性が確認され
たとする。
誤差項が自己相関性を持つ（分散不均一性の構造を持つ）ため、下記 2 通
りのモデルで検討する。
① AR(1)+ARCH(1) モデルのあてはめ
② AR(1)+GARCH(1,1) モデルのあてはめ
◎ モデルの検証
・ garchFit を利用
→パラメータの推定
・標準化残差の評価
→推定した標準化残差は標準正規分布に従っているはず。
－正規 QQ プロットによる評価
－ Shapiro-Wilk の検定による評価

7. 非正規な標準化残差
ARCH や GARCH では、標準化残差として標準正規分布を仮定している。
しかし、 garchFit や正規 QQ プロットによる検証の結果、標準化残差が標
準正規分布に従っていないことが判明したら、どうすればよいのだろう
か？
◎ 標準化残差の従う分布を、標準正規分布から変更する
※）モデルの検証は、これまでと同様に garchFit でパラメータを推定し
て、仮定した標準化残差の分布の適応度を QQ プロットで調べるとよい。
しかし、正規分布ではないため、 Shapiro-Wilk 検定は使えない。そこで
、汎用的な適合度検定である、 Kolmogorov-Smirnov 検定を使用する。
◎ GARCH モデルの構造に手を入れる
→今回は割愛