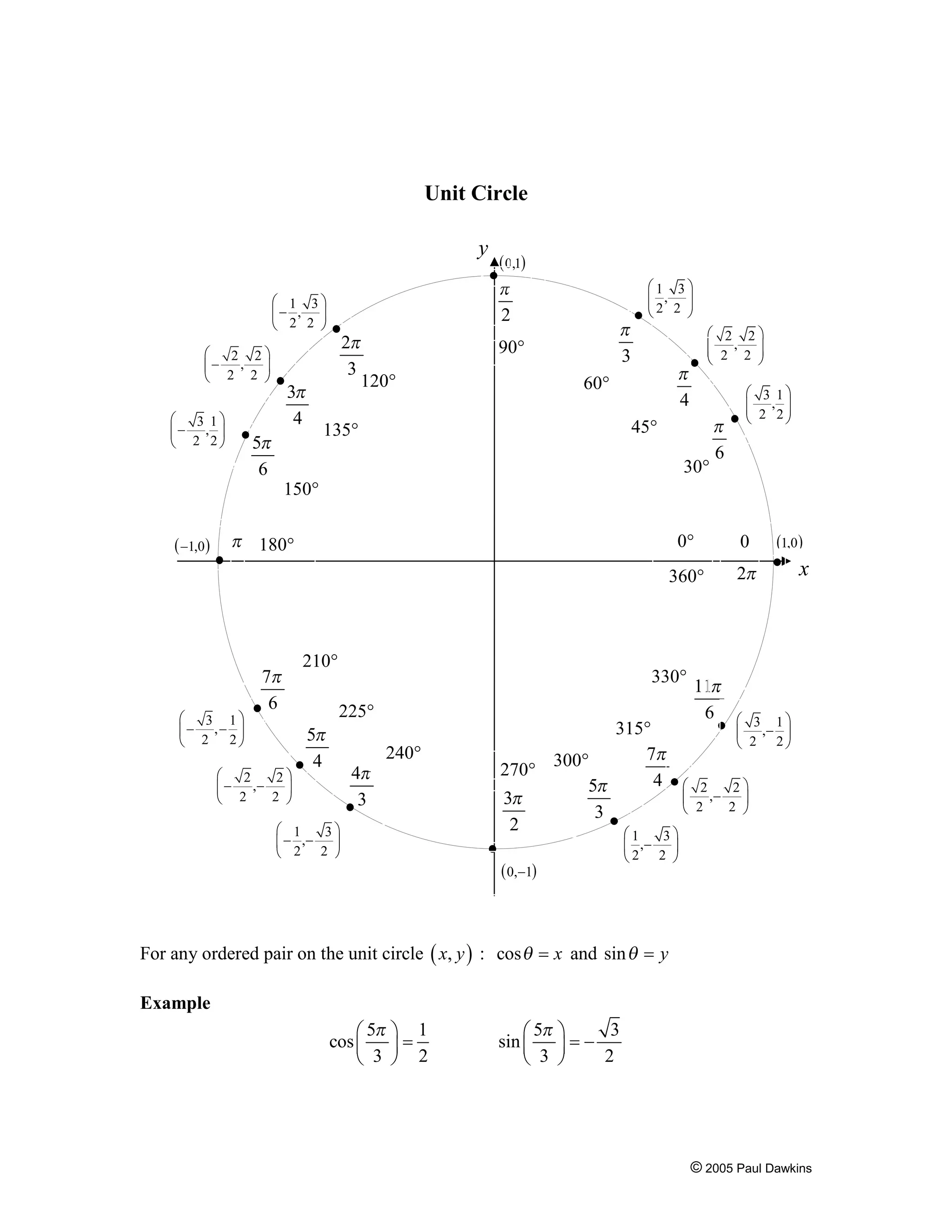
This document provides a trigonometry cheat sheet with definitions and properties of trig functions including: - Definitions of trig functions using right triangles and the unit circle. - Domain, range, and period of each trig function. - Important formulas and identities involving trig functions like sum and difference, double angle, and half angle formulas. - Information on inverse trig functions like domain, range, and alternative notations. - Laws involving trig functions like the Law of Sines, Cosines, and Tangents.

1. Trig Cheat Sheet
Definition of the Trig Functions
Right triangle definition
For this definition we assume that
p
0 < q < or 0° < q < 90° .
2
Unit circle definition
For this definition q is any angle.
y
( x, y )
hypotenuse
y
opposite
1
q
x
x
q
adjacent
opposite
hypotenuse
adjacent
cos q =
hypotenuse
opposite
tan q =
adjacent
sin q =
hypotenuse
opposite
hypotenuse
sec q =
adjacent
adjacent
cot q =
opposite
csc q =
y
=y
1
x
cos q = = x
1
y
tan q =
x
sin q =
1
y
1
sec q =
x
x
cot q =
y
csc q =
Facts and Properties
Domain
The domain is all the values of q that
can be plugged into the function.
sin q , q can be any angle
cos q , q can be any angle
1ö
æ
tan q , q ¹ ç n + ÷ p , n = 0, ± 1, ± 2,K
2ø
è
csc q , q ¹ n p , n = 0, ± 1, ± 2,K
1ö
æ
sec q , q ¹ ç n + ÷ p , n = 0, ± 1, ± 2,K
2ø
è
cot q , q ¹ n p , n = 0, ± 1, ± 2,K
Range
The range is all possible values to get
out of the function.
csc q ³ 1 and csc q £ -1
-1 £ sin q £ 1
-1 £ cos q £ 1 sec q ³ 1 and sec q £ -1
-¥ < tan q < ¥
-¥ < cot q < ¥
Period
The period of a function is the number,
T, such that f (q + T ) = f (q ) . So, if w
is a fixed number and q is any angle we
have the following periods.
2p
w
2p
=
w
p
=
w
2p
=
w
2p
=
w
p
=
w
sin ( wq ) ®
T=
cos (wq ) ®
T
tan (wq ) ®
T
csc (wq ) ®
T
sec (wq ) ®
T
cot (wq ) ®
T
© 2005 Paul Dawkins

2. Formulas and Identities
Tangent and Cotangent Identities
sin q
cos q
tan q =
cot q =
cos q
sin q
Reciprocal Identities
1
1
csc q =
sin q =
sin q
csc q
1
1
sec q =
cos q =
cos q
sec q
1
1
cot q =
tan q =
tan q
cot q
Pythagorean Identities
sin 2 q + cos 2 q = 1
tan 2 q + 1 = sec 2 q
1 + cot 2 q = csc 2 q
Even/Odd Formulas
sin ( -q ) = - sin q
csc ( -q ) = - csc q
cos ( -q ) = cos q
sec ( -q ) = sec q
tan ( -q ) = - tan q
cot ( -q ) = - cot q
Periodic Formulas
If n is an integer.
sin (q + 2p n ) = sin q
csc (q + 2p n ) = csc q
cos (q + 2p n ) = cos q sec (q + 2p n ) = sec q
tan (q + p n ) = tan q
cot (q + p n ) = cot q
Double Angle Formulas
sin ( 2q ) = 2sin q cos q
cos ( 2q ) = cos 2 q - sin 2 q
= 2 cos 2 q - 1
= 1 - 2sin 2 q
2 tan q
tan ( 2q ) =
1 - tan 2 q
Degrees to Radians Formulas
If x is an angle in degrees and t is an
angle in radians then
p
t
px
180t
=
Þ t=
and x =
180 x
180
p
Half Angle Formulas
1
sin 2 q = (1 - cos ( 2q ) )
2
1
cos 2 q = (1 + cos ( 2q ) )
2
1 - cos ( 2q )
tan 2 q =
1 + cos ( 2q )
Sum and Difference Formulas
sin (a ± b ) = sin a cos b ± cos a sin b
cos (a ± b ) = cos a cos b m sin a sin b
tan a ± tan b
1 m tan a tan b
Product to Sum Formulas
1
sin a sin b = écos (a - b ) - cos (a + b ) ù
û
2ë
1
cos a cos b = é cos (a - b ) + cos (a + b ) ù
û
2ë
1
sin a cos b = ésin (a + b ) + sin (a - b ) ù
û
2ë
1
cos a sin b = ésin (a + b ) - sin (a - b ) ù
û
2ë
Sum to Product Formulas
æa + b ö
æa - b ö
sin a + sin b = 2sin ç
÷ cos ç
÷
è 2 ø
è 2 ø
æa + b ö æa - b ö
sin a - sin b = 2 cos ç
÷ sin ç
÷
è 2 ø è 2 ø
æa + b ö
æa - b ö
cos a + cos b = 2 cos ç
÷ cos ç
÷
è 2 ø
è 2 ø
æa + b ö æa - b ö
cos a - cos b = -2sin ç
÷ sin ç
÷
è 2 ø è 2 ø
Cofunction Formulas
tan (a ± b ) =
æp
ö
sin ç - q ÷ = cos q
è2
ø
æp
ö
csc ç - q ÷ = sec q
è2
ø
æp
ö
cos ç - q ÷ = sin q
è2
ø
æp
ö
sec ç - q ÷ = csc q
è2
ø
æp
ö
tan ç - q ÷ = cot q
2
è
ø
æp
ö
cot ç - q ÷ = tan q
2
è
ø
© 2005 Paul Dawkins

3. Unit Circle
y
p
2
æ 1 3ö
ç- , ÷
è 2 2 ø
æ
2 2ö
,
ç÷
2 2 ø
è
æ
3 1ö
ç- , ÷
è 2 2ø
3p
4
5p
6
( 0,1)
2p
3
p
3
90°
120°
æ1 3ö
ç , ÷
ç2 2 ÷
è
ø
æ 2 2ö
ç
ç 2 , 2 ÷
÷
è
ø
p
4
60°
45°
135°
30°
p
6
æ 3 1ö
ç , ÷
ç 2 2÷
è
ø
150°
p 180°
æ
3 1ö
ç - ,- ÷
2ø
è 2
7p
6
æ
2
2ö
,ç÷
2
2 ø
è
0°
210°
0
360°
( -1,0 )
2p
330°
225°
5p
4
4p
3
240°
æ 1
3ö
ç - ,÷
è 2 2 ø
315°
7p
300°
270°
4
5p
3p
3
2
æ
(1,0 )
11p
6
x
æ 3 1ö
ç ,- ÷
è 2 2ø
æ 2
2ö
,ç
÷
2 ø
è 2
1
3ö
ç ,÷
è2 2 ø
( 0,-1)
For any ordered pair on the unit circle ( x, y ) : cos q = x and sin q = y
Example
æ 5p
cos ç
è 3
ö 1
÷=
ø 2
æ 5p
sin ç
è 3
3
ö
÷=2
ø
© 2005 Paul Dawkins

4. Inverse Trig Functions
Definition
y = sin -1 x is equivalent to x = sin y
Inverse Properties
cos ( cos -1 ( x ) ) = x
cos -1 ( cos (q ) ) = q
sin ( sin -1 ( x ) ) = x
y = tan -1 x is equivalent to x = tan y
Domain and Range
Function
Domain
y = sin -1 x
-1
-1 £ x £ 1
y = cos x
-1 £ x £ 1
y = tan -1 x
-¥ < x < ¥
sin -1 ( sin (q ) ) = q
tan ( tan -1 ( x ) ) = x
y = cos -1 x is equivalent to x = cos y
tan -1 ( tan (q ) ) = q
Alternate Notation
sin -1 x = arcsin x
Range
p
p
- £ y£
2
2
0£ y £p
p
p
- < y<
2
2
cos -1 x = arccos x
tan -1 x = arctan x
Law of Sines, Cosines and Tangents
c
b
a
a
g
b
Law of Sines
sin a sin b sin g
=
=
a
b
c
Law of Tangents
a - b tan 1 (a - b )
2
=
1
a + b tan 2 (a + b )
Law of Cosines
a 2 = b2 + c 2 - 2bc cos a
b - c tan 1 ( b - g )
2
=
b + c tan 1 ( b + g )
2
b 2 = a 2 + c 2 - 2ac cos b
c 2 = a 2 + b 2 - 2ab cos g
a - c tan 1 (a - g )
2
=
1
a + c tan 2 (a + g )
Mollweide’s Formula
a + b cos 1 (a - b )
2
=
c
sin 1 g
2
© 2005 Paul Dawkins