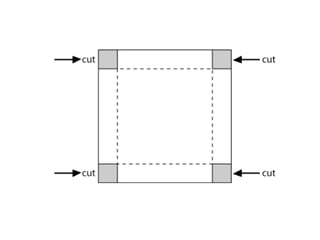
Solucion problema de caja
•Download as PPTX, PDF•
0 likes•520 views
Otras aplicaciones del cálculo en situaciones reales
Report
Share
Report
Share
Recommended
PIG/MIG: vers une définition commune? - Romain Boichat (Genolier Swiss Medica...

PIG/MIG: vers une définition commune? - Romain Boichat (Genolier Swiss Medica...Paianet - Connecting Healthcare
Recommended
PIG/MIG: vers une définition commune? - Romain Boichat (Genolier Swiss Medica...

PIG/MIG: vers une définition commune? - Romain Boichat (Genolier Swiss Medica...Paianet - Connecting Healthcare
More Related Content
Viewers also liked
Viewers also liked (20)
Accessoires agro-alimentaire - Food industry accessories - FG INOX

Accessoires agro-alimentaire - Food industry accessories - FG INOX
Robinetterie industrielle inox- Industrial stainless steel valves - FG INOX

Robinetterie industrielle inox- Industrial stainless steel valves - FG INOX
Presentation classe inversée en classe préparatoire

Presentation classe inversée en classe préparatoire
PyDayAsunción 2015 - Lightning Talks - OSM Paraguay

PyDayAsunción 2015 - Lightning Talks - OSM Paraguay
More from Mtra. Zoraida Gpe. Mtz
More from Mtra. Zoraida Gpe. Mtz (20)
Recently uploaded
Recently uploaded (20)
ACUERDO MINISTERIAL 078-ORGANISMOS ESCOLARES..pptx

ACUERDO MINISTERIAL 078-ORGANISMOS ESCOLARES..pptx
Éteres. Química Orgánica. Propiedades y reacciones

Éteres. Química Orgánica. Propiedades y reacciones
Plan Refuerzo Escolar 2024 para estudiantes con necesidades de Aprendizaje en...

Plan Refuerzo Escolar 2024 para estudiantes con necesidades de Aprendizaje en...
Planificacion Anual 2do Grado Educacion Primaria 2024 Ccesa007.pdf

Planificacion Anual 2do Grado Educacion Primaria 2024 Ccesa007.pdf
GUIA DE CIRCUNFERENCIA Y ELIPSE UNDÉCIMO 2024.pdf

GUIA DE CIRCUNFERENCIA Y ELIPSE UNDÉCIMO 2024.pdf
