More Related Content
PDF
PDF
FEPチュートリアル2021 講義3 「潜在変数が連続値、生成モデルが正規分布の場合」の改良版 PDF
数式を綺麗にプログラミングするコツ #spro2013 PDF
PDF
スパースモデリング、スパースコーディングとその数理(第11回WBA若手の会) PDF
Generative Adversarial Networks (GAN) の学習方法進展・画像生成・教師なし画像変換 PDF
[DL輪読会]Scalable Training of Inference Networks for Gaussian-Process Models PDF
What's hot
PDF
Ml professional bandit_chapter2 PDF
Sparse estimation tutorial 2014 PDF
「アクティブビジョンと フリストン自由エネルギー原理」@北大20170111 PDF
PDF
PDF
PDF
「3.1.2最小二乗法の幾何学」PRML勉強会4 @筑波大学 #prml学ぼう PDF
【輪読】Bayesian Optimization of Combinatorial Structures PDF
PDF
凸最適化 〜 双対定理とソルバーCVXPYの紹介 〜 PDF
PPTX
PPTX
古典的見解を越えたオーバーフィッティングの先の世界 PDF
PDF
PDF
PDF
[DL輪読会]Deep Learning 第18章 分配関数との対峙 PDF
時系列解析の使い方 - TokyoWebMining #17 PDF
NIPS2016論文紹介 Riemannian SVRG fast stochastic optimization on riemannian manif... PDF
Deep Learning 勉強会 (Chapter 7-12) Similar to はじめてのルベーグ積分
PDF
PDF
PDF
2015年度秋学期 応用数学(解析) 第14回 ルベーグ測度と完全加法性 (2016. 1. 14) PDF
2014年度秋学期 応用数学(解析) 第5部・測度論ダイジェスト / 第15回 ルベーグ積分 (2015. 1. 22) PDF
2014年度秋学期 応用数学(解析) 第5部・測度論ダイジェスト / 第14回 ルベーグ測度と完全加法性 (2015. 1. 15) PDF
2016年度秋学期 応用数学(解析) 第15回 ルベーグ積分 (2017. 1. 19) PDF
2018年度秋学期 応用数学(解析) 第4部・「その先の解析学」への導入 第15回 測度論(2) ルベーグ積分 (2019. 1. 15) PDF
2015年度秋学期 応用数学(解析) 第1回 イントロダクション (2015. 9. 24) PPTX
PDF
2015年度秋学期 応用数学(解析) 第15回 ルベーグ積分 (2016. 1. 21) PDF
2014年度秋学期 応用数学(解析) 第1回 イントロダクション (2014. 9. 25) はじめてのルベーグ積分
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
ルベーグ積分で計算 その2
有理数上0、無理数上1となる関数 の積分 を考える。ff(x)dμ∫
1
0
このままだと計算できないので、 (有理数上1、無理数上0)を考えると、
有理数は可算集合なので
1 − f
(1 − f)dμ∫
1
0
=
=
=
dμ∫
1
0
∑
a:rational
1{a}
dμ∑
a:rational
∫
1
0
1{a}
0 = 0∑
a:rational
従って
fdμ∫
1
0
=
=
(1 − (1 − f))dμ∫
1
0
1
- 17.
は計算できない∞ − ∞
f(x):= {
−1
1
(x < 0)
(x >= 0)
について を考えるfdμ∫
∞
−∞
fdμ∫
a+b
−a
=
=
=
fdμ + fdμ∫
0
−a
∫
a+b
0
− dμ + dμ∫
0
−a
∫
a+b
0
− a + (a + b) = b
従って
fdμ∫
∞
−∞
= fdμ = blim
a→∞
∫
a+b
−a
は任意の値をとれるので値が確定しない。b
- 18.
- 19.



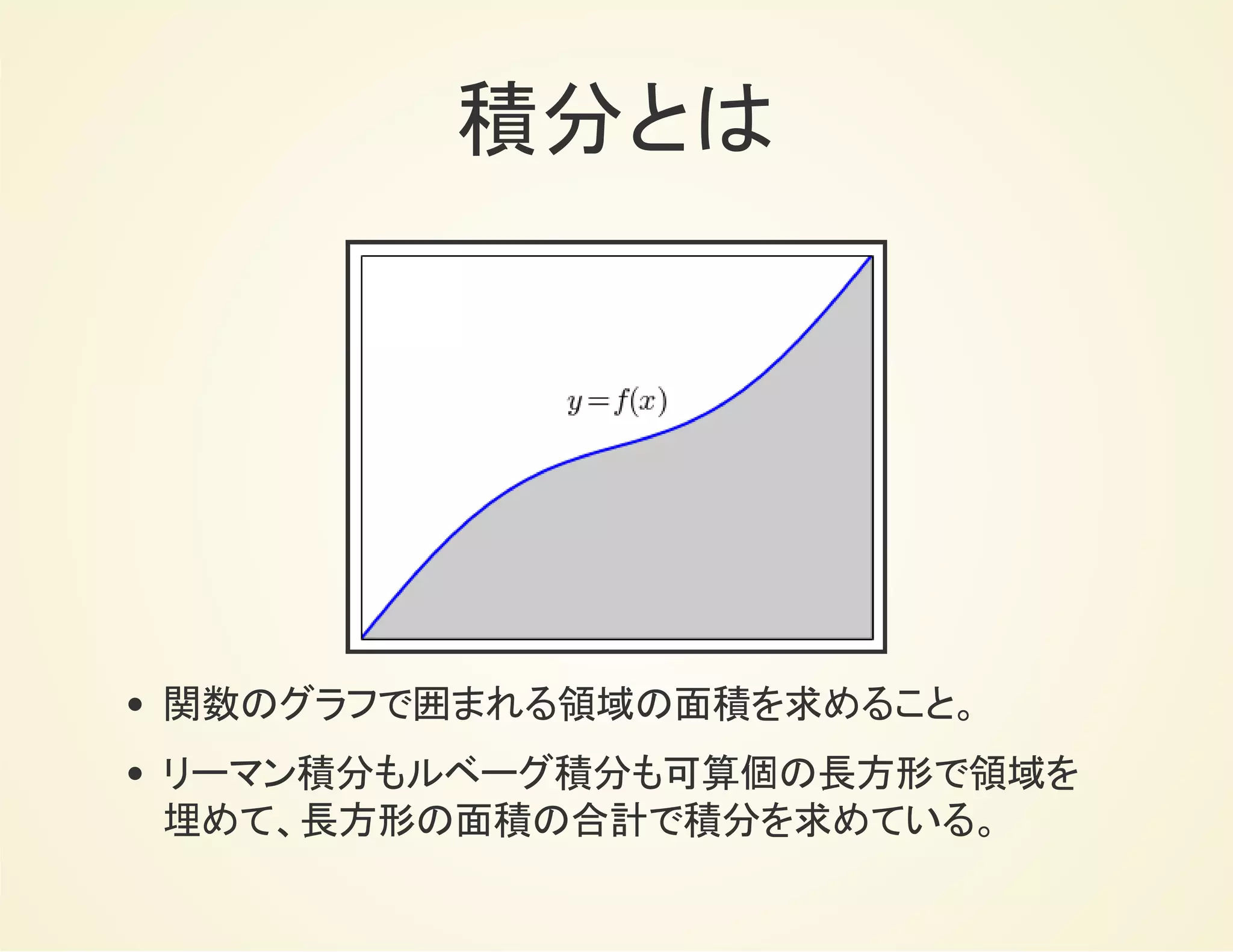
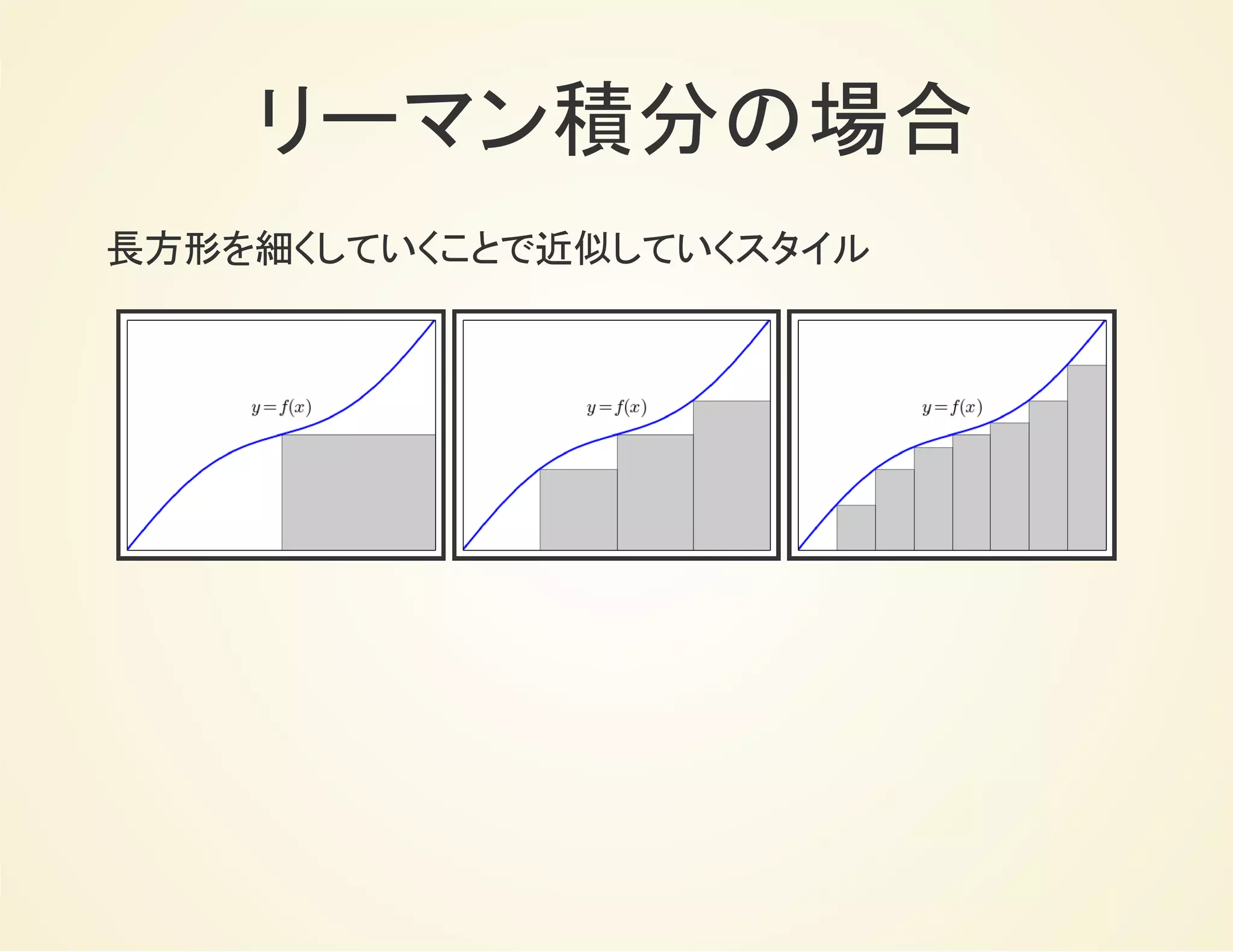
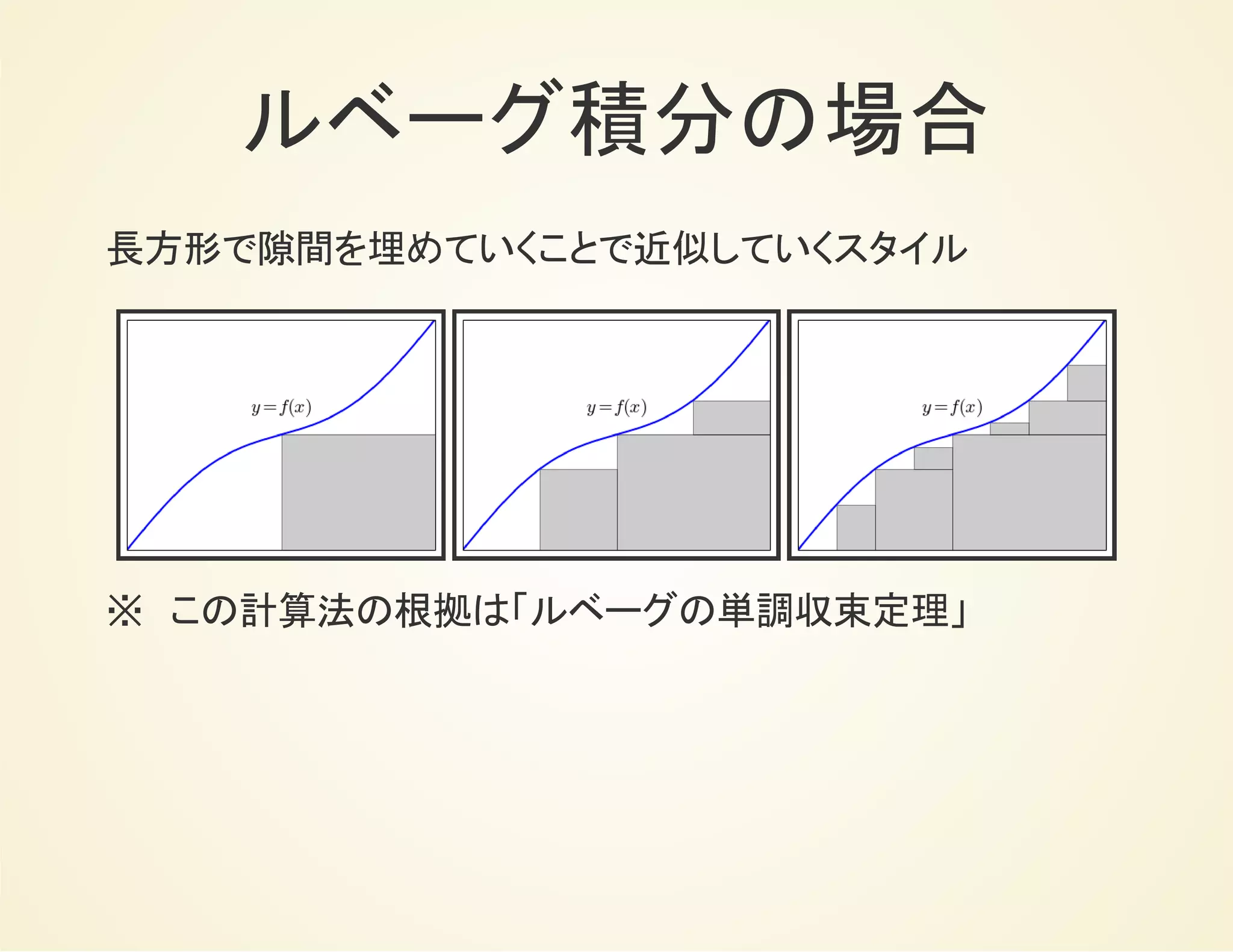
![ルベーグ積分の記法
ルベーグ積分強調したい場合は下記のような記法を用いる。
これは のときは下記に相当する
は測度(measure)のギリシア語の頭文字
fdμ∫
R
R = [a, b]
fdx∫
b
a
μ](https://image.slidesharecdn.com/random-150220180854-conversion-gate02/75/slide-7-2048.jpg)
![ルベーグ積分で計算 その1
xdμ∫
[0,1]
=
=
=
=
+ 2 + ⋯ + + ⋯( )
1
2
2
( )
1
4
2
2
n−1
( )
1
2
n
2
∑
n=0
∞
2
n−1
( )
1
2
2n
=
1
2
∑
n=0
∞
( )
1
2
n
1
4
∑
n=0
∞
( )
1
2
n−1
=
1
4
1
1 −
1
2
1
2](https://image.slidesharecdn.com/random-150220180854-conversion-gate02/75/slide-8-2048.jpg)










