Capítulo 5. Variación de funciones
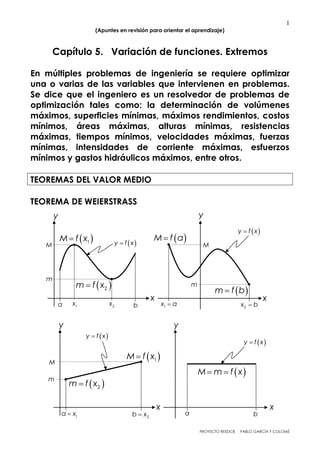
- 1. 1 PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ (Apuntes en revisión para orientar el aprendizaje) Capítulo 5. Variación de funciones. Extremos En múltiples problemas de ingeniería se requiere optimizar una o varias de las variables que intervienen en problemas. Se dice que el ingeniero es un resolvedor de problemas de optimización tales como: la determinación de volúmenes máximos, superficies mínimas, máximos rendimientos, costos mínimos, áreas máximas, alturas mínimas, resistencias máximas, tiempos mínimos, velocidades máximas, fuerzas mínimas, intensidades de corriente máximas, esfuerzos mínimos y gastos hidráulicos máximos, entre otros. TEOREMAS DEL VALOR MEDIO TEOREMA DE WEIERSTRASS x y f x y 2b x 1M f x 2m f x M m f x a b y f x 1a x M m y x x y f x y a b1x 2x 1M f x 2m f x m y M f a m f b M m 1x a 2x b M y f x x
- 2. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 2 TEOREMA DE ROLLE Se cumple para 1 2 3, ,x x x , donde la derivada vale cero. TEOREMA DE LAGRANGE (DEL VALOR MEDIO DEL C D) 1 2 3 4' ' ' ' f b f a f x f x f x f x b a Ejemplo. Verificar para las siguientes funciones que se cumple el teorema mencionado y obtener el o los valores de " "x que satisfacen la hipótesis: 3 ) en x -2 3,2 3 T. de Rolle 12 x i y x 3 ) 2 5 en 2,3 T. de Lagrangeii y x x x x y y f x 1' 0f x 1x 2x 3x f a f b a b 2' 0f x 3' 0f x 4x y f x y x b a f b f a 1x 2x 3x f b f a a b
- 3. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 3 Ejemplo. Comprobar que se cumple el teorema del Valor medio del Cálculo diferencial para la función 4 3 f x x en el intervalo 1,1 y obtener el o los valores de " "x que lo satisfacen.
- 4. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 4 Ejemplo. Investigar si la función f x sen x cumple las condiciones del teorema de Rolle en el intervalo 0,2 y en caso de hacerlo, obtener los valores de " "x en los que se satisface el teorema. Hacer una gráfica aproximada de la función en el intervalo considerado, señalando, si existen, los valores en los cuales se satisface el teorema.
- 5. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 5 FUNCIONES CRECIENTES Y DECRECIENTES DEFINICIÓN. Una función es creciente si para dos valores cualesquiera 1 2x y x de su dominio, se cumple que: 2 1 2 1x x f x f x DEFINICIÓN. Una función es decreciente si para dos valores cualesquiera 1 2x y x de su dominio, se cumple que: 2 1 2 1x x f x f x TEOREMA. Sea y f x una función continua en el intervalo cerrado ,a b , derivable en el intervalo abierto ,a b y tal que ' 0f x en el intervalo ,a b . Entonces la función es creciente en el intervalo ,a b . x y f 1f x 1x 2x 1' 0f x x y f 1f x 1f x 1x 2x 1' 0f x 2f x x y f 2f x 1f x 1x 2x 1' 0f x x y f 2f x 1f x 1x 2x 1' 0f x
- 6. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 6 TEOREMA. Sea y f x una función continua en el intervalo cerrado ,a b , derivable en el intervalo abierto ,a b y tal que ' 0f x en el intervalo ,a b . Entonces la función es decreciente en el intervalo ,a b . Ejemplo. Investigar para qué intervalos de " "x la siguiente función es creciente y decreciente. Hacer una gráfica aproximada. 3 29 6 1 2 f x x x x
- 7. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 7 SIGNO DE LA DERIVADA DE UNA FUNCIÓN BIYECTIVA 2 ) Sea la función: 1 ; : 0, 1, 2 x i f x f 2 2 1 2 2 2 2 1, 0 2 x y x y x y y 2 1 ' 0 0, 2 x f x f x x x 2 ) Sea la función: 4 ; : 0, 2 0,4ii f x x f 2 4 4 0,4y x x y y 2 4 ' 2 0 0, 2f x x f x x x 2 1 2 x y x y 0, 1 0,fD 1,f fR C ' 0 crecientef x 0, 4f fR C x y 2 4f x x 0, 4 2, 0 0,2fD ' 0 decrecientef x
- 8. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 8 EXTREMOS RELATIVOS Y ABSOLUTOS DEFINICIÓN. Una función f x tiene un máximo relativo 0f x para un valor 0x x en un intervalo ,a b , si se cumple que: 0 ,f x f x x a b DEFINICIÓN. Una función f x tiene un mínimo relativo 0f x para un valor 0x x en un intervalo ,a b , si se cumple que: 0 ,f x f x x a b 0 mínimo relativo f x 0 mínimo relativo f x f y 0' 0f x x a b0x a f 0'f x y a b0x x b f y 0' 0f x x a b0x a f 0'f x y a b0x x b 0 máximo relativo f x 0 máximo relativo f x
- 9. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 9 DEFINICIÓN. Se conocen como valores críticos de la variable independiente " "x a los valores del eje de las abscisas donde la derivada es cero o no existe. f 0'f x y x a 0x b f 0' 0f x y x a 0x b asíntota rM rM rM rM rm rm rm f x y AM Am 1x 2x 3x 4x 5x 6x 7x x y ' 0f x 'f x ' 0f x ' no existef x picorm no hay f r AM M no hay asíntota no hay máximos ni mínimos relativos
- 10. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 10 CRITERIO DE LA PRIMERA DERIVADA 1. Se calcula la derivada de la función. 2. Se obtienen los valores críticos donde la derivada vale cero o no existe. 3. Se analiza el posible cambio de signo de la derivada, antes y después de cada punto crítico, lo que manifestaría la presencia de un extremo relativo. Si la función no está definida o si la derivada no cambia de signo, no hay extremos relativos. Si la función está definida, entonces se pueden presentar los siguientes casos: Si la derivada cambia de positiva a negativa, quiere decir que la función cambia de creciente a decreciente y se tiene un máximo relativo. Si la derivada cambia de negativa a positiva, quiere decir que la función cambia de decreciente a creciente y se presenta un mínimo relativo. Ejemplo. Obtener los máximos y mínimos relativos de las funciones siguientes por medio del método de la primera derivada y hacer un trazo aproximado de sus gráficas a partir de los resultados obtenidos: 4 3 2 3 ) ; ) 2 2 ; 0 2 4 6 2 x x x i f x ii y senx sen x x 2 3 2 2 ) ; ) 3iii y iv f x x x x 2 2 4 2 2) ; ) 2 3 1 2 2 x si x v f x vi f x x x x si x
- 11. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 11
- 12. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 12
- 13. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 13 CRITERIO DE LA SEGUNDA DERIVADA TEOREMA. 0 0; ' 0 '' 0 M ry f x f x y f x TEOREMA. 0 0; ' 0 '' 0 ry f x f x y f x m Secuela de pasos del criterio de la segunda derivada: 1. Se calcula la derivada de la función. 2. Se obtienen los valores críticos donde la derivada vale cero o no existe. 3. Se calcula la segunda derivada de la función y se sustituye en ella cada uno de los valores críticos. Si la segunda derivada es negativa, la función presenta un máximo relativo en ese valor crítico. Si la segunda derivada es positiva, la función presenta un mínimo relativo en ese valor crítico. Nota. Si la segunda derivada es cero o no existe, entonces habría que utilizar el criterio de la primera derivada para ver si se presentan extremos relativos. Ejemplo. Determinar los extremos relativos de las siguientes funciones mediante el criterio de la segunda derivada y hacer un trazo aproximado de sus gráficas, utilizando los resultados obtenidos: 4 3 2 ) 4 4 1 ; ) 1i f x x x x ii y x x 5 24 3 3 ) ; ) 3 10 16 x iii f x iv y x x
- 14. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 14
- 15. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 15 Extremos absolutos Ejemplo. Determinar los extremos relativos y absolutos de la siguiente función, definida en el intervalo 3 5 , 2 2 . Hacer un trazo aproximado de su gráfica. 3 3 3f x x x
- 16. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 16 CONCAVIDAD Y PUNTOS DE INFLEXIÓN DEFINICIÓN. Se dice que una curva es cóncava hacia arriba cuando las rectas tangentes a todos sus puntos están situadas por debajo de su gráfica, y cóncava hacia abajo cuando las rectas tangentes están por encima de su gráfica. DEFINICIÓN. Al punto en el que una curva cambia su concavidad se le conoce como Punto de Inflexión y es en
- 17. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 17 este punto el único lugar en el cual la tangente corta a la curva sin tocar su gráfica en otro lugar. Relación entre la concavidad y la segunda derivada TEOREMA. Sea la función y f x y considérese que su segunda derivada existe y es positiva en el punto 0 0,P x y , es decir, 0'' 0f x . Entonces su gráfica es una curva " "C cóncava hacia arriba en dicho punto. TEOREMA. Sea la función y f x y considérese que su segunda derivada existe y es negativa en el punto 0 0,P x y , es decir, 0'' 0f x . Entonces su gráfica es una curva " "C cóncava hacia abajo en dicho punto. TEOREMA. Sea la función y f x cuya representación es la curva " "C . Y considérese que para 0x x se cumple que: 0 0'' 0 ''' 0f x y f x Entonces el punto 0 0,P x y es un punto de inflexión de la curva " "C . PI x y f concavidad hacia arriba concavidad hacia abajo PI (Punto de inflexión)
- 18. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 18 Criterio para determinar los puntos de inflexión y el sentido de la concavidad. Secuela de pasos: 1. Se calculan la primera, segunda y tercera derivadas. 2. Se iguala cero o se analiza la no existencia de la segunda derivada para determinar los valores " "x donde es posible que haya puntos de inflexión. y senx Máximo relativo Punto de Inflexión mínimo relativo y x x 4 2 3 4 5 4 3 2 7 4 2 x' cosy x x ''y senx ''' cosy x
- 19. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 19 3. En los valores donde puede haber punto de inflexión se analiza la tercera derivada que si es diferente de cero garantiza la existencia de punto de inflexión lo que se hace también al investigar si hay cambio de signo en la segunda derivada o cambio en la concavidad. Se hace el siguiente razonamiento: Si 2 2 d y dx cambia de negativa a positiva, entonces, si la función existe, se presenta un punto de inflexión y la gráfica de la función cambia de cóncava hacia abajo a cóncava hacia arriba. Si 2 2 d y dx cambia de positiva a negativa, entonces, si la función existe, se presenta un punto de inflexión y la gráfica de la función cambia de cóncava hacia arriba a cóncava hacia abajo. Ejemplo. Dada la siguiente función, investigar dónde es creciente o decreciente, determinar sus extremos relativos, calcular sus puntos de inflexión, decir en qué intervalos es cóncava hacia arriba y en cuáles hacia abajo, y hacer un trazo aproximado de su gráfica: 3 5 3 5 20 ) 3 5 ; ) 3 x i f x x x ii y x Se resolverá el primero.
- 20. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 20 x y y’ y’’ característica
- 21. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 21 SECUELA SUGERIDA PARA RESOLVER PROBLEMAS DE EXTREMOS - Leer cuidadosamente el enunciado para comprender la problemática presentada y ver qué se pretende optimizar. - Construir, cuando sea posible, un modelo geométrico del problema, que considere magnitudes constantes y variables. - Establecer un modelo matemático preliminar, que exprese como función al concepto que se desea optimizar. - Si este modelo matemático tiene más de una variable independiente, acudir a una o más ecuaciones auxiliares. - Sustituir las ecuaciones auxiliares en el modelo matemático preliminar y obtener el modelo matemático definitivo. - Se aplica cualquiera de los criterios para calcular extremos al modelo matemático definitivo y se resuelve el problema. - Cuando se obtienen los puntos críticos, alguno evidencia de inmediato el máximo o mínimo de la función y si se desea verificar su naturaleza, lo que no es indispensable, se prosigue con el criterio que se elija para ello. Ejemplo. La suma de dos números positivos es 40. Obtener los números tales que: )i Su producto sea máximo. )ii La suma de sus cuadrados sea mínima. )iii El producto del cuadrado de uno de ellos por el cubo del otro sea máximo.
- 22. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 22
- 23. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 23 Ejemplo. Un viaje de prácticas para realizar estudios geológicos, subsidiado por una escuela de ingeniería, costará a cada estudiante $15,000 si viajan no más de 150 estudiantes. Sin embargo, el costo por estudiante se reducirá en $ 50 por cada uno que exceda los 150. ¿Con cuántos estudiantes los ingresos de la escuela serían los máximos? Construir también una gráfica de los ingresos en función del número de estudiantes.
- 24. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 24 Ejemplo. Se tienen dos postes de 7 10m y m de altura, separados una distancia de 15 m en un piso horizontal. Deben sujetarse con cables que van de sus puntas a un solo punto en el suelo. ¿En qué lugar se deben fijar los dos cables al suelo para que la longitud total de cable sea mínima? ¿Cuál es la longitud mínima de cable?
- 25. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 25 Ejemplo. Una empresa petrolera desea construir un depósito en forma de cilindro circular recto, con tapa. El tanque debe contener 500,000 litros de crudo. El material para la superficie lateral tiene un costo de $ 400 por 2 m , para la tapa de $ 300 por 2 m y para base de $ 500 por 2 m . ¿Qué dimensiones debe tener el tanque para que el costo de los materiales empleados en su construcción sea el mínimo? Calcular también el costo mínimo del material.
- 26. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 26 Ejemplo. Un abrevadero de 6 m de largo tiene su sección transversal en forma de triángulo isósceles invertido, cuyos lados iguales miden 1.2 m c/u. Determinar el ancho en la parte superior de la sección, tal el volumen del abrevadero sea máximo. Calcular el valor de este volumen máximo.
- 27. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 27 Ejemplo. ¿Qué dimensiones tiene el cono circular recto de volumen máximo que se inscribe en una esfera de radio R?
- 28. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 28 Ejemplo. Una lámpara está colgada sobre el centro de una mesa redonda de radio igual a 1.4 m. Se requiere saber a qué altura deberá estar la lámpara para que la iluminación de un objeto en el borde sea la máxima. Considérese que la iluminación es directamente proporcional al coseno del ángulo de incidencia de los rayos luminosos e inversamente proporcional al cuadrado de la distancia al foco de luz.
- 29. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 29 Ejemplo. Se cuenta con 40 m de alambre para cercar un seto de flores en un jardín. El seto debe tener la forma de un sector circular. ¿Cuál será el radio y la longitud del arco del círculo si se desea que el seto tenga área máxima y cuál es el valor del área máxima?
- 30. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 30 Ejemplo. De un tronco recto de sección circular, de diámetro 100 cm, es necesario cortar una viga de sección rectangular. ¿Qué ancho y qué peralte (altura) debe tener la sección para que la viga ofrezca la resistencia máxima posible a la compresión y a la flexión? La resistencia de una viga a la compresión es proporcional al área de su sección transversal y a la flexión es proporcional al producto de su ancho por el cuadrado de su peralte.
- 31. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 31 Ejemplo. Determinar la base y la altura del triángulo de mínima área que en el primer cuadrante se puede formar al cortar los ejes coordenados una recta que pasa por el punto 3,4P .
- 32. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 32 VARIACIÓN DE UNA FUNCIÓN El estudio de la variación de una función consiste en analizar sus características geométricas como sus intersecciones con los ejes, sus simetrías, la existencia de asíntotas verticales y horizontales, sus extremos relativos, puntos de inflexión y sentido de la concavidad, concluyendo con el trazado aproximado de su gráfica. Se pretende estudiar la variación de la función: 2 12 9 x y x 1. Intersecciones a) Con el eje " "x : 0 0y x la curva interseca al eje " "x en el origen. b) Con el eje " "y : 0 0x y la curva interseca al eje " "y en el origen. 2. Simetrías a) Con el eje " "x : Se cambia y por –y y se tiene 2 12 9 x y x . Como se altera la función, no hay simetría. b) Con el eje " "y : Se cambia x por –x y se tiene 2 12 9 x y x . Como se altera la función, no hay simetría. c) Con el origen: Se cambia x por –x y y por –y y se tiene que 2 2 12 12 9 9 x x y y x x . Como no se altera la función, sí hay simetría con respecto al origen. 3. Asíntotas. Estas, si existen, se localizan como se vio en el tema II.
- 33. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 33 a) Asíntotas verticales. No tiene ya que no existe ningún valor real al cual tienda la " "x que haga que el límite de la función no exista. b) Asíntotas horizontales. Se calcula el valor numérico del límite de la función cuando la variable " "x tiende a y, 2 12 lim 0 9x x x por lo que la recta 0y (el eje x) es una asíntota horizontal de la función. 4. Extensión. Se despeja cada una de las variables y se obtiene su dominio. De esta manera, a) Extensión en " "x : 2 12 9 x y x x . b) Extensión en " "y : 2 2 12 144 36 12 9 0 2 y yx x y x y 2 144 36 0 12 6 12 6 0y y y Primera posibilidad: 12 6 0 2 12 6 0 2 y y y y Segunda posibilidad: 12 6 0 2 12 6 0 2 y y y y Por lo tanto, la extensión en " "y es: 2, 2 0y . 5. Extremos relativos, intervalos de creciente y decreciente, puntos de inflexión y concavidad. Se obtienen la primera, segunda y tercera derivadas y se procede como ya se estudió en el presente capítulo. 2 20 x 1 1 x 2 1 1 20
- 34. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 34 2 2 2 2 2 2 2 9 12 12 212 108 12 9 9 9 x x xx dy dy x y dx dxx x x 2 12 2 2 2 2 3108 12 0 108 12 0 9 39 xx x x xx 2 2 2 22 2 4 2 9 24 108 12 2 9 2 9 x x x x xd y dx x 2 3 3 2 3 2 3 2 3 2 2 24 216 432 48 24 648 9 9 d y x x x x d y x x dx dxx x 33 2 43 2 5 3 3 24 648 0 24 27 0 0 9 3 3 x x x x x x x x que son los posibles puntos de inflexión. 3 2 2 2 3 23 3 6 2 9 72 648 24 648 3 9 2 9 x x x x x xd y dx x 2 2 33 2 3 2 9 72 648 6 24 648 9 x x x x xd y dx x 3 4 2 3 3 2 72 3888 5832 9 d y x x dx x 3 3 3 3 3 0 3 3, 3 d y x PI dx 3 4 3 0 0 0, 0 d y x PI dx 3 3 3 3 3 0 3 3, 3 d y x PI dx En ocasiones puede resultar muy difícil calcular la tercera derivada para garantizar la existencia de un punto de inflexión cuando '' 0f x o no existe, por lo que es suficiente con saber si la función cambia su concavidad o bien, si su segunda derivada cambia de signo.
- 35. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 35 Ahora se construye la correspondiente tabla y, x y 'y ''y característica , 3 3 decrece 3 3x PI 0 3 3, 3PI 3 3, 3 decrece 3x mínimo 0 3, 2rm 3, 0 crece 0x PI 0 0, 0PI 0, 3 crece 3x máximo 0 3, 2rM 3, 3 3 decrece 3 3x PI 0 3 3, 3PI 3 3, decrece De acuerdo con la tabla, es posible decir que la curva que representa a la función dada: Es creciente en el intervalo 3, 3 Es decreciente en los intervalos , 3 3,y Es cóncava hacia arriba en 3 3, 0 3 3,y Cóncava hacia abajo en , 3 3 0, 3 3y Tiene un máximo relativo en el punto 3, 2 Tiene un mínimo relativo en 3, 2 Tiene tres puntos de inflexión en los puntos 3 3, 3 ; 0, 0 ; 3 3, 3
- 36. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 36 Cabe decir que a pesar de que la curva corta a los ejes coordenados en el origen, al crecer " "x en los dos sentidos, el eje de las abscisas, esto es, 0y , se convierte en asíntota de la curva, por lo que no se contradice el análisis realizado. Ejemplo. Estudiar la variación de las siguientes funciones: 2 2 1 4 ) ; ) 1 x x i y ii y x x y x 3, 2rM 0, 0PI 3 3, 3PI 3 3, 3PI 3, 2rm
- 37. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 37
- 38. PROYECTO REEDCB PABLO GARCÍA Y COLOMÉ 38
