Maximos, Minimos y Mutliplicadores de Lagrange
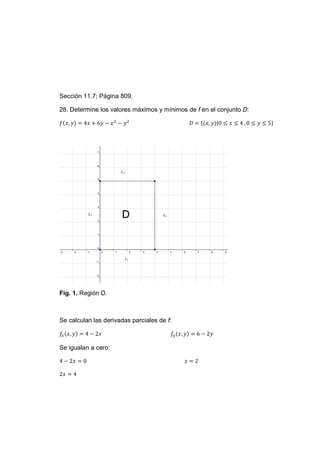
- 1. Sección 11.7; Página 809. 28. Determine los valores máximos y mínimos de f en el conjunto D: , 4 6 , |0 4 , 0 5 Fig. 1. Región D. Se calculan las derivadas parciales de f: , 4 2 , 6 2 Se igualan a cero: 4 2 0 2 2 4
- 2. 6−2 =0 2 =6 2 =6 =3 El único punto crítico de f en D es (2,3) donde 2,3 = 4 2 + 6 3 − 2 − 3 → 2,3 = 13 Ahora se hallan los puntos críticos en las fronteras de D. Para : = 0 y 0≤ ≤4 ℎ = ,0 = 4 − ℎ = 4 − 2 → 4 − 2 = 0 ↔ 2 = 4 ↔ =2 Comoℎ = −2 < 0 , 2,0 es un máximo. 2,0 = 4 2 + 6 0 − 2 − 0 =4 En los extremos de este intervalo: 0,0 = 4 0 + 6 0 − 0 − 0 =0 4,0 = 4 4 + 6 0 − 4 − 0 =0 Ambos son mínimos. Para : =4 y 0≤ ≤5 ℎ = 4, =6 − ℎ = 6 − 2 → 6 − 2 = 0 ↔ 2 = 6 ↔ = 3 Comoℎ = −2 < 0 → 4,3 es un máximo. 4,3 = 4 4 + 6 3 − 4 − 3 =9 En los extremos de este intervalo: 4,0 = 4 4 + 6 0 − 4 − 0 =0 4,5 = 4 4 + 6 5 − 4 − 5 =5
- 3. 4,5 es un mínimo. Para " : =5 y 0≤ ≤4 ℎ" = ,5 = 4 − +5 ℎ" = 4 − 2 → 4 − 2 = 0 ↔ 2 = 4 ↔ =2 Comoℎ" = −2 < 0 → 2,5 es un máximo. 2,5 = 4 2 + 6 5 − 2 − 5 =9 En los extremos de este intervalo: 0,5 = 4 0 + 6 5 − 0 − 5 =5 4,5 = 4 4 + 6 5 − 4 − 5 =5 Ambos son mínimos. Para #: =0 y 0≤ ≤5 ℎ# = 0, =6 − ℎ# = 6 − 2 → 6 − 2 = 0 ↔ 2 = 6 ↔ = 3 Comoℎ# = −2 < 0 → 0,3 es un máximo. 0,3 = 4 0 + 6 3 − 0 − 3 =9 En los extremos de este intervalo: 0,0 = 4 0 + 6 0 − 0 − 0 =0 0,5 = 4 0 + 6 5 − 0 − 5 =5 0,0 es un mínimo. Comparando todos los puntos hallados, se tiene: 2,3 = 13 es el máximo local de f en D. 0,0 = 4,0 = 0 son los mínimos locales de f en D.
- 4. 41. Encuentre el volumen de la caja rectangular más grande que este en el primer + 2 + 3$ = 6. octante y que tenga tres caras en los planos coordenados y un vértice en el plano Como la caja está en el primer octante: > 0 , > 0 , $ > 0. El volumen de la caja es & = $. Se tiene la siguiente restricción: + 2 + 3$ = 6 3$ = 6 − −2 $= '( ( " Reemplazando en V: &= ) *= '( ( ' ( + ( + " " Se hallan las derivadas parciales de V: 1 = 6 −2 −2 = 6−2 −2 3 3 1 = 6 − −4 = 6− −4 3 3 Se igualan a cero las derivadas parciales: = 0 ↔ 6−2 −2 = 0 ↔ = 0 ∨ 6 − 2 − 2 = 0 3 Pero, > 0 → 6 − 2 − 2 = 0 → 2 + 2 = 6 (ec.1) = 0 ↔ 6− −4 = 0 ↔ = 0 ∨ 6 − − 4 = 0 3 Pero, > 0 → 6 − − 4 = 0 → +4 =6 (ec.2) Si se multiplica (ec.2) por (-2), se tiene: −2 − 8 = −12. Luego se suma con (ec.1), se obtiene: −6 = −6 → =1
- 5. Se reemplaza este valor en (ec.2): 6 4 4 1 4 6 4 2 El valor de z que corresponde a un máximo es: '( ( '( ( '(# $ " " " " El volumen máximo es: # & 2 1 ) * ./012134 5ú70524 " " Sección 11.8; Página 819. 19. Encuentre los valores extremos de f en la región descrita por la desigualdad. , 3( ; 4 1 Fig. 2. Región 4 1
- 6. Para +4 < 1 (dentro de la región): = − 3( → − 3( = 0 ↔ =0 = − 3( → − 3( = 0 ↔ =0 Punto crítico: 0,0 → 0,0 = 3 (8 = 1 Para +4 = 1 (en la frontera): Se usa el método de los multiplicadores de Lagrange. , = 3( ; 9 , = +4 −1 − 3( , − 3( = : 2 ,8 Entonces: − 3( = 2: (1) − 3( = 8: (2) +4 =1 (3) De (1) y (2) se sabe que : ≠ 0, ya que si : = 0 → = 0 ∧ = 0, pero de (3) eso es una contradicción. = → = → 4 = ( = >?@ A ( = >?@ BA # Se divide (1) entre (2): Se reemplaza en (3): 1 1 4 +4 = 1 → 8 = 1 → = → = ± 8 2√2 Se reemplaza el valor de en (3): 1 1 1 1 + 4 E F = 1 → + = 1 → = → = ± 8 2 2 √2 Se tiene: 1 1 G G G E , F = 3 √+ +√+ = 3 ( H () *) * √2 2√2
- 7. 1 1 G G G E ,− F = 3 √+ +√+ = 3 H () *)( * √2 2√2 1 1 G G E− , F=3 = 3H G ()( *) * √+ +√+ √2 2√2 1 1 G G G E− ,− F=3 = 3 ( H ()( *)( * √+ +√+ √2 2√2 Entonces, el primer y último valor son mínimos, y el segundo y el tercero son máximos. 7 I J (I = K, donde Q es una constante. ¿Qué valores de L y K minimizan la 22. Con base en el ejercicio 21, supongamos ahora que la producción se fija en función costo L , J = M + /J? L , J = M + /J ; 9 ,J = 7 I J (I −K ∇L = :∇9 M, / = : 7O I( J (I ,7 1 − O I J (I Entonces: M = :7O I( J (I (1) / = :7 1 − O I J (I (2) 7 I J (I =K (3) De (1): M = :7O → : = PQ R SPR Q PR Q TIPQ R (4) De (2): / = :7 1 − O → : = PQ UR Q R Q T (I PQ (5) Igualando (4) y (5):
- 8. → = SPR Q UR Q SP U = TIPQ R T (I PQ IR (I Despejando a L: = UIR S (I (6) Reemplazando este valor en (3): /OJ I 7E F J (I =K M 1−O Se despeja K: /O I J I 7 J (I =K VM 1 − O WI KVM 1 − O WI JIJ (I = 7 /O I K M 1−O I J= X Y 7 /O Se reemplaza este valor en (6): /O K M 1−O I = X Y M 1−O 7 /O /O K VM 1 − O WI K (I V = = /O M 1 − O WI( M 1−O 7 /O I 7 39. El plano + + 2$ = 2 cruza el paraboloide $ = + en una elipse. Determine los puntos sobre esta elipse que están más cerca y los que estén más lejos del origen. Se hallan los extremos de la función que representa la distancia de un punto (x, y, z) al origen: 1 = , ,$ = + + $ , donde d es la distancia. Esta función está sujeta a dos restricciones:
- 9. 9 , ,$ = + −$ ; ℎ , ,$ = + + 2$ − 2 ∇ = :∇9 + Z∇ℎ 2 , 2 , 2$ = : 2 , 2 , −1 + Z 1,1,2 Entonces: 2 = 2: + Z (1) 2 = 2: + Z (2) 2$ = −: + 2Z (3) + =$ (4) + + 2$ = 2 (5) Se restan (1) y (2): 2 − 2 = 2: − 2: + Z − Z 2 − = 2: − Si: ≠ → : = 1 Reemplazando en (1): 2 = 2 + Z → Z = 0 De (3): 2$ = −: + 2Z 2$ = −1 + 0 1 $=− 2 Reemplazando en (4): 1 + = − →← 2 Esto es una contradicción.
- 10. Entonces: = Si = en (4): 2 =$ En (5): 2 + 2$ = 2 +$=1 $ =1− Igualando: 2 =1− 2 + −1=0 1 1 2E + − F=0 2 2 1 1 + − =0 2 2 1 1 1 1 + +E F ]− − =0 2 4 2 16 1 9 E + F = 4 16 1 3 + =± 4 4 Entonces: = ∨ = −1 Entonces: = ∨ = −1 $ = ∨ $ = 2
- 11. El punto más cercano es ) , , * : ) , , * = " # El punto más lejano es −1, −1,2 : −1, −1,2 = 6 Repaso: “Revisión de conceptos”. Página 825. 59. Use los multiplicadores de Lagrange para encontrar los valores máximos y mínimos de f sujetos a las restricciones dadas. , = ; + =1 2 , = : 2 ,2 2 = 2: (1) = 2: (2) + =1 (3) Si = 0 → : = 0 → _0 = 0, `ab 3 →← → : = 0 3 3 : = 1 → = ±1 → _3 c03/3: 0, ±1 = 0 De (1): _0 ≠ 0 → = : De (2): _0 = 0 → = 0 ; e3ba 3/ 3 : 0 + 0 = 1 →← Entonces: ≠ 0 → : ≠ 0 Se divide (2) entre (1) y se obtiene: =2 De (3): 2 + = 1 → 3 = 1 → = ± √" En (3): = 1 − " = " → = ±f" Entonces: 2 1 2 1 2 gh , i = g−h , i = → já 0Ma4 3 √3 3 √3 3√3
- 12. 2 1 2 1 2 gh , − i = g−h , − i = − → jí/0Ma4 3 √3 3 √3 3√3 0, ±1 /a 34 ./ Má 0Ma /0 ./ Mí/0Ma. 63. Determine los puntos de la superficie $ " = 2 más cercanos al origen. 1 = + +$ = , ,$ 9 , ,$ = $" − 2 → , , $ ≠ 0 2 , 2 , 2$ = : $", 2 $", 3 $ Entonces: 2 =: $" (1) 2 = 2: $" (2) 2$ = 3: $ (3) $" = 2 (4) De (2): 1 = $ ": (5) De (3): 1=3 $: (6) Se igualan: $ $" = 3 $ → $ = 3 → = ± √3 3 1 , 2 , 3 , 5 6 43 c03/3: : ≠ 0 Se dividen (1) y (3): 2 : $" = 2$ 3: $ $ = $ 3 3 =$
- 13. $ =± √3 Se reemplazan y en (4): $ $ ± E± F $" = 2 √3 √3 $ $ " $' ± $ = 2 → ± = 2 → $ ' = ±6√3 → $ = f6√3 o √3 3 3√3 o q'√" = = p o q'√" =± √" √" √" De aquí se concluye que y .
