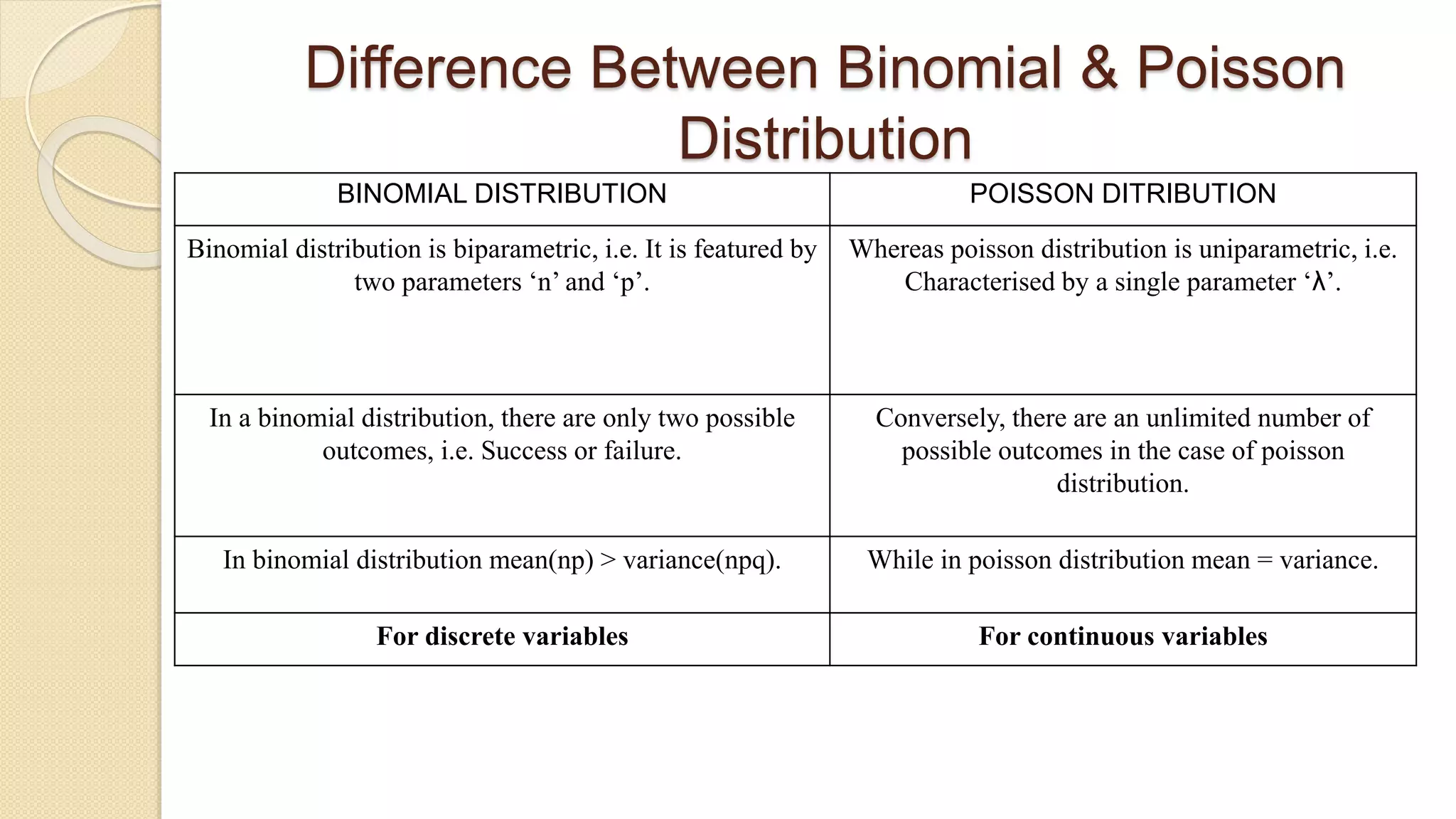
This document defines and provides information about the Poisson distribution: - The Poisson distribution results from Poisson experiments and is characterized by a single parameter λ, the expected number of events occurring in a fixed interval of time or space. - The Poisson distribution formula uses λ and e to calculate the probability of a given number of events (x) occurring. - Examples are provided to demonstrate calculating probabilities using the Poisson distribution for situations like births at a hospital and product failures. - Key properties of the Poisson distribution are that the mean and variance are both equal to λ.

2. RESENTED TO:
MAM FAIZA SAMI

3. OUTLINE
 DEFINATION
 PDF FOAM
 MEAN
 VARIACE
 USES

4. PRESENTED BY:
HAFIZ NAVEED ARSHAD(BCEF15008)
HAFIZ USMAN ALI SAIF(M016)
AHMAD SAEED(M007)
AMEER HAMZA(M020)
M. BILAL(E027)
GHULAM HAIDER(M009)

5. POISSON DISTRIBUTION
A POISSON DISTRIBUTION IS THE PROBABILITY
DISTRIBUTION THAT RESULTS FROM A POISSON
EXPERIMENT.
Siméon Denis Poisson
(1781–1840)

6.  Average number of accidents on any day on a
National Highway is 1.8.determine the
probability that the number of accidents are:
 At Least One.
 At Most One.

7. POISSON DISTRIBUTION
Poisson distribution only apply one formula:
Where:
 X = the number of events
 λ = mean of the event per interval
Where e is the constant, Euler’s Number or Napier's constant
(e = 2.71828...)
 This Is also called PDF form.

8. The Poisson distribution is defined by a
parameter, λ.

9. Difference Between Binomial & Poisson
Distribution
BINOMIAL DISTRIBUTION POISSON DITRIBUTION
Binomial distribution is biparametric, i.e. It is featured by
two parameters ‘n’ and ‘p’.
Whereas poisson distribution is uniparametric, i.e.
Characterised by a single parameter ‘λ’.
In a binomial distribution, there are only two possible
outcomes, i.e. Success or failure.
Conversely, there are an unlimited number of
possible outcomes in the case of poisson
distribution.
In binomial distribution mean(np) > variance(npq). While in poisson distribution mean = variance.
For discrete variables For continuous variables

10. Applications of Poisson distribution
 A practical application of this
distribution was made
by Ladislaus Bortkiewicz in
1898 when he was given the
task of investigating the
number of soldiers in the
Russian army killed
accidentally by horse kicks
this experiment introduced the
Poisson distribution to the
field of reliability engineering. Ladislaus Bortkiewicz

11. PRACTICAL EXAMPLE
Births Rate In A Hospital Occur Randomly At An
Average Rate Of 1.8 Births Per Hour.
What Is The Probability Of Observing 4 Births In A
Given Hour At The Hospital?

12. SOLUTION
Assuming
X = No. Of Births In A Given Hour
I) Events Occur Randomly
Ii) Mean Rate Λ = 1.8
Using The Poisson Formula, We Cam Simply Calculate
The Distribution.
P(x = 4) =( E^-1.8)(1.8^4)/(4!)
Ans: 0.0723

13. PRACTICAL EXAMPLE
If the probability of an item failing is
0.001, what is the probability of 3 failing
out of a population of 2000?

14. SOLUTION
Λ = n * p = 2000 * 0.001 = 2
Hence, use the Poisson formula
X = 3,
P(X = 3) =
Ans: 0.1804

15. MEAN

16. Variance of Poisson
distribution
The mean of any Poisson distribution is equal to its
variance, that is
m= v
m= mean
V= variance
which is a unique property of this distribution. (Note
that“ mean" here is the average of all values, and defines
the center of gravity of the distribution.
The mean and variance of a Poisson random variable
with parameter are both equal to :
E(X) = λ ;
V(X) = λ

17. Example
The number of flaws in a fibre optic cable follows a Poisson
distribution. The average number of flaws in 50m of cable
is 1.2.
(i) What is the probability of exactly three flaws in 150m of
cable?
(ii) What is the probability of at least two flaws in 100m of
cable?

19. Moment Generating
Function