processing

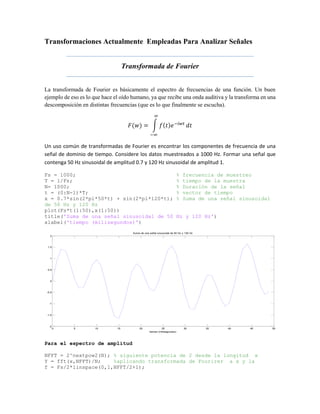
1. Transformaciones Actualmente Empleadas Para Analizar Señales
Transformada de Fourier
La transformada de Fourier es básicamente el espectro de frecuencias de una función. Un buen
ejemplo de eso es lo que hace el oído humano, ya que recibe una onda auditiva y la transforma en una
descomposición en distintas frecuencias (que es lo que finalmente se escucha).
𝐹(𝑤) = ∫ 𝑓(𝑡)𝑒−𝑖𝑤𝑡
∞
−∞
𝑑𝑡
Un uso común de transformadas de Fourier es encontrar los componentes de frecuencia de una
señal de dominio de tiempo. Considere los datos muestreados a 1000 Hz. Formar una señal que
contenga 50 Hz sinusoidal de amplitud 0.7 y 120 Hz sinusoidal de amplitud 1.
Fs = 1000; % frecuencia de muestreo
T = 1/Fs; % tiempo de la muestra
N= 1000; % Duración de la señal
t = (0:N-1)*T; % vector de tiempo
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % Suma de una señal sinusoidal
de 50 Hz y 120 Hz
plot(Fs*t(1:50),x(1:50))
title('Suma de una señal sinusoidal de 50 Hz y 120 Hz')
xlabel('tiempo (milisegundos)')
Para el espectro de amplitud
NFFT = 2^nextpow2(N); % siguiente potencia de 2 desde la longitud x
Y = fft(x,NFFT)/N; %aplicando transformada de Fourirer a x y la
f = Fs/2*linspace(0,1,NFFT/2+1);
0 5 10 15 20 25 30 35 40 45 50
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
Suma de una señal sinusoidal de 50 Hz y 120 Hz
tiempo (milisegundos)

2. % espectro de amplitud
plot(f,2*abs(Y(1:NFFT/2+1)))
title('espectro de amplitud de y(t)')
xlabel('Frecuencia (Hz)')
ylabel('|Y(f)|'
Transformada de Fourier Discreta
La transformada discreta de Fourier o DFT (del inglés, discrete Fourier transform) es un tipo de
transformada discreta utilizada en el análisis de Fourier. Transforma una función matemática en otra,
obteniendo una representación en el dominio de la frecuencia, siendo la función original una función
en el dominio del tiempo. Pero la DFT requiere que la función de entrada sea una secuencia discreta
y de duración finita. Dichas secuencias se suelen generar a partir del muestreo de una función
continua, como puede ser la voz humana.
𝑋 𝑘 = ∑ 𝑥 𝑛 𝑒−
2𝜋𝑖
𝑁
𝑘𝑛
𝑁−1
𝑛=0
𝑘 = 0, … , 𝑁 − 1
Donde i es la unidad imaginaria y es la N-ésima raíz de la unidad.
0 50 100 150 200 250 300 350 400 450 500
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
espectro de amplitud de y(t)
Frecuencia (Hz)
|Y(f)|

3. Transformada Rápida de Fourier
FFT es la abreviatura usual (del inglés Fast Fourier Transform) de un eficiente algoritmo que permite
calcular la transformada de Fourier discreta (DFT) y su inversa. La FFT es de gran importancia en
una amplia variedad de aplicaciones, desde el tratamiento digital de señales y filtrado digital en
general a la resolución de ecuaciones en derivadas parciales o los algoritmos de multiplicación rápida
de grandes enteros. El algoritmo pone algunas limitaciones en la señal y en el espectro resultante.
Uno de los algoritmos aritméticos más ampliamente utilizados es la transformada rápida de Fourier,
un medio eficaz de ejecutar un cálculo matemático básico y de frecuente empleo. La transformada
rápida de Fourier es de importancia fundamental en el análisis matemático y ha sido objeto de
numerosos estudios. La aparición de un algoritmo eficaz para esta operación fue una piedra angular
en la historia de la informática.
Transformada de Laplace
La transformada de Laplace es un operador LINEAL muy útil para la resolución de ecuaciones
diferenciales.
Laplace demostró como transformar las ecuaciones lineales NO HOMOGENEAS en ecuaciones
algebraicas que pueden resolverse por medios algebraicos.
La transformada de Laplace de una función f(t), 0 ≤ t ≤ 1 es una función ℒ[𝑓] de una variable real s
dada por:
(𝐹(𝑠) = ℒ[𝑓](𝑠) = ∫ 𝑓(𝑡)𝑒−𝑠𝑡
∞
0
𝑑𝑡 = lim
𝜏→∞
∫ 𝑓(𝑡)𝑒−𝑠𝑡
𝑑𝑡
𝜏
0
Está definida para todo 𝑠 ∈ ℝ donde la integral tenga sentido.
Transformada de Gabor

4. La transformada de Gabor realiza un análisis de la señal tal que es capaz de representar en cada
instante de tiempo, las componentes de la señal, de trata pues de un dominio tiempo-frecuencia.
La transformada de Gabor, el nombre de Dennis Gabor, es un caso especial de la corta duración de
transformada de Fourier. Se utiliza para determinar la frecuencia sinusoidal y contenido de fase de
las secciones locales de una señal, ya que cambia con el tiempo. La función a ser transformada se
multiplica primero por una función Gaussiana, que puede considerarse como una función de ventana,
y la función resultante se transforma a continuación, con una transformada de Fourier para obtener el
análisis de tiempo-frecuencia. La función de ventana significa que la señal cerca de la hora que se
analiza tendrá mayor peso.
𝐺(𝑤, 𝜏) = ∫ 𝑓(𝑡) ∙ 𝑔(𝑡 − 𝜏)𝑒−𝑗𝑤𝑡
𝑑𝑡
∞
−∞
Transformada Z
La Transformada Z convierte una señal real o compleja definida en el dominio del tiempo discreto en
una representación en el dominio de la frecuencia compleja.
Se usa la transformada z en el análisis y síntesis de sistemas de control en tiempo discreto de manera
similar a como se usa la transformada de Laplace en sistemas de tiempo continuo.
𝑋(𝑧) = 𝑍{𝑥[𝑛]} = ∑ 𝑥[𝑛]𝑧−𝑛
∞
𝑛=−∞
Transformada de Hilbert
La transformada de Hilbert conforma la señal con la mitad de la información en el dominio del tiempo
y la otra mitad en el dominio de la frecuencia.
La transformada de Hilbert esta definida como:
𝑠∗(𝑡) =
1
𝜋
∫
𝑠(𝜏)
𝑡 − 𝜏
𝑑𝜏

5. Que es equivalente a una rotación de 90° en la fase de cada componente armónica de la señal.
Esencialmente esta ecuación define la transformada de Hilbert como la convolución de la función s(t)
con 1/t, por consecuencia enfatiza las propiedades locales de s(t).
La transformada de Hilbert puede ser calculada de varias formas, entre ellas:
1. En el caso de tener una función (p.e.: funciones armónicas) se puede aplicar directamente la
transformada de Hilbert.
2. Determinación a partir de s(t) aplicando el operador lineal de convolución (operador
normalizado de Hilbert).
ℎ(𝑡) =
2
𝜋
sin2
(
𝜋𝑡
2
)
𝑡
, 𝑡 ≠ 0 𝑦 ℎ(𝑡) = 0, 𝑛 = 0,
de la forma s(t)*h(t), lo que es equivalente a aplicar un filtro.
3. Utilizando la transformada discreta
ℋ{𝑠(𝑡)} =
2
𝜋
∑ 𝑠(𝑡 − 𝑛∆𝑡)
sin2
(
𝜋𝑛
2 )
𝑛
, 𝑛 ≠ 0
∞
𝑛=−∞
4. Reduciendo a una representación de fasor si s(t) es un sinusoide, esto es, si s(t) = Acos(wt+ø)
entonces s*(t) = Asin(wt+ø) para valores reales de A y ø con w > 0
5. A partir de una transformada de Fourier, pasando al dominio de frecuencias la señal
analítica,𝐹+{𝑠̂( 𝑡)} con 𝑠̂( 𝑡) de la forma 𝑠̂( 𝑡) = 𝑠(𝑡) + 𝑖0, luego multiplicando por una
función escalón unitario(eliminando la parte negativa de w en el dominio de las frecuencias)
y finalmente haciendo una transformación inversa de Fourier (𝐹−
{𝑆̂(𝑤)}), con lo cual se
obtiene 𝑠̂( 𝑡) = 𝑠(𝑡) + 𝑖𝑠 ∗ (𝑡), que es equivalente a 𝜕𝑡 + 𝑖𝑠̂( 𝑡) ∙ 𝑠(𝑡)
Señales y Revisión de Sistemas

6. 2.1 Clasificación de señal
Una señal, x (t), se define como una función del tiempo (t ∈ R). Señales en ingeniería de sistemas
se describen típicamente con cinco diferentes clasificaciones
2.1.1 Energía versus Señales de Potencia
Definición 2.1 La energía, 𝑬 𝒙 , de una señal x (t) es
x (t) es llamada una señal de energía cuando 𝐸 𝑥 < ∞. Señales de energía están normalmente
asociadas con formas de onda de pulso o finito duración (por ejemplo, discurso o una transmisión
de información de longitud finita). En cambio, una señal es llamada una señal de potencia si no tiene
energía finita. En realidad, todas las señales son señales de energía (infinito es difícil de producir en
un sistema físico) pero a menudo es matemáticamente conveniente modelar ciertas señales como
señales de potencia Por ejemplo, cuando se considera una señal de voz por lo general es apropiado
considerar la señal como una señal de energía para aplicaciones de reconocimiento de voz, pero en
aplicaciones de transmisión de radio a menudo Modelizamos la voz como una señal de potencia.
Una señal común que se utilizará con frecuencia en este texto es la función sinc (seno cardinal).
Definición 2.2 La función sinc (seno cardinal) es:
𝑠𝑒𝑛𝑐(𝑥) =
𝑠𝑒𝑛(𝜋𝑥)
𝜋𝑥
Definición 2.3 La potencia de la señal, 𝑷 𝒙, es :
Tenga en cuenta que si 𝐸 𝑥 < ∞, entonces 𝑃𝑥 = 0 y si 𝑃𝑥 > 0, 𝐸 𝑥 = ∞.
La Energía normalmente se mide en julios y potencia normalmente se mide en Watts. La mayoría
de las señales de los ingenieros eléctricos consideran son tensiones (voltajes) o corrientes, así que
obtener energía y potencia en las unidades apropiadas una resistencia necesita ser especificado (por
ejemplo,𝑊𝑎𝑡𝑡𝑠 = 𝑉𝑜𝑙𝑡𝑠2
/𝑂ℎ𝑚𝑠). Para simplificar la notación, sólo definiremos la energía y la
potencia como antes, que es equivalente a tener la señal x (t) medido en voltios o amperios y la
resistencia siendo la unidad (𝑅 = 1Ω).
2.1.2 Periódica versus aperiódica

7. Una señal periódica es una que se repite en el tiempo.
Definición 2.4, x (t) es una señal periódica cuando:
Definición 2.5 El período de la señal es:
La frecuencia fundamental es entonces:
La mayoría de las señales periódicas son señales de potencia (Nota Si la energía en un período es
distinto de cero, entonces la señal periódica es una señal de potencia) y otra vez la periodicidad es
una conveniencia matemática que no es rigurosamente cierto para cualquier señal real. Utilizamos
el modelo de periodicidad cuando la señal tiene aproximadamente la propiedad en la ecuación de
la definición 2.4 sobre el intervalo de tiempo de interés. Una señal aperiódica se define como una
señal de que no es periódica.
2.1.2 Real versus Señales Complejas
Señales complejas ocurren a menudo en el análisis de sistemas de comunicación y diseño. El
ejemplo más común es la transformada de Fourier. Otra aplicación importante de la comunicación
de señales complejas es en la representación de las señales de paso de banda. Definir una señal
compleja y una exponencial compleja para ser:
donde x (t) y y (t) son ambas señales reales. Una magnitud (α (t)) y la fase (θ (t)) la representación
de una señal compleja también se utiliza comúnmente como:
donde
La operación conjugada compleja se define como:
Algunas fórmulas importantes para el análisis de señales complejas son:
Una señal, x (t), se define como una señal de tiempo continua si el dominio de la función que
define la señal que contiene intervalos de la línea real. Una señal, x (t), se define como una señal
de tiempo discreta si el dominio de la señal es un subconjunto de la línea real contable. A menudo

8. una señal discreta se denota por x(k), donde k es un número entero y una señal discreta surge con
frecuencia de muestreo (uniforme) de una señal continua de tiempo, por ejemplo,𝑥(𝑘) = 𝑥(𝑘𝑇𝑠),
donde 𝑇𝑠 es el periodo de muestreo.
2.2 Caracterización de dominio de frecuencia de las señales
2.2.1 Series de Fourier
Si x (t) es periódica con período T, entonces x (t) puede ser representado como
Donde 𝑓𝑇 = 1/𝑇 y
Esto se conoce como la serie de Fourier exponencial compleja. En general, tenga en cuenta que el
𝑥 𝑛 son números complejos. En palabras: una señal periódica, x (t), con período T se puede
descomponer en una suma ponderada de sinusoides complejos con frecuencias que son un número
entero múltiplo de la frecuencia fundamental (𝑓𝑇 = 1/𝑇).
Propiedades de la serie de fourier
Propiedad 2.1 Si x (t) es real, entonces 𝑥 𝑛 = 𝑥′−𝑛. En consecuencia la serie de Fourier de una
señal real es una función simétrica Herminia de frecuencia. Esto implica que la magnitud de la serie
de Fourier es una función par de la frecuencia
y la fase de la serie de Fourier es una función impar de frecuencia, es decir:
Propiedad 2.2 Si x (t) es real y una función es par de tiempo, es decir, 𝑥(𝑡) = 𝑥(−𝑡) entonces
todos los coeficientes de la serie de Fourier son números reales.
Teorema 2.1 (Parseval)
Teorema de Parseval establece que la potencia de una señal puede calcularse utilizando ya sea el
tiempo o la representación en el dominio de frecuencia de la señal y los dos resultados son idénticos.

9. 2.2.2 Transformada de Fourier
Si x (t) es una señal de energía, entonces la transformada de Fourier se define como:
X (f) se encuentra en el complejo general y da la representación en el dominio de la frecuencia de
x (t). La transformada inversa de Fourier es
Propiedades de la Transformas de Fourier
Propiedad 2.4 Si x (t) es real entonces la transformada de Fourier es simetrica Hermitiana , es
decir, 𝑋(𝑓) = 𝑋′
(−𝑓). Esto implica
Propiedad 2.5 Si x (t) es real y una función par de tiempo, es decir,𝑥(𝑡) = 𝑥(−𝑡), entonces 𝑋(𝑓)
es un valor real y una función par de la frecuencia.
Propiedad 2.6 Si x (t) es real e impar, es decir, 𝑥(𝑡) = −𝑥(−𝑡), entonces 𝑋(𝑓) es un imaginario
valorado y función impar de frecuencia
Teorema 2.2 (Enerdia de Rayleigh´s)
Teorema 2.3 (Convolucion) La Convolución de dos funciones de tiempo, x (t) y h (t), se define
como:
La transformada de Fourier de y(t) es dada como
Teorema 2.4 (Dualidad ) Si 𝑋(𝑓) = 𝐹{𝑥(𝑡)}, entonces
Teorema 2.5 Translación y Dilatación Si 𝑦(𝑡) = 𝑥(𝑎𝑡 + 𝑏) , entonces
Teorema 2.6 Translación de Frecuencia Multiplicar cualquier señal de una señal sinusoidal
resulta una translación de la frecuencia de las transformadas de Fourier

10. Definición 2.6 La función de correlación de una señal x (t) es
Son tres importantes características de la función de correlación
Definición 2.7 El espectro de energía de una señal x (t) es
La densidad espectral de energía es la transformada de Fourier de la función de correlación,
El espectro de energía es una descripción funcional de cómo la energía de la señal
x (t) se distribuye en función de la frecuencia. Las unidades en un espectro de energía son 𝐽 / 𝐻𝑧.
Debido a esta característica, dos propiedades importantes, de la densidad espectral de energía son
Definición 2.8 La potencia media durante un tiempo de medición, 𝑇 𝑚, es.
Definición 2.9 La transformada de Fourier de una señal truncada a una longitud de tiempo de Tm
es
Un analizador de espectro ideal produce la siguiente medición un periodo de frecuencias
El espectro de potencia muestreado es una descripción funcional de cómo la potencia en la señal
truncada x(t) se distribuye como una función de la frecuencia. Las unidades en un espectro de
potencia son 𝑊𝑎𝑡𝑡𝑠 / 𝐻𝑧. Debido a esta característica, dos características importantes de la
densidad espectral de potencia son

11. 2.2.4 Transformada de Fourier Representación de señales periódicas
La transformada de Fourier para señales eléctricas no está rigurosamente definida y sin embargo
a menudo queremos utilizar representaciones de la frecuencia de las señales electricas.
Normalmente las señales electricas que usaremos en este texto son típicamente señales periódicas
que tienen una representación de la serie de Fourier. Una serie de Fourier puede ser representada
en el dominio de la frecuencia con la ayuda de los siguientes resultados
En otras palabras, un complejo exponencial de frecuencia 𝑓1 puede ser representado en el
dominio de la frecuencia con un impulso en la 𝑓1 . Por lo tanto la transformada de Fourier de una
señal periódica se representa como
Durante el resto del texto será marcado el espectro de una señal periódica mediante líneas con
flechas en la parte superior para representar las funciones de delta.
2.2.5 Transformada de Laplace
Este texto utilizará la transformada de Laplace unilateral para el análisis de señales transitorias en
sistemas de comunicaciones. La unilateral transformada de Laplace de una señal x (t) es
El uso de la transformada de Laplace unilateral implica que la señal es cero para tiempo negativo.
La transformada inversa de Laplace se da como
La evaluación de la inversa general de transformada de Laplace requiere la evaluación de
integrales de contorno en el plano complejo. Para la mayoría de las transformadas de interés los
resultados están disponibles en tablas.

12. 2.3 Sistemas lineales invariantes del tiemp
Sistemas electrónicos se caracterizan a menudo por las relaciones de entrada-salida. Un diagrama
de bloques de un sistema electrónico se da en la siguiente figura , donde x(t) es la entrada y y(t) es
la salida
Definición 2.14 Un sistema lineal es uno en la cual la superposición se mantiene, es decir,
Figura 1.- Un diagrama de bloques del sistema.
Definición 2.15 Un sistema invariante en el tiempo es uno en el cual un cambio de tiempo en la
entrada sólo cambia la salida por un cambio del tiempo, es decir,
Un sistema lineal invariante en el tiempo (LTI) se describe completamente por una respuesta de
impulso, h (t). La salida del sistema lineal es la convolución de la señal de entrada con la respuesta
al impulso, es decir,
La transformada de Fourier (transformada de Laplace) de la respuesta del impulso se denota la
respuesta de frecuencia (función de transferencia), 𝐻(𝑓) = 𝐹{ℎ(𝑡)}(𝐻(𝑠)) = 𝐿{ℎ(𝑡)}, y por el
teorema de convolución para señales de energía tenemos que:
Del mismo modo el espectro de energía de salida del sistema lineal tiene una forma simple
Para una señal de entrada periódica la salida del sistema LTI será una señal periódica del mismo
periodo y tienen una representación de la serie de Fourier de
donde𝑦𝑛 = 𝐻 (
𝑛
𝑇
) 𝑥 𝑛 . En otras palabras la salida de un sistema LTI con una entrada periódica
también será periódica. Los coeficientes de la serie de Fourier son el producto de los coeficientes
de señal de entrada y la función de transferencia evaluados en las frecuencias harmónicas
Un sistema lineal importante para el estudio de las señales de frecuencia modulada (FM) es el
diferenciador. El diferenciador se describe con la siguiente función de transferencia

13. Espacios de Señales
2.1 Espacios métricos
Habiendo reunido en un conjunto de todas las señales que presentan alguna propiedad común.
Una señal particular solo interesa en relación con las demás señales del conjunto. Un método en
general, que es intuitivamente satisfactorio , para caracterizar la diferencia entre dos elementos de
un conjunto consiste en asignar a cada par de elementos un numero real positivo. Este se interpreta
como distancia entre los elementos y el propio conjunto comienza a tomar un carácter geométrico.
Al conjunto, con una distancia definida adecuadamente, le llamaremos espacio de señales. Para
definir una distancia, necesitamos un funcional que aplique todos los pares de elementos del
conjunto en el eje real. A dicho funcional, 𝑑: {𝑥, 𝑦} → 𝑅, se dice que es una métrica si posee las
siguientes propiedades:
a.- 𝑑(𝑥, 𝑦) ≥ 0 𝑦 𝑑(𝑥, 𝑦) = 0 si, y solo si, 𝑥 = 𝑦
b.- 𝑑(𝑥, 𝑦) = 𝑑(𝑦, 𝑥) (𝑠𝑖𝑚𝑡𝑟𝑖𝑎)
c.- 𝑑(𝑥, 𝑧) ≤ 𝑑(𝑥, 𝑦) + 𝑑(𝑦, 𝑧) (𝑑𝑒𝑠𝑖𝑔𝑢𝑎𝑙𝑑𝑎𝑑 𝑑𝑒𝑙 𝑡𝑟𝑖𝑎𝑛𝑔𝑢𝑙𝑜)
Estos requisitos no son mas que enunciados formalizados que reflejan las propiedades asociadas
intuitivamente a la distancia: (a) La distancia es un numero no negativo. (b) La distancia de x e y es
la misma que de y a x. (c) La longitud de un lado de un triangulo no puede ser mayor que la suma
de las longitudes de los otros dos (aquí interpretaremos geométricamente los elementos x, y y z
como vértices de un triangulo)
Un conjunto d elementos €, junto con una métrica d, se denomina espacio métrico ( € , d ). Debe
notarse que dos métricas diferentes , definidas sobre el mismo conjunto de elementos, forman dos
espacios métricos diferentes.
2.2 Convergencia y continuidad
En los problemas de análisis nos encontramos a menudo con sucesiones infinitas de elementos
{𝑥1, 𝑥2, 𝑥3, . . . . . } seleccionadas de un cierto conjunto €. El concepto de distancia de un espacio
métrico nos permite examinar dichas sucesiones en lo que respecta a la propiedad fundamental
llamada convergencia.
Decimos que una sucesión {𝑥 𝑛 ; 𝑥 𝑛 Є €, 𝑛 = 1,2, … … … } es convergente si existe una 𝑥 𝑛 Є € tal
que para todo 𝜀 > 0 , existe un entero positivo 𝑛0 tal que
𝑛 ≥ 𝑛0 → 𝑑(𝑥 𝑛, 𝑥) < 𝜀
Esto se expresa a menudo en la forma
lim
𝑛→∞
𝑥 𝑛 = 𝑥

14. Es intuitivamente aparente que puntos sucesivos de una sucesión convergente deben tener a estar
cada vez mas próximos al ir creciendo
n. Toda sucesión que tenga esta
propiedad se denomina sucesión de
Cauchy. Concretamente, si para todo
𝜀 > 0 existe un entero positivo 𝑛0 tal
que 𝑚, 𝑛 ≥ 𝑛0 → 𝑑(𝑥 𝑚, 𝑥 𝑛) < 𝜀 la
sucesión será una sucesión de cauchy.
De la desigualdad del triangulo
𝑑(𝑥 𝑛, 𝑥 𝑚) ≤ 𝑑(𝑥, 𝑥 𝑚) + 𝑑(𝑥 𝑛, 𝑥 )
queda claro que una sucesión
convergente debe ser una sucesión de
cauchy. En cambio, una sucesión de
cauchy puede no ser convergente simplemente por que el elemento al cual tiende la sucesión en el
limite puede no estar en el conjunto €. A continuación damos

15. ME FALTO LA PAGINA 31 PARA ESCRIBIR, Y TAMBIEN TIENE UN EJEMPLO QUE
ES EL 2.6
2.3 Espacios Vectoriales
Si como sistema de escalares se utilizan números reales, el espacio vectorial resultante se denomina
espacio vectorial. Utilizando los números complejos para los escalares, tenemos un espacio vectorial
complejo. El vector obtenido tomando la suma de n vectores particulares, multiplicando cada uno
de ellos por un coeficiente escalar
𝑥 = ∑ 𝛼𝑖 𝑥𝑖
𝑛
𝑖=1
Se denomina combinación lineal. Facil es ver que el conjunto de todas las combinaciones lineales de
{𝑥1, 𝑥2, … … … , 𝑥 𝑛} forman un espacio vectorial. Es mas, si tomamos un subconjunto de
{𝑥1, 𝑥2, … … … , 𝑥 𝑛}, 𝑝. 𝑒., {𝑥1, 𝑥2, … … … , 𝑥 𝑚}; 𝑚 < 𝑛
El conjunto de combinaciones lineales formara un espacio vectorial que es un subconjunto del
espacio vectorial formado a partir de las combinaciones lineales de {𝑥1, 𝑥2, … … … , 𝑥 𝑛}. A dicho
subconjunto se le llama subes pació vectorial. Un conjunto de vectores {𝑥𝑖; 𝑖 = 1,2, … … … , 𝑛} se
dice que es linealmente independiente si la relación
∑ 𝛼𝑖 𝑥𝑖
𝑛
𝑖=1
= 0
Solo puede satisfacerse siendo nulos todos los escalares 𝛼𝑖. Dicho de otro modo, un vector de un
conjunto linealmente independiente no puede expresarse como combinación lineal de los demás
vectores del conjunto. Sea M el espacio de las combinaciones lineales de los n vectores linealmente
independiente {𝑥𝑖; 𝑖 = 1,2, … … . . , 𝑛}. Cada vector de M es una combinación lineal única de los {𝑥𝑖}
(conjunto único de coeficientes escalares). Se dice que M es un espacio vectorial n-dimensional. Al
conjunto {𝑥𝑖} se le denomina base de M y se dice que M esta engendrado por esta base. Todo
conjunto de n vectores de M linealmente independientes servirá de base para M; por tanto, un
espacio vectorial no tendrá base única.
2.4 Espacios Vectoriales Normados
Vamos a combinar los conceptos geométricos asociados a los espacios métricos con los conceptos
algebraicos asociados a los espacios vectoriales. Ello se logra asignando un numero real que refleje
el “tamaño” de un elemento cualquiera de un espacio vectorial. A dicho numero e le llama norma
de un vector (se representa por ||𝑥||) y se puede definir en función de una aplicación cualquiera
del espacio vectorial en el eje real, la cual satisfaga las siguientes propiedades:
a.- ||𝑥|| ≥ 0 y ||𝑥|| = 0 si, y solo si, 𝑥 = 0
b.- ||𝑥 + 𝑦|| ≤ ||𝑥|| + ||𝑦||

16. c.- ||𝛼𝑥|| = |𝛼| ||𝑥||
2.5 Espacios con Producto Escalar
El paso final en el desarrollo de espacios de señales es proporcionar estructura geométrica
adicional en forma de una relación de producto interior entre pares de vectores. De ahora en
adelante trataremos de espacios vectoriales complejos, ya que los espacios reales se pueden tratar
siempre como caso particular. El producto interior es una aplicación de pares ordenados de vectores
del espacio vectorial es el plano complejo. Esta aplicación, con imágenes representaos por (x,y) en
]C, satisface las propiedades siguientes:
a. (𝑥, 𝑦) = (𝑦, 𝑥)∗
b. (𝛼𝑥 + 𝛽𝑦, 𝑧) = 𝛼(𝑥, 𝑧) + 𝛽(𝑦, 𝑧)
c. (𝑥, 𝑥) ≥ 0 y (𝑥, 𝑥) = 0 si, y solo si, 𝑥 = 0
De la ecuación del inciso (a) y (b), vemos que (𝛼𝑥, 𝑦) = 𝛼(𝑥, 𝑦), (𝑥, 𝛼𝑦) = 𝛼∗(𝑥, 𝑦), y que (𝑥, 𝑥)
es real. Al producto interior también se le llama producto escalar. Consecuencia importante de la
definición de producto interior es que
||𝑥|| = (𝑥, 𝑥)
1
2
Es noma valida para el espacio vectorial. Seve fácilmente que se cumplen las propiedades (a) y (c)
de las ecuaciones de espacio vectorial normada que definen una norma. La propiedad (b), o
desigualdad del triangulo, exige mayor esfuerzo. Establezcamos primeramente una relación muy
útil, conocida por el hombre de desigualdad de Schuartz.
|(𝑥, 𝑦)|2
≤ (𝑥, 𝑥)(𝑦, 𝑦)
Para demostrar, utilizamos la propiedad (c) de la ecuación del Espacios con Producto Escalar con el
vector 𝑥 + 𝛼𝑦 donde 𝛼 es un escalar cualquiera.
0 ≤ (𝑥 + 𝛼𝑦, 𝑥 + 𝛼𝑦)
= (𝑥, 𝑥) + 𝛼(𝑦, 𝑥) + 𝛼∗(𝑥, 𝑦) + |𝛼|2
(𝑦, 𝑦)
En particular, vale para 𝛼 = −(𝑥, 𝑦)/(𝑦, 𝑦), dando
(𝑥, 𝑥) −
|(𝑥, 𝑦)|2
(𝑦, 𝑦)
≥ 0

17. El producto escalar introduce, pues, una norma que a su vez introduce una métrica, por (2.25), (me
falta la pagina 38) por lo que un espacio con producto escalar será un espacio métrico que lleva
implícita un métrica particular. Un espacio con producto escalar que sea también completo, como
espacio métrico, se denomina espacio de Hilbert
A veces es útil pensar en el producto escalar como algo que proporciona una relación angular entre
vectores. Como la desigualdad de Schwartz podemos escribirla en la forma
|(𝑥, 𝑦)| ≤ ||𝑥||||𝑦||
Podemos definir un ángulo real θ formado por x e y tal que
𝐶𝑜𝑠𝜃 =
𝑅𝑒(𝑥, 𝑦)
||𝑥||||𝑦||
Sin embargo , para el análisis solo utilizaremos el concepto de ortogonalidad entre pares de
vectores. Diremos que x e y son ortogonales si, y solo si , (𝑥, 𝑦) = 0. Se ve en seguida la dificultad
que presenta en la ecuación anterior que es el cosθ aplicada a espacios complejos, ya que podríamos
tener 𝜃 = ±𝜋/2 con (𝑥, 𝑦) ≠ 0.En cambio, si sustituimos 𝑅𝑒(𝑥, 𝑦) por |(𝑥, 𝑦)| en la ecuación
anterior, no podemos generar en los cuadrantes segundo y tercero.
Los espacios de los que nos ocuparemos tienen productos escalares dados por
(𝑥, 𝑦) = ∑ 𝛼𝑖 𝛽𝑖
∗
; 𝑥, 𝑦𝜖𝐶 𝑛
𝑛
𝑖=1
Y
(𝑥, 𝑦) = ∫ 𝑥(𝑡)𝑦∗(𝑡)𝑑𝑡; 𝑥, 𝑦 ∈ 𝐿2
(𝑇)
𝑡
𝑇
El contenido energético de la señal no esta afectado por la traslación temporal;
||𝑥||
2
= ||𝑥 𝑟||2
; luego
𝑑2(𝑥, 𝑥 𝑟) = 2[||𝑥||
2
− 𝑅𝑒(𝑥, 𝑥 𝑟)]
= 2[𝑟𝑥(0) − 𝑟𝑥(𝜏)]
Donde hemos definido
𝑟𝑥(𝜏) = 𝑅𝑒(𝑥, 𝑥 𝑟)
= 𝑅𝑒 ∫ 𝑥(𝑡)𝑥∗
(𝑡 + 𝜏)
∞
−∞
𝑑𝑡
Luego, para cada señal x, existe una función real del traslado en el tiempo τ que caracteriza la
separación en el espacio de señales debida a la traslación en el tiempo. En el caso de una señal
rápidamente fluctuante, podríamos esperar que 𝑟𝑥(𝜏) disminuyera rápidamente con τ. En el caso
de un pulso de señal estrecho, esta claro que 𝑟𝑥(𝜏) es estrecha, pero la señal podría tener una larga
duración y seguir originando una 𝑟𝑥(𝜏) estrecha según indica en la figura 3. En muchas aplicaciones,
por ejemplo es sistemas de radar, conviene utilizar señales que den origen a una 𝑟𝑥(𝜏) estrecha de

18. manera que se pueda obtener una localización
precisa de la señal en el tiempo por medio de
medidas efectuadas sobre la seña
En consecuencia, a 𝑟𝑥(𝜏) le llamaremos
función ambigüedad en el tiempo de la señal
x(t). una ambigüedad pequeña significa que la
distancia es grande. La función 𝑟𝑥(𝜏) también
se denomina a veces función de auto
correlación parta x(t) por analogía con una
caracterización similar de los procesos
aleatorios. En el caso de señales reales, es fácil
tomar la transformada de Fourier, de la
siguiente manera:
𝑅 𝑥(𝑓) = ∫ 𝑟𝑥(𝜏)𝑒−𝑗2𝜋𝑓𝜏
𝑑𝜏
∞
−∞
= |𝑋(𝑓)|2
Y vemos que las señales que presentan la misma ambigüedad en el tiempo tienen transformadas
de Fourier que pueden diferir en un factor de fase arbitrario.
La característica mas importante de un espacio con producto escalar como espacio de señales es
que se proporciona una relación directa entre una señal y su representación. Supongamos que M
sea un espacio n dimensional arbitraria engendrado por la base {𝑢𝑖; 𝑖 = 1,2, … … , 𝑛}, entonces 𝑥 ∈
𝑀 viene dado por
𝑥 = ∑ 𝛼𝑖 𝑢𝑖
𝑛
𝑖=1
Tomando productos escalares en ambos miembros de la ec anterior,
(𝑥, 𝑢𝑖) = ∑(𝑢𝑖,
𝑛
𝑖=1
𝑢𝑗)𝛼𝑖; 𝑗 = 1,2, … … . . 𝑛
Este es un sistema de n ecuaciones escalares lineales del que puede despejarse la n-pla 𝛼 =
{𝛼1, 𝛼2, … … . . , 𝛼 𝑛} que proporciona la representacion (en 𝐶 𝑛
) de x relativa a la base {𝑢𝑖}. Otro
método, mas conveniente desde el punto de vista de la notación, consiste es establecer otra base
{𝑣𝑖} para M relacionada con {𝑢𝑖} de manera ortogonal por pares de acuerdo con
(𝑢𝑖, 𝑣𝑗) = 𝛿𝑖𝑗; 𝑖, 𝑗 = 1,2, … … . , 𝑛
Donde 𝜹𝒊𝒋 es la delta de Kronecker definida por 𝜹𝒊𝒋 = 𝟏 para 𝑖 = 𝑗, 𝜹𝒊𝒋 = 𝟎 para 𝑖 ≠ 𝑗.
(𝑥, 𝑣𝑗) = ∑ 𝛼𝑖(𝑢𝑖, 𝑣𝑗)
𝑛
𝑖=1
→ 𝛼𝑖 = (𝑥𝑖, 𝑣𝑗); 𝑗 = 1,2, … … … 𝑛
Las bases que satisfagan a la ecuación anterior se denominan bases reciprocas, y tenemos
𝑥 = ∑(𝑥, 𝑣𝑖)𝑢𝑖 =
𝑛
𝑖=1
∑(𝑥, 𝑢)𝑣𝑖
𝑛
𝑖=1

19. Para todo 𝑥 𝜖 𝑀 y todo par de base reciprocas para M. Otro método que posee muchas
características atractivas consiste en utilizar como base para M un conjunto orto normal. Diremos
que el conjunto {𝑢𝑖; 𝑖 = 1,2, … … . , 𝑛} es un conjunto orto normal si es autor reciproco, es decir, si
los vectores son mutuamente ortogonales y tiene norma unidad.
(𝑢𝑖, 𝑢𝑗) = 𝜹𝒊𝒋
Entonces para todo 𝑥 ∈ 𝑀
𝑥 = ∑(𝑥, 𝑢𝑖)𝑢𝑖
𝑛
𝑖=1
Con una base orto normal para M, no solo tenemos una correspondencia uno a uno entre los
vectores de M y su representación en 𝐶 𝑛
, sino una igualdad de productos escalares en ambos
espacios. Para
𝑥 = ∑ 𝛼𝑖 𝑢𝑖
𝑛
𝑖=1
𝑒 𝑦 = ∑ 𝛽𝑖 𝑢𝑖
𝑛
𝑖=1
2.6 Funcionales lineales
Una aplicación de un espacio vectorial complejo € en los escalares complejos 𝑓: € → 𝐶 wue tenga
la propiedad de que
𝑓(𝛼𝑥 + 𝛽𝑦) = 𝛼𝑓(𝑥) + 𝛽𝑓(𝑦)
Para todo 𝛼, 𝛽 ∈ 𝐶 y todo x,y ∈ € se denomina funcional lineal o forma lineal. Si es € un espacio con
producto escalar, por la propiedad (b) de espacios con producto escalar vemos que 𝑓𝜑 definido por
𝑓𝜑(𝒙) = (𝒙, 𝜑)
Es un funcional lineal. Es mas, si ||𝜑|| esta acotada, ||𝜑|| < 𝐾, 𝑓𝜑 sera un funcional lineal continuo.
Esto se deduce directamente de la desigualdad de Schwartz, ya que
|𝒇 𝜑(𝒙) − 𝒇 𝜑(𝒙 𝟎) |= |𝒙 − 𝒙 𝟎, 𝜑| ≤ ||𝑥 − 𝒙 𝟎||| |𝜑||< 𝐾||𝑥 − 𝒙 𝟎||
Para todo 𝒙 𝟎 ∈ € .
Rsulatdo mas importante es que si € es completo, es decir, es un espacio de Hilbert, todo funcional
lineal continuo se podrá expresar como producto interior en la forma de la ec anterior. Para cada
funcional lineal continuo existe un vector único 𝜑 ∈ €. La demostración de este enunciado puede
verse en la mayoría de textos de análisis funcional. Una parte fundamental de la demostración lleva
consigo el hecho de que el conjunto de vectores que un funcional lineal consigo el hecho de que el
conjunto de vectores que un funcional lineal aplica en cero es un subespacion vectorial de €.
Representamos por Mf, este subespacio para la funcional f; es decir, 𝑀𝑓 = {𝑥; 𝑓(𝑥) = 0}. Elijamos
ahora un vector no nulo x0 ortogonal al Mf.

20. (𝒚, 𝒙 𝟎) = 𝟎 para todo 𝑦 ∈ 𝑴 𝒇
Podemos normar este espacio mediante la definición siguiente:
||𝑓|| = sup{|𝑓(𝑥)|; ||𝑥|| ≤ 1, 𝑥 𝜖 €}
O, lo que es equivalente, por medio de
||𝑓|| = inf{𝐾; |𝑓(𝑥)| ≤ 𝐾||𝑥||, 𝑥 𝜖 €}
Si esta acotada la norma da un funcional, decimos que este acotado. Un funcional lineal acotado es
continuo puesto que tenemos |𝑓(𝑥) − 𝑓(𝑥0)| = |𝑓(𝑥 − 𝑥0)| ≤ ||𝑓||||𝑥 − 𝑥0|| para todo 𝒙 𝟎 ∈ €
. La continuidad en x0 implica continuidad puesto que ||𝑓|| es independiente de x0.
Recíprocamente, un funcional lineal continuo esta acotado, puesto que la continuidad en el origen
da
Con ||𝑦|| < 2. Luego la acotabilidad y la continuidad de un funcional lineal son equivalentes.
En el caso de un funcional lineal expresado como producto escalar, vemos que
Utilizando la desigualdad de schwartz y notando que la igualdad se cumple para x proporcional a 𝜑
Si restringimos nuestra consideración al espacio de todos los funcionales lineales continuos
definidos sobre un espacio de hilbert €, hallaremos que dicho espacio es un espacio de hilbert que
esta relacionado con € de manera muy sencilla. Al espacio en cuestión se le llama espacio conjugado
€. Hemos observado que existe una correspondencia uno a uno entre los elementos 𝑓𝜑 𝜖 € y
𝝋 ∈ € .Es mas, los escalares correspondientes son, simplemente, complejos conjugados, ya que
𝑓𝛼𝜑 = 𝛼𝑓𝜑. Esto sugiere que
La cual se demuestra fácilmente que es una definición valida para un producto interior en €. La
norma inducida por este producto interior ||𝑓𝜑|| = √(𝑓𝜑, 𝑓𝜑) = ||𝜑|| . Por ultimo, si es {𝑢𝑖} una
base para €, {𝑓𝜑,} sera una base para € donde {𝑣𝑖} es la base reciproca (𝑢𝑖, 𝑣𝑖) = 𝛿𝑖𝑗. Luego un
funcional lineal continuo arbitrario f podrá expresarse mediante la combinación lineal
Con ciertos espacios de señales, digamos 𝐿2
(𝑇), tendremos ocasión de utilizar funcionales lineales
que no sean continuos. Esta claro que 𝑓(𝑥) = 𝑥(𝑡0) describe un funcional lineal, pero también lo
esta que exciten funciones del tiempo de cuadrado integrable que no esta acotadas para todo 𝑡 ∈
𝑇. Podemos conservar aun la representación del funcional como producto interior , en este caso
definiendo la función d tal que

21. Procesos Estocásticos
3.1 Definición axiomática de probabilidad
Definición 3.1 eventos A y B son mutuamente excluyentes si 𝐴⋂𝐵 = Ǿ
Axiomas de probabilidad. Una medida de probabilidad, P, para un espacio probabilístico (Ω,F,P)
con eventos A,B Є F debe satisfacer los siguientes axiomas
Estos tres axiomas son los bloques de construcción para la teoría de la probabilidad y la
comprensión de eventos aleatorios que caracterizan el desempeño del sistema de comunicación.
Definicion 3.2 (Complemento) El complemento de un conjunto A, denota 𝐴 𝐶
, es el conjunto de
todos los elementos de Ω que no sean elementos A.
Teorema 3.1 Poincaré Para N eventos 𝐴1, 𝐴2, … … 𝐴 𝑁
Donde
Prueba: Los resultados se dan para N= 2 y la prueba para otros casos es similar (si no más tedioso).
Tenga en cuenta que los eventos 𝐴 𝑦 𝐵⋂𝐴 𝐶
son eventos mutuamente excluyentes. Por lo tanto
tenemos
Sumando las dos primeras ecuaciones y restando la tercera, tendremos la siguiente ecuacion
Definición 3.3 (Probabilidad Condicional) Sea (Ω,F,P) un espacio de probabilidad con conjuntos
A, B Є F y 𝑃[𝐵] ≠ 0 El condicional o probabilidad a posteriori del evento A dado un acontecimiento
B, denotado 𝑃 [𝐴 | 𝐵], se define como

22. 𝑃 [𝐴 | 𝐵] se interpreta como la probabilidad de eventos de A después de que el experimento se ha
realizado y el evento B se observa.
Definición 3.4 (Independencia) Dos eventos A, B Є F son independientes si y sólo si
La independencia es equivalente a
Para eventos independientes A y B, el a posteriori o probabilidad condicional 𝑃 [𝐴 | 𝐵] es igual a
la probabilidad a prioir 𝑃 [𝐴]. Por consiguiente, si A y B son independientes, entonces la observación
de B no revela nada acerca de la probabilidad relativa de la ocurrencia del evento A.
Definición 3.5 Un conjunto de eventos colectivamente exhaustivo es uno que
Teorema 3.2 Probabilidad Total Para N mutuamente exclusivo, colectivamente exhaustivas
eventos (𝐴1, 𝐴2 , … … … . 𝐴 𝑁) y B Є Ω, entonces
Teorema 3.3 (Bayes) Para N mutuamente exclusivo, eventos colectivamente exhaustivas
(𝐴1, 𝐴2 , … … … . 𝐴 𝑁) y B Є Ω, entonces la probabilidad condicional del evento Aj dado ese evento B
se observa
Prueba: La definición de probabilidad condicional da
3.2 Variables Aleatorias
En las comunicaciones, la transmisión de información a menudo es corrompida por el ruido
aleatorio. Este ruido aleatorio se manifiesta como una tensión al azar (un número real) en la salida
de los circuitos eléctricos en el receptor. El concepto de una variable aleatoria (RV) vincula la
definición axiomática de probabilidad con estos números al azar real observados. El conjunto de
todos los resultados experimentales se denomina Ω y un particular resultado del experimento
aleatorio se denota con ω.
Definición 3.6 (Ω, F, P) sea un espacio de probabilidad. Una variable aleatoria real X(ω) es una
función de un solo valor o asignación de Ω a la línea real (R).

23. Existen tres tipos de variables aleatorias: discretas, continuas y mixtos. Una variable aleatoria
discreta tiene un número finito (o infinito contable) de valores posibles. Una variable aleatoria
continua toma valores en un intervalo de la línea real de longitud diferente a cero. Una variable
aleatoria mixta es una combinación convexa de una variable aleatoria continua y discreta. Para
simplificar la notación cuando no existe ninguna ambigüedad, X representa la variable aleatoria X(ω)
(se cae el índice de resultados experimentales) y X = X (ω) representa una realización particular de
esta variable aleatoria.
Definición 3.7 Un número real observado como resultado del experimento aleatorio es
denotado una muestra de la variable aleatoria.
3.2.1 función de distribución acumulativa
Definición de 3.8 Para una variable aleatoria
X(ω), la CDF es una función 𝐹 𝑥(𝑥) definida como
Un vez mas para simplificar la notación cuando no
existe ninguna ambigüedad, la CDF de la variable
aleatoria X se escribirá como 𝐹𝑥(𝑥) = 𝑃(𝑋 ≤ 𝑥)
Figura 3.2 muestra diagramas de ejemplo de la
CDF para variables aleatorias discretas, continuas
y mixtas. La variable aleatoria discreta tiene un CDF con una forma escalonado, los pasos se
producen en los puntos de los valores posibles de la variable aleatoria. La variable aleatoria continua
tiene un CDF, que es una función continua y la variable aleatoria mixta tiene un CDF que contienen
ambos intervalos donde la función es continua con cero derivado y puntos donde la función hace
unos saltos.
Propiedades de un CDF

24. 3.2.2 función de densidad de probabilidad
Definición 3.9 Para una variable aleatoria continua X (ω), el PDF es una función 𝑓𝑥 (𝑥)
se define como
el PDF se puede considerar como la "densidad" de probabilidad en un intervalo muy pequeño
alrededor de X= x. Variables aleatorias discretas no tienen una "densidad" de probabilidad,
repartidas en un intervalo pero tienen probabilidad masa concentrada en los puntos. Así que la idea
de una función de densidad de una variable aleatoria discreta no es consistente. La cantidad análoga
a un PDF para un RV continua en el caso de un RV discreta es la función de masa de probabilidad
(PMF)
Propiedades de un PDF
De nuevo, si no hay ninguna ambigüedad en la expresión, el PDF de la variable aleatoria X se
escribe como f (x) y si no no hay ambigüedad sobre si un RV es continua o discreta, el PDF se escribe
p (x).
3.2.3 Momentos y promedios estadísticos
A menudo, un ingeniero de comunicaciones calcula la media estadística de una función de una
variable aleatoria. El valor medio o valor esperado de una función g (x) con respecto a una variable
aleatoria X es
Promedio o valores esperados son números, que proporcionan una información parcial sobre la
variable aleatoria. Los valores promedio son unos caracterizaciones números de variables aleatorias,
pero no una descripción completa en sí mismos como un PDF o CDF. Un buen ejemplo de un
promedio estadístico utilizado a menudo para caracterizar RVs viene dada por el valor medio. El
valor promedio se define como

25. La media es el valor promedio de la variable aleatoria. El momento n-ésima de una variable
aleatoria es una generalización de la media y se define como
El valor cuadrático medio,𝐸(𝑋2
) , se utiliza con frecuencia en el análisis de un sistema de
comunicación (por ejemplo, potencia media). Otra función de interés es un momento central (un
momento alrededor del valor medio) de una variable aleatoria. El momento central nth se define
como
El segundo momento central más comúnmente utilizado es la varianza, 𝜎X,2, que proporciona una
medida de la propagación de una variable aleatoria alrededor de la media. La varianza tiene la
notación abreviada 𝜎X,2 = 𝜎X,
2
= 𝑣𝑎𝑟(𝑥) La relación entre la varianza y el valor cuadrático medio
viene dada por
3.2.4 La variable aleatoria gaussiana
Esta RV es una muy buena aproximación a muchos de los fenómenos físicos que ocurren en las
comunicaciones electrónicas (por ejemplo, el voltaje de ruido generado por el movimiento térmico
de los electrones en los conductores). La razón para el uso común de la gaussiano RV es el teorema
de límite Central y que el análisis con gaussiano RV’s a menudo es manejable. Un RV Gaussiano o
normal RV, X, de la media 𝑚 𝑥 y varianza 𝜎X,
2
es denotado 𝑁(𝑚 𝑥, 𝜎X,
2
) El Gaussiano RV es una
continua toma valores de variables aleatorias sobre toda la recta real y un PDF de
El PDF Gaussiano se refiere a menudo como la curva en forma de campana. La media cambia el
centroide de la curva en forma de campana como se muestra en la figura 3.3(a). La varianza es una
medida de la dispersion en los valores que se da cuenta de la variable aleatoria. Una gran variación
implica que la variable aleatoria es probable que tome valores lejos de la media, mientras que una
pequeña variación implica que una gran mayoría de los valores de que una variable aleatoria toma
cerca de la media. Como ejemplo, la figura 3.3 (b) representa las funciones de densidad para tres
cero RVs gaussianas de medias con varianzas de 0,25, 1, y 4.

26. 3.2.5 Una transformación de una Variable aleatoria
En el análisis del funcionamiento del sistema de comunicación es a menudo necesario para
caracterizar una variable aleatoria, que es una transformación de otra variable aleatoria. Esta
transformación se expresa como
Paso 1: Encontrar el CDF de Y como una suma de integrales sobre la variable aleatoria X tal que
𝑔(𝑋) < 𝑦. Esto se expresa matemáticamente como
donde el 𝑅𝑖(𝑦) son intervalos en la línea real donde X es tal que 𝑔(𝑋) < 𝑦.
Paso 2: Encontrar el PDF mediante la diferenciación de la CDF que se encuentra en el paso 1
usando la regla de Leibniz del cálculo.
Regla de Leibniz
3.3 Variables Aleatorias Multiples
3.2.5 Densidad conjunta y funciones de distribución
Una vez más las variables aleatorias están completamente caracterizados tanto por el conjunto
CDF o el conjunto PDF. Tenga en cuenta, se utilizaran simplificaciones similares en notación con
conjunto CDF y PDFs, cuando no existía ninguna ambigüedad.
Definición 3.10 El conjunto CDF de dos variables aleatorias es
Propiedades del conjunto CDF

27. Definición 3.11 para dos variables aleatorias continuas X y Y, el conjunto PDF, 𝑓𝑋𝑌(𝑥, 𝑦), es
Nota, las variables aleatorias discretas distribuidas en forma conjunta tienen un conjunto PMF
,𝑃𝑋𝑌(𝑥, 𝑦) y como el conjunto PMF y PDF tienen características similares este texto a menudo utiliza
𝑃𝑋𝑌(𝑥, 𝑦) para ambas funciones.
Propiedades del conjunto PDF o PMF
3.3.2 Momentos conjuntos y promedios estadísticos
Momentos conjuntos y promedios estadísticos son también de interés en ingeniería de sistemas
de comunicación. El promedio estadístico general de una función 𝑔 (𝑋, 𝑌) de dos variables
aleatorias 𝑋 𝑒 𝑌 se da como
Un momento conjunto de uso común o promedio estadístico es la correlación entre dos variables
aleatorias X e Y, definido como
Un momento central conjunta de uso frecuentemente es la covarianza entre dos variables
aleatorias X e Y, definido como
Definición 3.14 El coeficiente de correlación es
El coeficiente de correlación es una medida de la similitud estadística de dos variables aleatorias.
Si |𝑝 𝑋𝑌| = 1 para variables aleatorias X e Y, entonces X es un múltiplo escalar de Y. Si 𝑝 𝑋𝑌 = 0,
entonces las variables aleatorias no están correlacionadas. Los valores de |𝑝 𝑋𝑌| entre estos dos
extremos proporcionan una medida de la similitud de las dos variables aleatorias (mayor |𝑝 𝑋𝑌| son
más similares).

28. 3.3.4 Transformaciones de Variables aleatorias
En general, el problema de encontrar una descripción probabilística (conjunto CDF o PDF) de
una transformación conjunta de las variables aleatorias es muy difícil. Para simplificar la
presentación, dos de las transformaciones más comunes y prácticos serán considerados: la sola
función de n variables aleatorias y el uno a uno la transformación o transformación individual.
Una sola función de n variables aleatorias
Una transformación única de función de n variables aleatorias se expresa como
Donde 𝑋1, … … … , 𝑋 𝑛 son la n variable aleatoria original. En esta sección se refiere a encontrar el
PDF o el CDF de la variable aleatoria 𝑌. La técnica general es el mismo proceso de dos paso idénticos
utilizado para una sola variable aleatoria (las regiones de integración ahora convertido en
volúmenes en lugar de intervalos).
Paso 1: Encontrar el CDF de 𝑌 como una suma de integrales sobre las variables aleatorias
𝑋1, … … , 𝑋 𝑛 . Esto se expresa matemáticamente como
donde el 𝑅𝑖(𝑦) son N volúmenes dimensionales donde 𝑋1, … … , 𝑋 𝑛 son tales que 𝑔(𝑋1, … … , 𝑋 𝑛 ) <
𝑦
Paso 2: Encontrar el PDF mediante la diferenciación de la CDF que se encuentra en el paso 1
usando la regla de Leibniz, es decir,

29. Modulación en banda base
2.6 Modulación por impulsos codificados
La modulación por impulsos codificados (PCM) es el nombre determinado a la clase de señales de
banda base obtenida desde la señales PAM cuantificadas codificando cada muestra cuantificada en
una palabra digital. La fuente de información es probada(muestreada) y cuantificada a uno de nivel
L; Entonces cada muestra cuantificada es digitalmente codificada en un l-bit (𝑙 = 𝑙𝑜𝑔2 𝐿) clave
(palabra código). Para la transmisión de banda base, los bits de clave (palabra código) serán
entonces transformados a pulsos de onda. Las características esenciales del binario PCM son
mostradas en la figura 1. Asumiendo eso una señal analógica 𝑥(𝑡) es limitada en sus excursiones al
rango de −4 a +4 𝑉. El tamaño de paso(escalon) entre niveles de cuantizacion se ha fijado a 1 𝑉.
Asi , ocho niveles de cuantizacion son empleados; Estos son localizados en
−3.5, −2.5, … … … . , +3.5 𝑉. Nosotros asignamos el numero de código 0 en el nivel −3.5 𝑉, el
numero de código 1al nivel −2.5 𝑉, etc., hasta al nivel 3.5 𝑉 , que es asignado al numero de código
7. Cada numero de código tiene su representación en aritmética binaria, que van desde 000 para el
numero de código de 0 a 111 para el numero de código 7. Por que tienen el niveles de voltaje
determinados en esta manera, comparado con el uso de una secuencia consecutiva de enteros, 1,
2, 3, … … . ? Los cambios de niveles de voltaje son guiados por dos restricciones. Primero, los
intervalos cuantil es entre los niveles deben ser iguales; y Segundo, Es Conveniente para los niveles
son simétricos aproximadamente cero.
Al ordenar en la figura 1, es etiquetada con niveles de cuantizacion y otros códigos de números.
Cada muestra de la señal analógica es asignada al nivel cuantizacion mas cercano al valor de la
muestra. Debajo de la onda analógica 𝑥(𝑡) son vistos cuatro representaciones de 𝑥(𝑡), como
siguiente: Las muestra de valores naturales, La muestra de valores cuantizaciones, los códigos de
números, y la secuencia PCM.
Note, que en el ejemplo de la figura 1, cada muestra es asignada a uno de los ocho niveles o una
secuencia de PCM de tercero-bit. Suponiendo que la señal analógica es un canal musical, que es
muestreada en el índice nyquist. Y, suponiendo que cuando nosotros escuchamos música en forma
digital, sus sonidos terribles. Que nosotros podemos improvisar la fidelidad? Rellamando el proceso
de cuantizacion recoloca la señal verdadera con una aproximación. De este modo, el numero
creciente de niveles son reducidos al cuantizacion de ruidos. Si nosotros duplicáramos el numero
de nivel a 16, Para este caso, cada muestra analógica son representadas como una secuencia PCM
de cuarto-bit. En tiempo real de sistemas de comunicación, los mensajes no son retrasados. Por lo
tanto, el tiempo de transmisión para cada muestra debe ser el mismo, A pesar de cuantos bits
representan la muestra. Asi que, cuanto hay mas bits por muestra, los bits deben moverse rápido,
en otras palabras, ellos deben ser remplazados por pequeños bits. Los índices de datos es asi
incrementado, y el costo es un súper transmisión de bandwidth

30. 2.7 Cuantizacion Uniforme o No-Uniforme
Estáticas de Amplitudes de Expresión
La comunicación de expresión es muy
importante y area especializada de
comunicaciones digitales. Humanos hablan esta
característica por único propiedad estadístico uno
de los tales propiedades es ilustrado en la figura 2.
La representación abscisa expresa señal de
magnitudes, normalizado a valores (RMS) de
magnitudes de com atravesar un canal típico de
comunicación. Y la probabilidad es ordenar.
Para mas voces de canales de comunicación , muy
lenta expresión de predominante volumen; 50%
del tiempo, el voltaje caracterizado es detectado en
expresión de energía, es menor que un cuarto (1/4) del valor RMS. Grandes valores de amplitud
son relativamente raros; el 15% del tiempo de voltaje escede al valor de RMS. Esto se ve en la
ecuación (aaaaaaa) y eso depende del ruido de cuantizacion en el paso de intensidad (Tamaño del
cuantil intervalo). Cuando los pasos son uniforme en tamaño de cuantizacion es conocido una
cuantizacion uniforme. En un sistema son usados igualmente espaciados en niveles cuantizacion, el
ruido de cuantizacion es lo mismo para todas las señales de magnitud. Por lo tanto, con cuantizacion
uniforme, la señal a ruido (SNR) es peor para señales de niveles bajos que para señales de altos
niveles. La cuantizacion No-Uniforme puede provenir bien cuantizacion de las señales débil y áspero
cuantizacion de la fuerte señal. De este modo en el caso de Cuantizacion No-Uniforme, Ruido de
cuantizacion pueden hacer proporcional a magnitud de la señal. El efecto es a mejorar el total SNR,
por reduciendo el ruido para el predominante señales débiles, en el gasto de un aumento en ruido
para el raramente ocurre en señales fuertes. En la figura (bbbbbb) se compara la cuantizacion de
una fuerte versus una débil señal para uniforme y No-uniforme cuantizacion. La forma escalera de
la onda representa la aproximación a la onda analógica (después de cuantizacion de distorsión ha
sido introducido ).Cuantizacion No-uniforme puede ser usado a hacer el SNR una constante para
todas las señales dentro del la entrada de rango. Para voces de señal, lo típico de señal de entrada
de rango dinámico es de 40 𝑑𝑒𝑐𝑖𝑏𝑒𝑙𝑒𝑠 (𝑑𝐵), donde un decibel es definido en términos del radio de
potencia 𝑃2 a potencia 𝑃1 :

31. 2.7.2 Cuantizacion No-Uniforme
Una forma de conseguir la cuantizacion No-Uniforme es usando una característica de
cuantizacion No-Uniforme, mostrando en la figura 4(a), Mas adelante la cuantizacion No-Uniforme
consiguiendo por primero distorsionando la señal original con una característica de comprensión
logarítmica , como se muestra en la figura 4(b) y por tanto esta usando una cuantizador uniforme.
Para pequeños señales de magnitud la característica de compresión tiene la pendiente mas
pronunciada que para grandes señales de magnitud. Asi, un dado señal de cambien pequeño
magnitudes llevara al cuantizador uniforme a través de mas escalones que el mismo cambio en
magnitudes grandes.. La característica de compresión efectivamente cambia la distribución de
magnitud de la señal de entrada de modo que no haya una preponderancia de baja señal de
magnitud en la salida del compresor. Después de la compresión, la señal distorsionada es usada en
la entrada a una característica cuantizador uniforme (lineal), que
se muestra en la figura ccccc(c). En el receptor, una característica
de compresión inversa, llamada expansión, es aplicada de modo
que el total transmisión no este distorsionada. El par de
procesamiento (compresión y expansión) es usualmente
referido como companding
Figura 4.- (a) Característica No-Uniforme cuantizador, (b)
Característica de compresión, (c) Característica Uniforme
cuantizadorµ-law
2.8 Transmisión Base Banda
Representación de onda de digitos binarios
Haremos representar que los dígitos binarios con pulsos eléctricos en orden a transmitir a través
de una canal base banda. Como una representación es mostrada en la figura 6. Ranuras de tiempo
clave son mostradas en la figura 6(a), donde la clave es un 4-bit representación de cada muestra
cuantizada. En la figura 6(b), cada binario, uno(1) es representado por un pulso y cada binario
cero(0) es representado por la falta de un pulso. De este modo una secuencia de pulsos eléctricos
tendrán el patrón mostrando la figura 6(b), puede ser usada a transmitir la información en el PCM
bit flujo.
En el receptor , una determinación se debe hacer como la presencia o absencia de un pulso en
cada bit ranura de tiempo. Por consiguiente hay una ventaja en elaboración al ancho de pulso T,
en la figura 6(b) lo mas amplio posible. Si nosotros incrementáramos el ancho de pulso al máximo
posible (igual al tiempo bit T), tendremos la onda que se muestra en la figura figura 6(c). Mejor
dicho que describe esta onda como una secuencia de presente o ausente pulsos, podremos describir

32. que es como una secuencia de transiciones entre
dos niveles. Cuando el voltaje esta en alto, ocupo
un 1 binario, y cuando el voltaje es bajo, ocupa un
0 binario.
Figura 6.- Representación de onda de dígitos
binarios (a) Secuencia PCM, (b) Representación
de pulsos PCM (c) Pulso de onda (transición de
dos niveles)
2.8.2 Tipos de Onda de PCM
Cuando la modulación de pulso es aplicado a un símbolo binario, la resultante onda binaria es
llamada un modulación pulso-código (PCM) de onda. Hay diferentes tipos de ondas de PCM que son
describidas a continuación y ilustradas en la figura fffff Cuando la modulación de pulso es aplicada
a un símbolo No-Binario la onda resultante es llamada un M-ary de la onda de modulación de pulso.
Las formas de onda PCM se dividen en 4 grupos:
1.- No-retorno a cero (NRZ)
2.- Retorno a Cero (RZ)
3.- Fase codificado
4.- Multinivel binario
El grupo NRZ es probablemente la mas comúnmente usada en ondas PCM. Esto puede ser
particionado en los siguientes subgrupos: NRZ-L (L para nivel), NRZ-M(M para marca, y NRZ-S(S para
espacio). NRZ-L es usada extensamente en circuitos lógicos digitales. Hay un cambio en nivel
siempre que el dato cambia desde a 1 a un 0 o desde un 0 a un 1. Con NRZ-M, el 1 , o marca , es
representado por un cmabio de nivel, y un 0 , o espacio, es representado por ningún cambio en
nivel. Esto es después referido a como codificación diferencial. NRZ-M es usada primordialmente en
grabación de cinta magnética. NRZ-S es el complemento de NRZ-M: A 1 es reprentado por ningún
cambio en nivel, y 0 es representado por un cambio de nivel.
Las ondas RZ consiste de unipolar -RZ, bipolar-RZ, y RZ-AMI Estos códigos encontrados su
aplicación en datos de transmisión de base banda. Con unipolar-RZ, un 1 es representado por un
Medio-bit-ancho de pulso, y un 0 es representado por la ausencia de un pulso. Con bipolar-RZ, los
1 y 0 son representados por el contrario de un pulso que son Uno-Medio bit de ancho. RZ-AMI
(AMI para “inversión de marca alternativa”) es una esquema de señalización usado en sistemas
telefónicos. Los 1 son representados por igual-amplitud de pulsos alternos. Los 0 son
representados por la ausencia de pulsos.
El grupo de fase codificado consiste de bi-Φ-L(bi-fase-nivel), y es conocido como código
manchester; bi-Φ-M(bi-fase-marca); bi-Φ-S(bi-fase-espacio) y modulación de retraso (DM), o código
miller. El bi-Φ-L, un 1 es representado por un medio-bit-ancho de pulso posicionado durante la
primera mitad del intervalo bit; un 0 es representado por un medio-bit-ancho de pulso posicionado
durante la segunda mitad del intervalo bit. Con el bi-Φ-M, una transición se produce al comienzo
de cada intervalo de bit. Un 1 es representado por un segundo transiscion Uno-medio depues del

33. 2.8.3 Atributos espectrales de ondas PCM
Se puede ver que las características espectrales de
algunas ondas mas populares del PCM. La grafica del
espesor de la potencia espectral en 𝑤𝑎𝑡𝑡𝑠/𝐻𝑧
versus ancho de banda normalizado, WT, donde W es
el ancho de banda, y T es la duración del pulso. WT es
referido como el producto de tiempo- ancho de
banda, de la señal. Sabiendo que la 𝑅 𝑠 es reciproca a
𝑇 =
1
𝑅 𝑠
, entonces se puede ver su ecuación siguiente
𝑊
𝑅 𝑠
⁄ , y sus expresiones de esta unidad normalizada
son 𝐻𝑧
(𝑝𝑢𝑙𝑠𝑜/𝑠)⁄ y así nos puede describir como es
eficiente la transmisión ancho de banda es la
existencia utilizada para cada onda de interés.. Cualquier tipo de onda se requiere menor que 1 𝐻𝑧
para enviar 1 𝑝𝑢𝑙𝑠𝑒/𝑠 que es relativamente eficiente ancho de banda.
Un importante parámetro para medición de eficiencia ancho de banda es 𝑅
𝑊⁄ teniendo como
unidades de 𝐵𝑖𝑡𝑠
𝑠/𝐻𝑧⁄ . Esta ecuación describe cuantos datos de rendimiento pueden ser
transmitido para cada 𝐻𝑧 de disponible bandwidth
2.8.4 Bits por palabra PCM y Bits por Símbolo
Cada muestra analógica es transformada en una palabra PCM formados por grupos de bits. El
tamaño de palabra de PCM puede describirse por el numero de niveles cuantizacion permitido para
cada muestra; este es idéntico al numero de valores que la palabra PCM pueda asumirse. O, la
cuantizacion puede ser describida por el numero de bits requeridos a identificar que ese conjunto
de niveles. La relación entre el numero de niveles por muestra y el numero de bits necesarios a
representar aquellos niveles es la misma como las relaciones de 𝑀 = 2 𝑘
entre el tamaño de un
conjunto de símbolos de mensajes y el numero de bits necesarios a representar al símbolo.
2.8.4 Bits por palabra PCM y Bits por Símbolo
La selección del numero de niveles, o bits por muestra, depende en cuantos cuantizacion de
distorsión están dispuestos a tolerar con el formato PCM. Permite que la magnitud de la
cuantizacion de error en distorsión , |𝑒| , ser especificado como una fracción de voltaje de pico a
pico como es lo siguiente:
|𝑒| ≤ 𝑝𝑉𝑝𝑝
Desde el error de cuantizacion no puede ser mayor que 𝑞/2 , donde 𝑞 es el intervalo cuantil, se
escribe de la siguiente manera:
|𝑒| 𝑚𝑎𝑥 =
𝑞
2
=
𝑉𝑝𝑝
2(𝐿 − 1)
≈
𝑉𝑝𝑝
2𝐿

34. Donde 𝐿 es el numero de niveles de cuantizacion. Para mas aplicaciones el numero de niveles es
suficiente grande de modo que 𝐿 − 1 puede ser reemplazado por 𝐿 , como se hizo anteriormente.
Entonces, de las ecuaciones anteriores, se puede describir de la siguiente manera:
𝑉𝑝𝑝
2𝐿
≤ 𝑝𝑉𝑝𝑝
2𝑙
= 𝐿 ≥
1
2𝑝
𝑛𝑖𝑣𝑒𝑙𝑒𝑠
Y
𝑙 ≥ 𝑙𝑜𝑔2 (
1
2𝑝
) 𝑏𝑖𝑡𝑠
2.8.5 M-ary Ondas de modulación de pulso
Hay tres formas básicas a información modulada en una secuencia de pulsos: Modulación de pulso
amplitud(PAM), Modulación de pulso posición(PPM), y modulación de pulso duración(PDM). PDM
es a veces llamada modulación de onda de pulso (PWM). Cuando la información de muestra sin
ningún cuantizacion son modulados en pulsos, el resultado modulación de pulso puede ser llamada
modulación de pulso analógico. Cuando la información muestreada son primero cuantizada,
produciendo símbolos desde un M-ary conjunto de alfabeto, y entonces modula en pulsos,
resultando pulsos de modulación digital y nos referimos a esto como M-ary modulación de pulso.
En este caso de M-ary PAM, 1 de M niveles de amplitud permitida son asignados a cada de lo M
posible valores simbólicos. Nótese que tales ondas de PCM que solo requiere dos niveles
representan lo especial caso (𝑀 = 2) de lo general M-ary PAM que requiere niveles M.
En este caso de ondas de M-ary PPM, modulación es efectuada por retrasar (o avanzar) una
ocurrencia de pulso, por una cantidad que corresponde al valor de los símbolos de información. En
este caso las ondas de M-ary PDM, modulación es efectuada variando el ancho de pulso por una
cantidad que corresponde al valor de los símbolos. Sabiendo que, PAM es similar a modulación de
amplitud (AM), mientras que PPM y PDM son similares a modulación de fase (PM) y frecuencia(FM).
Considerando el cometido que el pulso receptor debe llevar a cabo: debe distinguirse entre los
posibles niveles de cada pulso. El receptor puede distinguir entre los 8 posibles niveles de cada
pulso octal en la figura 9(a) tan fácilmente como puede distinguirse entre los dos posibles niveles
de cada pulso binario en la figura 9(b). La transmisión de un 8 − 𝑛𝑖𝑣𝑒𝑙 (comparado con un 2-nivel)
pulso requiere una mayor cantidad de energía para rendimiento de detección equivalente. Para
igualar la potencia media al binario y los pulsos octales, es mas fácil detectar los pulsos binarios por
que el detector tiene mas señal de energía por nivel para tomar una decisión binaria que una
decisión de 8 − 𝑛𝑖𝑣𝑒𝑙 .
2.9 Codificacion Correlativa
Señalizacion de DuoBinaria

35. Podemos pensar que la codificación de operación duobinaria puede ser implementada en la
siguiente figura 10. Asumiendo que una secuencia de símbolos binarios {𝑥 𝑘} es ser transmitida en
el índice de 𝑅 𝑠𝑖𝑚𝑏𝑜𝑙𝑜𝑠/𝑠 durante un sistema teniendo un espectro ideal rectangular de ancho
de banda 𝑊 =
𝑅
2
=
1
2𝑇
𝐻𝑧. Para un filtro ideal rectangular es solo la parte de nuestro equivalente
modelo que es usado para el desarrollo de un filtro que es mas fácil a aproximados. Pero antes de
estar en formar por un filtro ideal, los pulsos pasan a través de un simple filtro digital, como se
muestra en la figura. El filtro digital incorpora un Uno-Digito retraso a cada pulso de entrada el filtro
añade el valor del pulso anterior. En otras palabras, para cada pulso en el filtro digital, obtenemos
la suma de dos pulsos de salida. Cada pulso de la secuencia de salida {𝑦 𝑘} del filtro digital puede
expresarse como:
𝑦 𝑘 = 𝑥 𝑘 + 𝑥 𝑘−1
Por lo tanto, las amplitudes {𝑦 𝑘} no son independientes; cada digito de acarreo 𝑦 𝑘 lleva con el la
memoria el digito anterior (cada dígito lleva consigo el recuerdo de la cifra anterior). El introducido
el ISI a cada digito 𝑦 𝑘 viene solo del previo digito 𝑥 𝑘−1 . Esta correlación entre las amplitudes de
pulso de {𝑦 𝑘} se puede pensar de cómo el controlador ISI introduciendo por la codificación
duobinario. La interferencia del controlador es la esencia de este novedosa técnica debido en el
detector. En la figura 10, en la toma de muestras del receptor, y esperaríamos a recuperar la
secuencia {𝑦 𝑘} exactamente en la ausencia del ruido. Asi que todos los sistemas experimentan
ruidos de contaminación, y denotado en {𝑦̂ 𝑘}
2.9.2 Descodificación DuoBinaria
Si el digito binario 𝑥 𝑘 es igual a ± 1, entonces usando la ecuación anterior , 𝑦 𝑘 tiene 1 de 3 posibles
valores: + 2, 0, 𝑜 − 2 .El código Duobinario resulta en un tercer nivel de salida: en general , para
transmisión M-ary , los resultados de señalización de respuesta parcial en la salida de nivel en 2𝑀 −
1. El procedimiento de descodificación involucra el inverso del procedimiento de codificación , es
decir, restando la decisión de 𝑥 𝑘−1 desde el digito de 𝑦 𝑘
2.9.3 Pre codificación
Pre codificación es realizado por primera codificación diferencial la secuencia binaria {𝑥 𝑘} en el
nueva secuencia binaria {𝑤 𝑘} por medio de la ecuación:
𝑤 𝑘 = 𝑥 𝑘 ⊕ 𝑤 𝑘−1
Donde el símbolo ⊕ representa la adición del modulo 2 (equivalente a la lógica de operación XOR)
de los dígitos binarios. Las reglas de la modulo de adicion-2 son las siguientes:
0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 0
Sin embargo, con pre codificación, el proceso de detección es bastante diferente desde la detección
del ordinario duobinario, como puede verse en el siguiente ejemplo, El modelo de pre codificación

36. 2.9.6 Señalización Poli binario
La señalización duobinario puede ser extendida a mas que tres dígitos o niveles, resultando un
mayor ancho de banda eficientemente; que son llamadas como poli binario. Considerando que una
información binaria con dos señalización de niveles es transformada en una señal con j señalización
de niveles numeradas consecutivamente desde cero a (𝑗 − 1). La transformación desde el binario
al poli binario se lleva a cabo en dos simples pasos. Primero, la secuencia original {𝑥 𝑘}, que consiste
de binarios unos y ceros, es convertido en otra secuencia binaria {𝑦 𝑘}, como sigue. El digito binario
actual de la secuencia {𝑦 𝑘} es formada desde la adición de modulo-2 de los dígitos (𝑗 − 2)
inmediatamente anteriores de la secuencia {𝑦 𝑘} y el digito actual {𝑥 𝑘}. Por ejemplo, vemos que:
𝑦 𝑘 = 𝑥 𝑘 ⊕ 𝑦 𝑘−1 ⊕ 𝑦 𝑘−2 ⊕ 𝑦 𝑘−3
Aquí 𝑥 𝑘 representa la entrada de digito binario y 𝑦 𝑘 la 𝑘 𝑡ℎ
digito codificado. Ya que la expresión
implica (𝑗 − 2) = 3 bits anteriores de 𝑦 𝑘, hay 𝑗 = 5 niveles de señalización. La secuencia binaria
{𝑦 𝑘} es transformada en un tren de pulsos de poli binario {𝑧 𝑘} por adcion algebraicamente al bit
actual de la secuencia {𝑦 𝑘} al (𝑗 − 2) bits anteriores de {𝑦 𝑘}. Por lo tanto, 𝑧 𝑘 modulo -2 = 𝑥 𝑘, y los
elementos binarios unos y ceros son mapeados en valores de pulsos par e impar en la secuencia
{𝑧 𝑘}