Números Complejos
- 1. MATEMÁTICA IV NÚMEROS COMPLEJOS Alumna: THAYS YOSELIN HURTADO ESPINOZA C.I.: V.-17.748.086 MAYO 2020
- 2. ESQUEMA GENERAL 1. Concepto de números complejos y operaciones elementales. 2. Representar los números complejos 3. Forma canónica. Gráfica. 4. Definición de inversa, módulo y complejo conjugadas. 5. Desigualdad triangular, forma polar de un número complejo, teorema de Moivre Exponenciación y raíces de números complejos. Contenido
- 3. INTRODUCCIÓN En la presentación se estará tocando el siguiente tema: números complejos. Este tema a pesar de ser complejo, abarca o integra la trigonometría, algebra y la geometría. Los números complejos son utilizados en varios campos de las matemática, física, en la ingeniería, con mas ímpetu en la electrónica y las telecomunicaciones. Los números complejos surgen cuando se quiere resolver ecuaciones algebraicas en las que hay necesidad de calcular raíces cuadradas de números negativos, estos números se pueden suma, resta, multiplicar y dividir. Los números complejos reflejan aspectos como transformaciones y los movimientos de plano. Contenido
- 4. 1. Concepto de números complejos y operaciones elementales. Los números complejos son aquellos que resultan de la suma de un número real y un numero imaginario; entendiéndose como número real, aquel que puede expresarse de forma entera (s, 10, 300, etc.) o decimal (2,24; 3,10; etc.), mientras que el imaginario es aquel número cuyo cuadrado es negativo. Los números complejos son muy utilizados en el álgebra y en el análisis. hora bien, estos números que nos ocupan forman un conjunto de cifras que resultante sumas entre un número real y otro imaginario. En tanto, un número real será aquel que podrá expresarse a través de un número entero, o en su defecto de uno decimal. Mientras tanto el número imaginario será aquel cuyo cuadrado resulta ser negativo. Contenido
- 5. 1. Concepto de números complejos y operaciones elementales: Ejemplos de Números Complejos Suma de Números Complejos: (-3 + 3i) + (7 - 2i) −3 + 3i + 7 – 2i = −3 + 7 + 3i – 2i Reacomoda las sumas para juntar los términos semejantes. Respuesta −3 + 7 = 4 y 3i – 2i = (3 – 2)i = i Signos iguale ( -,- y +,+) se suman, signos diferentes se restan (+,- y -,+) Respuesta: (−3 + 3i) + (7 – 2i) = 4 + i Combina los términos semejantes. Contenido
- 6. 1. Concepto de números complejos y operaciones elementales: Ejemplos de Números Complejos Resta de Números Complejos: (−3 + 3i) – (7 – 2i) (−3 + 3i) – (7 – 2i) = −3 + 3i – 7 + 2i Asegúrate de distribuir el signo de resta a todos los términos del sustraendo. −3 – 7 + 3i + 2i Reacomoda las sumas para juntar los términos semejantes. Respuesta: −3 – 7 = −10 y 3i + 2i = (3 + 2)i = 5i (−3 + 3i) – (7 – 2i) = - 10 + 5i Combina los términos semejantes. Contenido
- 7. 1. Concepto de números complejos y operaciones elementales: Ejemplos de Números Complejos Multiplicación de Números Complejos: (3i)(2i) (3i)(2i) = (3)(2)(i)(i)= 6i2 Multiplica los coeficientes de i y luego multiplica i por i. Reemplaza i2 = –1. 6i2 = 6(−1) 6(−1) = −6 Respuesta (3i)(2i) = −6 Contenido
- 8. 2. Representar los números complejos. Representación Binómica: La forma binómica de un número complejo es la expresión a+bi, a se llama la parte real y b la parte imaginaria. Si la parte imaginaria es nula, entonces el número es real. Por tanto, los números reales están contenidos en los números complejos. Se llaman números imaginarios puros a los que tienen parte real igual a cero. La parte real del número complejo y la parte imaginaria, se pueden expresar de varias maneras, como se muestra a continuación: Contenido
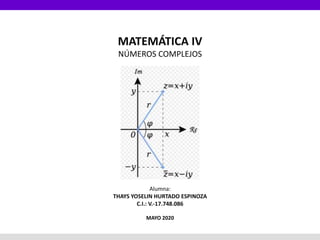
- 9. 2. Representar los números complejos. Representación Polar: La forma polar de un número complejo es otra forma de representar un número complejo. La forma z = a + bi es llamada la forma coordenada rectangular de un número complejo El eje horizontal es el eje real y el eje vertical es el eje imaginario. Encontramos los componentes reales y complejos en términos de r y donde r es la longitud del vector y θ es el ángulo hecho con el eje real. Contenido
- 10. 2. Representar los números complejos. Representación Exponencial: También conocida como Euler es ampliamente usado en la rama del Cálculo, y tiene un papel muy importante en el crecimiento exponencial y por lo tanto en procesos de la naturaleza y de la vida cotidiana. Contenido
- 11. 2. Representar los números complejos. Representación Trigonométrica: La forma trigonométrica del complejo z= a + bi z = a + bi es: Cuando tenemos un complejo escrito en forma trigonométrica, ya lo tenemos casi en forma binómica. Falta calcular el seno y el coseno del argumento y multiplicar por el módulo. Contenido
- 12. 2. Representar los números complejos: Diagrama de Argand El concepto de plano complejo permite interpretar geométricamente los números complejos. La suma de números complejos se puede relacionar con la suma con vectores, y la multiplicación de números complejos puede expresarse simplemente usando coordenadas polares, donde la magnitud del producto es el producto de las magnitudes de los términos, y el ángulo contado desde el eje real del producto es la suma de los ángulos de los términos pudiendo ser vista como la transformación del vector que rota y cambia su tamaño simultáneamente. Contenido
- 13. 2. Representar los números complejos: Diagrama de Argand Los diagramas de Argand se usan frecuentemente para mostrar las posiciones de los polos y los ceros de una función en el plano complejo. El análisis complejo, la teoría de las funciones complejas, es una de las áreas más ricas de la matemática, que encuentra aplicación en muchas otras áreas de la matemática así como en física, electrónica y muchos otros campos. Multiplicar cualquier complejo por i corresponde con una rotación de 90º en dirección contraria a las agujas del reloj. Asimismo el que (-1)·(-1)=+1 puede ser entendido geométricamente como la combinación de dos rotaciones de 180º (i al cuadrado = -1), dando como resultado un cambio de signo al completar una vuelta. Contenido
- 14. 2. Representar los números complejos: Algunos Ejemplos Determinar la parte real y la parte imaginaria de los siguientes números complejos: Contenido
- 15. 2. Representar los números complejos: Algunos Ejemplos Representar los siguientes números imaginarios: Contenido Representación del complejo z=1+2iz=1+2i: Representación del complejo w=3−iw=3−i:
- 16. 3. Forma canónica. Gráfica. El adjetivo canónico se usa con frecuencia en matemática para indicar que algo es natural, como debe ser e independiente de elecciones arbitrarias, que es absoluto y no relativo a un observador, que es intrínseco y no depende de un sistema de referencia o de un sistema de coordenadas, que pertenece a la estructura propia de lo que estudiamos. Decir de algo que es canónico es decir que no es arbitrario, que todos coincidimos en ello si lo miramos con atención. Aunque siempre se use en sentido impreciso, es un concepto central en matemáticas, ciencia que aspira a desentrañar con rigor lo que se entiende por canónico y a sacar a la luz todo lo que es canónico. Contenido
- 17. 3. Forma canónica. Gráfica. En forma canónica (o forma exponencial), un número complejo es z = r · eiφ Explicación En la forma trigonométrica un número complejo se representa con z = r (φ + i sin φ) Sustitución de la fórmula de Euler eiφ = cos φ + i sin φ deducen z = r · eiφ Ejemplo 1 En forma canónica el número complejo z = 1 + i se deducen Contenido
- 18. 3. Forma canónica. Gráfica. FORMA CANONICA: (a,b) , a es la parte real y b es la parte imaginaria. NUMERO REAL : (a,0). IMAGINARIO PURO: (0,b). Un complejo esta compuesto por una parte real y una imaginaria. NUMERO COMPLEJO: (a,0)+(0,b). - Todo complejo esta representado por un punto del plano de Argand, o plano cartesiano. - Todo complejo se asocia a un vector en el plano, cuyas componentes son a y b. - Todo complejo queda definido por su modulo y dirección. - El modulo corresponde a la medida del vector expresado en unidades de longitud del plano. - La dirección del complejo corresponde al ángulo que forma el vector con el eje positivo de las componentes reales. Contenido
- 19. 3. Forma canónica. Gráfica. Ejemplo - Par ordenado (-4, -5) se puede expresar en su forma canónica o biónica como z = -4 -5i entonces (-4, -5) = -4 – 5i - Su forma grafica es: Contenido
- 20. 3. Forma canónica. Gráfica: Aplicaciones Soluciones de ecuaciones polinómicas: Una raíz o un cero del polinomio p es un complejo z tal que p(z)=0. Un resultado importante de esta definición es que todas las ecuaciones polinómicas (algebraicas) de grado tienen exactamente n soluciones en el cuerpo de los números complejos, esto es, tiene exactamente n complejos z que cumplen la igualdad p(z)=0, contados con sus respectivas multiplicidades. Contenido Variable compleja o análisis complejo Al estudio de las funciones de variable compleja se lo conoce como el Análisis complejo. Tiene una gran cantidad de usos como herramienta de matemáticas aplicadas así como en otras ramas de las matemáticas. El análisis complejo provee algunas importantes herramientas para la demostración de teoremas incluso en teoría de números; mientras que las funciones reales de variable real, necesitan de un plano cartesiano para ser representadas.
- 21. 4. Definición de inversa, módulo y complejo conjugadas. Módulo Se define el módulo de un número complejo como el módulo del vector que lo representa, es decir, si z = x + iy entonces el módulo de Z es Conjugado El conjugado de un número complejo se define como su simétrico respecto del eje real, es decir, si z = x + iy entonces el conjugado de Z es Contenido
- 22. 4. Definición de inversa, módulo y complejo conjugadas. Propiedades El conjunto ℂ de los números complejos satisface las leyes de la axiomática que define un cuerpo: • Propiedad conmutativa: z+w = w+z; zw= wz. • Propiedad asociativa: v+(w+z)= (v+w)+ z; v(wz)= (vw)z • Propiedad distributiva: v(w+z) = vw+vz; (w+z)v = wv+zv Inversos: cada número complejo tiene su inverso aditivo -z tal que z +(-z) = 0 y cada número complejo, distinto de cero, tiene su inverso multiplicativo z-1, tal que z·z-1 = 1.9 Si identificamos el número real a con el complejo (a, 0), el cuerpo de los números reales R aparece como un subcuerpo de C. Más aún, C forma un espacio vectorial de dimensión 2 sobre los reales. Los complejos no pueden ser ordenados como, por ejemplo, los números reales, por lo que C no puede ser convertido de ninguna manera en un cuerpo ordenado. Contenido
- 23. 5. Desigualdad triangular, forma polar de un número complejo, teorema de Moivre. Exponenciación y raíces de números complejos. La desigualdad triangular o desigualdad de Minkowski es un teorema de geometría euclidiana que establece: Este resultado ha sido generalizado a otros contextos más sofisticados como espacios vectoriales. En todo triángulo la suma de las longitudes de dos lados cualquiera es siempre mayor a la longitud del lado restante. Este hecho es una consecuencia de otro teorema de la geometría plana clásica que afirma que la distancia más corta entre dos puntos es la línea recta. Contenido
- 24. 5. Desigualdad triangular, forma polar de un número complejo, teorema de Moivre. Exponenciación y raíces de números complejos. La fórmula de De Moivre, nombrada así por Abraham Moivre afirma que para cualquier número complejo (y en particular, para cualquier número real) x y para cualquier entero n se verifica que: Esta fórmula es importante porque conecta a los números complejos (i significa unidad imaginaria) con la trigonometría. La expresión "cos x + i sen x" a veces se abrevia como cis x. Contenido
- 25. 5. Desigualdad triangular, forma polar de un número complejo, teorema de Moivre. Exponenciación y raíces de números complejos. Raíces de un número complejo Para hallar las raíces de un número complejo se aplica la fórmula de Moivre, teniendo en cuenta que para que dos complejos coincidan han de tener el mismo módulo y la diferencia de sus argumentos ha de ser un múltiplo entero de 360º. Sea Ra un número complejo y considérese otro complejo R'a', tal que Ra = (R' a' ) n = ((R' )n )n a‘ Aunque esto parece aportar una infinidad de soluciones, nótese que si a k se le suma un múltiplo de n, al dividir el nuevo argumento, éste aparece incrementado en un número entero de circunferencias. Por tanto, basta con dar a k los valores 1, 2, 3, ..., n - 1, lo que da un total de n - 1 raíces, que junto a k = 0 da un total de n raíces. Contenido
- 26. CONCLUSIÓN La introducción de los números complejos tiene gran importancia en la Matemática, ya que te proporciona herramientas de trabajo para resolver ecuaciones que no tenían solución en el dominio de los números reales. También te permite resolver ejercicios utilizando los símbolos ya estudiados para los conjuntos numéricos. Como has podido apreciar, la adición y sustracción de números complejos es muy similar a como lo haces en el trabajo con variables, solo que en lugar de una variable, encuentras la unidad imaginaria.
- 27. BIBLIOGRAFÍA Mario Hernández (2011) ensayo números complejos. Disponible: https://es.scribd.com/doc/66197935/ensayo-de-los-Numeros-complejos Juan canos morales (2016) ensayo números complejos. Disponible: https://www.academia.edu/32257280/Ensayo_N%C3%BAmeros_Complejos Yúnior castillo Silverio (2012) los números complejos. Disponible:https://www.monografias.com/trabajos107/numeroscomplejostrigonometria/ numeros-complejos-trigonometria.shtml Ricardo Fernández (2018) números complejos. Disponible: https://html.rincondelvago.com/numeros-complejos_5.html Julián Pérez(2012) Modulo. Disponibles: https://definicion.de/modulo/