Matricial1

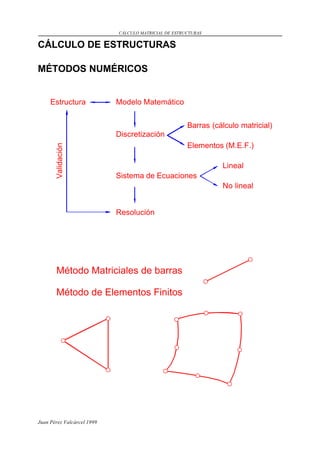
CÁLCULO MATRICIAL DE ESTRUCTURAS

CÁLCULO DE ESTRUCTURAS

MÉTODOS NUMÉRICOS

Estructura Modelo Matemático

Barras (cálculo matricial)
Discretización
Elementos (M.E.F.)
Validación

Lineal
Sistema de Ecuaciones
No lineal

Resolución

Método Matriciales de barras

Método de Elementos Finitos

Juan Pérez Valcárcel 1999

CALCULO MATRICIAL DE ESTRUCTURAS

INTRODUCCIÓN AL CÁLCULO MATRICIAL

IDEALIZACIÓN DE LA ESTRUCTURA

Estructura real ↔ Modelo matemático
Discretización ↔ Elementos conectados por nudos

ELEMENTOS LINEALES Pórticos
Emparrillados
Celosías

SUPERFICIALES Pantallas
Losas
Láminas

VOLUMÉTRICOS Losas gruesas
Macizos
Presas

Elementos lineales Discretización en barras
(matricial)

Elementos superficiales Discretización en elementos
finitos
y volumétricos



IDEALIZACIÓN GEOMÉTRICA

Consiste en la simplificación de las dimensiones y formas de la estructura
real.

Se sustituyen las piezas por su directriz, simplificando en los casos de
sección variable o directriz curva Supone errores.
Problemas Dimensión finita de los nudos
Luces reales de cálculo

Piezas de Sección Variable

Piezas de Sección Constante Piezas de Sección Curva
8

8

K= K=

L1
L

Pilares de distinta sección Zonas rígidas de viga



La idealización geométrica no tiene por qué ser inmediata

En la idealización geométrica deben figurar las condiciones de
apoyo, sea rígido o elástico.

Apoyos Rígidos Apoyos Elásticos



IDEALIZACIÓN MECÁNICA: ESTRUCTURA.

C APROXIMACIÓN DEL COMPORTAMIENTO MECÁNICO DE LA
ESTRUCTURA.

Se define por los DESPLAZAMIENTOS de los nudos

En el espacio: 3 traslaciones + 3 giros

En el plano: Según el problema

Estructuras articuladas planas: 2 traslaciones
Pórticos planos: 2 traslaciones + 1 giro
Emparrillados planos: 1 traslación + 2 giros.

- Hay que elegir los grados de libertad en función del problema
analizado.
- Los desplazamientos se suponen infinitesimales con respecto a
las dimensiones de la estructura.
- Si los desplazamientos son grandes se precisa análisis no lineal.

Se analiza a través de las DEFORMACIONES de las barras.

Según el problema analizado.

- Deformación por axil.
Importante en estructuras de nudos articulados y pilares de
pórticos.
- Deformación por flexión.
Es la más importante en casi todos los casos.
- Deformación por cortante.
Despreciable salvo en casos muy particulares.
- Deformación por torsión.
Sólo importante en emparrillados y pórticos espaciales.

C TIPOS DE CONEXIÓN ENTRE BARRAS.

Nudo rígido Cierto grado de articulación
Nudo articulado Cierto grado de empotramiento



IDEALIZACIÓN MECÁNICA: ESTRUCTURA.

C UNA MISMA ESTRUCTURA ADMITE DIVERSAS
MODELIZACIONES CON DISTINTO GRADO DE PRECISIÓN.

ARCO

Estructura Real

Idealización como
Elementos Lineales

Idealización por
Elementos Finitos

E.F. de E.F. de
4 nodos 8 nodos



IDEALIZACIÓN MECÁNICA: MATERIALES

DIAGRAMAS TENSIÓN-DEFORMACIÓN REALES
Acero

TENSIONES
en N/mm2
σ CURVA TENSIÓN-DEFORMACIÓN
de BARRAS CORRUGADAS

700

600

500
fy

400

300

200

100

ε
0 2 4 6 8 10 12 14 16 18 20%
ALARGAMIENTOS

ACERO DE DUREZA NATURAL

TENSIONES
en N/mm2
σ CURVA TENSIÓN-DEFORMACIÓN
de BARRAS CORRUGADAS

600

500

fy
400

300

200

100

ε
0 2 4 6 8 10 12 14 16%
ALARGAMIENTOS

ACERO ESTIRADO en FRIO

El acero estirado en frío no se utiliza en obra nueva


Hormigón

TENSIONES σc CURVA TENSIÓN-DEFORMACIÓN
del HORMIGÓN
fc

1.0

Ec
0.8

0.6

0.4

0.2
E co εc
Ec ε cu
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4
DEFORMACIONES

DIAGRAMA NOVAL

TENSIONES σc CURVA TENSIÓN-DEFORMACIÓN
del HORMIGÓN
fc

1.0

0.8

0.6

0.4

0.2
εc
0 0' Ec ε cu
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4
DEFORMACIONES

DIAGRAMA con CARGAS REITERADAS




DIAGRAMAS TENSIÓN-DEFORMACIÓN SIMPLIFICADOS.- Son
necesarios por la excesiva complejidad de los reales.

ACERO ESTRUCTURAL

fyd fyd
TENSIONES

TENSIONES

0 εyd DEFORMACIONES 0 εyd DEFORMACIONES
ELASTO PLÁSTICO RÍGIDO PLÁSTICO
ELASTO PLÁSTICO
con ENDURECIMIENTO

HORMIGÓN

0'85.fcd 0'85.fcd 0'85.fcd
TENSIONES

TENSIONES

TENSIONES

0 -2%o -3'5%o 0 -2%o -3'5%o 0 -0'7%o -2%o -3'5%o
DEFORMACIONES DEFORMACIONES DEFORMACIONES
BIPARABOLICO PARABOLA-RECTANGULO RECTANGULAR

0'85.fcd 0'85.fcd
TENSIONES

TENSIONES

0 -2%o -3'5%o 0 -0'7%o -2%o -3'5%o
DEFORMACIONES DEFORMACIONES
RAMA DECRECIENTE BIRRECTILÍNEO

Lo más frecuente en considerar el material perfectamente elástico
y lineal.




DIAGRAMAS MOMENTO-CURVATURA.- Son los diagramas que
permiten determinar las ecuaciones constitutiva a flexión de las
barras. Son fundamentales en el cálculo matricial.

Acero.- Diagrama bilineal.

MOMENTOS M
Mu
1.00

.75

Diagrama
Bilineal

.50

.25

χ
0 .0001 .0002 .0003 .0004 .0005 .0008
CURVATURA

DIAGRAMAS MOMENTO-CURVATURA (ACERO)

Hormigón.- Diagrama trilineal.
MOMENTOS M
Mu
1.00

L1 L2
.75
Diagrama
Diagrama Experimental
Bilineal

.50

Diagrama
L0 Trilineal

.25

χ
0 .01 .02 .03 .04 .05 .08
CURVATURA

DIAGRAMAS MOMENTO-CURVATURA (HORMIGÓN)



IDEALIZACIÓN DEL TERRENO DE CIMENTACIÓN

- Propiedades del terreno.

- Interacción cimiento-estructura.

Conexión rígida.
Conexión elástica Coeficientes de balasto.

- Problemas de asientos diferenciales.

Grandes momentos en los dinteles.

- Problemas de giros de la cimentación.

- Influencia de las zapatas de medianería y de esquina.

Generalmente se considera la estructura rígidamente empotrada en
la base.

u=0
v=0
w=0

En cálculo matricial es muy fácil introducir deformaciones
impuestas en los vínculos a condición de que puedan expresarse
directamente en coordenadas globales.



BASES DEL CÁLCULO MATRICIAL.

1.- Desarrollo histórico.

C Planteamientos iniciales (1850- 1875)

Maxwell.
Castigliano.
Mohr.
(No progresaron por la dificultad de resolver grandes
sistemas de ecuaciones)

C Planteamiento general del método (1915- 1926)

Maney (USA)
Ostenfeld (Dinamarca)

C Método iterativo de Hardy Cross (1932)

C Formulación matricial actual (1944)

G. Kron “Tensorial analysis of elastic structures”

C Método de elementos finitos.

Turner
Clough

C Desarrollo y generalización del uso de los ordenadores



SUPUESTOS PREVIOS.
- Linearidad.- Los movimientos y esfuerzos son funciones
lineales de las cargas aplicadas.

Ventajas Simplifica el análisis
Permite la superposición de soluciones

Condiciones Materiales elásticos
Desplazamientos pequeños

n.P

P

+
+
P.l n. P.l
4 4
f

n.f

- Superposición.- Los esfuerzos y movimientos que produce un
conjunto de sistemas de carga actuando a la vez es igual a la suma
de los que producirían actuando por separado.

En cálculo matricial es fundamental este principio de
superposición, puesto que en general hemos de superponer dos
estados:
C Estado de empotramiento perfecto
C Estado final de cálculo.



MÉTODOS MATRICIALES.

En estructuras la relación determinista
CAUSA ↔ EFECTO
se establece como
FUERZA ↔ MOVIMIENTO

Es una relación biunívoca que debe satisfacer:

1.- Ecuaciones constitutivas del material Ley de Hooke
2.- Ecuaciones de compatibilidad
3.- Ecuaciones de equilibrio

ESTRUCTURAS ISOSTÁTICAS Ecuación 3
ESTRUCTURAS HIPERESTÁTICAS Ecuaciones 1,2, 3

Lo que diferencia los métodos matriciales es el ORDEN de
utilización de las ecuaciones

1 → 2→ 3
MÉTODO DE EQUILIBRIO
O DE RIGIDEZ

1 → 3→ 2
MÉTODO DE LAS FUERZAS
O DE FLEXIBILIDAD



MÉTODO DE FLEXIBILIDAD

INCÓGNITAS BÁSICAS FUERZAS HIPERESTÁTICAS

DATOS FUERZAS EN LOS NUDOS

APLICACIÓN DEL MÉTODO

1.- Expresar las deformaciones en función de los esfuerzos en los
extremos de las barras. (Ecuación constitutiva).

2.- Expresar los esfuerzos en los extremos de las barras en función
de las incógnitas hiperestáticas y de las fuerzas exteriores
conocidas. (Ecuación de equilibrio).

3.- Aplicar las ecuaciones de compatibilidad de las deformaciones.
(Ecuación de compatibilidad).

SE GENERA UN SISTEMA LINEAL DE ECUACIONES

X = T ⋅ L
X = matriz de deformaciones
T = matriz de flexibilidad en coordenadas globales
L = matriz incógnita (fuerzas hiperestáticas)

RESOLUCIÓN L = T -1.X Fuerzas hiperestáticas

↓
Se aplica 2 Esfuerzos en barras

↓
Se aplica 1 Deformaciones



MÉTODO DE RIGIDEZ

INCÓGNITAS BÁSICAS MOVIMIENTOS EN LOS NUDOS

DATOS FUERZAS EN LOS NUDOS

APLICACIÓN DEL MÉTODO

1.- Expresar las esfuerzos en los extremos de las barras en función
de los movimientos en dichos extremos. (Ecuación constitutiva).

2.- Aplicar las ecuaciones de compatibilidad de las deformaciones.
Se ponen los movimientos de los extremos de las barras
(coordenadas locales) en función de los movimientos de los nudos
(coordenadas globales). (Ecuación de compatibilidad).

3.- Aplicar las ecuaciones de equilibrio de nudos. (Ecuación de
equilibrio).

SE GENERA UN SISTEMA LINEAL DE ECUACIONES

L = S ⋅ X
L = matriz de cargas en los nudos
S = matriz de rigidez en coordenadas globales
X = matriz incógnita (desplazamientos en los nudos)

RESOLUCIÓN X = S -1.L Desplazamientos en
coord. globales

↓
Se aplica 2 Desplazamientos en
coord. locales

↓
Se aplica 1 Esfuerzos



SISTEMAS DE REFERENCIA Y CONVENIOS DE SIGNOS

SISTEMA DE COORDENADAS GLOBALES
SISTEMA DE COORDENADAS LOCALES

+
z'

+
+
+ Fuerzas y desplazamientos
+ y'
+
+
+
+
Momentos y giros
x'

Eje x Directriz de la barra
z Ejes y,z Ejes principales de
inercia de la sección

DATOS DE LA BARRA
L, A, I y , I z ,I T

(ángulos con ejes globales)

y
i

j

x



CAMBIOS DE SISTEMAS DE REFERENCIA

Para resolver una estructura es preciso cambiar las variables de
coordenadas locales a globales y viceversa m a t r i z d e
transformación

O’x’y’z’ Sistema global
Oxyz Sistema local

CAMBIO DE EJES

 x'  x'⋅x x'⋅y x'⋅z  x
     
 y' =  y'⋅x y'⋅y y'⋅z ⋅  y
     
 z'  z'⋅x z'⋅y z'⋅z   z
144 2444
4 3
cosenos directores

En forma matricial X’ = D . X

Generalmente el cambio de ejes es una rotación. En el plano

 cos α -sen α 0
 
y' ∆ =  sen α cos α 0
y  0
 0 1


x

x'



CÁLCULO MATRICIAL: PRINCIPIOS GENERALES.

P'1
x P'
x2

1 2
d'x1 d'x2
Px1 Px1 Px3 Px3
Px2 2 Px2
1 3

Ecuación constitutiva relaciona los esfuerzos con los
desplazamientos Coord. locales

Px1 = k1 ⋅ dx1   Px1  k 1 0 0   dx1 
      
Px2 = k 2 ⋅ dx2   Px2  =  0 k 2 0  ⋅  dx2 
     
Px3 = k 3 ⋅ dx3 
  Px3   0 0 k 3   dx3 
132 14 244 1 3
4 3 2
~ ~ ~
P K d

P = matriz de fuerzas internas
K = matriz de rigidez
d = matriz de desplazamientos de elementos

Ecuación de compatibilidad relaciona los desplazamientos de
elementos (coordenadas locales)
con los de los nudos
(coordenadas globales)

dx1 = d'x1 - 0   dx1   1 0
      d' 
dx2 = d'x2 - d'x1   dx2  =  -1 0  ⋅  x1 
     d'x2 
dx3 = 0 - d'x2    dx3   0 -1 1 3 2
132 4 3 ~
1 24 d'
~ ~
d A
A = matriz de compatibilidad
d’ = matriz de desplazamientos de nudos



Ecuación de equilibrio las fuerzas externas has de equilibrarse
co las fuerzas internas (coordenadas
globales)

 Px1 
P'x1 = Px1 - Px2   P'x1   1 -1 0   
   =   ⋅ Px2
P'x2 = Px2 - Px3   P'x2   0 1 -1  
132 1 4243  Px3 
 
~ ~t 132
P' A ~
P
P’ = matriz de fuerzas exteriores
At = Matriz traspuesta de A

Se formulan tres ecuaciones matriciales

~ ~ ~
P = K ⋅ d Ecuacion constitutiva
~ ~ ~
d = A ⋅ d' Ecuacion de compatibilidad
~ ~ ~
P' = A t ⋅ P Ecuacion de equilibrio
Proceso
~ ~ ~
1 P’ = At . P
~ ~ ~ ~
2 P’ = At . K . d
~ ~ ~ ~ ~ ~ ~ ~
3 P’ = At . K . A . d’ P’ = S . d’

~ ~ ~
P’ = S . d’ Expresa la ecuación matricial en coordenadas
globales de la estructura completa.



ECUACIÓN CONSTITUTIVA

C Expresa la relación entre los esfuerzos sobre un elemento y
los desplazamientos de dicho elemento. Para materiales
elásticos es la ley de Hooke.
C Al referirse a cada elemento se formula en coordenadas
locales.
C Su grado de complejidad depende del número de esfuerzos
que definan el estado de la barra.

ESTRUCTURAS ARTICULADAS Sólo esfuerzo axil

 E⋅ A - E ⋅ A
Pxi i j Pxj  Pxi     dxi 
  =  El⋅ A E ⋅lA  ⋅  
 Pxj  -   dxj 
{  l  {
d xi dxj 144244 l 3
~ ~ ~
P K d
Puesto en forma matricial
Pxi = - Pxj
Pxj ⋅ l
∆ l = dxj - dxi =
E⋅ A
E⋅ A
Pxj = - Pxi =
l
(dxj - dxi )
ESTRUCTURAS RETICULADAS Axil, cortante y flector

 Pxi   dxi 
Pyi Pyj    
mi mj  Pyi   dyi 
 mi  ~  θi 
Pxi i j Pxj   = K⋅ 
 Pxj   dxj 
 Pyj   dyj 
   
 m j  θj 



CÁLCULO DE LA ECUACIÓN CONSTITUTIVA POR
MEDIO DE LA MATRIZ DE FLEXIBILIDAD

z' Esfuerzos
Pzj m yj
m xj Axil
Pzi m yi Pxj
m zj Momentos flectores
m xi Pyj Esfuerzos cortantes
Pxi m zi Momento torsor
Pyi
y'

x'

La matriz de flexibilidad relaciona los desplazamientos del
elemento con sus esfuerzos Inversa de la matriz de rigidez.
~ ~ ~
P = K⋅d (rigidez) ~
 ~ -1 ~ ~ -1
~ ~ ~ T = K ⇒ K = T
d = T ⋅P (Flexibilidad) 


La ventaja de este método es que la matriz de flexibilidad puede
obtenerse siempre por simple aplicación del teorema de
Castigliano.

Energía elástica del elemento

1 l N2 MT 
2
M2 V2
U = ∫0 + + +  ⋅ dx
2  E⋅ A E ⋅I G ⋅ Ae G ⋅ J

Derivando la energía elástica con respecto a cada esfuerzo se
puede obtener el desplazamiento correspondiente.

∂U ~ ~ ~
di = ⇒ d = T ⋅P
∂ Pi
E invirtiendo la matriz de flexibilidad se obtiene la matriz de rigidez.



ECUACIÓN DE COMPATIBILIDAD.

Los esfuerzos internos
y' llevan la dirección de
Pyj mj los ejes locales.
y
Pyi Pxj
mi x Las fuerzas externas
llevan la dirección de
Pxi los ejes globales.

Las leyes de cambio de
x' coordenadas son las
mismas que para ejes.

Se trata de una rotación de ejes de ángulo a

 x  cos α sen α 0  x'
     
 y =  -sen α cos α 0 ⋅  y'
     
 z  0 0 1  z'
{ 1444 2 444 3
4 4 {
~
x ~ ~
x'
A

Para los esfuerzos
 Px   cos α sen α 0  Px '
     
 Py  =  -sen α cos α 0 ⋅  Py '
     
 m  0 0 1  m'
{ 1444 24444
4 3 {
~ ~ ~
P A P'

Para los desplazamientos
 dx   cos α sen α 0  dx '
     
 dy  =  -sen α cos α 0 ⋅  dy '
     
θ  0 0 1  θ' 
{ 1444 2444 3
4 4 132
~ ~ ~
d A d'

Las mismas relaciones pueden generalizarse para cualquier
sistema de coordenadas.


ECUACIÓN DE EQUILIBRIO

P' P'  P'x1 
y1 y2  
m'1 m'2  P'y1 
 M'1 
 
P' 1
x1 2 P'
x2
 ......
 P'x2 
 
~  P'y2 
P' = 
M' 
 2
 ......
3 4  . 
 
 . 
 . 

 ......

 
Estructura cualquiera con cargas en los nudos

Fuerzas exteriores Fuerzas interiores
se equilibran

~ ~
Fuerzas P' ↔ P
~ ~
Desplazamientos d'
{ ↔ d
{
exteriores internas

Aplicando el principio de trabajos virtuales
1 1
⋅ ∑ P'i ⋅d'i = ⋅ ∑ Pj ⋅ d
24 4
1 2 3
i 24 4 j
1 j2 3
trabajo fuerzas trabajo fuerzas
externas internas
~ ~ ~ ~
En forma matricial P't ⋅d' = Pt ⋅ d
~ ~ ~
Aplicando la ecuación de compatibilidad d = A ⋅ d'
~t~ ~ ~ ~ ~ ~ ~
P' ⋅d' = Pt ⋅ A ⋅ d ⇒ P't = Pt ⋅ A

Y trasponiendo esta ecuación
~ ~ ~
Ecuación de equilibrio P' = A ⋅ P


PLANTEAMIENTO GENERAL DEL CÁLCULO
MATRICIAL
~ ~ ~
Ecuación constitutiva P = K ⋅ d
~ ~
Ecuación de compatibilidad d = A ⋅ d'
~ ~ ~
Ecuación de equilibrio
P' = A t ⋅ P

~ ~ ~ ~ ~ ~ ~
P = K⋅d ⇒ P = K ⋅ A ⋅ d'
multiplicando a la izquierda por A t
~ ~ ~ ~ ~ ~
A2P = 1 ⋅ K4 ⋅ d' ⇒ P' = S ⋅ d'
t
13 ⋅ A t 2 ⋅3
4 A
~ ~
P' S

Sistema lineal de ecuaciones

n datos Fuerzas en los nudos
n incógnitas Desplazamientos en los nudos
El problema se reduce a resolver un sistema lineal de n ecuaciones
con n incógnitas, por cualquiera de los métodos matemáticos
disponibles.

 s11 s12 s13 ... s1 n   x 1   p1 
     
 s 21 s 22 s 23 ... s 2n   x 2   p2 
 s 31 s 32 s 33 ... s 3n  ⋅  x 3  =  p3 
     
 : : : ... :   :   :
     
 sn1 sn2 sn3 ... snn   x n   pn 

Una vez resuelto el sistema se conocen los desplazamientos de los
nudos en coordenadas globales.



ENSAMBLAJE POR BLOQUES

Matriz de un elemento Coordenadas globales

~ ~ ~ ~
 Pi '  Sii Sij   di '
~  = ~ ~  ⋅~ 
 Pj '  S ji Sjj   dj '

Situación en la matriz de rigidez de la totalidad de la estructura

 • • 
 
 • • 
 • • 
 
 • • • +Sii • • • • +Sij • • • fila i
 • • 
 
 • • 
 • • 
 
 • • • +S ji • • • • +Sjj • • • fila j
 • • 
 
 • • 
 • • 

 

 • • 
columna columna
i j



EJEMPLO DE ENSAMBLAJE POR BLOQUES DE LA
MATRIZ DE RIGIDEZ DE UNA ESTRUCTURA

1 1 2 2 3

3 4 5

4 5 6

1 3 1 3
P'
1 S 11+ S 11 S 12 0 S 14 0 0 d'1
1 1 2 4 2 4
P'
2 S 21 S 22+ S 22+ S 22 S 23 0 S 25 0 d'2
2 2 5 5
P'
3 0 S 32 S 33+ S 33 0 0 S 36 d'3
= .
3 3
P'
4 S 41 0 0 S 44 0 0 d'4
4 4
P'
5 0 S 52 0 0 S 55 0 d'5 =0

5 5
P'
6 0 0 S 63 0 0 S 66 d'6 =0

En los nudos 5 y 6 los tres desplazamientos son nulos al tratarse
de empotramientos. Pueden eliminarse del sistema de ecuaciones.

El nudo 4 tiene dos desplazamientos nulos (articulaciones). Las
filas correspondientes a esos desplazamientos también pueden
eliminarse.



EFECTO DE LOS VÍNCULOS.

Una vez efectuado el ensamblaje de matrices se obtiene un sistema
lineal de ecuaciones del tipo

 s11 s12 s13 ... s1 n   x 1   p1 
     
 s 21 s 22 s 23 ... s 2n   x 2   p2 
 s 31 s 32 s 33 ... s 3n  ⋅  x 3  =  p3 
     
 : : : ... :   :   :
     
 sn1 sn2 sn3 ... snn   x n   pn 

La existencia de un vínculo supone un desplazamiento conocido.
La ecuación correspondiente a esa incógnita no necesita ser
resuelta.

Desplazamientos
nulos

Son ecuaciones que
pueden eliminarse del
sistema. En la práctica
es mucho más simple
formar la ecuación pero
saltarla a la hora de
d y =0 d x =0 d x =0 resolver el sistema.
d y =0 d y =0
0 =0

Desplazamientos conocidos pero no nulos
Es preciso modificar la matriz de rigidez global.

Supongamos conocido el valor de x 2 x2=b

Métodos de resolución Resolución directa
Factores de penalización



Método de resolución directa.- Se modifica el sistema de
ecuaciones en forma tal que mantenga la simetría.

 s11 0 s13 ... s1n   x 1   p1 - s12β 
     
 0 1 0 ... 0   x 2   β 
 s 31 0 s33 ... s3n  ⋅  x 3  =  p 3 - s 32β
     
 : : : ... :   :   : 
     
 sn1 0 sn3 ... snn   xn   pn - sn2 β

Si hay más desplazamientos conocidos se repite este proceso las
veces que haga falta.

Método de los factores de penalización.- Se modifica el sistema de
ecuaciones utilizando un factor de penalización muy grande, por
ejemplo 1010.

 s11 s12 s13 ... s1n   x 1   p1 
     
 s 21 s 22 ⋅ 1010 s 23 ... s 2n   x 2   p2 ⋅ 1010 ⋅ β
 s 31 s32 s 33 ... s 3n  ⋅  x 3  =  p3 
     
 : : : ... :   :   : 
     
 sn1 s n2 sn3 ... snn   x n   pn 

Si dividimos la segunda ecuación por s 22.1010 obtendremos

s21 s s
⋅ 10 -10 ⋅ x 1 + x 2 + 23 ⋅ 10-10 ⋅ x 3 + ... + 2n ⋅ 10-10 ⋅ x n = β
s 22 s 22 s22

Que es prácticamente equivalente a x2=b que es la ecuación del
desplazamiento impuesto



RESOLUCIÓN DE SISTEMAS DE ECUACIONES

Métodos directos.- Son algoritmos que proporcionan una solución
exacta del sistema tras un número finito de operaciones.

C Método de Gauss
C Método de Gauss-Jordan
C Método frontal
C Método de Cholesky

Método iterativos.- Son algoritmos que suponen una solución
inicial inexacta que va convergiendo a la solución exacta por
aproximaciones sucesivas.

C Método de Jacobi
C Método de Gauss-Seidel
C Método de gradientes conjugados

El problema principal de los métodos iterativos es asegurar la convergencia de la
solución en un número finito de pasos.



MÉTODO DE GAUSS

S11.x 1 + s 12.x 2 + s 13.x 3 + ........ + s 1n.x n = p 1 pivotes
S21.x 1 + s 22.x 2 + s 23.x 3 + ........ + s 2n.x n = p 2 X f21=-s 21/s 11
S31.x 1 + s 32.x 2 + s 33.x 3 + ........ + s 3n.x n = p 3 X f31=-s 31/s 11
. . . . .
. . . . .
. . . . .
Sn1.x 1 + s n2.x 2 + s n3.x 3 + ........ + s nn.x n = p n X fn1=-s n1/s 11

C Se multiplica la ecuación pivote por cada pivote y se suma a
cada ecuación
s11.(-s 21/s 11) + s 11 = -s 11 + s 11 = 0

C La ecuación pivote se mantiene y cada una de las demás se
modifica anulando la primera columna

S11.x 1 + s 12 .x 2 + s 13 .x 3 + ........ + s 1n .x n = p 1 pivotes
0.x 1 + s’22.x 2 + s’23.x 3 + ........ + s’2n.x n = p’2
0.x 1 + s’32.x 2 + s’33.x 3 + ........ + s’3n.x n = p’3 X f’32=-s’32/s’22
. . . . .
. . . . .
. . . . .
0.x 1 + s’n2.x 2 + s’n3.x 3 + ........ + s’nn.x n = p’n X f’n2=-s’n2/s’22

C Se toma la segunda ecuación como pivote
C Se reitera el proceso anulando la segunda columna
C Se toma la tercera ecuación como pivote
C Se reitera el proceso anulando la tercera columna
C Se repite con todas las ecuaciones hasta que todos los
términos bajo la diagonal principal sean nulos (matriz
triangular)

s11.x 1 + s 12 .x 2 + s 13 .x 3 + ........ + s 1n-1 .x n-1 + s 1n .x n = p 1
+ s 22 .x 2 + s 23 .x 3 + ........ + s 2n-1 .x n-1 + s 2n .x n = p 2
+ s 33 .x 3 + ........ + s 3n-1 .x n-1 + s 3n .x n = p 3
. . . . .
. . . . .
. . . . .
+ s n-1,1 .x n-1 + s n-1,n .x n = p n-1
+ s nn .x n = p n
C De la última ecuación se despeja x n
C Llevando este valor a la penúltima se despeja x n-1
C Procediendo sucesivamente se obtienen todas las incógnitas


CÁLCULO DE ESFUERZOS
~ ~ ~
P' = S ⋅ d' Se obtienen los desplazamientos en los
nudos , pero interesa conocer los
esfuerzos en la barras.

Para cada barra

y'
Pyj mj
y
Pyi Pxj
mi x

Pxi Se conocen d’i y d’j

x' Interesa conocer P i y P j

~ ~ ~ ~ ~ ~
P = K ⋅d pero d = A ⋅ d'

Calculamos los desplazamientos en coordenadas locales

~ ~ ~
d = A ⋅ d'

Llevando estos desplazamientos a la ecuación constitutiva se
obtienen los esfuerzos sobre la barra

~ ~ ~
P = K ⋅d

Al afectar a las barras una por una no es necesario recurrir a las
matrices completas de la estructura, sino sólo a las de cada barra,
lo que supone una gran simplificación de cálculo.



COMPROBACIÓN DE RESULTADOS

Los resultados del cálculo matricial nunca son rigurosamente
exactos.

Errores de truncadura 
 SIEMPRE es preciso comprobar que

 la estructura está en equilibrio
Problemas de mal 
condicionamiento 

ESTRUCTURAS DE NUDOS ARTICULADOS.- Se comprueba el
equilibrio de los nudos, para las fuerzas horizontales y verticales
externas.

y'

Fi Pi

x'

n

∑F x
= 0 ⇒ Fix + ∑ P ⋅ cos α
i=1
i i
= 0
n

∑ Fy = 0 ⇒ Fiy + ∑ P ⋅ sen α
i=1
i i
= 0



ESTRUCTURAS DE NUDOS RÍGIDOS.- Se comprueba el equilibrio de
los nudos para las fuerzas horizontales y verticales y para los
momentos externos.

y'

Mi Pyi
mi
Fi Pxi

x'

n

∑F x = 0 ⇒ Fix + ∑ (P
i=1
xi ⋅ cos α i - Pyi ⋅ sen αi ) = 0
n

∑F y
= 0 ⇒ Fiy + ∑ (P xi
⋅ sen αi + Pyi ⋅ cos αi ) = 0
i=1
n

∑M = 0 ⇒ Mi + ∑m
i=1
i
= 0



ESTRUCTURAS PLANAS DE NUDOS ARTICULADOS

y' j
y
i x

x'

Ecuación de la barra
Pxi = - Pxj
Pxj ⋅ l
Pxi i j Pxj ∆ l = dxj - dxi =
E⋅ A
E⋅ A
dxi dxj Pxj = - Pxi =
l
(dxj - dxi )
Puesto en forma matricial

 E⋅ A - E ⋅ A ~ ~ ~ ~ ~
 Pxi   l l  ⋅  dxi  Pi = Kii ⋅ di + Kij ⋅ dj
  =  E⋅ A E ⋅ A   
 Pxj  -   dxj 
~ ~ ~ ~ ~
Pj = K ji ⋅ di + K jj ⋅ dj
{  l  {
144244 l 3
~ ~ ~
P K d



Cambio de ejes

P'xi = Pxi ⋅ cos α
y' j P'yi = Pyi ⋅ sen α
y En forma matricial
x
 P'xi   cos α 
i   =   ⋅ (Pxi )
P'xi
 P'yi   sen α  {
P'yi 132 1 24 ~
4 3
~ ~ Pi
P xi
P'i At

x'

Proyectando sobre el eje de la barra

 P' 
Pxi = P'xi cos α + P'yi sen α ⇒ (
{
Pxi ) = (cos α sen α ) ⋅  xi 
144 443  P'yi 
2
~ ~ 132
Pi A ~
P'i
Para los desplazamientos las relaciones son idénticas

~ ~ ~ ~ ~ ~
di = A ⋅ d'i di ' = A t ⋅ di

Aplicando la transformación de coordenadas a las ecuaciones

~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Pi = Kii ⋅ di + Kij ⋅ dj ⇒ Pi = Kii ⋅ A ⋅ d'i + Kij ⋅ A ⋅ d' j
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Pj = K ji ⋅ di + K jj ⋅ dj ⇒ Pj = K ji ⋅ A ⋅ d'i + K jj ⋅ A ⋅ d' j
Multiplicando a la izquierda por At

~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
P'i = A t ⋅ Pi = A t ⋅ Kii ⋅ A ⋅ d'i + A t ⋅ Kij ⋅ A ⋅ d' j = Sii ⋅ d'i + Sij ⋅ d' j
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
P'j = A t ⋅ Pj = A t ⋅ K ji ⋅ A ⋅ d'i + A t ⋅ K jj ⋅ A ⋅ d'j = S ji ⋅ d'i + Sjj ⋅ d' j



Efectuando las multiplicaciones matriciales

 EA
cos 2α
EA
sen α cos α 
 cos α   EA   
Sii = Sjj =   ⋅  ⋅ ( cos α sen α ) =  l l 
 sen α   l  
EA EA

 l sen α cos α l
sen2 α 

 EA EA 
 cos α   EA   - cos 2 α - sen α cos α 
Sij = S ji =   ⋅ -  ⋅ (cos α sen α ) =  l l 
 sen α   l  -
EA
sen α cos α -
EA
sen2 α 
 l l 

La matriz de rigidez en coordenadas globales de la barra será

 EA EA EA EA 
 cos 2α sen α cos α : - cos 2α - sen α cos α 
 P'xi 
 EA
l l l l
  xi 
d'
  EA EA EA  
 P'yi   sen α cos α sen 2α : - sen α cos α - sen α 2
  d' yi 
 ...... =  ......................... ......................... 
l l l l
 : ......................... ........................  ⋅  ......
   
 P'xj   -
EA
cos 2 α -
EA
sen α cos α :
EA
cos2 α
EA
sen α cos α   d' xj 
   l l l l   
 P'yj   EA EA EA EA   d' yj 
- sen α cos α - sen2α : sen α cos α sen α 2

 l l l l 



CÁLCULO DE ESFUERZOS: ESTRUCTURAS
ARTICULADAS PLANAS

Para cada barra se
y' j aplica la ecuación de
y compatibilidad
x ~ ~ ~
d = A ⋅ d'
P'xi i
P'yi
P xi

x'

 d'xi 
(d )
{ xi = (cos α sen α ) ⋅  
1442443  d'yi 
4 4
~ ~ 132
d A ~
d'

Nudo origen i dxi = cos α ⋅ d'xi + sen α ⋅ d'yi

Nudo extremo j dxj = cos α ⋅ d'xj + sen α ⋅ d'yj

Aplicando la ecuación constitutiva

 P = EA ⋅ d - EA ⋅ d
~ ~ ~  xi
 l
xi
l
xj
P = K ⋅d 
 Pxj = - EA ⋅ dxi + EA ⋅ dxj

 l l



COMPROBACIÓN DE RESULTADOS: ESTRUCTURAS
ARTICULADAS PLANAS.

Se comprueba el equilibrio de los nudos, para las fuerzas
horizontales y verticales externas.

y'

P'xi
P'yi
Fi Pi

x'

Es preciso pasar los esfuerzos sobre las barras a coordenadas
globales

~ ~ ~  P'xi   cos α 
P'i = A t ⋅ Pi ⇒   =  . (Pi )
 P'yi   sen α 
P'xi = Pi ⋅ cos α ; P'yi = Pi ⋅ sen α

Aplicando las condiciones de equilibrio

n

∑F x
= 0 ⇒ Fix + ∑ P ⋅ cos α
i=1
i i
= 0
n

∑F y
= 0 ⇒ Fiy + ∑ P ⋅ sen α
i=1
i i
= 0



ESTRUCTURAS DE PÓRTICOS PLANOS

y' y j
i x

x'

Matriz de cargas Matriz de fuerzas
exteriores internas
 Pxi 
 
 Pyi 
 Fxi   mi 
~   ~  
P'i =  Fyi  Pi =  ....
  P 
 Mi 
 xj 
 Pyj 
m 
 j
Desplazamientos en Desplazamientos en
coord. locales coordenadas globales
 dxi   d'xi 
   
 dyi   d'yi 
 θi   θ 'i 
~   ~  
di =  .... d'i =  .... 
 dxj   d'xj 
   
 dyj   d'yj 
θ   θ' 
 j  j



y Estado 1
1
Pyj mi i
j

Pyi i j
1
Pxj j
mj
i
d yj Estado 2
Pxi dyi
i j
2
x mi
dxi dxj
d yi - dyj
2
mj

Momentos producidos por el estado 1.- Giro de los extremos.
mi ⋅ l mj ⋅ l 
1 1
4EI 2EI
θi = ⋅ θi + ⋅θj
1
-  mi =
3EI 6EI  ⇒ l l
mi ⋅ l mj ⋅l
1
1
2EI 4EI
⋅ θi + ⋅ θj
1
θj = - + mj =
3EI 6EI   l l

Momentos producidos por el estado 2.- Desplaz. de los extremos.
2
mi = m j =
2 6EI
l2
(dyi - dyj ) = 6EI ⋅ dyi - 6EI ⋅ dyj
l2 l2

El estado total es la suma de ambos

6EI 4EI 6EI 2EI
mi = ⋅ dyi + ⋅ θi - ⋅ dyj + ⋅ θj
l2 l l2 l
6EI 2EI 6EI 4EI
mj = ⋅ dyi + ⋅ θi - 2 ⋅ dyj + ⋅θj
l2 l l l



Esfuerzos cortantes.- Se plantea la ecuación de equilibrio de la
barra
mi + mj 12E I 6E I 12E I 6E I
Pyi = - Pyj = = 3 ⋅ d yi + 2 ⋅ θ i - 3 ⋅ dyj + 2 ⋅ θ j
l l l l l

Esfuerzos axiles.- Su formulación es idéntica a las estructuras
articuladas
EA EA
Pxi = - Pxj = ⋅ dxi - ⋅ dxj
l l

Poniendo todas estas ecuaciones en forma matricial

 EA   EA 
 0 0  - 0 0 
 Pxi   l
    dxi   l
12E I 6EI       dxj 
12E I 6EI   
 Pyi  =  0 ⋅  dyi  + 0 - 3 ⋅d 
   l3 l2     l l2   yj 
 mi   6EI 4EI   θ i   6EI 2EI   θ j 
{  0  {  0 - 2  {
 l 2 444 
l3  l 4444
l3
1444 2 1444 2
4
~ ~ ~ ~ ~
Pi Kii di Kij dj
 EA   EA 
 - 0 0  - 0 0 
 Pxj   l   dxi   l   dxj 
  12EI 6EI   12EI 6EI  
 Pyj  =  0 - 3 - 2  ⋅  dyi  +  0 - 2  ⋅  dyj 
m   l l     l3 l   
 j  6EI 2EI  { θi   6E I 4EI   θ j 
{  0   0 - 2  {
 l2 l   l l 
1444 24444
4 3 1444 24444
4 3
~ ~ ~ ~ ~
Pj K ji di K jj dj
Que pueden ponerse en la forma

~ ~ ~ ~ ~
Pi = Kii ⋅ di + Kij ⋅ dj  
~ ~ ~ ~ ~ ⇒ En coordenadas locales
Pj = K ji ⋅ di + K jj ⋅ dj 




Cambio de coordenadas.- Se pasan de coordenadas locales (x,y)
a globales (x’,y’) por medio de una matriz de rotación.

 Px   cos α sen α 0  P'x 
     
 Py  =  -sen α cos α 0 ⋅  P'y 
 m  0 1  m 
   0   

Como en las matrices de
~ ~ ~ ~ ~ ~
P = A ⋅ P' P' = A t ⋅ P rotación la inversa es igual a la
traspuesta


~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Multiplicando a la izquierda por A t
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

Para calcular las submatrices S se aplica la transformación de
coordenadas a cada una de las submatrices K



 EA 
 0 0 
 cos α -sen α 0  l   cosα senα 0
~   12EI 6E I  
Sii =  sen α cos α 0 ⋅  0 ⋅  -senα cosα 0
 0   l3 l2   
 0 1  6EI 4E I  44424441
0 0
14442444  0 3  1 3
 l2 l 
1444 444
2 3
~t ~ ~
A Kii A
El resultado final de efectuar estas multiplicaciones matriciales a
las cuatro submatrices será

 a c d : -a -c d
 
 c b e : -c -b e
 d e f : -d -e g
~  
S =  ... ... ... ... ... ... ... Siendo
 -a -c -d : a c -d
 
 -c -b -e : c b -e 
 
 d e g : -d -e f

EA 12EI
a= ⋅ cos2 α + 3 ⋅ sen2 α
l l
EA 12E I
b= ⋅ sen2α + 3 ⋅ cos2 α
l l
EA 12EI
c= ⋅ senα ⋅ cosα - 3 ⋅ sen α ⋅ cos α
l l
6EI 6EI
d = - 2 ⋅ sen α ; e = 2 ⋅ cos α
l l
4EI 2EI
f= ; g=
l l



CÁLCULO DE ESFUERZOS: ESTRUCTURAS DE PÓRTICOS PLANOS

Para cada barra se aplica la ecuación de compatibilidad

~ ~ ~  dxi   cosα sen α 0  d'xi 
d = A ⋅ d'
     
 dyi  =  -senα cos α 0 ⋅  d'yi 
     
 θi   0 0 1  θ 'i 
Aplicando esta ecuación a los
nudos origen y extremo de la barra

Nudo origen i dxi = cos α ⋅ d'xi + sen α ⋅ d'yi
dyi = - sen α ⋅ d'xi + cos α ⋅ d'yi
θ i = θ 'i

Nudo extremo j dxj = cos α ⋅ d'xj + sen α ⋅ d'yj
dyj = - sen α ⋅ d'xj + cos α ⋅ d'yj
θ j = θ 'j

~ ~ ~
Aplicando la ecuación constitutiva P = K ⋅d

EA EA
Pxi = - Pxj = ⋅ dxi - ⋅ dxj
l l
mi + m j 12E I 6EI 12EI 6E I
Pyi = - Pyj = = ⋅ d yi + 2 ⋅ θi - ⋅ dyj + 2 ⋅ θ j
l l3 l l3 l
6EI 4EI 6E I 2E I
mi = 2 ⋅ dyi + ⋅ θi - 2 ⋅ dyj + ⋅ θj
l l l l
6EI 2E I 6E I 4EI
mj = 2
⋅ dyi + ⋅ θi - 2 ⋅ dyj + ⋅θj
l l l l



COMPROBACIÓN DE RESULTADOS: ESTRUCTURAS DE PÓRTICOS
PLANOS.

Se comprueba el equilibrio de los nudos, para las fuerzas
horizontales y verticales externas y para los momentos exteriores.

y'

Mi Pyi
mi
Fi Pxi

x'

Es preciso pasar los esfuerzos sobre las barras a coordenadas
globales
 P'xi   cos α i -sen α i 0  Pxi 
~ ~ ~      
P'i = A t ⋅ Pi ⇒  P'yi  =  sen α i cos α i 0 . Pyi 
 m'   0 1  mi 
 i  0   
P'xi = Pxi ⋅ cos α i - Pyi ⋅ sen α i
P'yi = Pxi ⋅ sen α i + Pyi ⋅ cos α i
m'i = mi
Aplicando las condiciones de equilibrio
n

∑F x = 0 ⇒ Fix + ∑ (P
i=1
xi ⋅ cos α i - Pyi ⋅ sen αi ) = 0
n

∑F y
= 0 ⇒ Fiy + ∑ (P xi
⋅ sen αi + Pyi ⋅ cos αi ) = 0
i=1
n

∑M = 0 ⇒ Mi + ∑m
i=1
i
= 0



ACCIONES SOBRE LAS BARRAS.- PÓRTICOS PLANOS

Estado general
P
q
i j

P -Vi -Vj
-m i q -mj
i j +
Estado I i Estado II j
-Vi +Vj -m i mj

Estado I .- Se emplea el
convenio de signos de flectores
y cortantes
Py i Pyj
Mi Mj

Estado II.- Se emplea el Pxi i j Px j
convenio de signos de matricial

Diagrama de flectores Diagrama de cortantes

-mi -Mi -Vi - Pyi
-
- - -mj + Mj
+ + V + Pyj
j

Resultado final Superposición E I + E II



ESTRUCTURAS DE EMPARRILLADOS PLANOS

P
P
q
P M

Condiciones

C Estructura plana, horizontal, de nudos rígidos.
C Cargas perpendiculares al plano.
C Momentos contenidos en el planos

Hipótesis

C Los desplazamientos son sólo verticales.
C No se producen giros de eje vertical

y
y'

x' x
z=z'



Matriz de cargas Matriz de fuerzas
exteriores internas
 mxi 
 
 Pzi 
 M xi   myi 
~   ~  
P'i =  FZi  Pi =  .... 
M  m 
 yi   xj 
 Pzj 
m 
 yj 
Desplazamientos en Desplazamientos en
coord. locales coordenadas globales
 θ xi   θ 'xi 
   
 dzi   d'zi 
 θ yi   θ 'yi 
~   ~  
di =  ....  d'i =  .... 
θ   d' 
 xj   xj 
 dzj   d'zj 
θ   θ' 
 yj   yj 
La diferencia principal con los pórticos planos consiste en el efecto
del momento torsor que es análogo al del esfuerzo axil.

m xi m xj
xj
- xi

GJ GJ
mxi = - mxj = ⋅ θ xi - ⋅ θ xj
l l



i
Estado 1
j x
mxi dzi tj m1
yi
j m1
yj
i
dzj
mxj
ti j i
Pzi
Pzj
Estado 2 m2
yj
y
d zi - dzj
m2
yi

Momentos producidos por el estado 1.- Giro de los extremos.

m 1 ⋅l m 1⋅l 
yi yj  4EI 2EI
θ = - m 1 = ⋅θ + ⋅θ
yi 3EI 6EI  ⇒ yi l yi l yj

m 1 ⋅l m 1⋅l  m 1 =
2EI
⋅θ +
4EI
⋅θ
yi yj  yj yi yj
θ = - + l l
yj 3EI 6EI 
Momentos producidos por el estado 2.- Desplaz. de los extremos.
2
myi = myj =
2 6E I
l2
(dzi - dzj ) = 6EI ⋅ dzi - 6EI ⋅ dzj
l2 l2

El estado total es la suma de ambos

6E I 4E I 6E I 2E I
myi = 2 ⋅ dzi + ⋅ θ yi - 2 ⋅ dzj + ⋅ θ yj
l l l l
6E I 2E I 6E I 4E I
myj = 2 ⋅ dzi + ⋅ θ yi - 2 ⋅ dzj + ⋅ θ yj
l l l l



Esfuerzos cortantes.- Se plantea la ecuación de equilibrio de la
barra
mi + m j 12EI 6EI 12E I 6EI
Pzi = - Pzj = = 3 ⋅ dzi + 2 ⋅ θ yi - 3 ⋅ dzj + 2 ⋅ θyj
l l l l l

Momentos torsores.- Su formulación es análoga a las estructuras
de pórticos planos
GJ GJ
mxi = - mxj = ⋅ θ xi - ⋅ θxj
l l

Poniendo todas estas ecuaciones en forma matricial

 GJ   GJ 
 0 0   - 0 0 
 mxi   l  θxi   l
     θxj 
  12E I 6EI  12E I 6EI   
 Pzi  =  0 ⋅  dzi  +  0 - 3 ⋅  dzj 
m   l     l   
3 2 2
l l
 yi   6EI 4EI   θyi   6EI 2EI   θyj 
13  0
2  {  0 - 2  {
 l2
l3  l4
1444 444
2 4l
1444 2444 3
~ ~ ~ ~ ~
Pi Kii di Kij dj
 GJ   EA 
 - 0 0  - 0 0 
 mxj   l   θ xi   l   θ xj 
  12EI 6EI   12EI 6EI  
 Pzj  = 0 - 3 - 2  ⋅  dzi  +  0 - 2  ⋅  dzj 
m   l l     l3 l   
 yj   0 6EI 2EI  { θ yi   6E I 4EI   θ yj 
132    0 - 2  {
 l2 4444
l 3  l 4444
l 3
1444 24 1444 2
4
~ ~ ~ ~ ~
Pj K ji di K jj dj
Que pueden ponerse en la forma

~ ~ ~ ~ ~
Pi = Kii ⋅ di + Kij ⋅ dj  
~ ~ ~ ~ ~ ⇒ En coordenadas locales
Pj = K ji ⋅ di + K jj ⋅ dj 




Cambio de coordenadas.- Se pasan de coordenadas locales (x,y)
a globales (x’,y’) por medio de una matriz de rotación.

 mx   cosα 0 sen α  m'x 
y'      
 Pz  =  0 1 0  ⋅  P'z 
 m   -senα 
0 cosα  m'y 
 y   

x' x
z=z'

Como en las matrices de rotación la inversa es igual a la traspuesta
~ ~ ~ ~ ~ ~
P = A ⋅ P' P' = A t ⋅ P

~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
Multiplicando a la izquierda por A t
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~
~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~ ~

Para calcular las submatrices S se aplica la transformación de
coordenadas a cada una de las submatrices K



 GJ 
 0 0 
 cosα 0 -senα   l   cosα 0 senα
~   12EI 6EI   
Sii =  0 1 0  ⋅ 0 ⋅ 0 1 0 
 senα 0 cosα   l  
3 2

0 cosα
l

1444 444  0
2 3
  6EI 4EI   -senα 2444 
 1444 3
 l2 444 
l3
1444 2
~t ~ ~
A Kii A
El resultado final de efectuar estas multiplicaciones matriciales a
las cuatro submatrices será como en el caso del pórtico plano

a c d : g -c h 
 
c b e : c -b i 
d e f : h -i j 
~  
S =  ... ... ... ... ... ... ... Siendo los coeficientes
g c h : a -c d 
 
 -c -b -i : -c b -i 
h i
 j : d -i f 

GJ 4EI 12EI
a= ⋅ cos 2 α + ⋅ sen2 α ; b=
l l l3
6EI GJ 4EI
c = - 2 ⋅ senα ; d= ⋅ senα ⋅ cosα - ⋅ senα ⋅ cosα
l l l
6EI GJ 4EI
e = 2 ⋅ cosα ; f= ⋅ sen2 α + ⋅ cos2 α
l l l
GJ 2EI GJ 2EI
g=- ⋅ cos2 α + ⋅ sen2 α ; h=- ⋅ senα ⋅ cosα + ⋅ senα ⋅ cosα
l l l l
6EI GJ 2EI
i = 2 ⋅ cosα ; j=- ⋅ sen2 α + ⋅ cos2 α
l l l



CÁLCULO DE ESFUERZOS: ESTRUCTURAS DE EMPARRILLADOS
PLANOS

Para cada barra se aplica la ecuación de compatibilidad

~ ~ ~  θ xi   cosα 0 sen α  θ 'xi 
d = A ⋅ d'
     
 dzi  =  0 1 0  ⋅  d'zi 
 θ   -senα 0 cos α  θ ' 
 yi     yi 

Aplicando esta ecuación a los nudos origen y extremo de la barra

Nudo origen i θ xi = cos α ⋅ θ 'xi + sen α ⋅ θ 'yi
dzi = d'zi
θ yi = - sen α ⋅ θ 'xi + cos α ⋅ θ 'yi

Nudo extremo j θ xj = cos α ⋅ θ 'xj + sen α ⋅ θ 'yj
dzj = d'zj
θ yj = - sen α ⋅ θ 'xj + cos α ⋅ θ 'yj
Aplicando la ecuación constitutiva ~ ~ ~
P = K ⋅d
GJ GJ
mxi = - mxj = ⋅ θ xi - ⋅ θ xj
l l
m yi + m yj 12EI 6E I 12EI 6EI
Pzi = - Pzj = = 3
⋅ dzi + 2 ⋅ θ yi - 3
⋅ dzj + 2 ⋅ θ yj
l l l l l
6EI 4E I 6E I 2E I
myi = 2 ⋅ dzi + ⋅ θ yi - 2 ⋅ d zj + ⋅ θ yj
l l l l
6EI 2E I 6E I 4E I
myj = ⋅ dzi + ⋅ θ yi - 2 ⋅ d zj + ⋅ θ yj
l2 l l l


Matricial1

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Viewers also liked

Viewers also liked (20)

More from Andrea Espinosa

More from Andrea Espinosa (9)

Matricial1