07Decoders121

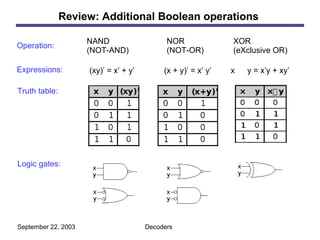
Review: Additional Boolean operations September 22, 2003 Decoders NAND (NOT-AND) NOR (NOT-OR) XOR (eXclusive OR) (xy)’ = x’ + y’ (x + y)’ = x’ y’ x  y = x’y + xy’ Operation: Expressions: Truth table: Logic gates:

XOR gates ,[object Object],[object Object],[object Object],September 22, 2003 Decoders x  y = x’ y + x y’

More XOR tidbits ,[object Object],[object Object],[object Object],September 22, 2003 Decoders x  (y  z) = x  (y’z + yz’) [ Definition of XOR ] = x’(y’z + yz’) + x(y’z + yz’)’ [ Definition of XOR ] = x’y’z + x’yz’ + x(y’z + yz’)’ [ Distributive ] = x’y’z + x’yz’ + x((y’z)’ (yz’)’) [ DeMorgan’s ] = x’y’z + x’yz’ + x((y + z’)(y’ + z)) [ DeMorgan’s ] = x’y’z + x’yz’ + x(yz + y’z’) [ Distributive ] = x’y’z + x’yz’ + xyz + xy’z’ [ Distributive ]

XNOR gates ,[object Object],[object Object],September 22, 2003 Decoders (x  y)’ = x’y’ + xy

Design considerations, and where they come from ,[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders

Decoders ,[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders

What is a decoder ,[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders

What a decoder does ,[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders

How can you build a 2-to-4 decoder? ,[object Object],[object Object],September 22, 2003 Decoders Q0 = S1’ S0’ Q1 = S1’ S0 Q2 = S1 S0’ Q3 = S1 S0

A picture of a 2-to-4 decoder September 22, 2003 Decoders

Enable inputs ,[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders

An aside: abbreviated truth tables ,[object Object],[object Object],September 22, 2003 Decoders

[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],Blocks and abstraction September 22, 2003 Decoders Q0 = S1’ S0’ Q1 = S1’ S0 Q2 = S1 S0’ Q3 = S1 S0

A 3-to-8 decoder ,[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders Q0 = S2’ S1’ S0’ Q1 = S2’ S1’ S0 Q2 = S2’ S1 S0’ Q3 = S2’ S1 S0 Q4 = S2 S1’ S0’ Q5 = S2 S1’ S0 Q6 = S2 S1 S0’ Q7 = S2 S1 S0

So what good is a decoder? ,[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders Q0 = S1’ S0’ Q1 = S1’ S0 Q2 = S1 S0’ Q3 = S1 S0

Design example: addition ,[object Object],[object Object],[object Object],September 22, 2003 Decoders 1 + 1 + 1 = 11 0 + 1 + 1 = 10 C(X,Y,Z) = m(3,5,6,7) S(X,Y,Z) = m(1,2,4,7)

[object Object],[object Object],Decoder-based adder September 22, 2003 Decoders C(X,Y,Z) = m(3,5,6,7) S(X,Y,Z) = m(1,2,4,7)

Using just one decoder ,[object Object],September 22, 2003 Decoders C(X,Y,Z) = m(3,5,6,7) S(X,Y,Z) = m(1,2,4,7)

Building a 3-to-8 decoder ,[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders Q0 = S2’ S1’ S0’ = m 0 Q1 = S2’ S1’ S0 = m 1 Q2 = S2’ S1 S0’ = m 2 Q3 = S2’ S1 S0 = m 3 Q4 = S2 S1’ S0’ = m 4 Q5 = S2 S1’ S0 = m 5 Q6 = S2 S1 S0’ = m 6 Q7 = S2 S1 S0 = m 7

Decoder expansion ,[object Object],September 22, 2003 Decoders

Modularity ,[object Object],[object Object],[object Object],September 22, 2003 Decoders

A variation of the standard decoder ,[object Object],[object Object],September 22, 2003 Decoders

Separated at birth? ,[object Object],[object Object],[object Object],September 22, 2003 Decoders Q3 = S1 S0 Q2 = S1 S0’ Q1 = S1’ S0 Q0 = S1’ S0’ Q3’ = (S1 S0)’ = S1’ + S0’ Q2’ = (S1 S0’)’ = S1’ + S0 Q1’ = (S1’ S0)’ = S1 + S0’ Q0’ = (S1’ S0’)’ = S1 + S0

Active-low decoder example ,[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders

Summary ,[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],[object Object],September 22, 2003 Decoders

07Decoders121

Recommended

Recommended

More Related Content

What's hot

What's hot (20)

Similar to 07Decoders121

Similar to 07Decoders121 (20)

More from Tatyana Remayeva

More from Tatyana Remayeva (20)

07Decoders121