Resistencia extrema al cobre por un consorcio bacteriano conformado por Sulfo...
Magnitudes Proporcionales
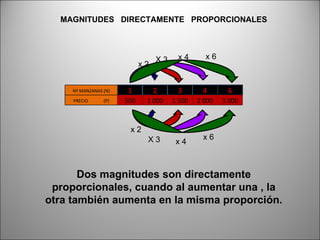
1. 1 2 3 4 6 500 1 000 1 500 2 000 3 000 MAGNITUDES DIRECTAMENTE PROPORCIONALES Dos magnitudes son directamente proporcionales, cuando al aumentar una , la otra también aumenta en la misma proporción. x 2 X 3 x 4 x 6 x 2 X 3 x 4 x 6 Nº MANZANAS (N) PRECIO (P)
2. 1 2 3 4 6 500 1 000 1 500 2 000 3 000 MAGNITUDES DIRECTAMENTE PROPORCIONALES 500 3 000 2 500 1 000 1 500 2 000 1 6 5 4 3 2 Dos magnitudes son directamente proporcionales, si al representarlas gráficamente obtenemos una línea recta que pasa por el origen. Nº MANZANAS (N) PRECIO (P)
3. 1 2 3 4 6 500 1 000 1 500 2 000 3 000 MAGNITUDES DIRECTAMENTE PROPORCIONALES P N = 500 1 = 1 000 2 = 1 500 3 = 2 000 4 = 3 000 6 = 500 = k P N = k P = k N Dos magnitudes son directamente proporcionales, si están ligadas por un cociente constante. Nº MANZANAS (N) PRECIO (P)
4. 120 60 40 30 20 1 2 3 4 6 MAGNITUDES INVERSAMENTE PROPORCIONALES Dos magnitudes son inversamente proporcionales, cuando al aumentar una , la otra disminuye en la misma proporción, y viceversa. ÷ 2 ÷ 3 ÷ 4 ÷ 6 x 2 X 3 x 4 x 6 X = 120 km VELOCIDAD (V) TIEMPO (t)
5. MAGNITUDES INVERSAMENTE PROPORCIONALES 20 120 100 40 60 80 1 6 5 4 3 2 Dos magnitudes son inversamente proporcionales, si al representarlas gráficamente obtenemos una curva llamada hipérbola. 120 60 40 30 20 1 2 3 4 6 VELOCIDAD (V) TIEMPO (t)
6. = k k t = V V · t = k Dos magnitudes son inversamente proporcionales, si están ligadas por un producto constante. MAGNITUDES INVERSAMENTE PROPORCIONALES 120 60 40 30 20 1 2 3 4 6 V · t = (120)(1) = (60)(2) = (40)(3) = (30)(4) = (20)(6) = 120 VELOCIDAD (V) TIEMPO (t)
